Zagadnienia opracowane są na podstawie książki, nagrania z ostatniego wykładu i trochę na podstawie notatek Marzenki. Nie wiem czy się to komuś przyda, nie wiem czy jest tu wszystko to, co powinno być (szczerze mówiąc, wątpię ;), ale wysyłam, co udało mi się skleić. Jak znajdziecie błędy lub braki, to dajcie znać, żebym mogła poprawić. Miłej lektury, edi

1. Podać przykład modelu matematycznego do badania przemieszczeń (statyczny lub kinematyczny)

Model matematyczny jest to układ zależności zachodzących między wielkościami charakteryzującymi odkształcenia (deformacje) lub przemieszczenie obiektu [deformowanie się lub przemieszczenie obiektu jest zjawiskiem fizycznym zachodzącym pod wpływem obciążeń działających na obiekt np. ciężaru własnego, użytkowego, parcia wiatru, zmiany temperatury otoczenia, drań podłoża].

Modele w ogólności składa się z kilku modeli szczegółowych różnych elementów, które wchodzą w dane zagadnienie:

- model badanego obiektu (jaki obiekt np. belka, która będzie odkształcana)

- model samego zjawiska (czyli z jakim zjawiskiem, deformującym lub przemieszczającym obiekt będziemy mieli do czynienia )

- model sieci kontrolnej (jaki ma kształt, jaki wymiar) wraz z modelem błędu obserwacji (czy obserwacje są skorelowane, niezależne, z jakim rozkładem błędu)

- model układu odniesienia (układ odniesienia to baza odniesienia, układ współrzędnych oraz związki wiążące punkty bazy z układem współrzędnych)

Najczęściej jest tak, że nie wszystkie elementy mamy (często nie znamy modelu badanego obiektu oraz modelu samego zjawiska) i ograniczamy się do modelu sieci, błędu i układu odniesienia.

Model statyczny sieci jest to model, wykorzystywany w przypadku pomiarów okresowych wtedy, gdy zmiany położenia punktów obiektu zaistniałe w czasie trwania pomiaru można uznać za zaniedbywane wobec osiągalnej dokładności pomiaru. W takim modelu wynikowi pomiaru każdego z elementów sieci można przypisać jeden wspólny moment czasu.

Model kinematyczny sieci to model, wykorzystywany wtedy, gdy nie możemy zaniedbać zmian położenia punktów obiektu zaistniałych w czasie trwania pomiaru. Wtedy każdej obserwacji musimy przypisać moment jej wykonania.

W związku ze znacznym przemieszczeniem punktu sieci kontrolnej ΔH (tp-tk) , jakie zaszło między momentem rozpoczęcia pomiaru tp, a jego zakończenia tk, każdej obserwacji w interwale czasu <tp, tk> przypisujemy moment jej wykonania ti Dopiero gdy wprowadzimy do modelu jako niewiadome prędkości poszczególnych punktów, to będziemy mogli sprowadzić obserwacje do wspólnego momentu czasu.

Modelu statycznego można użyć zamiast kinematycznego, gdy skrócimy czas trwania pomiaru (np. zwiększając liczbę zespołów pomiarowych) . Gdy zaś zwiększymy dokładność pomiaru, trzeba będzie zastąpić model statyczny modelem kinematycznym.

2. Jak, w odniesieniu do badania przemieszczeń, można interpretować pojęcie „model przyczynowo - skutkowy”?

Schemat modelu:

Przyczyną jest Obciążenie		Obiekt		Skutkiem jest deformacja lub przemieszczenie obiektu

Przykładem może być belka obustronnie podparta:

Mając model opisujący związek przyczynowo - skutkowy możemy wyznaczyć deformacje i przemieszczenia obiektu, które zajdą w wyniku określonego układu obciążeń. Możemy również określić parametry wytrzymałościowe tej belki.

Modele przyczynowo - skutkowe mają tą zaletę, że w miarę gromadzenia coraz większej ilości informacji na temat zachowania się obiektu możemy zmniejszać błędy modelu, a więc go „udokładniać” . Uwzględniamy przy tym błędy samych pomiarów, rozróżniając rzeczywiste przemieszczenia i deformacje od wyznaczonych.

Model przyczynowo -skutkowy nazywany jest również objaśniającym lub opisowym.

Wśród modeli przyczynowo - skutkowych wyróżniamy modele dwuetapowe. Pozwalają one na oddzielne wyznaczenie błędności samych pomiarów od błędności modelu. Ta `dwuetapowość' oznacza, że najpierw wyznaczamy przemieszczenia na podstawie pomiarów geodezyjnych (wyrównanie, diagnostyka błędów grubych, oszacowanie dokładności wyznaczeń), a dopiero po wprowadzeniu tych wyników do modelu przyczynowo - skutkowego, określamy błędność pomiarów i samego modelu.

Inną specyficzną odmianą modeli przyczynowo - skutkowych są modele typu wejście - wyjście. Bazują one wyłącznie na wielkościach wejściowych i wielkościach wyjściowych i ustalają zależności między nimi wyłącznie poprzez operacje matematyczne. Przykładem mogą być sieci neuronowe.

3. Czym różnią się pomiary rozproszone od pomiaru okresowego?

Zarówno pomiary rozproszone, jak i pomiary ciągłe się pomiarami w trybie dyskretnym.

Pomiar rozproszony - dyskretny zbiór momentów wykonania poszczególnych obserwacji, rozłożonych z nieregularną intensywnością w całym interwale monitorowania obiektu.

Pomiary okresowe - skupiska dyskretnych momentów wykonania poszczególnych obserwacji, dające się wydzielić w całym interwale monitowania obiektu. Ważnym czynnikiem jest tu relacja między czasem trwania i dokładnością pomiaru na kontrolowanym obiekcie, a przewidywanymi prędkościami przemieszczania się punktów na obiekcie.

4. Podać postać równania obserwacyjnego dla różnicy wysokości w modelu kinematycznym sieci.

gdzie: t - moment wykonania obserwacji, t0 - moment odniesienia, ui, uj - wektory prędkości

5. Omówić pojęcia defektu sieci w odniesieniu do modelu kinematycznego (sieć pionowa, sieci poziome).

Defekt sieci występuje, gdy w zbiorze danych do wyrównania obserwacji tej sieci brakuje pewnej liczby wielkości geometrycznych, które są niezbędne do wyznaczenia położenia punktów sieci w przyjętym układzie współrzędnych. Charakteryzujemy go przez podanie liczby oraz rodzaju brakujących wielkości. Rozróżniamy defekt zewnętrzny d_z i wewnętrzny d_w. Całkowity defekt sieci d jest sumą obu: d = d_z + d_w

Pod względem ilościowym całkowity defekt sieci jest równy sumie defektu statycznego i kinematycznego: d = d_s + d_k

Defekt kinematyczny d_k- defekt związany z wyznaczeniem prędkości ruchu. Zależny jest od geometrii i struktury obserwacyjnej sieci (czyli tak jak defekt statyczny) oraz od rozkładu momentów wykonania obserwacji do poszczególnych punktów sieci.

dk = dk(s) + dk(t)

dk(s) - składnik ilościowo i jakościowo odpowiadający defektowi statycznemu ds, czyli suma defektu zewnętrznego i wewnętrznego brak zaczepienia dla parametrów kinematycznych, czyli 0 dla pędkości dk(t) - składnik wynikający z niewłaściwego rozkładu momentów wykonania obserwacji w sieci, defekt strukturalny np. dla jednego punktu są wykonane 2 obserwacje w tym samym czasie, Δt = 0, prędkości tego punktu nie da się wyznaczyć; defekt ten powinien być równy zero.

Dla sieci pionowej defekt w modelu kinematycznym wynosi 2 (2 razy więcej niż w modelu klasycznym). Pierwszy defekt to brak zorientowania w układzie wysokości dla niewiadomych statycznych, drugi to brak zaczepienia dla parametrów dynamicznych w tym modelu.

Dla sieci poziomej defekt w modelu kinematycznym wynosi 6, gdyż:

d = ds +dk = ds + dk(s) + dk(t)

dażymy do tego, by dk(t) = 0,

więc d = ds + dk(s), przy czym z natury ds = dk(s), a co za tym idzie d = 2 ds

Z analizy wzajemnej wyznaczalności punktów w sieci wynika, że nie ma ona defektu wewnętrznego, a jako sieć lokalna ma pełny defekt zewnętrzny równy 3, zatem

d = ds + dk = ds + dk(s) = 2ds = 6

6. Jak rozpoznać, że obliczeniowy model statyczny sieci nie jest odpowiednim modelem dla opisu ruchu jej punktów? (przyjąć, że dane są wyniki pomiarowe)

Wyrównujemy sieć. Nie wprowadzając milionowych kinematycznych otrzymujemy niezgodność między obserwacjami (występują bardzo zróżnicowane wartości poprawek obserwacyjnych), i otrzymujemy duże m₀ (przekraczające wartośc krytyczną) nie jest spełniony test globalny. Może to oznaczać, że model sieci jest zły, ale może również oznaczać występowanie błędów grubych - dlatego trzeba zrobić testy lokalne.

Jeśli po przeprowadzeniu testów lokalnych otrzymamy, że przynajmniej 30 - 40% poprawek zunifikowanych przekracza wartości krytyczne, to podejrzewamy, że coś jest nie tak z modelem.

Ze statystyki matematycznej wiemy, że prawdopodobieństwo, że wartość błędu grubego będzie więcej niż 3 razy większa niż wartość błędu średniego wynosi 0,997 (czyli 3 na 1000 przekroczą wartość krytyczną). Jeśli więc w naszych testach lokalnych otrzymujemy przynajmniej 30-40% to zdecydowanie jest to za dużo wtedy wiemy, że model statyczny nie jest odpowiedni.

7. Jakie składowe przemieszczenia obiektu można wyznaczyć na podstawie przemieszczeń pionowych jego wybranych punktów?

Pionowe przemieszczenia punktów to pionowa składowa wektora przemieszczenia punktów. Gdy wyznaczamy tylko składową pionową i stwierdzamy, że ma zerową wartość, nie możemy założyć, że punkt się nie przemieścił, gdyż nie mamy informacji na temat składowej poziomej.

Składowe przemieszczenia obiektu, jakie można wyznaczyć na podstawie przemieszczeń pionowych: obroty wokół dwóch osi oraz przesunięcie: δα_x, δαy, δz₀ (z₀ dotyczy przesunięcia pionowego początku układu współrzędnych - żeby to dotyczyło obiektu, trzeba układ współrzędnych sprowadzić do środka ciężkości obiektu i wtedy środek ciężkości będzie miał parametr δz₀)

8. Co to jest zmiana układu odniesienia w badaniu przemieszczeń? (podać własne przykłady)

Układ odniesienia jest to baza odniesienia oraz związany z nią w sposób jednoznaczny układ współrzędnych (czyli 3 elementy składające się na układ odniesienia: baza odniesienia, układ współrzędnych oraz związki wiążące punkty z układem współrzędnych) Zapisywane są w nich: pozycja punktów, wektory przemieszczeń oraz charakterystyki dokładnościowe tych wielkości.

Zmiana układu odniesienia wynika ze zmiany jednego z elementów układu odniesienia (baza odniesienia, układ współrzędnych oraz związki wiążące punkty z układem współrzędnych) zazwyczaj oznacza przyjęcie innej bazy odniesienia, czasem połączone ze zmianą zorientowania układu współrzędnych.




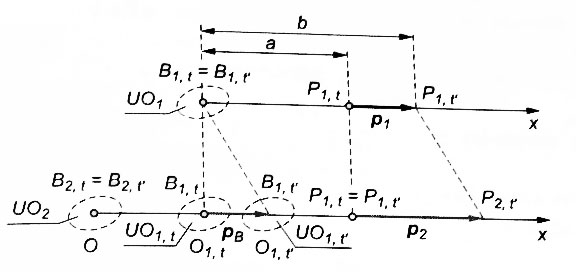
Przenoszenie się przemieszczeń na przykładzie przestrzeni jednowymiarowej.

Układ odniesienia UO₁(B₁,Ox₁); obserwacje z bazy B₁ w momentach t, t'; rejestracja pozycji punkt P, odpowiednio P_t, P_t' wektor przemieszczenia p₁ dla interwału czasu <t,t'>. Jednocześnie baza B₁ była obserwowana z układu UO₂(B₂,Ox₂); obserwacje w momentach t, t'; rejestracja pozycji punkt P, odpowiednio P_1,t i P_1,t' wektor przemieszczenia p_B dla interwału czasu <t, t'>. Jeśli w układzie UO₂(B₂,Ox₂) zaznaczymy pozycje punktu P obserwowane w pierwszym układzie odniesienia to otrzymamy wektor przemieszczenia p₂ punktu P w drugim układzie odniesienia. Otrzymamy:

a+ p₂ = p_B + b p₂ = p_B + b - a = p_B + p₁

9. Jakie korzyści daje zastosowanie wzorów transformacyjnych dla wektora przemieszczeń i jego macierzy kowariancji?

Wzory transformacyjne z układu odniesienia i na układ odniesienia j

S to macierze warunków, S₀ to macierz warunków swobodnych. Z macierzy warunków można uformować macierz G i ona może być wykorzystana do przetransformowania wektora x i jego macierzy kowariancji na nowy układ.

W sieci wysokościowej jest to szczególnie proste (jeśli chcemy przejść z jednego punktu odniesienia na drugi to wystarczy średnia arytmetyczna z wektora x i od tego co było, odjąć tą średnią i już mamy inny układ)

Korzyści: Nie trzeba powtarzać całej procedury wyrównawczej (układać równań, rozwiązywać układu, definiować na nowo układu odniesienia) wystarczy raz utworzyć tą macierz, przemnożyć ją w tych dwóch wzorach i mamy wyrównanie przy innym układzie odniesienia, czyli oszczędność czasu i obliczeń.

10. Jak charakteryzowany jest płaski stan odkształceń w danym punkcie ośrodka

Tensor odkształceń w punkcie bryły:

ε_xx

γ_xy

T_ε =

γ_yx

ε_yy

εxx, εyy - odkształcenia liniowe kier. Osi OX i PY γ - odkształcenia postaciowe, zmiana kąta między 2 liniami w punkcie

Elementy Tensora T_ε ulegają zmianie przy obrocie układu współrzędnych.

ε_φ = ε_xx cos ² φ + 2 γ_xy sin φ cos φ + ε_yysin² φ

Ekstremalne wartości ε_φ to odkształcenia liniowe główne ε_max i ε_min. Zaś ekstremalna wartość γ_φ to maksymalna wartość odkształcenia postaciowego γ_max.




Stan odkształceń bryły - rozmaitość wielkości ε i γ, które charakteryzują intensywność zmian wymiarów liniowych oraz zmian parametrów kształtu w różniczkowym otoczeniu danego punktu.

11. Omówić sposób wyznaczenia odkształceń poziomych terenu na podstawie pomiarów tensometrycznych w geodezyjnej konstrukcji pomiarowej w kształcie gwiazdy.

Konstrukcja jest w kształcie gwiazdy, na ramionach mierzy się długości w dwóch różnych momentach, a z nich przechodzimy na odkształcenia liniowe w danym kierunku (azymucie).

Układamy układ równań obserwacyjnych, gdzie niewiadomymi są ε_x, ε_y oraz γ_xy i te trzy niewiadome wyznaczamy z tego układu równań.

(Nie musimy się przejmować defektem strukturalnym sieci, ponieważ informacja na temat wszystkich niewiadomych (ε_x, ε_y, γ_xy) jest zawarta w obserwacjach.)

Trzeba sprawdzić czy nie występują błędy grube, czy każda z obserwacji, ε, nadaje się do dalszego przetworzenia - jeśli nie, to usunąć. Ostateczne wartości, liczone z tych trzech parametrów, czyli elementów tensora płaskiego to ε_min, ε_max, γ_max

---