SZUKANIE ZER W FUNKCJACH NIELINIOWYCH
METODA POŁOWIENIA
Po n -krokach mamy przedział ![]()
o długości ![]()
.
Szybkość zbieżności nie zależy od funkcji. W algorytmie tym, nie wykorzystuje się żadnej własności funkcji, oprócz informacji, że posiada tylko jedno 0 w przedziale ![]()
.
METODA NEWTONA
Startuję z tego końca przedziału, w którym f(x) ma ten sam znak co f''(x). Tworzę ciąg przybliżeń pierwiastka ![]()
w następujący sposób:
funkcję f(x) aproksymuję styczną w punkcie ![]()
, styczna przecina oś x w punkcie ![]()
bliższym pierwiastkowi ![]()
. W punkcie ![]()
wyznaczam następną styczną - przecina ona oś x w punkcie ![]()
, i tak dalej...
![]()
![]()
(1a)
Przerywamy, gdy: ![]()
![]()
maleje dość szybko do momentu, aż dominują błędy zaokrągleń
Szybkość zbieżności metody:
Założenia:
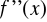
ciągła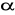
- pierwiastek pojedynczy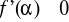
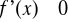
w otoczeniu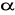
![]()
- błąd przybliżenia ![]()
![]()
- jakie są zależności
Rozwijamy w szereg Taylore'a:
![]()
, gdzie ![]()
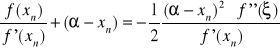
![]()
(patrz 1a) ![]()
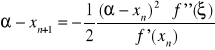
![]()
![]()
(2)
![]()
const.
Jeśli ![]()
:
![]()
p c
im większy
wykładnik
tym metoda
szybciej zbieżna
DEFINICJA:
Niech ![]()
będzie ciągiem zbieżnym do ![]()
; ![]()
Jeśli istnieją takie dwie liczby p, c ,gdzie ![]()
, że 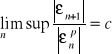
, to p nazywamy wykładnikiem zbieżności ciągu, a c - stałą asymptotyczną błędu.
Dla p = 1, lub 2 lub 3, mówimy o zbieżności odpowiednio, liniowej, kwadratowej i sześciennej.
Załóżmy, że I jest otoczeniem pierwiastka ![]()
i że w tym otoczeniu zachodzi własność:
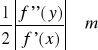
![]()
![]()
Można udowodnić, że jeśli ![]()
i przedział ![]()
, to każde ![]()
, wyznaczone metodą Newtona, należy do przedziału I oraz ![]()
Zatem metoda Newtona jest zbieżna do pojedynczego pierwiastka, jeśli tylko ![]()
jest dostatecznie blisko pierwiastka ![]()
, ściślej jeśli:
![]()
A teraz praktyczny wzór:
To metoda jest zbieżna dla dowolnego przybliżenia początkowego ![]()
należącego do [a,b].
METODA SIECZNYCH
Otrzymujemy z metody Newtona, aproksymując ![]()
ilorazem ![]()
.
Startujemy z dwóch przybliżeń początkowych: ![]()
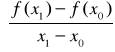
Tworzy się rekurencyjnie ciąg ![]()
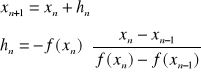
Pierwsza iteracja musi zaczynać się od punktów, w których funkcja ma różne znaki - inaczej może być wykryte fałszywe 0 (ta metoda nie jest dobra w pobliżu 0).
Można wyprowadzić zależność:
![]()
gdzie ![]()
Metoda siecznych nie jest zbieżna kwadratowo (jest wolniejsza od metody Newtona).
Można wykazać, że nie istnieje metoda iteracyjna, rzędu II, używając tylko jednej nowej wartości w każdym kroku.
f(x) = 0
![]()
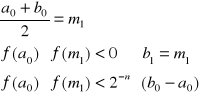
![]()
to ![]()
i ![]()
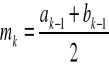
![]()
to ![]()
i ![]()
Założenia:
I i II pochodna funkcji mają stały znak w
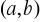
istnieje tylko jedno zero w
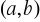
Twierdzenie:
Założenia:
![]()
![]()
ma stały znak w [a,b]
![]()
Jeśli 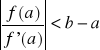
oraz 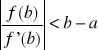
Wyszukiwarka
Podobne podstrony:
marcinka all, 20021008
marcinka all, 20021112, INTERPOLACJA FUNKCJAMI SKLEJANYMI:
Funkcje nieliniowe?z ograniczeń
marcinka all, 20030107
marcinka all, 20021203, Ciąg dalszy:
marcinka all, 20021119
Funkcje nieliniowe
marcinka all, 20030121
Przykładowe transformacje liniowe funkcji nieliniowych
marcinka all, 20021126, (RYSUNEK)
Funkcje internetu w życiu rodziny, wrzut na chomika listopad, Informatyka -all, INFORMATYKA-all, Inf
Wybrane funkcje programu graficznego GIMP do obróbki zdjęć c, wrzut na chomika listopad, Informatyka
Wójcik, Marcin Funkcjonalizm w geograficznych badaniach wsi (2013)
biernacki,algorytmy przetwarzania sygnałów L, wpływ rozmieszczebnia zer i biegunów na funkcję transm
BANK CENTRALNY I JEGO FUNKCJE
Zaburzenia funkcji zwieraczy
Genetyka regulacja funkcji genow
więcej podobnych podstron