XIII Konferencja Naukowa - Korbielów' 2001

"Metody Komputerowe w Projektowaniu i Analizie Konstrukcji Hydrotechnicznych"

O wyznaczaniu naprężeń kontaktowych między

fundamentem obciążonym mimośrodowo a podłożem

gruntowym

Marian Łupieżowiec

1

1.

WSTĘP

Bardzo ważnym zadaniem podczas projektowania posadowienia dowolnej konstrukcji

budowlanej lub inżynierskiej jest wyznaczenie nacisków, jakie poprzez fundament wywiera
budowla na grunt. Dynamiczny rozwój metod komputerowych przy coraz bardziej
powszechnym dostępie do komputerów każe inżynierom szerzej spojrzeć na możliwości
dokładniejszego symulowania zjawisk występujących podczas wznoszenia i użytkowania
konstrukcji. Okazuje się, że najprostsze metody obliczeń dotychczas stosowane często nie
dają zadawalających nas dokładności. Konieczne jest więc sięgnięcie do bardziej
wyrafinowanych metod, jaką jest Metoda Elementów Skończonych wraz z jej
modyfikacjami.

W niniejszej pracy porównano kilka różnych metod znalezienia nacisków, jakie

wywiera na podłoże fundament obciążony mimośrodowo. Metodami analizowanymi w
pracy są:


założenie liniowego rozkładu naprężeń,



liniowy rozkład nacisków przy braku naprężeń rozciągających (sposób wg normy PN-
81\B-03020),



wg nomogramów Gorbunowa,



analiza MES przy założeniu modelu liniowo sprężystego,



analiza MES z modelem sprężysto – plastycznym,



ograniczenie rozciągania poprzez umożliwienie rozejścia się siatki w modelu liniowo
sprężystym MES.

W dalszej części zostanie przedstawione wyznaczanie nacisków ławy na grunt

(założono płaski stan odkształceń) w przypadku mimośrodowego obciążenia siłą rozłożoną
na długości ławy .

2.

LINIOWY ROZKŁAD NAPRĘŻEŃ

1

Mgr inż, Katedra Geotechniki Politechniki Śląskiej, Gliwice

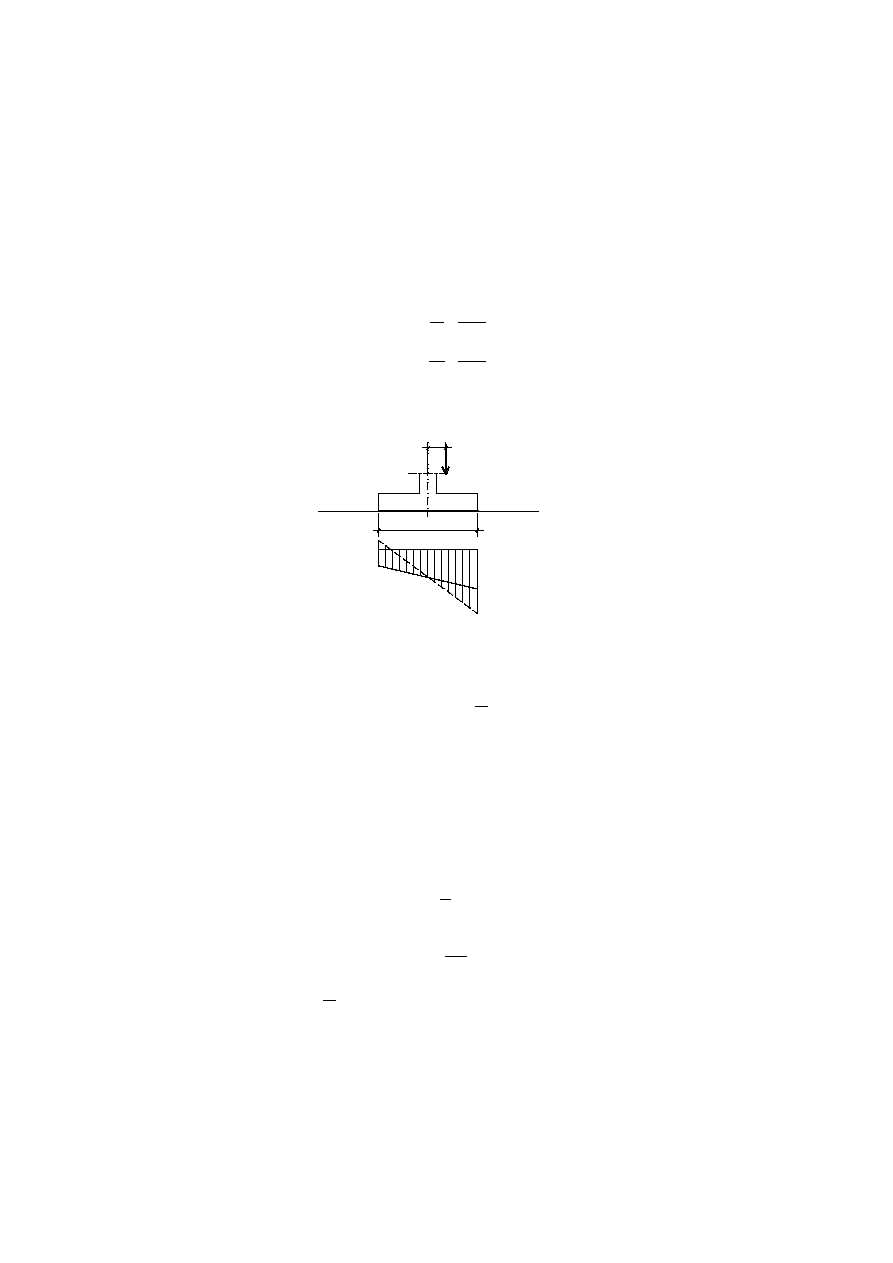
Jest to najprostszy sposób wyznaczenia naprężeń, którym się często posługują

inżynierowie przy rozwiązywaniu typowych problemów. W sytuacji opisanej we wstępie, a
przedstawionej na rys. 1 naciski q

max

i q

min

obliczymy ze znanych z Wytrzymałości

Materiałów wzorów:

2

max

6

B

Ne

B

N

q





(1’)

2

min

6

B

Ne

B

N

q





(1’’)

gdzie:

N [kN/m]

– siła przypadająca na metr długości ławy,

e [m]

– mimośród,

B [m]

– szerokość ławy.

N

e

q

max

q

min

B

Rys. 1

Oczywiście powyższa metoda jest bliska prawdy, jeśli mimośród e jest mały – siła znajduje
się w rdzeniu. Odpowiada to warunkowi:

0

min



q



6

B

e



.

(2)

3.

ROZKŁAD NAPRĘŻEŃ WG NORMY

W przypadku większych mimośrodów licząc powyższą metodą otrzymujemy naprężenia
q

min

ujemne (por. linię przerywaną na rys. 1), które nie mogą być przeniesione przez grunt.

W takiej sytuacji opierając się na normie PN-81\B-03020 możemy „obciąć” naprężenia
ujemne odpowiednio zwiększając nacisk maksymalny (rys. 2). Wartość nacisku znajdziemy
rozważając równanie momentów, z którego dostajemy:

B

e

c

2

1

3





,

(3)

a następnie z równania rzutu sił wyznaczymy poszukiwany maksymalny nacisk:

a

N

q

3

2



(4)

gdzie:

e

B

a





2

– jest odległością siły od bliższej krawędzi.

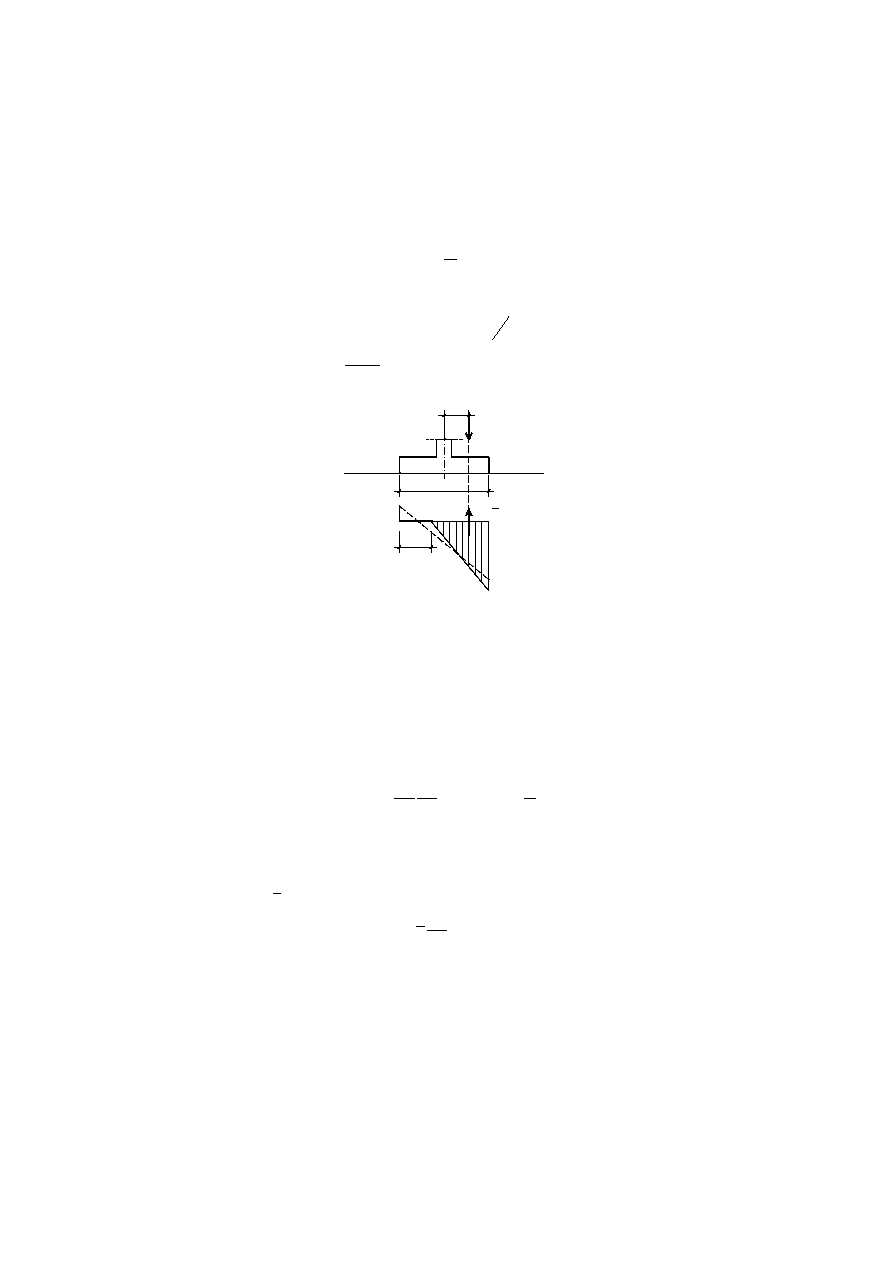
Daje to ograniczenie:

2

B

e



(5)

Kiedy mamy do czynienia z większym mimośrodem, to nie jesteśmy w stanie wyznaczyć
nacisków tą metodą, ponieważ otrzymujemy naprężenia dążące do nieskończoności. Zresztą
norma [5] ogranicza wartość mimośrodu tylko do 4

B . Istnieją też wymagania żądające

spełnienia warunku:

4

max

min







, który bardzo rygorystycznie ogranicza rdzeń przekroju

(bardziej niż ograniczenie (2) ).

B

e

N

c

R = q (B-c)

1

2

q

Rys. 2

4.

WYZNACZENIE NAPRĘŻEŃ Z NOMOGRAMÓW GORBUNOWA

W okresie, kiedy specjalistyczne programy komputerowe nie były tak

powszechne i łatwo dostępne jak obecnie, nomogramy opracowane przez Gorbunowa
[2] były bardzo użyteczne dla projektantów. W metodzie przyjmuje się, że linia wpływowa
rozkładu naprężeń zależy od wskaźnika wiotkości pasma t oraz od mimośrodu względnego
ławy

. Wielkości te są zdefiniowane następująco (por. rys. 3):

L

e

α

h

L

E

E

10

t

3

3

1

0





(6)

gdzie:

E

0

– moduł sprężystości pierwotnej gruntu, E

1

– moduł sprężystości betonu,

L – połowa szerokość pasma fundamentu,
h – wysokość ławy fundamentowej,

e – mimośród siły.

Mając powyższe dane odczytujemy z odpowiedniej tabeli [2] współczynniki

linii wpływowej p , a poszukiwaną wartość naprężenia wyznacza się z zależności:

bL

N

p

σ



(7)

w której:

N – działająca siła,

b – długość rozpatrywanego pasma.

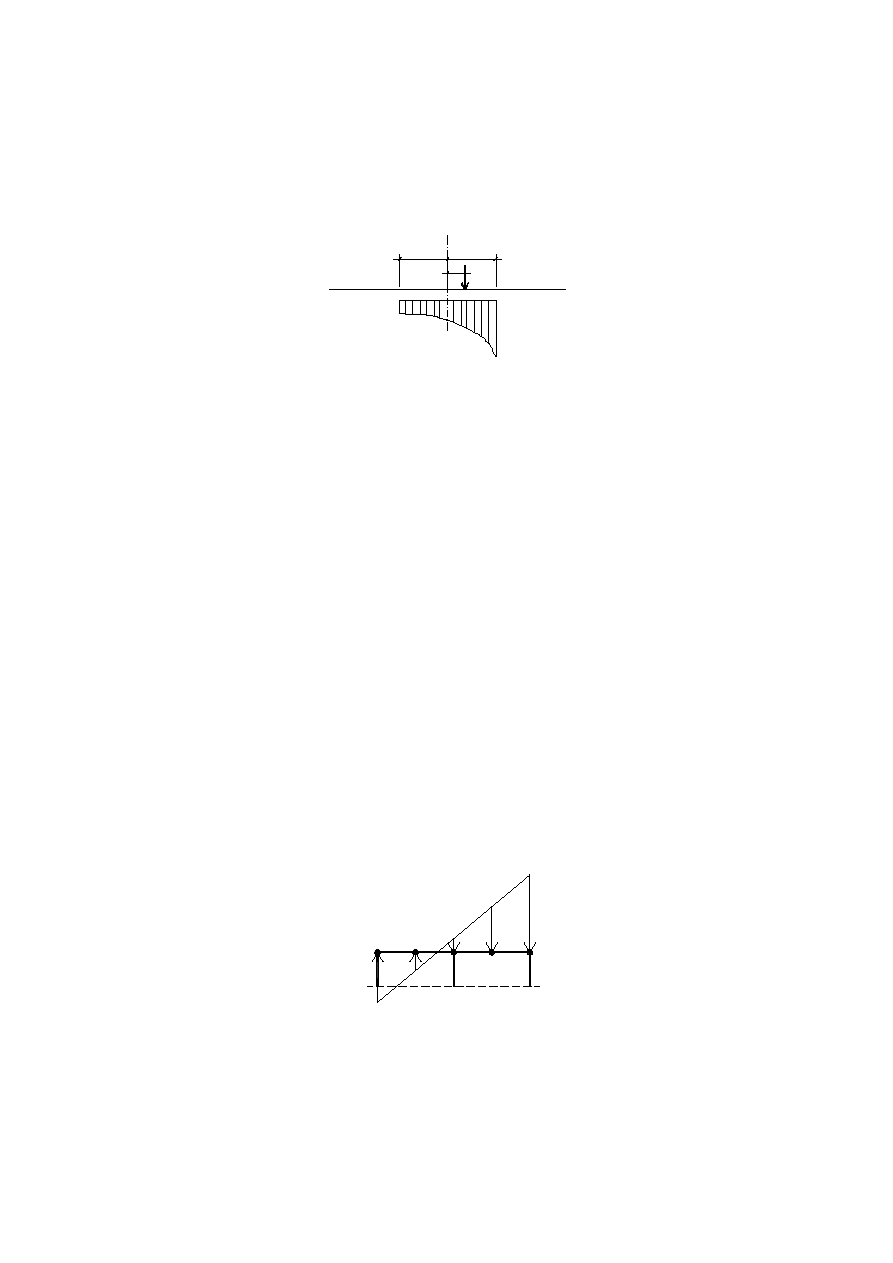
L

e

N

L



z

Rys. 3

Monogramy podane przez Gorbunowa są analitycznym rozwiązaniem

problemu obciążenia półprzestrzeni sprężystej przez sztywną konstrukcję. Wyniki uzyskane
z tej analizy w miarę dobrze opisują sytuację obserwowaną w praktyce, jednak ograniczenie
się do liniowych związków konstytutywnych powoduje powstawanie osobliwości w
rozwiązaniu (nieskończone wartości naprężeń pod krawędziami fundamentu).

5.

ANALIZA METODĄ ELEMENTÓW SKOŃCZONYCH

Współczesne techniki obliczeniowe pozwalają na dokładniejsze wykonanie

analizy pracy konstrukcji. Rozwiązując zagadnienie techniką MES możemy uwzględnić nie
tylko odkształcalność fundamentu i podłoża, ale także wpływ gruntu zalegającego ponad
poziomem posadowienia budynku. Możemy więc spotkać się także z sytuacją, w której
obliczenie nacisków wzorami (1’) i (1’’) daje odrywanie fundamentu, natomiast analiza
MES z uwzględnieniem wcześniejszych uwag nie wykazuje występowania naprężeń
rozciągających. Może to mieć szczególne doniosłe znaczenie, przy rozpatrywaniu
fundamentów posadowionych na większych głębokościach (np [4]). Takie postawienie
problemu powoduje konieczność dokładnego podania parametrów mechanicznych
rozpatrywanych materiałów, które to parametry istotnie rzutują na uzyskiwane wyniki.
Model analizowanej sytuacji opisanej w pierwszym rozdziale pokazany jest na rysunku 5.
W obliczeniach założono trzy strefy materiałowe (zróżnicowane na rysunku) o
następujących parametrach :

Beton

Grunt rodzimy

Grunt zasypowy

E = 20 GPa

 = 0.3

E = 60 MPa

 = 0.25

E = 20 MPa

 = 0.25

Q

1

Q

2

3

Q

Q

4

Q

5

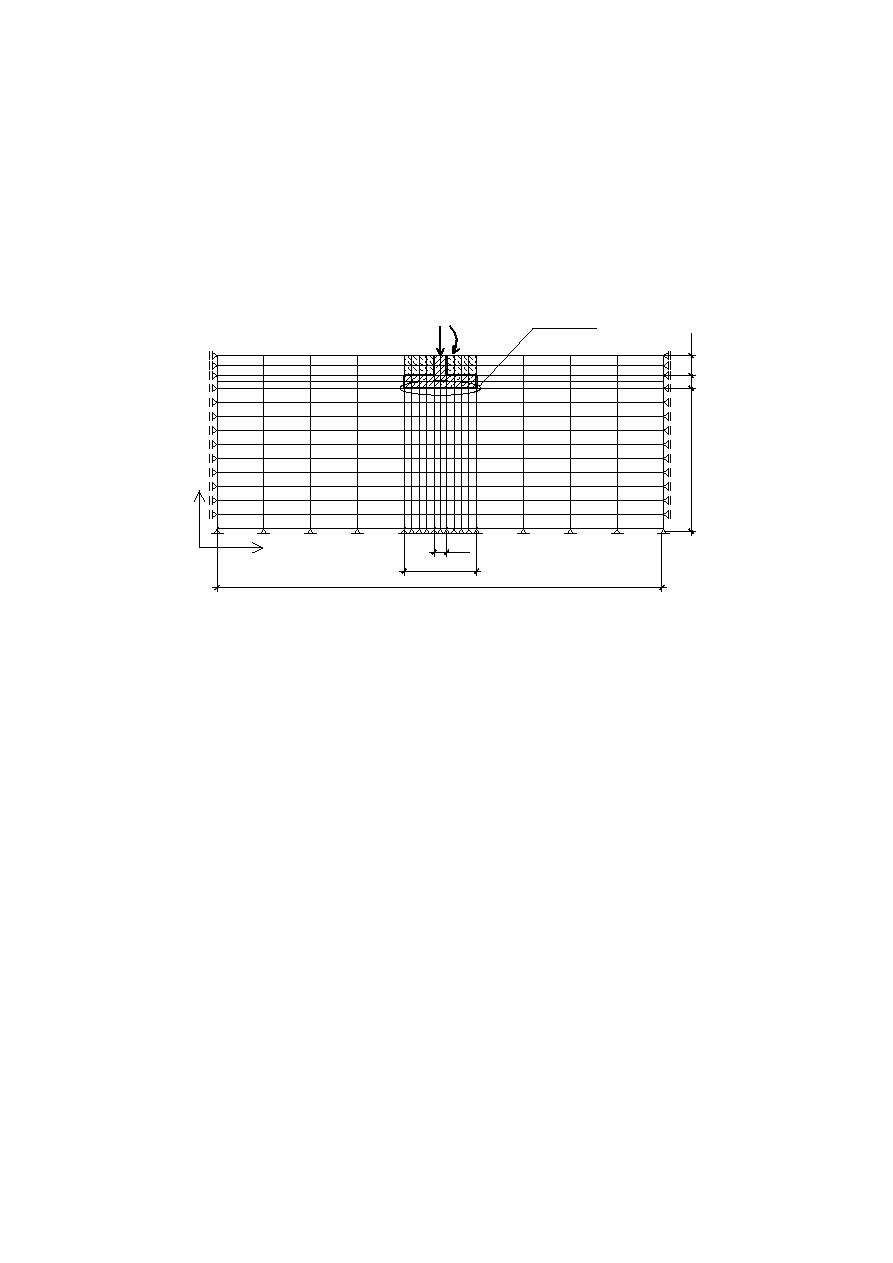
Zadane obciążenie przyłożono jako „trójkątne” do górnej krawędzi elementu (rys 4).

W pracy analizowano trzy warianty obciążeń – odpowiadających obciążeniu stałą siłą na
trzech różnych mimośrodach.

N

M

1.0

5.0

25.0

0.

7

0.

5

20

.0

Dyskretyzacja

x

y

Analizowany
fragment

Rys. 5

Oczywiście także w tej metodzie, w przypadku większych mimośrodów, otrzymamy w

wynikach naprężenia rozciągające w gruntach, jeśli ograniczymy się w analizie do modelu
liniowo – sprężystego. Wynika stąd wniosek, że jeśli chcemy uzyskać inny rozkład
nacisków powinniśmy odwołać się do analizy materiałów o charakterystykach nieliniowych,
co przedstawimy w dalszej części.

6.

ROZWIĄZANIE Z UWZGLĘDNIENIEM MODELU DRUCKERA–
PRAGERA

Rozważając stwierdzenia wypowiedziane we wcześniejszych rozdziałach, należałoby

stwierdzić, że przyjęcie do rozważań modelu liniowo – sprężystego, w przypadku dużych
mimośrodów nie prowadzi do wyników zgodnych z rzeczywistością. Dlatego więc celowe
jest sformułowanie problemu nieliniowego. W pracy zaproponowałem dwa z wielu ogólnie
dostępnych modeli – jest to model ciała sprężysto–idealnie plastycznego Druckera–Pragera
(nieliniowość fizyczna) oraz model no–tension, który umożliwia powstanie szczeliny w
modelu (nieliniowość geometryczna).

W modelach sprężysto–plastycznych ograniczamy dopuszczalne stany naprężenia do

takich, których odwzorowanie w przestrzeni naprężeń zawiera się wewnątrz pewnej
powierzchni, zwanej powierzchnią plastyczności (rys. 6). W modelu Druckera–Pragera
przyjmuje się, że ta powierzchnia jest stożkiem obrotowym o osi pokrywającej się z linią
ciśnienia hydrostatycznego. Jak pokazano to na rysunku, stany ujemne wartości naprężeń,

Rys. 4







1

2

3

F( 

)

Rys. 6

poza “małym kawałkiem”, znajdują się poza powierzchnią plastyczności, a więc są
fizycznie niemożliwe. W takim razie jesteśmy w stanie wyznaczyć taki rozkład naprężeń
kontaktowych pod fundamentem, w którym występują wyłącznie naciski.

W modelu Druckera–Pragera powierzchnia plastyczności dana jest równaniem [3]:

H

Mp

q

)

σ

,

σ

,

F(σ

3

2

1







,

(8)

gdzie współczynniki M i H występujące powyżej zależą od spójności c i kąta tarcia
wewnętrznego

 poprzez zależności:









sin

3

cos

c

6

H

sin

3

sin

6

M









,

(9)

natomiast naprężenie średnie oraz intensywność naprężenia wyrażamy poprzez:





2

1

2

1

3

2

3

2

2

2

1

3

2

1

)

σ

(σ

)

σ

(σ

)

σ

(σ

2

1

q

)

σ

σ

(σ

3

1

p



















(10)

W powyższym

i

σ

oznacza i–te naprężenie główne.

Podczas rozwiązywania problemu zastosowano iterację Newtona–Raphsona (zaszyta

w pakiecie MES), która pozwala na „sprowadzenie” punktów na powierzchnię
plastyczności, które znalazły się poza stanami fizycznie dopuszczalnymi.

Rozwiązując zagadnienie postawione w rozdziale pierwszym przyjęto współczynniki

sprężystości dla poszczególnych stref materiałowych identyczne jak w rozdziale czwartym.
Ponadto założono model Druckera–Pragera dla obydwu stref gruntowych przyjmując
(niezerowa wartość spójności została przyjęta ze względów numerycznych):

Grunt rodzimy

Grunt zasypowy

c = 0.5 kPa
 = 40

c = 1.0 kPa
 = 30

7.

ROZWIĄZANIE Z UWZGLĘDNIENIEM MODELU DRUCKERA–
PRAGERA

Innym podejściem, mającym na celu ograniczenie naprężeń ujemnych jest

zastosowanie modelu no–tension, który pozwala na „rozerwanie” siatki MES przy
zachowaniu liniowo sprężystych związków fizycznych (por. rys.7).

u

A

A

v

A

B

B

u

B

v

v

C

C

u

C

I

II

IV

III

I

III

II

IV

A

u

A

v

A

v

B

u

B

B

C

u

C

v

C

D

D

u

v

D

Naprężenia
kontaktowe dodatnie

Odrywanie
fundamentu

Rys. 7a

Rys. 7b

„Rozejście się” siatki umożliwiamy poprzez przypisanie sąsiadującym elementom
skończonym (np. elementy I i III na rys. 7b) punktów o różnych numerach, ale tych
samych współrzędnych (punkty A i B). Oczywiście w przypadku, kiedy nie dochodzi do
odrywań, mamy do czynienia ze zwykłym zagadnieniem sprężystym (rys.7a). Ponieważ
większość pakietów MES nie posiada tego modelu analizy, dlatego konieczne było najpierw
rozwiązanie problemu przy założeniu sprężystości, a następnie tam, gdzie występowały
naprężenia ujemne, należało dodać kolejne punkty, aby umożliwić oderwanie, tak długo,
aby wszystkie naprężenia miały wartości dodatnie. Trudnością przy rozwiązywaniu
zagadnienia był fakt, że w pobliżu punktu styku oderwanego fundamentu z podłożem
powstawał znaczny skok naprężeń, który został złagodzony poprzez uśrednienie
otrzymanych nacisków.

8.

OTRZYMANE WYNIKI

W pracy porównano otrzymane naciski przedstawionymi wcześniej metodami.

Analizowano metr długości ławy fundamentowej (płaski stan odkształceń), przyjęta
szerokość fundamentu: B = 5.0 m, posadowionego na D = 1.2 m. Zagadnienie rozwiązano
przy pomocy pakietu CRISP93 [1]. Rozważano trzy warianty obciążeń:

Schemat I

Schemat II

Schemat III

N = 800 kN
M = 1000 kNm
(e = 1.25 m)

N = 800 kN
M = 2000 kNm
(e = 2.50 m)

N = 800 kN
M = 3000 kNm
(e = 3.75 m)

Poniżej przedstawiono wykresy nacisków fundamentu na grunt (por. zaznaczony

fragment na rys. 5) dla wszystkich trzech schematów znalezione wymienionymi wcześniej
metodami, ponadto dla trzeciego schematu pokazano otrzymane osiadania.

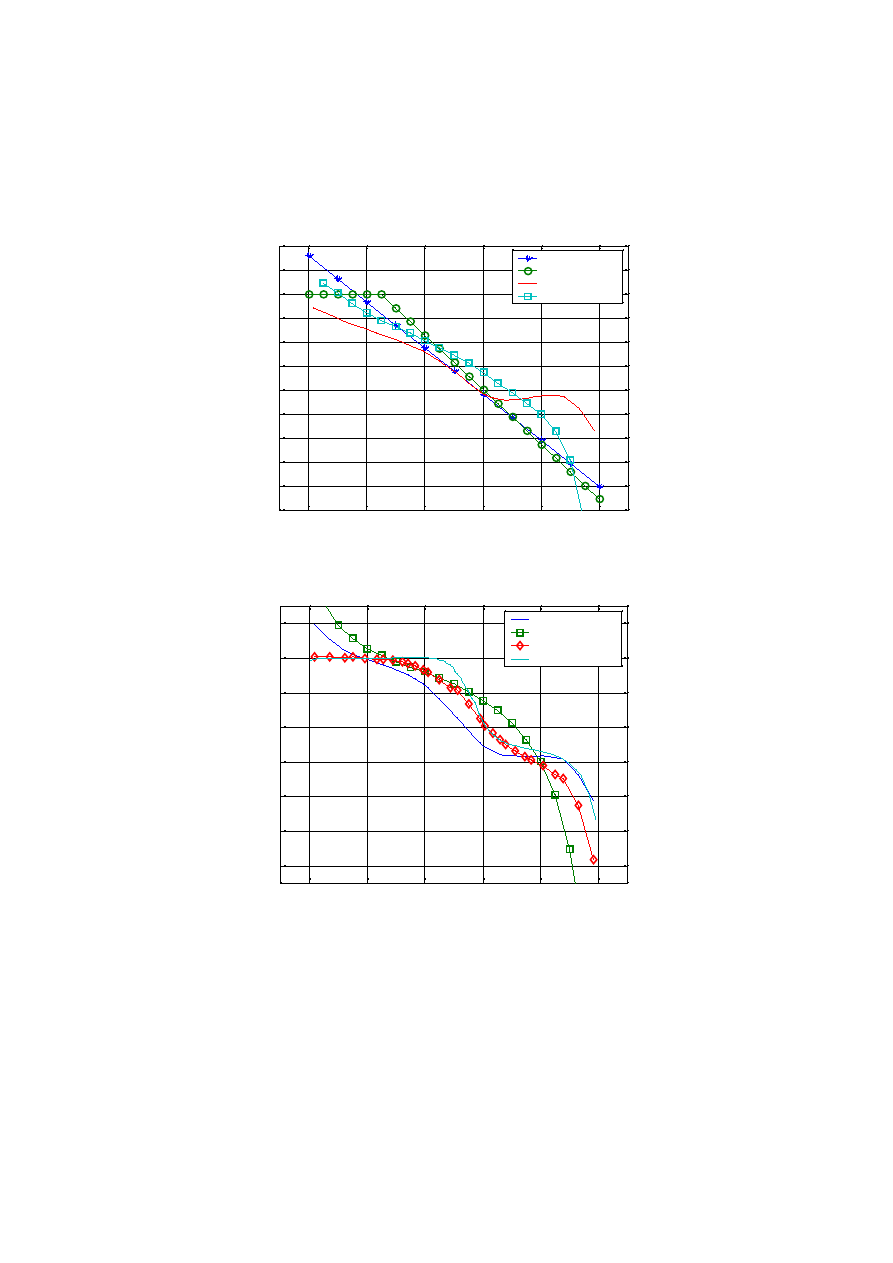
10

11

12

13

14

15

-100

-50

0

50

100

150

200

250

300

350

400

450

R oz k ?ady napr??e? pod fundam ent em (N = 800 k N/ m , M = 1000k Nm / m )

x [ m ]

N

a

c

is

k

[

k

P

a

]

Roz k ?ad liniowy

wg norm y

M odel lin. s pr.

wg G orbunowa

Rys. 8

1 0

1 1

1 2

13

14

1 5

-1 00

0

1 00

2 00

3 00

4 00

5 00

6 00

R o z k ?ad y n ap r?? e? po d fu ndam en te m (N = 8 00 k N /m , M = 20 00 k N m /m )

x [ m ]

N

a

c

is

k

[

k

P

a

]

M o de l lin. s pr.

w g G orbu now a

M o de l D -P

M o de l n o-te ns io n

Rys. 9

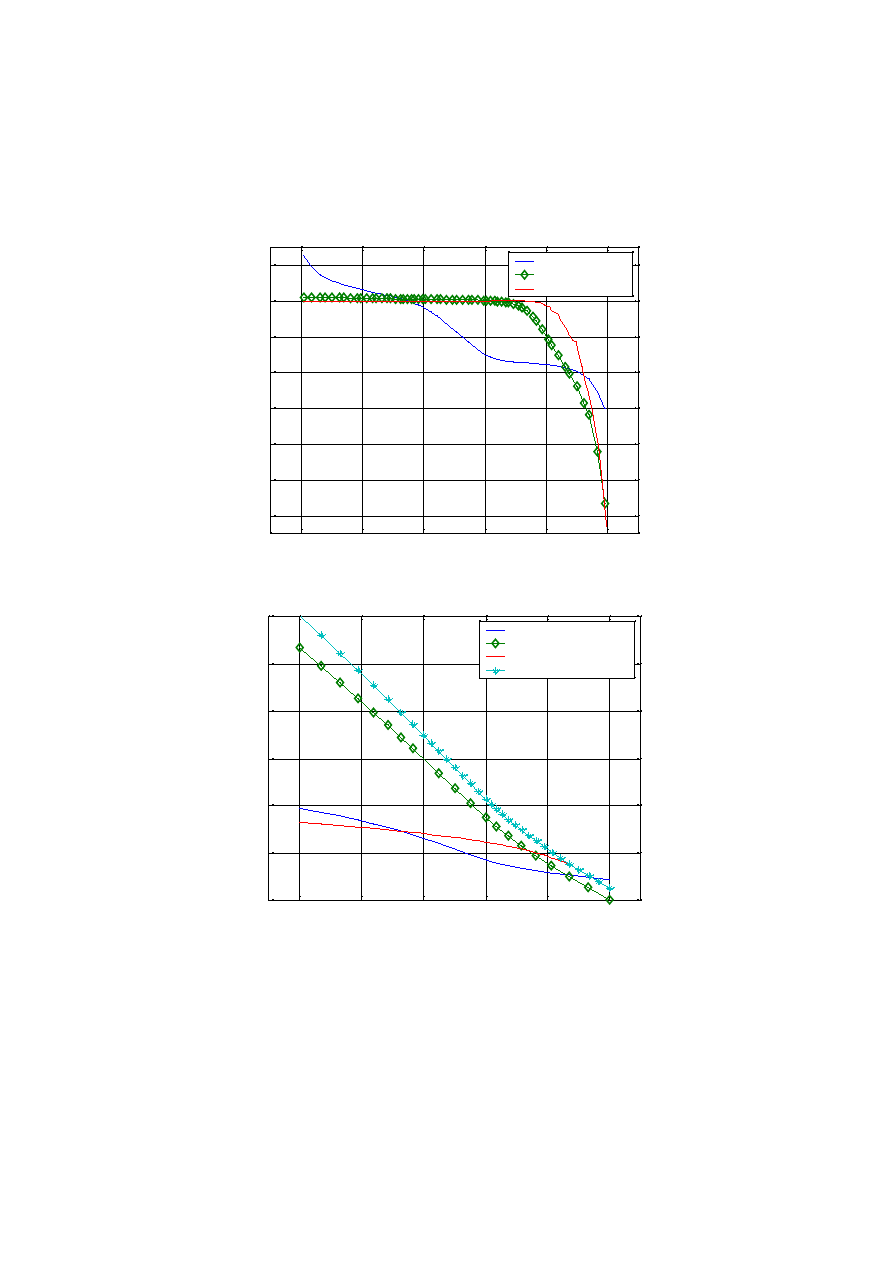
1 0

11

1 2

13

1 4

15

-2 0 0

0

2 0 0

4 0 0

6 0 0

8 0 0

10 0 0

12 0 0

R o z k ?ad y n ap r?? e ? p od fu n d am e n te m (N = 8 0 0 k N/ m , M = 3 00 0k Nm / m )

x [m ]

N

a

c

is

k

[

k

P

a

]

M od el lin. s p r.

M od el D -P

M od el n o-te ns io n

Rys. 10

10

11

12

13

14

15

-4

-2

0

2

4

6

8

Roz k ?ad os iada ? pod fundam entem (N = 80 0 k N/m , M = 3 000k N m /m )

x [m ]

p

rz

e

m

ie

s

z

c

z

e

n

ie

[

c

m

]

Liniowa s pr??y s to? ?

M odel D-P

No-tens io n - grun t

No-tens io n - fund am ent

Rys. 11

9.

PODSUMOWANIE

Analizując przedstawione powyżej wyniki obliczeń dla różnych wariantów modeli

można pokusić się o kilka słów komentarza na temat ich przydatności. Tak więc:


wyznaczenie nacisków przy założeniu liniowego rozkładu naprężeń jest najprostszym i
najczęściej stosowanym sposobem rozwiązania zagadnienia w praktyce inżynierskiej;
w przypadku małych mimośrodów daje wyniki zadawalające projektantów; jednak w
przypadku większych mimośrodów dostaje się naprężenia rozciągające, których nie
obserwujemy w rzeczywistości, ponadto przy wyznaczaniu naprężeń tą metodą
obserwujemy niedoszacowanie maksymalnych dodatnich nacisków,



analizując normowy sposób obliczeń – założenie liniowego rozkładu nacisków przy
braku naprężeń rozciągających (por. norma [5]), należy zauważyć, że ten przypadek
może być użyteczny tylko w niewielkim przedziale – norma ta dopuszcza odrywanie
fundamentu do jednej czwartej jego szerokości, gdyż przy większej jego wartości
otrzymamy bardzo duże naciski przy przeciwnej krawędzi,



zastosowanie Metody Elementów Skończonych pozwala na dokładniejszą analizę
współpracy konstrukcji z gruntem, szczególnie korzystne jest uwzględnienie gruntu
zalegającego powyżej poziomu posadowienia; jednak ograniczenie się do modelu
liniowo sprężystego również daje naprężenia ujemne, które nie występują w
rzeczywistości,



analiza MES z założeniem modelu sprężysto – plastycznego (tutaj Druckera–Pragera)
pozwala otrzymać wyniki bardzo bliskie rzeczywistości; ponadto jest ona dostępna w
większości znanych pakietów komputerowych,



model no–tension również pozwala na wyeliminowanie naprężeń rozciągających,
ponadto możliwe w tej metodzie jest wyznaczenie szczeliny, co może mieć znaczenie
praktyczne; wadą modelu jest czasochłonność obliczeń – model ten jest niedostępny w
większości pakietów i zachodzi konieczność samodzielnego ustalania odcinka, na
którym to odrywanie występuje,



nomogramy Gorbunowa do wyznaczania rozkładu nacisków mają w obecnych czasach
mniejsze znaczenie praktyczne ze względu na dostępność programów komputerowych,
przyjęcie liniowej sprężystości powiela wady opisane powyżej.

10.

LITERATURA

[1] Britto A. M., Gunn M. J. „Crisp 90. User’s and Programmers Guide”, Cambridge

University.

[2] Gorbunow–Posadow M. I. „Obliczanie konstrukcji na podłożu sprężystym”,

Wydawnictwo „Budownictwo i Architektura, Warszawa 1956.

[3] Gryczmański M. „Wprowadzenie do sprężysto–plastycznych modeli gruntów”, Studia

z zakresu inżynierii, 40, KILiW, IPPT PAN, Warszawa 1995.

[4] Gryczmański M., Chmielniak S., Bzówka J., Jastrzębska M., Łupieżowiec M., Sternik

K.: Analiza geotechniczna warunków posadowienia obiektów budowlanych nowej
instalacji MCOS3 i ZOWB na terenie Huty KATOWICE NB–183 / RB–7 / 2000,
Katedra Geotechniki Pol. Śl,.Gliwice, grudzień 2000.

[5] PN-81/B03020 „Posadowienie bezpośrednie budowli. Obliczenia statyczne i

projektowanie”.

STRESZCZENIE

W pracy analizowano naciski wywołane przez fundament obciążony mimośrodowo.

Przyjęcie założenia o liniowym rozkładzie naprężeń przy większych mimośrodach daje w
wyniku naprężenia rozciągające, które nie występują w rzeczywistości. Okazuje się, że
zachodzi konieczność obliczeń MES z uwzględnieniem nieliniowych związków fizycznych.
W artykule rozważano model sprężysto–idealnie plastyczny oraz no–tension, który
pozwalał na nieciągłość siatki elementów skończonych.

SUMMARY

In this it was analysed the pressures produced by the foundation under the load with

eccentricity. If we admit the assumption about the linear distribution of the stresses by more
eccentricity we will get the tension stresses, which are not in the reality. It is needed to solve
using FEM with non-linear physical equation. In this article it was solved the problem with
elastic perfect plastic model and no–tension one, which let for discontinuity the finite
elements net.