Rachunek prawdopodobieństwa MAP1151

Wydział Elektroniki, rok akad. 2009/10, sem. letni

Wykładowca: dr hab. A. Jurlewicz

Przykłady do listy 1: Przestrzeń probabilistyczna. Prawdopodobieństwo

klasyczne. Prawdopodobieństwo geometryczne. Twierdzenie o

prawdopodobieństwie całkowitym. Wzór Bayesa. Niezależność zdarzeń

Przykłady do zadania 1.1 :

(a) Przy dwukrotnym rzucie monetą zaobserwowano, że konfiguracja OR (tzn. „orzeł” w jednym z

rzutów, „reszka” w drugim) pojawia się w

1
3

przypadków. Czy moneta, którą wykonywano rzut,

jest symetryczna?

• Przyjmujemy Ω = {(O, O), (O, R), (R, O), (R, R)}, F = 2

Ω

, P określone przez p

1

=

P {(O, O)}, p

2

= P {(O, R)}, p

3

= P {(R, O)}, p

4

= P {(R, R)}.

• Niech p oznacza szansę na wyrzucenie „orła”, 0 < p < 1. Wtedy 1 − p ta szansa na „reszkę”.

Moneta jest symetryczna, gdy p = 0, 5.

• Rzuty są niezależne, więc mamy p

1

= p

2

, p

2

= p

3

= p(1 − p), p

4

= (1 − p)

2

.

(Spr. p

i

­ 0 dla i = 1, 2, 3, 4 oraz

4

P

i=1

p

n

= p

2

+ 2p(1 − p) + (1 − p)

2

= (p + 1 − p)

2

= 1.)

• W takim modelu prawdopodobieństwo konfiguracji OR wynosi

P (OR) = P ((O, R), (R, O)) = p

2

+ p

3

= 2p(1 − p).

Szukamy takiego p, dla którego P (OR) = 1/3.

• Rozwiązujemy równanie 2p(1 − p) = 1/3, czyli równanie kwadratowe 6p

2

− 6p + 1 = 0.

Otrzymujemy ∆ = 12, p =

3 −

√

3

6

≈ 0, 21 lub

3 +

√

3

6

≈ 0, 79.

(Zauważmy, że wartości p sumują się do 1. Nie ma w tym nic dziwnego. Wynika to z
symetrycznej roli „orła” i „reszki” w modelu i badanym zdarzeniu.)

• W obu przypadkach p 6= 0, 5, zatem w ramach modelu wnioskujemy, że moneta nie jest

symetryczna.

(b) Hasło potrzebne do uzyskania połączenia w sieci komputerowej składa się z jednej cyfry i

następnie pięciu dużych liter alfabetu angielskiego. Znaleźć prawdopodobieństwo, że osoba po-
stronna odgadnie hasło, jeśli wiadomo, że cyfra jest nieparzysta, a wśród liter są dokładnie trzy
litery E.

•

Ω = {(c, l

1

, . . . , l

5

), gdzie c ∈ {1, 3, 5, 7, 9}, l

i

to duże litery, dokładnie 3 wśród nich to E}

,

F = 2

Ω

, P - prawdopodobieństwo klasyczne.

• #Ω = 5 ·

5
3

· (25)

2

= 31250,

bo jest 5 możliwości wyboru cyfry,

5
3

możliwości wyboru miejsc na E,

(26 − 1)

2

możliwości wyboru liter innych niż E na każde z dwóch pozostałych miejsc

• zdarzenie, że osoba postronna odgadnie hasło, A = {właściwe hasło}, #A = 1

• P (A) =

#A

#Ω

=

1

31250

≈ 0, 000032.

1

(c) Użytkownik karty kredytowej używa czterocyfrowego hasła dostępu. Bankomat blokuje kartę,

gdy po raz trzeci hasło zostanie nieprawidłowo podane. Jakie jest prawdopodobieństwo, że
złodziej karty dostanie się na nasze konto nie znając hasła?

•

Ω = {{h

1

, h

2

, h

3

}, gdzie h

i

to trzy różne hasła spośród 10

4

możliwych haseł}.

F = 2

Ω

, P - prawdopodobieństwo klasyczne.

• A = {dostęp do konta} = {{właściwe hasło,h

2

, h

3

}}

• #Ω =

10

4

3

, #A =

10

4

−1

2

.

• P (A) =

#A

#Ω

=

(10

4

− 1)!

2!(10

4

− 3)!

·

3!(10

4

− 3)!

(10

4

)!

= 0, 0003.

(d) Drewniany sześcian, którego wszystkie boki są pomalowane na niebiesko, rozpiłowano na 64 =

4

3

jednakowej wielkości mniejsze sześcianiki. Sześcianiki te dokładnie wymieszano, następnie

wylosowano 10 z nich. Jakie jest prawdopodobieństwo, że dokładnie jeden z wylosowanych
sześcianików będzie miał 3 niebieskie ściany? Odpowiedź uzasadnić.

• Ω = {{s

1

, . . . , s

10

}, gdzie s

i

to różne sześcianiki spośród 64 możliwych}

F = 2

Ω

, P - prawdopodobieństwo klasyczne.

•

A = {dokładnie jeden narożny} = {{narożny,s

2

, . . . , s

10

}, gdzie s

i

nie są narożne}

• #Ω =

64
10

, #A =

8
1

56

9

• P (A) =

#A

#Ω

=

24597300

61474519

≈ 0, 4.

Przykłady do zadania 1.2 :

(a) Rzucamy monetą tak długo, aż upadnie dwa razy pod rząd na tę samą stronę. Określić Ω i P

odpowiadające temu eksperymentowi dla monety symetrycznej. Obliczyć prawdopodobieństwo,
że wykonamy mniej niż 7 i więcej niż 2 rzuty.

• Ω = {OO, ROO, OROO, . . .} ∪ {RR, ORR, RORR, . . .}, F = 2

Ω

,

p

n,O

= P (n rzutów+OO) =

1
2

n+2

, p

n,R

= P (n rzutów+RR) =

1
2

n+2

dla monety symetrycznej.

• Przestrzeń probabilistyczna jest dobrze określona, bo p

n,O

, p

n,R

­ 0 dla dowolnego n oraz

∞

P

n=0

(p

n,O

+ p

n,R

) =

∞

P

n=0

2 ·

1
4

·

1
2

n

=

1
2

·

1

1 −

1
2

= 1.

•

P (mniej niż 7 i więcej niż 2 rzuty) = P ( 3, 4, 5 lub 6 rzutów) =

4

P

n=1

(p

n,O

+ p

n,R

) =

15

32

(ilość rzutów= n + 2).

2

(b) Niech Ω = {ω

n

, n = 1, 2, . . .}, F = 2

Ω

. Weźmy ciąg p

n

= cz

−n

, n = 1, 2, . . ., gdzie z > 1 jest

ustalone. Dobrać stałą c tak, aby ciąg (p

n

) określał prawdopodobieństwo P na zbiorze Ω tak,

że p

n

= P ({ω

n

}). Obliczyć P ({ω

1

, . . . , ω

10

}).

• p

n

­ 0 dla każdego n wtedy i tylko wtedy, gdy c ­ 0

•

∞

P

n=1

p

n

= c

∞

P

n=1

1
z

n

= c ·

1

z

·

1

1 −

1
z

=

c

z − 1

= 1 wtedy i tylko wtedy, gdy c = z − 1 ­ 0

• Oba warunki na ciąg określający prawdopodobieństwo na Ω są spełnione

dla c = z − 1

• P ({ω

1

, . . . , ω

10

}) =

10

P

n=1

p

n

=

10

P

n=1

(z − 1)

1
z

n

= (z − 1) ·

1

z

·

1 −

1
z

10

1 −

1
z

= 1 −

1

z

10

Przykłady do zadania 2.3 :

(a) Na okręgu wybieramy „losowo” cięciwę. Uściślić na kilka sposobów pojęcie „losowo” i dla każdego

z nich obliczyć prawdopodobieństwo, że długość cięciwy będzie większa od promienia okręgu.

1. sposób Ustalamy kierunek i wybieramy spośród cięciw o tym samym kierunku od średnicy do

cięciwy „zerowej”, przy czym nie wyróżniamy żadnej z nich. Odpowiada to jednostajnemu
wyborowi punktu x z odcinka [0, R], gdzie R to promień okręgu.

−1.5

−1

−0.5

0

0.5

1

1.5

−1.5

−1

−0.5

0

0.5

1

1.5

x

R

l(x)

• Ω = [0, R], F to rodzina zbiorów borelowskich z tego odcinka,

P to prawdopodobieństwo geometryczne.

• Dla wybranego x długość odpowiadajęcej mu cięciwy wynosi l(x) = 2

√

R

2

− x

2

• l(x) > R wtedy i tylko wtedy, gdy x ∈ [0,

√

3R/2).

• Zatem P (l(x) > R) = P ([0,

√

3R/2)) =

√

3R/2

R

=

√

3

2

.

3

2. sposób Ustalamy punkt A

0

na okręgu i wybieramy spośród cięciw o punkcie początkowym A

0

,

przy czym nie wyróżniamy żadnej z nich. Odpowiada to jednostajnemu wyborowi punktu
A (końcowego punktu cięciwy) z okręgu, albo równoważnie wyborowi kąta ϕ z przedziału
[−π, π], patrz rysunek.

−1.5

−1

−0.5

0

0.5

1

1.5

−1.5

−1

−0.5

0

0.5

1

1.5

A

0

A

fi

R

l(fi)

0

• Ω = [−π, π], F to rodzina zbiorów borelowskich z tego odcinka,

P to prawdopodobieństwo geometryczne.

• Dla wybranego ϕ długość odpowiadajęcej mu cięciwy wynosi l(ϕ) = 2

q

2R

2

(1 + cos ϕ).

• l(ϕ) > R wtedy i tylko wtedy, gdy ϕ ∈ (−2π/3, 2π/3).

• Zatem P (l(ϕ) > R) = P ((−2π/3, 2π/3)) =

2 · 2π/3

2π

=

2

3

.

3. sposób Wybieramy bez wyróżniania punkt A z koła bez środka. Punkt ten potraktowany jako

środek cięciwy jednoznacznie ją wyznacza (wyjątkiem byłby środek koła odpowiadający
średnicom, odrzucając środek koła na początku przyjęliśmy, że prawdopodobieństwo wy-
losowania średnicy wynosi 0).

−1.5

−1

−0.5

0

0.5

1

1.5

−1.5

−1

−0.5

0

0.5

1

1.5

.

0

R

R

r

A

l(A)

• Ω =koło o promieniu R, F to rodzina zbiorów borelowskich na tym kole,

P to prawdopodobieństwo geometryczne.

• Dla wybranego A długość odpowiadajęcej mu cięciwy wynosi l(A) = 2

√

R

2

− r

2

,

gdzie r to odległość punktu A od środka koła.

• l(A) > R wtedy i tylko wtedy, gdy r <

√

3R/2, tzn. gdy A leży w otwartym kole

K(A) o tym samym środku co Ω i promieniu

√

3R/2.

• Zatem P (l(A) > R) = P (K(A)) =

π · 3R

2

/4

πR

2

=

3

4

.

4

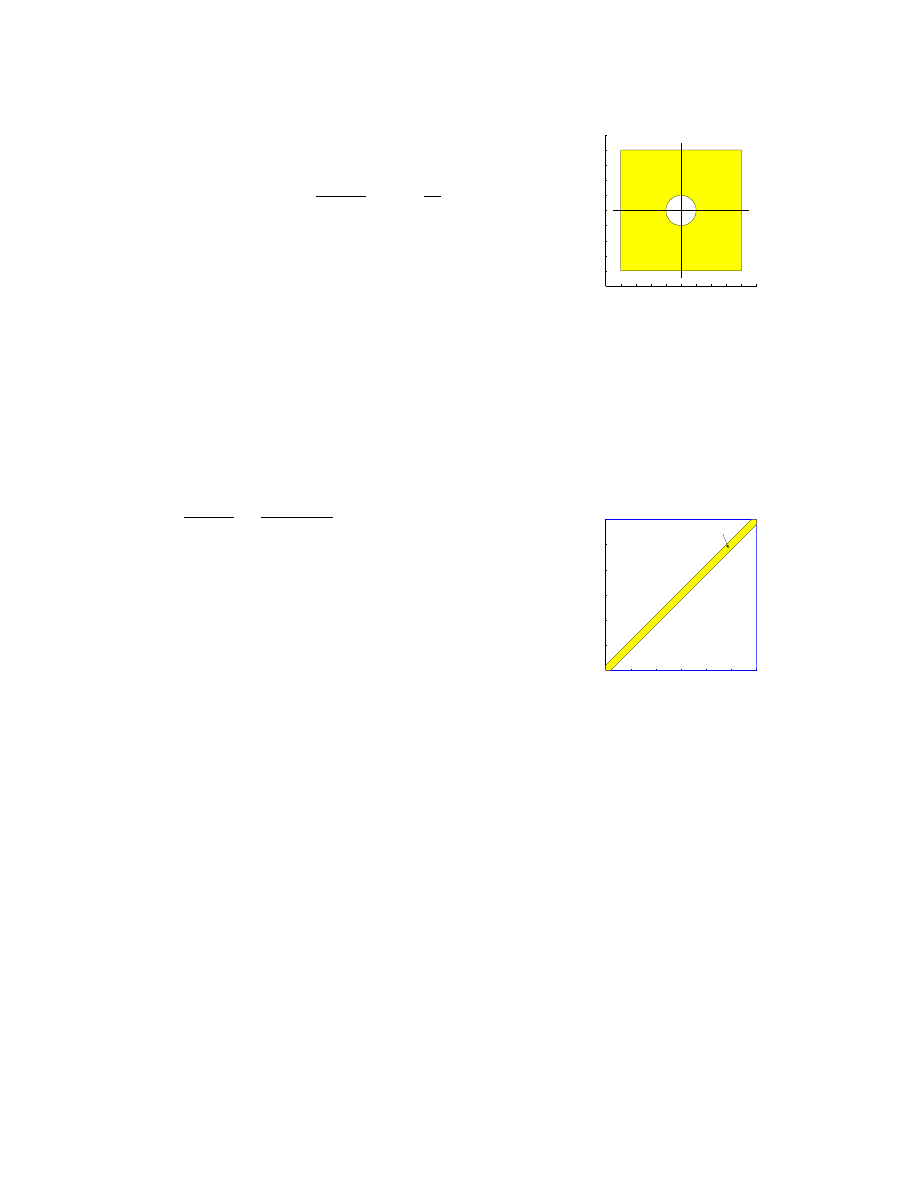
(b) Obliczyć prawdopodobieństwo tego, że wybrany losowo punkt kwadratu |x| < 4, |y| < 4 leży

na zewnątrz koła x

2

+ y

2

< 1.

• Ω = {(x, y) : |x| < 4, |y| < 4} - kwadrat, F to borelowskie podzbiory Ω,

P - prawdopod. geometryczne.

• A = {(x, y) : x

2

+ y

2

< 1} - koło.

• P (A

c

) = 1 − P (A) = 1 −

pole A

pole Ω

= 1 −

π

64

≈ 0, 951.

−5

−4

−3

−2

−1

0

1

2

3

4

5

−5

−4

−3

−2

−1

0

1

2

3

4

5

1

4

A

A

c

Ω

−4

−4

4

(c) W przypadkowych chwilach z przedziału czasu [0, 60] minut mogą nadejść do odbiornika dwa

sygnały. Odbiornik zostaje uszkodzony, jeśli różnica w czasie między tymi dwoma sygnałami
jest mniejsza od 2 minut. Obliczyć prawdopodobieństwo uszkodzenia odbiornika.

• Ω = {(t

1

, t

2

) : t

1

, t

2

∈ [0, 60]}, F to borelowskie podzbiory Ω, P - prawdopod. geometrycz-

ne.

• A - zdarzenie, że odbiornik został uszkodzony. A = {(t

1

, t

2

) ∈ Ω : |t

1

− t

2

| < 2}

• P (A) =

pole A

pole Ω

=

60

2

− 58

2

60

2

≈ 0, 0655.

0

10

20

30

40

50

60

0

10

20

30

40

50

60

t

2

=t

1

+2

t

2

=t

1

−2

t

1

t

2

A

Ω

5

Przykłady do zadania 1.4 :

(a) Zakład pracuje na trzy zmiany. Zmiany produkują odpowiednio n

1

= 200, n

2

= n

3

= 150

wyrobów, przy czym szansa wyprodukowania wadliwego wyrobu wynosi odpowiednio p

1

=

p

2

= 0, 1, p

3

= 0, 3. Obliczyć prawdopodobieństwo, że wyrób wylosowany z całej produkcji jest

wadliwy. Obliczyć prawdopodobieństwo, że wylosowany wadliwy wyrób wyprodukowała druga
zmiana.

• Wprowadzamy oznaczenia:

A - zdarzenie, że wylosowany wyrób jest wadliwy;
B

n

- zdarzenie, że wylosowany wyrób wyprodukowała n-ta zmiana, n = 1, 2, 3.

• Mamy P (B

1

) =

n

1

n

1

+ n

2

+ n

3

=

200

500

= 0, 4; P (B

2

) = P (B

3

) = 0, 3;

P (A|B

1

) = P (A|B

2

) = 0, 1; P (A|B

3

) = 0, 3.

• Z tw. o prawdop. całkowitym

P (A) = P (A|B

1

)P (B

1

) + P (A|B

2

)P (B

2

) + P (A|B

3

)P (B

3

) =

= 0, 1 · 0, 4 + 0, 1 · 0, 3 + 0, 3 · 0, 3 = 0, 16.

• Szukamy teraz P (B

2

|A).

Ze wzoru Bayesa P (B

2

|A) =

P (A|B

2

)P (B

2

)

P (A)

=

0, 1 · 0, 3

0, 16

=

3

16

= 0, 1875.

(b) Prawdopodobieństwo trafienia w cel w jednym strzale wynosi 1/2, natomiast prawdopodobień-

stwo zniszczenia celu przy k trafieniach wynosi 1 −

1
3

k

, k = 0, 1, . . .. Wyznaczyć prawdopo-

dobieństwo zniszczenia celu przy oddaniu 10 strzałów.

• Wprowadzamy oznaczenia:

A - zdarzenie, że zniszczono cel przy oddaniu 10 strzałów,
B

k

- zdarzenie, że w 10 strzałach jest k trafień, k = 0, 1, . . . , 10.

• B

0

, B

1

, . . . , B

10

stanowią rozbicie przestrzeni probabilistycznej (są parami rozłączne i w

sumie są zdarzeniem pewnym Ω).

• Mamy P (B

k

) =

10

k

1
2

k

1 −

1
2

10−k

=

10

k

1
2

10

; P (A|B

k

) = 1 −

1
3

k

.

• Z tw. o prawdop. całkowitym P (A) =

10

P

k=0

P (A|B

k

)P (B

k

) =

10

P

k=0

(1 −

1
3

k

)

10

k

1
2

10

=

=

1
2

10

10

P

k=0

10

k

1

k

1

10−k

−

10

P

k=0

10

k

1
3

k

1

10−k

=

1
2

10

(1 + 1)

10

−

1
3

+ 1

10

=

= 1 −

2
3

10

≈ 0, 983,

gdzie korzystaliśmy ze wzoru (a + b)

10

=

P

10
k=0

10

k

a

k

b

10−k

.

6

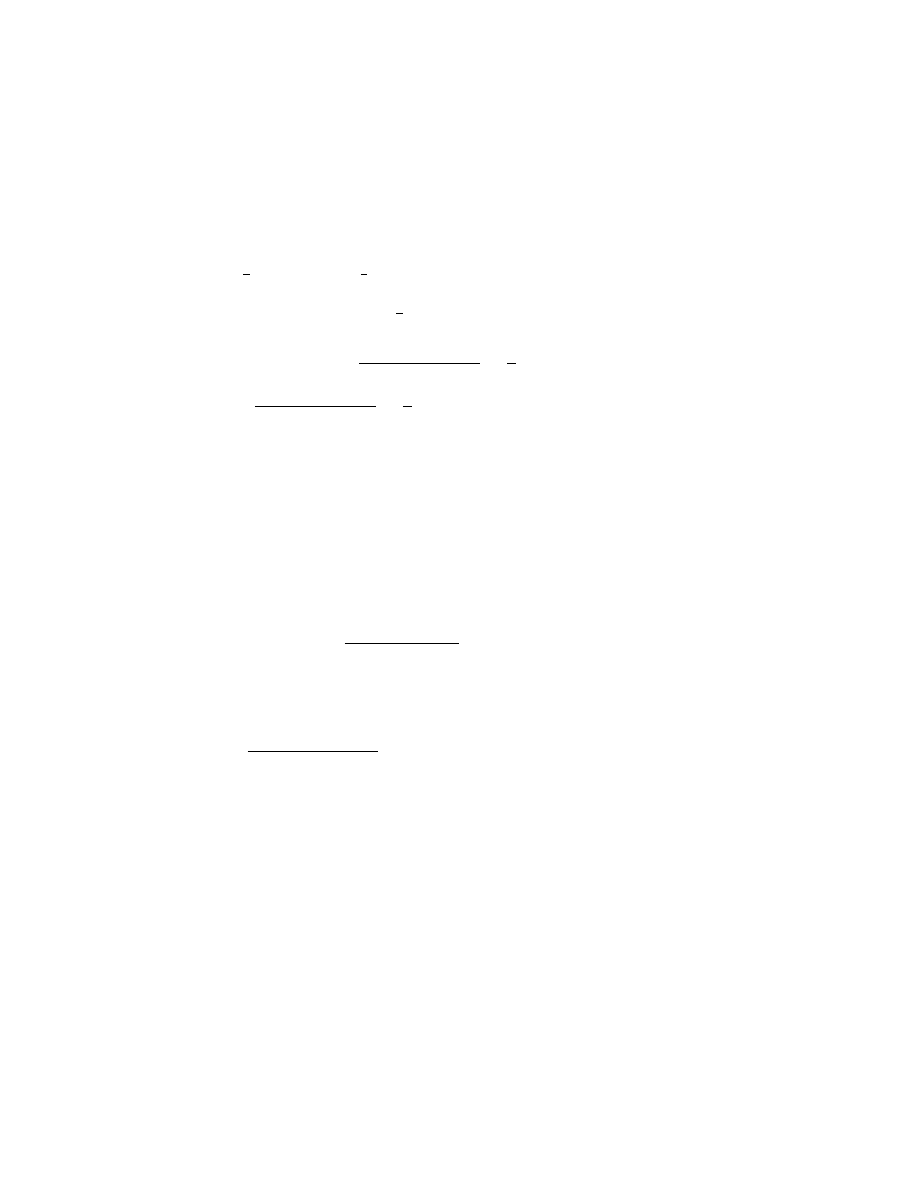
(c) W pewnym teleturnieju za jednymi z trzech zamkniętych drzwi znajduje się samochód, a za

pozostałymi dwoma kozy. Prowadzący grę wie, które drzwi kryją samochód. Gracz wskazuje
na jedne z drzwi, prowadzący otwiera jedne z pozostałych odkrywając kozę i następnie pyta
gracza, które z zamkniętych drzwi otworzyć (tzn. czy gracz zmienia wybór, czy nie). Jeżeli
gracz wskaże na odpowiednie drzwi, wygrywa samochód.

Powiedzmy, że gracz wskazał na początku na drzwi nr 1, a prowadzący grę otworzył drzwi nr 3
z kozą. Czy graczowi opłaca się zmienić decyzję i wskazać na drzwi nr 2? Odpowiedź uzasadnić.

• Wprowadzamy oznaczenia: A

i

- zdarzenie, że samochód jest za drzwiami nr i,

B

i

- zdarzenie, że prowadzący otworzył drzwi nr i, i = 1, 2, 3

• Mamy P (A

i

) =

1
3

, P (B

3

|A

1

) =

1
2

, P (B

3

|A

2

) = 1, P (B

3

|A

3

) = 0.

• Stąd P (B

3

) =

3

P

i=1

P (B

3

|A

i

)P (A

i

) =

1
2

z tw. o prawdop. całkowitym,

• i ze wzoru Bayesa P (A

1

|B

3

) =

P (B

3

|A

1

)P (A

1

)

P (B

3

)

=

1

3

oraz P (A

2

|B

3

) =

P (B

3

|A

2

)P (A

2

)

P (B

3

)

=

2

3

• Wniosek: Graczowi opłaca się zmienić decyzję, bo zwiększa swoją szansę na wygraną.

(d) Pewna choroba jest obecna w 0,01% populacji. Opracowano test, który daje wynik dodatni

u 90% chorych i u 5% zdrowych. Jakie jest prawdopodobieństwo tego, że pacjent z wynikiem
dodatnim jest zdrowy? Czy ma on powody do obaw?

• Wprowadzamy oznaczenia:

A - zdarzenie, że test daje wynik dodatni; B - zdarzenie, że pacjent jest chory.
Szukamy P (B

c

|A).

• Ze wzoru Bayesa P (B

c

|A) =

P (A|B

c

)P (B

c

)

P (A)

• Mamy P (B) = 0, 0001 = 1 − P (B

c

); P (A|B) = 0, 9; P (A|B

c

) = 0, 05.

• Zatem P (A) = P (A|B)P (B) + P (A|B

c

)P (B

c

) = 0, 050085 z tw. o prawdop. całkowitym.

• oraz P (B

c

|A) =

0, 05(1 − 0, 0001)

0, 050085

≈ 0, 9982

• Wniosek: Test w istocie nie wykrywa choroby, bo pacjent z wynikiem dodatnim jest zdrowy

na ponad 99% i raczej nie ma powodów do obaw.

7

Przykłady do zadania 1.5 :

(a) Dwa razy kontrolowana jest jakość pewnego urządzenia przez niezależne kontrole. Wynik kon-

troli to jedna z dwóch opinii: S - urządzenie sprawne lub N - urządzenie niesprawne. Szansa
na to, że S będzie wynikiem pierwszej kontroli, wynosi p, drugiej kontroli - q, 0 ¬ p, q ¬ 1.
Zbadać niezależność zdarzenia A, że wynik pierwszej kontroli to S, oraz zdarzenia B, że obie
kontrole stwierdziły to samo.

• Ω = {SS, SN, N S, N N }, F = 2

Ω

,

P (SS) = pq, P (SN ) = p(1 − q), P (N S) = (1 − p)q, P (N N ) = (1 − p)(1 − q),
gdyż kontrole są niezależne.

• A = {SS, SN }, B = {SS, N N }, A ∩ B = {SS}

• P (A ∩ B) = P (A)P (B) wtedy i tylko wtedy, gdy pq = (pq + p(1 − q))(pq + (1 − p)(1 − q)),

czyli gdy pq = p(1 − p − q + 2pq).

• Równość zachodzi dla p = 0 albo p = 1 albo q = 1/2.

• Zatem zdarzenia A i B są niezależne w skrajnych przypadkach p = 0 lub p = 1 bez

względu na q oraz w ciekawszym przypadku q = 1/2 bez względu na p.

(b) Elektron emitowany jest w losowej chwili τ przedziału [0, T ]. Dla ustalonej chwili t przedziału

(0, T ) niech A będzie zdarzeniem, że emisja nastąpi po chwili t, a B zdarzeniem, że emisja
nastąpi przed chwilą T − t. Czy zdarzenia A, B są niezależne?

• Ω = [0, T ], F to zbiory borelowskie z tego odcinka,

P to prawdopodobieństwo geometryczne.

• A = [t, T ], B = [0, T − t]

• P (A) · P (B) =

T − t

T

2

.

• A ∩ B =

(

∅,

gdy T − t < t,

[t,T-t], gdy T − t ­ t;

i stąd P (A ∩ B) =







0,

gdy T /2 < t < T,

T − 2t

T

, gdy 0 < t ¬ T /2.

• Ponieważ P (A ∩ B) 6= P (A)P (B), zdarzenia A i B nie są niezależne.

(Zauważmy, że wniosek ten nie zależy od wyboru t.)

(c) Prawdopodobieństwo zestrzelenia samolotu przez wystrzał z karabinu wynosi p = 0, 004. Jakie

jest prawdopodobieństwo zestrzelenia samolotu przez salwę z 250 karabinów?

• Wprowadzamy oznaczenia:

A

i

= {zestrzelenie samolotu z i-tego karabinu }, i = 1, 2, . . . , 250,

B = {zestrzelenie samolotu przez salwę z 250 karabinów }.
Zakładamy, że zdarzenia A

i

, i = 1, 2, . . . , 250, są niezależne.

• B =

250

S

i=1

A

i

, a stąd B

c

=

250

T

i=1

A

c
i

.

• Z niezależności P (B

c

) =

250

Q

i=1

P (A

c
i

) = (1 − 0, 004)

250

≈ 0, 3671

• Stąd P (B) = 1 − P (B

c

) ≈ 0, 6329

8