Rachunek prawdopodobieństwa MAP1151

Wydział Elektroniki, rok akad. 2009/10, sem. letni

Wykładowca: dr hab. A. Jurlewicz

Wykład 3: Zmienna losowa. Dystrybuanta.

Definicja.

Zmienna losowa

X to funkcja X : Ω −→

R

, dla której dla dowolnego borelowskiego

zbioru B ⊂

R

zbiór

{ω : X(ω) ∈ B}

ozn.

= {X ∈ B} ∈ F ,

tzn. zbiór {X ∈ B} jest zdarzeniem losowym.

Innymi słowy, jest to taka funkcja X na zbiorze zdarzeń elementarnych o wartościach licz-
bowych, dla której określone są (teoretycznie) prawdopodobieństwa przyjmowania przez
X wartości z każdego dowolnego zakresu.

(Uwaga: z analizy matematycznej przyzwyczajeni jesteśmy do zupełnie innej informacji:
znamy zwykle przepis na wartość funkcji dla danego argumentu, badamy wykres funkcji,
monotoniczność, różniczkowalność itd.)

W rachunku prawdopodobieństwa interesuje nas rozkład zmiennej losowej, ewentualnie
jej charakterystyki liczbowe (takie jak wartość średnia, wariancja i inne momenty,
mediana i inne kwantyle, mody).

cała informacja

(Ω, F , P )

'

&

$

%

przestrzeń probabilistyczna

X

-

fragment informacji;

ten, który nas interesuje

(

R

, B, P

X

)

nowa przestrzeń

probabilistyczna,

B to zbiory borelowskie,

P

X

to rozkład zmiennej

losowej X

1

Rozkład zmiennej losowej

Definicja.

Rozkład zmiennej losowej X

to funkcja określona na zbiorach borelowskich w

następujący sposób:

P

X

(B) := P (X ∈ B) dla dowolnego borelowskiego zbioru B.

P

X

to funkcja o własnościach prawdopodobieństwa dla przestrzeni stanów

R

i rodziny

zdarzeń losowych B (zbiorów borelowskich).

Przykłady zmiennych losowych:

1. Ilość ”szóstek” w n rzutach kostką do gry.

2. Ilość rzutów potrzebnych do uzyskania pierwszej ”szóstki”.

3. Numer orbity, na której znajduje się elektron.

4. Zachowanie dziewczyny, gdy jej chłopak spóźnia sie na randkę, opisane liczbowo,

np. −1 - gniewa się; 0 - nie zauważa; 1 - cieszy się, że wreszcie przyszedł.

5. Czas bezawaryjnej pracy komputera liczony w godzinach.

Typy zmiennych losowych:

1. Zmienna losowa

dyskretna

(in. o rozkładzie dyskretnym)

to taka zmienna losowa, która przyjmuje z dodatnim prawdopodobieństwem jedynie
skończoną lub nieskończoną przeliczalną liczbę różnych wartości.

2. Zmienna losowa

ciągła

(in. rozkładzie ciągłym)

to taka zmienna losowa, dla której istnieje taka nieujemna funkcja f (x), że dla
każdego borelowskiego zbioru B

P

X

(B) =

Z

B

f (x)dx.

Funkcja f (x) zwana jest wtedy gęstością rozkładu X.

3. Zmienna losowa

osobliwa

(in. o rozkładzie osobliwym)

to zmienna losowa, której rozkład skupiony jest na nieprzeliczalnym zbiorze o dłu-
gości 0 (np. na zbiorze Cantora), tzn. prawdopodobieństwo tego, że zmienna ta
przyjmuje wartość z tego zbioru, wynosi 1, przy czym P (X = x) = 0 dla każdego
x ∈

R

.

4. Dowolna zmienna losowa albo jest jednego z tych trzech typów, albo ma rozkład

mieszany

składający się z rozkładów tych typów.

2

Technika określania rozkładu zmiennej losowej X
za pomocą dystrybuanty:

Pełna informacja o rozkładzie zmiennej losowej X zawarta jest w funkcji

F (x) = P (X < x), x ∈

R

,

nazywanej

dystrybuantą

.

Zauważmy, że F (x) = P (X < x) = P

X

(B) dla B = (−∞, x).

Z dystrybuanty możemy dostać informację o wartościach funkcji P

X

na innych zbiorach

borelowskich:

• P (X < b) = F (b)

• P (X ¬ b) = lim

x→b+

F (x);

• P (X ­ b) = 1 − F (b);

• P (X > b) = 1 − lim

x→b+

F (x);

• P (a ¬ X < b) = F (b) − F (a);

• P (a < X < b) = F (b) − lim

x→a+

F (x);

• P (a < X ¬ b) = lim

x→b+

F (x) − lim

x→a+

F (x);

• P (a ¬ X ¬ b) = lim

x→b+

F (x) − F (a).

Funkcja F (x) spełnia następujące warunki:

• jest lewostronnie ciągła;

• jest niemalejąca;

•

lim

x→−∞

F (x) = 0, lim

x→∞

F (x) = 1.

Jeżeli pewna funkcja F (x) spełnia te warunki, to dla pewnej zmiennej losowej X mamy
F (x) = P (X < x). Funkcja F ma wtedy probabilistyczną interpretację, reprezentację,
może być używana w modelach w roli dystrybuanty.

3

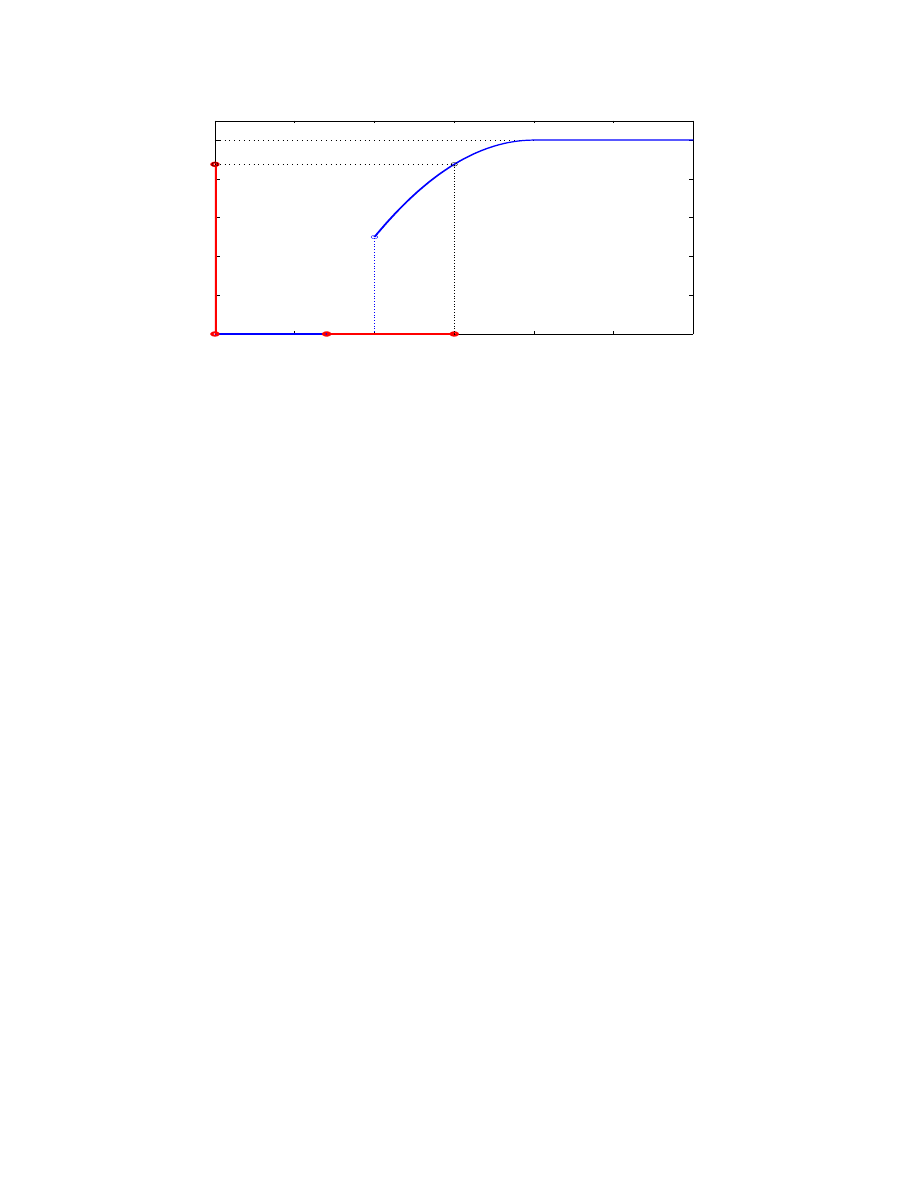
Przykładowy wykres dystrybuanty (X - płaca losowo wybranego pracownika pewnej du-
żej grupy zawodowej w stosunku do płacy minimalnej):

0

0.5

1

1.5

2

2.5

3

0

0.2

0.4

0.6

0.8

1

F(x)

x

B

P(B)=

dlugosc

X

Przykłady do zad. 2.1 - 2.3

4