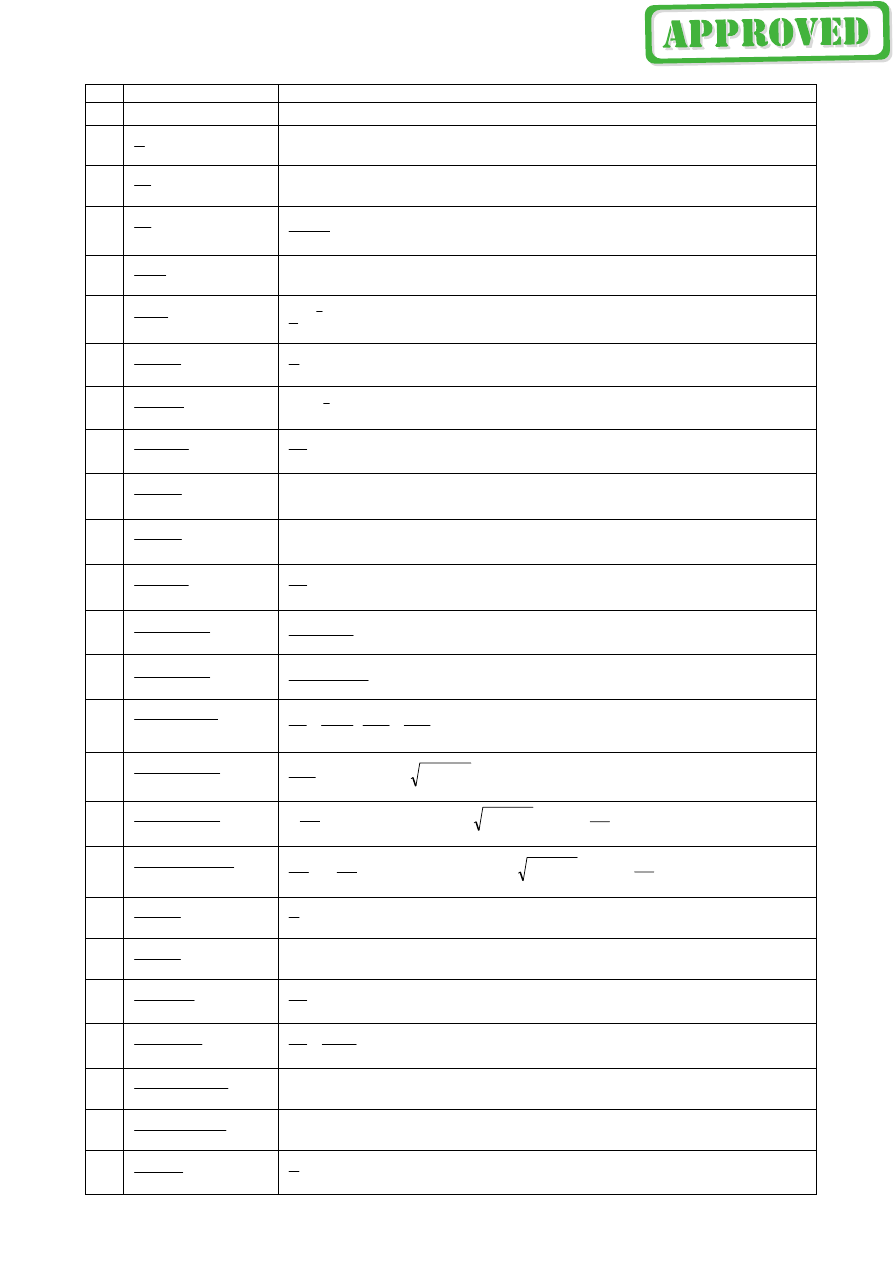
Tablica przekształceń Laplace’a
Lp. F(s)
f(t)
1
1
( )
t
δ
- funkcja impulsowa
2
s
a
a
3
2
1
s
t
4
n
s
1
(
)
!
1
1
−
−
n
t
n
dla n=1,2,3,...
5
a
s
+
1
at
−
e
6
τ
+ s
1
1
τ
−
τ
t
e
1
7
(
)
a
s
s
+
1
(
)
at
a
−
− e
1
1
8
(
)
τ
+ s
s 1
1
τ
−
−
t
e
1
9
(
)
a
s
s
+
2
1
(
)
1
e
1
2
−
+
−
at
a
at
10
(
)
2
1
a
s
+
at
t
−
e
11
(
)
2
a
s
s
+
(
)
at
at
−
−
e
1
12
(
)
2
1
a
s
s
+
(
)
(
)
at
at
a
−
+
−
e
1
1
1
2
13
(
)(
)
b
s
a
s
+
+
1
b
a
a
b
bt
at
≠
−
−
−
−
,
e
e
14
(
)(
)
b
s
a
s
s
+
+
b
a
b
a
b
a
bt
at
≠
−
−
−
−
,
e
e
15
(
)(
)
b
s
a
s
s
+
+
1
b
a
b
a
b
a
ab
bt
at
≠
−
−
+
−
−
,
e
e
1
1
16
2
2
2
1
n
s
s
ω
+
α
+
α
>
ω
α
−
ω
=
ω
ω
ω
−
n
n
o
o
o
at
t
e
,
,
sin
2
2
17
2
2
2
n
s
s
s
ω
+
α
+
(
)
α
>
ω
α
ω
=
Θ
α
−
ω
=
ω
Θ
−
ω
ω
ω
−
−
n
o
n
o
o
at
o
n
t
,
tg
,
,
sin
e
2
2
18
(
)
2
2
2
1
n
s
s
s
ω
+
α
+
(
)
α
>
ω
α
ω
=
Θ
α
−
ω
=
ω
Θ
+
ω
ω
ω
−
ω
−
n
o
n
o
o
at
o
n
n
t
,
tg
,
,
sin
e
1
1
2
2
2
19
2
2
1
a
s
+
at
a
sin
1
20
2
2
a
s
s
+
at
cos
21
(
)
2
2
1
a
s
s
+
(
)
at
a
cos
1
1
2
−
22
(
)
2
2
2
1
a
s
s
+
3
2
sin
a
at
a
t −
23
2
2
sin
cos
b
s
b
s
+
ϕ
−
ϕ
(
)
ϕ
+
bt
cos
24
2
2
cos
sin
b
s
b
s
+
ϕ
+
ϕ
(
)
ϕ
+
bt
sin
25
2
2
1
a
s
−
at
a
sinh
1

26
2
2
a
s
s
−
at
cosh
27
(
)
2
2
1
a
s
s
−
(
)
1
cosh
1
2
−
at
a
28
(
)
2
2
2
1
a
s
s
−
2
3
sinh
a
t
a
at −
29
(
)
2
2
1
b
a
s
+
+
b
bt
at
sin
e
−
30
(
)
2
2
b
a
s
s
+
+
at
bt
b
a
bt
−
−
e
sin
cos
31
(
)
2
2
b
a
s
a
s
+
+
+
bt
at
cos
e
−
32
(
)
(
)
2
2
sin
cos
b
a
s
b
a
s
+
+
ϕ
−
ϕ
+
(
)
ϕ
+
−
bt
at
cos
e
33
(
)
(
)
2
2
cos
sin
b
a
s
b
a
s
+
+
ϕ
+
ϕ
+
(
)
ϕ
+
−
bt
at
sin
e
34
(
)
2
2
1
b
a
s
−
+
b
bt
at
sinh
e
−
35
(
)
2
2
b
a
s
a
s
−
+
+
bt
at
cosh
e
−
36
(
)
3
1
a
s
+
at
t
−
e
2
1
2
37
(
)
3
a
s
s
+
at
at
t
−
−
e
2
1
1
38
(
)
(
)
2
2
1
b
s
a
s
+
+
(
)
[
]
2
2
2
2
arcsin
,
sin
sin
e
1
b
a
b
bt
b
a
b
at
+
=
Θ
Θ
−
+
Θ
+
−
39
(
)
(
)
2
2
1
b
s
a
s
−
+
2
2
e
sinh
cosh
a
b
bt
b
a
bt
at
−
−
−
−
40
(
)(
)
2
1
b
s
a
s
+
+
(
)
[
]
(
)
2
e
1
e
b
a
t
b
a
bt
at
−
−
−
−
−
−
41
(
)(
)
2
b
s
a
s
s
+
+
(
)
[
]
(
)
2
e
e
b
a
a
t
b
a
b
a
at
bt
−
−
−
−
−
−
42
(
)
2
2
2
1
a
s
+
2
3
2
cos
2
sin
a
at
t
a
at −
43
(
)
2
2
2
a
s
s
+
at
t
a
sin
2
1
44
(
)
2
2
2
2
a
s
s
+
(
)
at
at
at
a
cos
sin
2
1
+
45
(
)
2
2
2
2
2
a
s
a
s
+
−
at
t cos
46
(
)
2
2
2
1
a
s
−
3
2
2
sinh
2
cosh
a
at
a
at
t
−
47
(
)
2
2
2
a
s
s
−
at
t
a
sinh
2
1
48
(
)
n
a
s
+
1
(
)
,..
3
,
2
,
1
,
!
1
e
1
=
−
−
−
n
n
t
at
n
Wyszukiwarka
Podobne podstrony:
Obliczanie transformat Laplace'a
Transformaty Laplacka
Transformata Laplacea oryginaly i transformaty funkcji [tryb zgodności]
AM23 w13 Transformata Laplace'a
Transformaty Laplace a
Transformacja Laplace wyprowadzenie wzorów
9 transformata Laplace'a + Transmitancja Operatorowa
Transformacja Laplacea
cps tablica transformat, Edukacja, studia, Semestr IV, Podstawy i Algorytmy Przetwarzania Sygnałów
AM23 w14 Zastosowania transformaty Laplace'a
transformaty Laplace'a
Podstawowe regu y transformacji Laplace's (wzory)
transformata Laplaca
Transformata Laplace, Studia, Semestr 1, Sygnały i Systemy, Sprawozdanie 4
3 Cwiczenia zadania4 transformata Laplacea id 606491 (2)
3 Podstawy automatyki Transformata Laplacea, algebra blok
Podstawowe transformaty Laplace'a
!Tablice transformaty Z i jej wlasnoci
Egz systemy ściaga, Transformaty Laplace`a [f(t) ; F(t)]
więcej podobnych podstron