Nazwisko i imię:

Zespół:

Data:

Ćwiczenie nr 9: Swobodne spadanie

Cel ćwiczenia: Obserwacja swobodnego spadania z wykorzystaniem elektronicznej rejestracji czasu
przelotu kuli przez punkty pomiarowe. Wyznaczenie przyspieszenia ziemskiego.

Literatura

[1] Kąkol Z., Fizyka dla inżynierów, OEN Warszawa, 1999.

[2] Zięba A. (red), Pracownia Fizyczna Wydziału Fizyki i Techniki Jądrowej SU1642, AGH, Kraków

2002 (ew. wydania wcześniejsze).

Zagadnienia do opracowania

Ocena i

podpis

1.

Prawo powszechnego ciążenia.

2.

Swobodne spadanie – opis ruch w próżni.

3.

Jakie siły działają na ciało spadające w powietrzu?

4.

Dlaczego przyspieszenie ciała spadającego swobodnie jest mniejsze od wartości
przyspieszenia ziemskiego?

5.

Podaj wielkości, od których zależy siła oporu powietrza?

6.

Co to jest siła wyporu powietrza i jaki jest jej możliwy wpływ na wartość przy-
spieszenia spadającego ciała?

7.

Wyjaśnij znaczenie pojęcia „ekstrapolacja liniowa”, zastosowanego jako element
opracowania wyników pomiaru.

8.

Wartość przyspieszenia ziemskiego zmienia się od 9, 832 m

s

2

na biegunach, poprzez

9, 811 m

s

2

na szerokości geograficznej Krakowa, do 9, 780 m

s

2

na równiku. Dlaczego?

Ocena z odpowiedzi:

9-1

1

Opracowanie ćwiczenia

Opracuj i opisz zagadnienia nr

i

podpis:

9-2

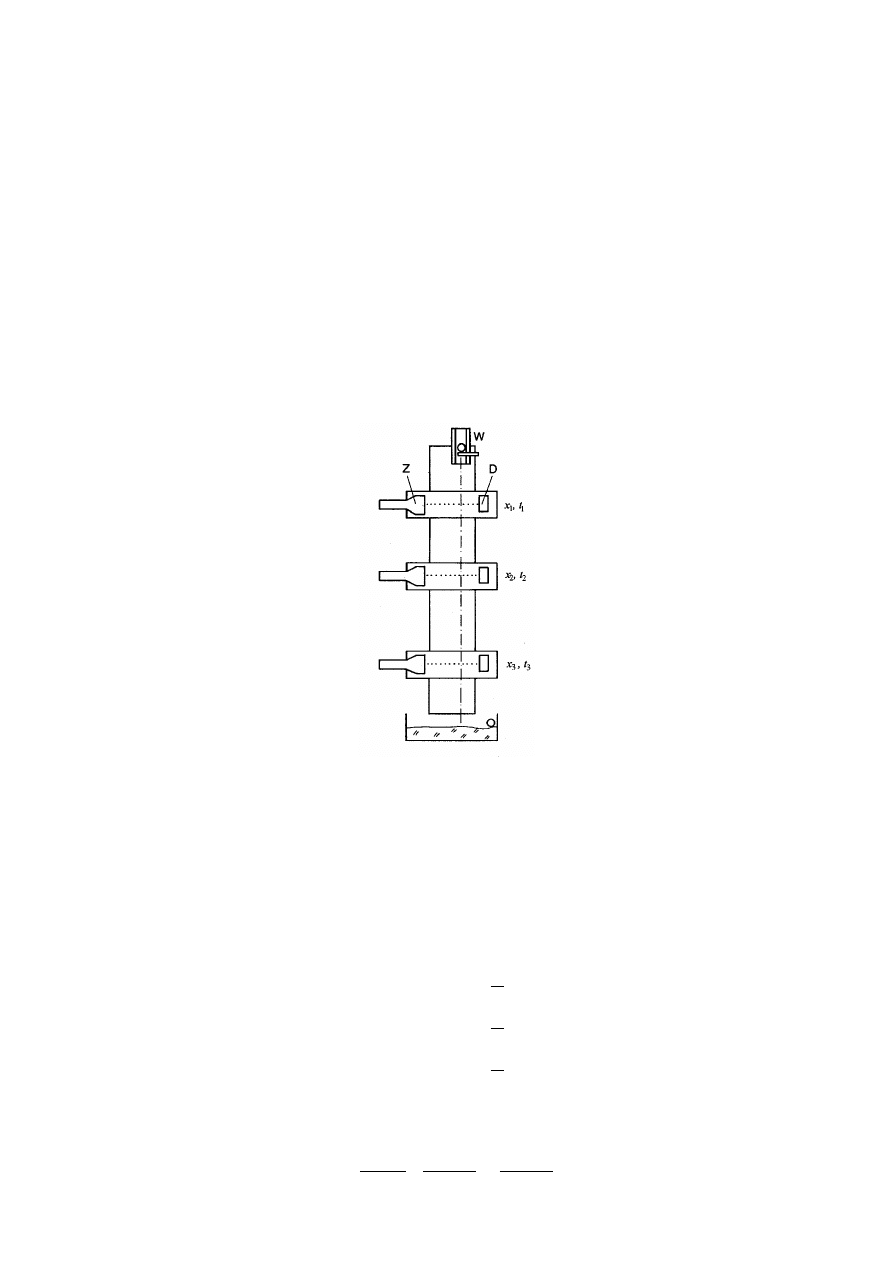
2

Oznaczenia, podstawowe definicje i wzory

Stosowane oznaczenia:

x

1

, x

2

, x

3

współrzędne przestrzenne trzech fotokomórek,

t

1

, t

2

, t

3

czas przelotu kuli przez kolejne fotokomórki,

x

0

wartość początkowa położenia kuli (w chwili t = 0),

v

0

wartość początkowa prędkości kuli (w chwili t = 0),

a

pozorna wartość przyspieszenia ziemskiego (wzór 2 )

ρ

gęstość materiału kul,

r

promień kuli,

v

prędkość (chwilowa) kuli,

ρ

p

gęstość powietrza,

C

współczynnik oporu,

g

wartość rzeczywista przyspieszenia ziemskiego.

Układ pomiarowy

Rysunek 9-1: Schemat mechaniczny układu pomiarowego: Z – reflektor lub laser, D – detektor światła,
W – wyrzutnik kul.

Użyteczne wzory
Równania ruchu jednostajnie przyspieszonego dla swobodnego spadania w próżni, zapisane dla trzech
fotokomórek:

x

1

= x

0

+ v

0

t

1

+ a

t

2

1

2

x

2

= x

0

+ v

0

t

2

+ a

t

2

2

2

(1)

x

3

= x

0

+ v

0

t

3

+ a

t

2

3

2

Pozorna wartość przyspieszenia ziemskiego (rozwiązanie ww. układu równań ze względu na a).

a =

2

t

3

− t

1

x

3

− x

2

t

3

− t

2

−

x

2

− x

1

t

2

− t

1

(2)

9-3

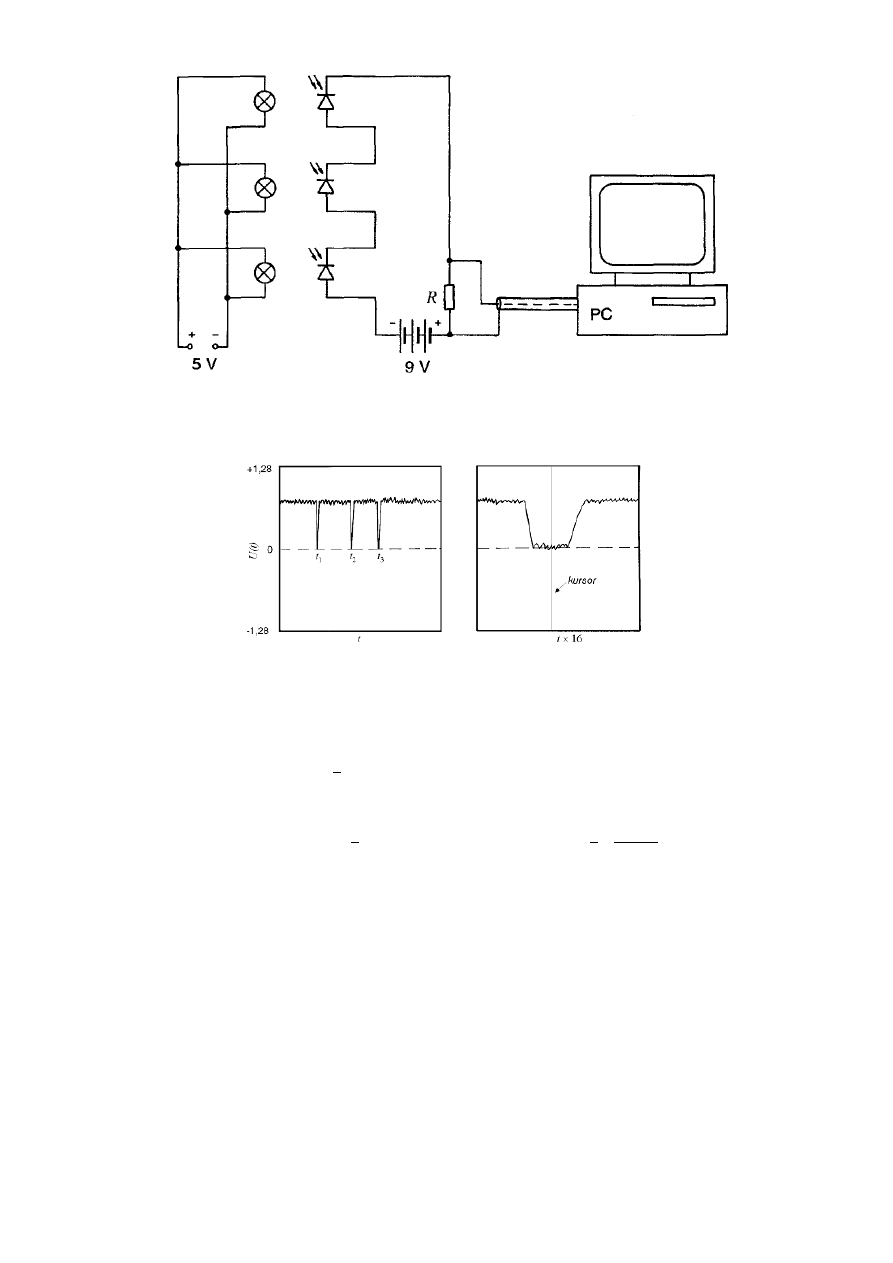
Rysunek 9-2: Schemat elektryczny dla źródeł i detektorów światła

Rysunek 9-3: Zarejestrowany przebieg U (t) na monitorze: (a) po pomiarze, (b) określenie czasów t

1

,

t

2

lub t

3

po 16-krotnym rozciągnięciu skali czasu

Równanie prostej ekstrapolacji a

1

ρ

pozwalającej obliczyć przyspieszenie ziemskie g z wyeliminowa-

niem wpływu siły oporu powietrza i siły wyporu Archimedesa:

a = g − const ·

1

ρ

,

gdzie

const = gρ

p

+

3

8

·

Cρ

p

v

2

r

.

(3)

3

Wykonanie ćwiczenia

1. Włącz zasilanie układu reflektorów (zestaw 1) lub laserów (zestaw 2).

2. Uruchom komputer z kartą oscyloskopową. Program obsługujący kartę winien zgłosić się sa-

moczynnie. Sprawdź działanie programu (przez kolejne naciśnięcie ENTER, SPACJA, ENTER,
HOME).

3. Zestaw (lub sprawdź) układ elektryczny detekcji światła według schematu z Rys.9-1. Sprawdź

działanie układu pomiarowego wyzwalając kartę przy długim czasie pomiaru (8, 192 s) i przery-
wając w tym czasie ręką światło padające na kolejne fotokomórki.

4. Właściwy eksperyment polega na jednoczesnym wyzwoleniu karty i przesunięciu zasuwki po-

wodującej spadanie kulki. Należy stosować czas pomiaru 819, 2 ms (Taki czas pomiaru wynika
z faktu, że pracująca w układzie dwójkowych pamięć karty ma 2

13

= 8192 komórek pamię-

ci, na każdą przypada czas dokładnie 0, 1ms). Jeżeli nie uda się zarejestrować trzech pików za
pierwszym razem, należy powtarzać doświadczenie aż do skutku.

9-4

5. Współrzędne położenia x

1

, x

2

, x

2

odczytujemy z dokładnością nie gorszą niż 1mm. Do tabeli

wpisujemy również różnice x

2

− x

1

oraz x

3

− x

2

.

6. Dla zarejestrowanego sygnału wykonujemy odczyt czasów t

1

, t

2

i t

3

. W tym celu:

(a) najeżdżamy kursorem na dany pik wykorzystując przyciski < i > (przesuw co 4 pkt ekranu)

oraz → i ← (przesuw co 1 pkt),

(b) przy użyciu lupy czasowej (kilkakrotne naciśnięcie +) rozciągamy 16-krotnie skalę czasu,

(c) ustawiamy kursor na środek piku (rys.9-3),

(d) czas spisujemy z odpowiedniego okienka na monitorze (z dokładnością do 0, 1 ms),

(e) wykonujemy odczyt czasu dla dwu pozostałych pików (pierwotną skalę czasu przywraca

kilkakrotne naciśnięcie — ).

7. Dla każdego pomiaru obliczamy na bieżąco różnice t

2

− t

1

, t

3

− t

2

, i t

3

− t

1

i wpisujemy do

tabeli. Na bieżąco obliczamy też wartość a. Jeżeli otrzymana wartość nie mieści się w granicach
około 9 ÷ 10 m

s

2

, trzeba sprawdzić czy nie została popełniona omyłka przy pomiarze, zapisie lub

w obliczeniach.

8. Pomiar (czynności 4÷7) powtarzamy dla kolejnych kul. Przed każdym pomiarem należy zmieniać

nieznacznie położenia x

1

, x

2

i x

3

(w granicach kilku centymetrów). Uwaga: jeżeli nie zdążymy

dla wszystkich, należy wybierać kule o wyraźnie różnych gęstościach. Gęstości kul są podane.

Wersja do wykonania

Wykonaj ćwiczenie dla kul ................................................. i dla odległości między fotodiodami około
....... centymetrów. (Im większa odległość tym wyraźniej widać efekt oporu powietrza). Dopasować
prostą ekstrapolacji metodą:

Graficzną
Najmniejszych kwadratów – obliczenia ręczne
Najmniejszych kwadratów – zaimplementowana w kalkulatorze
Najmniejszych kwadratów – przy pomocy komputera

podpis

9-5

4

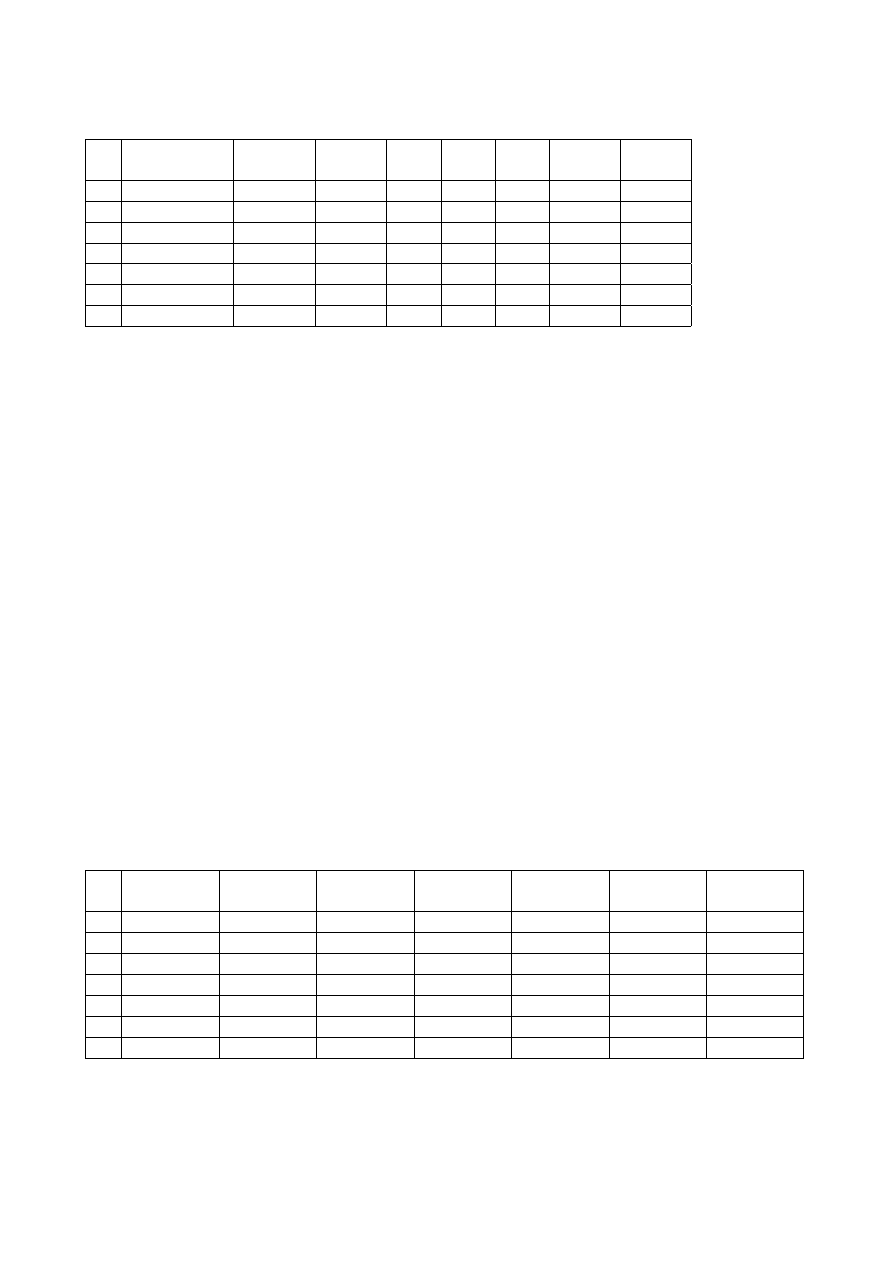
Wyniki pomiarów

Tabela 1a: Własności kul oraz zapis odległości (przedłużeniem jest tabela na dole strony)

Nr

Materiał kuli

gęstość ρ

1/ρ

x

1

x

2

x

3

x

2

− x

1

x

3

− x

2

[g/cm

3

]

[g/cm

3

]

[mm]

[mm]

[mm]

[mm]

[mm]

1
2
3
4
5
6
7

5

Opracowanie wyników

1. Zestaw rezultaty pomiarów i obliczeń w tabelach 1a – 1b.

2. Wykonaj wykres a w funkcji 1/ρ. (Skali osi pionowej nie należy zaczynać od zera!)

3. Dopasuj prostą ekstrapolacji metodą wyznaczoną przez prowadzącego.

4. Podaj wartość przyspieszenia ziemskiego jako składnik stały równania prostej

g = ............................. ......

5. W przypadku użycia metody najmniejszych kwadratów podaj niepewność g jako odchylenie

standardowe składnika stałego równania prostej.

u(g) = .......................... ........

6. Oblicz niepewność rozszerzoną dla wartości współczynnika rozszerzenia k = 3,

U (g) = k · u(g) = ............................ ......

7. Czy uzyskana wartość g jest zgodna, w granicach niepewności rozszerzonej, z wartością tablico-

wą?

Tabela 1b: Zapis czasów i wartość pozorna przyspieszenia ziemskiego (przedłużenie tabeli
z góry strony)

Nr

t

1

t

2

t

3

t

2

− t

1

t

3

− t

2

t

3

− t

1

a

[ms]

[ms]

[ms]

[ms]

[ms]

[ms]

[ms]

1
2
3
4
5
6
7

9-6

Miejsce na wykres a

1

ρ

Wnioski:

Uwagi prowadzącego:

Ocena za opracowanie wyników:

ocena

podpis

6

Załączniki: dodatkowe wykresy, obliczenia, ewentualna poprawa.

9-7