1. CIĄGI LICZBOWE

1.1. Definicja ciągu i ciągu liczbowego

Definicja 1.1.

• Ciągiem nieskończonym nazywamy każdą funkcję określoną na zbiorze liczb naturalnych.
• Jeśli funkcja a jest ciągiem, to wartości tej funkcji nazywamy wyrazami ciągu i oznaczamy

przez

a

n

def

= a(n),

n

∈ N.

• Ciąg o wyrazach a

n

zapisujemy symbolem

(a

n

) lub a

1

, a

2

, . . . ,

zaś zbiór wartości tego ciągu oznaczamy przez

{a

n

}

n

∈N

.

Ciągi, których wszystkie wyrazy są liczbami nazywamy ciągami liczbowymi (np. ciągi liczbowe

o wyrazach rzeczywistych, ciągi liczbowe o wyrazach zespolonych).

Ciągi, których wszystkie wyrazy są funkcjami nazywamy ciągami funkcyjnymi.

1.2. Własności ciągów liczbowych o wyrazach

rzeczywistych: monotoniczność, ograniczo-

ność, zbieżność.

Definicja 1.2.

• Ciąg (a

n

) jest rosnący

def

⇔

V

n

∈N

a

n+1

> a

n

.

• Ciąg (a

n

) jest niemalejący

def

⇔

V

n

∈N

a

n+1

­ a

n

.

• Ciąg (a

n

) jest malejący

def

⇔

V

n

∈N

a

n+1

< a

n

.

• Ciąg (a

n

) jest nierosnący

def

⇔

V

n

∈N

a

n+1

¬ a

n

.

Twierdzenie 1.3.

Jeśli a

n

> 0 dla n

∈ N, to

ciąg (a

n

) jest rosnący

⇔

V

n

∈N

a

n+1

a

n

> 1.

Ćwiczenie 1.4. Sformułować analogiczne własności dla ciągu niemalejącego, malejącego i nierosną-
cego.

Definicja 1.5.

• Ciąg (a

n

) jest ograniczony z dołu

def

⇔

W

m

∈R

V

n

∈N

a

n

­ m.

• Ciąg (a

n

) jest ograniczony z góry

def

⇔

W

M

∈R

V

n

∈N

a

n

¬ M.

1

1. CIĄGI LICZBOWE

2

• Ciąg (a

n

) jest ograniczony

def

⇔ (a

n

) jest ograniczony z dołu i z góry.

Ćwiczenie 1.6. Zbadać własności ciągów o wyrazach ogólnych:

a) a

n

=

√

n;

c) a

n

=

(

−1)

n

n

−1

;

b) a

n

= (

−3)

n

;

d) a

n

=

1

n

2

+ 1

.

Definicja 1.7.

Ciąg liczbowy (a

n

) jest zbieżny do a

∈ R, gdy

V

ε>0

W

K

∈N

V

n

­K

|a

n

− a| < ε,

czyli

V

ε>0

W

K

∈N

V

n

­K

a

− ε < a

n

< a + ε.

Liczbę a nazywamy granicą właściwą ciągu (a

n

) i zapisujemy

lim

n

→∞

a

n

= a lub a

n

→ a.

Przykład 1.8. Wykazać, że zachodzą równości:

a) lim

n

→∞

1

n

= 0;

b) lim

n

→∞

1

n

3

= 0.

Definicja 1.9.

• Mówimy, że ciąg (a

n

) jest rozbieżny do +

∞ i zapisujemy

lim

n

→∞

a

n

= +

∞,

gdy

V

ε>0

W

K

∈N

V

n

­K

a

n

> ε.

• Mówimy, że ciąg (a

n

) jest rozbieżny do

−∞ i zapisujemy

lim

n

→∞

a

n

=

−∞),

gdy

V

ε>0

W

K

∈N

V

n

­K

a

n

<

−ε.

• Mówimy, że ciąg (a

n

) jest rozbieżny, gdy nie posiada granicy (właściwej lub niewłaściwej).

Przykład 1.10. Wykazać, że lim

n

→∞

n

2

= +

∞.

Twierdzenie 1.11.

Każdy ciąg posiada conajwyżej jedną granicę (właściwą lub niewłaściwą).

Ćwiczenie 1.12. Wykazać, że:

a) lim

n

→∞

a

n

=

±∞ ⇒ lim

n

→∞

1

a

n

= 0;

{

1

±∞

= 0

}

1. CIĄGI LICZBOWE

3

b) lim

n

→∞

a

n

= 0

⇒ lim

n

→∞

1

a

n

=

(

+

∞, gdy a

n

> 0 dla prawie wszystkich n

∈ N,

−∞, gdy a

n

< 0 dla prawie wszystkich n

∈ N.

{

1

0

+

= +

∞}

{

1

0

−

=

−∞}

Ćwiczenie 1.13. Wykazać, że

a) lim

n

→∞

q

n

=



















nie istnieje dla q

¬ −1,

0

dla q

∈ (−1; 1),

1

dla q = 1,

+

∞

dla q > 1.

b) lim

n

→∞

n

α

=











0

dla α < 0,

1

dla α = 0,

+

∞ dla α > 0.

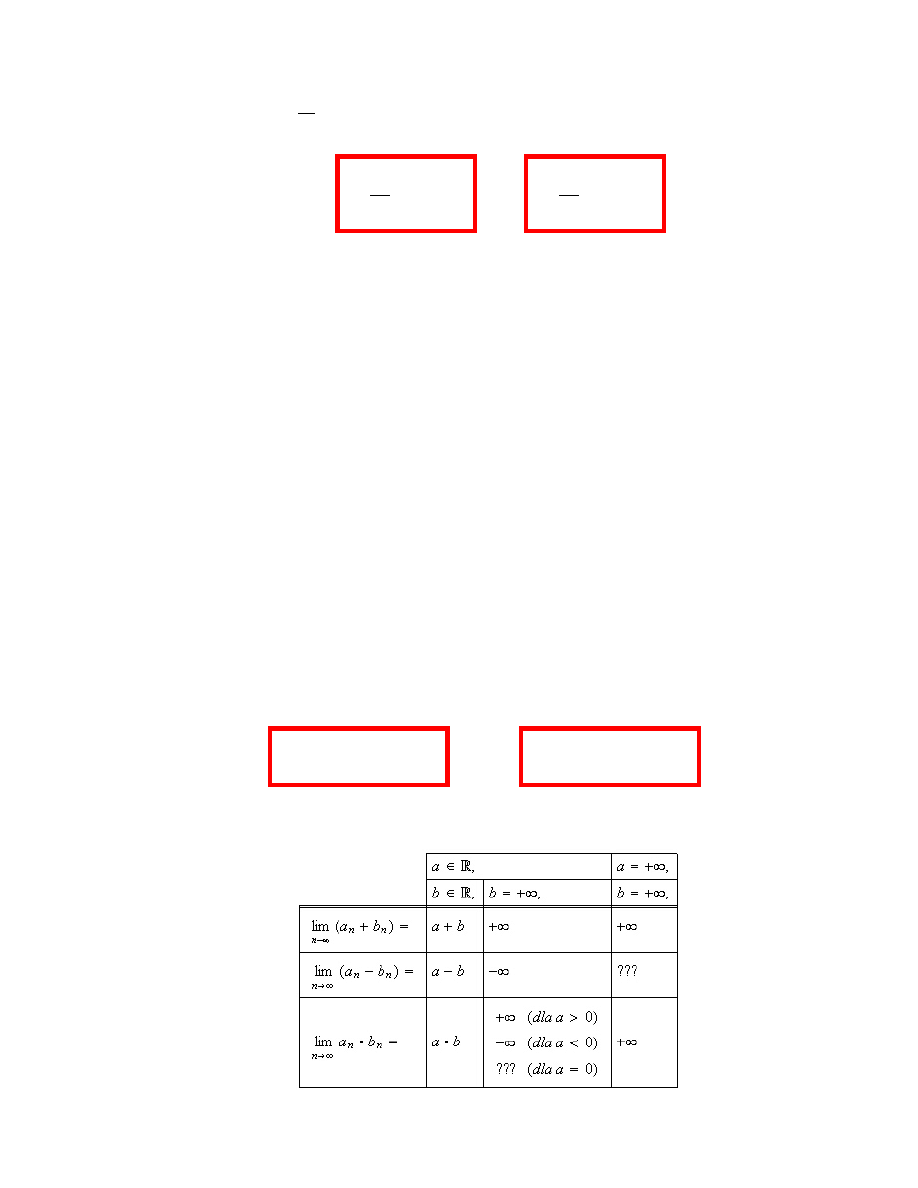
1.3. Arytmetyka granic

Twierdzenie 1.14.

Jeśli lim

n

→∞

a

n

= a oraz c

6= 0, to

lim

n

→∞

c

· a

n

=

(

c

· a, gdy a ∈ R,

±∞, gdy a = ±∞.

W szczególności dla c > 0 mamy

{c · (+∞) = +∞}

oraz

{c · (−∞) = −∞}

Twierdzenie 1.15.

Jeśli lim

n

→∞

a

n

= a oraz

lim

n

→∞

b

n

= b, to

1. CIĄGI LICZBOWE

4

Twierdzenie 1.16.

Jeśli lim

n

→∞

a

n

= a,

lim

n

→∞

b

n

= b oraz b

n

6= 0 dla n ∈ N, to

Twierdzenie 1.17.

Jeśli lim

n

→∞

a

n

= a,

lim

n

→∞

b

n

= b oraz b

n

­ 0 dla n ∈ N, to

Symbole nieoznaczone:

∞ − ∞ 0 · ∞

∞
∞

0

0

0

0

∞

0

1

∞

1.4.

Twierdzenia

o

ciągach

zbieżnych

i roz-

bieżnych

Definicja 1.18.

Podciągiem ciągu (a

n

) nazywamy każdy ciąg (a

k

n

), gdzie (k

n

) jest dowolnym ro-

snącym ciągiem liczb naturalnych.

Np. Podciągami ciągu (a

n

) są ciągi:

a

1

, a

3

, a

5

, . . .

a

2

, a

4

, a

6

, . . .

a

3

, a

4

, a

5

, . . .

(a

2n

−1

)

∞

n=1

(a

2n

)

n

∈N

(a

n

)

n

­3

Twierdzenie 1.19.

Każdy podciąg ciągu zbieżnego jest zbieżny i ma tę samą granicę, co dany ciąg.

Przykład 1.20. Wykazać, że nie istnieją granice:

a) lim

n

→∞

(

−1)

n

;

b) lim

n

→∞

cos

nπ

2

.

Twierdzenie 1.21.

Jeśli ciąg liczbowy jest zbieżny, to jest ograniczony.

Uwaga 1.22. Twierdzenie odwrotne do Tw.1.21 nie jest prawdziwe.

Twierdzenie 1.23 (Bolzano-Weierstrassa).

Jeśli ciąg liczbowy jest ograniczony, to istnieje pod-

ciąg zbieżny. Jeśli ciąg liczbowy jest nieograniczony, to posiada podciąg rozbieżny do

−∞ lub +∞.

1. CIĄGI LICZBOWE

5

Twierdzenie 1.24.

Jeśli ciąg liczbowy jest ograniczony i monotoniczny, to jest zbieżny.

Lemat 1.25. Jeśli ciągi (a

n

), (b

n

) są zbieżne oraz

W

K

∈N

V

n

­K

a

n

¬ b

n

,

to lim

n

→∞

a

n

¬ lim

n

→∞

b

n

.

Twierdzenie 1.26 (o trzech ciągach).

Załóżmy,że

(

∗)

W

K

∈N

V

n

­K

a

n

¬ b

n

¬ c

n

,

1) Jeśli lim

n

→∞

a

n

= lim

n

→∞

c

n

= a, to istnieje granica ciągu (b

n

), przy czym lim

n

→∞

b

n

= a.

2) Jeśli lim

n

→∞

a

n

= +

∞, to lim

n

→∞

b

n

= +

∞.

3) Jeśli lim

n

→∞

c

n

=

−∞, to lim

n

→∞

b

n

=

−∞.

1.5. Zbieżność pewnych ciągów specjalnych.

Liczba

e.

Twierdzenie 1.27.

1) lim

n

→∞

n

√

n = 1.

2) lim

n

→∞

n

√

a = 1.

3) Jeśli a

n

­ 0 dla każdego n ∈ N oraz lim

n

→∞

a

n

= a > 0, to lim

n

→∞

n

√

a

n

= 1.

Uwaga 1.28. Tw. 1.27 3) nie zachodzi w przypadku, gdy a = +

∞ lub a = 0.

Twierdzenie 1.29.

Ciąg a

n

= (1 +

1

n

)

n

dla n

∈ N jest ograniczony i monotoniczny.

Definicja 1.30.

Liczbą e nazywamy granicę ciągu (1 +

1

n

)

n

, n

∈ N.

Twierdzenie 1.31.

a)

∗

lim

n

→∞

n

X

k=0

1

k!

= e.

b) Liczba e jest liczbą niewymierną.

e = 2, 7182818284 . . .

Twierdzenie 1.32.

Jeśli a

n

6= 0 dla każdego n ∈ N oraz lim

n

→∞

a

n

=

±∞, to lim

n

→∞

(1 +

1

a

n

)

a

n

= e.

Definicja 1.33.

Logarytm o podstawie równej e nazywamy logarytmem naturalnym i oznaczamy

symbolem ln.

ln x

def

= log

a

x dla x > 0

1. CIĄGI LICZBOWE

6

1.6. Zbiory ograniczone na prostej. Kresy górny

i dolny.

Definicja 1.34.

Niech E

⊂ R, E 6= ∅.

• Liczbę M

0

∈ E taką, że

∧

x

∈E

x

¬ M

0

nazywamy elementem największym w zbiorze E i oznaczamy przez max E.

• Liczbę m

0

∈ E taką, że

∧

x

∈E

x

­ m

0

nazywamy elementem najmniejszym w zbiorze E i oznaczamy przez min E.

Definicja 1.35.

Niech E

⊂ R, E 6= ∅.

• Zbiór E jest ograniczony z góry, gdy

∨

M

∈R

∧

x

∈E

x

¬ M.

Lczbę M nazywamy ograniczeniem górnym zbioru E.

• Zbiór E jest ograniczony z dołu, gdy

∨

m

∈R

∧

x

∈E

x

­ m.

Liczbę m nazywamy ograniczeniem dolnym zbioru E.

• Zbiór E jest ograniczony, gdy zbiór E jest ograniczony z góry i z dołu.

Definicja 1.36.

Niech E

⊂ R, E 6= ∅.

• Jeśli zbiór E jest ograniczony z góry, to liczbę M ∈ R taką, że

(1)

∧

x

∈E

x

¬ M,

(2)

∧

M

1

<M

∨

x

∈E

x > M

1

nazywamy kresem górnym zbioru E i oznaczamy przez sup E.

(Liczba sup E jest najmniejszym ograniczeniem górnym zbioru E.)

W przypadku gdy E nie jest ograniczony z góry przyjmujemy sup E = +

∞.

• Jeśli zbiór E jest ograniczony z dołu, liczbę m ∈ R taką, że

(1)

∧

x

∈E

x

­ m,

(2)

∧

m

1

>m

∨

x

∈E

x < m

1

nazywamy kresem dolnym zbioru E i oznaczamy przez inf E.

(Liczba inf E jest największym ograniczeniem dolnym zbioru E.)

W przypadku gdy E nie jest ograniczony z dołu przyjmujemy inf E =

−∞.

Twierdzenie 1.37.

Każdy niepusty zbiór E

⊂ R posiada kresy górny i dolny, które należą do zbioru

R

.

1. CIĄGI LICZBOWE

7

Twierdzenie 1.38.

a) Jeśli ciąg (a

n

) jest niemalejący, to

sup

{a

n

: n

∈ N} = lim

n

→∞

a

n

,

inf

{a

n

: n

∈ N} = a

1

.

b) Jeśli ciąg (a

n

) jest nierosnący, to

sup

{a

n

: n

∈ N} = a

1

,

inf

{a

n

: n

∈ N} = lim

n

→∞

a

n

.