KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Ćwiczenie 6
Zad. 6.1
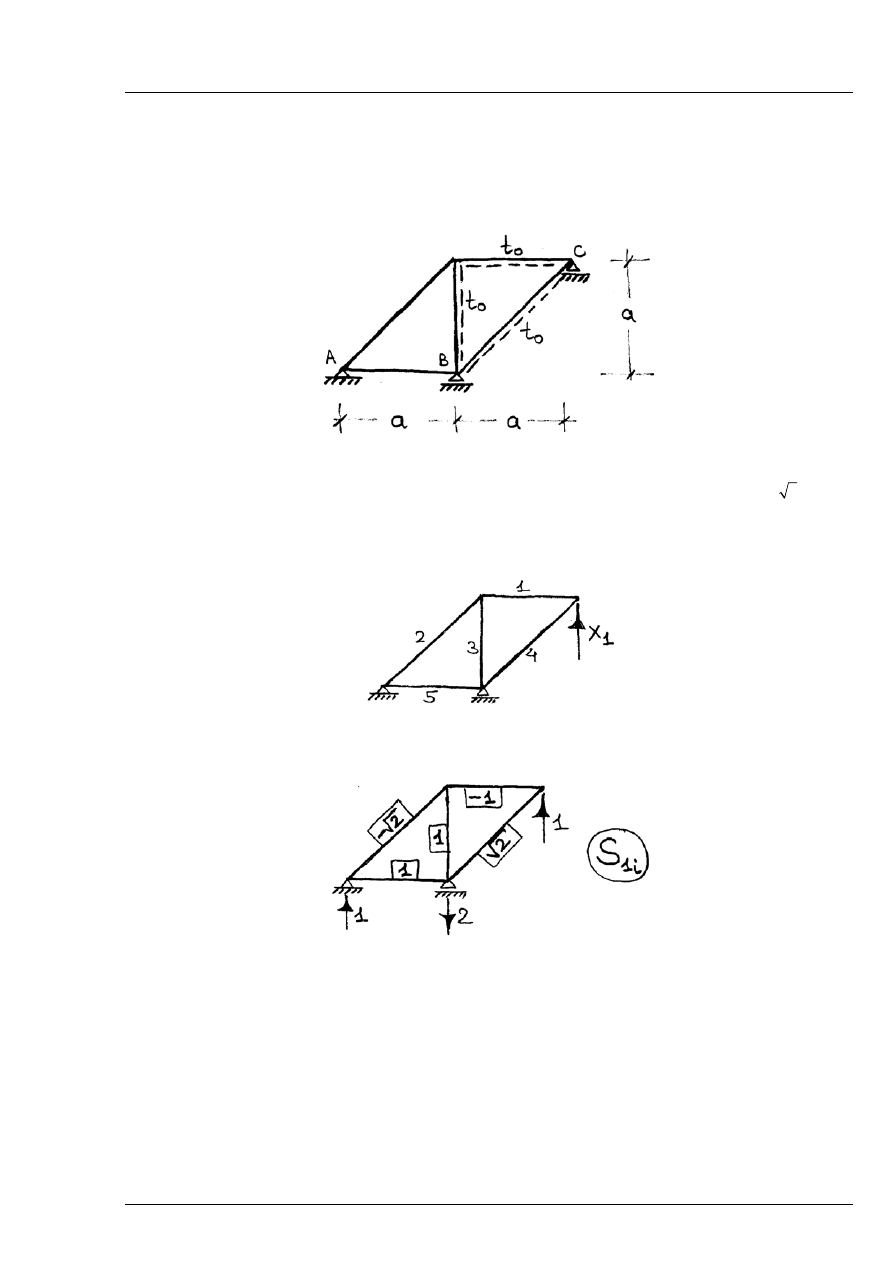
Obliczyć siły w prętach kratownicy powstałe na skutek równomiernego ogrzania zaznaczonych
prętów o wielkość względem temperatury montażu.
o
t
Rys. 6.1.1
Pola przekrojów prętów poziomych i pionowych równe są
A
, prętów ukośnych - równe
2
A
.
Dane :
4
1
30
2 10 [deg ]
7000
3 [ ]
o
o
t
t
C
EA
kN
a
α
−
−
=
= ⋅
=
= m
Układ podstawowy metody sił (na rysunku podana numeracja prętów):
Rys. 6.1.2
Siły w prętach układu podstawowego wywołane obciążeniem
1
1
X
=
Rys. 6.1.3
C16-2005-cw06
44
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
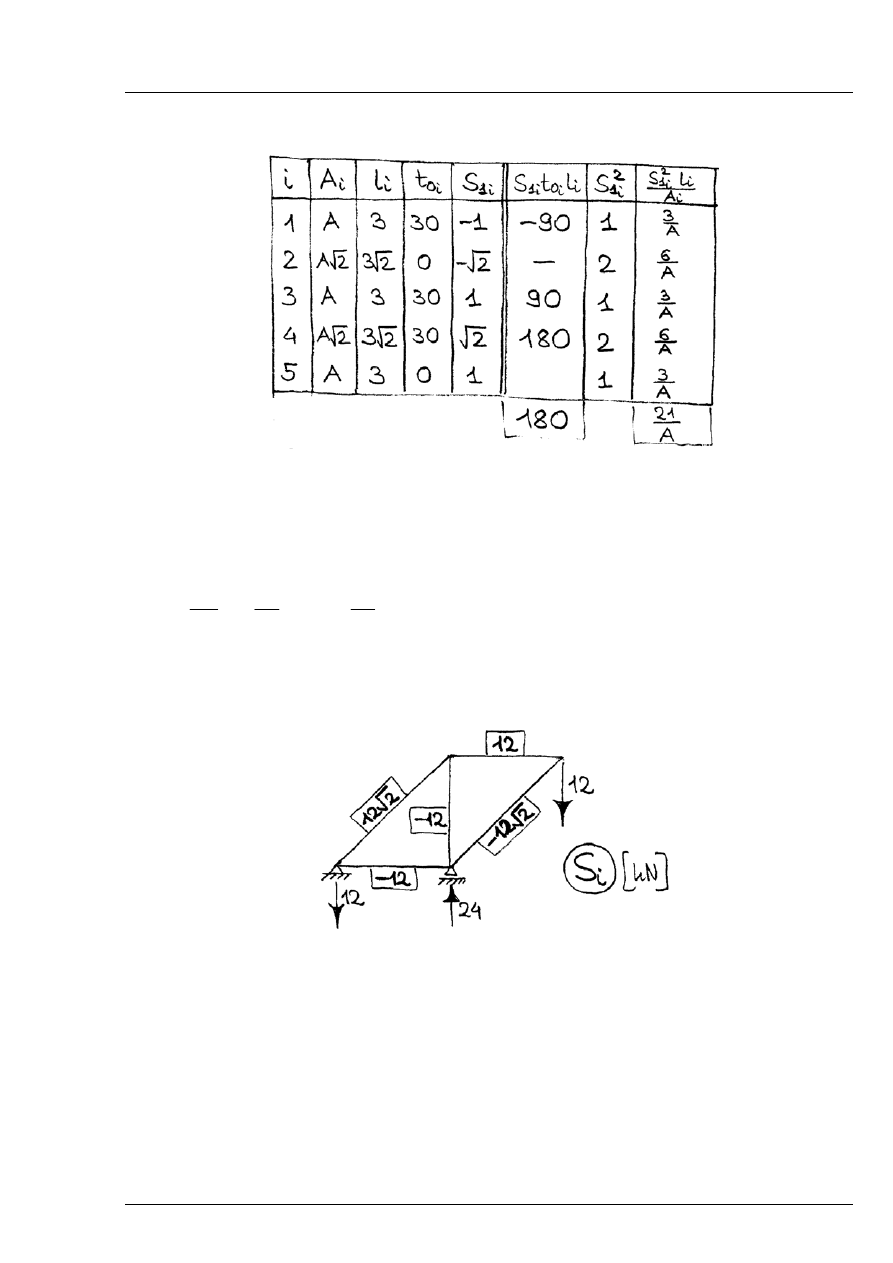
Przemieszczenia w układzie podstawowym (obliczenia w tabelce):
Rys. 5.1.4
Przemieszczenie pionowe w punkcie C wywołane równomiernym ogrzaniem:
5
4
10
1
1
2 10
180 0,036 [ ]
i
ti
oi i
i
S
t l
δ
α
−
=
=
⋅
⋅
= ⋅
⋅
=
∑
m
Przemieszczenie pionowe w punkcie C wywołane obciążeniem
1
1
X
=
2
5
1
11
1
21
0,003
i
i
i
i
S
m
l
EA
EA
kN
δ
=
⎡
=
⋅ =
=
⎢⎣ ⎦
∑
⎤
⎥
Z równania zgodności przemieszczeń
1
10
11
1
0
X
δ
δ
δ
=
+
=
otrzymujemy
1
12 [
]
X
kN
= −
.
Rozwiązanie:
Rys. 6.1.5
Inny sposób:
0
1
i
i
i
S
S
S
X
=
+
⋅
1
W przypadku oddziaływania pozastatycznego (temperatury) zachodzi
, więc
0
oi
S
=
1
1
1
12
[
]
i
i
i
S
S
X
S
kN
=
⋅
= −
C16-2005-cw06
45
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Zad. 6.2
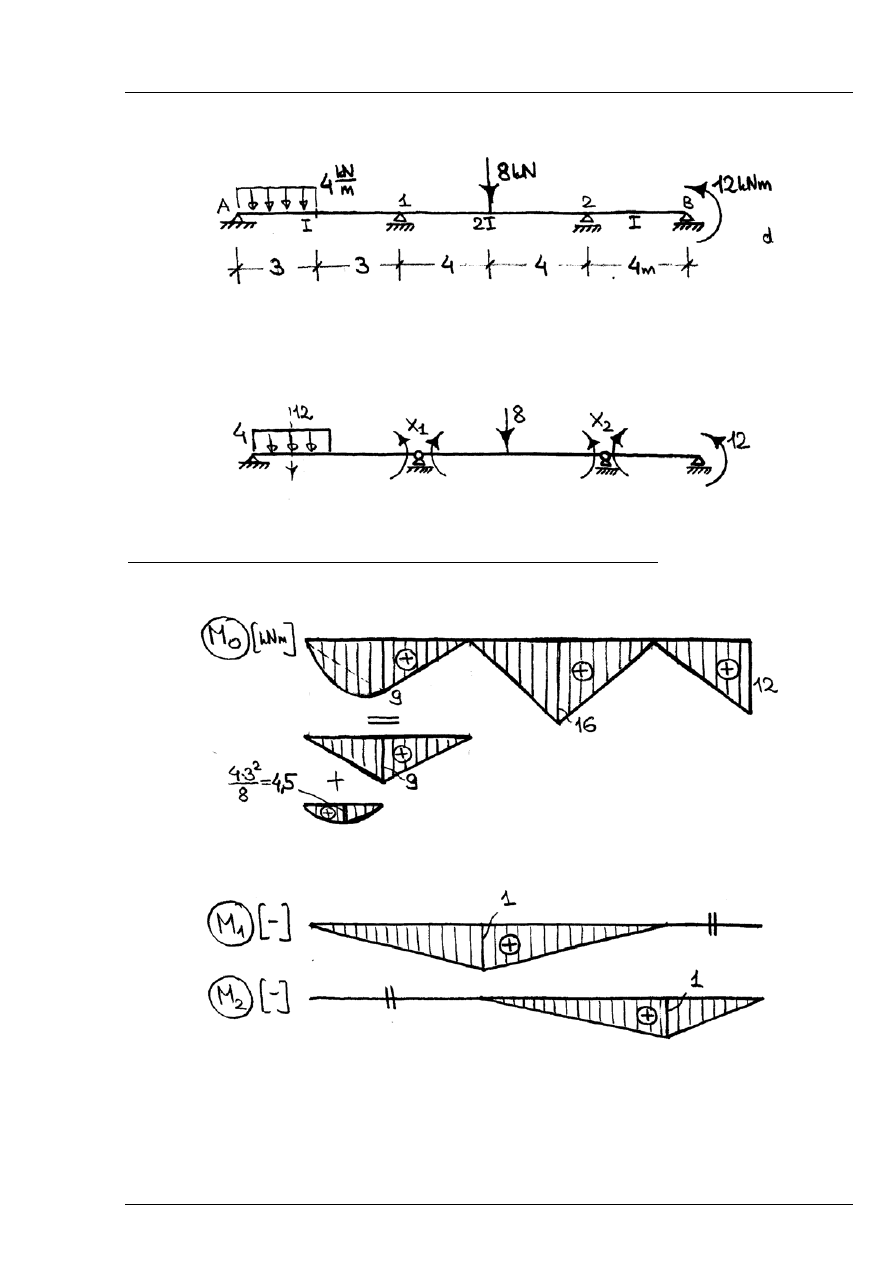
Sporządzić wykresy sił wewnętrznych w belce ciągłej.
Rys. 6.2.1
Układ jest dwukrotnie statycznie niewyznaczalny.
Układ podstawowy metody sił
Rys. 6.2.2
Momenty zginające w układzie podstawowym w poszczególnych stanach:
- stan obciążenia zewnętrznego
Rys. 6.2.3
- stany
oraz
:
1
1
X
=
2
1
X
=
Rys. 6.2.4
Równania zgodności przemieszczeń - układ równań (1):
C16-2005-cw06
46
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
- zmiana kąta obrotu w p.1 :
10
11
1
12
2
0
X
X
δ
δ
δ
+
⋅
+
⋅
=
- zmiana kąta obrotu w p.2 :
20
21
1
22
2
0
X
X
δ
δ
δ
+
⋅
+
⋅
=
Wyznaczenie współczynników układu równań:
1
10
1 1
1 2
9 1
1
1
31,75
6 9
3
8 16
2
2 3
2 4
2
2
o
L
M M
ds
EI
EI
EI
EI
δ
⎡
⎤
=
=
⋅ ⋅ ⋅ + ⋅ ⋅ ⋅
+
⋅ ⋅ ⋅
=
⎢
⎥
⎣
⎦
∫
2
20
1
1
1
1 1
1
24
8 16
4 12
1
2
2
2
2
3
o
L
M M
ds
EI
EI
EI
EI
δ
=
=
⋅ ⋅ ⋅ ⋅ +
⋅ ⋅ ⋅ ⋅ ⋅
∫
=
1
1
1
2
2
2
11
12
21
22
10
2
8
;
;
3
3
L
L
L
M M
M M
M M
ds
ds
ds
EI
EI
EI
EI
EI
EI
δ
δ
δ
δ
=
=
=
=
=
=
=
∫
∫
∫
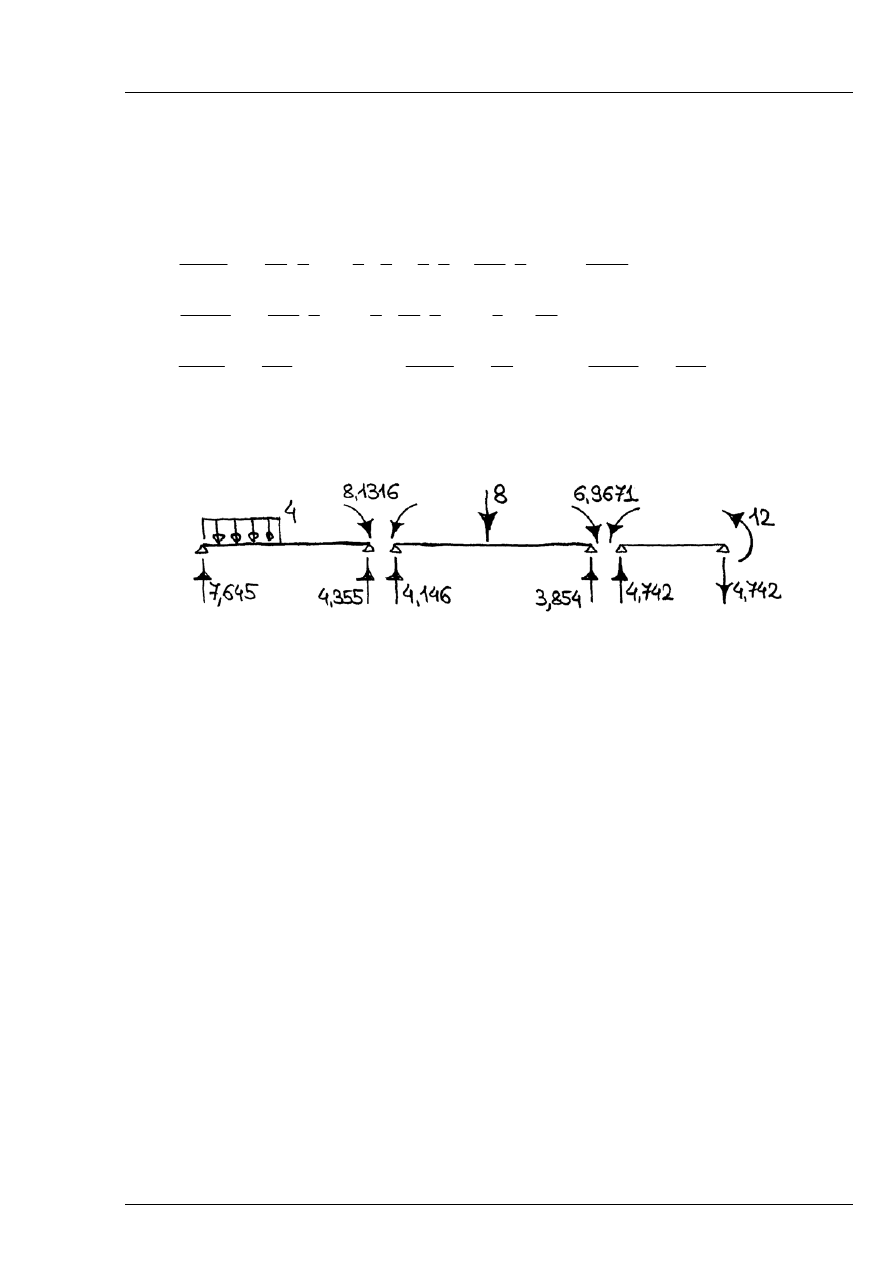
Z układu równań (1) otrzymujemy :
1
2
8,1316 [
]
6,9671[
]
X
kNm
X
kNm
= −
= −
Rozwiązanie:
Rys. 6.2.5
Wykresy - do samodzielnego wykonania.
C16-2005-cw06
47
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Zad. 6.3
Sporządzić wykres momentów zginających powstałych w układzie pod wpływem przemieszczenia
podpory B. Dane:
, ,
a
E
∆ I
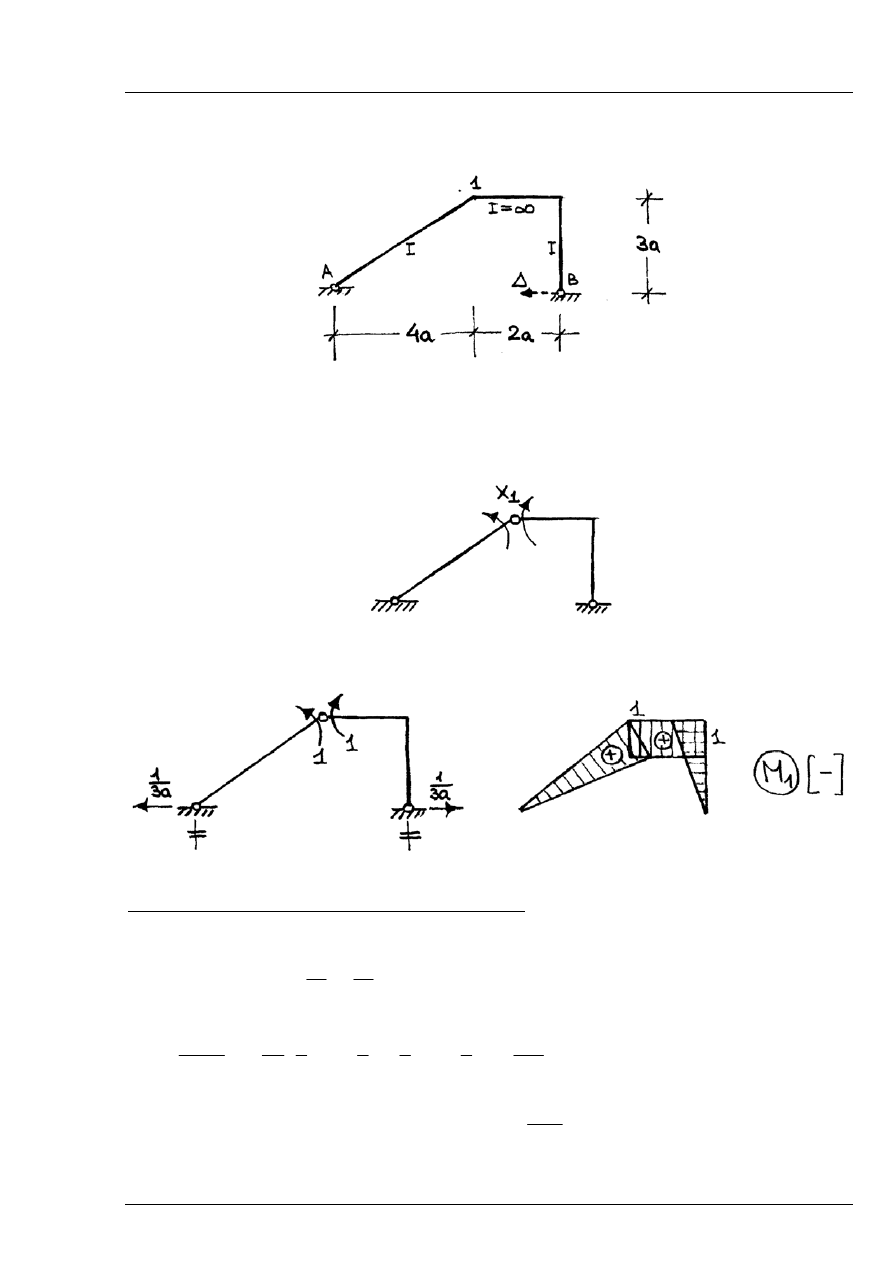
Rys. 6.3.1
Układ jest jednokrotnie statycznie niewyznaczalny.
Układ podstawowy metody sił przedstawiono na rys. 6.3.2 -
nadliczbową jest moment zginający w p.1
Rys. 6.3.2
Momenty zginające w układzie podstawowym wywołane działaniem nadliczbowej
1
1
X
=
Rys. 6.3.3
Przemieszczenia uogólnione w układzie podstawowym:
- zmiana kąta obrotu w p.1 wywołana przemieszczeniem podpory
10
1
1
3
3
i
i
i
R
a
a
δ
∆
⎛
⎞
= −
∆
= −∆ ⋅ −
=
⎜
⎟
⎝
⎠
∑
- zmiana kąta obrotu w p.1 wywołana działaniem nadliczbowej
1
1
X
=
1
1
11
1 1
2
1
2
8
5 1
1
3 1
1
2
3
2
3
3
L
M M
a
ds
a
a
EI
EI
EI
δ
⎛
⎞
=
=
⋅
⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ ⋅ =
⎜
⎟
⎝
⎠
∫
Z równania zgodności przemieszczeń obliczamy
1
2
8
EI
X
a
⋅ ∆
= −
C16-2005-cw06
48
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
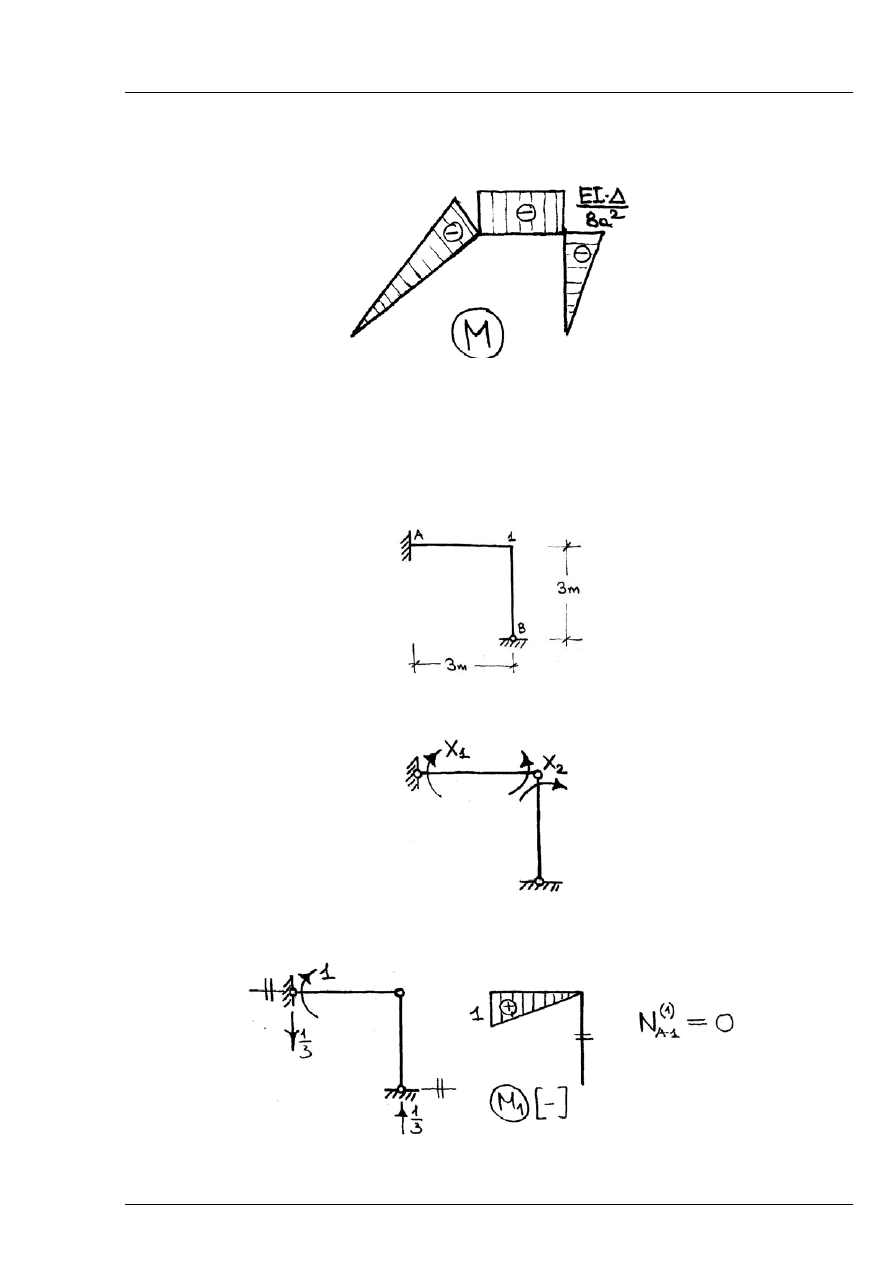
Rozwiązanie:
0
1
1
M
M
M X
=
+
0
M
−
momenty
wywołane oddziaływaniem zewnętrznym – zerowe
1
M
−
momenty
wywołane obciążeniem
1
1
X
=
Rys. 6.3.4
Zad. 6.4
Sporządzić wykresy sił wewnętrznych powstałych w układzie ramowym na skutek wmontowania
pręta A-1 dłuższego o
. Przyjąć
3
l
cm
∆ =
2
1400
EI
kNm
const
=
=
Rys. 6.4.1
Stopień statycznej niewyznaczalności (n=2).
Układ podstawowy metody sił:
Rys. 6.4.2
Układ podstawowy poddany działaniu nadliczbowej
1
1
X
=
Rys. 6.4.3
C16-2005-cw06
49
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
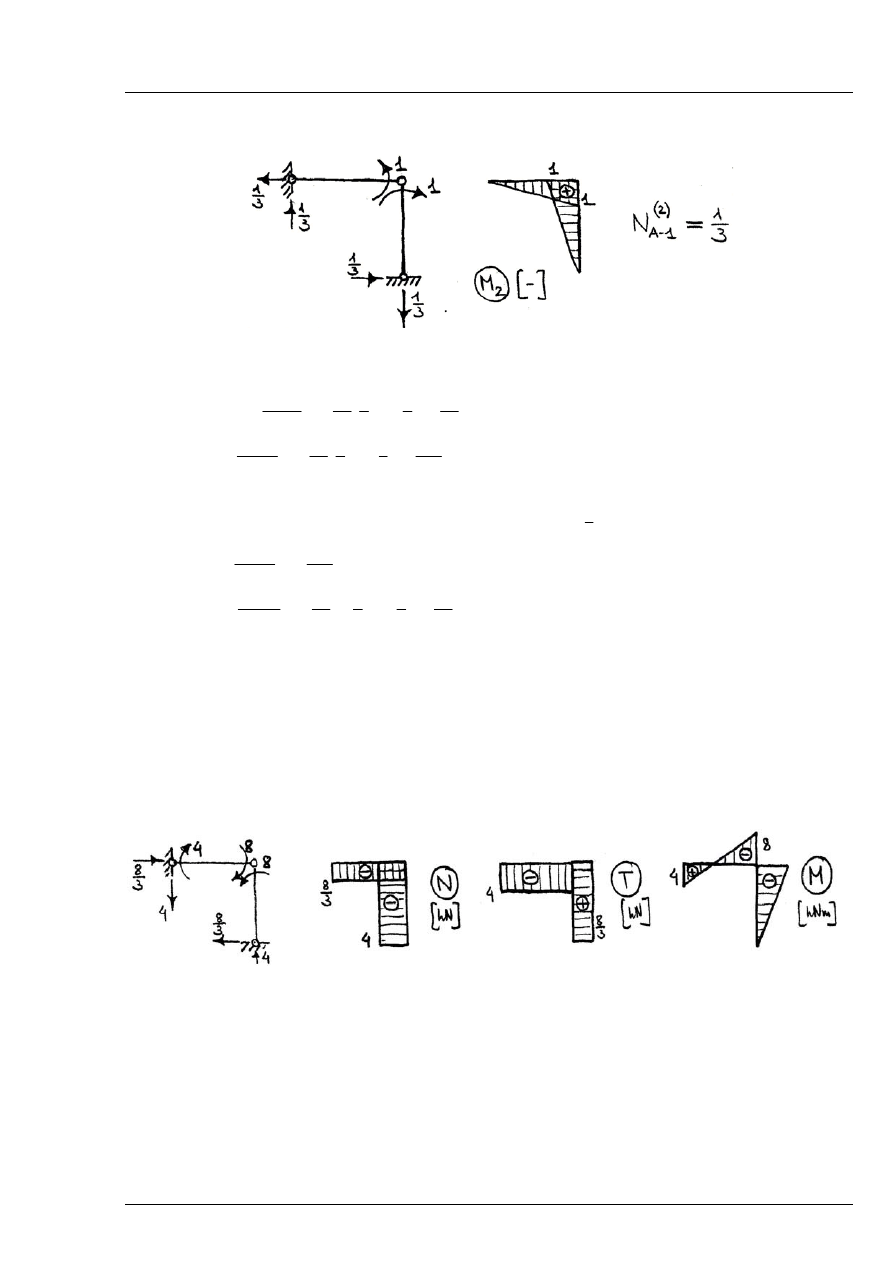
Układ podstawowy poddany działaniu nadliczbowej
2
1
X
=
Rys. 6.4.4
Kąt obrotu w p. A w poszczególnych stanach:
- oddziaływanie zewnętrzne (imperfekcja):
(1)
10
1
0
A
l N
δ
−
= ∆ ⋅
=
- stan
:
1
1
X
=
1
1
11
1 1
2
1
1 3
1
2
3
L
M M
ds
EI
EI
EI
δ =
=
⋅ ⋅ ⋅ ⋅ ⋅
∫
=
-
:
2
1
X
=
1
2
12
1 1
1
1
1 3
1
2
3
2
L
M M
ds
EI
EI
EI
δ =
=
⋅ ⋅ ⋅ ⋅ ⋅ =
∫
Zmiany katów obrotu p. 1 w poszczególnych stanach
- oddziaływanie zewnętrzne (imperfekcja)
(2)
20
1
1
0,03
0,01
3
A
l N
m
δ
−
= ∆ ⋅
=
⋅ =
-
:
1
1
X
=
2
1
21
1
2
L
M M
ds
EI
EI
δ =
=
∫
-
:
2
1
X
=
2
2
22
1
1
2
2
2
3 1
1
2
3
L
M M
ds
EI
EI
EI
δ =
=
⋅ ⋅ ⋅ ⋅ ⋅ ⋅
∫
=
0
Równania zgodności przemieszczeń:
(1)
10
11
1
12
2
1
2
0
2
X
X
X
X
δ
δ
δ
+
⋅
+
⋅
=
⇒
+
=
(2)
20
21
1
22
2
1
2
0
4
X
X
X
X
28
δ
δ
δ
+
⋅
+
⋅
=
⇒
+
= −
Stąd
1
2
4
,
8
X
kNm
X
kNm
=
= −
Rozwiązanie:
układ podstawowy poddany działaniu nadliczbowych (brak zewnętrznego obciążenia czynnego)
Rys.6.4.5
C16-2005-cw06
50
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Zad. 6.5 (*zadanie dodatkowe)
Obliczyć siły w prętach podpierających sztywną tarczę.
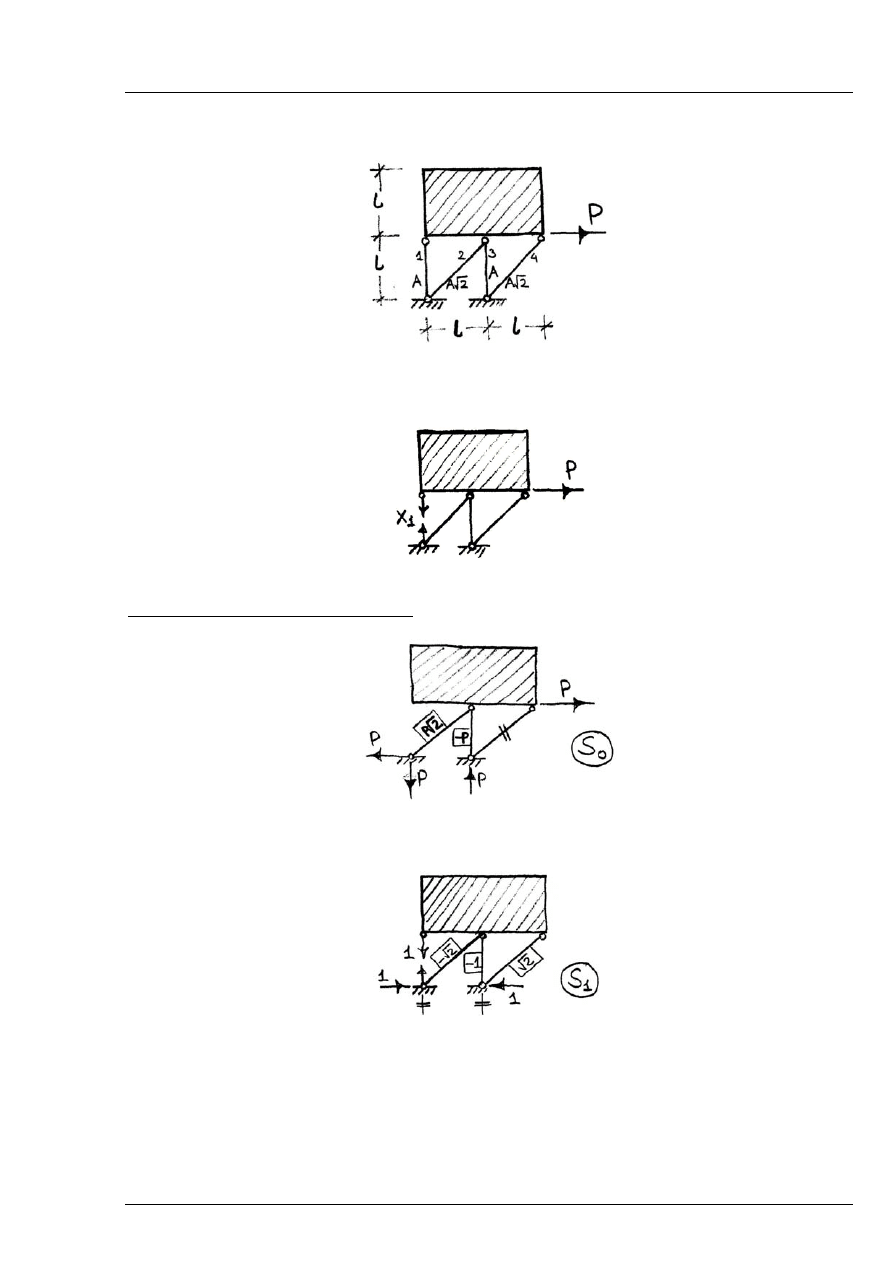
Rys. 6.5.1
Układ jest jednokrotnie statycznie niewyznaczalny.
Układ podstawowy metody sił:
Rys. 6.5.2
Rozwiązania w układzie podstawowym:
- siły w prętach układu podstawowego wywołane obciążeniem zewnętrznym
Rys. 6.5.3
- siły w prętach układu podstawowego wywołane obciążeniem
1
1
X
=
Rys. 6.5.4
C16-2005-cw06
51
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
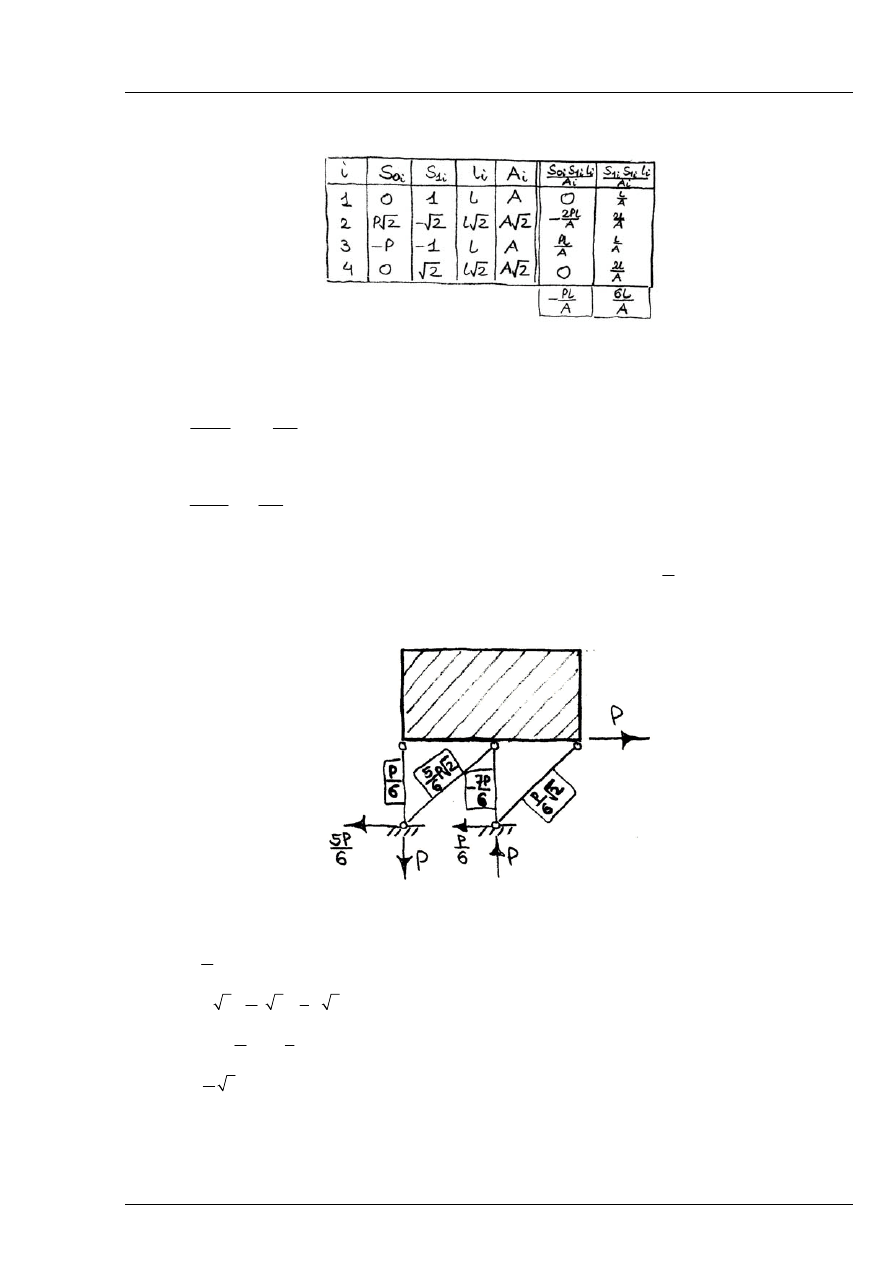
Obliczenie przemieszczeń w układzie podstawowym przy pomocy tabelki:
Rys. 6.5.5
Przemieszczenia w układzie podstawowym:
- wywołane obciążeniem zewnętrznym:
4
1
10
1
oi
i
i
i
i
S S
Pl
l
EA
EA
δ
=
=
=
∑
−
- wywołane nadliczbową
:
1
1
X
=
4
1
1
11
1
6
i
i
i
i
i
S S
l
l
EA
EA
δ
=
=
=
∑
Z równania zgodności przemieszczeń
1
10
11
1
0
X
δ
δ
δ
=
+
=
otrzymujemy
1
6
P
X
=
Rys. 6.5.6
Rozwiązanie otrzymujemy z superpozycji:
0
1
i
i
i
S
S
S
X
1
=
+
⋅
1
2
3
4
6
5
2
2
6
6
7
1
6
6
2
6
P
S
P
S
P
P
P
S
P
P
P
S
=
=
− ⋅
=
= − − ⋅ = −
=
2
C16-2005-cw06
52
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Zad. 6.6
Sporządzić wykresy
s
M
i
M
w dźwigarze załamanym w planie. Przyjąć
.
6
s
GI
EI
=
Rys. 6.6.1
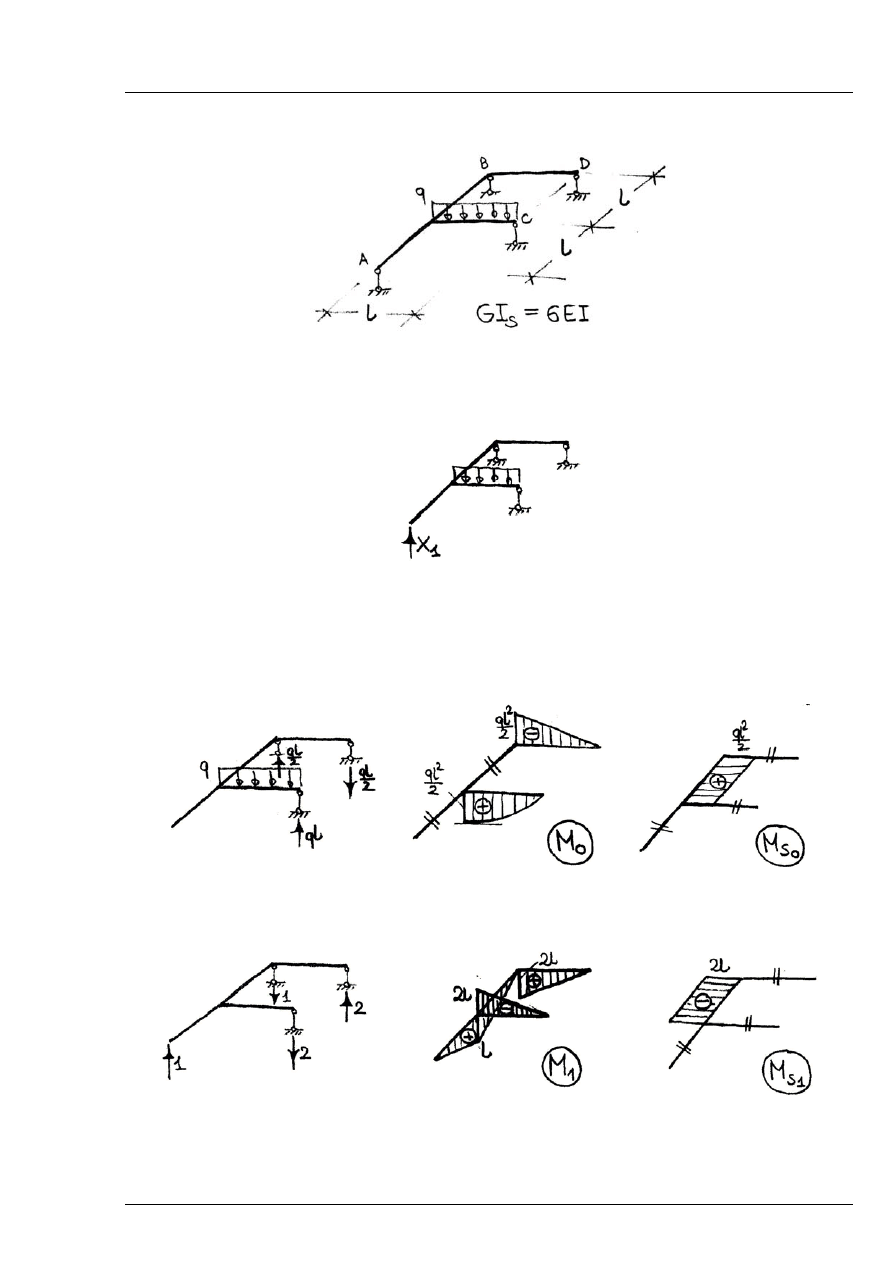
Układ jest jednokrotnie statycznie niewyznaczalny.
Układ podstawowy metody sił:
Rys. 6.6.2
Rozwiązanie w układzie podstawowym
Układ podstawowy poddany działaniu obciążenia zewnętrznego:
Rys. 6.6.3
Układ podstawowy poddany działaniu nadliczbowej
1
1
X
=
:
Rys. 6.6.4
C16-2005-cw06
53
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Przemieszczenia w układzie podstawowym:
- wywołane obciążeniem zewnętrznym:
( )
2
2
2
0
1
0
1
10
4
4
4
1
2
5
1
2
1
( 2 )
2
2
3 2
8
2
2
3
2
5
1
11
12 3
6
12
s
s
L
L
M M
M M
ql
ql
ql
ds
ds
l
l
l
l
l
l
EI
GI
EI
GI
gl
ql
ql
EI
EI
EI
δ
⎡
⎤
⎛
⎞
=
+
=
⋅
⋅
⋅ ⋅ ⋅ −
+ ⋅ ⋅ −
⋅ ⋅
+
⋅
⋅ ⋅ −
⎢
⎥
⎜
⎟
⎝
⎠
⎣
⎦
⎛
⎞
= −
+
−
= −
⋅
⎜
⎟
⎝
⎠
∫
∫
=
- wywołane nadliczbową
:
1
1
X
=
1
1
1
1
11
3
3
3
1
1
2
1
2
1
2
2
2
2
2
2
3
2
3
2 8
4
4
3 3
6
s
s
L
L
M M
M M
ds
ds
l l
l
l l
l
l l
l
EI
GI
EI
GI
l
l
l
EI
EI
EI
δ
⎡
⎤
=
+
=
⋅ ⋅ ⋅ ⋅ ⋅
+ ⋅ ⋅ ⋅ ⋅ ⋅
+
⋅ ⋅ ⋅ =
⎢
⎥
⎣
⎦
⎛
⎞
=
+
+
=
⎜
⎟
⎝
⎠
∫
∫
2
Z równania zgodności przemieszczeń
1
10
11
1
0
X
δ
δ
δ
=
+
=
otrzymujemy
1
11
48
X
ql
=
.
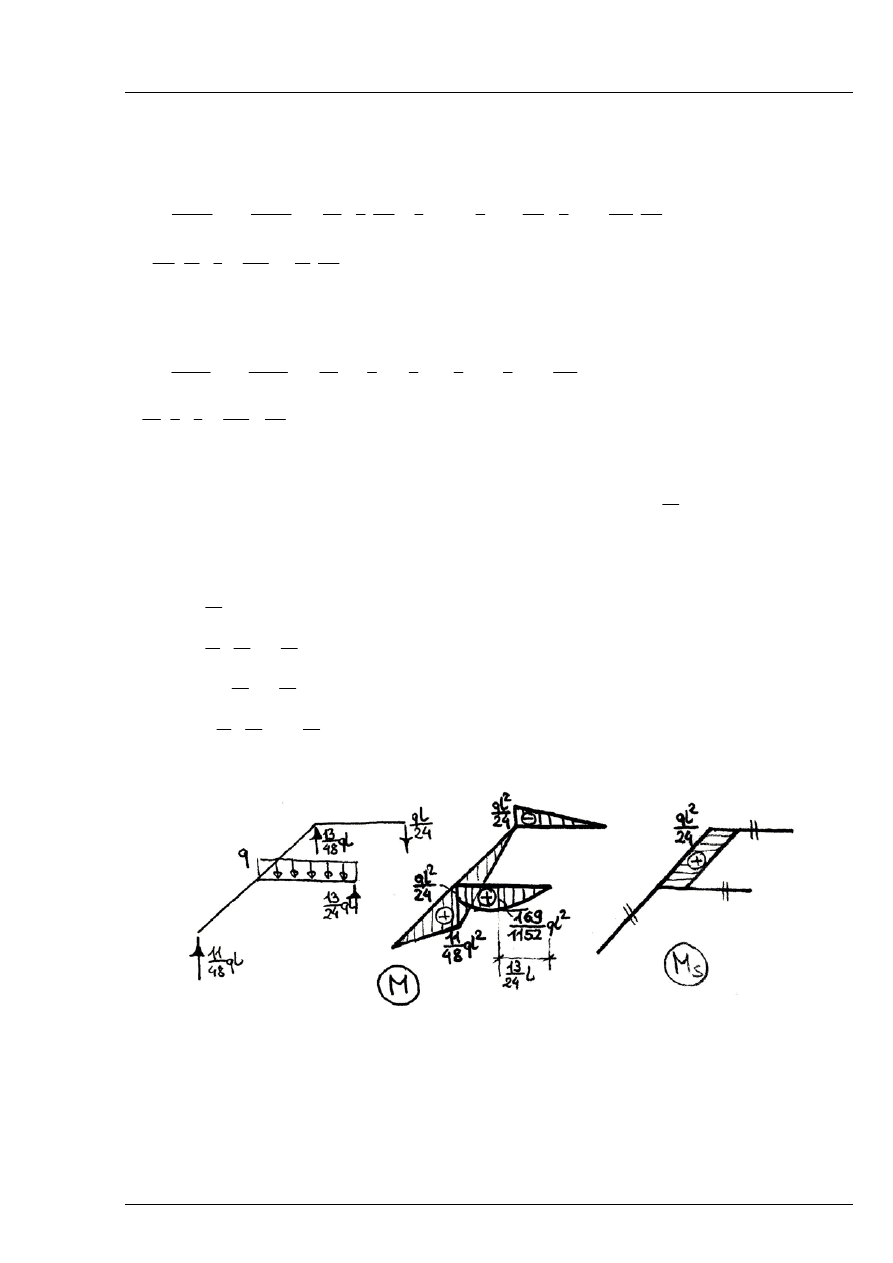
Reakcje podporowe uzyskujemy z superpozycji:
11
48
11
13
2
48
48
11
13
24
24
11
1
2
24
24
A
B
C
D
R
ql
ql
R
ql
q
R
ql
ql
ql
ql
R
ql
=
=
−
=
=
−
=
= −
+
= −
l
ql
Rozwiązanie:
Rys. 6.6.5
C16-2005-cw06
54
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
Zad. 6.7
Sporządzić wykresy
M
dla rusztu belkowego.
EI
const
=
.
Rys. 6.7.1
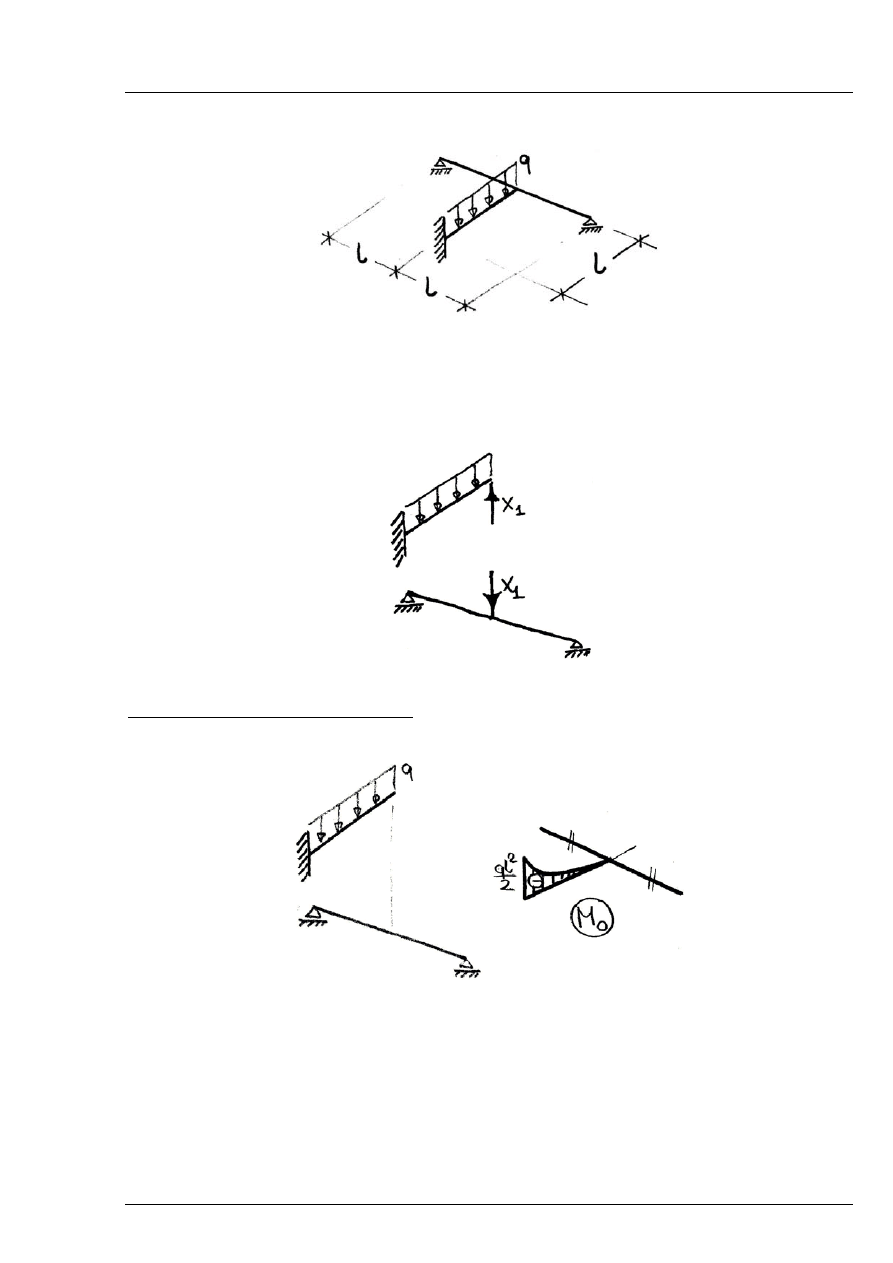
Układ jest jednokrotnie statycznie niewyznaczalny.
Układ podstawowy metody sił: rozdzielenie obu części układu, siła wzajemnego oddziaływania
(reakcja) jest nadliczbową
1
X
Rys. 6.7.2
Rozwiązanie w układzie podstawowym:
- układ podstawowy poddany działaniu obciążenia zewnętrznego
Rys. 6.7.3
C16-2005-cw06
55
KMB, WILiŚ, PG
MECHANIKA BUDOWLI I (C16)
Rok II, semestr IV (letni 2005)
Wykłady:
P. Iwicki, M. K. Jasina
Ćwiczenia:
M. Dudek, A. Kozakiewicz, T. Mikulski, M. Miśkiewicz, A. Sitarski, M. Skowronek, M. Szafrański, M. Zasada
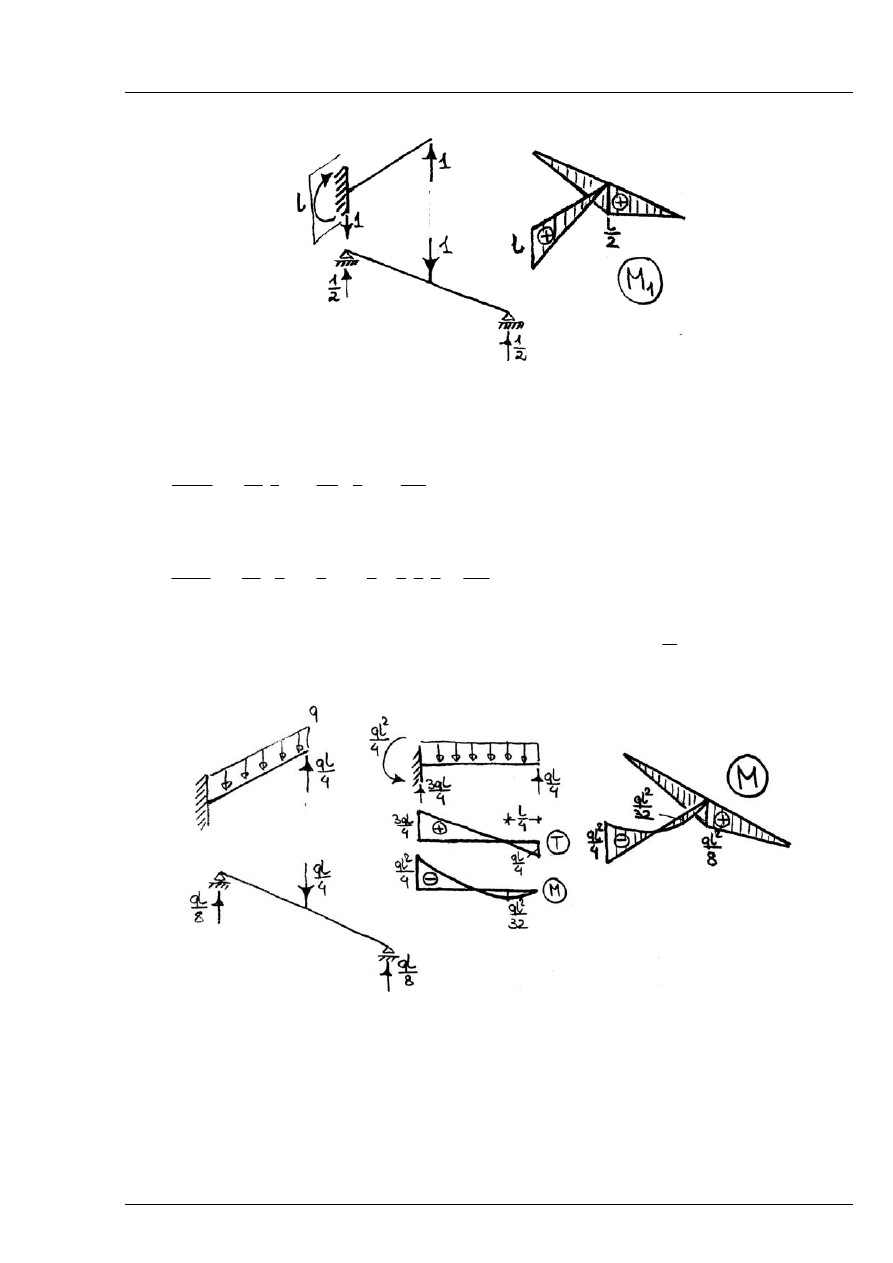
- układ podstawowy poddany działaniu nadliczbowej
1
1
X
=
Rys. 6.7.4
Przemieszczenia w układzie podstawowym:
- wywołane obciążeniem zewnętrznym:
2
4
0
1
10
1 1
3
3
2
4
8
L
M M
ql
ql
ds
l
l
EI
EI
EI
δ
⎛
⎞
=
=
⋅ ⋅ ⋅ −
⋅ ⋅ = −
⎜
⎟
⎝
⎠
∫
- wywołane nadliczbową
:
1
1
X
=
3
1
1
11
1
1
2
1
2
2
2
3
2
2 3 2
2
L
M M
l
l
l
ds
l l
l
l
EI
EI
EI
δ
⎡
⎤
=
=
⋅
⋅ ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ ⋅ ⋅
=
⎢
⎥
⎣
⎦
∫
Z równania zgodności przemieszczeń
1
10
11
1
0
X
δ
δ
δ
=
+
=
otrzymujemy
1
4
ql
X
=
.
Rozwiązanie:
Rys. 6.7.5
C16-2005-cw06
56
Document Outline