
1
Rachunek prawdopodobieństwa
1. Pojęcie prawdopodobieństwa.
2. Prawdopodobieństwo warunkowe. Niezależność zdarzeń. Schemat Bernoulli’ego. Prawdopodobieństwo
całkowite.
Literatura podstawowa
1. Z. Hellwig Elementy rachunku prawdopodobieństwa i statystyki matematycznej. Warszawa 1977.
2. W. Kordecki Rachunek prawdopodobieństwa i statystyka matematyczna. Definicje, twierdzenia,
wzory. Wrocław 2002.
3. H. Jasiulewicz, W. Kordecki Rachunek prawdopodobieństwa i statystyka matematyczna. Przykłady i
zadania. Wrocław 2002.
4. W. Krysicki, J. Bartos, W. Dyczka, K. Królikowska. M. Wasilewski Rachunek prawdopodobieństwa i
statystyka matematyczna w zadaniach. Część 1 i część 2. Warszawa 1986.
Zdarzenia i prawdopodobieństwa zdarzeń
Rachunek prawdopodobieństwa to dział matematyki zajmujący się badaniem zjawisk losowych. Ze
zjawiskami takimi mamy do czynienia, gdy wykonujemy np. doświadczenie, którego wyniku z góry nie znamy,
ale możemy je wielokrotnie powtarzać w tych samych warunkach. Dzięki temu jesteśmy w stanie przewidzieć
różne zakończenia tego doświadczenia i określić ich szanse.
Jeżeli np. wykonujemy doświadczenie polegające na rzucie monetą, to z góry nie wiemy, czy wypadnie orzeł
czy reszka. Jednak po wielu powtórzeniach tego doświadczenia możemy nabrać podejrzeń, że szanse
wypadnięcia orła są takie same jak wypadnięcia reszki, czyli mówimy, że każde z tych zjawisk zachodzi z
prawdopodobieństwem ½. Inne przykłady doświadczeń losowych: rzut kostką do gry, rozdanie kart, losowanie
toto-lotka, strzelanie do tarczy itp.
Rachunek prawdopodobieństwa zajmuje się też zjawiskami masowymi.
Np. interesuje nas, kto wygra wybory prezydenckie. Oczywiście wyniku z góry nie znamy, ale na podstawie
sondaży przedwyborczych możemy przewidzieć jakie są szanse każdego z kandydatów.
Widzimy więc, że z określaniem prawdopodobieństw różnych zdarzeń mamy do czynienia na co dzień.
Przestrzeń zdarzeń elementarnych
W każdej teorii istnieją pewne pojęcia pierwotne, czyli te, których się nie definiuje, np.
w arytmetyce – liczba, w geometrii – punkt, prosta, płaszczyzna.
Pojęciem pierwotnym w rachunku prawdopodobieństwa jest pojęcie:
przestrzeń zdarzeń elementarnych (zbiór zdarzeń elementarnych).
Oznaczamy ją literą Ω, a jej elementy zwane zdarzeniami elementarnymi oznaczać będziemy małą literą ω.
Przestrzeń zdarzeń elementarnych Ω
– jest to kompletna i rozłączna lista możliwych wyników rozważanego
doświadczenia losowego.
Przestrzeń zdarzeń elementarnych Ω może być zbiorem skończonym lub nieskończonym, przeliczalnym albo
nieprzeliczalnym.
W praktyce zainteresowani jesteśmy nie tyle pojedynczymi zdarzeniami elementarnymi, ale ich zbiorami, a
więc podzbiorami zbioru Ω.
Taką rodzinę podzbiorów Ω, którą wyróżniamy, nazywamy rodziną S podzbiorów przestrzeni zdarzeń
elementarnych ( tzw. zbiór zbiorów).

2
Zdarzeniami będziemy nazywać jedynie elementy rodziny
S.
Przykłady:
- rzucając jednokrotnie monetą: zdarzenia elementarne O i R, przestrzeń {O,R}
- rzucając dwukrotnie monetą zdarzenia np.: (O,R), (O,O), przestrzeń to: {(O,O); (O,R);
(R,O); (R,R)},
- losowanie totolotka zdarzenia to szóstki: (1,2,3,4,5,6), (1,3,23,21,43,5) ... ,
przestrzeń to 13 983 816 możliwych szóstek.
Silnia.
Symbol n! ( czytaj n –silnia) określamy rekurencyjnie:
1! = 1, n! = n · (n-1)!,
więc: n!= n · n · (n-1) · (n-2) · .....· 3 · 2 · 1 i przyjmujemy: 0! = 1.
Przykłady:
(1) 2! = 1 · 2 = 2
(2) 3! = 1 · 2 · 3 = 6
(3) 5! = 120
,
)...
2
)(
1
(
!
!
n
k
k
k
n
+
+
=
gdzie n > k
Symbol Newtona.
Przyjmijmy następującą definicję symbolu
k
n
(czytamy n nad k) gdzie
k
n
N
k
n
>
∈
,
,
zwanego symbolem
Newtona:
n
k
N
n
k
n
k
n
k
n
≤
≤
∈
−
=
0
,
,
)!
(
!
!
Uwaga:
1
0
=
=
n
n
n
n
k
gdzie
k
n
k
n
k
n
≤
≤
+
=
−
+
1
:
,
1
1
−
=
k
n
n
k
n
n
n
n
n
=
−
=
1
1
n
n
k
k
n
2
0
=
∑
=
Przykłady:
(1)
35
3
2
1
!
4
7
6
5
!
4
!
4
!
3
!
7
3
7
=
⋅
⋅
⋅
⋅
=
=
(2)
1
!
3
!
0
!
3
0
3
=
=
(3)
1
!
0
!
6
!
6
6
6
=
=
(4)
4
!
3
!
1
!
4
1
4
=
=
3
Algebra zdarzeń. Działania na zdarzeniach
Zdarzenie pewne – jest to podzbiór przestrzeni zdarzeń elementarnych Ω, zawierający wszystkie elementy tej
przestrzeni. Zdarzenie pewne oznaczamy tą samą literą Ω.
Zdarzenie niemożliwe
– jest to podzbiór pusty przestrzeni zdarzeń elementarnych Ω. Zdarzenie to będziemy
oznaczać symbolem
∅
.
Przykład:
Rzucając raz kostką do gry : zdarzenia elementarne: 1,2,3,4,5,6 ,
przestrzeń zdarzeń{1,2,3,4,5,6}
Przykłady zdarzeń:
A - wyrzucenie parzystej liczby oczek, A = { 2
,
4
,
6}
B - wyrzucenie co najwyżej 4 oczek, B = { 1, 2
,
3
,
4 }
C - wyrzucenie dokładnie 4 oczek, C = { 4 }
D - wyrzucenie co najmniej jednego oczka, D = { 1, 2
,
3
,
4
,
5
,
6} - zdarzenie pewne
F - wyrzucenie więcej niż 6 oczek, F =
∅
- zdarzenie niemożliwe
Zdarzenia losowe jako podzbiory przestrzeni Ω są zbiorami i będziemy je oznaczać literami A, B, C,... bądź
literami ze wskaźnikami: A
1
, A
2
,...
Relacje i działania na zdarzeniach są więc po prostu relacjami i działaniami na zbiorach.
1. Mówimy, że zdarzenie losowe A jest zawarte w zdarzeniu losowym B, jeśli każde zdarzenie
elementarne należące do A należy też do B (relacja implikacji). Oznaczamy to jako:
B
A
⊂
A
B
2. Sumą (alternatywą) dwu zdarzeń losowych A i B nazywamy zbiór złożony z tych i tylko tych zdarzeń
elementarnych, które należą co najmniej do jednego ze zdarzeń losowych A oraz B. Oznaczamy jako:
B
A
∪
A
B
Oczywiście suma dwóch zdarzeń jest również zdarzeniem, więc uogólniając ją na n składników,
otrzymamy:
i
n
i
n
A
A
A
A
C
U
1
2
1
...
=
=
∪
∪
∪
=
3. Iloczynem (koniunkcją) dwu zdarzeń losowych A oraz B nazywamy zbiór złożony z tych i tylko tych
zdarzeń elementarnych, które należą zarówno do A, jak i do B. Oznaczamy to:
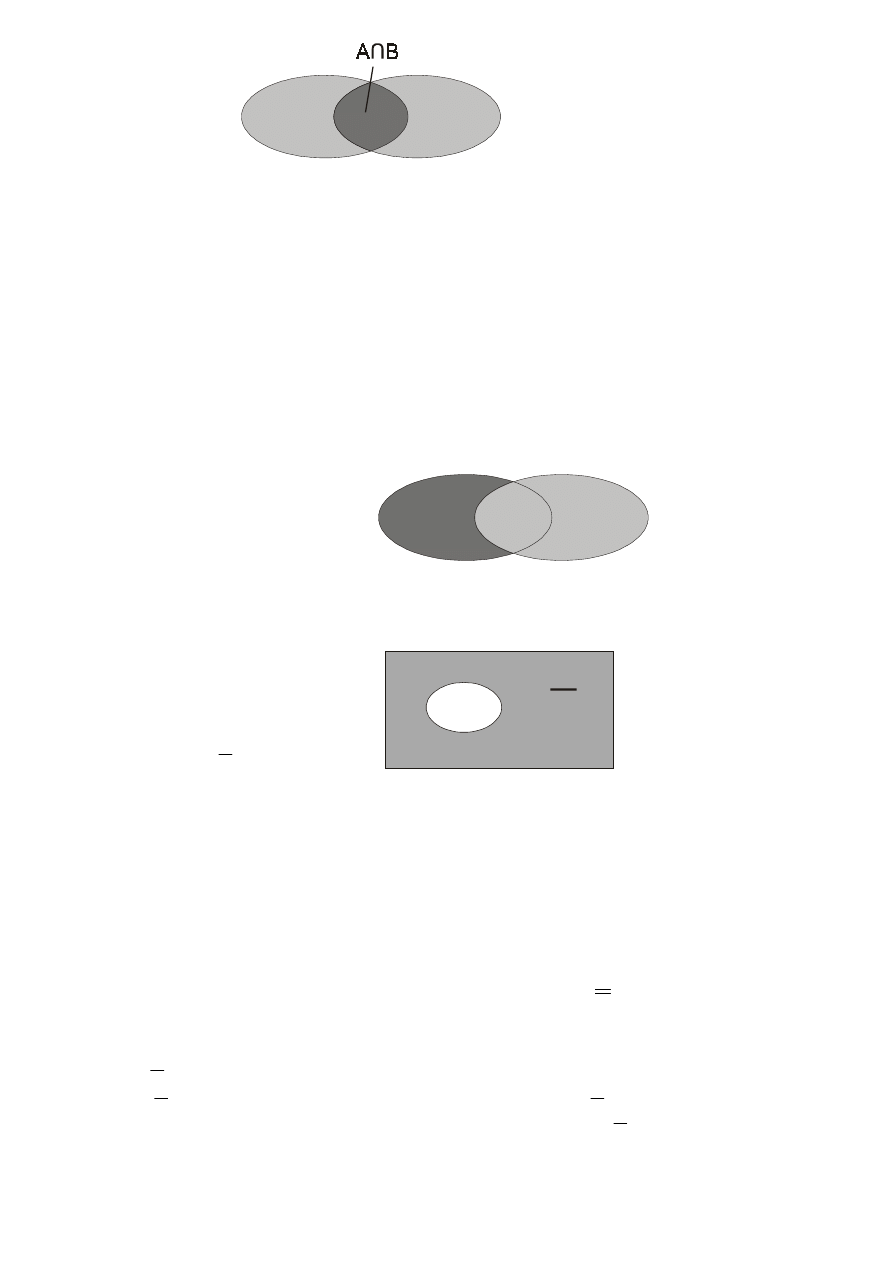
4
B
A
∩
A
B
Uogólnienie iloczynu na n zdarzeń:
i
n
i
n
A
A
A
A
C
I
1
2
1
...
=
=
∩
∩
∩
=
Przykład:
Rzut kostką:
{2,4,6} - zdarzenie polegające na wyrzuceniu parzystej liczby oczek,
{4,5,6} - zdarzenie polegające na wyrzuceniu więcej niż 3-ch oczek.
Iloczyn tych dwóch zdarzeń, to: {4,6}.
4. Różnicą dwóch zdarzeń losowych A oraz B nazywamy zbiór złożony z tych i tylko tych zdarzeń
elementarnych, które należą do zdarzenia A i nie należą do zdarzenia B. Oznaczamy:
B
A
−
lub
B
A \
A
B
5. Zdarzenie przeciwne do zdarzenia A ( dopełnienie zdarzenia A ) – nazywamy zdarzenie obejmujące te
wszystkie zdarzenia elementarne, które nie należą do zdarzenia A. Oznaczamy:
A
A
−
Ω
=
A
A
Przykład:
Dopełnieniem zdarzenia polegającego na wyrzuceniu parzystej liczby oczek: {2,4,6} jest zdarzenie
polegające na wyrzuceniu nieparzystej liczby oczek: {1,3,5}.
6. Zdarzenia rozłączne (wykluczające się) A i B jeżeli ich iloczyn jest zdarzeniem niemożliwym, czyli:
=
∩
B
A
∅
7. Liczność zbioru A ( moc zdarzenia A ), oznaczamy: Card A lub
A
.
Związki między wprowadzonymi działaniami na zdarzeniach
1.
Ω
=
∪
A
A
- suma zdarzenia i jego dopełnienia jest zdarzeniem pewnym,
2.
=
∩
A
A
∅
- zajście zdarzenia A wyklucza zajście zdarzenia
A
. Iloczyn zdarzenia i jego
dopełnienia jest zdarzeniem niemożliwym. Zdarzenie A i jego dopełnienie
A
są zdarzeniami rozłącznymi,
3.
A
A
A
=
∪
- suma dowolnego zdarzenia z samym sobą jest równoważna zajściu tego zdarzenia,

5
4.
A
A
A
=
∩
- iloczyn dowolnego zdarzenia z samym sobą jest równoważny temu zdarzeniu,
5.
A
A
=
)
(
- dopełnienie dopełnienia dowolnego zdarzenia jest równoważne temu zdarzeniu,
6.
B
A
B
A
∩
=
−
- różnica dwóch zdarzeń jest równa iloczynowi jednego ze zdarzeń i dopełnienia
drugiego zdarzenia.
7.
A
B
B
A
∪
=
∪
8.
A
B
B
A
∩
=
∩
9.
A
A
=
∪
0
10.
0
0
=
∩
A
11.
)
(
)
(
C
B
A
C
B
A
∪
∪
=
∪
∪
12.
)
(
)
(
C
B
A
C
B
A
∩
∩
=
∩
∩
13.
)
(
)
(
)
(
C
B
C
A
C
B
A
∩
∪
∩
=
∩
∪
- prawo rozdzielności mnożenia wzgl. dodawania
14.
)
(
)
(
)
(
C
B
C
A
C
B
A
∪
∩
∪
=
∪
∩
- prawo rozdzielności dodawania wzgl. mnożenia
15.
B
A
=
- równość zdarzeń
16. Jeśli zbiór A ma n elementów, to ma
n
2
podzbiorów.
Prawa de Morgana:
1.
B
A
B
A
∩
=
∪
- dopełnienie sumy zdarzeń jest równe iloczynowi dopełnień tych zdarzeń,
2.
B
A
B
A
∪
=
∩
- dopełnienie iloczynu zdarzeń jest równe sumie dopełnień tych zdarzeń.
Po omówieniu relacji i działań na zdarzeniach losowych powróćmy do problemu, jakie podzbiory
przestrzeni Ω będziemy nazywać zdarzeniami losowymi.
Rozważmy 2 przypadki:
A. Zdarzenia losowe w skończonej przestrzeni zdarzeń elementarnych Ω
Jeśli Ω – zawiera skończoną liczbę elementów, to jako rodzinę S przyjmujemy rodzinę wszystkich
podzbiorów przestrzeni zdarzeń elementarnych Ω, czyli dowolny podzbiór jest zdarzeniem losowym.
Przykład:
Na egzaminie student uzyskuje jedną z 4-ch ocen: 2, 3, 4, 5. Określić przestrzeń zdarzeń elementarnych
i wypisać wszystkie zdarzenia losowe występujące przy zdawaniu egzaminu.
Są 4 zdarzenia elementarne. Niech:
k
ω
- zdarzenie otrzymania oceny.
Przestrzeń zdarzeń elementarnych: Ω={ 2, 3, 4, 5 }.
Wszystkich możliwych zdarzeń losowych jest: 2
4
=16.
Rodzina S
k Zdarzenia losowe k- elementowe
Liczba zdarzeń losowych k- elem.
0
zdarzenie niemożliwe
∅
1
1
{2}, {3}, {4}, {5}
4
2
{2,3},{2,4},{2,5},{3,4},{3,5},{4,5}
6
3
{2,3,4},{2,3,5},{2,4,5},{3,4,5}
4
4
{2,3,4,5} – zdarzenie pewne Ω
1
Suma zdarzeń: 16
Zdarzenie niemożliwe - student nie otrzymał żadnej oceny ( k=0 ),
{3,4,5} - student zdał,

6
{4,5} - student otrzymał ocenę co najmniej dobrą.
Ogólnie: jeśli: Ω = {
n
ω
ω
ω
,...,
,
2
1
} jest zbiorem n – elementowym, to zdarzeń losowych jest:
n
2
: są to
podzbiory: 0-elementowe, 1- elementowe, ... ,k – elementowe, ... , n- elementowe.
Zdarzeń k- elementowych jest:
n
k
k
n
,...,
1
,
0
,
=
.
B. Zdarzenia losowe w n- wymiarowej przestrzeni euklidesowej
Niech przestrzenią zdarzeń elementarnych Ω będzie n- wymiarowa przestrzeń euklidesowa
n
ℜ
lub jej
podzbiór. Oznaczmy przez S
*
- rodzinę podzbiorów przestrzeni Ω, spełniającą następujące warunki:
1.
*
S
∈
Ω
,
2. Jeśli
*
S
A
∈
, to
*
S
A
∈
−
Ω
,
3. Jeśli
,...,
,
*
2
*
1
S
A
S
A
∈
∈
to
*
1
S
A
i
i
∈
∞
=
U
.
Rodzinę zbiorów S
*
nazywamy przeliczalnie addytywnym ciałem zdarzeń.
Niech S – oznacza najmniejsze przeliczalnie addytywne ciało zdarzeń, zawierające wszystkie zbiory
otwarte; takie ciało nazywamy ciałem zbiorów borelowskich, a jego elementy zbiorami borelowskimi.
Czyli zdarzenia losowe są to zbiory borelowskie.
Reasumując:
- jeśli Ω jest zbiorem przeliczalnym, to S składa się ze wszystkich podzbiorów Ω,
- jeśli Ω jest zbiorem nieprzeliczalnym, to S jest pewną rodziną podzbiorów Ω, zwaną σ- ciałem
zdarzeń, spełniającą powyższe 3 warunki.
Elementy kombinatoryki
Kombinatoryka jest działem matematyki, który zajmuje się różnorodnymi zestawieniami elementów.
Termin ten pochodzi z pracy G. W. Leibniza (1646-1716) "Dissertatio de arte combinatoria" (Rozprawa o
sztuce kombinacji), która została wydana w 1666 roku.
Początki kombinatoryki spotykamy w pracach arabskich matematyków z przełomu X i XI wieku, natomiast już
Arystoteles rozważał ustawienia liter alfabetu.
Wzory na liczbę permutacji oraz wariacji zostały podane w XIII wieku.
Prace "De ludo aleae" (O grze w kości) G. Cardano (1564-1643) oraz "Consideratione sopra il guioco dei
dadi" (Rozważania nad grą w kości) Galileusza (1564-1642) zapoczątkowały rozwój kombinatoryki.
Kombinatoryka jest gałęzią wiedzy, zajmującą się zestawieniami, czyli grupami utworzonymi z danej grupy
przedmiotów zwanych elementami. Mówiąc dokładniej, kombinatoryka odpowiada na pytanie, ile da się
zbudować zestawień określonego rodzaju z dostępnych elementów.
Pojęcie zestawienia nie jest formalnie definiowane; nie należy go też utożsamiać z pojęciem zbioru, znanym z
innych dziedzin matematyki. W literaturze polskiej rozróżnia się na ogół 3 rodzaje zestawień: permutacje,
wariacje i kombinacje. Tak oto przedstawiają się te pojęcia w klasycznym rozumieniu ( zob. np. J. Królikowski,
C. Steckiewicz: Matematyka. Wzory, definicje i tablice ).
Permutacje
to zestawienia spełniające dwa następujące warunki
:
•
każda permutacja obejmuje wszystkie dane elementy,
•
istotna jest tylko kolejność elementów permutacji.

7
Z trzech danych elementów: a, b, c, można utworzyć następujące permutacje: {a, b, c}, {a, c, b}, {b, a, c}, {b, c, a}, {c, a, b}, {c, b, a}.
Wariacje
to zestawienia spełniające dwa następujące warunki:
•
obejmują jedynie określoną liczbę k spośród danych n elementów (mniejszą niż liczba elementów
danych, k < n, zob. jednak niżej),
•
istotna jest kolejność elementów wariacji.
Z trzech danych elementów: a, b, c, można utworzyć następujące dwuelementowe wariacje: {a, b}, {a, c}, {b, a}, {b, c}, {c, a}, {c, b}.
Kombinacje
to zestawienia spełniające dwa następujące warunki:
•
obejmują jedynie określoną liczbę k spośród danych n elementów (mniejszą niż liczba elementów
danych, k < n),
•
nie jest istotna kolejność elementów kombinacji.
Z trzech danych elementów: a, b, c, można utworzyć następujące dwuelementowe kombinacje: {a, b}, {a, c}, {b, c}.
Zdefiniowane powyżej pojęcia można również rozszerzyć na przypadki, gdy brane są pod uwagę powtórzenia
elementów. W przypadku permutacji rozpatrujemy przypadki, gdy ilość powtórzeń danego elementu jest ściśle
określona. A zatem, jeżeli spośród elementów: a, b i c, element a weźmiemy dwa razy, element b jeden raz i
element c jeden raz, możemy utworzyć następujące permutacje z powtórzeniami:
{a, a, b, c}, {a, a, c, b}, {a, b, a, c}, {a, b, c, a}, {a, c, a, b}, {a, c, b, a}, {b, a, a, c}, {b, a, c, a}, {b, c, a, a}, {c,
a, a, b}, {c, a, b, a}, {c, b, a, a}.
Z trzech danych elementów: a, b, c, można utworzyć następujące dwuelementowe wariacje z powtórzeniami:
{a, a}, {a, b}, {a, c}, {b, a}, {b, b}, {b, c}, {c, a}, {c, b}, {c, c}. Zwróćmy uwagę, że ilość elementów wariacji
z powtórzeniami może być równa całkowitej ilości elementów, a nawet od niej większa.
Z podanych trzech elementów możemy więc tworzyć wariacje z powtórzeniami trójelementowe: {a, a, a}, {a, a,
b}, …, a także np. czteroelementowe: {a, a, a, a}, {a, a, a, b}, itd.
Z trzech danych elementów: a, b, c, można utworzyć następujące dwuelementowe kombinacje z
powtórzeniami: {a, a}, {a, b}, {a, c}, {b, b}, {b, c}, {c, c}.
Również i w wypadku kombinacji z powtórzeniami odpada warunek, że ilość elementów tworzących
kombinację musi być mniejsza niż całkowita dostępna ilość elementów (np. z trzech elementów możemy
tworzyć kombinacje dziesięcioelementowe).
Współczesne podręczniki często definiują powyższe pojęcia kombinatoryki przy pomocy pojęć „zbiór” i
„ciąg”, jednak takie podejście nie wydaje się najlepsze, z co najmniej dwóch powodów, o czym niżej. Najpierw
jednak zastanówmy się, czym są zbiory i ciągi.
Zbiór i element to pojęcia pierwotne. Nie możemy podać tu definicji zbioru, mimo to możemy podać dwie cechy zbioru:
•
w zbiorze kolejność elementów nie jest istotna,
•
zbiór nie zawiera dwóch identycznych elementów,
to znaczy każdy element traktujemy tak, jakby występował tylko jeden raz. Zauważmy, że kombinacje bez powtórzeń są zbiorami.
Multizbiór różni się z kolei tym od zbioru, że może zawierać elementy identyczne, a więc innymi słowy, każdy
z różnych elementów multizbioru może występować więcej niż jeden raz. Zauważmy, że kombinacje z
powtórzeniami są multizbiorami. Skoro kombinacje z powtórzeniami nie są zbiorami, lecz multizbiorami,
rezygnowanie w definicji kombinacji z pojęcia „zestawienie” i zastępowanie go pojęciem „zbiór” nie jest
najszczęśliwszym rozwiązaniem.

8
Ciąg definiuje się formalnie jako funkcję na danym zborze, można też określić ciąg jako „zbiór
uporządkowany” (takie określenie jest jednak nieścisłe, bo ciąg nie jest zbiorem, por. jednak „a sequence is an
ordered set of mathematical objects” –
tutaj
). Intuicyjnie przez ciąg należy rozumieć obiekt podobny do zbioru,
w którym „elementy” (zwane tu wyrazami) ułożone są po kolei. Ciąg może zawierać wyrazy identyczne lub
nie.
Zauważmy, że permutacje i wariacje są ciągami. Permutacje i wariacje bez powtórzeń są ciągami nie
zawierającymi wyrazów identycznych. Permutacje i wariacje z powtórzeniami są ciągami zawierającymi
wyrazy identyczne.
Zauważmy, że elementy, z których tworzyć będziemy zestawienia (permutacje, wariacje, kombinacje) bez
powtórzeń, pobieramy zawsze (bez zwracania) z jakiegoś zbioru.
Elementy, z których tworzyć będziemy zestawienia z powtórzeniami, pobieramy z jakiegoś multizbioru (w
przypadku wariacji i kombinacji możemy pobierać ze zbioru, zwracając pobrane elementy; w przypadku
permutacji z powtórzeniami nie jest to możliwe). Jest to drugi powód, dla którego opieranie definicji
poszczególnych rodzajów zestawień na pojęciu zbioru, nie jest najszczęśliwsze.
Permutacje określane są też jako przestawienia, wariacje jako przemiany albo rozmieszczenia,
kombinacje jako połączenia.
Najbardziej elementarną metodą kombinatoryki, często stosowaną intuicyjnie jest reguła mnożenia i
dodawania. Możemy ją sformułować w następujący sposób.
Jeżeli mamy k możliwości wykonania jednej operacji oraz l możliwości wykonania drugiej, to wykonując:
- jedną operację i drugą mamy k * l możliwości;
- jedną operację albo drugą mamy k + l możliwości.
Oczywiście w przypadku większej liczby operacji wykorzystujemy regułę mnożenia i dodawania wielokrotnie.
Zastosowanie reguły dodawania i mnożenia ilustruje następujący przykład:
Przykład
Dziewczyna wybierając się na dyskotekę może wybrać bluzkę spośród czterech oraz spódnicę, których
ma trzy albo spodnie, których ma pięć. Ile wariantów ubioru ma do dyspozycji ?
Rozwiązanie
W przykładzie wykonujemy trzy operacje: wybór bluzki (operacja 1 ), wybór spódnicy (operacja 2 )
oraz wybór spodni (operacja 3 ). Nietrudno zauważyć, że operacje te można połączyć następująco:
operacja 1 i (operacja 2 albo operacja 3)
Stosując regułę mnożenia i dodawania, otrzymamy, że liczba wariantów ubioru będzie wynosić:
4 * ( 3 + 5 ) = 4 * 8 = 32
Stosując w odpowiedni sposób regułę mnożenia i dodawania bez trudności można określić inne podstawowe
pojęcia kombinatoryki.
Permutacje bez powtórzeń
Często spotykamy się z sytuacją, gdy musimy elementy pewnego zbioru ustawić w określonej kolejności.
Rozważmy prosty przykład:

9
Przykład
Trzy osoby wybierają nagrody (różne) w konkursie w kolejności według zajętych miejsc. Na ile
sposobów mogą to zrobić?
Rozwiązanie
Pierwsza osoba ma trzy możliwości, druga już tylko dwie (jedną z nagród wybrała już pierwsza osoba),
a trzecia tylko jedną. Ponieważ nagrodę wybiera pierwsza osoba i druga, jak i trzecia, to do obliczenia
liczby możliwych wariantów stosujemy regułę mnożenia i otrzymujemy, że nagrody mogą być wybrane
na: 3 * 2 * 1 sposobów.
Rozumując analogicznie dochodzimy do wniosku, że gdy mamy ustawić w określonej kolejności elementy
-elementowego zestawienia, to liczba możliwych wariantów będzie wynosić:
n * (n-1)*...* 2* 1 = n!
Definicja
Permutacją bez powtórzeń zestawienia skończonego nazywamy każde ustawienie wszystkich jego
elementów w określonej kolejności. Dwie permutacje uważamy za różne, gdy przynajmniej dwa
elementy występują w nich na różnych miejscach.
Liczbę permutacji zestawienia n- elementowego obliczamy według wzoru:
P
n
=n!
Permutacje z powtórzeniami
Jeśli zestawienie X składa się z n elementów podzielonych na k grup, gdzie liczby elementów w
poszczególnych grupach wynoszą odpowiednio:
n
1
, n
2
, n
3
, n
4
, ..., n
k
i n
1
+ n
2
+ n
3
+...+ n
k
= n
to liczba permutacji tego zestawienia wynosi:
P
n
n1,n2....nk
=
n !
n
1
!*n
2
!*...*n
k
!
Przykład
Ile jest 3- elementowych permutacji elementów a i b , w których element a powtarza się 2 razy?
Rozwiązanie
3 - elementowe permutacje tych elementów, to: ( a, a, b ) , ( b, a, a ), ( a, b, a )
Ilość tych permutacji, to:
3
!
2
!*
1
!
3
2
,
1
3
=
=
P
Wariacje bez powtórzeń
Następnym problemem kombinatorycznym, które pojawia się w naturalny sposób jest ustawianie w określonej
kolejności elementów zestawienia, ale niekoniecznie wszystkich. Przykładem może być losowanie, w którym
elementy zestawienia losujemy bez zwracania (bez powtórzeń) i kolejność wylosowanych elementów jest
istotna. Rozważmy następujący przykład:

10
Przykład
Pan X ma wybrać kod PIN złożony z czterech nie powtarzających się cyfr. Ile ma możliwości?
Rozwiązanie
Pierwszą cyfrę może wybrać na dziesięć sposobów, drugą już tylko na dziewięć (cyfry nie mogą się
powtarzać), trzecią na osiem i czwartą na siedem. Ponieważ wybiera pierwszą i drugą i trzecią i czwartą
cyfrę, to stosując regułę mnożenia otrzymujemy, że pan X ma 10 * 9 * 8 * 7 możliwości.
Ten iloczyn można uzupełnić do następującej postaci:
)!
4
10
(
!
10
!
6
!
10
1
*
2
*
...
*
5
*
6
1
*
2
*
...
*
6
*
7
*
8
*
9
*
10
7
*
8
*
9
*
10
−
=
=
=
Widzimy więc, że liczbę wszystkich permutacji zbioru 10-elementowego należy podzielić przez liczbę
permutacji zbioru ( 10 – 4 )-elementowego.
Definicja
Wariacją bez powtórzeń k- elementów z zestawienia n- elementowego nazywamy każde ustawienie w
określonej kolejności k nie powtarzających się elementów wybranych z zestawienia n- elementowego,
przy czym
n
k
≤
≤
1
.
Liczbę wariacji bez powtórzeń k - elementowych wybranych z zestawienia n- elementowego oznaczamy
symbolem
k
n
V
i obliczamy ze wzoru:
)!
(
!
k
n
n
V
k
n
−
=
Zauważmy, że gdy k = n to wariacja bez powtórzeń staje się permutacją i oczywiście:
n
n
n
P
n
n
n
n
n
V
=
=
=
−
=
!
!
0
!
)!
(
!
Wariacje z powtórzeniami
W tym momencie pojawia się pytanie, jak można wyrazić liczbę wariantów gdy elementy zestawienia
ustawiane w określonej kolejności mogą się powtarzać. Proste zastosowanie reguły mnożenia daje natychmiast
odpowiedź. Rozważmy przykład:
Przykład
Pan X wybierając kod PIN może powtarzać cyfry. Ile ma możliwości?
Rozwiązanie
Wybierając pierwszą cyfrę ma 10 możliwości, wybierając drugą nadal ma 10 możliwości, podobnie jest
z trzecią i czwartą cyfrą. Stosując regułę mnożenia łatwo obliczymy, że liczba możliwych wariantów
wynosi:
10 * 10 * 10 * 10 = 10
4

11
Definicja
Wariacją z powtórzeniami k- elementów z zestawienia n- elementowego nazywamy każde ustawienie
w określonej kolejności k elementów mogących się powtarzać wybranych z zestawienia
n- elementowego.
Liczbę wariacji z powtórzeniami k- elementowych wybranych z zestawienia n - elementowego oznaczamy
symbolem
k
n
W
i obliczamy ze wzoru:
k
k
n
n
W
=
Kombinacje bez powtórzeń
We wszystkich dotychczasowych rozważaniach zakładaliśmy, że kolejność elementów jest istotna. W wielu
przypadkach jednak tak nie jest, wystarczy rozważyć choćby losowanie Dużego Lotka. Nie interesuje nas czy
skreślona na kuponie liczba zostanie wylosowana jako pierwsza, czwarta czy też szósta. Ważne jest jedynie to,
czy wybrana przez nas liczba znajdzie się w zbiorze wylosowanych liczb. Stąd w kombinatoryce pojawia się
kolejne pojęcie, które zilustrujemy następującym przykładem:
Przykład
Z grupy dziewięciu osób mamy wybrać czteroosobową delegację. Na ile sposobów możemy to zrobić?
Rozwiązanie
Na początek obliczmy na ile sposobów można wybrać delegacje w sytuacji gdy kolejność wyboru jest
istotna. Można to oczywiście zrobić na
)!
4
9
(
!
9
4
9
−
=
V
sposobów - jest to liczba wariacji
czteroelementowych z zestawienia dziewięcioelementowego. Jednak nas kolejność wyboru tych
czterech osób nie interesuje, zatem niepotrzebnie uwzględniliśmy liczbę ustawień czterech osób w
określonej kolejności. Liczba takich ustawień wynosi P
4
= 4! , dlatego ostateczna liczba możliwych
wyborów będzie równa:
126
!
5
*
1
*
2
*
3
*
4
!
5
*
6
*
7
*
8
*
9
!
5
!*
4
!
9
)!
4
9
!*(
4
!
9
4
4
9
=
=
=
−
=
P
V
Definicja
Kombinacją bez powtórzeń k- elementową z zestawienia n- elementowego nazywamy każdy wybór
podzbioru k- elementowego spośród elementów zestawienia n- elementowego, przy czym
n
k
≤
≤
0
.
Liczbę kombinacji bez powtórzeń k- elementowych wybranych z zestawienia n- elementowego oznaczamy
symbolem
k
n
C
i obliczamy ze wzoru:
)!
(
!
!
k
n
k
n
k
n
C
k
n
−
=
=
12
Kombinacje z powtórzeniami
Definicja
Kombinacją z powtórzeniami k- elementową z zestawienia n- elementowego A nazywamy
zestawienia złożone z różnych lub nie różniących się elementów zestawienia A . Ich liczba wynosi:
( )
)!
1
(
!
)!
1
(
1
−
−
+
=
=
−
+
n
k
k
n
C
k
n
k
k
n
Przykład
Kości do gry w domino są oznaczone dwoma liczbami. Ile różnych kości można utworzyć z liczb 0, 1,
2, 3, 4, 5, 6 ?
Rozwiązanie:
Z 7- elementowego zestawienia liczb należy wybierać 2- elementowe podzbiory, w których elementy
mogą się powtarzać a uporządkowanie nie odgrywa roli. Kości jest więc:
( )
28
!
6
*
2
8
*
7
!*
6
!
6
!
2
!
8
)!
1
7
(
!
2
)!
1
2
7
(
1
2
7
2
2
7
=
=
=
−
−
+
=
=
−
+
C
Rozpoznawanie rodzaju zestawień
Właściwości poszczególnych typów zestawień obrazuje tabela:
spośród
wyciągamy
czy zwracamy? czy notujemy kolejność?
permutacje bez powtórzeń
n różnych elementów
wszystkie
nie
tak
permutacje z powtórzeniami
n elementów, w tym identyczne wszystkie
nie
tak
wariacje bez powtórzeń
n różnych elementów
k elementów, k < n nie
tak
wariacje z powtórzeniami
n różnych elementów
k elementów
tak
tak
kombinacje bez powtórzeń
n różnych elementów
k elementów, k < n nie
nie
kombinacje z powtórzeniami
n różnych elementów
k elementów
tak
nie
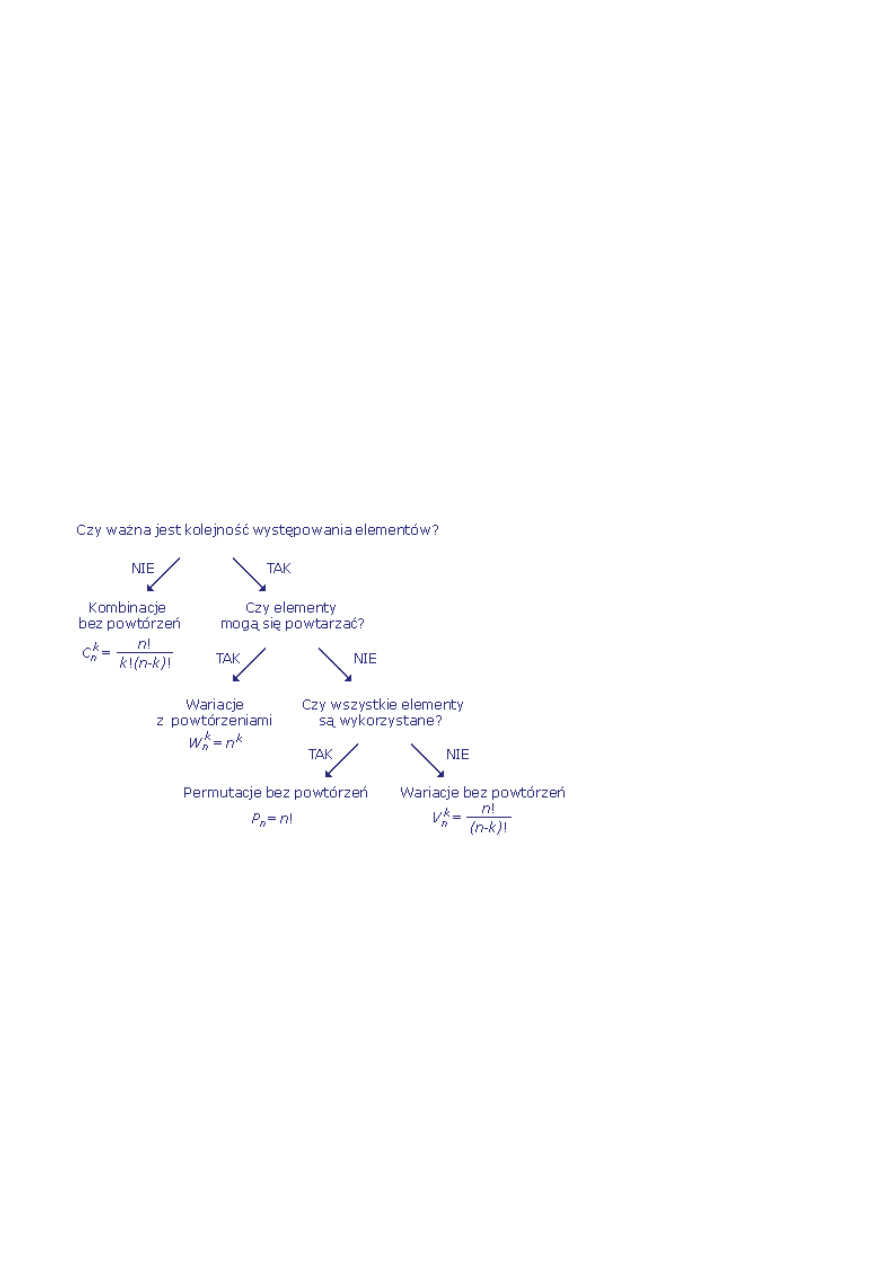
Aby ustalić rodzaj zestawień, które będziemy analizować, należy postępować według następującego algorytmu:
a. Ustalamy, czy kolejność elementów w zestawieniach jest istotna, czy też nie. Jeżeli nie jest istotna, a zestawienia różnią się tylko składem, mamy
do czynienia z kombinacjami i omijamy punkt b.
b. Ustalamy, czy zestawienia różnią się tylko kolejnością elementów. Jeżeli tak, mamy do czynienia z permutacjami. Jeżeli różnią się nie tylko
kolejnością elementów, ale także składem, nasze zestawienia to wariacje.
c. Ustalamy, czy w zestawieniach elementy powtarzają się, czy też nie.
Obliczanie ilości zestawień
Ilość zestawień danego typu obliczamy według następujących wzorów:
permutacje
wariacje
kombinacje
bez powtórzeń
!
n
P
n
=
)!
(
!
k
n
n
V
k
n
−
=
n
k
k
n
k
n
k
n
C
n
k
≤
≤
−
=
=
0
,
)!
(
!
!
z powtórzeniami
!
!...
!
!
2
1
...,
,
,
2
1
k
n
n
n
n
n
n
n
n
P
k
=
k
k
n
n
W
=
)!
1
(
!
)!
1
(
1
1
−
−
+
=
=
−
−
+
n
k
k
n
C
C
n
k
n
k
n
13
Uwagi do wzorów:
•
n oznacza ilość elementów, z których tworzymy zestawienie,
•
k oznacza ilość elementów w zestawieniu ,
•
dla permutacji z powtórzeniami: n
1
to ilość powtórzeń elementu pierwszego, n
2
– elementu drugiego, itd., n
= n
1
+ n
2
+ … + n
k
.
Ilość permutacji z powtórzeniami oznacza się też symbolem P
n
(n
1
,n
2
,…,n
k
). W mianowniku można pominąć
elementy, które występują tylko jeden raz, gdyż 1! = 1, a dzielenie przez 1 nie zmienia wyniku.
Ilość wariacji bez powtórzeń wyraża równoważny wzór V
n
k
= n (n – 1) (n – 2) … (n – r + 1). W dobie
kalkulatorów z wbudowaną funkcją silnia (n!) wygodniej jest jednak posługiwać się wzorem podanym w
tabeli. Zauważmy, że istotnie P
n
= V
n
n
, a więc permutacje bez powtórzeń można uznać za rodzaj wariacji bez
powtórzeń. Jednak ilość permutacji z powtórzeniami wcale nie jest równa ilości wariacji z powtórzeniami.
Dlatego lepiej przyjąć określenie klasyczne, w myśl którego permutacje i wariacje to jednak pojęcia
rozłączne.
Zauważmy również, że ilość k- elementowych kombinacji bez powtórzeń z n elementów równa jest
stosunkowi liczby k- elementowych wariacji bez powtórzeń z n elementów do liczby permutacji z k:
C
n
k
= V
n
k
/ P
k
Rozpoznawanie rodzaju zestawień (wersja 2)
Wyszukiwarka
Podobne podstrony:
ĆW 04, Elementy kombinatoryki, Elementy kombinatoryki
Probablistyczne wymiarowanie elementów żelbetowych z uwzględnieniem trwałości
MAD2 V Elementy kombinatoryki
jurlewicz,probabilistyka, zmienne losowe wielowymiarowe
jurlewicz,probabilistyka, zmien Nieznany
jurlewicz,probabilistyka, zmienne losowe wielowymiarowe
jurlewicz,probabilistyka, zadania
sciaga elementy kombinatoryki. wariacje.d
jurlewicz,probabilistyka, rozkl Nieznany
ELEMENTY KOMBINATORYKI
Przestrzeń zdarzeń elementarnych
jurlewicz,probabilistyka, twierdzenia graniczne
jurlewicz,probabilistyka, rozkład typu skokowego
jurlewicz,probabilistyka, test
Elementy kombinatoryki
więcej podobnych podstron