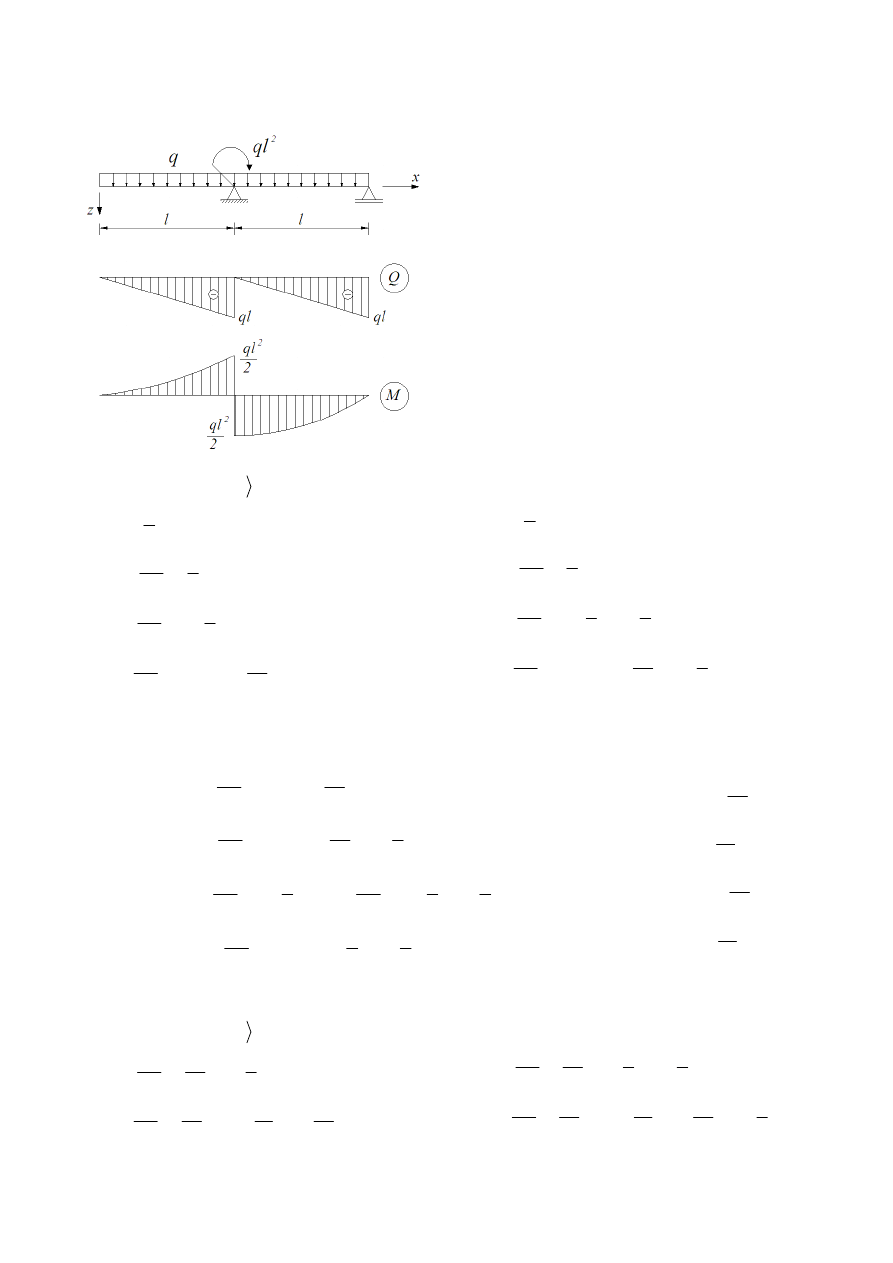
Wyznaczanie przemieszczeń Metodą Klasyczną
Przedział 1:
(
l
x
;
0
1
∈
2
1
2
1
qx
M
−
=
−
−
=
′′
2
1
2
1
1
qx
EJ
z
−
−
=
′
3
1
1
6
1
1
qx
C
EJ
z
−
+
−
=
4
1
1
1
1
24
1
1
qx
D
x
C
EJ
z
Przedział 2:
( )
l
l
x
2
;
2
∈
(
)
2
2
2
2
2
1
ql
l
x
ql
qx
M
+
−
+
−
=
(
)
+
−
+
−
−
=
′′
2
2
2
2
2
1
1
ql
l
x
ql
qx
EJ
z
+
−
+
−
−
=
′
2
2
2
2
2
2
3
2
2
2
1
6
1
1
x
ql
x
ql
qlx
qx
C
EJ
z
+
−
+
−
=
3
2
4
2
2
2
2
6
1
24
1
1
qlx
qx
D
x
C
EJ
z
Warunki brzegowe
+
−
+
−
=
→
=
+
−
−
=
−
−
→
′
=
′
+
−
+
−
=
→
=
−
+
−
=
→
=
=
=
=
=
=
4
4
2
2
2
3
3
2
3
1
3
4
2
2
4
1
1
3
4
3
2
2
1
0
0
2
1
6
1
1
6
1
1
6
1
24
1
1
0
0
24
1
1
0
0
2
2
1
2
1
ql
ql
l
C
D
EJ
z
ql
ql
C
EJ
ql
C
EJ
z
z
ql
ql
l
C
D
EJ
z
ql
l
C
D
EJ
z
l
x
l
x
l
x
l
x
l
x
→
=
−
=
=
−
=
4
2
3
2
4
1
3
1
12
5
24
13
12
1
24
1
ql
D
ql
C
ql
D
ql
C
Równania kąta obrotu i osi ugiętej:
Przedział 1:
(
l
x
;
0
1
∈
−
−
−
=
′
3
1
3
6
1
24
1
1
qx
ql
EJ
z
−
+
−
−
=
4
1
4
1
3
24
1
12
1
24
1
1
qx
ql
x
ql
EJ
z
Przedział 2:
( )
l
l
x
2
;
2
∈
+
−
+
−
−
−
=
′
2
2
2
2
2
2
3
2
3
2
1
6
1
24
13
1
x
ql
x
ql
qlx
qx
ql
EJ
z
+
−
+
−
−
=
3
2
4
2
4
2
3
6
1
24
1
12
5
24
13
1
qlx
qx
ql
x
ql
EJ
z
Wyszukiwarka
Podobne podstrony:
Badanie czystości metodą klasyczną
Pomiary wysokiego napiecia przemiennego metodami posrednimi
cwicz mechanika budowli przemieszczen metoda pracy wirtualnej
cwicz mechanika budowli przemieszczen metoda pracy wirtualnej
RKO prowadzona tylko za pomocą masażu serca a RKO metodą klasyczną, MEDYCYNA, RATOWNICTWO MEDYCZNE,
Ćwiczenie 7 Identyfikacja bakterii (metoda klasyczna i testy API)
Ćw, TO2 ETK Lista1 Metoda Klasyczna
Obliczanie wielomianu metodą klasyczną i metodą Hornera Temat 1
Badanie czystości metodą klasyczną
Linda Schubert GODZINA PRZEMIANY (Metoda modlitwy, która może zmienić twoje życie)
Wcięcie katowe metodą klasyczną z analizą
Przemieszczenia Metoda Clebscha
Zbiór zadań z mechaniki budowli Metoda przemieszczeń i metoda elementów skończonych Tadeusz Chmiel
belka obroty i przesuwy metoda przemieszczeń
Linie wpływu Metoda przemieszczeń mmp belka lw
więcej podobnych podstron