Teoria Obwodów 2 - Wydział Elektryczny

Lista 1 – Stany nieustalone – Metoda klasyczna

A.G.,T.S.,Z.W. ‘07

Wyznaczanie stanu nieustalonego w obwodach z jednym elementem zachowawczym:
W układach z jednym elementem zachowawczym, przedstawionych na schematach, dla t<0 panował stan ustalony.
Wyznaczyć przebiegi wskazanych wielkości dla t>0.

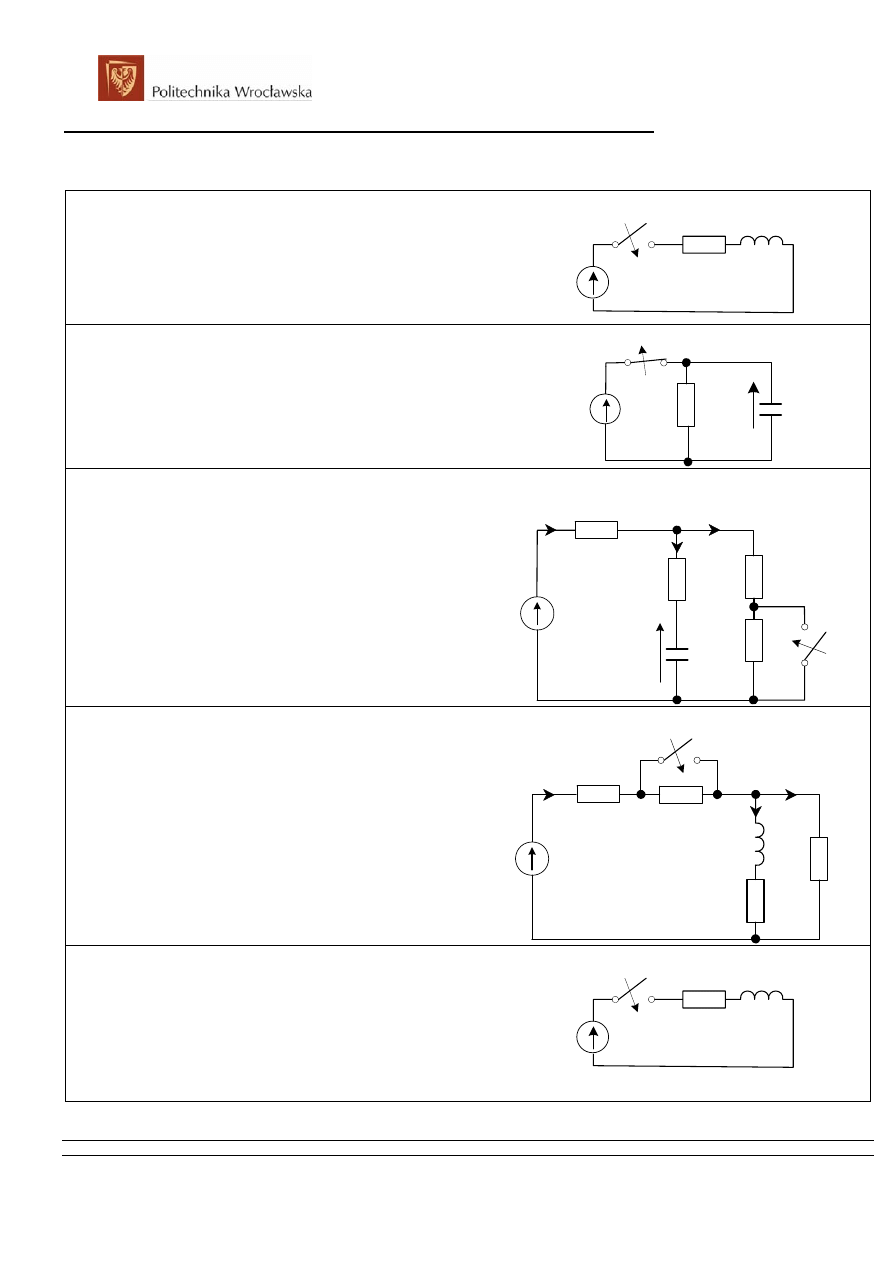
zad. 1

Cewkę o danych L=0.1H, R=10Ω załączono na napięcie stałe
U=100V. Obliczyć i naszkicować przebieg prądu w obwodzie
po zamknięciu wyłącznika. Znaleźć i naszkicować przebiegi
napięć na elementach R i L.
Wyznaczyć stałą czasową obwodu oraz obliczyć po jakim
czasie prąd osiągnie 0.5 i 0.99 wartości ustalonej.

L

R

E

t=0

zad. 2

Kondensator o pojemności C=0.02µF po naładowaniu i
odłączeniu rozładowuje się przez swoją izolację. Po 140s
napięcie na jego zaciskach zmalało dwukrotnie. Znaleźć
oporność izolacji oraz stałą czasową rozładowania
kondensatora.

E

R

u

C

(t )

C

zad. 3

W stanie ustalonym zamknięto wyłącznik „w”. Obliczyć
przebiegi prądów oraz napięcie na kondensatorze.
Dane R

1

=R

3

=10

Ω; R

2

=5

Ω; R

4

=15

Ω; C=1μF; E=15V

Odp.

;

;

;

4

12*10

1

( ) 1 0, 2

t

i t

e

A

−

= −

4

12*10

2

( ) 1 0,1

t

i t

e

A

−

= +

4

12*10

3

( )

0,3

t

i t

e

A

−

= −

4

12*10

( ) 10 2,5

t

C

u t

e

V

−

=

+

t=0

E

R

C

i

3

(t)

i

2

(t)

2

R

3

R

4

i

1

(t)

R

1

u

C

(t )

w

zad. 4

W stanie ustalonym zamknięto wyłącznik „w”. Obliczyć
przebiegi prądów.
Dane R

1

=8

Ω; R’

1

=R

2

=10

Ω; R

3

=30

Ω; L=25mH; E=60V.

Odp.

;

;

653

1

( ) 3,87 0,9

t

i t

e

A

−

=

−

653

2

( ) 2,905 1,14

t

i t

e

A

−

=

−

653

3

( ) 0,965 0, 24

t

i t

e

A

−

=

+

R

1

R

3

i(t)

E

i

2

(t)

L

R

2

i

3

(t)

1

R'

1

t=0

w

zad. 5

Zwojnica o indukcyjności 364mH i rezystancji 10Ω została
włączona w chwili t=0 na napięcie e(t)=160sin(314t+60)V.
Obliczyć wartość chwilową prądu po dwóch okresach od
momentu załączenia napięcia.
Przeanalizować wpływ momentu załączenia w stosunku do fazy
początkowej napięcia zasilającego. Rozważyć:

ψ=0

0

,

ψ=30

0

,

ψ=-60

0

.

L

R

e(t)

t=0

A.S. Cz.S. P.R.®

TS’13

- 1 -

Teoria Obwodów 2 - Wydział Elektryczny

Lista 1 – Stany nieustalone – Metoda klasyczna

A.G.,T.S.,Z.W. ‘07

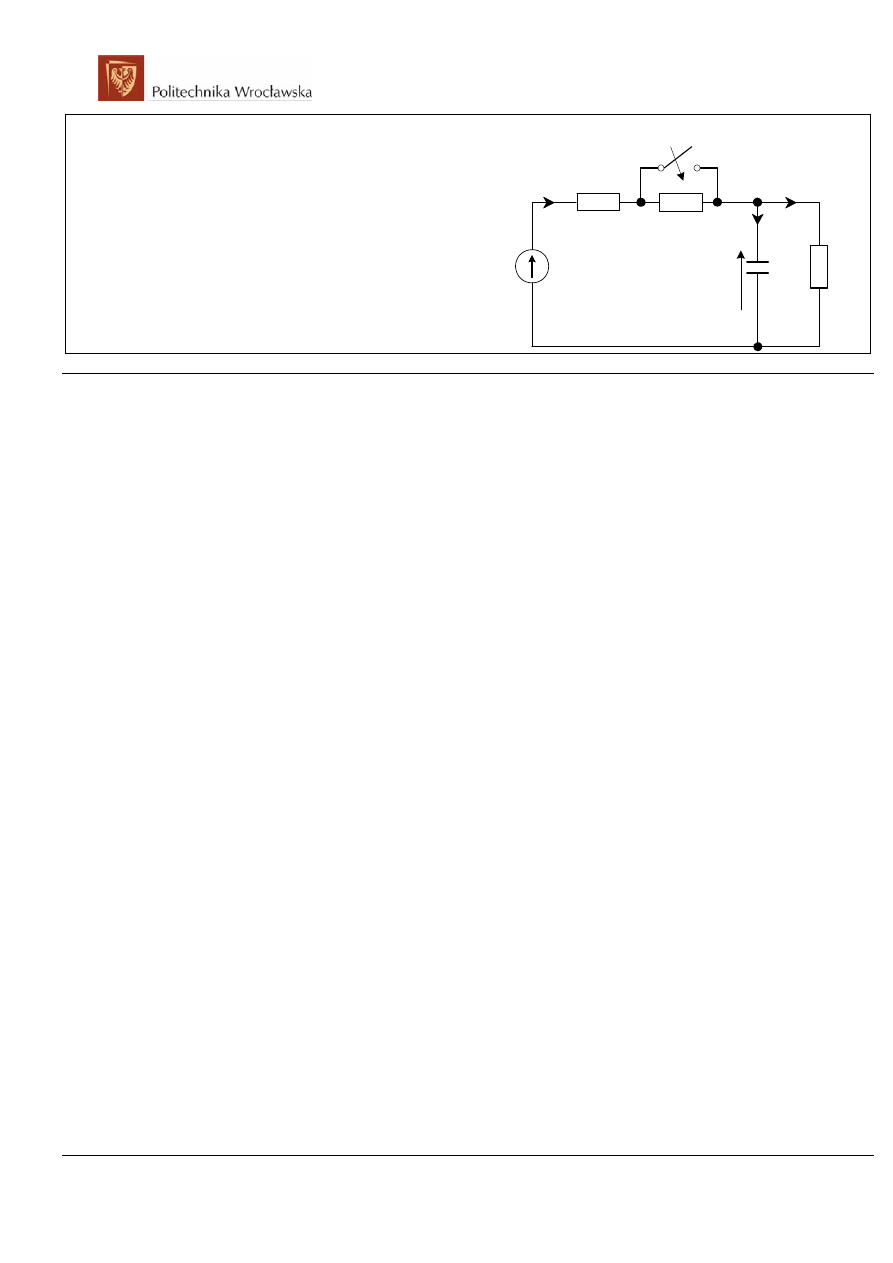
zad. 6

W stanie ustalonym zamknięto wyłącznik „w”. Obliczyć
przebieg prądu zasilającego oraz przebieg napięcia na
kondensatorze.
Dane: R

1

=R’

1

=20

Ω; R2=16Ω; C=11,1μF; ω=5000s-1;

( ) 25sin(

30 )

o

e t

t

V

ω

=

−

Odp.

;

4

1,01*10

1

( ) 0,84sin(

15 20 ') 1,11

o

t

i t

t

e

A

ω

−

=

+

−

4

1,01*10

( ) 9,8sin(

55 40 ') 2,8

o

t

C

u t

t

e

V

ω

−

=

−

+

R

1

R

3

i(t)

e(t)

i

2

(t)

i

3

(t)

1

R'

1

t=0

C

w

u

C

(t )

A.S. Cz.S. P.R.®

TS’13

- 2 -

Teoria Obwodów 2 - Wydział Elektryczny

Lista 1 – Stany nieustalone – Metoda klasyczna

A.G.,T.S.,Z.W. ‘07

Wyznaczanie stanu nieustalonego w obwodach z dwoma elementami zachowawczymi
W układach z dwoma elementami zachowawczymi, przedstawionych na schematach, dla t<0 panował stan ustalony.
Wyznaczyć przebiegi wskazanych wielkości dla t>0.

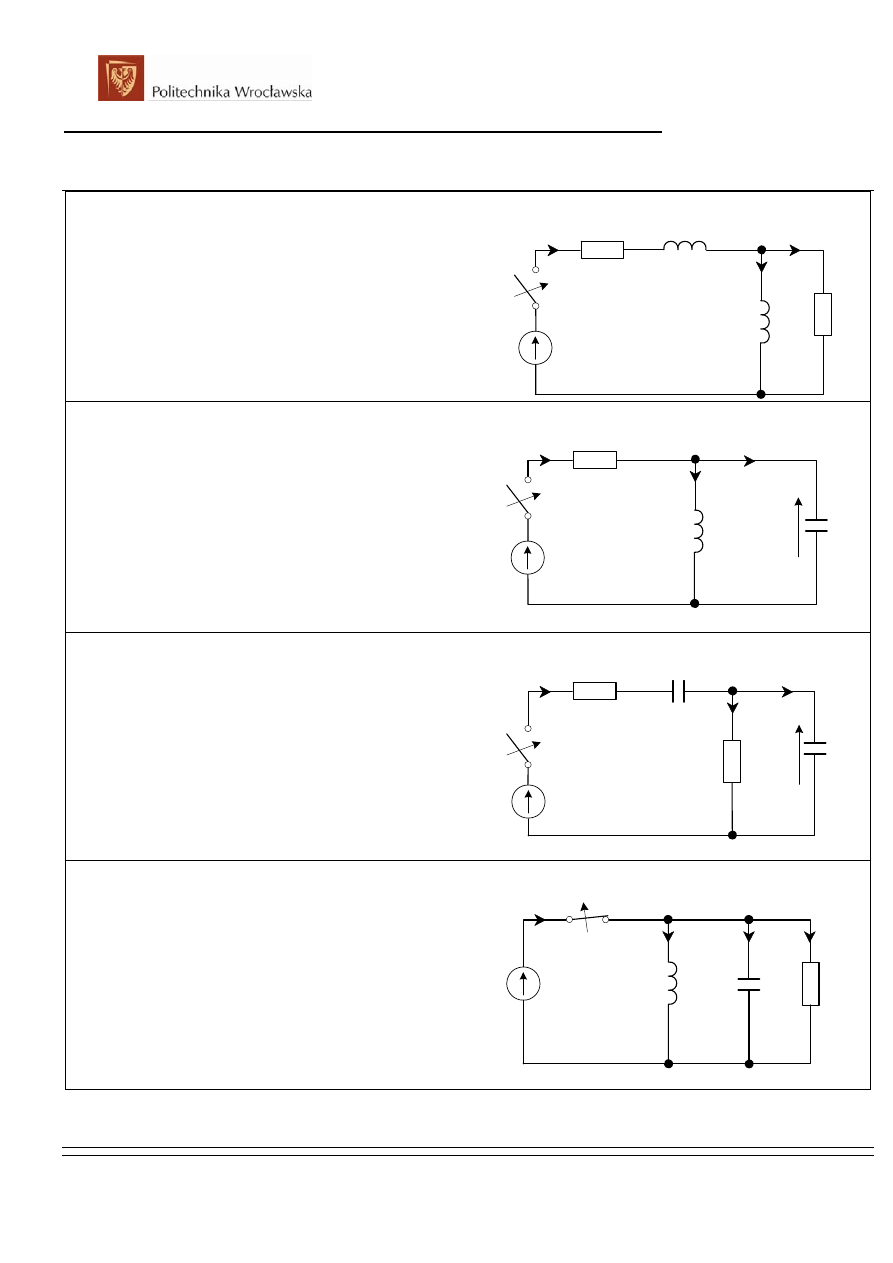
zad. 7

Obwód przedstawiony na rys. obok załączono na napięcie stałe
E=48V. Obliczyć przebiegi chwilowe prądów.
Dane : R

1

=160

Ω; L

1

=100mH; R

3

=90

Ω; L

2

=36mH

Odp.:

;

1000

400

1

( ) 0,3 0, 24

0, 06

t

t

i t

e

e

A

−

−

=

−

−

1000

400

2

( ) 0,3 0, 4

0,1

t

t

i t

e

e

A

−

−

=

−

+

1000

400

3

( ) 0,16

0,16

t

t

i t

e

e

A

−

−

=

−

R

1

R

3

i(t)

E

i

2

(t)

i

3

(t)

1

L

t=0

L

1

2

w

zad. 8

Przy zerowych warunkach początkowych elementów
zachowawczych, załączono obwód na napięcie stałe E=125V.
Obliczyć przebieg napięcia na kondensatorze w trzech
przypadkach:
1 - R=250

Ω; L=667mH; C=2μF

2 - R=100

Ω; L=40mH; C=1μF

3- R=100

Ω; L=40mH; C=5μF

Odp.:1-

; 2-

;

3-

500

1500

( ) 250

t

t

C

u t

e

e

V

−

=

−

5000

( ) 1, 25

t

C

u t

e

MV

−

=

1000

( ) 125

sin(2000 )

t

C

u t

e

t V

−

=

R

C

i(t)

E

i

2

(t)

i

3

(t)

1

t=0

L

u

C

(t )

w

zad. 9

Przy nie naładowanych kondensatorach włączono zasilanie
E=100V. Obliczyć przebieg napięcia na kondensatorze C

2

,

jeżeli C

1

=100

μF, C

2

=20

μF, R

1

=10

Ω, R

2

=100

Ω.

(Odp. u

C2

=81.3(exp(-175t)-exp(-6325t) V

zad. 10

W stanie ustalonym, w chwili, gdy faza napięcia zasilającego
wynosiła

π/6 odłączono zasilanie. Obliczyć przebiegi prądów

licząc czas od t=0 (odłączenie) oraz energię wydzieloną w
postaci ciepła na rezystancji. Dane są e(t)=10sin5000t V,
R=100

Ω, L=40mH, C=1F.

(Odp. i

C

=(-0.0065-92.5t)exp(-5000t) A, i

R

=(0.05+185t)exp(-

5000t), i

L

=(-0.0435-92.5t)exp(-5000t), W=50

μJ )

R

1

i(t)

E

i

2

(t)

C

R

2

i

3

(t)

1

C

1

2

t=0

w

u

C

(t )

R

i(t)

e(t)

i

C

(t)

i

R

(t)

C

L

i

L

(t)

t=0

w

A.S. Cz.S. P.R.®

TS’13

- 3 -

Teoria Obwodów 2 - Wydział Elektryczny

Lista 1 – Stany nieustalone – Metoda klasyczna

A.G.,T.S.,Z.W. ‘07

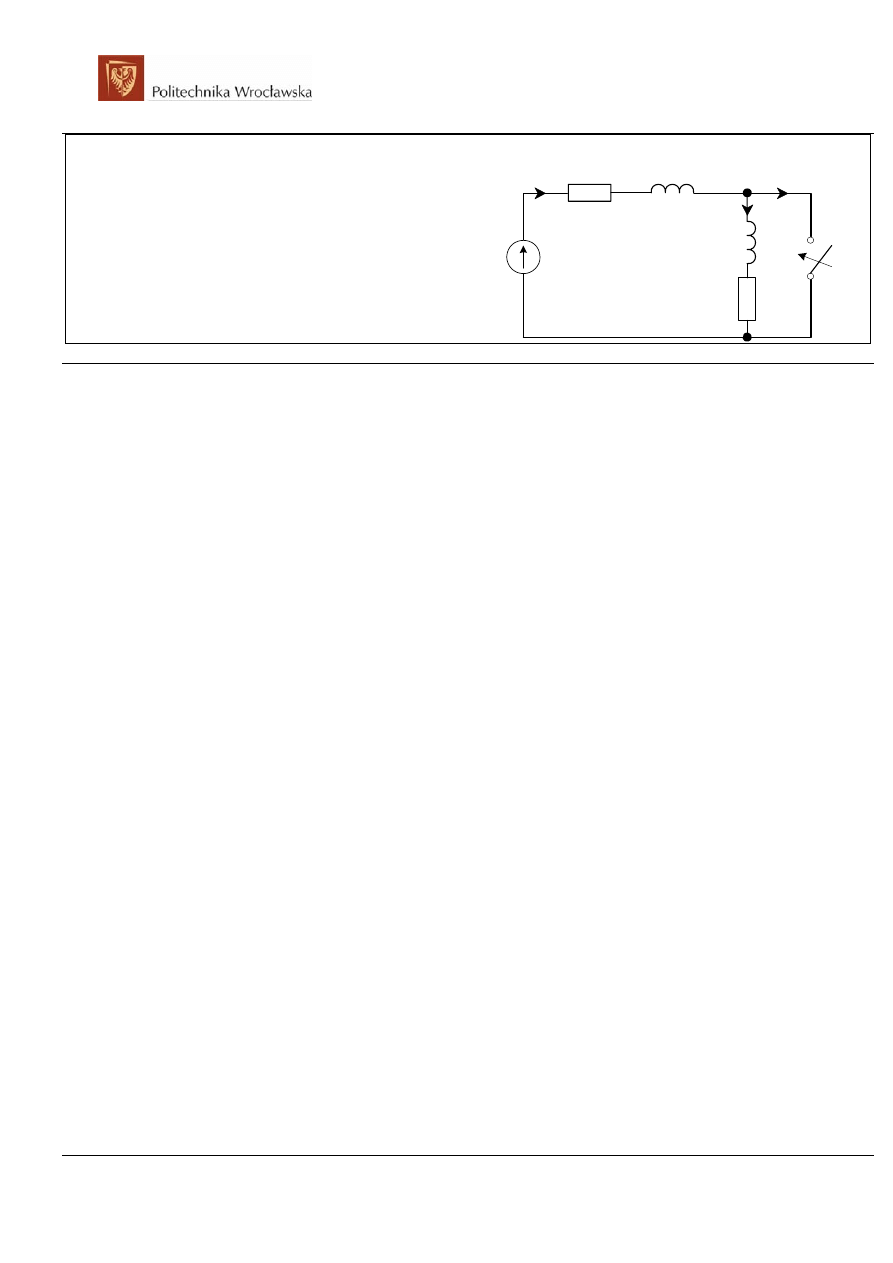
zad. 11

W stanie ustalonym, w chwili, gdy prąd osiągnął wartość
maksymalną zamknięto wyłącznik. Wyznaczyć przebiegi
prądów w zwojnicach. Dane: R

1

=3

Ω, R

2

=4

Ω, L

1

=0.8mH,

L

2

=4mH, e(t)=10sin(5000t+

ψ) V.

(Odp. i

1

=2cos(5000t+20

°35′)-1.47exp(-3750t) A,

i

2

=0.4exp(-1000t) A)

R

1

i(t)

e(t)

i

2

(t)

L

R

2

i

3

(t)

1

L

1

2

t=0

w

A.S. Cz.S. P.R.®

TS’13

- 4 -