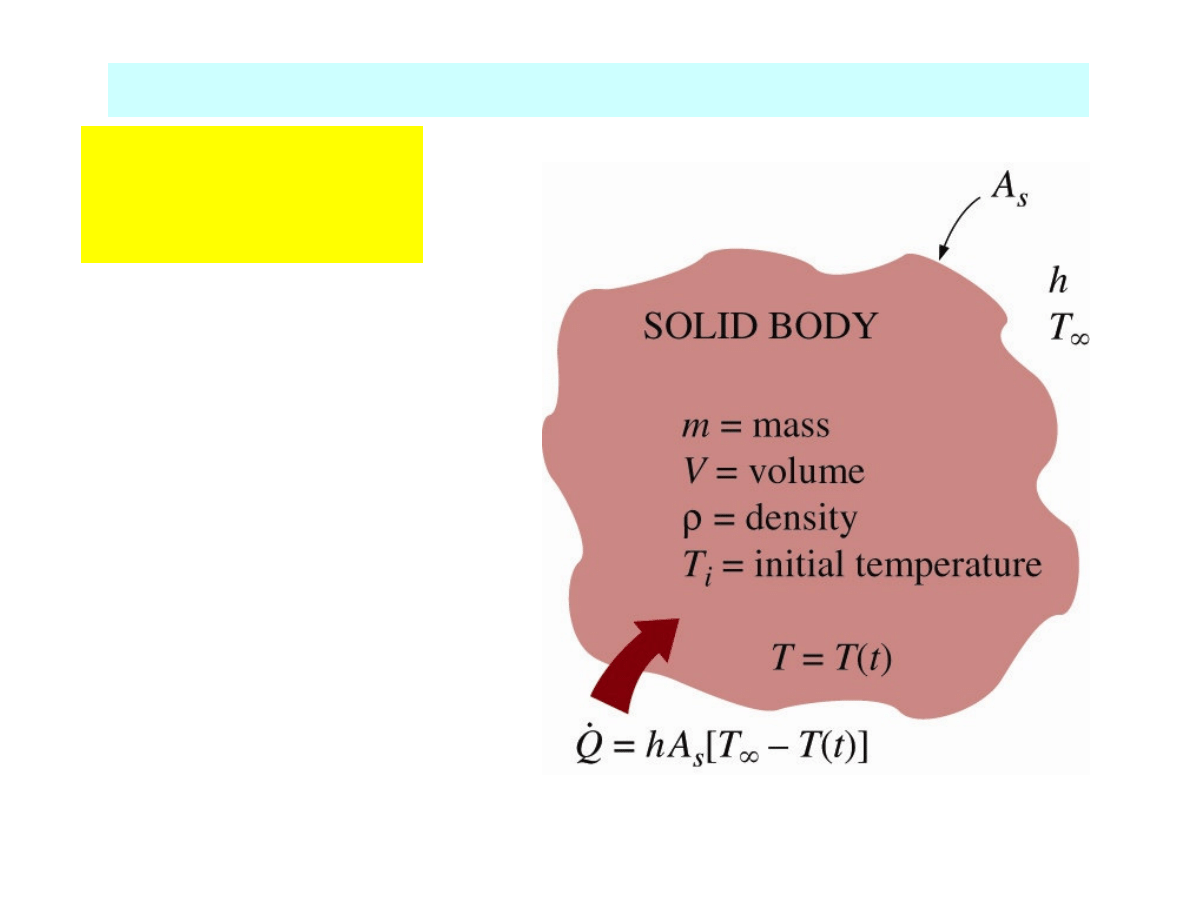
Modelling
Lumped systems:
T = f(t)
but
T = const
throughout the
solid at any time
Temperature of a body, in general, varies with time and
position: T = f(x,y,z,t)
→
→
→
→ unsteady conditions
TRANSIENT HEAT CONDUCTION
T = f(x,y,z,t)
in:
• 1D systems – a large plane wall, a long cylinder, a sphere,
a semi-infinite medium
• multidimensional systems
LUMPED SYSTEM
const
z
y
x
T
t
f
T
=
=
)
,
,
(
)
(
h
– heat transfer coefficient
Assumption:
temperature of a medium
T
∞
∞
∞
∞
>
>
>
> T
i
During a differential time
dt
–
temperature rising by a
differential amount
dT
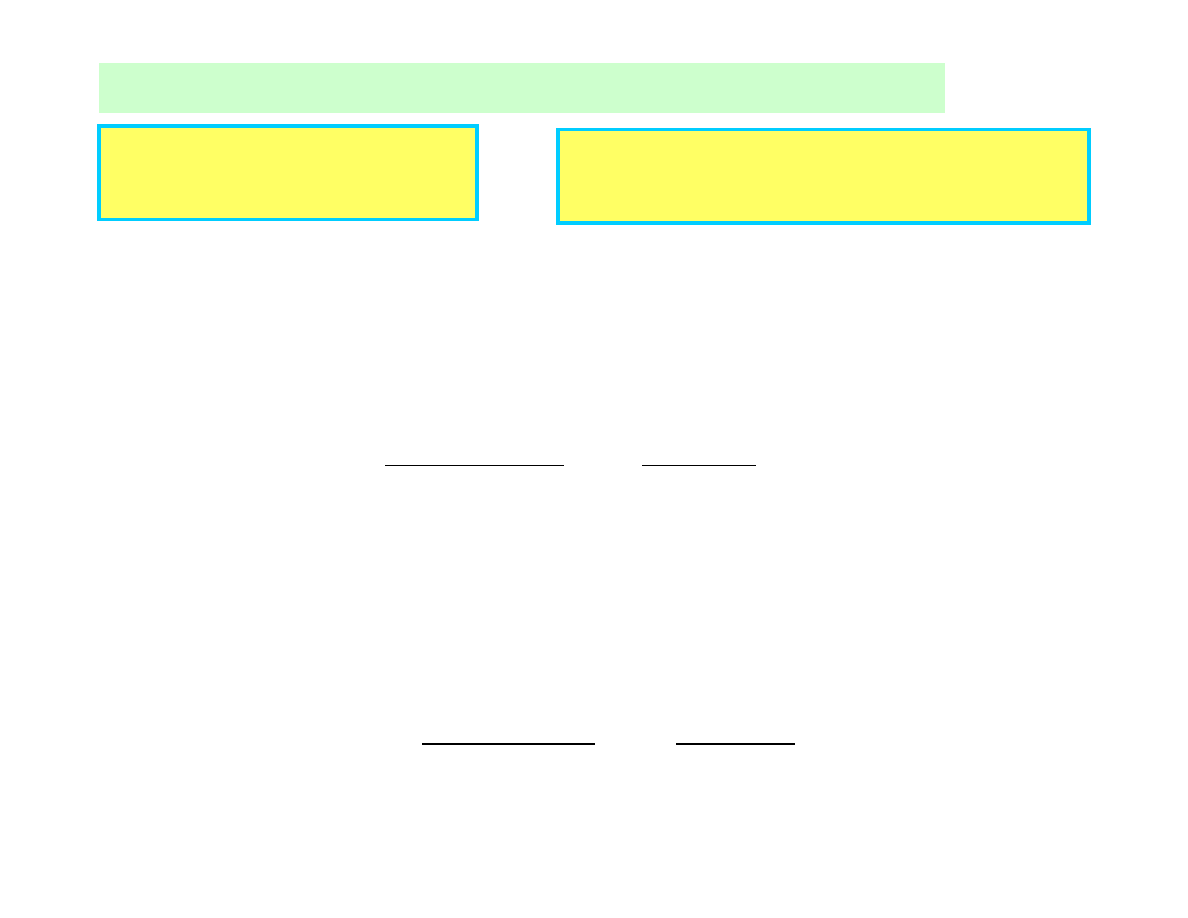
Energy balance of the solid for the time interval
dt
:
Heat transfer into the
body during
dt
The increase in the energy of
the body during
dt
=
or:
dT
mC
dt
T
T
hA
p
S
=
−
∞
)
(
Integrating from t = 0, at which T = T
i
, to any time t, at which
T = T(t), gives
t
VC
hA
T
T
T
t
T
p
S
i
ρ
−
=
−
−
∞
∞
)
(
ln
V
m
ρ
=
Since:
and
)
(
∞
−
=
T
T
d
dT
, because
const
T
=
∞
dt
VC
hA
T
T
T
T
d
p
S
ρ
−
=
−
−
∞
∞
)
(
we obtain:
Thus:
bt
i
e
T
T
T
t
T
−
∞
∞
=
−
−
)
(
where:
p
S
VC
hA
b
ρ
=
)
/
1
(
s
b
/
1
=
τ
- time constant
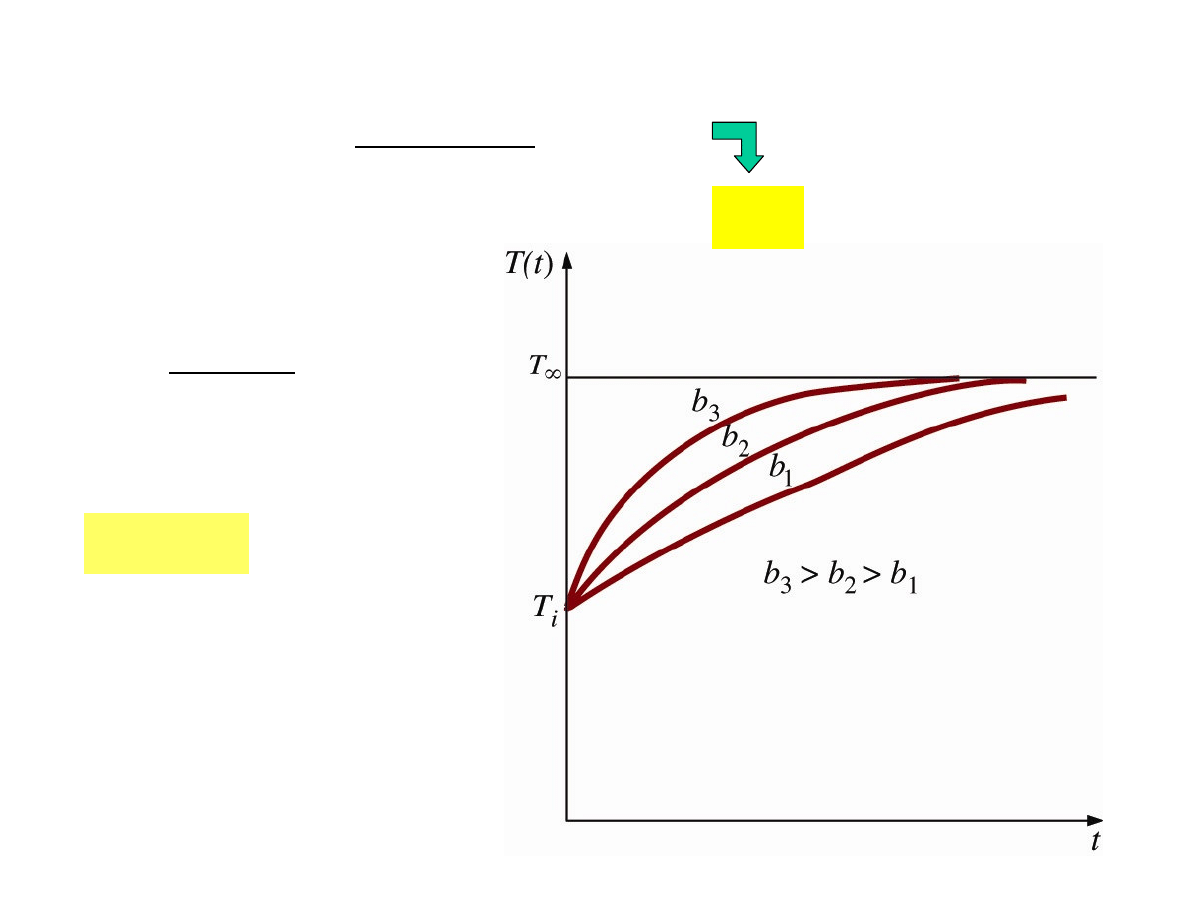
The
T
of a body approaches the
ambient temperature
T
∞
∞
∞
∞
exponentially:
- the larger
b
value, the higher
rate of
T
decay.
)
(t
T
temperature
of a body at
time
t
The
actual rate
of convection heat transfer between the body
and its environment – from Newton`s law of cooling:
]
)
(
[
)
(
∞
•
−
=
T
t
T
hA
t
S
Q
)
(W
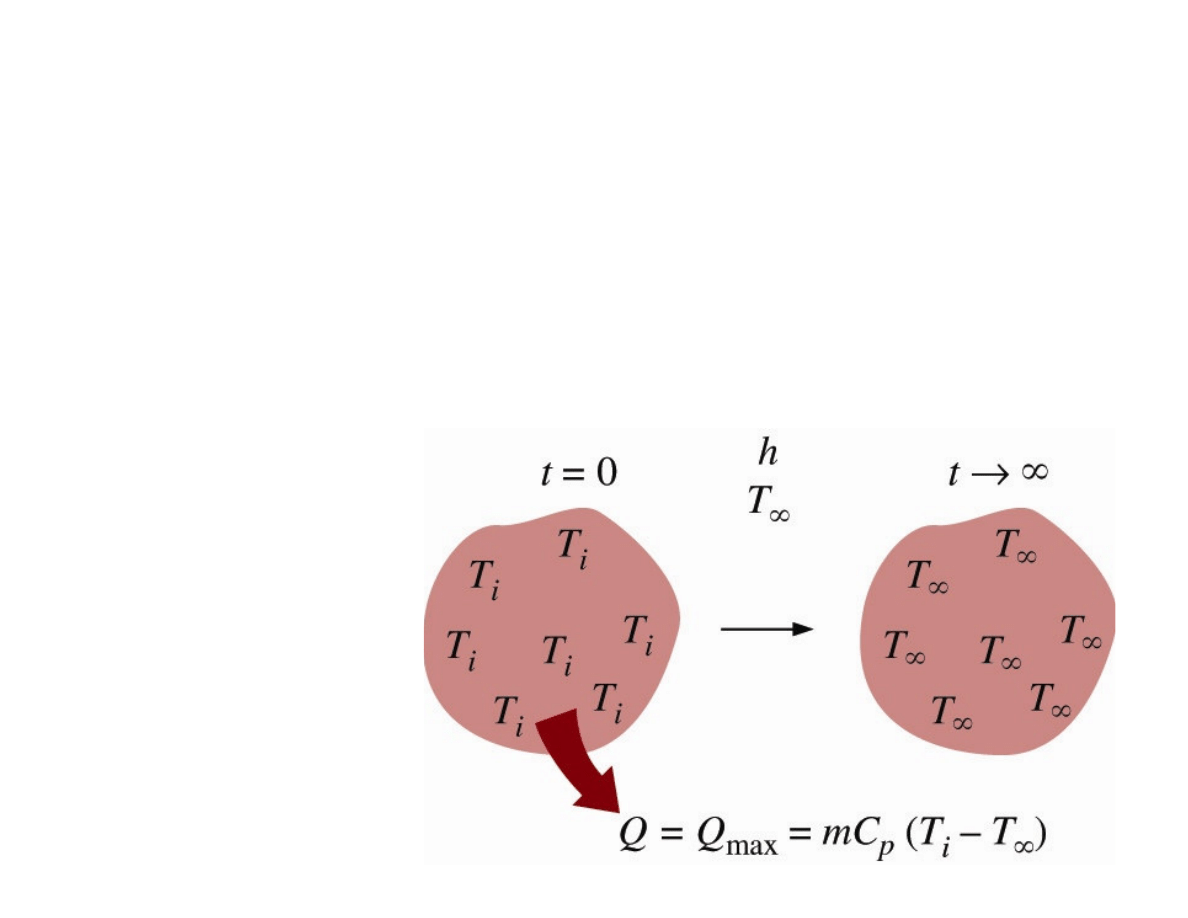
The
total amount
of heat transfer between the body and the
surrounding medium over the time interval (0 – t) is the
change in the energy content of the body:
]
)
(
[
i
p
T
t
T
mC
Q
−
=
)
(kJ
Heat transfer to
or from a body
reaches its
maximum value
when the body
reaches the
environment
temperature
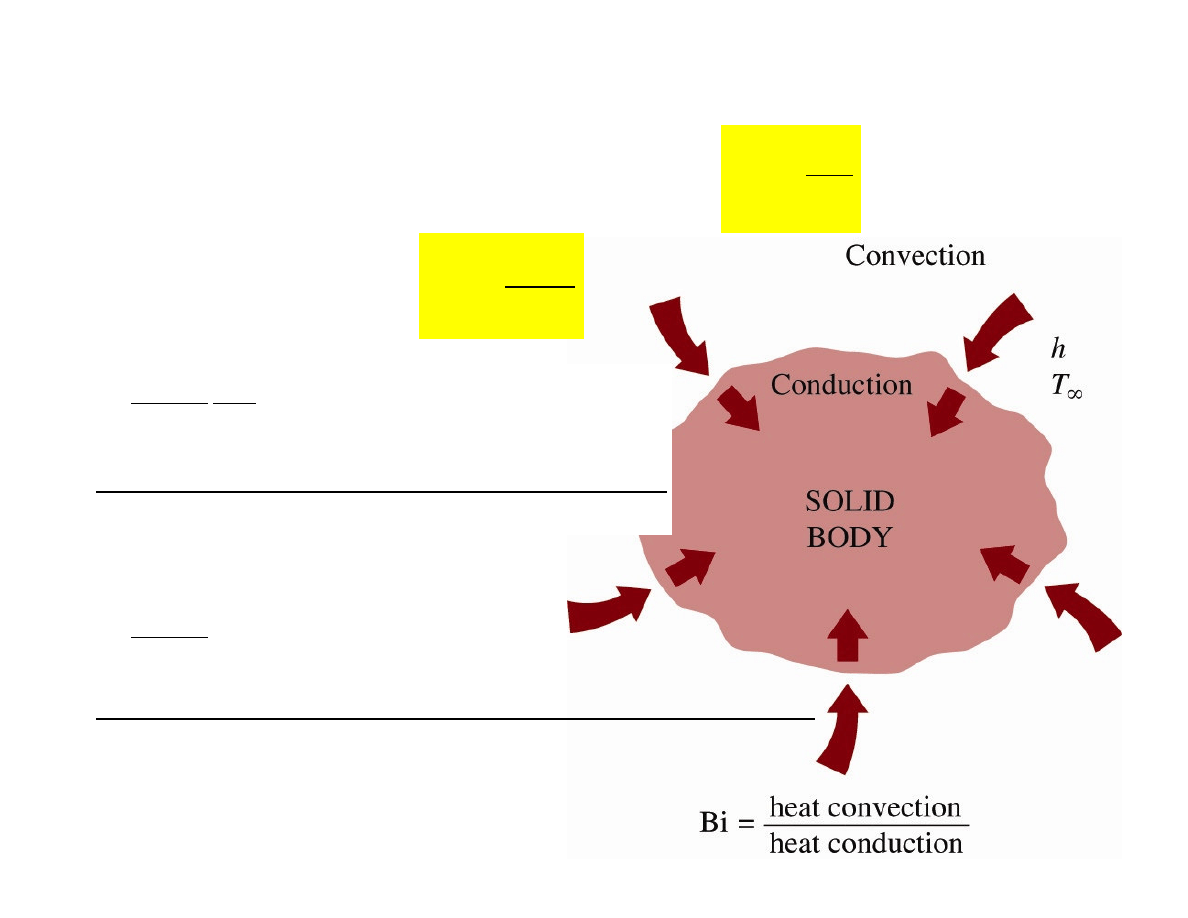
Lumped system
– great convenience in heat transfer analysis
Criterion for the applicability
→
→
→
→ definition of a
characteristic length
S
C
A
V
L
=
and a
Biot number
Λ
=
C
hL
Bi
Also:
body
the
within
Conduction
body
the
of
surface
the
at
Convection
T
T
L
h
Bi
C
_
_
_
_
_
_
_
_
_
/
=
∆
∆
Λ
=
or:
body
the
of
surface
the
at
ce
tan
resis
Convection
body
the
within
ce
tan
resis
Conduction
h
L
Bi
C
_
_
_
_
_
_
_
_
_
_
_
/
1
/
=
Λ
=
Meaning of Biot number
→
→
→
→
• Small Biot number represents small resistance to heat
conduction
→
→
→
→ small T gradients within the body
• Lumped system - a uniform T distribution throughout the body
→
→
→
→ conduction resistance = 0
Thus, lumped system analysis is exact when Bi = 0
and approximate when Bi
>
>
>
> 0.
Estimation of an accuracy of lumped system analysis
→
→
→
→ Typical uncertainty in the convection heat transfer coefficient
h
is about
20%
It is generally accepted that lumped system analysis is applicable
if
1
.
0
≤
Bi
The temperature variations with location within the body is
slight (
<
<
<
< 5%) →
→
→
→ small bodies with high thermal conductivity in
a medium that is a poor conductor of heat (air)
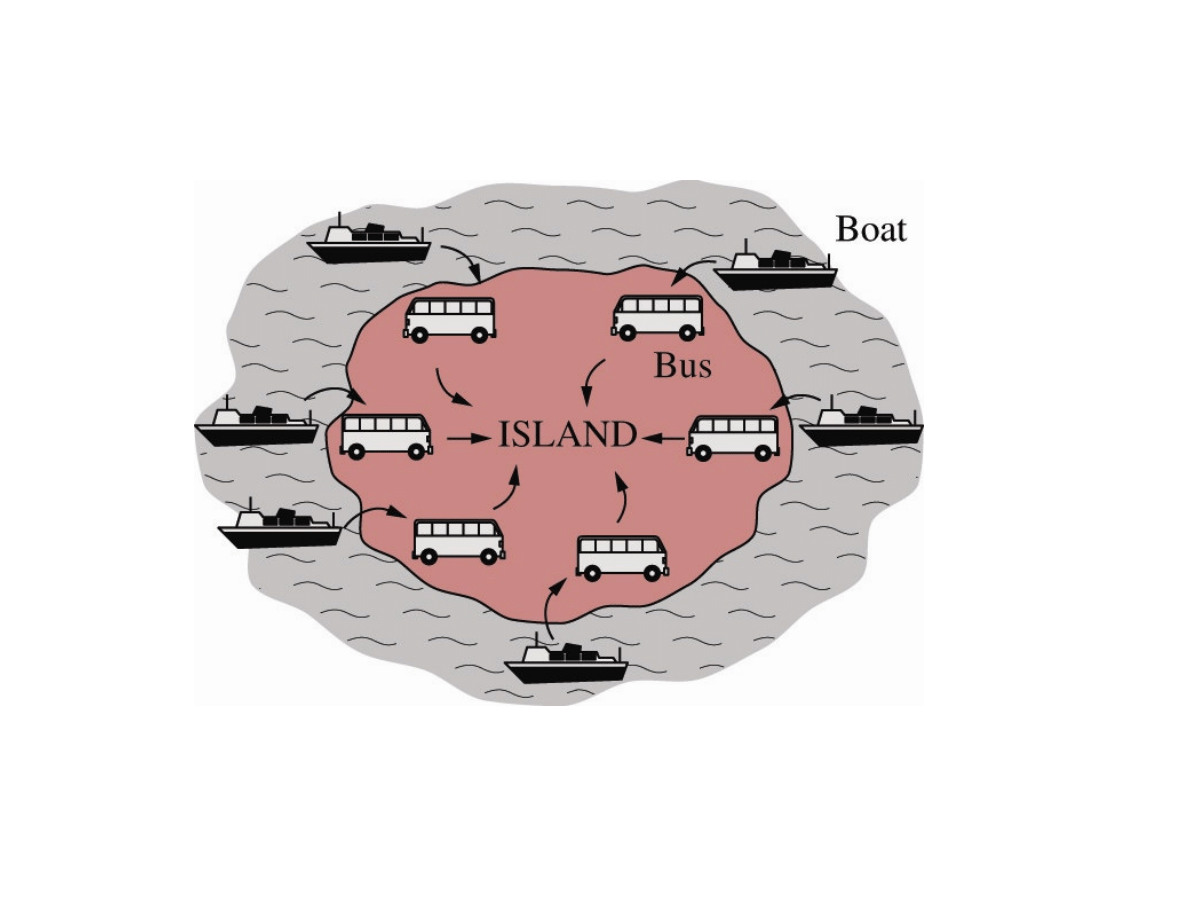
Analogy between heat transfer to a solid and
passenger traffic to an island
Lumped system – small island with plenty of fast buses
(no overcrowding at the harbour = accumulation of heat)
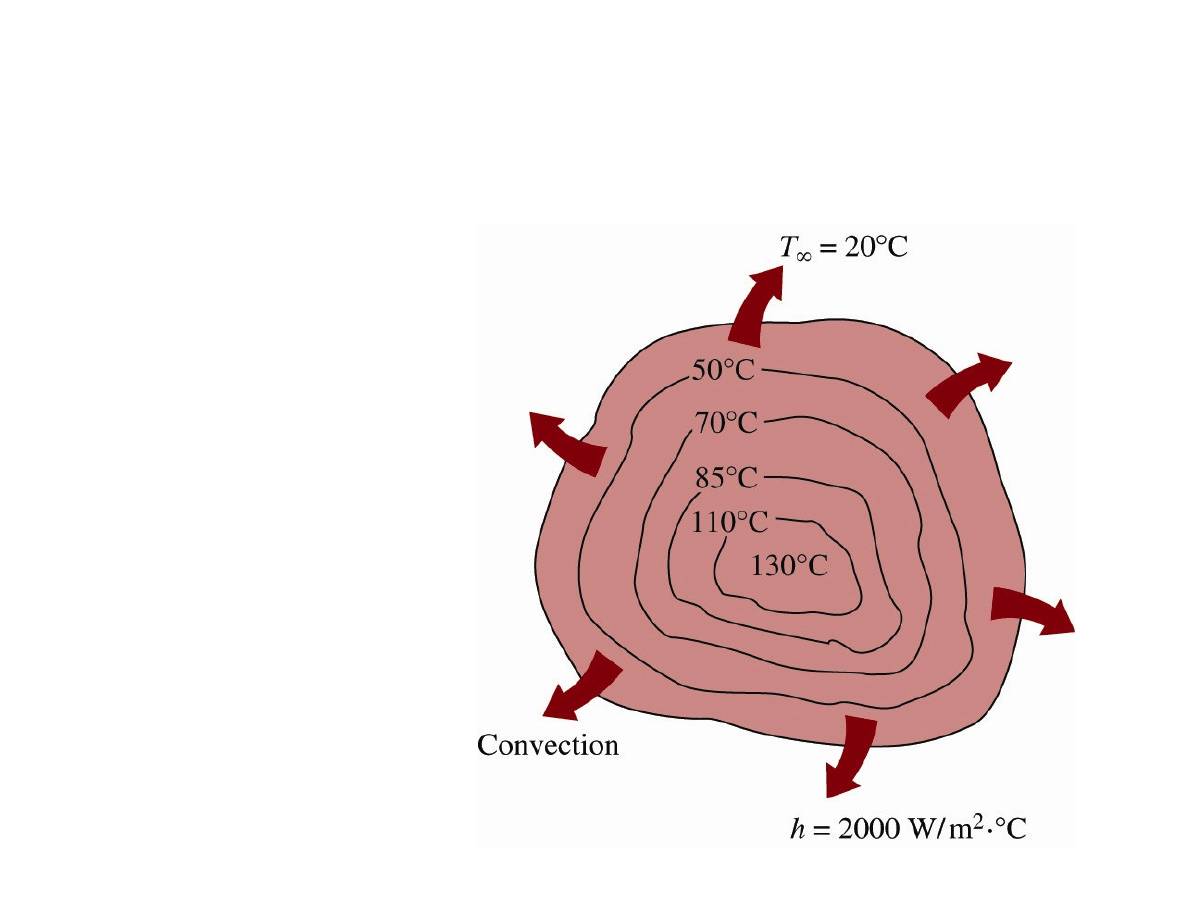
Example of non-lumped system
:
high value of the convection heat transfer coefficient
h
→
→
→
→ large T difference between the inner and outer regions
On the other hand:
The larger the thermal conductivity
Λ
Λ
Λ
Λ
,
the smaller the temperature gradient
within the body.
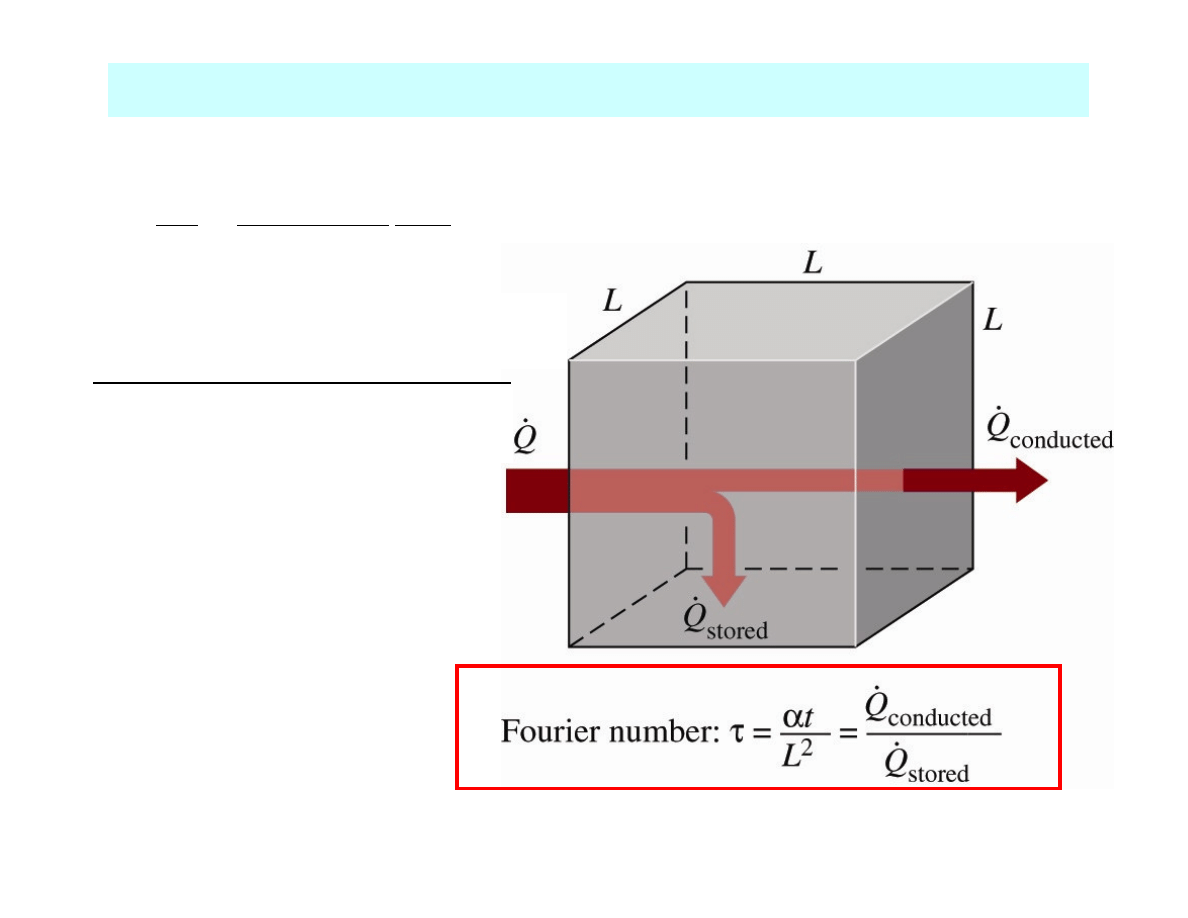
TRANSIENT SYSTEMS
The variation of the T profile with time in the plane etc.
where:
α
α
α
α
is the thermal diffusivity in (m
2
/s)
T
T
t
L
C
L
L
L
t
p
∆
∆
Λ
=
=
/
)
/
1
(
3
2
2
ρ
α
τ
The rate at which heat is conducted
across L of a body of volume L
3
The rate at which heat is stored
in a body of volume L
3
=
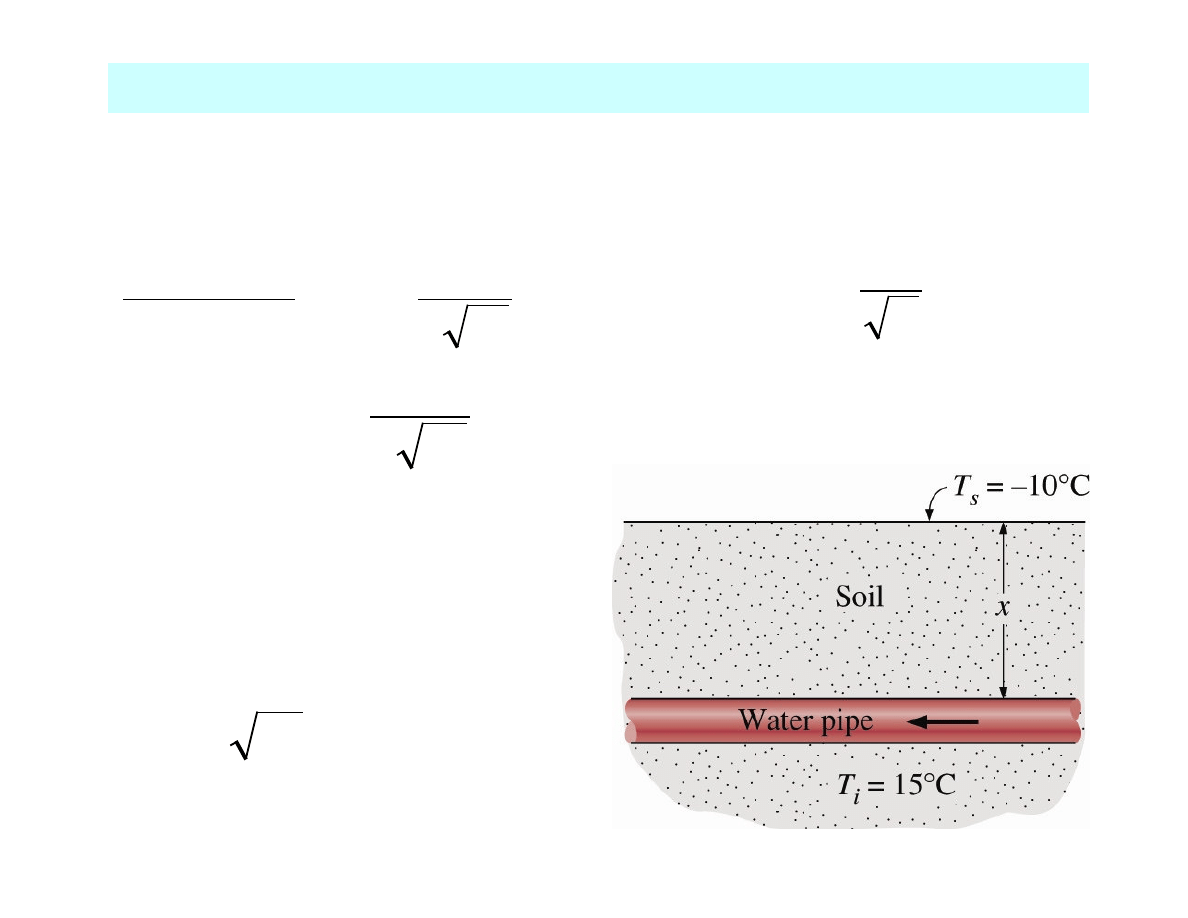
TRANSIENT HEAT CONDUCTION IN SEMI-INFINITE SOLIDS
For the special case of
h
→
→
→
→ ∞
∞
∞
∞
, the surface temperature
T
S
becomes equal to the fluid temperature
T
∞
∞
∞
∞
, and
=
−
−
t
x
erfc
T
T
T
t
x
T
i
S
i
α
2
)
,
(
du
e
erfc
u
∫
−
−
=
ξ
π
ξ
0
2
2
1
)
(
The complementary error function
t
x
α
ξ
2
=
Example
Minimum burial depth of water
pipes to avoid freezing
m
t
x
80
.
0
2
=
=
α
ξ
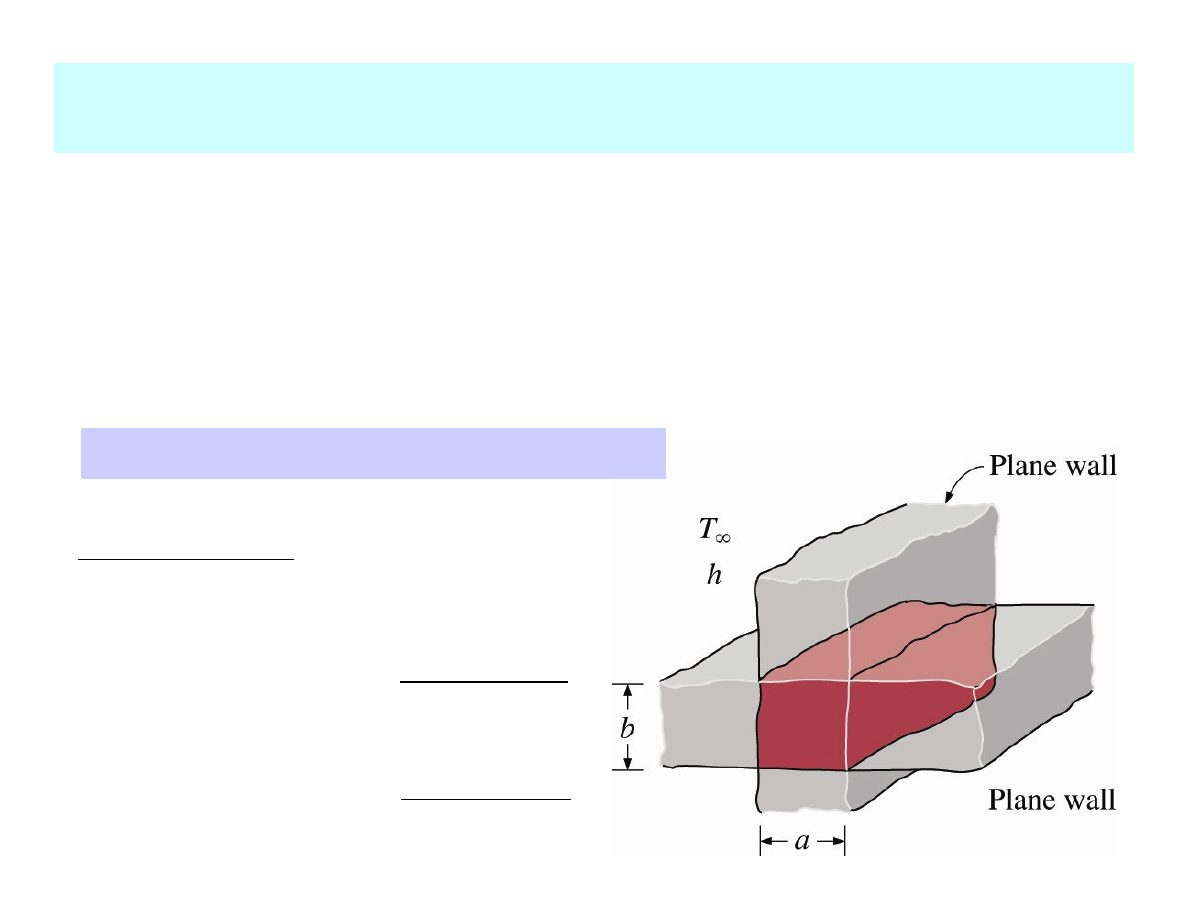
TRANSIENT HEAT CONDUCTION IN MULTIDIMENSIONAL
SYSTEMS
For 2D and 3D systems – a superposition approach called a
product solution (based on charts containing numerical
solutions for 1D systems)
Example
A solid bar of rectangular profile a
×
×
×
× b is the intersection of two
plane walls of thickness a and b.
Transient T distribution in the bar:
)
,
(
)
,
(
)
,
,
(
t
y
t
x
T
T
T
t
y
x
T
wall
wall
bar
i
θ
θ
=
−
−
∞
∞
where:
∞
∞
−
−
=
T
T
T
t
x
T
t
x
i
wall
)
,
(
)
,
(
θ
∞
∞
−
−
=
T
T
T
t
y
T
t
y
i
wall
)
,
(
)
,
(
θ