Jesteś tu:

Bossa.pl

»

Edukacja

»

AT

»

Techniki

» Gann

Wybrane zagadnienia teorii Ganna

William D. Gann (1878 - 1955) był legendą rynków kapitałowych i towarowych pierwszej połowy

ubiegłego stulecia. W ciągu swojej błyskotliwej kariery często osiągał kilkusetprocentową stopę zwrotu w

stosunkowo krótkim czasie :

[1]

1908 r. - w ciągu 30 dni rachunek o początkowej wysokości 130 USD zwiększył do 12 000 USD

1923 r.- w ciągu 60 dniu kwota 973 USD została powiększona do 30 000 USD

1933 r.- spośród 479 transakcji, jakie przeprowadził w tym roku, aż 422 okazały się udanymi

(88%). Uzyskana w ten sposób stopa zwrotu wyniosła ponad 4000%

1946 r. - w ciągu 3 miesięcy zysk netto przy wykorzystaniu początkowego kapitału w postaci 4500

USD wyniósł 13 000 USD (stopa zwrotu osiągnęła zatem prawie 300%).

Jego teorię można określić jako ścisłe połączenie zasad arytmetyki i geometrii. W latach 50-tych i 60-tych

większość jego prac była niedostępna w formie pisanej. Dopiero, kiedy w 1976 r. B. Jones nabył firmę

wydawniczą Lambert - Gann Publishing Company, a wraz z nią prawa autorskie Ganna, wiele z teorii

tego geniusza giełdy zostało przypomnianych społeczeństwu. Najbardziej popularnymi z nich okazały się

analiza cykli Ganna , linie Ganna i liczby Ganna .

[2]

[3]

[4]

Wachlarz Ganna

Istotne znaczenie przywiązywał Gann do połączenia koncepcji ceny i czasu. Przypuszczał on, że

pomiędzy tymi dwoma aspektami istnieją określone relacje. Według koncepcji równowagi czasu i ceny,

wyrażona w jednostkach pieniężnych wartość istotnego szczytu cenowego zostaje przełożona na liczbę

jednostek kalendarzowych (dni, tygodni, miesięcy) jakie muszą upłynąć aby doszło do utworzenia

kolejnego znaczącego ekstremum cenowego. Jeśli zatem rynek osiągnął istotny szczyt na poziomie X

jednostek pieniężnych, należy odmierzyć od tego momentu 100 dni, tygodni, miesięcy lub lat, uzyskując

w ten sposób daty potencjalnych punktów zwrotnych na rynku.

W. D. Gann był twórcą technik będących połączeniem kątów geometrycznych z danymi cenowymi i

szeregami czasowymi . Był on przekonany, że istnieje idealna równowaga między upływem czasu a

[5]

zmianami cen na rynku kapitałowym. Taka równowaga ma miejsce, gdy ceny rosną lub spadają pod

kątem 45 stopni w stosunku do osi czasu. Jest to tzw. kąt 1*1 (jednostce upływu czasy towarzyszy zmiana

ceny o jednostkę). Linie kątów Ganna wykreśla się pomiędzy istotnymi minimum i maksimum cenowym

i prowadzi się je pod różnymi kątami.

Pełen zestaw kątów Ganna przedstawia się następująco:

1*8 - 82,5 stopnia

1*4 - 75 stopni

1*3 - 71,25 stopnia

1*2 - 63,75 stopnia

1*1 - 45 stopni

2*1 - 26,25 stopnia

3*1 - 18,75 stopnia

4*1 - 15 stopni

8*1 - 7,5 stopnia

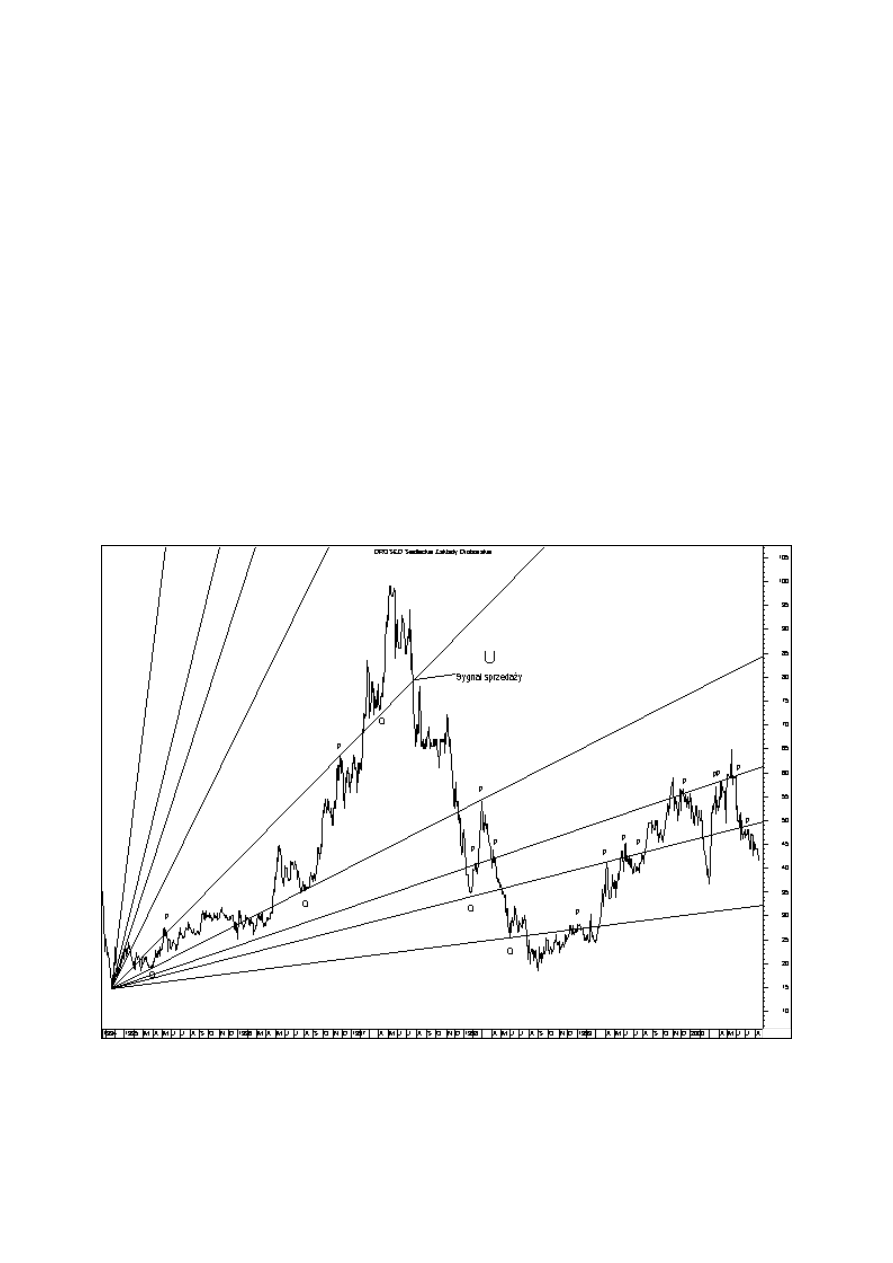
Rysunek 1. Przykład zastosowania wachlarza (kątów) Ganna na wykresie spółki Drosed.

Źródło: opracowanie własne

Wg Ganna linia 1*1 jest silną linią wsparcia dla trendu wzrostowego a moment jej przełamania stanowi

kluczowy sygnał znaczącego odwrócenia trendu. Jeśli cena aktywu znajduje się powyżej wzrastającej linii

45 stopni, mamy do czynienia z rynkiem byka, natomiast jeśli plasuje się ona poniżej zniżkującej linii 1*1

- z rynkiem niedźwiedzia. Kiedy podczas trendu wzrostowego ceny spadają do tej linii, czas i cena

znajdują się w doskonałej równowadze. Przełamanie linii 45 stopni wskazuje na zakłócenie tej

równowagi i możliwe staje się odwrócenie trendu. Posługując się linią 1*1 można wtedy wyznaczyć linię

kanału prowadząc je od istotnego szczytu lub dołka - równolegle do podstawowej linii trendu. Przykład

wachlarza Ganna przedstawiony został poniżej (Rysunek 1). Poszczególne linie wachlarza stanowią

poziomy wsparcia lub oporu (oznaczone strzałkami w górę i w dół), bardzo często wyznaczając

krótkoterminowy trend wzrostowy lub spadkowy, jak to ma miejsce na wykresie cen kontraktów

terminowych na półtusze wieprzowe (Rysunek 2) i indeksie S&P 500 (Rysunek 3). Na kolejnym rysunku

przedstawiona została tzw. siatka Ganna o wymiarach 80*80

na wykresie indeksu S&P. Każda z

linii reprezentuje linię 1*1 z wachlarza Ganna. Odległość między przecięciami poszczególnych

kwadratów wynosi 80 jednostek (w naszym przypadku tygodni). Poszczególne linie siatki stają się liniami

wsparcia i oporu.

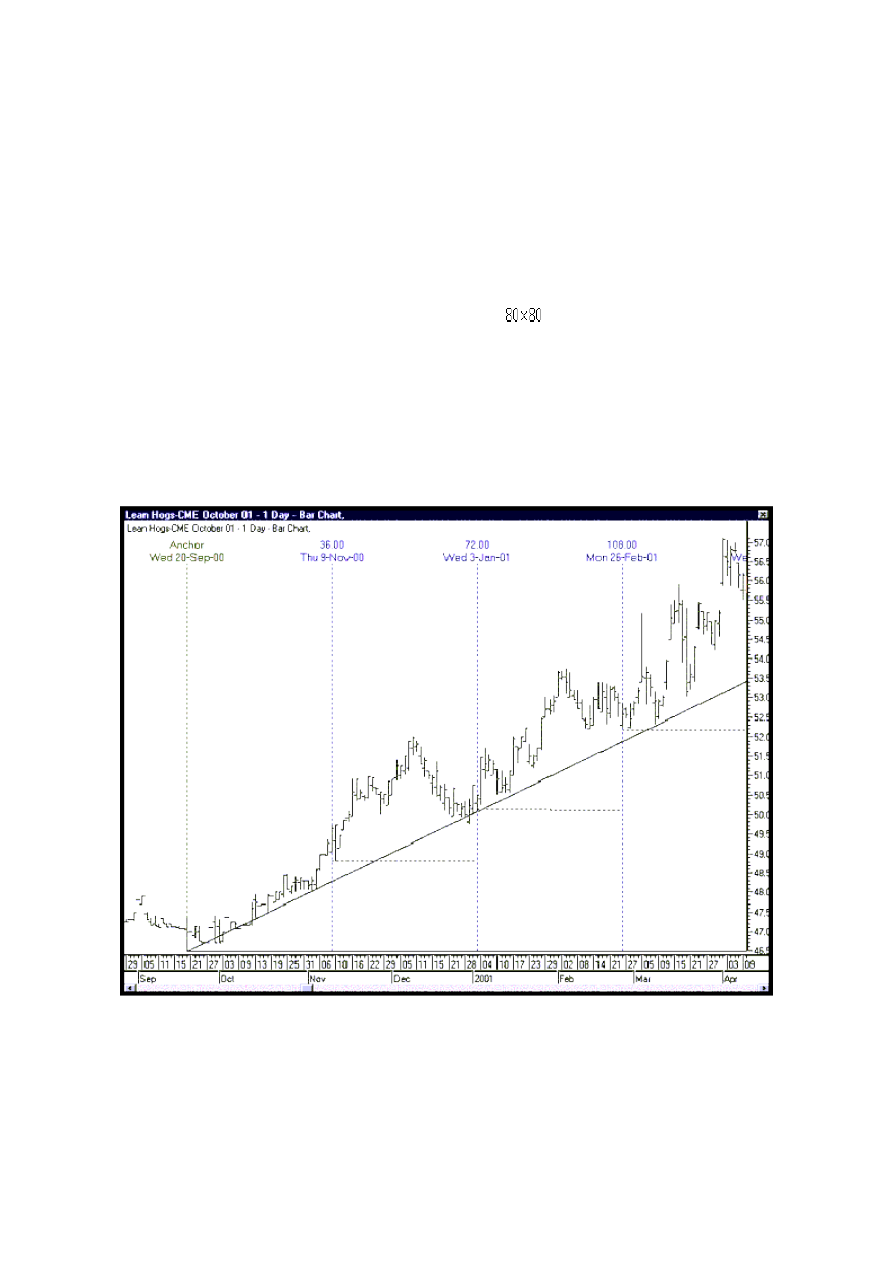
Rysunek 2. Linia 2*1 wachlarza Ganna stanowiąca trend wzrostowy na wykresie

kontraktu terminowego na półtusze wieprzowe wygasającego w październiku 2001.

Źródło: opracowanie własne

Rysunek 3. Linia 2*1 wachlarza Ganna stanowiąca trend wzrostowy na wykresie indeksu S&P500.

Układ tygodniowy.

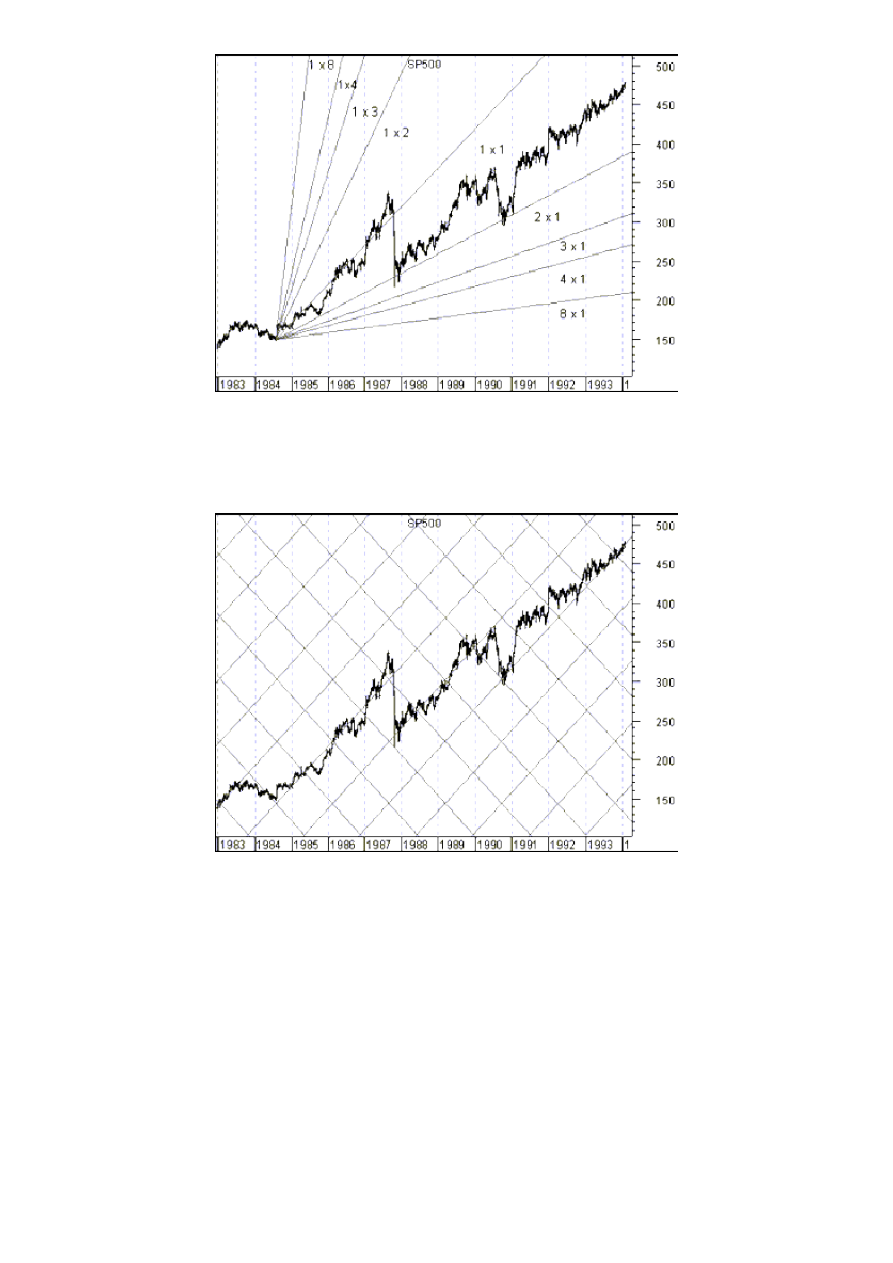
Źródło: opracowanie własne

Rysunek 4. Siatka Ganna na wykresie indeksu S&P500.

Układ tygodniowy.

Źródło: opracowanie własne

W zależności od trendu, każdy z kątów stosowanych przez Ganna może stać się poziomem wsparcia lub

oporu. Po przełamaniu linii tworzonej przez jeden z kątów, ceny zmieniają położenie i konsolidują się

wokół poziomu wyznaczonego przez następny z kątów. Zdaniem twórcy metody linie 1*3 oraz 3*1 są

najbardziej przydatne na wykresach długoterminowych sporządzanych w ujęciu tygodniowym i

miesięcznym. Geometryczne linie Ganna wykorzystywane są analogicznie do linii tempa (tj. linii

wachlarza) Fibonacciego. W trendzie wzrostowym stanowią one obszary wsparcia, a w trendzie

spadkowym obszary oporu. W tendencji zwyżkującej przełamanie jednej z linii zapowiada dalszy spadek

do kolejnej, niższej linii. Podobnie, jeśli ceny przebiją się ponad jedną linię, można oczekiwać, że dotrą

do kolejnej, wyższej linii.

Kwadrat, koło, heksagon i trójkąt

Najważniejszymi figurami geometrycznymi w koncepcji Ganna są: koło, trójkąt i kwadrat.

[6]

Kwadrat zwany też kardynalnym jest metodą wyznaczania poziomów przyszłego oporu lub wsparcia.

Polega ona na odmierzaniu pewnych jednostek czasu od historycznie najniższego poziomu ceny danego

aktywu. Cena wyjściowa zostaje umieszczona w środku kwadratu, po czym zgodnie z ruchem wskazówek

zegara wprowadza się kolejne ceny systematycznie wzrastające o pewną stałą wielkość (skok ceny).

Liczby wypadające w ramionach krzyża powstałego z poziomych i pionowych linii przecinających się w

środku kwadratu, stanowią najbardziej prawdopodobne obszary zatrzymania ceny w przyszłości. Pewną

modyfikacją tej metody jest wykorzystywanie na wykresie kwadratu kardynalnego również linii ukośnych

(przekątnych) wyznaczających potencjalne punkty zwrotne. Poniżej przedstawiony został kwadrat

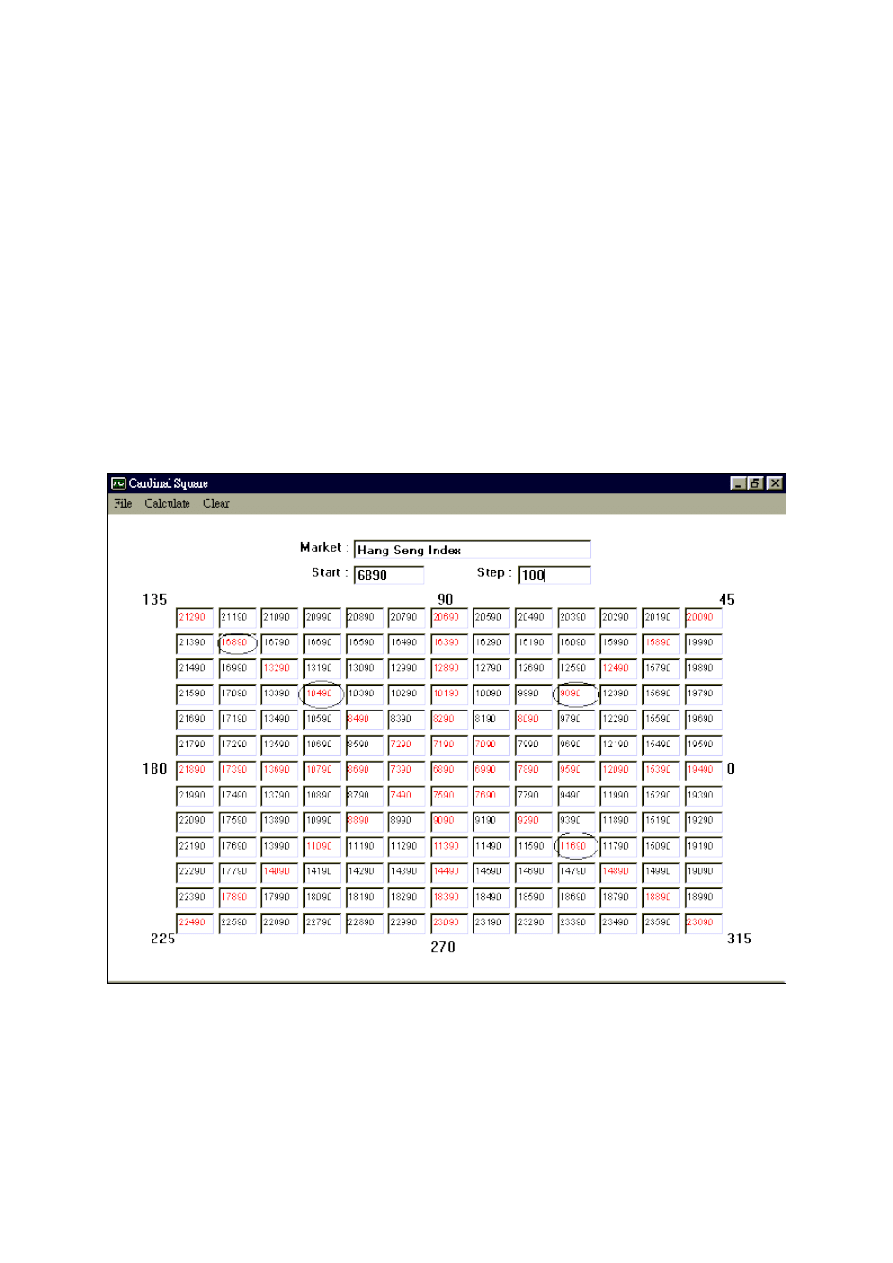
cenowy dla dołka indeksu Hang Seng 6890 punktów i krokiem 100 punktów - Rysunek 5.

Rysunek 5. Kwadrat cenowy utworzony dla indeksu Hang Seng

Źródło: opracowanie własne

Punkty znajdujące się w polach zakreślonych stanowią najważniejsze poziomy oporu - rysunek poniżej.

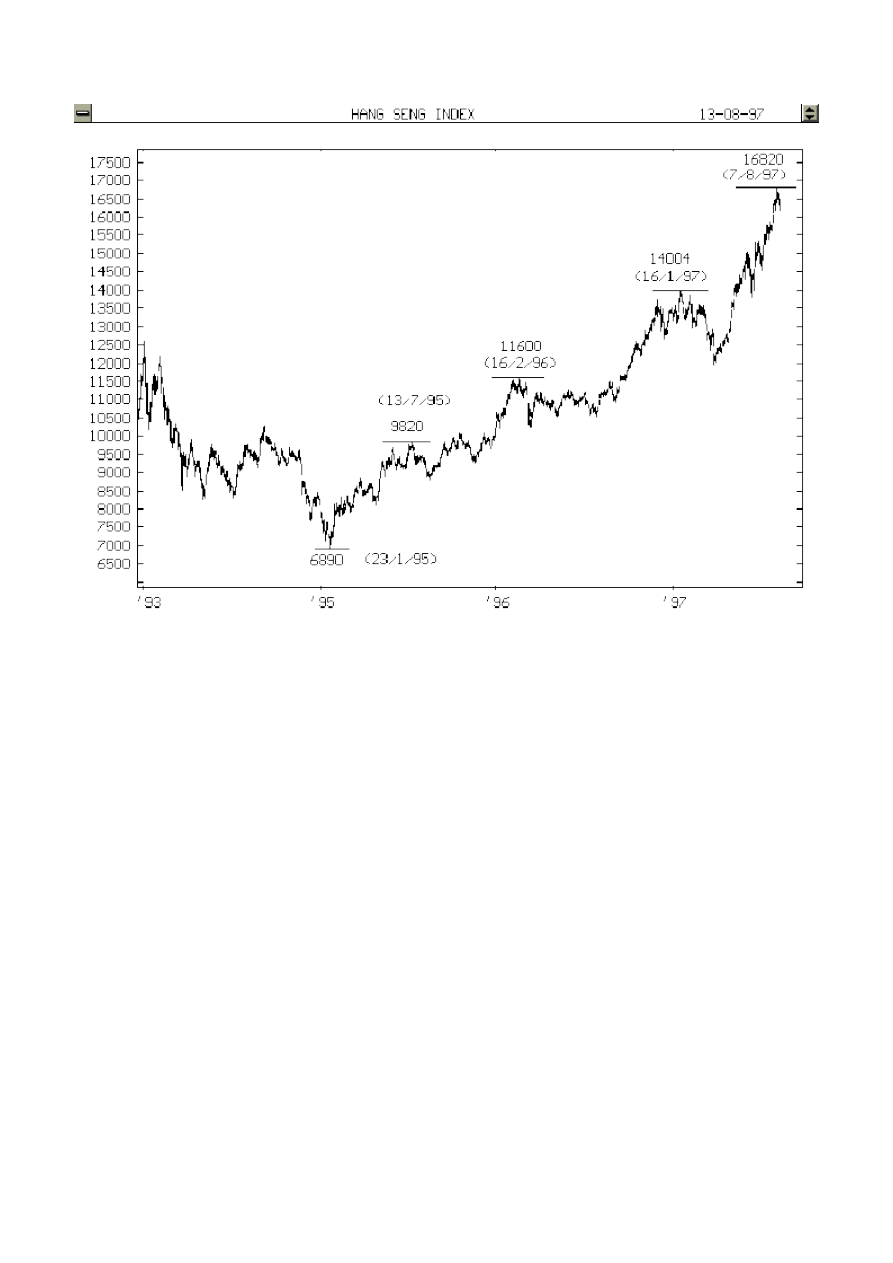
Rysunek 6. Poziomy oporu zaznaczone na wykresie indeksu Hang Seng

Źródło: opracowanie własne

Postępując w analogiczny sposób możemy otrzymać również poziomy wsparcia.

Konstrukcja koła i heksagonu jest analogiczna do konstrukcji kwadratu kardynalnego. Na kolejnych

rysunkach przedstawione zostały przykłady koła i heksagonu Ganna.

Koła i heksagony Ganna stanowią bezpośrednie połączenie ceny z czasem (innymi słowy jest to

rozwijanie spirali cenowej od środka figury). Brzeg zewnętrzny koła i heksagonu zostały podzielone wg

zasady, że upływ 365 dni roku reprezentuje obrót o 360 stopni.

Kwadraty służą do wyznaczania punktów wsparcia i oporu - w tym przypadku należy w środku figury

umieścić wartość historycznego dołka lub szczytu. Jeśli jednak w środku takiej figury umieścimy datę

istotnego punktu zwrotnego, wtedy na wybranych osiach otrzymamy daty potencjalnych punktów

zwrotnych. Rysunek 9 zawiera przykład kwadratu kardynalnego wyznaczającego istotne czasowe punkty

zwrotne dla cen kontraktów terminowych na indeks giełdy australijskiej.

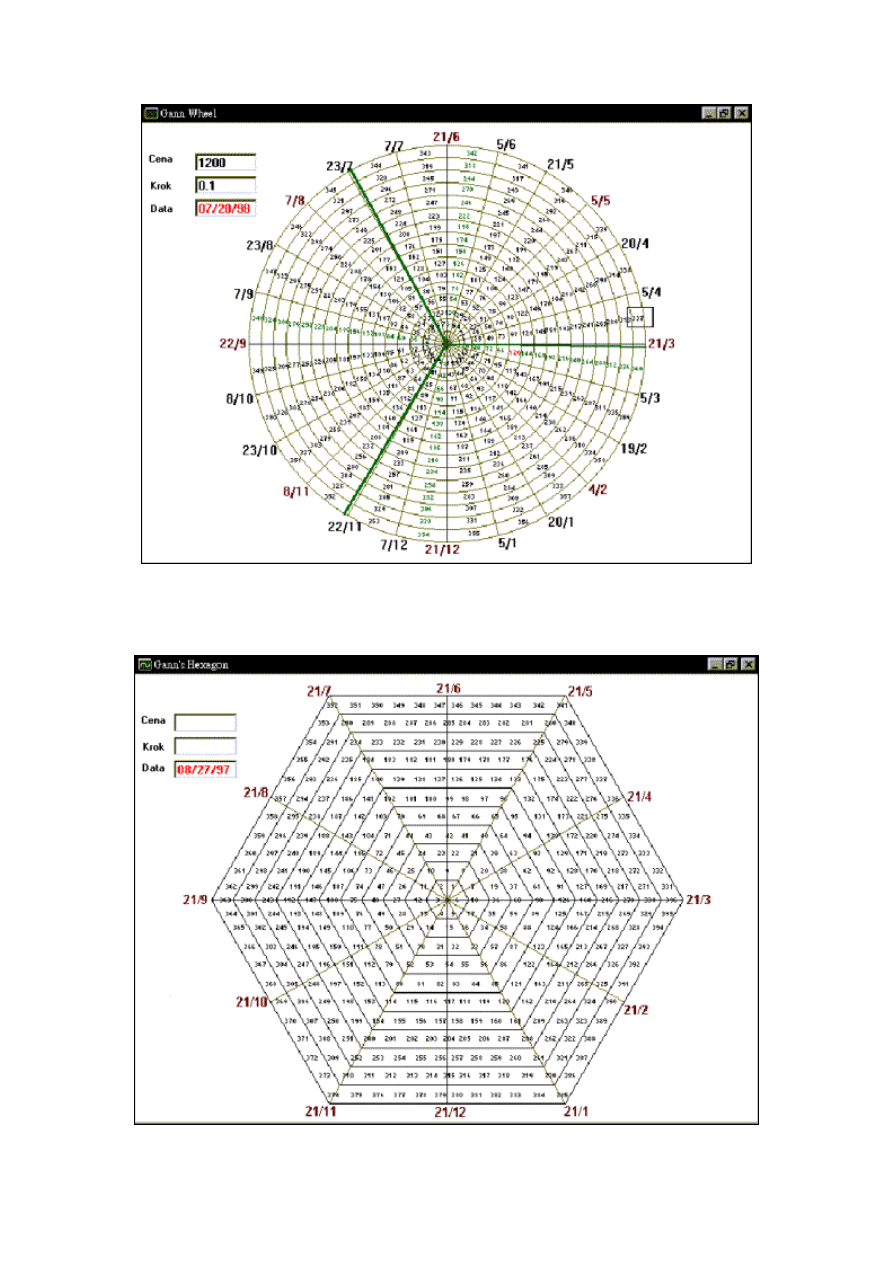
Rysunek 7. Koło Ganna - połączenie ruchu ceny z upływem czasu

Źródło: opracowanie własne

Rysunek 8. Heksagon Ganna - połączenie ruchu ceny z upływem czasu

Źródło: opracowanie własne

Rysunek 9. Przykład kwadratu kardynalnego z czasową projekcją punktów zwrotnych.

Źródło: opracowanie własne

Rysunek 10 ilustruje połączenie kwadratu kardynalnego z podziałem koła na 360 stopni.

Rysunek 10. Połączenie kwadratu kardynalnego z kołem.

Źródło: opracowanie własne

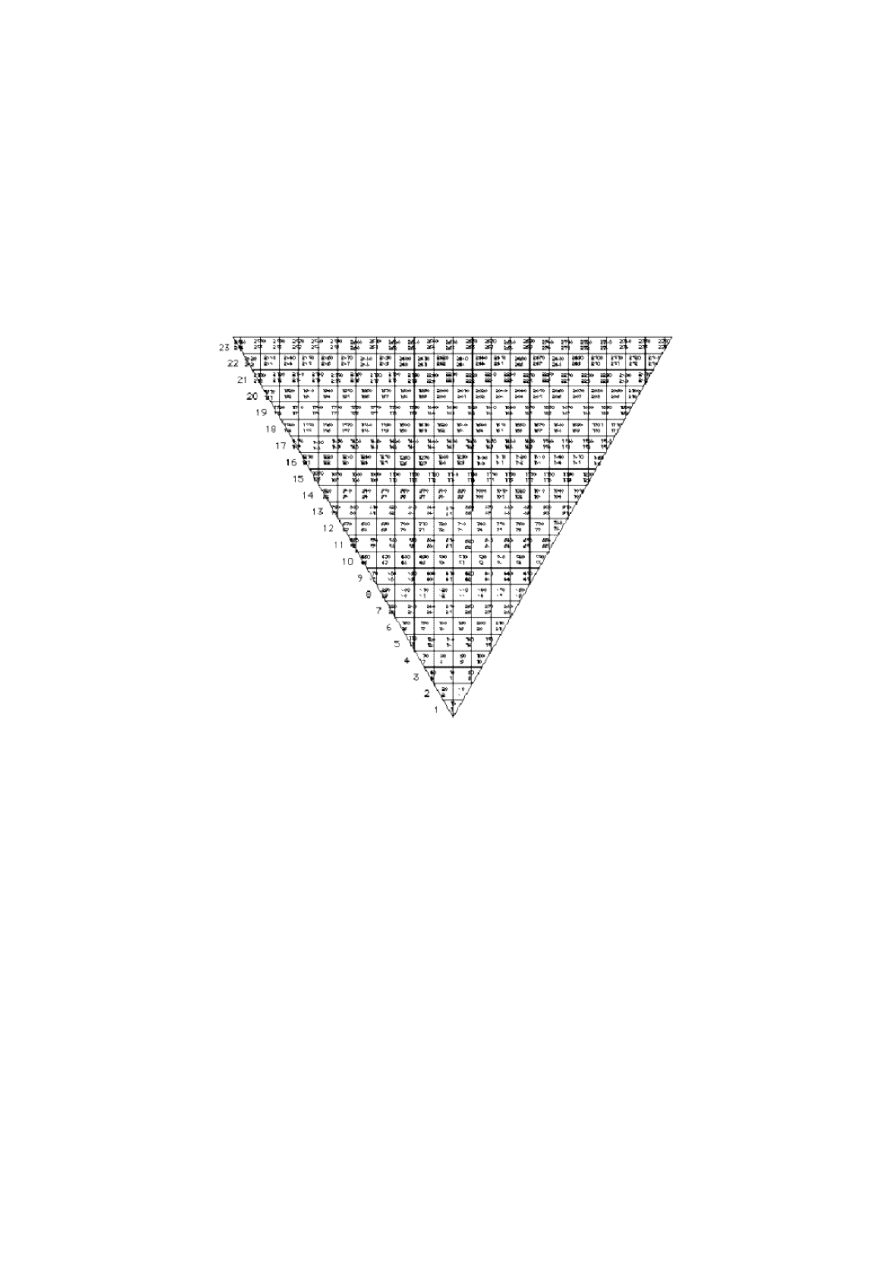
Ostatnią figurą wykorzystywaną przez Ganna był trójkąt. W dolnym polu wpisana została wartość

minimum cenowego danego aktywu. Następnie przechodząc do kolejnego wiersza, wpisujemy ceny

zwiększając każdą z nich o wartość ustalonego wcześniej kroku (skok ceny). Ceny leżące na brzegach

trójkąta stanowią potencjalne punkty zwrotne. Przy ich obliczeniu należy uwzględnić fakt podziału

poszczególnych małych kwadracików cenowych przez linie ograniczające. Stosunek pola nie wyciętego

przez linię ograniczającą do całkowitej wartości pola kwadracika, wyznacza precyzyjnie wartość

potencjalnego punku zwrotnego.

Rysunek 11. Przykład trójkąta cenowego Ganna.

Źródło: opracowanie własne

Cykle Ganna

Szczególną rolę w teorii Ganna odgrywa podział koła na 360 stopni. Harmonia pełnego okręgu została

wykorzystana do wyznaczenia przyszłych punktów zwrotnych rynku. Gann odliczał do przodu: 30, 45,

60, 72,

, 121, 152,

, 213, 243,

, 304, 335 i 

dni od istotnych dołków lub szczytów, uzyskując

91

182

273

360

w ten sposób potencjalne punkty zwrotne (liczby wytłuszczone miały dla niego szczególne znaczenie) .

[ ]

7

Najważniejszy moment przypada według niego dokładnie po upływie roku kalendarzowego od lokalnego

ekstremum . Metoda Ganna sprawdzała się najlepiej na rynkach produktów rolnych, które są w oczywisty

sposób powiązane z cyklami pór roku.

Istotne dni zmiany trendu mogą przypadać także po upływie okresu czasu mierzonego od istotnego

szczytu lub dołka, będącego wielokrotnością liczby 7. Z uwagi na fakt, że tydzień liczy 7 dni,

a kwadratem tej liczby jest 49, to najważniejsze odwrócenia trendów obserwowane na rynku, znajdują się

w odległości od 49 do 52 dni od początku ruchu.

Szczególne znaczenie mają wg Ganna punkty zwrotne położone w odległości 7 miesięcy od kluczowego

ekstremum cenowego. Nie należy też jego zdaniem lekceważyć istotnych rocznic ważnych szczytów lub

dołków.

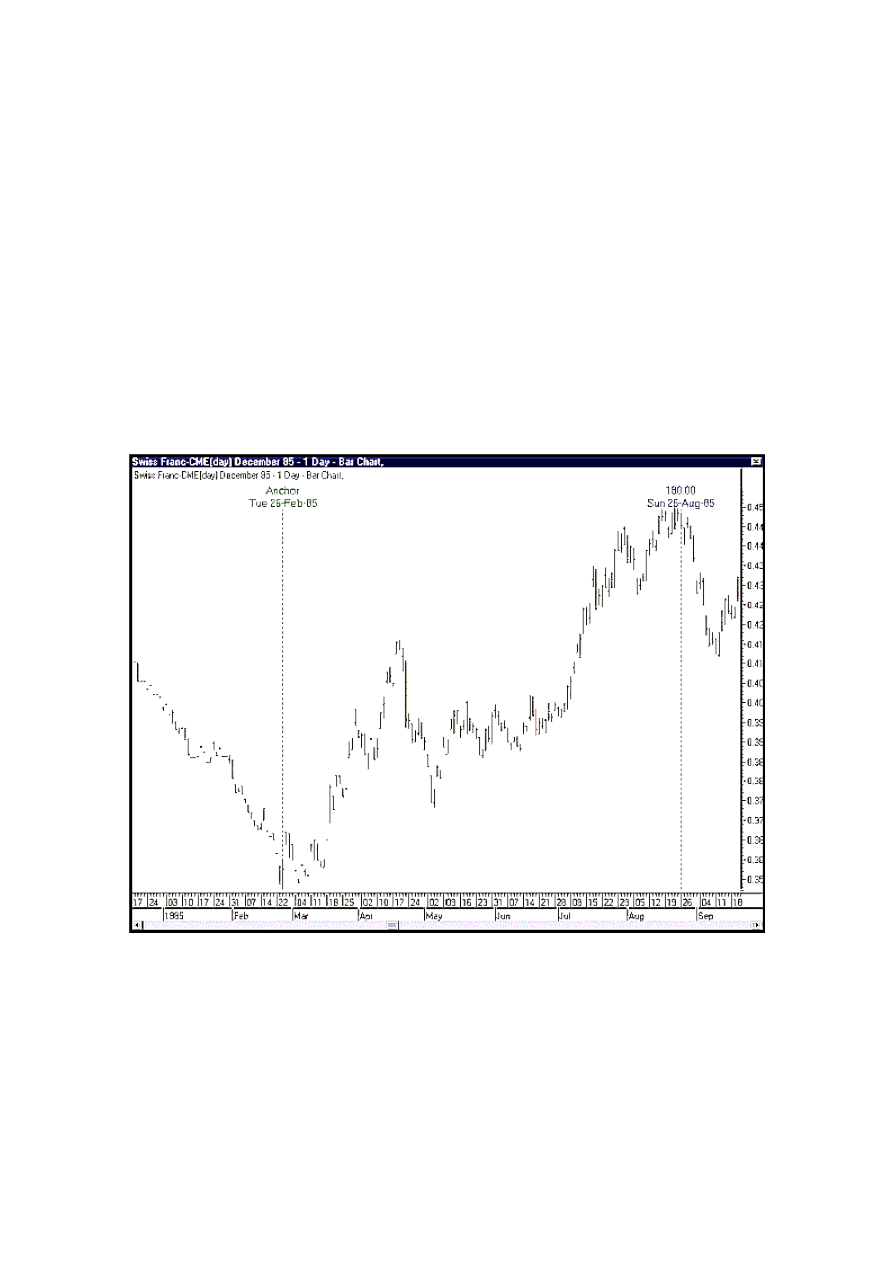
Rysunek 12. Przykład kontraktu na kurs franka szwajcarskiego do dolara amerykańskiego.

Dno utworzone zostało 25 lutego 1985 r.

Odległość 180 dni od tego punktu zwrotnego przypada 25 sierpnia 1985 r.

Okazało się, że istotny punkt zwrotny wystąpił 22 sierpnia.

Źródło: obliczenia własne na podstawie programu komputerowego Market Analyst III.

Rysunek 13. Wyznaczanie dnia docelowego na bazie odległości między punktami zwrotnymi A i B oraz

współczynnika G.

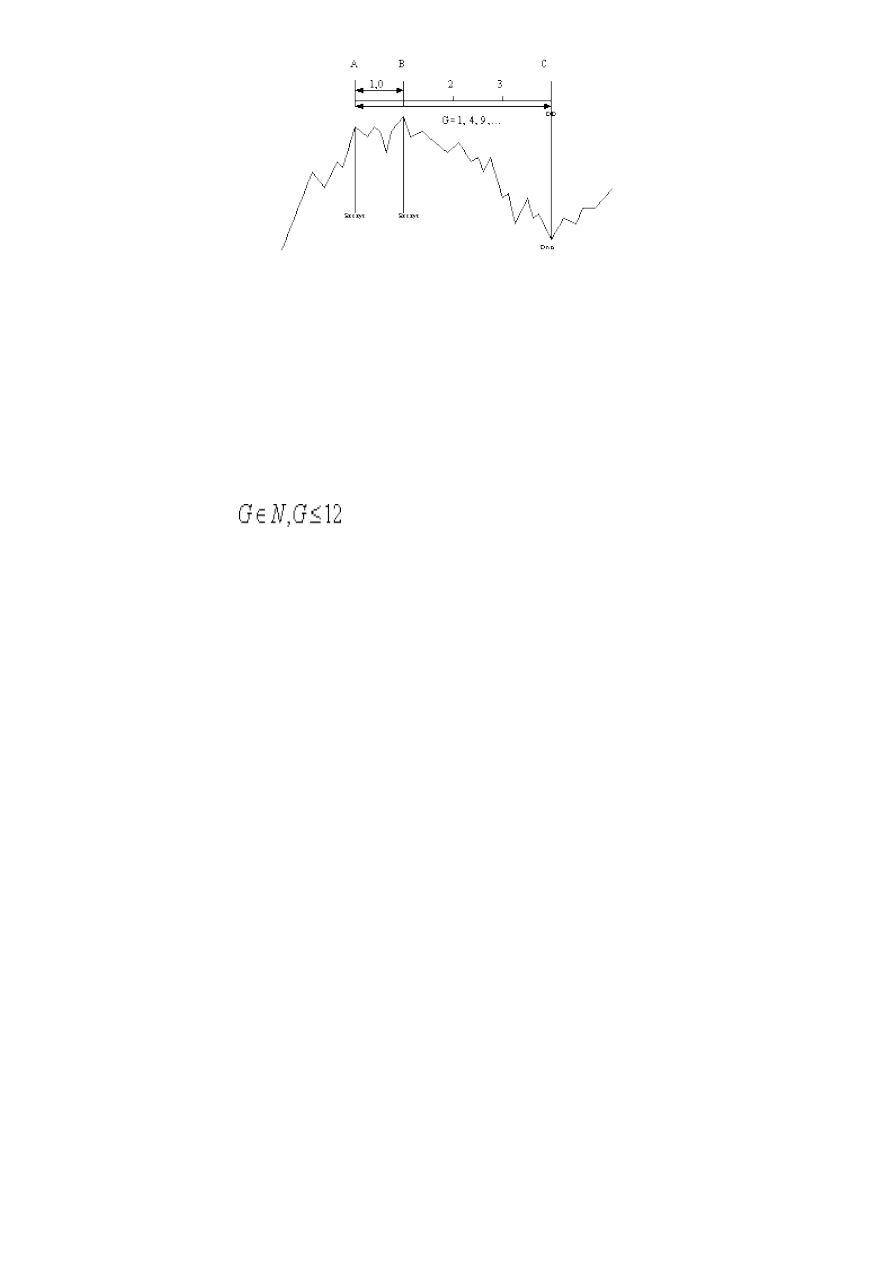
Źródło: opracowanie własne

Trzeci szereg, z którego korzystał Gann był oparty na kwadratach liczb od 1 do 12 tj.: 1, 4, 9, 16, 25, 36,

49, 64, 81, 100, 121, 144. Szereg ten był pierwowzorem dla stworzonej później metody Fischera -

Rysunek 13. Potencjalny dzień zmiany trendu określany był przez Ganna jako:

DD = D + k * (D - D )

G

A

G

B

A

gdzie:

DD - dzień docelowy (

)

G

D - data pierwszego punktu zwrotnego

A

D - data drugiego punktu zwrotnego

B

k - kolejna liczba ciągu Ganna; k = 1, 4, 9,... 144.

G

G

Następnym ciągiem liczb jaki znajdujemy w opisach metod wykorzystywanych przez Ganna jest

podwojenie i potrojenie poprzednika. Odległości potencjalnych punktów zwrotnych od dnia istotnego

ekstremum cenowego wynoszą w dniach:

1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024...

1, 3, 9, 18, 27, 81, 243, 729, 2187, 6561...

Kwadrat cenowo - czasowy

Rysunek 14. Kwadrat cenowo - czasowy dla indeksu Wig20 w okresie maj - lipiec 2002.

Miesiące widoczne na wykresie obejmują okres od maja do października 2002 r.

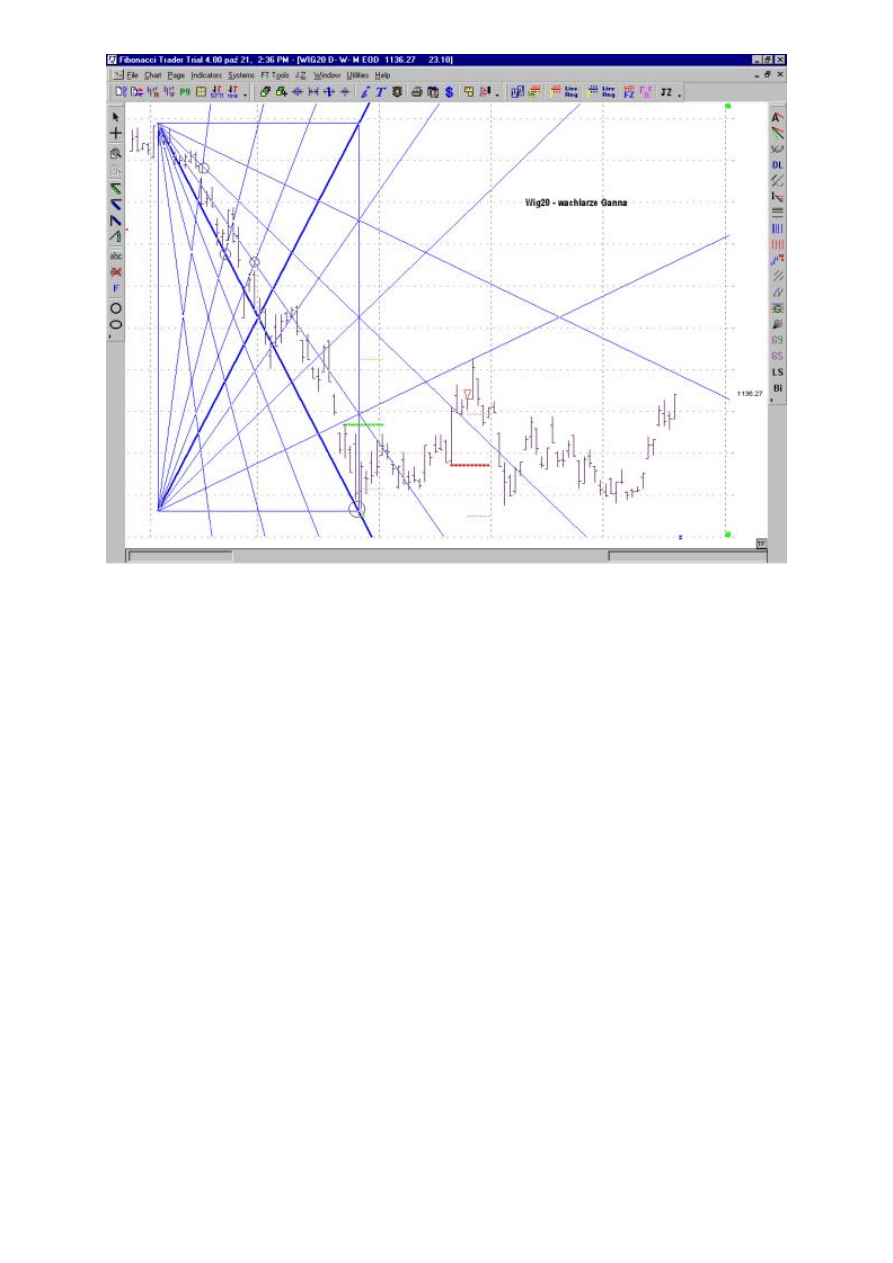
Źródło: opracowanie własne

Kwadrat cenowo - czasowy tworzony jest na akcjogramie w taki sposób, że pionowa linia łącząca

najwyższe i najniższe notowanie w przyjętym okresie staje się lewym brzegiem kwadratu. Pozostała

część kwadratu zostaje dorysowana w oparciu o znajomość tego jednego obszaru. W kwadracie znaczenie

posiadają również przekątne - tworzące kąty Ganna. Zasadniczy opór na rynkach z określonym wyraźnie

trendem następuje na linii nachylonej pod kątem Ganna. Przykład kwadratu cenowo - czasowego dla

zmiany indeksu Wig20 na przestrzeni maj - lipiec 2002, przedstawiony został na rysunku poniżej

(Rysunek 14). Wewnątrz kwadratu narysowane zostały dwa wachlarze Ganna, których niektóre przecięcia

(oznaczone kółeczkami) wyznaczają krótkoterminowe punkty zwrotne indeksu Wig20. Przedłużenie linii

wachlarza Ganna poza kwadrat cenowo - czasowy określa również ważne poziomy wsparcia i oporu - np.

dwukrotne zatrzymanie na linii wachlarza w miesiącu sierpniu.

Gann i liczby Fibonacciego.

Odwrócenie trendu jest bardzo prawdopodobne jeśli jednocześnie zbiegają się co najmniej trzy okresy

mierzone w identycznych jednostkach (dni, tygodnie lub miesiące). Od kluczowych punktów zwrotnych

w przeszłości (niezależnie czy są to dołki czy też szczyty) odlicza się okresy równe kolejnym liczbom

ciągu Fibonacciego. Zbieżność co najmniej trzech okresów sugeruje powstanie istotnego punktu

zwrotnego - Rysunek 15. Modyfikację tej metody na osi pionowej przedstawiono na kolejnym rysunku

(Rysunek 16).

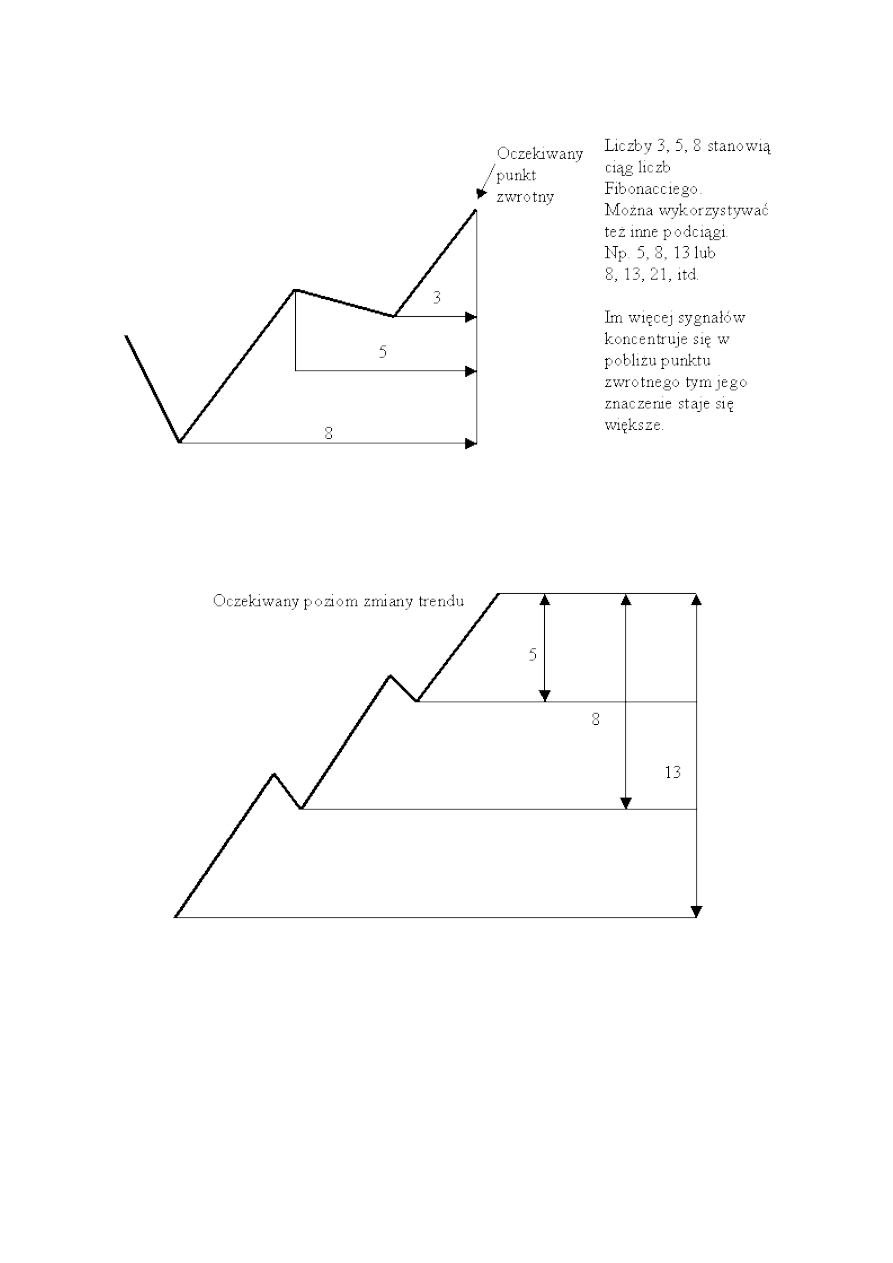
Rysunek 15. Prognozowanie istotnego punku zwrotnego przy pomocy ciągu Fibonacciego na osi

czasowej.

Źródło: opracowanie własne

Rysunek 16. Prognozowanie istotnego punku zwrotnego przy pomocy ciągu Fibonacciego na osi

pionowej.

Źródło: opracowanie własne

Wykorzystanie technik Ganna na osi pionowej

Rysunek 17. Osiem poziomów zniesienia Ganna dla fali spadkowej indeksu Wig20 z maja do lipca 2002

r.

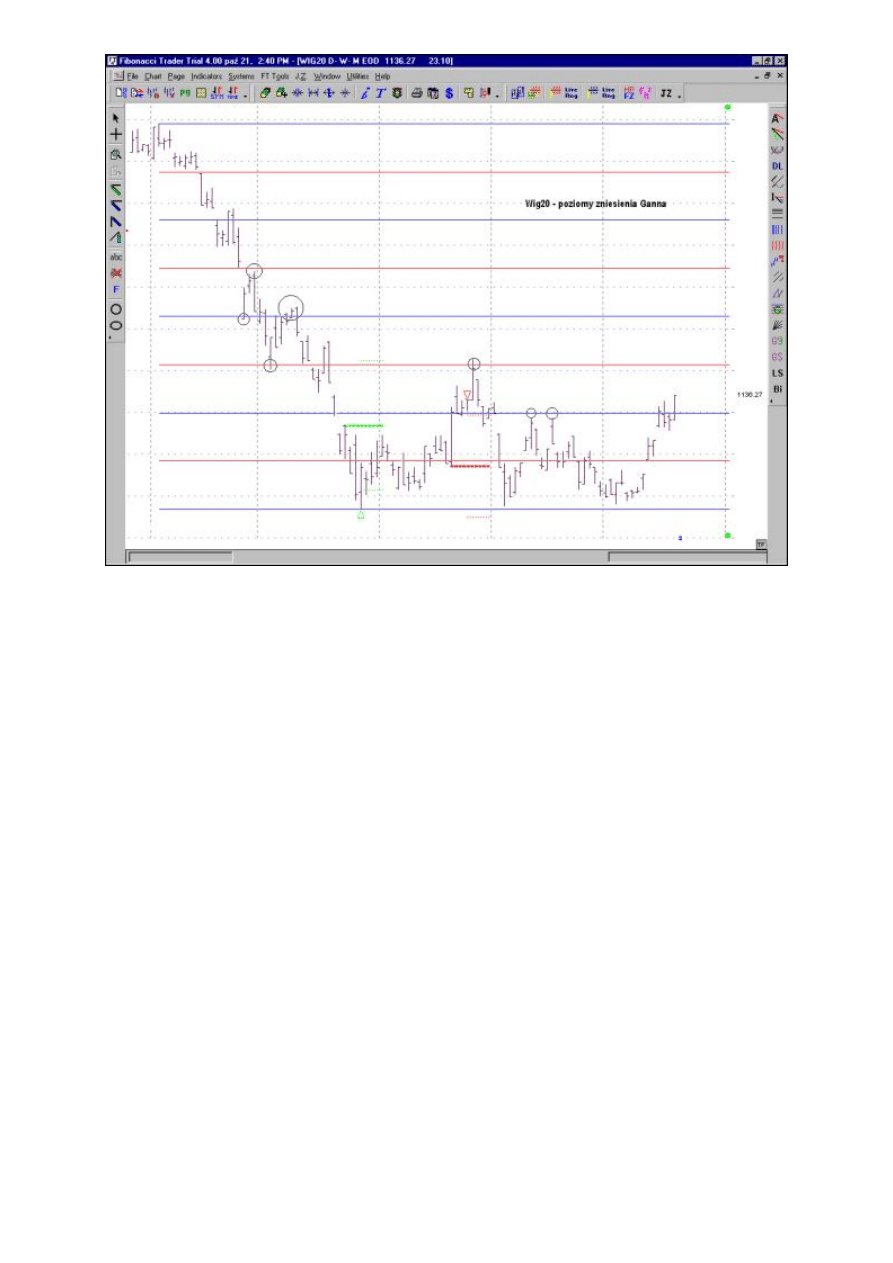
Źródło: opracowanie własne

Dowolny ruch cenowy został podzielony przez Ganna na następujące części:

1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8 i 8/8.

Dużą wagę przywiązywał on także do poziomów zniesienia wyznaczonych przez 1/3 i 2/3 długości ruchu.

Najważniejszym był wg niego poziom 50%. Kolejne pod względem znaczenia są poziomy 37,5% (=3/8)

oraz 62,5% (=5/8), które odpowiadają proporcjom Fibonacciego. Pozostałe poziomy procentowe

odgrywają pewną rolę w ruchach cen, ale nie mają już tak istotnego znaczenia. Znajdują się one poza

granicami wyznaczonymi przez poziomy 33 i 67 procent, którymi posługuje się znaczne grono

analityków technicznych.

Rysunek 17 przedstawia 8 poziomów cenowych zniesienia Ganna dla fali spadkowej z maja do lipca 2002

r. dla indeksu WIG20.

Podsumowując rozdział poświęcony pracom W. D. Ganna należy zauważyć, że w czasie swojej kariery

giełdowej poszukiwał on harmonii rynków finansowych opartej głównie na kombinacjach liczb

naturalnych.

Krzysztof Borowski.

[1] Marisch G. "The W. D. Gann Method of Trading", Windsor Books, Brightwaters, N. Y. 1993.

[2] Gann miał kilka ulubionych sekwencji np. 91,182, 273 i 365 dni, co odpowiada poszczególnym

kwartałom kalendarza połączonym z sezonowością. Cykle Ganna można zakwalifikować jako

specyficzną podgrupę cykli uzyskiwanych przy zastosowaniu innych metod pomiaru cykli np. analizy

Fouriera.

[3] Vodopich D. "Trading for Profit with Precision Timing", Precision Timing, Atlanta 1984.

[4] Gately E. "Cena i czas", WIG-Press, Warszawa 1999 także Arnold C. "Gann", Technical Analysis of

Stock & Commodities", March 1982, Volume 1, Number 3. oraz Pardo R. "Gann Lines and Angels",

Technical Analysis of Stock and Commodities", May 1995, Volume 13, Number 5. także Lamarr D.

"Trading with Gann Lines", Technical Analysis of Stock & Commodities", April 1990, Volume 8,

Number 4.

[5] Murphy J. "Analiza techniczna", WIG - Press, Warszawa 1999.

[6] John J. Murphy "Analiza techniczna", WIG - Press, Warszawa 1999 oraz Gann W. "Master Calculator

for Weekly Time Periods to Determine the Trends of Stock and Commodities", Lambert - Gann, Pomeroy

WA 1976; oraz Gannsoft Publishing "Ganntrader I", Technical Analysis of Stock & Commodities,

January / February 1984, Volume 2, Number 1/2.

[7] Niektóre źródła podają też liczby 30,90, 180 i 360 dni - np. John J. Murphy "Analiza techniczna",

WIG - Press, Warszawa 1999.