
GENEROWANIE LICZB LOSOWYCH
o wybranych
ROZK
àADACH PRAWDOPODOBIEēSTWA
Prezentacja materiaáów pomocniczych do wykáadu
adam.kadzinski@put.poznan.pl
Plik: 1_AK_Generowanie_Liczb_Losowych_2007_s_p_[v6].doc
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
Plik: 1 AK Generowanie Liczb Losow
(1)
PODSTAWOWE ZASADY I PODSTAWY TEORETYCZNE GENEROWANIA
LICZB LOSOWYCH
Ogólna zasada generowania liczb losowych
Generowanie liczb losowych o zadanym nierównomiernym rozk
áadzie prawdopodobieĔstwa polega na
generowaniu ci
ągu liczb o rozkáadzie równomiernym na przedziale ¢0;1² i przeksztaáceniu go w ciąg liczb
o zadanym rozk
áadzie nierównomiernym.
ych 2007 s p [v6].doc
A.
KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
2/26
Rozk
áad
równomierny
Rozk
áad
na przedziale
¢0;1²
zadany
x
i
x
2
x
1
f(x)
1
0
x
0
1
1
p(x)
x
x
i
x
1
x
2
Metoda
przeksztaácania
Plik: 1 AK Generowanie Liczb Losow
(2)
PODSTAWOWE ZASADY I PODSTAWY TEORETYCZNE GENEROWANIA
LICZB LOSOWYCH
Podstawa teoretyczna generowania liczb losowych
ych 2007 s p [v6].doc
A.
KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
3/26
Schemat ideowy
Je
Īeli ciąg
^ `
n
i
r
i
,
,
2
,
1
,
liczb losowych jest ci
ągiem o rozkáadzie równomiernym na przedziale
¢0;1² a (a;b) jest czĊĞcią przedziaáu ¢0;1², oraz
- = -(a,b) jest liczbą elementów skoĔczonego podciągu
ci
ągu
^ `
n
i
r
i
,
,
2
,
1
,
le
Īących w przedziale (a;b), to prawdziwa jest zaleĪnoĞü graniczna:
a
b
r
5
r
2
1,0
r
1
r
3
0,0
r
4
n
- (a;b)
^ `
n
i
r
i
,
,
2
,
1
,
a
b
a
b
n
b
a
n
f
o
0
1
)
,
(
lim
-
,
tzn.
je
Īeli ciąg
ma w przedziale domkni
Ċtym ¢0;1² rozkáad równomierny, to graniczna czĊstoĞü
wzgl
Ċdna przyjmowania przez wyrazu ciągu
^ `
i
r
^ `
warto
Ğci z przedziaáu (a;b) bĊdącego podprzedziaáem
przedzia
áu ¢0;1², jest równa dáugoĞci przedziaáu (a;b).
i
r
Plik: 1 AK Generowanie Liczb Losow
(3)
PODSTAWOWE ZASADY I PODSTAWY TEORETYCZNE GENEROWANIA
LICZB LOSOWYCH
Podstawy teoretyczne metody odwracania dystrybuanty
Je
Īeli
^ `
,
2
,
1
,
i
r
i
jest ci
ągiem liczb losowych o rozkáadzie równomiernym na przedziale ¢0;1², to ciąg
^ `
,
2
,
1
,
i
x
i
taki,
Īe
,
,
2
,
1
),
(
1
i
r
F
x
i
i
jest ci
ągiem liczb losowych o rozkáadzie prawdopodobieĔstwa z dystrybuantą F.
F(x)
ych 2007 s p [v6].doc
A.
KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
4/26
r
2
x
2
x
r
i
x
i
1,0
r
3
r
1
x
4
x
3
x
1
Plik: 1 AK Generowanie Liczb Losow
(4)
PODSTAWOWE ZASADY I PODSTAWY TEORETYCZNE GENEROWANIA
LICZB LOSOWYCH
Metoda odwracania dystrybuanty
a
dystrybuanta
ych 2007 s p [v6].doc
A.
KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
5/26
1.
2.
3.
r
2
x
2
x
r
i
x
i
F x
( )
F(x)
1,0
x
3
x
1
r
1
r
3
x
4
r
4
r
2
x
2
x
r
i
1,0
x
i
r
3
r
1
x
3
x
1
x
4
r
4
r
1
x
2
x
x
i
F(x)
x
3
x
1
x
4
r
2
r
i
r
3
1,0
Plik: 1 AK Generowanie Liczb Losow
(1)
GENEROWANIE LICZB LOSOWYCH
O ROZK
àADZIE RÓWNOMIERNYM NA PRZEDZIALE ¢0;1²
Po co te liczby?
r
i
r
3
r
4
r
1
x
2
x
x
i
x
3
x
1
x
4
r
2
F(x)
1,0
x
x
3
x
i
x
1
f(x)
1
0
0
1
1
x
4
x
2
Mo
ĪliwoĞci pozyskiwania liczb losowych
o rozk
áadzie równomiernym na przedziale
¢0;1²
!
Tablice liczb losowych
!!
Standardowe podprogramy bibliotek j
Ċzyków programowania lub aplikacji
!!!
Inne algorytmy
ych 2007 s p [v6].doc
A.
KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
6/26
Plik: 1 AK Generowanie Liczb Losowych 2007 s p [v6].doc
(2)
GENEROWANIE LICZB LOSOWYCH O ROZK
àADZIE RÓWNOMIERNYM NA ¢0;1²
!
Tablice liczb losowych
FRAGMENT TABLICY CYFR LOSOWYCH
98520
17767
14905
68607
22109
40558
60970
93433
50500
73998
11805
05431
39808
27732
50725
68248
29405
24201
52775
68851
83452
99634
06288
98083
13746
70078
18475
40610
68711
77817
88685
40200
86507
58401
36766
67951
90364
76493
29609
11062
99594
67348
87517
64969
91826
08928
93785
61368
23478
34113
65481
17674
17468
50950
58047
76974
73039
57186
40218
16544
80124
35635
17727
08015
45318
22374
21115
78253
14385
53763
74350
99817
77402
77214
43236
00210
45521
64237
96286
02655
69916
26803
66252
29148
36936
87203
76621
13990
94400
56418
09893
20505
14225
68514
46427
56788
96297
78822
54382
14598
91499
14523
68479
27686
46162
83554
94750
89923
37089
20048
80336
94598
26940
36858
70297
34135
53140
33340
42050
82341
44104
81949
85157
47954
32979
26575
57600
40881
22222
06413
12550
73742
11100
02040
12860
74697
96644
89439
28707
25813
63606
49329
16505
34484
40219
52563
43651
77082
07207
31790
A.
KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
7/26
1
2
3
4
5
6
7
8
9
10
0,36766
0,67951
0,90364
0,76493
0,29609
0,11062
0,99594
0,67348
0,87517
0,64969
36766 / 10
5
64969 / 10
5
Plik: 1 AK Generowanie Liczb Losow
(3)
GENEROWANIE LICZB LOSOWYCH
O ROZK
àADZIE RÓWNOMIERNYM NA PRZEDZIALE ¢0;1²
!
Kalkulatory elektroniczne
ych 2007 s p [v6].doc
A.
KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
8/26
0,215
0,855
0,667
0,357
RANDOM
Plik: 1 AK Generowanie Liczb Losow
(4)
GENEROWANIE LICZB LOSOWYCH
O ROZK
àADZIE RÓWNOMIERNYM NA PRZEDZIALE ¢0;1²
!!
Standardowe podprogramy bibliotek j
Ċzyków programowania lub aplikacji
2.
1.
3.
ych 2007 s p [v6].doc
A.
KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
9/26
i
LP1
LP2
LP1 + 2
.
LP2
LLi = LP1 +2
.
LP2
- Zaokr.Do.Całk(LP1 + 2
.
LP2)
LLi = Zaokr(LLi ; 11)
1
0,34567891234 0,56789123456 1,48146138146
0,48146138146
0,48146138146
2
0,56789123456 0,48146138146 1,53081399748
0,53081399748
0,53081399748
3
0,48146138146 0,53081399748 1,54308937642
0,54308937642
0,54308937642
4
0,53081399748 0,54308937642 1,61699275032
0,61699275032
0,61699275032
5
0,54308937642 0,61699275032 1,77707487706
0,77707487706
0,77707487706
6
0,61699275032 0,77707487706 2,17114250444
0,17114250444
0,17114250444
7
0,77707487706 0,17114250444 1,11935988594
0,11935988594
0,11935988594
8
0,17114250444 0,11935988594 0,40986227632
0,40986227632
0,40986227632
9
0,11935988594 0,40986227632 0,93908443858
0,93908443858
0,93908443858
10
0,40986227632 0,93908443858 2,28803115348
0,28803115348
0,28803115348
11
0,93908443858 0,28803115348 1,51514674554
0,51514674554
0,51514674554
12
0,28803115348 0,51514674554 1,31832464456
0,31832464456
0,31832464456
13
0,51514674554 0,31832464456 1,15179603466
0,15179603466
0,15179603466
14
0,31832464456 0,15179603466 0,62191671388
0,62191671388
0,62191671388
15
0,15179603466 0,62191671388 1,39562946241
0,39562946241
0,39562946241
16
0,62191671388 0,39562946241 1,41317563870
0,41317563870
0,41317563870
17
0,39562946241 0,41317563870 1,22198073981
0,22198073981
0,22198073981
18
0,41317563870 0,22198073981 0,85713711832
0,85713711832
0,85713711832
19
0,22198073981 0,85713711832 1,93625497645
0,93625497645
0,93625497645
20
0,85713711832 0,93625497645 2,72964707123
0,72964707123
0,72964707123
21
0,93625497645 0,72964707123 2,39554911891
0,39554911891
0,39554911891
22
0,72964707123 0,39554911891 1,52074530906
0,52074530906
0,52074530906
23
0,39554911891 0,52074530906 1,43703973703
0,43703973703
0,43703973703
24
0,52074530906 0,43703973703 1,39482478311
0,39482478311
0,39482478311
25
0,43703973703 0,39482478311 1,22668930325
0,22668930325
0,22668930325
26
0,39482478311 0,22668930325 0,84820338962
0,84820338962
0,84820338962
27
0,22668930325 0,84820338962 1,92309608250
0,92309608250
0,92309608250
28
0,84820338962 0,92309608250 2,69439555463
0,69439555463
0,69439555463
29
0,92309608250 0,69439555463 2,31188719175
0,31188719175
0,31188719175
30
0,69439555463 0,31188719175 1,31816993814
0,31816993814
0,31816993814
31
0,31188719175 0,31816993814 0,94822706803
0,94822706803
0,94822706803
32
0,31816993814 0,94822706803 2,21462407419
0,21462407419
0,21462407419
33
0,94822706803 0,21462407419 1,37747521640
0,37747521640
0,37747521640
34
0,21462407419 0,37747521640 0,96957450698
0,96957450698
0,96957450698
35
0,37747521640 0,96957450698 2,31662423036
0,31662423036
0,31662423036
36
0,96957450698 0,31662423036 1,60282296770
0,60282296770
0,60282296770
37
0,31662423036 0,60282296770 1,52227016577
0,52227016577
0,52227016577
38
0,60282296770 0,52227016577 1,64736329924
0,64736329924
0,64736329924
39
0,52227016577 0,64736329924 1,81699676425
0,81699676425
0,81699676425
40
0,64736329924 0,81699676425 2,28135682773
0,28135682773
0,28135682773
41
0,81699676425 0,28135682773 1,37971041971
0,37971041971
0,37971041971
42
0,28135682773 0,37971041971 1,04077766715
0,04077766715
0,04077766715
43
0,37971041971 0,04077766715 0,46126575401
0,46126575401
0,46126575401
44
0,04077766715 0,46126575401 0,96330917517
0,96330917517
0,96330917517
45
0,46126575401 0,96330917517 2,38788410436
0,38788410436
0,38788410436
46
0,96330917517 0,38788410436 1,73907738389
0,73907738389
0,73907738389
47
0,38788410436 0,73907738389 1,86603887213
0,86603887213
0,86603887213
48
0,73907738389 0,86603887213 2,47115512814
0,47115512814
0,47115512814
49
0,86603887213 0,47115512814 1,80834912841
0,80834912841
0,80834912841
50
0,47115512814 0,80834912841 2,08785338497
0,08785338497
0,08785338497
51
0,80834912841 0,08785338497 0,98405589836
0,98405589836
0,98405589836
52
0,08785338497 0,98405589836 2,05596518169
0,05596518169
0,05596518169
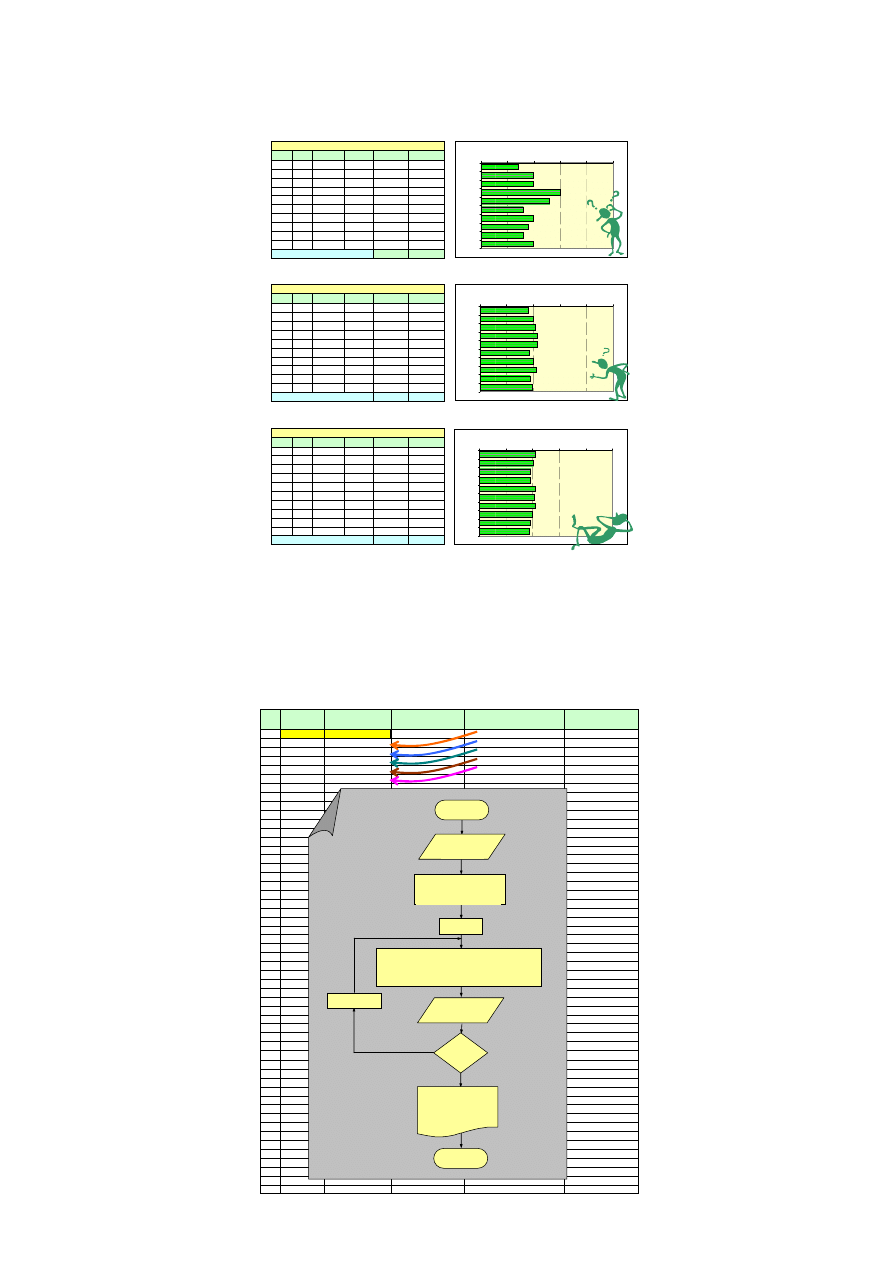
GENERATOR
<BOB>
LICZB LOSOWYCH
O ROZKŁADZIE RÓWNOMIERNYM NA PRZEDZIALE <0;1>
N
T
START
Wczytaj
ILL
LP1 := 0,34567891234
LP2 := 0,56789123456
i := 1
i := i + 1
LP1 := LP2
LLi := LP1 + 2.LP2 - Zaokr.Do.Całk (LP1 + 2.LP2)
LP := LLi
LLi := Zaokr(LLi ;11)
Wypisz
LLi
i ≥ ILL
Wydruk liczb losowych
LL1: 0,48146138146
LL2: 0,53081399748
LL3: 0,54308937642
…
STOP
LP2 := LP
Plik: Generatory_BOB_i_RAJ_Przykłady_obl.xls
Opr. Adam Kadziński
GENERATOR
<BOB>
LICZB LOSOWYCH
O ROZK
àADZIE RÓWNOMIERNYM NA PRZEDZIALE <0;1>
BOB
100
x
d
x
g
x
d
-x
g
n
sk
n
i
p
i
0,0
0,1
0,0-0,1
7
7
0,070
0,1
0,2
0,1-0,2
17
10
0,100
0,2
0,3
0,2-0,3
27
10
0,100
0,3
0,4
0,3-0,4
42
15
0,150
0,4
0,5
0,4-0,5
55
13
0,130
0,5
0,6
0,5-0,6
63
8
0,080
0,6
0,7
0,6-0,7
73
10
0,100
0,7
0,8
0,7-0,8
82
9
0,090
0,8
0,9
0,8-0,9
90
8
0,080
0,9
1,0
0,9-1,0
100
10
0,100
RAZEM
100
1,000
BOB
500
x
d
x
g
x
d
-x
g
n
sk
n
i
p
i
0,0
0,1
0,0-0,1
45
45
0,090
0,1
0,2
0,1-0,2
95
50
0,100
0,2
0,3
0,2-0,3
147
52
0,104
0,3
0,4
0,3-0,4
201
54
0,108
0,4
0,5
0,4-0,5
255
54
0,108
0,5
0,6
0,5-0,6
301
46
0,092
0,6
0,7
0,6-0,7
351
50
0,100
0,7
0,8
0,7-0,8
404
53
0,106
0,8
0,9
0,8-0,9
451
47
0,094
0,9
1,0
0,9-1,0
500
49
0,098
RAZEM
500
1,000
BOB 5000
x
d
x
g
x
d
-x
g
n
sk
n
i
p
i
0,0
0,1
0,0-0,1
523
523
0,105
0,1
0,2
0,1-0,2
1032
509
0,102
0,2
0,3
0,2-0,3
1515
483
0,097
0,3
0,4
0,3-0,4
1991
476
0,095
0,4
0,5
0,4-0,5
2515
524
0,105
0,5
0,6
0,5-0,6
3030
515
0,103
0,6
0,7
0,6-0,7
3558
528
0,106
0,7
0,8
0,7-0,8
4052
494
0,099
0,8
0,9
0,8-0,9
4532
480
0,096
0,9
1,0
0,9-1,0
5000
468
0,094
RAZEM
5000
1,000
0,00
0,05
0,10
0,15
0,20
0,25
0,0-0,1
0,1-0,2
0,2-0,3
0,3-0,4
0,4-0,5
0,5-0,6
0,6-0,7
0,7-0,8
0,8-0,9
0,9-1,0
0,00
0,05
0,10
0,15
0,20
0,25
0,0-0,1
0,1-0,2
0,2-0,3
0,3-0,4
0,4-0,5
0,5-0,6
0,6-0,7
0,7-0,8
0,8-0,9
0,9-1,0
0,00
0,05
0,10
0,15
0,20
0,25
0,0-0,1
0,1-0,2
0,2-0,3
0,3-0,4
0,4-0,5
0,5-0,6
0,6-0,7
0,7-0,8
0,8-0,9
0,9-1,0
Plik: Generatory_BOB_i_RAJ_Przyk
áady_obl.xls
Opr. Adam Kadzi
Ĕski
i
LPS
LPZ
LPS
.
LPZ
LLi = LPS
.
LPZ
- Zaokr.Do.Całk(LPS
.
LPZ)
LLi = Zaokr(LLi ; 11)
1
31999
0,12345678501
3950,49366353499
0,49366353498999
0,49366353499
2
31999
0,49366353498999 15796,73945614470
0,73945614474178
0,73945614474
3
31999
0,73945614474178 23661,85717559220
0,85717559221666
0,85717559222
4
31999
0,85717559221666 27428,76177534100
0,76177534100134
0,76177534100
5
31999
0,76177534100134 24376,04913670190
0,04913670185488
0,04913670185
6
31999
0,04913670185488
1572,32532265421
0,32532265421469
0,32532265421
7
31999
0,32532265421469 10409,99961221580
0,99961221578997
0,99961221579
8
31999
0,99961221578997 31986,59129306310
0,5912930631311610
0,59129306313
9
31999
0,59129306313
18920,78672713400
0,7867271340219300
0,78672713402
10
31999
0,78672713402
25174,48156156780
0,4815615677507590
0,48156156775
11
31999
0,48156156775
15409,48860645660
0,4886064565507700
0,48860645655
12
31999
0,48860645655
15634,91800316810
0,9180031680734830
0,91800316807
13
31999
0,91800316807
29375,18337518340
0,1833751833764840
0,18337518338
14
31999
0,18337518338
5867,82249286410
0,8224928640993310
0,82249286410
15
31999
0,82249286410
26318,94915831450
0,9491583144990730
0,94915831450
16
31999
0,94915831450
30372,11690565580
0,1169056558283050
0,11690565583
17
31999
0,11690565583
3740,86408084992
0,8640808499185370
0,86408084992
18
31999
0,86408084992
27649,72311654330
0,7231165432604030
0,72311654326
19
31999
0,72311654326
23139,00626778960
0,0062677896348760
0,00626778963
20
31999
0,00626778963
200,56300052640
0,5630005263956260
0,56300052640
21
31999
0,56300052640
18015,45384413360
0,4538441336480900
0,45384413365
22
31999
0,45384413365
14522,55843260520
0,5584326052339750
0,55843260523
23
31999
0,55843260523
17869,28493488200
0,2849348819581790
0,28493488196
24
31999
0,28493488196
9117,63128777978
0,6312877797754480
0,63128777978
25
31999
0,63128777978
20200,57766503460
0,5776650345651430
0,57766503457
26
31999
0,57766503457
18484,70344105000
0,7034410500200470
0,70344105002
27
31999
0,70344105002
22509,41015959150
0,4101595914689820
0,41015959147
28
31999
0,41015959147
13124,69676741600
0,6967674159677700
0,69676741597
29
31999
0,69676741597
22295,86054355270
0,8605435526696970
0,86054355267
30
31999
0,86054355267
27536,53314187760
0,5331418776186180
0,53314187762
31
31999
0,53314187762
17060,00694191820
0,0069419181672856
0,00694191817
32
31999
0,00694191817
222,13443943497
0,1344394349725920
0,13443943497
33
31999
0,13443943497
4301,92747968796
0,9274796879617500
0,92747968796
34
31999
0,92747968796
29678,42253508800
0,4225350880296900
0,42253508803
35
31999
0,42253508803
13520,70028186210
0,7002818620530890
0,70028186205
36
31999
0,70028186205
22408,31930383680
0,3193038367899130
0,31930383679
37
31999
0,31930383679
10217,40347344040
0,4034734404413030
0,40347344044
38
31999
0,40347344044
12910,74662068130
0,7466206812532620
0,74662068125
39
31999
0,74662068125
23891,11517942310
0,1151794231263920
0,11517942313
40
31999
0,11517942313
3685,62636062142
0,6263606214197350
0,62636062142
41
31999
0,62636062142
20042,91352481010
0,9135248101083560
0,91352481011
42
31999
0,91352481011
29231,88039865730
0,8803986572893340
0,88039865729
43
31999
0,88039865729
28171,87663460140
0,8766346013871950
0,87663460139
44
31999
0,87663460139
28051,43060978890
0,4306097888620570
0,43060978886
45
31999
0,43060978886
13779,08263379700
0,0826337969629094
0,08263379696
46
31999
0,08263379696
2644,19886901614
0,1988690161379050
0,19886901614
47
31999
0,19886901614
6363,60964739684
0,6096473968354990
0,60964739684
48
31999
0,60964739684
19508,10705133910
0,1070513391168790
0,10705133912
49
31999
0,10705133912
3425,53580040100
0,5358004010049630
0,53580040100
50
31999
0,53580040100
17145,07703175780
0,0770317577989772
0,07703175780
51
31999
0,07703175779898
2464,93921780947
0,93921780947130
0,93921780947
52
31999
0,93921780947130 30054,03068527220
0,03068527218420
0,03068527218
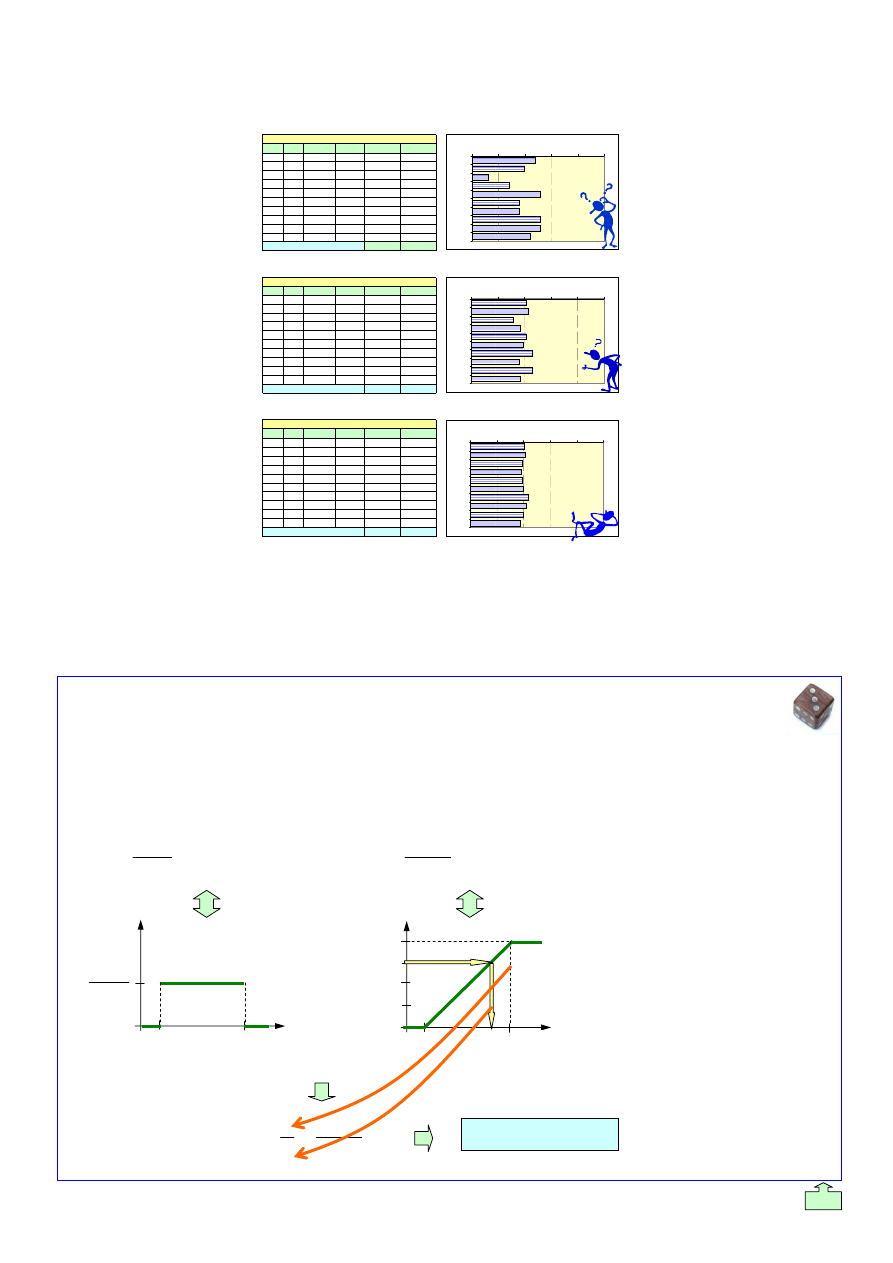
GENERATOR
<RAJ>
LICZB LOSOWYCH
O ROZKŁADZIE RÓWNOMIERNYM NA PRZEDZIALE <0;1>
N
T
START
Wczytaj
ILL
LPS := 31999
LPZ := 0,12345678501
i := 1
i := i + 1
LL
i := LPS
.
LPZ - Zaokr.Do.Całk (LPS
.
LPZ)
LPZ := LL
i
LL
i := Zaokr(LLi
;11)
Wypisz
LLi
i ≥ ILL
Wydruk liczb losowych
LL1: 0,49366353499
LL2: 0,73945614474
LL3: 0,85717559222
…
STOP
Plik: Generatory_BOB_i_RAJ_Przykłady_obl.xls
Opr. A. Kadziński
GENERATOR
<RAJ>
LICZB LOSOWYCH
O ROZK
àADZIE RÓWNOMIERNYM NA PRZEDZIALE <0;1>
RAJ
100
x
d
x
g
x
d
-x
g
n
sk
n
i
p
i
0,0
0,1
0,0-0,1
12
12
0,120
0,1
0,2
0,1-0,2
22
10
0,100
0,2
0,3
0,2-0,3
25
3
0,030
0,3
0,4
0,3-0,4
32
7
0,070
0,4
0,5
0,4-0,5
45
13
0,130
0,5
0,6
0,5-0,6
54
9
0,090
0,6
0,7
0,6-0,7
63
9
0,090
0,7
0,8
0,7-0,8
76
13
0,130
0,8
0,9
0,8-0,9
89
13
0,130
0,9
1,0
0,9-1,0
100
11
0,110
RAZEM
100
1,000
RAJ
500
x
d
x
g
x
d
-x
g
n
sk
n
i
p
i
0,0
0,1
0,0-0,1
52
52
0,104
0,1
0,2
0,1-0,2
106
54
0,108
0,2
0,3
0,2-0,3
146
40
0,080
0,3
0,4
0,3-0,4
192
46
0,092
0,4
0,5
0,4-0,5
244
52
0,104
0,5
0,6
0,5-0,6
293
49
0,098
0,6
0,7
0,6-0,7
351
58
0,116
0,7
0,8
0,7-0,8
396
45
0,090
0,8
0,9
0,8-0,9
454
58
0,116
0,9
1,0
0,9-1,0
500
46
0,092
RAZEM
500
1,000
RAJ
5000
x
d
x
g
x
d
-x
g
n
sk
n
i
p
i
0,0
0,1
0,0-0,1
507
507
0,101
0,1
0,2
0,1-0,2
1019
512
0,102
0,2
0,3
0,2-0,3
1508
489
0,098
0,3
0,4
0,3-0,4
1988
480
0,096
0,4
0,5
0,4-0,5
2475
487
0,097
0,5
0,6
0,5-0,6
2970
495
0,099
0,6
0,7
0,6-0,7
3512
542
0,108
0,7
0,8
0,7-0,8
4037
525
0,105
0,8
0,9
0,8-0,9
4530
493
0,099
0,9
1,0
0,9-1,0
5000
470
0,094
RAZEM
5000
1,000
0,00
0,05
0,10
0,15
0,20
0,25
0,0-0,1
0,1-0,2
0,2-0,3
0,3-0,4
0,4-0,5
0,5-0,6
0,6-0,7
0,7-0,8
0,8-0,9
0,9-1,0
0,00
0,05
0,10
0,15
0,20
0,25
0,0-0,1
0,1-0,2
0,2-0,3
0,3-0,4
0,4-0,5
0,5-0,6
0,6-0,7
0,7-0,8
0,8-0,9
0,9-1,0
0,00
0,05
0,10
0,15
0,20
0,25
0,0-0,1
0,1-0,2
0,2-0,3
0,3-0,4
0,4-0,5
0,5-0,6
0,6-0,7
0,7-0,8
0,8-0,9
0,9-1,0
Plik: Generatory_BOB_i_RAJ_Przyk
áady_obl.xls
Opr. A. Kadzi
Ĕski
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[
(1)
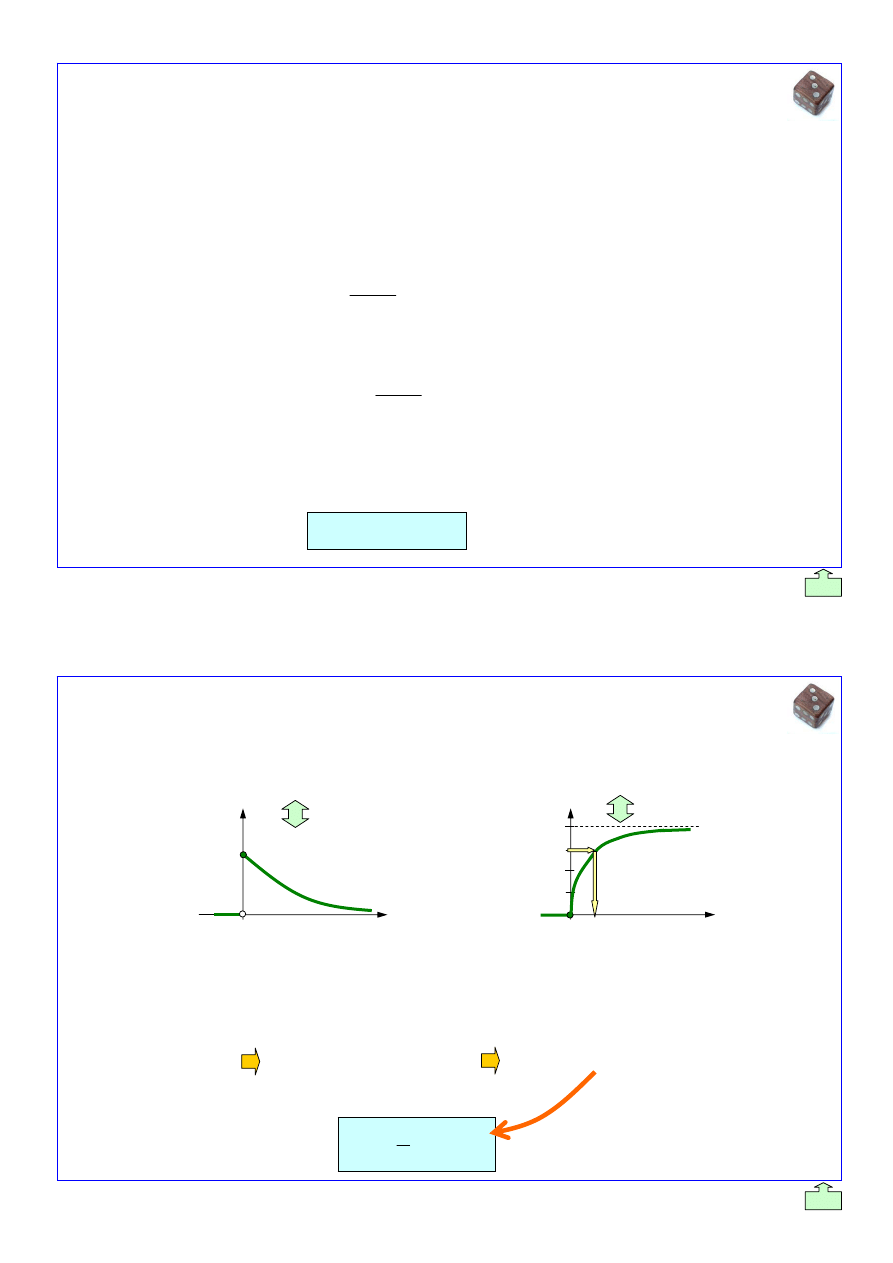
GENEROWANIA LICZB LOSOWYCH
O ROZK
àADZIE RÓWNOMIERNYM NA PRZEDZIALE (a;b)
Do generowania liczb losowych o rozk
áadzie równomiernym na przedziale (a;b) zastosowaü moĪna
generator pozyskany metod
ą odwracania dystrybuanty zmiennej losowej o tym rozkáadzie.
Odwracanie dystrybuanty metod
ą graficzną
)
;
(
,
1
)
(
b
a
x
dla
a
b
x
f
i
i
)
;
(
,
)
(
b
a
x
dla
a
b
a
x
x
F
i
i
i
f(x)
b
a
x
a
b
1
v9].doc
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
12/26
a
x
a
b
r
i
i
1
)
(
a
b
r
a
x
i
i
, gdzie i = 1,2,...
(1)
r
i
x
i
F(x)
b
a
x
0,0
1,0
0,5
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(2)
GENEROWANIA LICZB LOSOWYCH
O ROZK
àADZIE RÓWNOMIERNYM NA PRZEDZIALE (a;b)
Do generowania liczb losowych o rozk
áadzie równomiernym na przedziale (a;b) zastosowaü moĪna
generator pozyskany metod
ą odwracania dystrybuanty zmiennej losowej o tym rozkáadzie.
Odwracanie dystrybuanty metod
ą analityczną
Niech dystrybuant
Ċ zmiennej losowej o rozkáadzie równomiernym na przedziale (a;b) przedstawia
zale
ĪnoĞü postaci:
a
b
a
x
x
F
i
i
)
(
, gdzie
)
;
( b
a
x
i
i = 1,2,... .
(2)
Je
Īeli zaáoĪy siĊ, Īe dystrybuanta przyjmowaü bĊdzie wartoĞci r
i
(i=1,2,...) nale
Īące do rozkáadu
równomiernego na przedziale
¢0;1², to mamy:
a
b
a
x
r
i
i
, gdzie i = 1,2,... ,
(3)
a st
ąd otrzymuje siĊ:
)
(
a
b
r
a
x
i
i
, gdzie i = 1,2,... ,
(4)
a na tej podstawie ostateczna posta
ü matematyczna generatora liczb losowych o rozkáadzie
równomiernym na przedziale (a;b) przedstawia si
Ċ nastĊpująco:
)
(
a
b
r
a
x
i
i
, gdzie i = 1,2,...
(5)
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
13/26
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
14/26
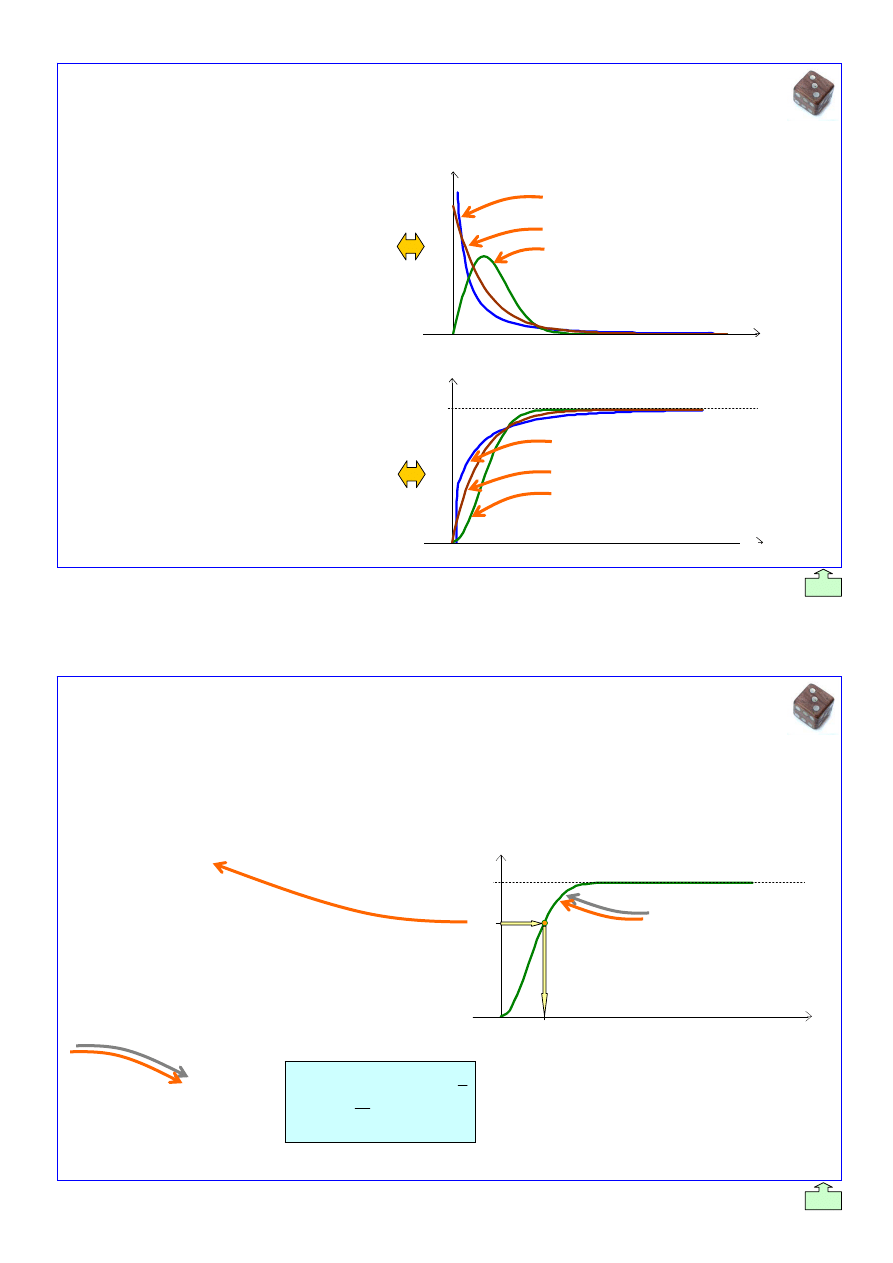
GENEROWANIE LICZB LOSOWYCH O ROZK
àADZIE WYKàADNICZYM
Zmienna losowa ma rozk
áad wykáadniczy jeĪeli funkcjĊ gĊstoĞci prawdopodobieĔstwa i dystrybuantĊ
przedstawiaj
ą nastĊpujące formuáy matematyczne oraz ich reprezentacje graficzne:
0
dla
,
)
(
t
i
i
x
i
x
e
x
f
O
O
0
dla
,
1
)
(
t
i
i
x
i
x
e
x
F
O
Do generowania liczb losowych o rozk
áadzie wykáadniczym zastosowaü moĪna formuáĊ pozyskaną
metod
ą analitycznego odwracania dystrybuanty zmiennej losowej o tym rozkáadzie (schemat ideowy takiej
metody pokazano na rysunku).
Je
Īeli zaáoĪy siĊ, Īe dystrybuanta rozkáadu wykáadniczego przyjmowaü bĊdzie wartoĞci r
i
(i=1,2,...)
nale
Īące do rozkáadu równomiernego na przedziale ¢0;1², to mamy:
i
x
i
e
r
O
1
,
)
ln(
)
1
ln(
i
x
i
e
r
O
i
i
x
r
O
)
1
ln(
, gdzie i = 1,2,... ,
a na tej podstawie ostateczna posta
ü matematyczna generatora liczb losowych o rozkáadzie wykáadniczym
przedstawia si
Ċ nastĊpująco:
)
1
ln(
1
i
i
r
x
O
, gdzie i = 1,2,... .
(1)
O
f(x)
x
x
r
i
x
i
F(x)
1,0
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
15/26
(1)
GENEROWANIE LICZB LOSOWYCH O ROZK
àADZIE WEIBULLA
Zmienna losowa ma rozk
áad Weibulla jeĪeli funkcjĊ gĊstoĞci prawdopodobieĔstwa i dystrybuantĊ
przedstawiaj
ą pokazane dalej formuáy matematyczne oraz ich reprezentacje graficzne.
f(x)
x
D
D
D!
0
dla
)
(
1
t
i
i
x
i
i
x
e
x
x
f
D
E
D
E
D
F(x)
1,0
D
0
dla
1
)
(
t
i
i
x
i
x
e
x
F
D
E
D
D!
x
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(2)
GENEROWANIE LICZB LOSOWYCH O ROZK
àADZIE WEIBULLA
Do generowania liczb losowych o rozk
áadzie Weibulla zastosowaü moĪna formuáĊ pozyskaną metodą
analitycznego odwracania dystrybuanty zmiennej losowej o tym rozk
áadzie (schemat ideowy takiej metody
pokazano na rysunku).
Je
Īeli zaáoĪy siĊ, Īe dystrybuanta rozkáadu Weibulla przyjmowaü bĊdzie wartoĞci r
i
(i=1,2,...) nale
Īące
do rozk
áadu równomiernego na przedziale ¢0;1², to mamy:
D
E ix
i
e
r
1
, gdzie i = 1,2,... ,
(1)
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
16/26
i kolejno
D
E ix
i
e
r
1
, gdzie i = 1,2,... ,
¸
¹
·
¨
©
§
D
E ix
i
e
r
ln
)
1
ln(
, gdzie i = 1,2,... ,
D
E
i
i
x
r
)
1
ln(
, gdzie i = 1,2,... ,
F(x)
1,0
x
r
i
x
i
D
E ix
i
e
x
F
1
)
(
a st
ąd ostatecznie
D
E
1
)
1
ln(
1
¿
¾
½
¯
®
i
i
r
x
, gdzie i = 1,2,... .
(2)
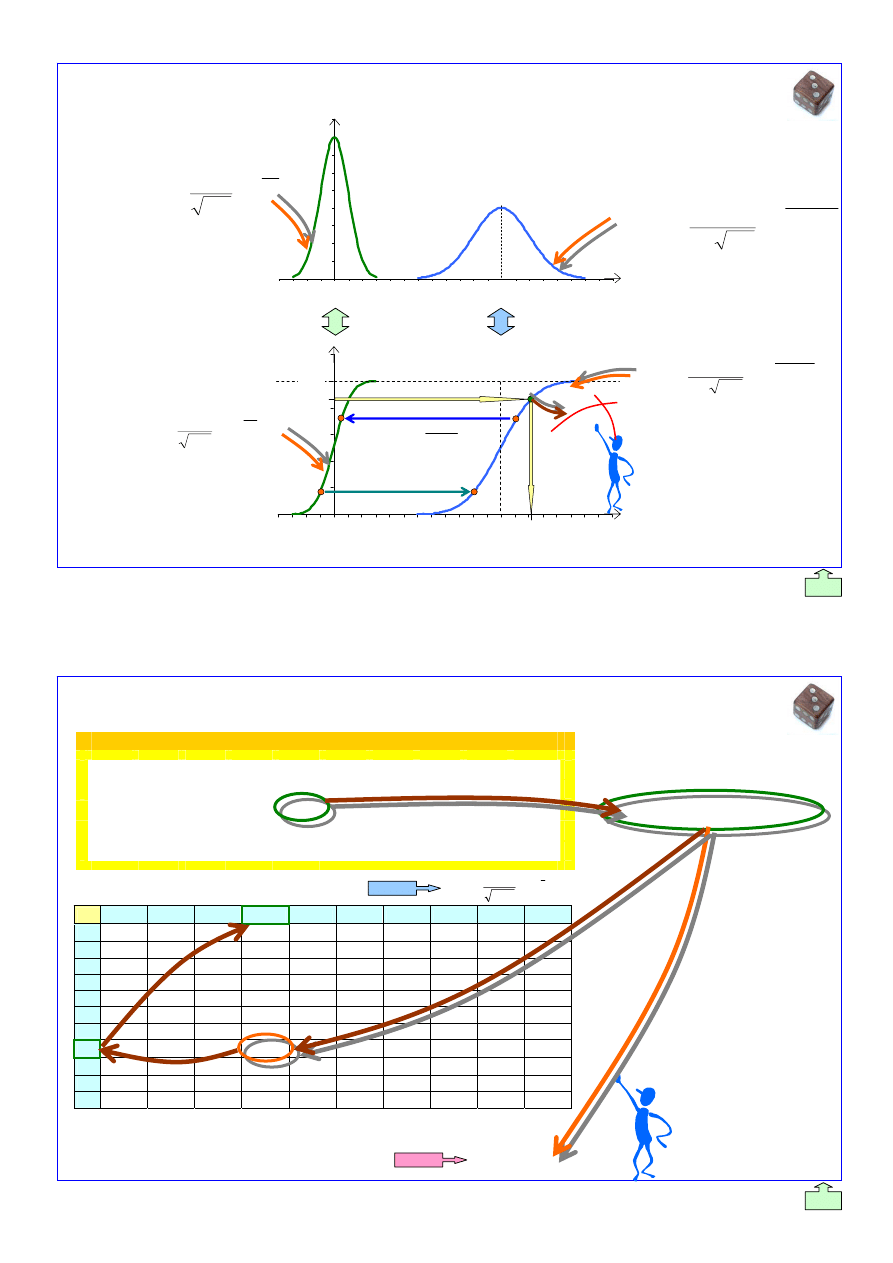
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(1)
GENEROWANIE LICZB LOSOWYCH O ROZK
àADZIE NORMALNYM
(1)
GENEROWANIE LICZB LOSOWYCH O ROZK
àADZIE NORMALNYM
f( )
x
1
2
~
2
2
1
)
(
i
x
i
x
e
x
f
3
2
2
2
)
(
2
1
)
(
V
P
V
3
i
x
i
e
x
f
1
PV
P
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
17/26
x
0
x
P
0
F(x)
1
PV
1
V
P
x
x
~
P
V
x
x
~
x
i
r
i
dz
e
x
F
i
x
z
i
³
f
3
2
2
2
)
(
2
1
)
(
V
P
V
dz
e
x
F
i
x
z
i
x
³
f
3
2
~
2
2
1
)
(
)
(
1
i
i
r
F
x
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(2)
GENEROWANIE LICZB LOSOWYCH O ROZK
àADZIE NORMALNYM
1
FRAGMENT TABLICY CYFR LOSOWYCH
10097
32533
76520
13586
34673
54876
80959
09117
39292
74945
37542
04805
64894
74296
24805
24037
20636
10402
00822
91665
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
18/26
08422
68953
19645
09303
23209
02560
15953
34764
35080
33606
99019
02529
09376
70715
38311
31165
88676
74397
04436
27659
12807
99970
80157
36147
64032
36653
98951
16877
12171
76833
Dystrybuanta rozk
áadu
N(0;1)
u
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
dx
e
u
F
u
x
³
f
3
2
2
1
2
1
)
(
0,0
0,50000 0,49601 0,49202 0,48803 0,48405 0,48006 0,47608 0,47210 0,46812 0,46414
-0,1
0,46017 0,45620 0,45224 0,44828 0,44433 0,44038 0,43644 0,43251 0,42858 0,42465
-0,2
0,42074 0,41683 0,41294 0,40905 0,40517 0,40129 0,39743 0,39358 0,38974 0,38591
-0,3
0,38209 0,37828 0,37448 0,37070 0,36693 0,36317 0,35942 0,35569 0,35197 0,34827
-0,4
0,34458 0,34090 0,33724 0,33360 0,32997 0,32636 0,32276 0,31918 0,31561 0,31207
0,30854
-0,5
0,30503 0,30153 0,29806 0,29460 0,29116 0,28774 0,28434 0,28096 0,27760
-0,6
0,27425 0,27093 0,26763 0,26435 0,26109 0,25785 0,25463 0,25143 0,24825 0,24510
-0,7
0,24196 0,23885 0,23576
0,23270
0,22965 0,22663 0,22363 0,22065 0,21770 0,21476
-0,8
0,21186 0,20897 0,20611 0,20327 0,20045 0,19766 0,19489 0,19215 0,18943 0,18673
-0,9
0,18406 0,18141 0,17879 0,17619 0,17361 0,17106 0,16853 0,16602 0,16354 0,16109
-1,0
0,15866 0,15625 0,15386 0,15151 0,14917 0,14686 0,14457 0,14231 0,14007 0,13786
lub
=ROZK
àAD.NORMALNY.S.ODW(
0,23209
)
– 0,73198
23209 / 10
5
=
0,23209
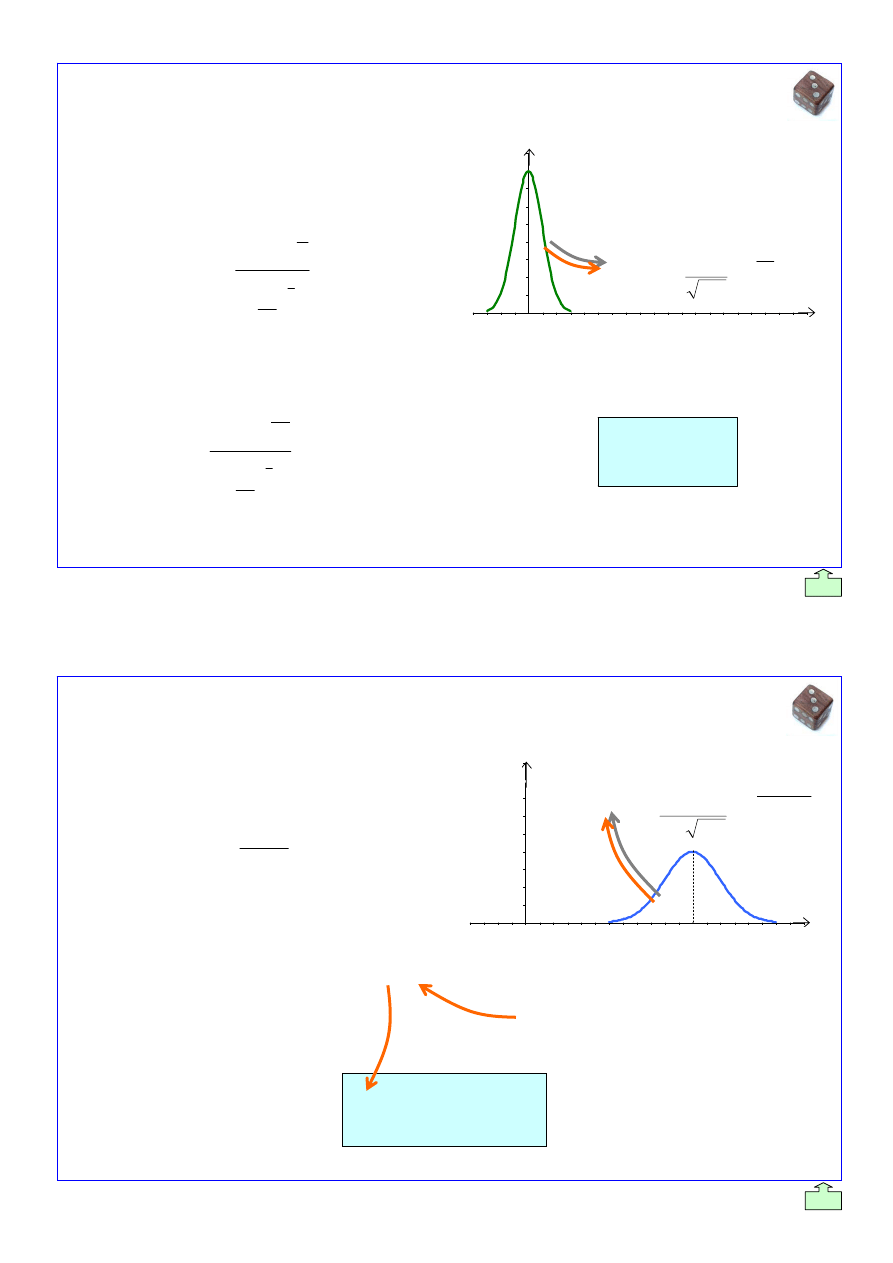
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(3)
GENEROWANIE LICZB LOSOWYCH O ROZK
àADZIE NORMALNYM
1
Liczby losowe o rozk
áadzie normalnym
1
pozyskuje si
Ċ z
k
(
f
o
k
)
liczb losowych
y
x
f(x)
0
1
2
~
2
2
1
)
(
i
x
i
x
e
x
f
3
j
o rozk
áadzie równomiernym na przedziale
¢0;1²
przekszta
áconych zgodnie z zaleĪnoĞcią
2
1
1
12
2
~
¸
¹
·
¨
©
§
¦
k
k
y
x
k
j
j
i
Zauwa
Īono, Īe dogodną wartoĞcią
k
jest 12 (
k
=12) i wtedy
2
1
12
1
12
12
2
12
~
¸
¹
·
¨
©
§
¦
j
j
i
y
x
a st
ąd ostatecznie
0
,
6
~
12
1
¦
j
j
i
y
x
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
19/26
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(4)
GENEROWANIE LICZB LOSOWYCH O ROZK
àADZIE NORMALNYM
1
PV
Liczby losowe o rozk
áadzie normalnym
1
PV
pozyskuje si
Ċ wykorzystując zaleĪnoĞü na
standaryzacj
Ċ zmiennej losowej o rozkáadzie
normalnym postaci
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
20/26
V
P
i
i
x
x
~
oraz formu
áĊ generatora liczb losowych o
rozk
áadzie normalnym standaryzowanym
1
x
f(x)
P
0
1
PV
2
2
2
)
(
2
1
)
(
V
P
V
3
i
x
i
e
x
f
Na tej podstawie mamy
P
V
i
i
x
x
~
a st
ąd ostatecznie
P
V
¸
¸
¹
·
¨
¨
©
§
¦
0
,
6
12
1
j
j
i
y
x
0
,
6
~
12
1
¦
j
j
i
y
x
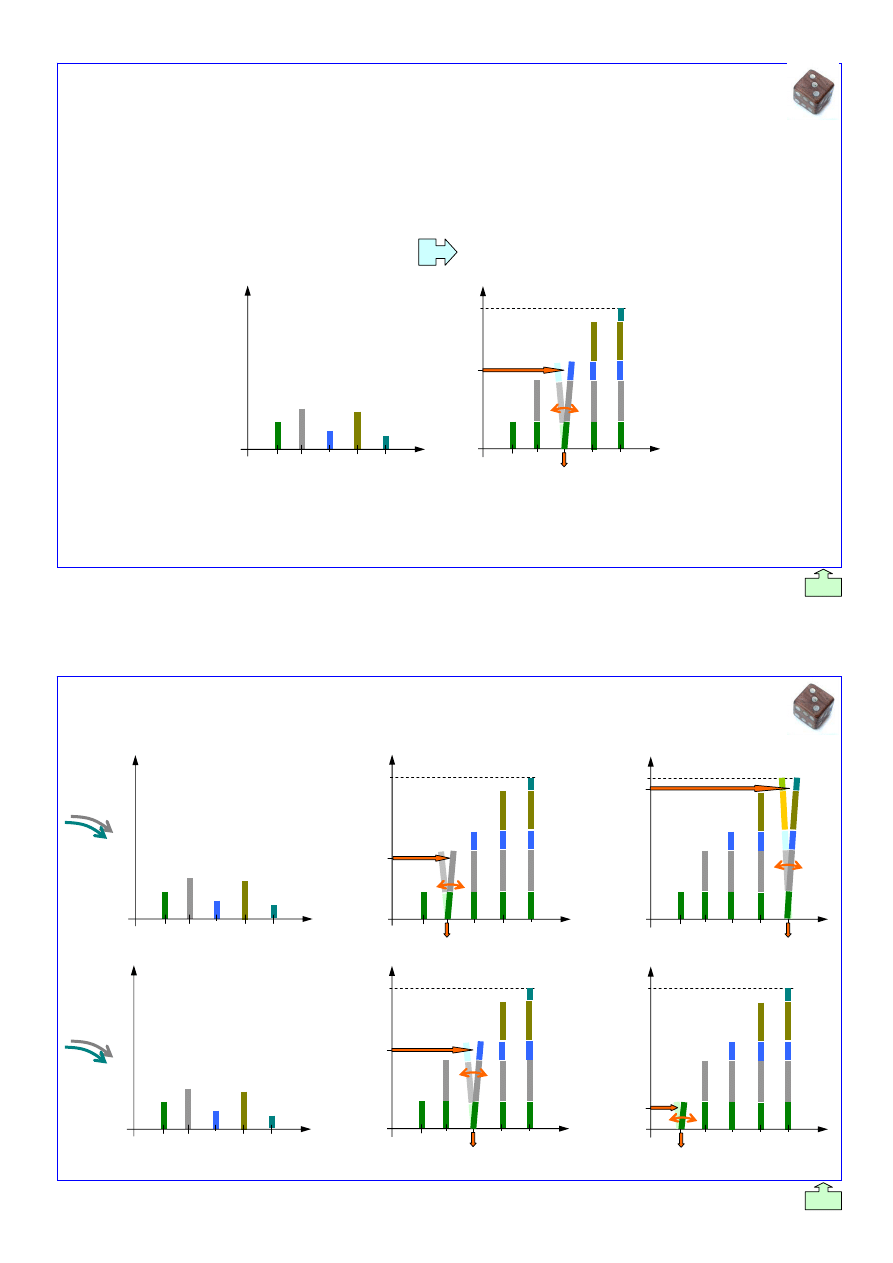
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(1)
GENEROWANIE LICZB LOSOWYCH
O ROZK
àADZIE EMPIRYCZNYM ZMIENNEJ SKOKOWEJ
Do generowania liczb losowych o rozk
áadzie empirycznym zmiennej skokowej stosuje siĊ generator
pozyskany metod
ą odwracania dystrybuanty zmiennej losowej o tym rozkáadzie.
Dalej pokazano ide
Ċ generowania liczb losowych o rozkáadzie empirycznym zmiennej skokowej
(rys. 1).
p(x)
F(x)
x
1
x
F(x)
1,0
0,0
r
i
x
i
=x
3
x
2
x
4
x
5
x
1
x
x
2
x
4
x
5
p(x)
x
3
Idea generowania liczb losowych o rozk
áadzie
empirycznym zmiennej skokowej
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
21/26
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(2)
PRZYK
àADY GENEROWANIA LICZB LOSOWYCH
O ROZK
àADZIE EMPIRYCZNYM ZMIENNEJ SKOKOWEJ
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
22/26
F(x)
x
1
x
1,0
0,0
r
i
x
i
=x
2
x
5
x
4
x
3
x
1
x
x
2
x
4
x
5
p(x)
x
3
x
1
x
F(x)
1,0
0,0
r
i
x
i
=x
5
x
2
x
4
x
3
1.
x
1
x
F(x)
1,0
0,0
r
i
x
i
=x
3
x
2
x
4
x
5
x
1
x
x
2
x
4
x
5
p(x)
x
3
x
F(x)
1,0
0,0
r
i
x
i
=x
1
x
2
x
4
x
5
x
3
2.

Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(1)
GENEROWANIE LICZB LOSOWYCH
O ROZK
àADZIE EMPIRYCZNYM ZMIENNEJ CIĄGàEJ
(1)
GENEROWANIE LICZB LOSOWYCH
O ROZK
àADZIE EMPIRYCZNYM ZMIENNEJ CIĄGàEJ
Do generowania liczb losowych o rozk
áadzie empirycznym zmiennej ciągáej stosuje siĊ generator
pozyskany metod
ą odwracania dystrybuanty zmiennej losowej o tym rozkáadzie.
Do generowania liczb losowych o rozk
áadzie empirycznym zmiennej ciągáej stosuje siĊ generator
pozyskany metod
ą odwracania dystrybuanty zmiennej losowej o tym rozkáadzie.
Dalej pokazano ide
Ċ generowania liczb losowych o rozkáadzie empirycznym zmiennej ciągáej (rys. 1).
Dalej pokazano ide
Ċ generowania liczb losowych o rozkáadzie empirycznym zmiennej ciągáej (rys. 1).
x
i
0,00
0,20
0,40
0,60
0,80
1,00
F (x )
0,00
0,20
0,40
0,60
0,80
1,00
p (x )
r
i
x
k
x
k+1
x
k
x
k+1
[x
k
, F(x
k
)]
[x
k+1
, F(x
k+1
)]
k
i
k
k
k
k
k
i
x
F
r
x
F
x
F
x
x
x
x
1
1
x
i
=?
0,00
0,20
0,40
0,60
0,80
1,00
F (x )
0,00
0,20
0,40
0,60
0,80
1,00
p (x )
r
i
x
1
x
2
x
3
x
4
x
1
x
2
x
3
x
4
Schemat ideowy
generowania liczb losowych
o rozk
áadzie empirycznym
zmiennej ci
ągáej
Schemat ideowy
generowania liczb losowych
o rozk
áadzie empirycznym
zmiennej ci
ągáej
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
23/26
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(2)
GENEROWANIE LICZB LOSOWYCH
O ROZK
àADZIE EMPIRYCZNYM ZMIENNEJ CIĄGàEJ
Z trójk
ątów, które moĪna zauwaĪyü na rysunku obok wynika, Īe
x
i
0,00
0,20
0,40
0,60
0,80
1,00
F (x )
r
i
x
k
x
k+1
[x
k
, F(x
k
)]
[x
k+1
, F(x
k+1
)]
k
k
k
k
x
x
x
F
x
F
tg
1
1
D
k
i
k
i
x
x
x
F
r
tg
D
,
(1)
Porównuj
ąc stronami równania (1) otrzymuje siĊ:
k
i
k
i
k
k
k
k
x
x
x
F
r
x
x
x
F
x
F
1
1
, (2)
a st
ąd ostateczna postaü modelu matematycznego generatora liczb losowych o rozkáadzie empirycznym
zmiennej ci
ągáej, przedstawia siĊ nastĊpująco:
k
i
k
k
k
k
k
i
x
F
r
x
F
x
F
x
x
x
x
1
1
, gdzie i = 1,2,... .
(3)
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
24/26
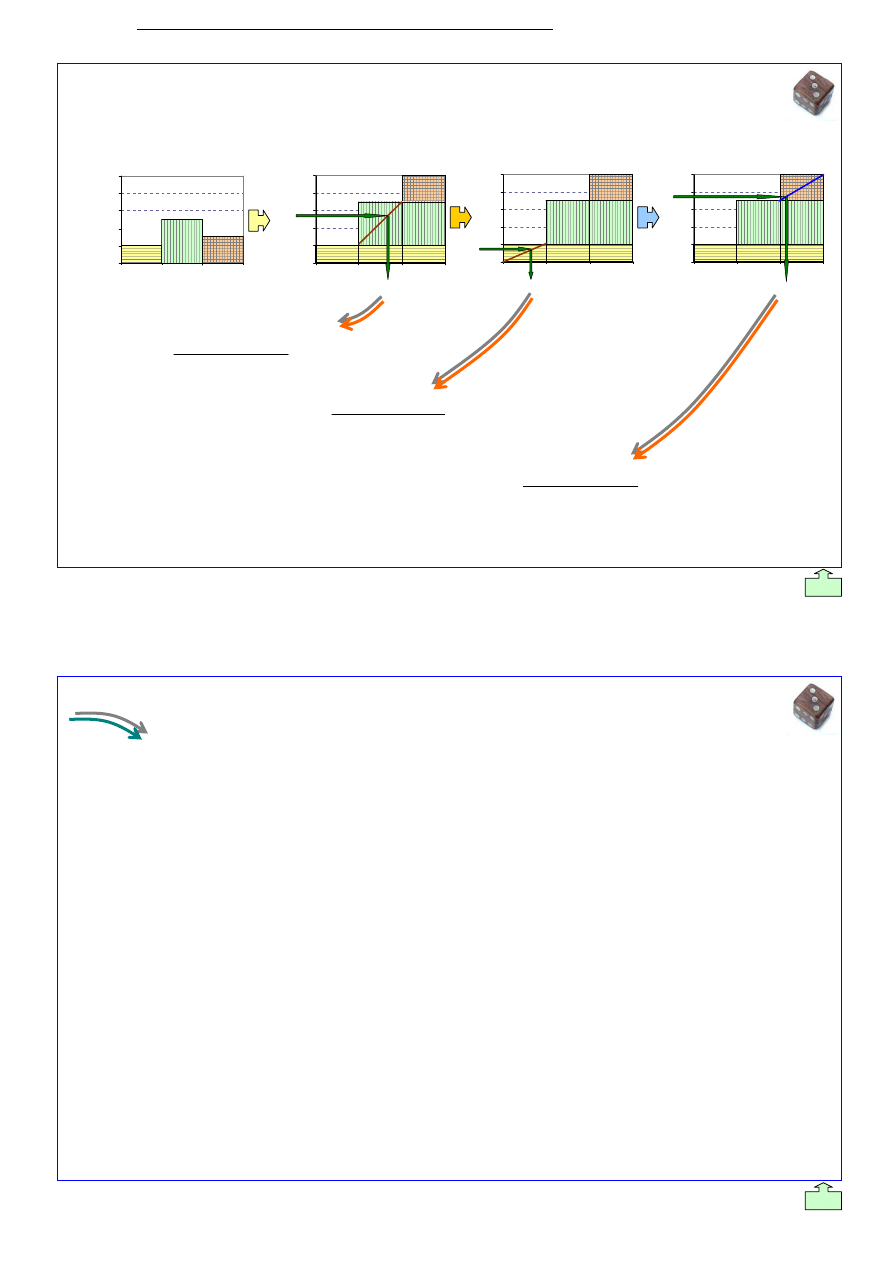
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
(3)
GENEROWANIE LICZB LOSOWYCH O ROZK
àADZIE
EMPIRYCZNYM ZMIENNEJ CI
ĄGàEJ – PRZYKàADY
0,00
0,20
0,40
0,60
0,80
1,00
p (x )
x
1
x
2
x
3
x
4
x
i
0,00
0,20
0,40
0,60
0,80
1,00
F (x )
r
i
x
1
x
2
x
3
x
4
x
i
0,00
0,20
0,40
0,60
0,80
1,00
F (x )
r
i
x
1
x
2
x
3
x
4
x
i
0,00
0,20
0,40
0,60
0,80
1,00
F (x )
x
1
x
2
x
3
x
4
r
i
1
1
2
1
2
1
x
F
r
x
F
x
F
x
x
x
x
i
i
2
2
3
2
3
2
x
F
r
x
F
x
F
x
x
x
x
i
i
3
3
4
3
4
3
x
F
r
x
F
x
F
x
x
x
x
i
i
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
25/26
Plik: 2_AK_Generowanie_Liczb_Losowych_2007_s_p_[v9].doc
NOTATKI
A. KADZI
ēSKI
,
GENEROWANIE LICZB LOSOWYCH O WYBRANYCH ROZKàADACH PRAWDOPODOBIEēSTWA
26/26
Wyszukiwarka
Podobne podstrony:
14 BO 2 1 PP Generowanie Liczb Losowych 2008 s p [v9]
14 BO 2 1 PP Generowanie Liczb Losowych 2008 s p [v9]
Generowanie liczb losowych
LEP BY TVN MED, Zestaw LEP - TVN MED - PEDIATRIA II, Zestaw LEP: Zestaw losowy (2008-03-29 14:38:06)
LEP BY TVN MED, Zestaw LEP - TVN MED - PEDIATRIA III, Zestaw LEP: Zestaw losowy (2008-03-29 14:45:57
2 BO 2 1 PP Przykłady Segregator [v1]
9 BO 2 1 PP MODEL A s p [v2]
tablica liczb losowych
8 BO 2 1 PP ZASOBY Wprowadzenie s p [v3]
1 BO 1 1 PP Modelowanie Opisowe Segregator [v1]
12 BO 2 1 PP Segregator Polityka Odnawiania Zasobów w Stacji Paliw s p [v2]
0 BO 3 1 PP Dzienne 2014 AK&BK Plan cyklu wykładowego [v2]
4 BO 2 1 PP M M 1 oo Analityczne p s [v3]
Fak 1 PP'16 10'12'2008
13 BO 1 1 PP 1plus2 Paliwa 6000
5 BO 2 1 PP M M n oo Analityczne p s [v3]
3 BO 2 1 PP Klasyfikacje systemów masowej obsługi s p
11 BO 2 1 PP MODEL D s p [v2]
więcej podobnych podstron