
Strona 1111 z 16
16
16
16
Sprawozdanie z zadania domowego wykonanego w ramach przedmiotu
Fizyka I- ćwiczenia audytoryjne.
Doświadczalne wyznaczenie wykładnika potęgi n przy wysokości h słupa cieczy we
wzorze na czas t wypływu cieczy ze zbiornika w funkcji tej wysokości h.
Wykonała:
Nr albumu:
Kierunek:
studia stacjonarne, pierwszego stopnia
rok , sem.
Sprawdziła:
Strona 2222 z 16
16
16
16
1.
Cel doświadczenia.
Celem tego ćwiczenia było eksperymentalne wyznaczenie wykładnika potęgowego czasu
wypływu wody ze zbiornika w zależności od wysokości oraz porównanie go z wykładnikiem
potęgowym występującym we wzorze.
Celem pośrednim było też wykorzystanie metod analizy wymiarowej do wyprowadzenia
wzoru na potrzeby doświadczenia.
2.
Wstęp teoretyczny.
Rozważając zjawisko przepływu nieodzownym jest, zastosowanie równania Bernoulliego,
czyli jednego z podstawowych równań mechaniki płynów, wyrażającego zmiany energii
mechanicznej strumienia płynu. Aby wyprowadzić takie równanie dla cieczy idealnej, należy
porównać energię płynu między dwoma przekrojami poprzecznymi strugi, przy założeniach,
ż
e:
•
przepływający płyn jest doskonały (nielepki η = 0, nieściśliwy ρ = const.)
•
przepływ jest stacjonarny (pochodna cząstkowa dowolnego parametru przepływu
względem czasu jest równa zeru)
•
przepływ odbywa się bez wymiany ciepła i masy
•
do płynu nie jest dostarczana z zewnątrz żadna energia mechaniczna
•
przepływ ma miejsce w jednorodnym polu grawitacyjnym.
Wypływ ustalony cieczy ze zbiornika zachodzi wówczas, gdy powierzchnia swobodna
(zwierciadło) pozostaje na niezmienionej wysokości
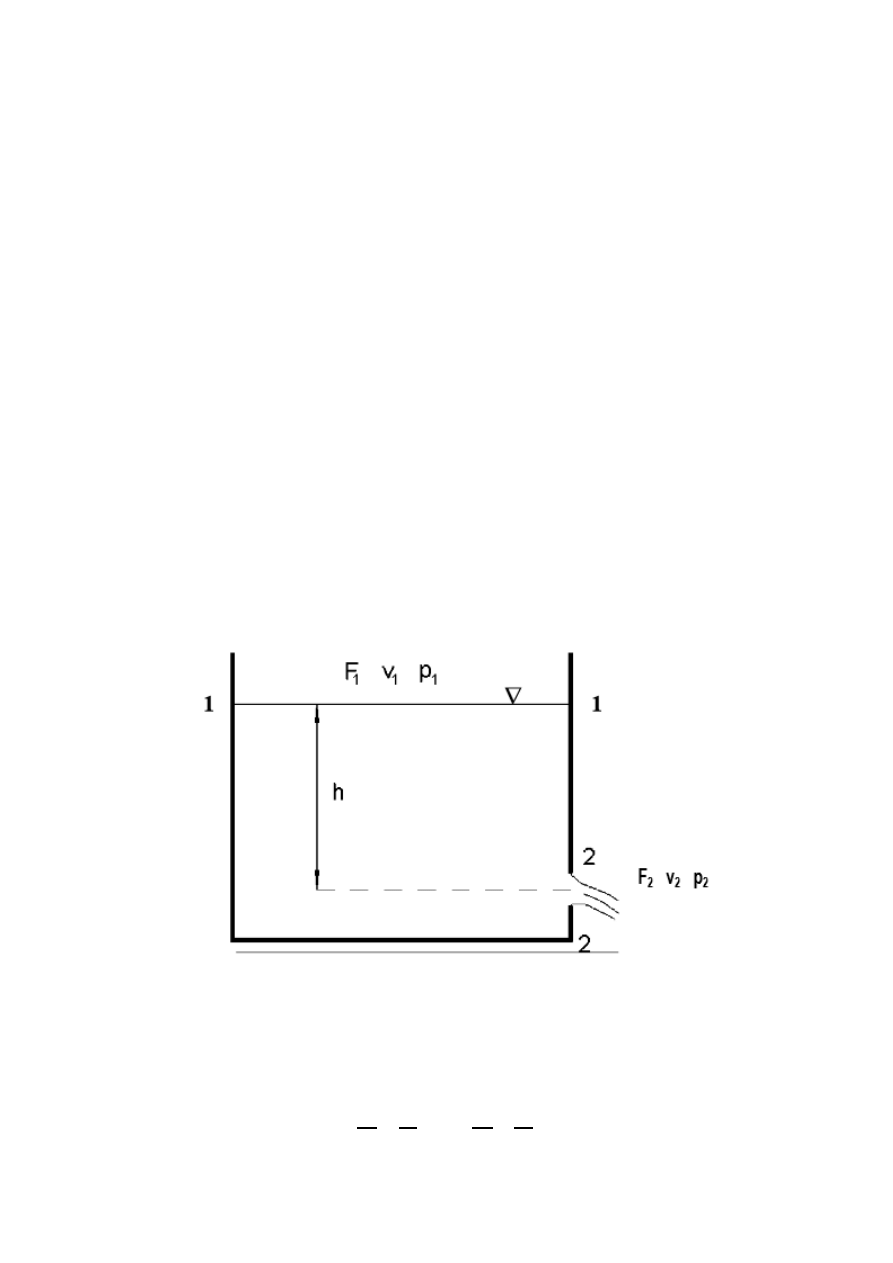
h=const (rys.1)
.
Rys. 1. Schemat rozważanego zbiornika.
Oznaczając przez F
1
pole powierzchni zwierciadła cieczy w zbiorniku, v
1
prędkość i p
1
ciśnienie w przekroju 1-1, (rys.1) natomiast F
2
, v
2
, p
2
pole powierzchni otworu, prędkość
wypływu i ciśnienie w przekroju wylotowym (2-2) równanie Bernoulliego będzie miało
postać:
v
2g +
p
gρ + h =
v
2g +
p
gρ.

Strona 3333 z 16
16
16
16
Zależność ta prawdziwa jest nie tylko dla samych cieczy, ale i dla płynów.
Prędkości v
1
i v
2
powiązane są wzajemnie równaniem ciągłości:
F ∙ v = F ∙ v ,
skąd: v =
F
F ∙ v .
Wówczas z równania Bernoulli’ego otrzymuje się zależność:
v =
2g p − p
gρ + h"
1 − #FF $
,
Dla
%
&
%
'
≪ 1, równanie przyjmuje postać:
v = )2g
p
*
γ + h" .
Ponieważ
, ≪ , można pominąć (, /, ) jako wielkość bardzo małą w porównaniu
z jednością. Jeżeli ponadto uwzględni się wypływ ze zbiornika otwartego do atmosfery
wówczas
0 = 0 = 0
1
(p
a –
ciśnienie atmosferyczne), wtedy równanie upraszcza się do
postaci:
v = 22gh,
znanego również jako równanie Torricellego.
W rzeczywistości prędkość wypływu jest mniejsza od wyznaczonej ze wzoru Torricellego.
Wpływ na to ma istnienie sił masowych oraz sił stycznych (lepkości) w płynach rzeczywistych.
Owe straty niweluje się wprowadzając do wzory Torricellego współczynnik poprawkowy:
φ =
v
45
v
6
,
gdzie v
rz
- wyznaczona doświadczalnie prędkość wypływu, v
t
- prędkość wypływu
wyznaczona ze wzoru
.
gh
2
Po wprowadzeniu współczynnika
φ
<1 do równania, przedstawia
się ono w postaci:
.
gh
2
v
rz
⋅
ϕ
=
Ze wzoru Torricellego wynika, że zmniejszanie prędkości wypływu płynu ze zbiornika
odbywa się w sposób ciągły. Jeśli przyjąć prostokątny układ współrzędnych z początkiem (0,0)
na poziomie otworu i osią OZ zorientowaną pionowo ku górze, to w chwili początkowej
opróżniania zbiornika zwierciadło płynu znajduje się na wysokości h nad otworem. Po upływie
pewnego czasu spada on do wysokości z, przy czym pole powierzchni F
Z
pozostaje stałe, zaś
prędkość wypływu wynosi:
v = φ ∙ 22gz.
W czasie dt przez otwór (ostro krawędziowy) przepływa płyn w ilości Q:
Q = κ ∙ F
9
22gz ∙ dt,
gdzie
κ
jest współczynnikiem wydatku takim, że
µ
⋅
ϕ
=
κ
.
ϕ
to omówiony wcześniej
współczynnik strat prędkości, zaś
µ−
dodatkowy współczynnik korekcyjny związany ze
zjawiskiem kontrakcji (przewężenia strugi). Obserwuje się bowiem, że w pewnej odległości od
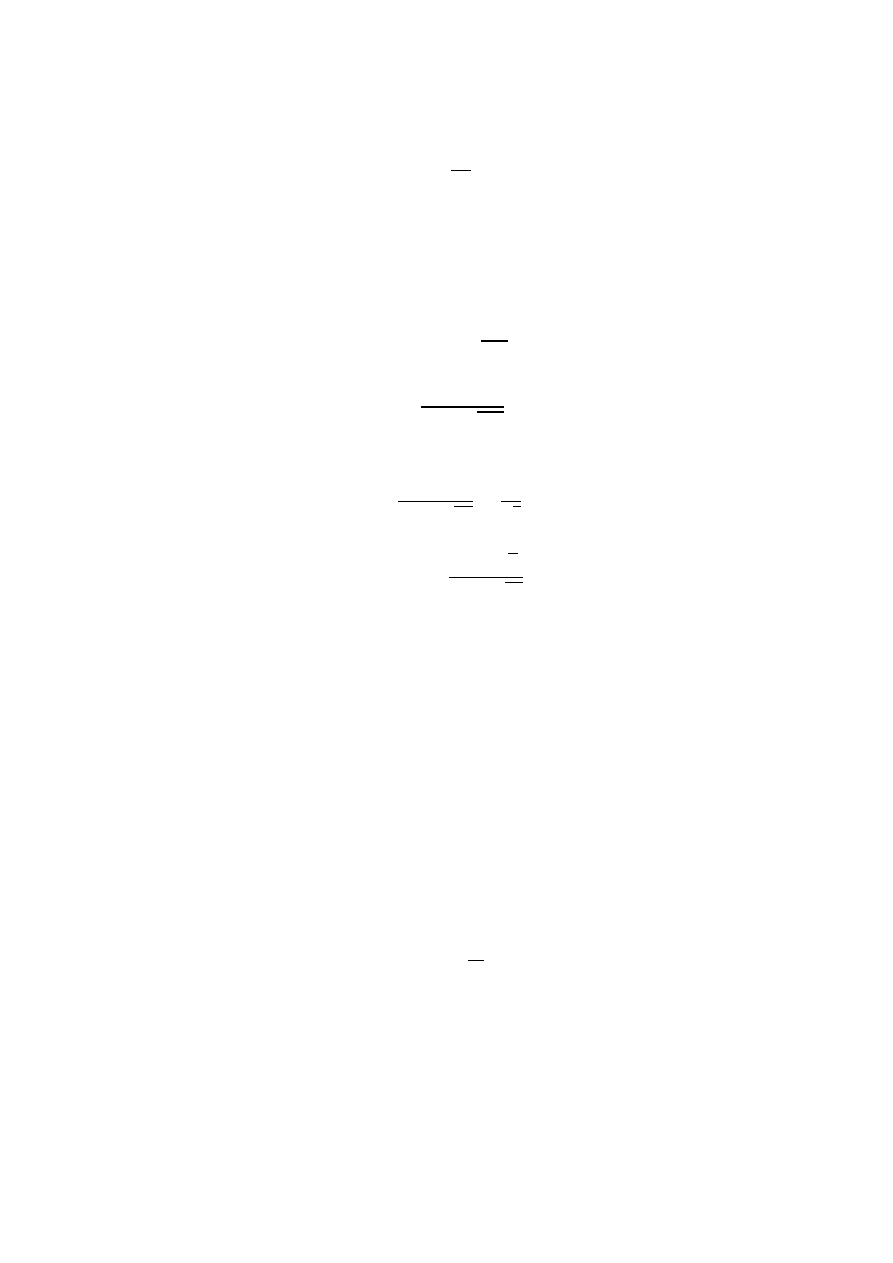
Strona 4444 z 16
16
16
16
otworu przekrój strumienia jest mniejszy niż przekrój samego otworu. Jest to związane z
istnieniem sił masowych w płynach. Współczynnik przewężenia wyznacza się jako:
μ =
F
9
F
<
,
gdzie F
S
- to przekrój strugi. Wartość współczynnika kontrakcji zależy od ukształtowania
krawędzi otworu, zaokrąglenia jego brzegów oraz chropowatości. Zjawisko kontrakcji
uwidacznia się najbardziej dla otworów ostro krawędziowych. Dla otworu okrągłego o
delikatnie zaokrąglonych krawędziach i małej chropowatości wartość współczynnika
kontrakcji może osiągnąć jedność.
W czasie dt przez otwór przepływa płyn w ilości Q, a zwierciadło obniża się o dz, to bilans
masy prowadzi do równania:
F
=
∙ dz = κ ∙ F
9
22gz ∙ dt.
Jest to równanie różniczkowe o zmiennych rozdzielonych. Stąd:
dt =
F
=
∙ dz
κ ∙ F
9
22gz
.
Podczas opróżniania zbiornika wysokość z zmienia się od h do 0. Czas t
0
wypływu płynu
ze zbiornika oblicza się jako całkę:
t
>
=
F
=
κ ∙ F
9
22g
?
dz
√z
A
>
,
skąd: t
>
=
2F
=
∙ √h
κ ∙ F
9
22g
.
Wynika z tego, że całkowity czas wypływu płynu ze zbiornika o stałym przekroju jest
wprost proporcjonalny do pierwiastka początkowej wysokości słupa cieczy.
Zatem poszukiwany wykładnik potęgi ma wartość n= 0,5.
Możliwe jest wyznaczenie współczynnika nawet bez znajomości równania Bernoulliego
oraz wzoru Torricellego, a mianowicie posługując się analizą wymiarową zjawiska. Analizując
przepływ można wysunąć wniosek, że czas wypływu zależy bezpośrednio od wysokości słupa
cieczy (h) oraz grawitacji, co można zapisać:
t = f(h, g)
Zależność da się przedstawić w następującej postaci:
t = c ∙ h
*
∙ g
D
,
gdzie t- całkowity czas wypływu płynu ze zbiornika, h- początkowa wysokość słupa płynu,
g- przyspieszenie ziemskie, n
−
wykładnik potęgi, stojącej przy wysokości (czyli poszukiwana
wartość), p
−
wykładnik potęgi, stojącej przy przyspieszeniu ziemski, c- bezwymiarowy, stały
współczynnik proporcjonalności.
Dokonując rachunku jednostek miar powyższych wielkości fizycznych otrzymujemy
zależność:
s = m
*
∙ #
m
s $
D
s ∙ m
>
= m
*FD
∙ s
G ∙D
.
Z równości wykładników potęg stojących przy tych samych czynnikach po lewej i prawej
stronie równania wynika, że:
H 1 = −2p
0 = n + p
Oznacza to, że:

Strona 5555 z 16
16
16
16
K
n =
1
2
p = −
1
2 .
Zatem:
t = c ∙ )
h
g.
W konsekwencji poszukiwany wykładnik potęgi ma wartość n=
.
2
1
3.
Opis wykonanego ćwiczenia laboratoryjnego.
3.1.
Zastosowane materiały.
Jako ciecz w doświadczeniu wykorzystano wodę użytkową.
3.2.
Zastosowane urządzenia.
Posłużono się następującymi urządzeniami pomiarowymi: przymiarem liniowym z
podziałką milimetrową oraz dwoma stoperami.
3.3.
Opis stanowiska.
Przygotowano stanowisko pomiarowe: od
plastikowej butelki (o grubościach ścianek
pomijalnie małych w stosunku do średnic
wewnętrznej i zewnętrznej) odcięto dno,
następnie plastycznym korkiem zaczopowano
szyjkę. W korku spreparowano okrągły otwór,
który usztywniono plastikową słomką. Takie
przygotowanie odpływu miało gwarantować
małą wartość stosunku średnicy odpływu do
ś
rednicy zwierciadła cieczy, czyli w tym
przypadku do średnicy butelki, a także zapobiec
wypływowi
turbulentnemu
w
możliwie
największym stopniu.
Na zewnętrzną ściankę butelki naniesiono
podziałkę ze skokiem co 1cm, przy czym za
wartość zerową przyjęto koniec przewężenia
szyjki.
Całość zamontowano do statywu, tak że
odpływ był skierowany w dół. Pod zbiornikiem
umieszczono kuwetę.
Stanowisko
pomiarowe
zostało
przedstawione na rys. 2 obok.

Strona 6666 z 16
16
16
16
3.4.
Wykonane operacje.
Pomiar wykonano w następujący sposób:
1)
określono średnicę naczynia na podstawie jego obwodu;
2)
zamknięto otwór odpływu, zapobiegając wypływowi wody;
3)
napełniono zbiornik do żądanej wysokości;
4)
usunięto przesłonę i jednocześnie rozpoczęto pomiar czasu wypływu wody na dwóch
niezależnych stoperach;
5)
po osiągnięciu przez wodę poziomu oznaczonego jako h=0 zatrzymano stopery i zapisano
pomiar (tab. 1.);
6)
powtórzono czynności od 1) do 4) trzy razy;
7)
powtórzono czynności od 1) do 5) dla dwudziestu jeden różnych poziomów wody;
8)
wykonano obliczenia
4.
Wyniki pomiarów oraz obliczenia.
4.1.
Wyniki pomiarów elementów stanowiska pomiarowego oraz wyznaczenie
niepewności maksymalnych.
Pomiar średnicy odpływu d i wyznaczeni pola jego przekroju F
O
.
Ś
rednicę zmierzono, porównując przymiar liniowy (z podziałką milimetrową)
bezpośrednio z wymiarem otworu. Wynik pomiaru: 4mm=0,004m. Niepewność
maksymalna pomiaru (jako najmniejszy skok podziałki na przymiarze):
∆
d=1mm=0,001. Zatem średnica odpływu: d=(0,004±0,001)m.
Pole przekroju otworu F
O
, wyznaczono ze wzoru:
.
4
d
F
2
O
⋅
π
=
Wynik obliczeń dla
d=0,004m wynosił 0,000013m
2
. Niepewność maksymalna pomiaru pola:
.
m
000007
,
0
F
2
m
004
,
0
m
001
,
0
F
2
d
d
F
d
F
d
F
2
O
O
O
O
O
≈
∆
⇒
⋅
π
⋅
=
∆
⇒
⋅
π
⋅
∆
=
∆
⇒
∂
∂
⋅
∆
=
∆
Ostatecznie pole przekroju odpływu F
O
=(0,000013 ±0,000007) m
2
.
Pomiar średnicy zbiornika i wyznaczenie jego pola przekroju F
Z
.
Ś
rednicę zmierzono, porównując przymiar liniowy (z podziałką milimetrową)
bezpośrednio z zewnętrznym wymiarem zbiornika. Wynik pomiaru: 106mm=0,106m.
Niepewność maksymalna pomiaru (jako najmniejszy skok podziałki na przymiarze):
∆
D=1mm=0,001m. Zatem średnica pojemnika: D=(0,106±0,001)m.
Pole przekroju zbiornika F
Z
, wyznaczono ze wzoru:
.
4
D
F
2
Z
⋅
π
=
Wynik obliczeń dla
D=0,106m wynosił 0,008825m
2
. Niepewność maksymalna pomiaru pola:
.
m
000167
,
0
F
2
m
106
,
0
m
001
,
0
F
2
D
D
F
D
F
D
F
2
O
Z
O
Z
Z
≈
∆
⇒
⋅
π
⋅
=
∆
⇒
⋅
π
⋅
∆
=
∆
⇒
∂
∂
⋅
∆
=
∆
Ostatecznie pole przekroju odpływu F
Z
=(0,008825 ±0,000167) m
2
.
Niepewność maksymalna pomiaru wysokości słupa wody
∆∆∆∆
h.
∆
h=±1mm, jako najmniejszy skok na przymiarze liniowym.
Strona 7777 z 16
16
16
16
Niepewność maksymalna pomiaru czasu wypływu
∆∆∆∆
t.
Niepewność maksymalna pomiaru czasu
∆
t wyznaczono jako niepewność
standardową całkowitą z niepewności systematycznej
∆
t
S
oraz związanej z czasem
reakcji eksperymentatora
∆
t
R
.
Za wartość niepewności systematycznej przyjęto najmniejsza jednostkę czasu na
stoperze:
∆
t
S
=0,01s. Wartość niepewności związanej z czasem reakcji ustalono na
podstawie informacji zawartych w instrukcji przeprowadzenia niepewności analizy
pomiarowej www.typjan.zut.edu.pl
:
∆
t
R
=0,2s.
Zatem niepewność maksymalna pomiaru czasu:
( ) ( )
(
) (
)
s
20
,
0
t
s
20025
,
0
t
s
20
,
0
s
01
,
0
t
t
t
t
2
2
2
R
2
S
≈
∆
⇒
=
∆
⇒
+
=
∆
⇒
∆
+
∆
=
∆
4.2.
Wyniki pomiaru czasu t dla zadanych względnych wysokości słupa wody h.
Tabela 1.
L. p.
Względna
wysokość
słupa wody h
Czas wypływu wody t
i
Ś
redni czas
wypływu
wody
ln(h) ln(t)
[-]
[m]
[s]
[s]
[-]
[-]
t
1
t
2
t
3
t
4
t
5
1
0,22
100,33
100,33
101,06
101,04
101,20
100,79
-1,51 4,61
2
0,21
97,05
97,13
95,63
95,74
96,01
96,31
-1,56 4,57
3
0,20
92,36
92,36
92,36
92,45
92,40
92,39
-1,61 4,53
4
0,19
88,27
88,27
88,56
88,12
89,12
88,47
-1,66 4,48
5
0,18
85,16
85,16
87,45
87,52
87,85
86,63
-1,71 4,46
6
0,17
81,74
81,74
84,05
84,12
84,42
83,21
-1,77 4,42
7
0,16
77,87
77,87
79,21
79,76
79,55
78,85
-1,83 4,37
8
0,15
73,45
73,45
73,08
73,23
74,08
73,46
-1,90 4,30
9
0,14
69,58
69,58
69,12
69,23
69,45
69,39
-1,97 4,24
10
0,13
65,74
65,86
66,32
66,21
65,18
65,86
-2,04 4,19
11
0,12
61,74
61,88
61,92
61,85
61,86
61,85
-2,12 4,12
12
0,11
57,51
57,60
57,35
58,29
58,11
57,77
-2,21 4,06
13
0,10
53,41
53,45
53,66
54,17
53,16
53,57
-2,30 3,98
14
0,09
49,72
49,53
49,25
49,47
49,58
49,51
-2,41 3,90
15
0,08
44,32
44,10
44,45
44,34
44,19
44,28
-2,53 3,79
16
0,07
39,82
39,89
38,93
38,85
39,09
39,32
-2,66 3,67
17
0,06
34,83
34,86
34,58
34,63
34,72
34,72
-2,81 3,55
18
0,05
29,09
28,84
29,45
29,52
29,64
29,31
-3,00 3,38
19
0,04
24,16
24,17
24,72
24,80
24,98
24,57
-3,22 3,20
20
0,03
18,23
18,67
19,60
19,55
18,57
18,92
-3,51 2,94
21
0,02
12,33
12,33
12,80
12,89
12,79
12,63
-3,91 2,54
22
0,01
6,16
6,20
6,63
6,76
6,88
6,53
-4,61 1,88
Strona 8888 z 16
16
16
16
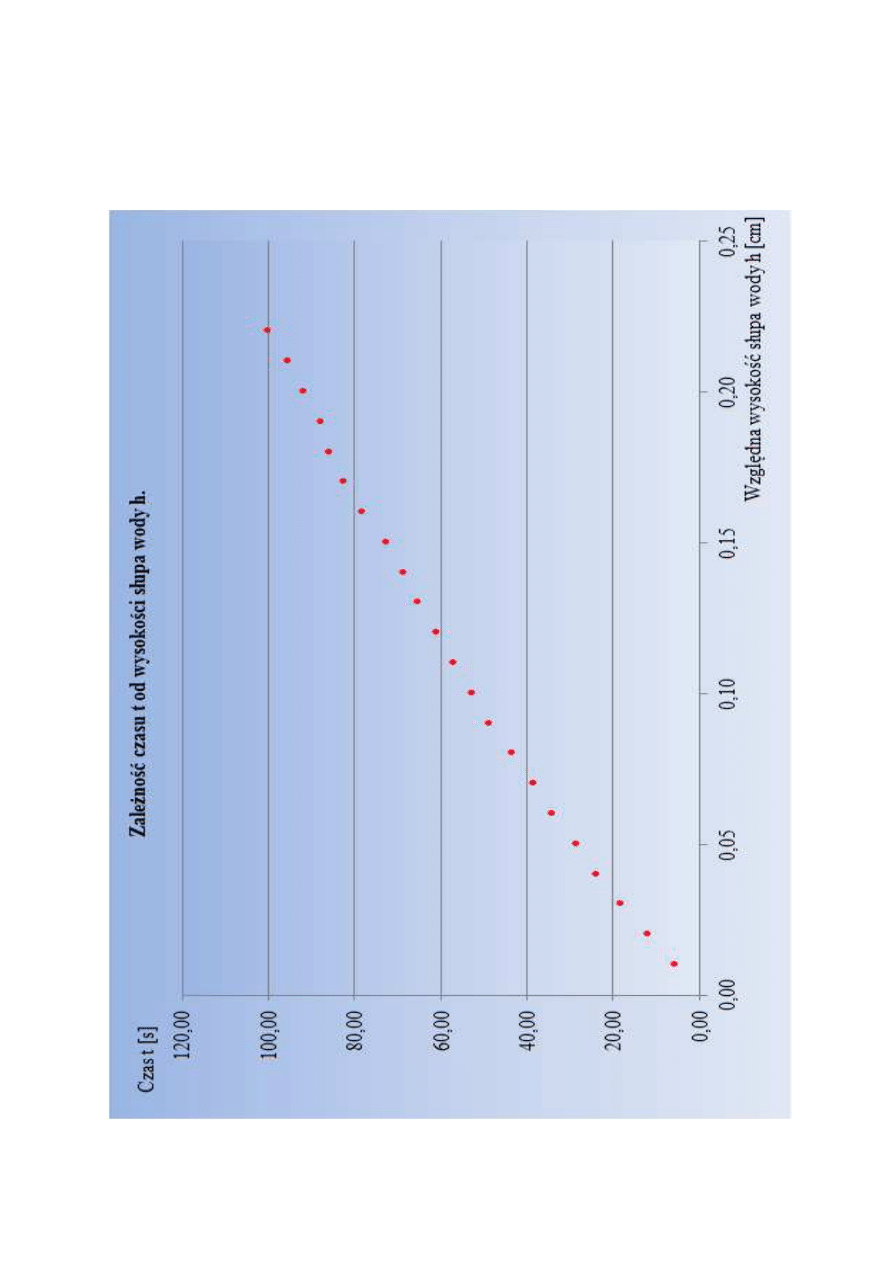
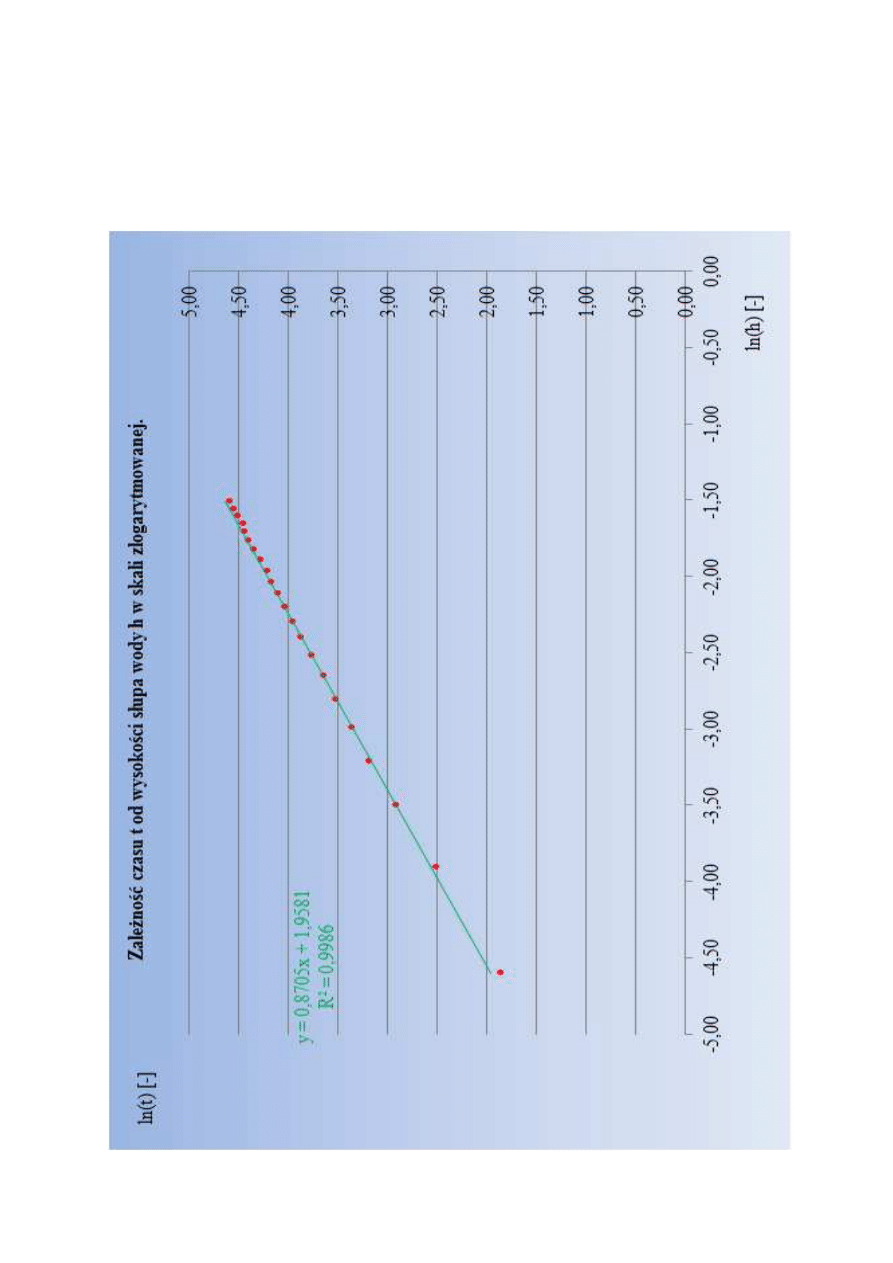
4.3.
Wykres zależności całkowitego czasu t wypływu wody ze zbiornika w zależności od
początkowej wysokości słupa wody h.
Wykres wykonano w programie Excel 2007 na podstawie wyników przedstawionych
w tab.1.
Strona 9999 z 16
16
16
16
4.4.
Wykres zależności całkowitego czasu t wypływu wody ze zbiornika w zależności od
początkowej wysokości słupa wody h w skali zlogarytmowanej.
Wykres wykonano w programie Excel 2007 na podstawie wyników przedstawionych
w tab.1. Zielonym kolorem zaznaczono prostą regresji, jej równanie, a także współczynnik
korelacji R
2
, wyznaczonych za pomocą funkcji: ,,Linia trendu”.
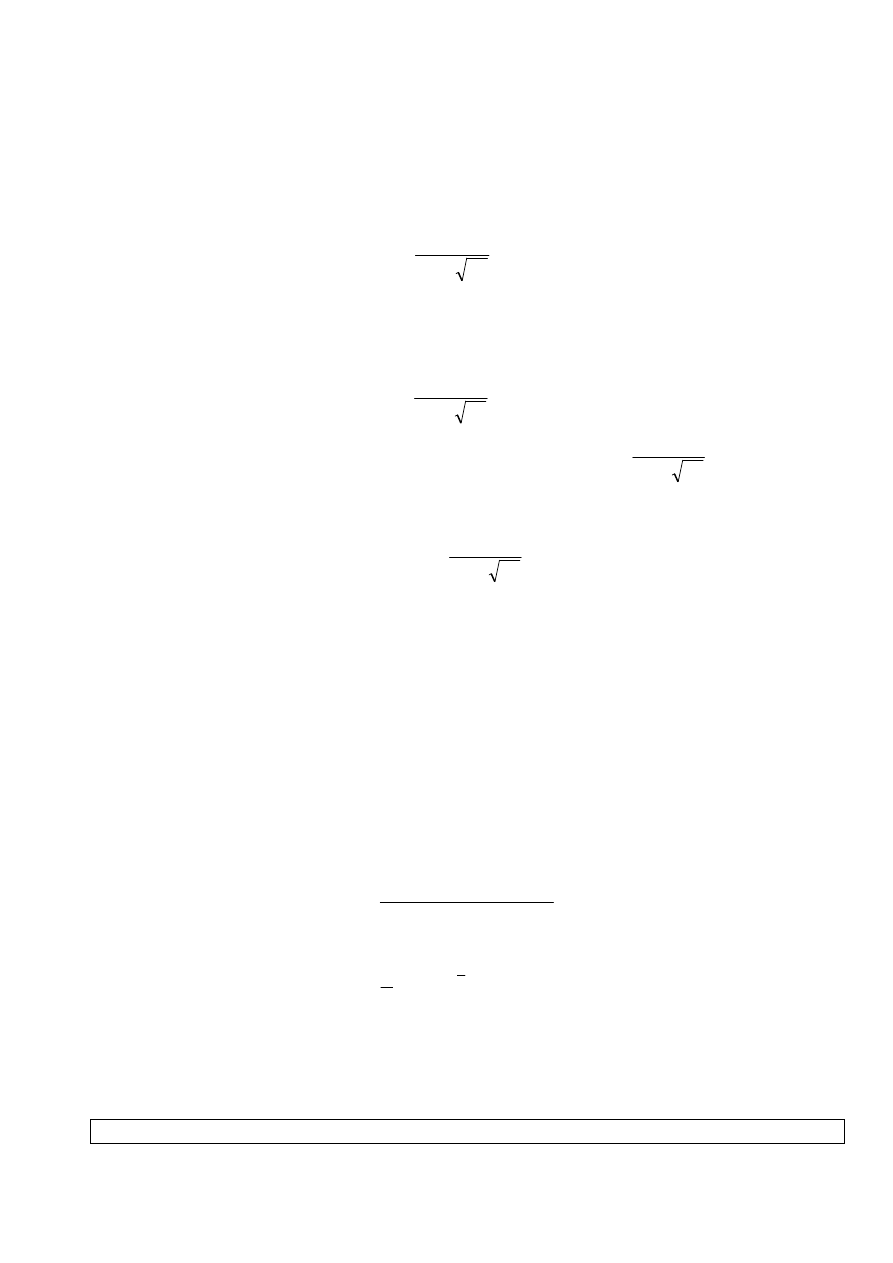
Strona 10
10
10
10 z 16
16
16
16
4.5.
Wyznaczenie szukanego wykładnika potęgi n.
Poszukiwany wykładnik potęgi przy wysokości słupa cieczy we wzorze na czas wypływu
cieczy ze zbiornika w funkcji tej wysokości oznaczono jako n. Wówczas wzór przedstawiony
w punkcie 2. przybrał postać:
,
h
g
2
F
F
2
t
n
O
Z
⋅
⋅
κ
=
gdzie t- czas wypływu wody ze zbiornika, F
Z
- pole powierzchni swobodnego zwierciadła
wody,
κ
- współczynnik wydatku zależny od kształtu odpływu, F
O
- pole powierzchni
odpływu, g- przyspieszenie ziemskie, h- początkowa wysokość słupa wody nad odpływem.
W celu wyznaczenia wykładnika potęgi n, obie strony równania zlogarytmowano:
).
h
ln(
n
g
2
F
F
2
ln
)
t
ln(
O
Z
⋅
+
⋅
κ
=
Dla niezmiennego przekroju poprzecznego zbiornika składnik
⋅
κ
g
2
F
F
2
ln
O
Z
był stały,
zatem równanie miało charakter liniowy, gdzie ln(t) można było traktować jako zmienną
zależną y, ln(h)- zmienną niezależną x, poszukiwane n- jako współczynnik kierunkowy a,
stojący przy zmiennej niezależnej, zaś stałą
⋅
κ
g
2
F
F
2
ln
O
Z
jako wolny wyraz b:
.
b
x
a
y
+
⋅
=
W tej sytuacji oczekiwano, że rozkład wyników pomiarów w skali zlogarytmowanej będzie
prostą, o współczynniku kierunkowym a=n, tj. stanowiącym poszukiwany wykładnik potęgi.
Ponieważ tak się nie stało, co zaprezentowano na wykresie w podpunkcie 4.3., metodą
najmniejszych kwadratów wyznaczono regresję liniową dla rozkładu wyników pomiarów
w skali zlogarytmowanej (zgodnie z instrukcją zawartą na stronie www.typjan.zut.edu.pl).
Z metody tej wiadomo było, że jeśli pomiędzy mierzonymi wielkościami x oraz y (czyli
w tym przypadku pomiędzy ln(h) i ln(t)) istniała zależność liniowa taka, że:
,
b
x
a
y
+
⋅
=
to
empiryczne współczynniki regresji liniowej a oraz b można było wyznaczyć z warunku:
(
)
.
min
b
x
a
y
n
1
i
2
i
i
=
−
⋅
−
∑
=
Z różniczkowego warunku na minimum otrzymano:
⋅
−
=
−
⋅
⋅
−
⋅
=
∑
∑
∑
∑
∑
∑
∑
=
=
=
=
=
=
=
k
1
i
i
k
1
i
i
2
n
1
i
i
k
1
i
2
i
k
1
i
i
k
1
i
i
k
1
i
i
i
x
a
y
k
1
b
,
x
x
k
y
x
y
x
k
a
gdzie i= 1, 2, 3,..,k, zaś k stanowił liczbę wykonanych pomiarów. Obliczenia dotyczące
wyznaczenia współczynnika
a oraz wyrazu wolnego b przedstawiono w tab.2. oraz tab.3.
Tabela.2
Strona 11
11
11
11 z 16
16
16
16
∑
∑
=
=
⋅
k
1
i
i
k
1
i
i
y
x
2
n
1
i
i
x
∑
=
Lp. ln(h)= x
i
ln(t)=
y
i
x
i
· y
i
a
[-]
[-]
[-]
[-]
[-]
[-]
[-]
[-]
[-]
[-]
1
-1,51
4,61
-6,98
-4229,19
-4500,56
2,29
3104,63
2792,34 0,87
2
-1,56
4,57
-7,13
2,44
3
-1,61
4,53
-7,28
2,59
4
-1,66
4,48
-7,44
2,76
5
-1,71
4,46
-7,65
2,94
6
-1,77
4,42
-7,83
3,14
7
-1,83
4,37
-8,00
3,36
8
-1,90
4,30
-8,15
3,60
9
-1,97
4,24
-8,34
3,87
10
-2,04
4,19
-8,54
4,16
11
-2,12
4,12
-8,75
4,50
12
-2,21
4,06
-8,95
4,87
13
-2,30
3,98
-9,17
5,30
14
-2,41
3,90
-9,40
5,80
15
-2,53
3,79
-9,57
6,38
16
-2,66
3,67
-9,76
7,07
17
-2,81
3,55
-9,98
7,92
18
-3,00
3,38
-10,12
8,97
19
-3,22
3,20
-10,30
10,36
20
-3,51
2,94
-10,31
12,30
21
-3,91
2,54
-9,92
15,30
22
-4,61
1,88
-8,64
21,21
Tabele 3.
Lp.
ln(h)= x
i
ln(t)= y
i
L. p.
ln(h)= x
i
ln(t)= y
i
b
[-]
[-]
[-]
[-]
[-]
[-]
[-]
1
-1,51
4,61
12
-2,21
4,05
5,95
2
-1,56
4,58
13
-2,30
3,98
3
-1,61
4,53
14
-2,41
3,91
4
-1,66
4,48
15
-2,53
3,79
5
-1,71
4,44
16
-2,66
3,68
6
-1,77
4,40
17
-2,81
3,55
7
-1,83
4,36
18
-3,00
3,37
8
-1,90
4,30
19
-3,22
3,18
9
-1,97
4,24
20
-3,51
2,90
10
-2,04
4,19
21
-3,91
2,51
11
-2,12
4,12
22
-4,61
1,82
Zatem równanie prostej regresji miało następującą postać:
∑
=
⋅
k
1
i
i
i
y
x
k
2
i
x
∑
=
⋅
k
1
i
2
i
x
k

Strona 12
12
12
12 z 16
16
16
16
95
,
5
)
ln(
87
,
0
)
ln(
+
⋅
=
h
t
Oznaczało to, że dla zbioru wyznaczonych danych poszukiwany wykładnik potęgowy
n=0,87 miał wartość inną niż oczekiwana.
Dla porównania, w punkcie 4.3., na wykresie zależności czasu t od początkowej wysokości
słupa wody h w skali zlogarytmowanej zielonym kolorem zaznaczono prostą regresji, jej
równanie oraz współczynnik korelacji R
2
.
4.6.
Wyznaczenie niepewności standardowej empirycznych współczynników a oraz b
regresji liniowej.
Odchylenia średnie kwadratowe u(a) oraz u(b) empirycznych współczynników regresji
liniowej a oraz b wyznaczono ze wzorów zawartych w instrukcji na stronie
www.typjan.zut.edu.pl
:
,
x
k
1
)
a
(
u
)
b
(
u
,
x
x
k
y
b
y
x
a
y
2
k
k
)
a
(
u
k
1
i
2
i
2
n
1
i
i
k
1
i
2
i
k
1
i
i
i
k
1
i
i
k
1
i
2
i
∑
∑
∑
∑
∑
∑
=
=
=
=
=
=
⋅
⋅
=
−
⋅
⋅
−
⋅
⋅
−
−
=
gdzie i=1,2,3,...,k, zaś k to ilość pomiarów, y- zmienna zależna, czyli ln(t), x- zmienna
niezależna, czyli ln(h). Obliczenia dotyczące wielkości u(a) oraz u(b) zawarto w tabelach 4. i
5.
4.7.
Wyznaczenie wartości stałego składnika
2
F
κ
2F
C
O
Z
⋅
=
.
W podpunkcie 4.5. przyjęto oznaczenie, że wyraz wolny w równaniu na czas t wypływu
wody ze zbiornika w funkcji wysokości słupa cieczy h w formie zlogarytmowanej był równy b:
.
g
2
F
F
2
ln
b
O
Z
⋅
κ
=
Jeśli stały składnik
2
F
κ
2F
O
Z
⋅
oznaczyć jako C, to powyższa równość przybierała postać:
.
g
C
ln
b
g
2
F
F
2
C
O
Z
=
⋅
κ
=
Wartość b wyznaczono jako wartość empirycznego współczynnika regresji liniowej,
ponieważ rezultat doświadczenia był różny od założeń teoretycznych:
b = 5,95 ± 0,07
Zakładając, że przyspieszenie ziemskie
,
s
m
81
,
9
g
2
=
a podstawa logarytmu naturalnego
e≈2,718, szukana wartość C wynosiła:
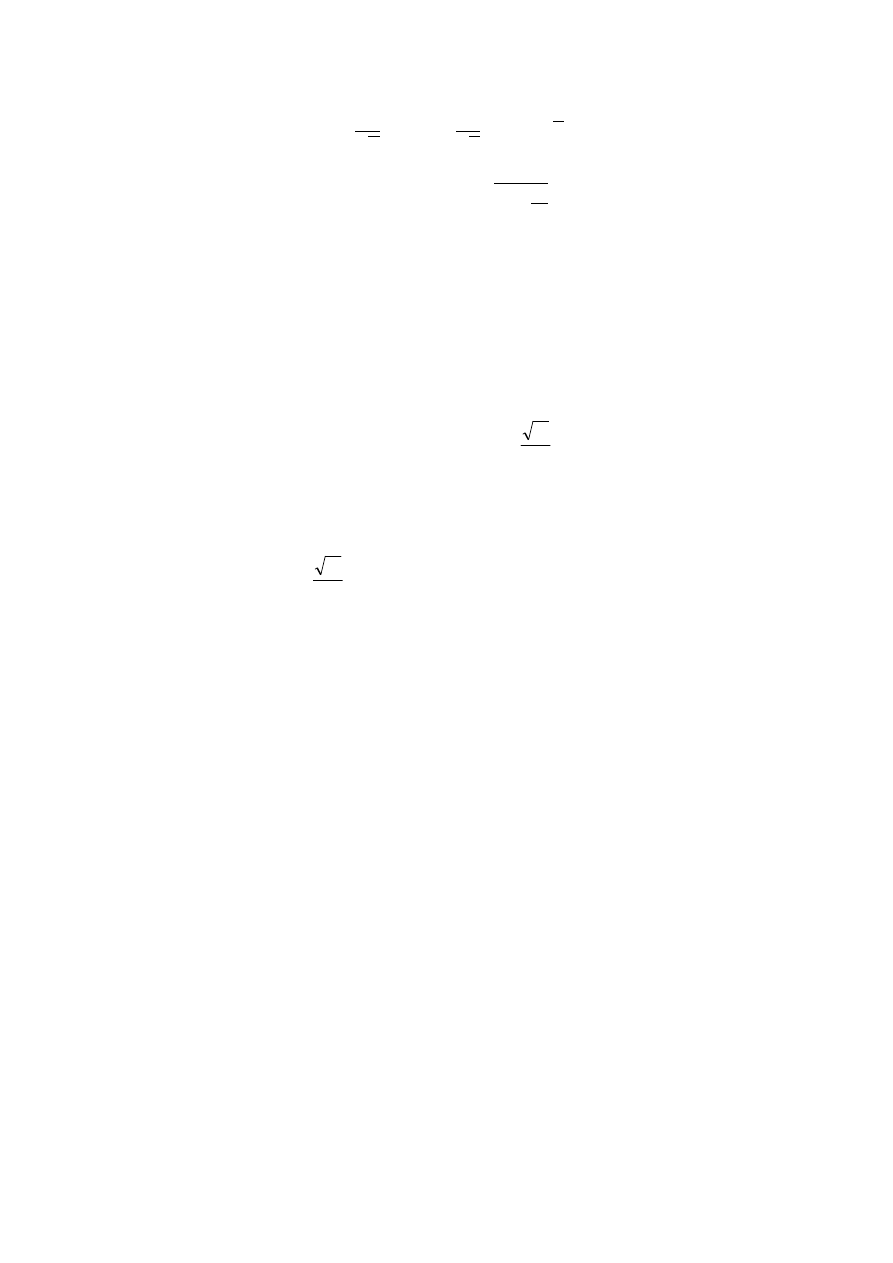
Strona 13
13
13
13 z 16
16
16
16
O = ln Q
R
2S
T U V
W
=
R
2S
U V
W
∙ 2S = R
R = (2,718)
X,YX
∙ Z9,81
[
\
R = 1201,209
Niepewność standardowa dla stałej C:
](R) = R ∙ ](O)
](R) = 1201,209 ∙ 0,07 U ](R) = 84,08466
Ostatecznie wartość:
C=(1201,209±84,08466)
s
m
.
4.8.
Wartości szukanych wielkości n- wykładnika potęgi przy wysokości słupa wody oraz
C- stałego składnika wyrazu wolnego.
n=a±u(a)=0,87±0,03
C=(1201,209±84,08466)
s
m
Strona 14
14
14
14 z 16
16
16
16
Tabela 4.
Lp.
ln(h)=
x
i
ln(t)=
y
i
u(a)
[-]
[-]
[-]
[-]
[-]
[-]
[-]
[-]
[-]
1
-1,51
4,61
339,42
-166,52
505,74
3104,63
2792,34
0,03
2
-1,56
4,58
3
-1,61
4,53
4
-1,66
4,48
5
-1,71
4,44
6
-1,77
4,40
7
-1,83
4,36
8
-1,90
4,30
9
-1,97
4,24
10
-2,04
4,19
11
-2,12
4,12
12
-2,21
4,05
13
-2,30
3,98
14
-2,41
3,91
15
-2,53
3,79
16
-2,66
3,68
17
-2,81
3,55
18
-3,00
3,37
19
-3,22
3,18
20
-3,51
2,90
21
-3,91
2,51
22
-4,61
1,82
Tabela 5.
Lp.
ln(h)= x
i
Lp.
ln(h)= x
i
u(b)
[-]
[-]
[-]
[-]
[-]
1
-1,51
12
-2,21
0,07
2
-1,56
13
-2,30
3
-1,61
14
-2,41
4
-1,66
15
-2,53
5
-1,71
16
-2,66
6
-1,77
17
-2,81
7
-1,83
18
-3,00
8
-1,90
19
L. p.
9
-1,97
20
-3,51
10
-2,04
21
-3,91
11
-2,12
22
-4,61
∑
=
k
1
i
2
i
y
i
k
1
i
i
y
x
a
⋅
⋅
∑
=
∑
=
⋅
k
1
i
i
y
b
∑
=
⋅
k
1
i
2
i
x
k
2
n
1
i
i
x
∑
=

Strona 15
15
15
15 z 16
16
16
16
5.
Wnioski.
Teoretyczną wartością współczynnika potęgowego jest n=0,5. Jednakże doświadczenie
dało wynik inny niż zakładany, mianowicie n=0,87. Wpływ na różnicę mogło mieć:
•
błędy ludzkie, tj. niepoprawnie przygotowane stanowisko pomiarowe (nieprecyzyjnie
zaznaczona podziałka na ściance zbiornika, a także niedokładność wzorcowa);
nieprecyzyjne napełnienie zbiornika w kolejnych pomiarach; zbyt wczesne lub późne
uruchamianie stopera, co wpłynęło na niewłaściwy pomiar czasu, zaokrąglenia
przyjmowane podczas obliczeń, które kompensując się, wpłynęły na dodatkowe wielkości
pomiarowe.
•
niewłaściwy dobór cieczy modelowej- w doświadczeniu stanowiła ją woda o temperaturze
18,5
°
C, która z oczywistych względów posiada swoją lepkość i ściśliwość. Natomiast wzór
Torricellego dotyczy tylko cieczy idealnych. Tarcie powstałe na skutek lepkości, między
cieczą, a ściankami naczynia wpłynęło na powstanie różnicy między wartościami
teoretycznymi, a doświadczalnymi poszukiwanego wykładnika potęgi.
•
obserwacje strugi cieczy wypływającej przez otwór dowodzą, że przekrój strugi w pewnej
niewielkiej odległości od przekroju otworu wylotowego jest na ogół mniejszy od samego
otworu. Zjawisko to nosi nazwę kontrakcji strugi i spowodowane jest bezwładnością strugi
płynu. Zjawisko kontrakcji w doświadczeniu, powodowane było przede wszystkim tym, że
niektóre elementy cieczy wewnątrz zbiornika dopływały do otworu promieniowo wzdłuż
ś
cian i po osiągnięciu brzegów otworu nie mogły nagle zmienić swojego dotychczasowego
kierunku na osiowy.
•
zastosowanie przystawki, czyli krótkiej rurki o dowolnych kształtach stanowiącej
obramowanie otworu wypływowego, mogło w dużym stopniu wpłynąć na zmiany
współczynnika wypływu, gdyż zaistniało, wspomniane wcześniej, zjawisko kontrakcji.
6.
Literatura.
a)
,,Mechanika płynów.”, Ryszard Gryboś, Gliwice 1991r.,
b)
www.typjan.zut.edu.pl- instrukcja odnośnie przeprowadzenia analizy niepewności
pomiarowej
c)
,,Metrologia elektryczna.”, A. Chwaleba, M. Poniński, A. Siedlecki, Warszawa 2003.
Spis treści
1.
Cel doświadczenia. ......................................................................................................... 1
2.
Wstęp teoretyczny. ......................................................................................................... 2
3.
Opis wykonanego ćwiczenia laboratoryjnego. ............................................................... 5
3.1.
Zastosowane materiały. ......................................................................................... 5
3.2.
Zastosowane urządzenia. ...................................................................................... 5
3.3.
Opis stanowiska. ................................................................................................... 5
3.4.
Wykonane operacje. .............................................................................................. 6
4.
Wyniki pomiarów oraz obliczenia. ................................................................................. 6
4.1.
Wyniki pomiarów elementów stanowiska pomiarowego oraz wyznaczenie
niepewności maksymalnych. ................................................................................ 6
4.2.
Wyniki pomiaru czasu t dla zadanych względnych wysokości słupa wody h. ..... 7
4.3.
Wykres zależności całkowitego czasu t wypływu wody ze zbiornika w zależności
od początkowej wysokości słupa wody h. ............................................................ 8

Strona 16
16
16
16 z 16
16
16
16
4.4.
Wykres zależności całkowitego czasu t wypływu wody ze zbiornika w zależności
od początkowej wysokości słupa wody h w skali zlogarytmowanej. ................... 9
4.5.
Wyznaczenie szukanego wykładnika potęgi n.................................................... 10
4.6.
Wyznaczenie niepewności standardowej empirycznych współczynników a oraz b
regresji liniowej................................................................................................... 12
5.
Wnioski. ........................................................................................................................ 14
6.
Literatura. ..................................................................................................................... 15
Spis ilustracji
Rys. 1. Schemat rozważanego zbiornika. .......................................................................................... 2
Rys. 2. Widok stanowiska pomiarowego. ........................................................................................... 5
Wyszukiwarka
Podobne podstrony:
Doswiadczalne wyznaczenia mom Nieznany
DOSWIADCZENIA id 141037 Nieznany
O doświadczalnym wyznaczaniu nośności krytycznej płyt na modelach obarczonych imperfekcjami geome
Doświadczalne wyznaczenie sił w prętach karatownicy płaskiej, Studia, Mibm, semestr II, Mechanika, L
doswiadczenia klasa 2 konkurs20 Nieznany
Doświadczalne wyznaczenie siły krytycznej przy wyboczeniu sprężystym pręta prostego
teoretyczne i doswiadczalne wyznaczanie refrakcji molowej wody i glice XW53GBRV4RDPBNU4DEQ43NREVKKNT
Wyznaczanie ładunku właściwego, Wyznaczanie ładunku właściwego e do m metodą magnetronową 7, Doświad
WPROWADZENIE DO PSYCHOLOGI WYKL Nieznany
doswiadczenia klasa 4 konkurs20 Nieznany
instrukcja doswiadczenia id 216 Nieznany
macierze i wyznaczniki, wyklad Nieznany
Chemia organiczna podstawy wykl Nieznany
Metodyka wyznaczania niezawodno Nieznany
Ćwiczenie nr 2 Doświadczalne wyznaczanie masowego momentu?zwładności
Doswiadczalne wyznaczanie sil w pretach kratownicy plaskiej , Księgozbiór, Studia, Mechnika Doświadc
Ćw.2 Doświadczalne wyznaczanie masowego momentu bezwładności, studia, semestr 3 (2011), Mechanika i
więcej podobnych podstron