
:\NáD
3U]HNV]WDáFHQL
PDFLHU]RZ
SU]HVWU]HQ
WUyMZ\PLDURZHM
WUDQVODFM
XNáD
ZVSyáU]GQ\FK
zmiana skali, obroty,
VNáDGDQL
SU]HNV]WDáFH
SU]HNV]WDáFHQL
OLQLRZH
rzutowanie.

•
ZVSyáU]GQ MHGQRURGQH
x
=
x
y
z
1
•
p
U]HVXQLFL SRF]WN
NáD
ZVSyáU]GQ\FK
T
=
−
−
−
1
0
0
0
1
0
0
0
1
0
0
0
1
T
T
T
x
y
z
•
zmiana skali
S
=
S
S
S
x
y
z
0
0
0
0
0
0
0
0
0
0
0
0
1
]DPLDQ
XNáD
OHZRVNUWQH
XNáD
UDZRVNUWQ\
1
0
0
0
0
1
0
0
0
0
1 0
0
0
0
1
−

•
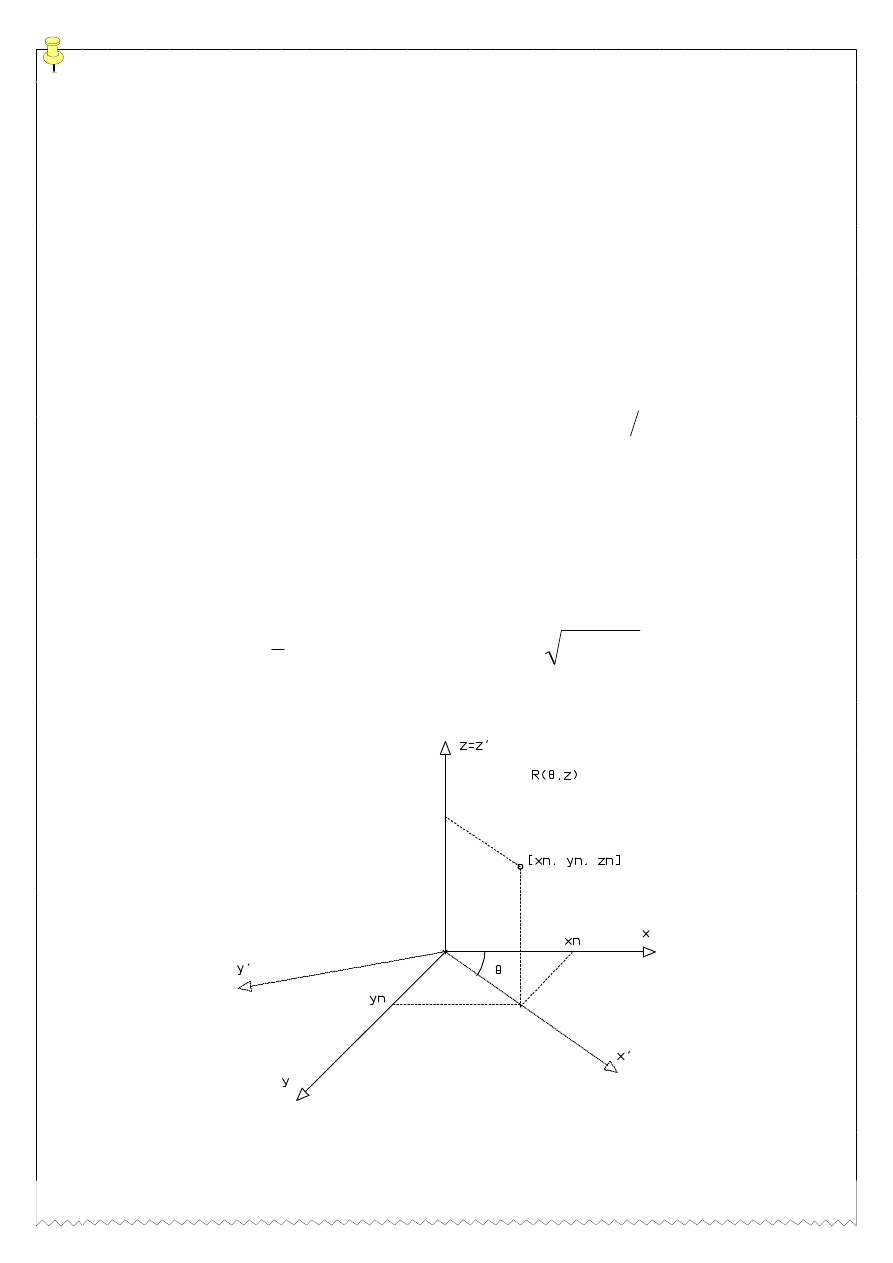
REUy
N
Θ
ZRNy
RV
z, (y, x)
(
)
( )
(
)
R
R
R
Θ
Θ
Θ
Θ
Θ
Θ
Θ
Θ
Θ
Θ
Θ
Θ
Θ
Θ
Θ
,
cos
sin
sin
cos
,
,
cos
sin
sin
cos
,
,
cos
sin
sin
cos
z
y
x
=
−
=
−
=
−
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
1
•
REUy SU]HVWU]HQ
N
ψ
ZRNy
GRZROQH
SURVWH
S
+
µ
d
•
Translacja do punktu p
F
=
−
−
−
1
0
0
0
1
0
0
0
1
0
0
0
1
1
2
3
p
p
p
•
2EUy
ZRNy
RV
z
(
)
Θ =
arctg d d
2
1
SU]HNV]WDáFHQL
SXQNW
(
)
d d d
1
2
3
,
,
w
(
)
ν
, ,
0
3
d
(
)
G
Θ
,
,
z
d
d
d
d
d
d
=
−
=
+
1
0
0
0
0
0
0
0
0
0
0
1
2
2
1
2
1
2
2
2
ν
ν
ν
ν
•
2EUy
ZRNy
RV
y
(
)
Φ =
arctg
ν
d
3
SU]HNV]WDáFHQL
SXQNW
(
)
ν
, ,
0
3
d
w
(
)
0 0
, , w
H
=
−
=
+
=
+
+
1
0
0
0
0
0
0
0
0
0
0
3
3
2
2
3
2
1
2
2
2
3
2
w
d
w
d
w
w
d
d
d
d
ν
ν
ν
,
iloczyn macierzy H
×
G
×
F
SU]HNV]WDá
GRZROQ
SXQN
Q
SURVWH
p+
µ
d w
SXQN
]QDMGXMF
VL Q
RV
z
QRZH
áD
!"
ZVSyáU]GQ\FK

•
]DJDGQLHQL REURW
U]HVWU]HQ
ZRNy
GRZROQH
RV
VSURZDG
VL
URW
U]HVWU]HQ
ZRNy
QRZH
RV
z
ψ
W
=
−
cos
sin
sin
cos
ψ
ψ
ψ
ψ
0
0
0
0
0
0
1
0
0
0
0
1
•
SLHUZRWQ\
XNáDG]L ZVSyáU]GQ\F
Uy
UHDOL]XMHP
SRPRF ]áR*HQL
QDVWSXMF\F
U]
e
NV]WDáFH
P
F
G
H
W
H G
F
=
×
×
×
× × ×
−
−
−
1
1
1
•
RZUTOWANIE
•
dwie klasy:
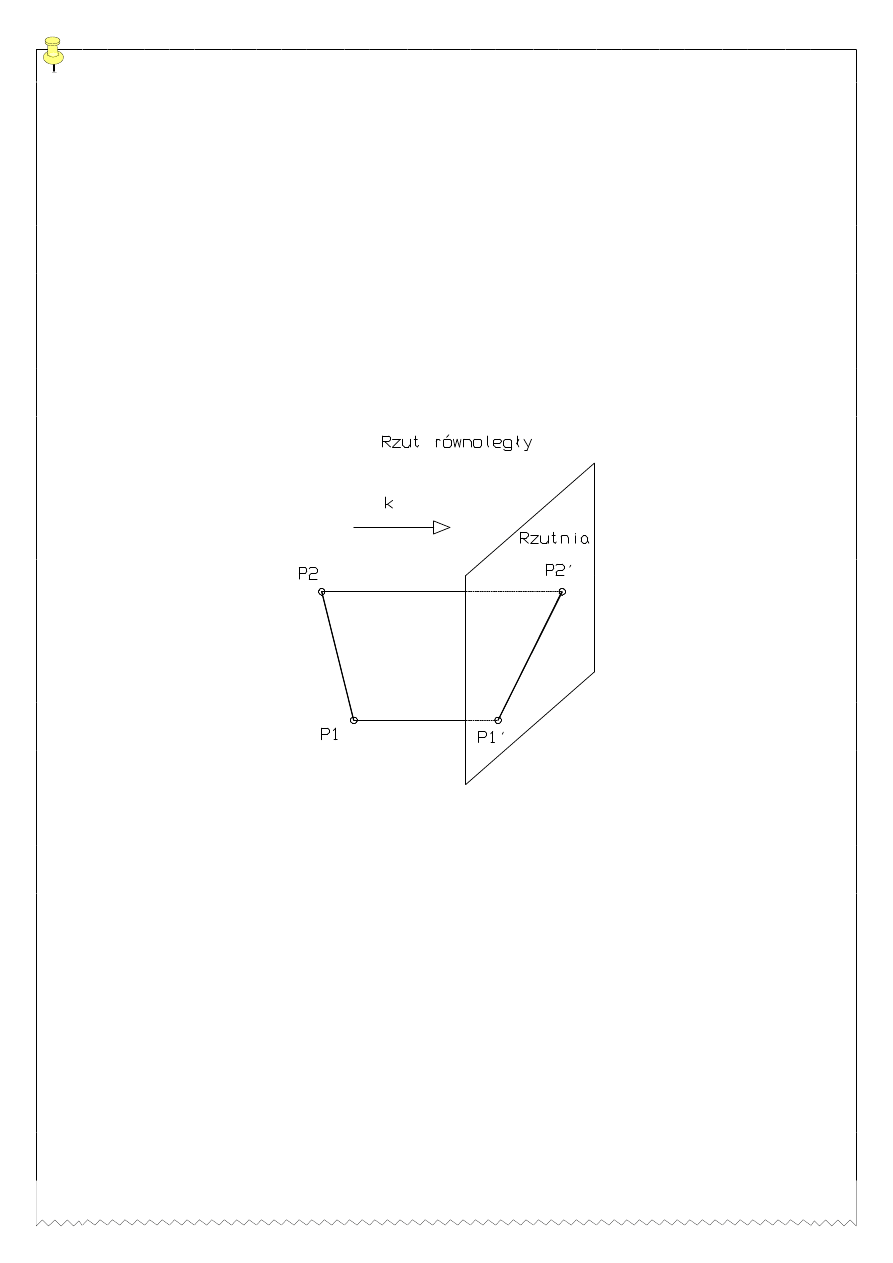
U]XW
UyZQROHJáH
-
]DFKRZXM UyZQROHJáR
SURVW\FK
VWRVXQH
GáXJRF
RGFLQNy
UyZQROHJá\F
]ZL]N
PLDURZ
ILJX
SáDVNLF
UyZQROHJá\F
áDV]F]\]Q
U]XWRZDQL
(rysunek techniczny)
•
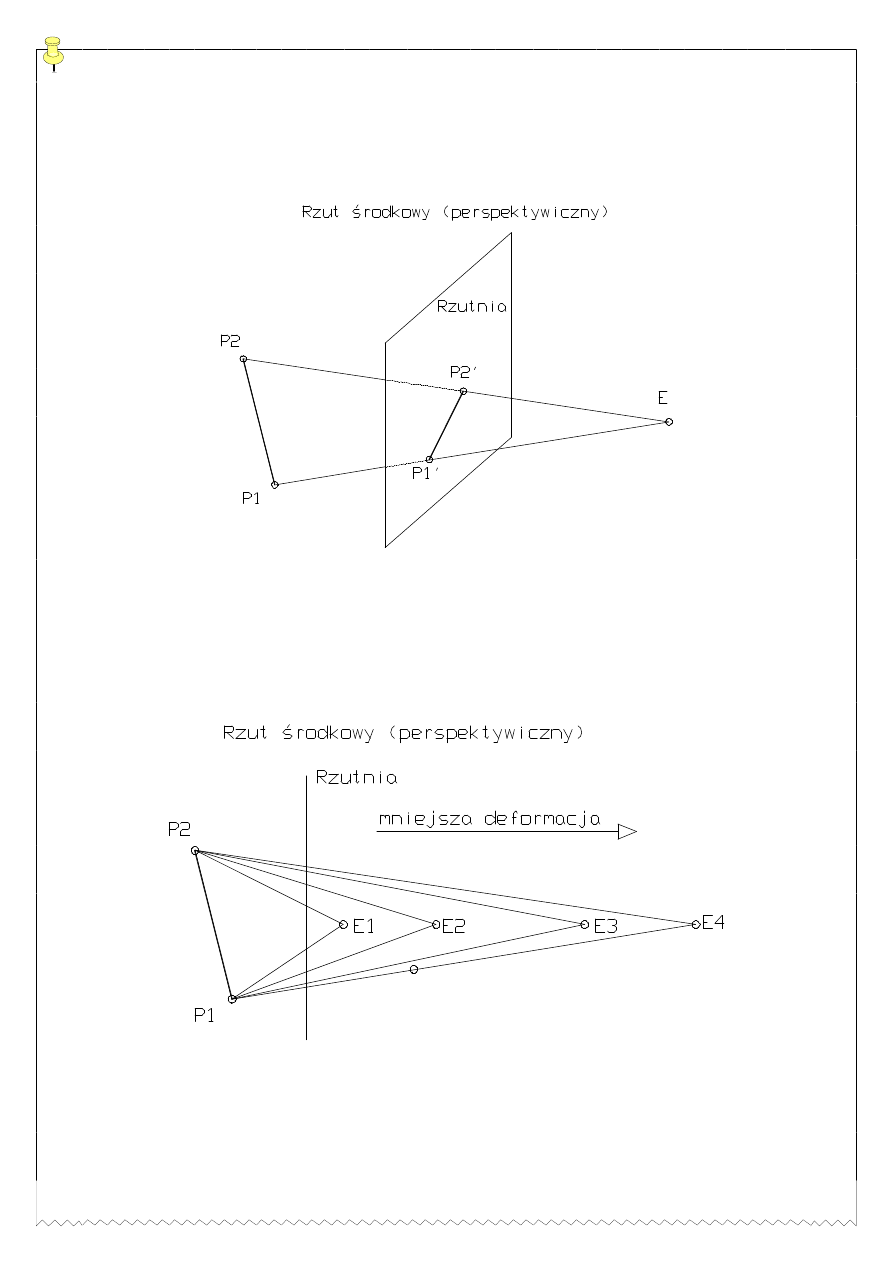
U]XW URGNRZ
SHUVSHNW\ZLF]QH
- realistyczna wizualizacja
RELHNWy
'ZUD*HQL
JáEL
W rzucie perspektywicznym wszystkie proste (promienie rzutowania)
PDM SXQN
ZVSyOQ
QD]\ZDQ
URGNLH
U]XWRZDQLD
2GOHJáR
URGN
U]XWRZDQL
áDV]F]\]Q
U]XWRZDQL
U]XWQL
GHF\GXM
deformacji rysunku.

U]XFL
UyZQROHJá\
ZV]\VWNL
SURVW
U]XWRZDQL
PDM WH
VD
ustalony kierunek (k). W szczególnym przypadku kiedy jest on
SURVWRSDGá
U]XWQ
PyZLP
U]XFL
ortogonalnym
(
SURVWRNWQ\P
).
Rzutowanie punktu P
VSURZDG
VL
]QDOH]LHQL
ZVSyáU]GQ\F
punktu P'
EGFH
WH
SU]HFLFL
U]XWQ
SURVW U]XWRZDQL
RNUHORQ SXQNWH
P i kierunkiem k
SU]\SD
U]XW
UyZQROHJáH
lub punktem P i
URGNLH
U]XWRZDQL
SU]\SD
U]XW
perspektywicznego.
Z\QL
HUDF
!
U]XWRZDQL
RWU]\PXMHP
"
ZVSyáU]GQ
#
SXQNW
P'
$
DNWXDOQH
%
SU]HVWU]HQ
&
RELHNWX
'
3U]HNV]WDáFDP
(
M
)
*+
XNá
,-.
obserwatora
/
NWyU
(
GHILQLXMHP
(
$
WDN
&
VSRVyE
/
*
)
U]XWQL
0
SRNU\Z
0
VL
$
QL
132
SáDV]F]\]Q
z=0.
Zaleta -
$
U]XFL
)
SURVWRNWQ\
1
Z\VWDUF]
(
SRPLQ
4
ZVSyáU]GQ
z
punktu P'.
=DáR*HQLD
1. P
RF]WH
5765
áD
896;:<
VHUZDWRU
=
SRNU\Z
=
VL
>
SRF]WNLH
?
DNWXDOQH
@:
XNáD
896A:<
LHNWX
2. P
U]
B
U]XFL
C
SHUVSHNW\ZLF]Q\
?
REVHUZDWR
D
]QDMGXM
C
VL
E
U
:856
rzutowania
(
)
E x y z
e
e
e
,
,
=
U]XWQL
=
MHV
F
SURVWRSDGá
=G8:
ZHNWRU
=
OE
3. P
U]
B
U]XFL
C
SURVWRNWQ\
?
U]XWQL
=
MHV
F
SURVWRSDGá
=H8:I5
LHU
6J56
rzutowania k
4. P
U]
B
GRZROQ\
?
U]XFL
C
UyZQROHJá\
?
U]XWQL Z\]Q
=LKM>=N>=
GDQ
B
wektor normalny n.
3U]HNV]WDáFHQL
XNáD
VHUZDWRU
SROHJ
Q
Z\NRQDQL
WDNLF
obrotów przestrzeni by wektor
[
]
n
=
x y z
e
e
e
, ,
RNUHODMF
U]XWQL
SRNU\ZD
VL
RVL
z
QRZH
áD
PLD
LH
SU]HFLZQ
]ZURW
•
GO
U]XW
URVWRNWQH
n=k
•
dla rzutu perspektywicznego
[
]
n
=
x y z
e
e
e
, ,
-
XMHPQ
osi z
XNáD
VHUZDWRUD
Realizacja
→
dwa etapy:
•
REUy
XNáD
( )
xyz
ZRNy
RV
z
(
)
Θ =
arctg y x
n
n
wektor
[
]
x y z
n
n
n
,
,
przechodzi w wektor
[
]
s
z
n
, ,
0
RWU]\PXMHP
QRZ
XNáD
ZVSyáU]GQ\F
(
)
x y z
' ' '
(
)
R
Θ
,
,
z
s
x
y
y
x
s
s
s
x
y
n
n
n
n
n
n
=
−
=
+
1
0
0
0
0
0
0
0
0
0
0
2
2
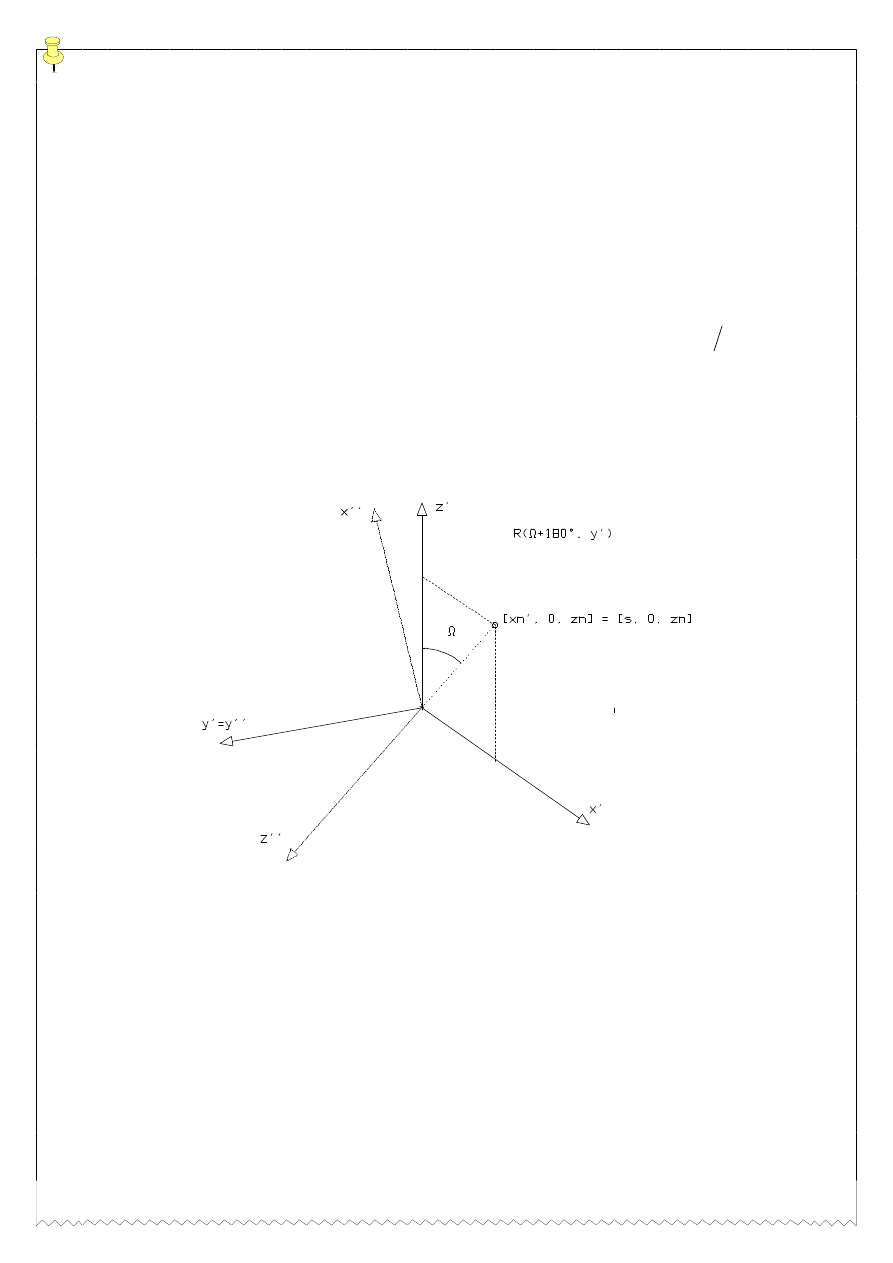
•
REUy XNáD
(
)
x y z
' ' '
ZRNy
RV
y'
( )
Ω
Ω
+
=
180
,
arctg s z
n
wektor
[
]
s
z
n
, ,
0
przechodzi w wektor
[
]
0 0
, ,
−
t
RWU]\PXMHP
QRZ
XNáD
(
)
x y z
' ' ' ' ' '
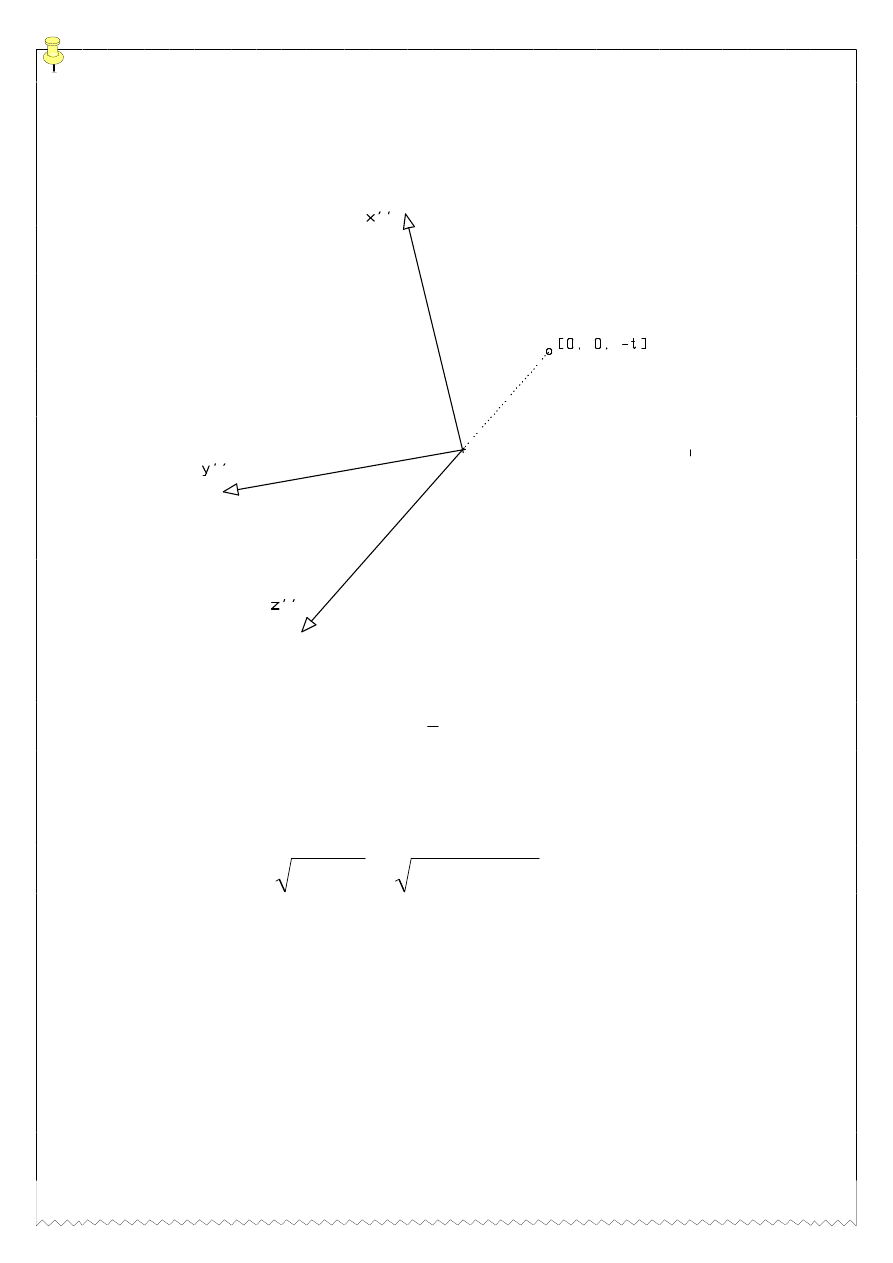
(
)
R
Ω +
=
−
−
−
=
+
=
+
+
180
1
0
0
0
0
0
0
0
0
0
0
2
2
2
2
2
, '
,
y
t
z
s
t
s
z
t
t
s
z
x
y
z
n
n
n
n
n
n
=áR*HQL
SU]HNV]WDáFH
(
)
(
)
R
R
R
=
+
Ω
Θ
180
, '
,
y
z
SU]HNV]WDá
NWXDOQ
XNáD
LHNW
XNáD
VHUZDWRUD
3LRQRZR OLQ
]DSHZQLDP
Z\NRQXM
NROHMQ
REUyW
wybieramy punkt
[
]
P
=
0 1 0 1
, , ,
T
XNáDG]L
NWXDOQ\
RELHNW
XNáDG]L
REVHUZDWRU
SXQN
P
SRZLQLH
PL
ZVSyáU]GQ
x
UyZQ ]HUX
macierz R
R
=
r
r
r
r
r
r
r
r
r
11
12
13
21
22
23
31
32
33
0
0
0
0
0
0
1
pr
]HNV]WDá
SXQN
P w
[
]
r r r
12
22
32
1
,
,
,
PDFLHU
GRGDWNRZH
URW
ZRNy
RV
z,
(
)
R
η
, ' '
z
(
)
η
= −
arctg r
r
12
22
(
)
R
η
, ' '
,
z
u
r
r
r
r
u
u
u
r
r
=
−
=
+
1
0
0
0
0
0
0
0
0
0
0
22
12
12
22
12
2
22
2
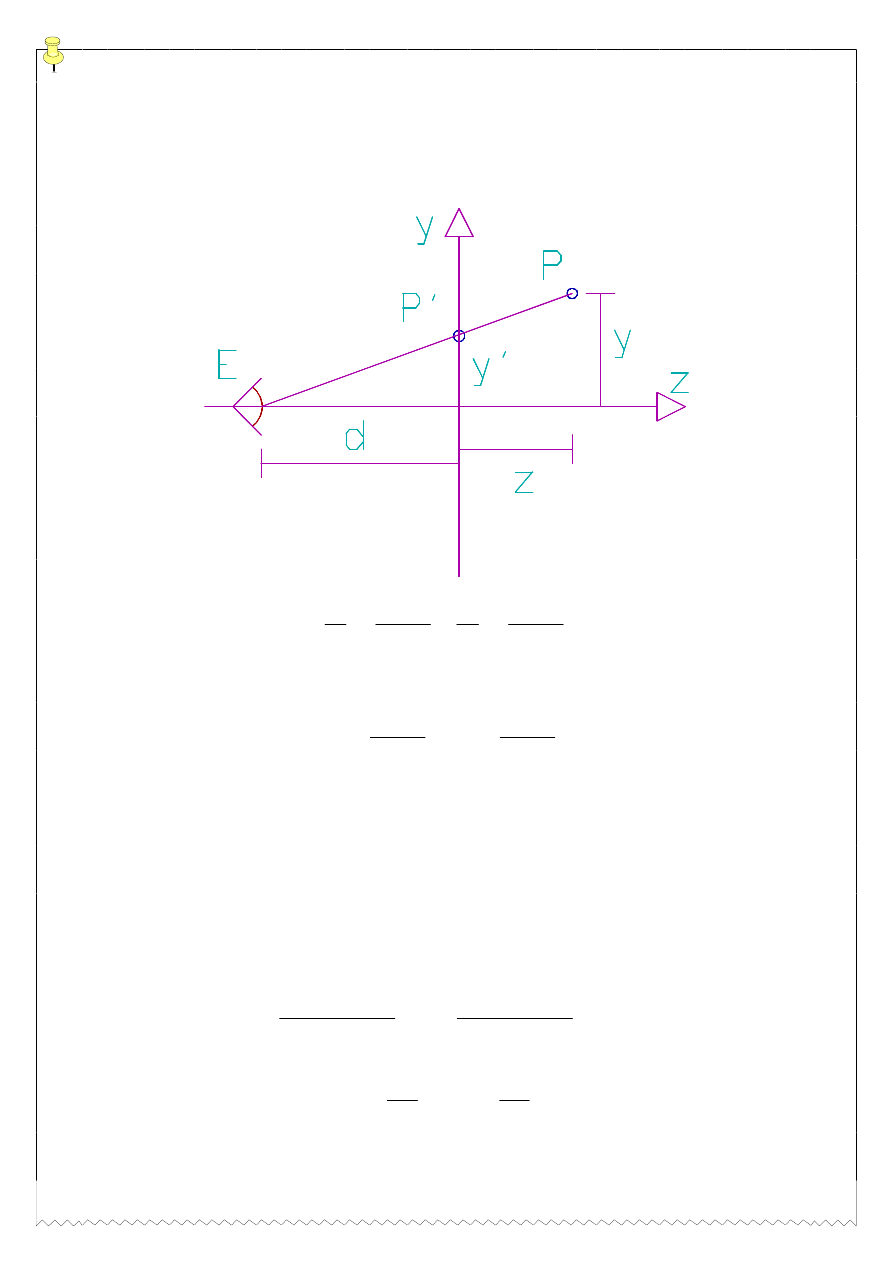
Rzut perspektywiczny (
URGNRZ\
)
y
d
y
z
d
x
d
x
z
d
x
xd
z
d
y
yd
z
d
'
,
'
'
,
'
=
+
=
+
=
+
=
+
:áDVQRü
S
URVW\F
UyZQROHJá\F
ZHNWRU
[
]
w
=
w w w
x
y
z
,
,
ma punkt
ZVSyOQ
MH*H
w
z
≠
0
[
]
P
p
w
( )
,
,
'
(
)
'
(
)
'
, '
t
t
x
tw y
tw z
tw
x
x
tw d
z
tw
d
y
y
tw d
z
tw
d
t
x
w
w
d y
w
w
d
x
y
z
x
z
y
z
x
z
y
z
= +
= +
+
+
=
+
+
+
=
+
+
+
→ ∞ ⇒ =
=
Wyszukiwarka
Podobne podstrony:
Przeksztalcenia macierzowe id 4 Nieznany
Przeksztalcenia macierzowe id 4 Nieznany
M[1] 5 Przeksztalcenia elementarne macierzy
M[1].5. Przeksztalcenia elementarne macierzy
M[1] 5 Przeksztalcenia elementarne macierzy
Przeksztalcanie wzorow
Ustawa z dnia 25 06 1999 r o świadcz pien z ubezp społ w razie choroby i macierz
macierz BCG
macierze 2
04 Analiza kinematyczna manipulatorów robotów metodą macierz
5 Przekształcenie Fouriera
Dyskretne przeksztaĹ'cenie Fouriera
macierze i wyznaczniki lista nr Nieznany
GK 9 Przekształcenia geometryczne
macierze 1
10 Laczenie, podzial, przekszta lcanie spolek FOLIE
Macierz przykrycia testów akceptacyjnych Jasiek
więcej podobnych podstron