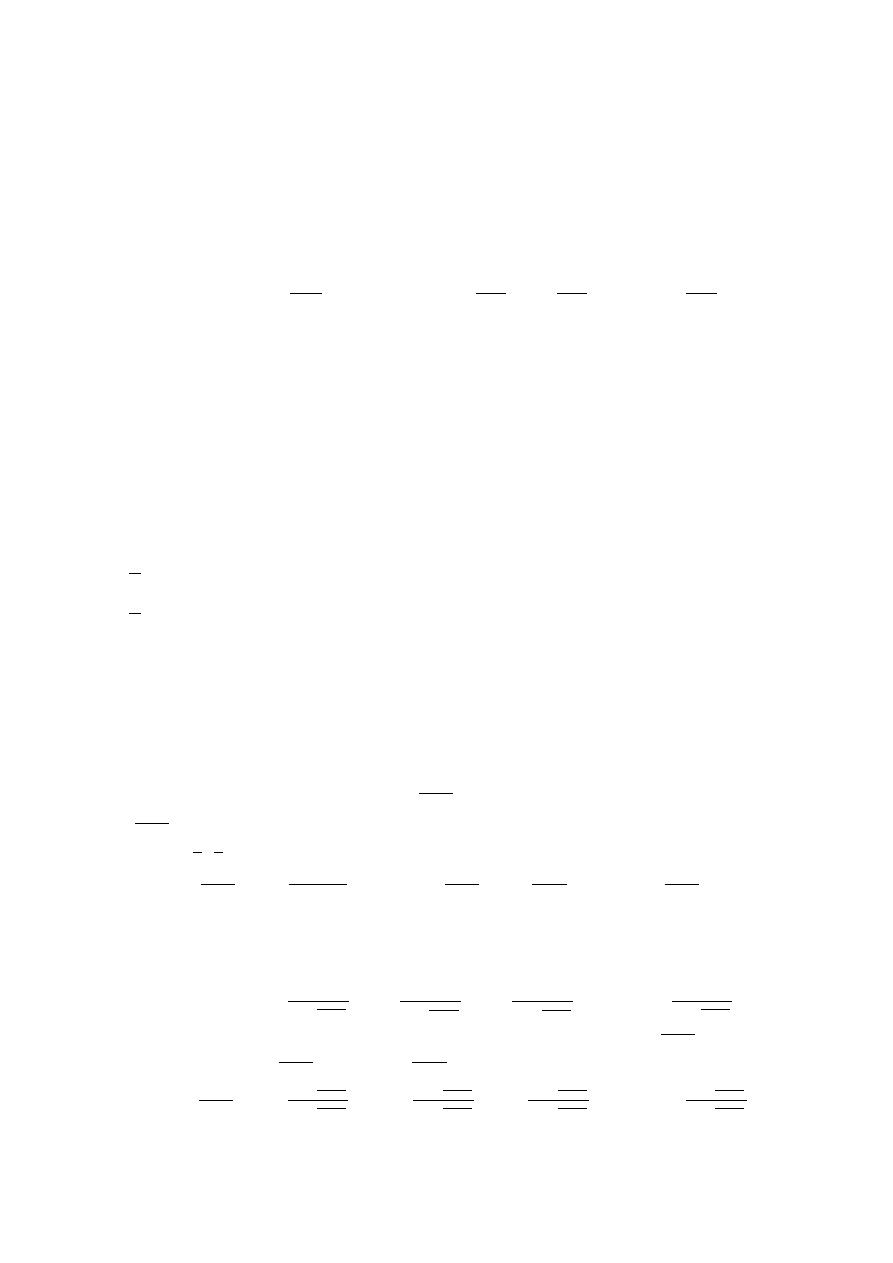
Funkcje analityczne — przykÃlady

ostatnia aktualizacja:

11 czerwca 2014, 00:14

Twierdzenie 14.1 (

rozwinie

,

cie sinusa w iloczyn niesko´

nczony

)

Dla ka˙zdej liczby zespolonej z zachodzi r´owno´s´c

sin z = z ·

∞

Y

n=1

1 −

z

2

n

2

π

2

:= z · lim

n→∞

1 −

z

2

1

2

π

2

1 −

z

2

2

2

π

2

· . . . · 1 −

z

2

n

2

π

2

przy czyn iloczyn jest zbie˙zny niemal jednostajnie, czyli jednostajne na ka˙zdym zbio-

rze zwartym K ⊆ C .

Dow´

od. Najpierw wyka˙zemy, ˙ze dla ka˙zdej liczby naturalnej n istnieje taki wielo-

mian W

n

stopnia 2n + 1 , ˙ze dla ka˙zdej liczby zespolonej z zachodzi r´owno´s´c:

sin(2n + 1)z = W

n

(sin z) .

Mo˙zna udowodni´c istnienie wielomianu W

n

przez indukcje

,

, ale zamiast tego skorzy-

stamy z wzor´ow Eulera. Mamy

sin(2n + 1)z =

=

1

2i

cos(2n + 1)z + i sin(2n + 1)z

− cos(2n + 1)z − i sin(2n + 1)z

=

=

1

2i

cos z + i sin z

2n+1

− cos z − i sin z

2n+1

=

=

n

X

k=0

(−1)

k 2n+1

2k+1

cos

2n+1−2k−1

z sin

2k+1

z =

=

n

X

k=0

(−1)

k 2n+1

2k+1

(1 − sin

2

z)

n−k

sin

2k+1

z := W

n

sin(z)

.

Oczywi´scie stopie´

n wielomianu W

n

nie jest wie

,

kszy ni˙z 2n + 1 . Dla ka˙zdej liczby

ca lkowitej k zachodzi r´owno´s´c W sin

kπ

2n+1

= sin(kπ) = 0 . Oznacza to, ˙ze liczba

sin

kπ

2n+1

jest pierwiastkiem wielomianu W

n

. Funkcja sinus ro´snie (´sci´sle) na prze-

dziale

−

π

2

,

π

2

. Wobec tego

sin

−nπ

2n+1

< sin

(−n+1)π

2n+1

< . . . < sin

0·π

2n+1

< sin

π

2n+1

< . . . < sin

nπ

2n+1

.

Wskazali´smy wie

,

c 2n + 1 parami r´

o˙znych pierwiastk´ow wielomianu W

n

, wie

,

c jego

stopie´

n nie jest mniejszy ni˙z 2n + 1 . Pierwiastki wielomianu W

n

le˙za

,

symetrycznie

wzgle

,

dem punktu 0 na osi rzeczywistej. Mo˙zna go przedstawi´c jako iloczyn:

W

n

(u) = A

n

u 1 −

u

2

sin

2

π

2n+2

1 −

u

2

sin

2

2π

2n+2

1 −

u

2

sin

2

3π

2n+2

· . . . · 1 −

u

2

sin

2

nπ

2n+2

,

A

n

oznacza tu pewna

,

sta la

,

, kt´ora

,

niebawem znajdziemy. Niech u = sin

z

2n+1

. Wtedy:

sin z = sin (2n + 1) ·

z

2n+1

= W

n

sin

z

2n+1

=

= A

n

· sin

z

2n+1

·

1 −

sin

2

z

2n+1

sin

2

π

2n+1

·

1 −

sin

2

z

2n+1

sin

2

2π

2n+1

1 −

sin

2

z

2n+1

sin

2

3π

2n+1

· . . . ·

1 −

sin

2

z

2n+1

sin

2

nπ

2n+1

.

Z tej r´owno´sci wynika, ˙ze

1

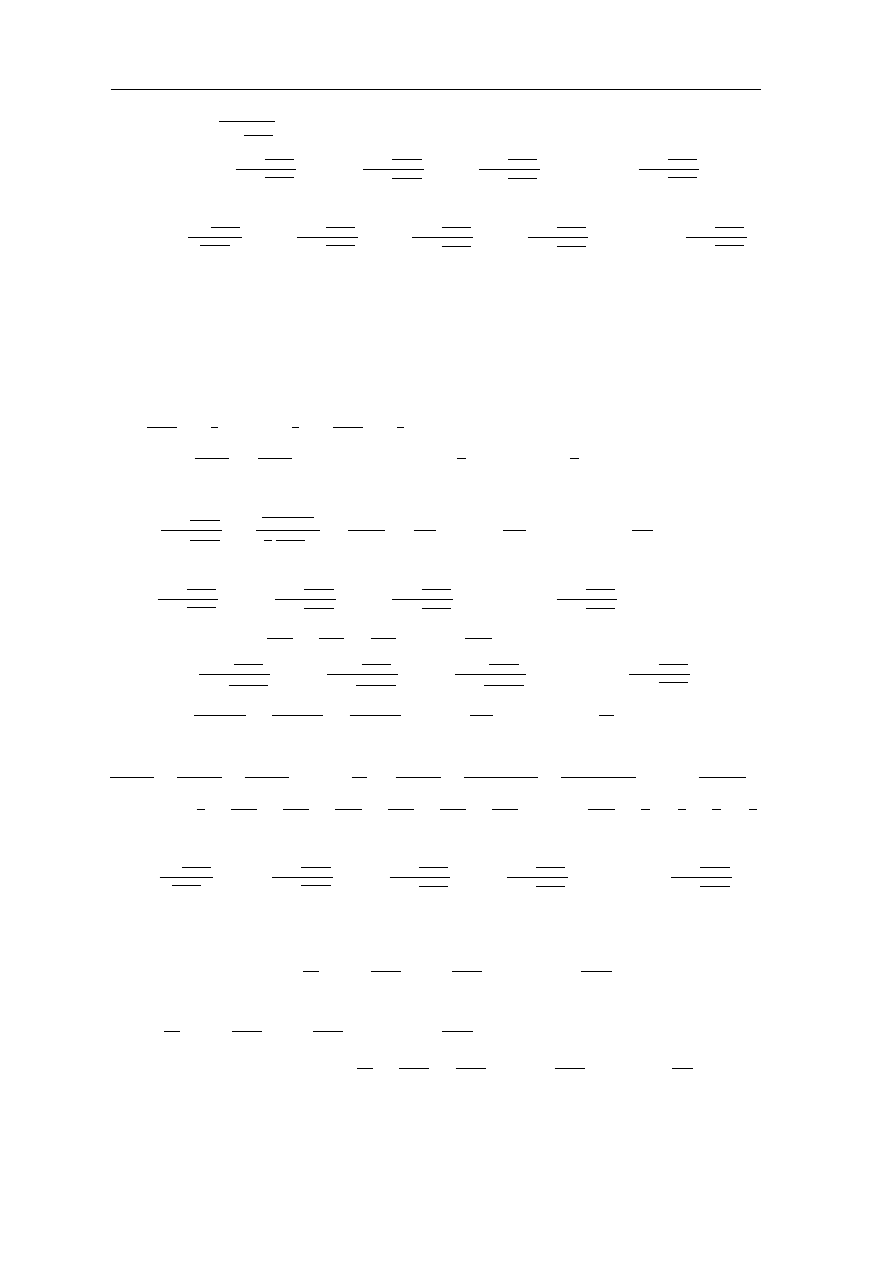
Funkcje analityczne — przyk lady

Micha l Krych

2n + 1 = lim

z→0

sin z

sin

z

2n+1

=

= lim

z→0

A

n

·

1 −

sin

2

z

2n+1

sin

2

π

2n+1

·

1 −

sin

2

z

2n+1

sin

2

2π

2n+1

1 −

sin

2

z

2n+1

sin

2

3π

2n+1

· . . . ·

1 −

sin

2

z

2n+1

sin

2

nπ

2n+1

= A

n

.

Znale´zli´smy wie

,

c A

n

i mo˙zemy napisa´c wz´or:

sin z = z ·

sin

z

2n+1

z

2n+1

·

1 −

sin

2

z

2n+1

sin

2

π

2n+1

1 −

sin

2

z

2n+1

sin

2

2π

2n+1

1 −

sin

2

z

2n+1

sin

2

3π

2n+1

· . . . ·

1 −

sin

2

z

2n+1

sin

2

nπ

2n+1

.

W dalszym cia

,

gu skorzystamy z nier´owno´sci

(1 + z

1

)(1 + z

2

) · . . . · (1 + z

m

) − 1

¬

¬ (1 + |z

1

|)(1 + |z

2

|) · . . . · (1 + |z

m

|) − 1 ¬ e

|z

1

|+|z

2

|+···+|z

m

|

− 1,

(♠)

kt´ora

,

ka˙zdy student z latwo´scia

,

sam udowodni (np. przez indukcje

,

wzgle

,

dem m ).

Za l´o˙zmy, ˙ze |z| ¬ r , r > 0 . Istnieje taka liczba δ > 0 , ˙ze je´sli 0 < |α| < δ , to

1 −

sin α

α

<

1
3

, zatem

2
3

<

sin α

α

<

4
3

. Istnieje taka liczba naturalna ν > r , ˙ze je´sli

n > ν , to

|z|

2n+1

¬

r

2n+1

< δ . Je´sli 0 < β <

π

2

, to sin β >

2

π

β , bo funkcja sinus jest

´sci´sle wkle

,

s la na przedziale [0, π] . Niech n > ν oraz 0 < j ¬ n . Wtedy

sin

2

z

2n+1

sin

2

jπ

2n+1

¬

16|z|2

9(2n+1)2

(

2

π

jπ

2n+1

)

2

=

16|z|

2

36j

2

¬

|z|

2

2j

2

¬ exp

|z|

2

2j

2

− 1 ¬ exp

r

2

2j

2

− 1

(♣) .

Z nier´owno´sci (♠) i (♣) wynika, ˙ze je´sli 0 < k ¬ n , to

1 −

sin

2

z

2n+1

sin

2

π

2n+1

1 −

sin

2

z

2n+1

sin

2

2π

2n+1

1 −

sin

2

z

2n+1

sin

2

3π

2n+1

· . . . ·

1 −

sin

2

z

2n+1

sin

2

kπ

2n+1

− 1

¬

¬ exp

r

2

2·1

2

+

r

2

2·2

2

+

r

2

2·3

2

+ · · · +

r

2

2·k

2

− 1 ¬ exp(r

2

) − 1

(i) ,

oraz

1 −

sin

2

z

2n+1

sin

2 (k+1)π

2n+1

1 −

sin

2

z

2n+1

sin

2 (k+2)π

2n+1

1 −

sin

2

z

2n+1

sin

2 (k+3)π

2n+1

· . . . ·

1 −

sin

2

z

2n+1

sin

2

nπ

2n+1

− 1

¬

¬ exp

r

2

2(k+1)

2

+

r

2

2(k+2)

2

+

r

2

2(k+3)

2

+ · · · +

r

2

2n

2

− 1 ¬ exp

r

2

2k

− 1−−−−→

k→∞

0 (ii) ,

ostatnie nier´owno´sci wynikaja

,

z tego, ˙ze je´sli k ­ 1 , to

1

(k+1)

2

+

1

(k+2)

2

+

1

(k+3)

2

+ · · · +

1

n

2

<

1

k(k+1)

+

1

(k+1)(k+2)

+

1

(k+2)(k+3)

+ · · · +

1

(n−1)n

=

=

1
k

−

1

k+1

+

1

k+1

−

1

k+2

+

1

k+2

−

1

k+3

+

1

k+3

+ · · · +

1

n−1

−

1

n

=

1
k

−

1

n

<

1
k

.

Jasne jest, ˙ze iloczyn

z ·

sin

z

2n+1

z

2n+1

·

1 −

sin

2

z

2n+1

sin

2

π

2n+1

1 −

sin

2

z

2n+1

sin

2

2π

2n+1

1 −

sin

2

z

2n+1

sin

2

3π

2n+1

· . . . ·

1 −

sin

2

z

2n+1

sin

2

kπ

2n+1

ustalonej liczby czynnik´ow (jest ich k + 2 , teraz k nie zmieniamy) przy n −→ ∞

da

,

˙zy jednostajnie na zbiorze {z:

|z| ¬ r} do funkcji

z 1 −

z

2

π

2

1 −

z

2

2

2

π

2

1 −

z

2

3

2

π

2

· . . . · 1 −

z

2

k

2

π

2

.

Mamy oczywi´scie

z 1 −

z

2

π

2

1 −

z

2

2

2

π

2

1 −

z

2

3

2

π

2

· . . . · 1 −

z

2

k

2

π

2

¬

¬ r exp

r

2

π

2

+

r

2

2

2

π

2

+

r

2

3

2

π

2

+ · · · +

r

2

k

2

π

2

¬ r exp

2r

2

π

2

< re

r

2

.

Otrzymali´smy oszacowanie zale˙zne jedynie od liczby r . Niech ε > 0 . Przyj-

mijmy, dla uproszczenia oznacze´

n, ˙ze

2

Funkcje analityczne — przyk lady

Micha l Krych

M = re

r

2

,

P

n

(z) = z ·

sin

z

2n+1

z

2n+1

·

1 −

sin

2

z

2n+1

sin

2

π

2n+1

1 −

sin

2

z

2n+1

sin

2

2π

2n+1

1 −

sin

2

z

2n+1

sin

2

3π

2n+1

· . . . ·

1 −

sin

2

z

2n+1

sin

2

kπ

2n+1

,

Q

n

(z) = z 1 −

z

2

π

2

1 −

z

2

2

2

π

2

1 −

z

2

3

2

π

2

· . . . · 1 −

z

2

k

2

π

2

,

R

n

(z) =

1 −

sin

2

z

2n+1

sin

2 (k+1)π

2n+1

1 −

sin

2

z

2n+1

sin

2 (k+2)π

2n+1

1 −

sin

2

z

2n+1

sin

2 (k+3)π

2n+1

· . . . ·

1 −

sin

2

z

2n+1

sin

2

nπ

2n+1

,

r

n

(z) = 1 −

z

2

(k+1)

2

π

2

1 −

z

2

(k+2)

2

π

2

1 −

z

2

(k+3)

2

π

2

· . . . .

Bez trudu stwierdzi´c mo˙zna, ˙ze |r

n

(z) − 1| < exp

r

2

kπ

2

− 1 < exp

r

2

2k

− 1 , wcze´sniej

udowodnili´smy (ii), ˙ze |R

n

(z)| ¬ exp

r

2

2k

oraz ˙ze |P

n

(z)| ¬ r exp(r

2

) .

Niech k > ν be

,

dzie tak du˙za

,

liczba

,

naturalna

,

, ˙ze M · exp

r

2

2k

− 1

<

ε
3

.

Istnieje taka liczba n

0

> k , ˙ze je´sli n > n

0

, to |P

n

(z) − Q

n

(z)| <

ε
3

dla wszystkich

liczb z , dla kt´orych |z| ¬ r . W takiej sytuacji mamy:

| sin z − z(1 −

z

2

π

2

)(1 −

z

2

2

2

π

2

) · . . . | = |P

n

(z)R

n

(z) − Q

n

(z)r

n

(z)| ¬

¬ |P

n

(z)R

n

(z) − P

n

(z)| + |P

n

(z) − Q

n

(z)| + |Q

n

(z) − Q

n

(z)r

n

(z)| ¬

¬ M · |R

n

(z) − 1| +

ε
3

+ M · |1 − r

n

(z)| < M exp

r

2

2k

− 1

+

ε
3

+ M exp

r

2

2k

− 1

< ε .

Z otrzymanej nier´owno´sci wynika dowodzona teza.

Lemat 12.2

Funkcja ctg x −

1

x

jest analityczna w pewnym otoczeniu punktu 0 .

Dow´

od. Zachodzi r´owno´s´c: ctg x −

1

x

=

x cos x−sin x

x sin x

. Mamy

x cos x − sin x = x 1 −

1

2!

x

2

+

1

4!

x

4

−

1

6!

x

6

+ · · ·

− x −

1

3!

x

3

+

1

5!

x

5

−

1

7!

x

7

+ · · ·

=

= −

2

3!

x

3

+

4

5!

x

5

−

6

7!

x

7

+ · · · = x

3

−

2

3!

+

4

5!

x

2

−

6

7!

x

4

+ · · ·

oraz x sin x = x x −

1

3!

x

3

+

1

5!

x

5

−

1

7!

x

7

+ · · ·

= x

2

1 −

1

3!

x

2

+

1

5!

x

4

−

1

7!

x

6

+ · · ·

,

wie

,

c po skr´oceniu przez x

2

otrzymujemy iloraz

−

2

3!

x +

4

5!

x

3

−

6

7!

x

5

+ · · ·

1 −

1

3!

x

2

+

1

5!

x

4

−

1

7!

x

6

+ · · ·

.

Wobec tego istnieja

,

takie liczby b

1

, b

3

, . . . , ˙ze

ctg x −

1

x

=

−

2

3!

x +

4

5!

x

3

−

6

7!

x

5

+ · · ·

1 −

1

3!

x

2

+

1

5!

x

4

−

1

7!

x

6

+ · · ·

= b

1

x + b

3

x

3

+ b

5

x

5

+ · · ·

dla wszystkich x dostatecznie bliskich liczbie 0 . Z r´owno´sci

−

2

3!

x +

4

5!

x

3

−

6

7!

x

5

+ · · · = 1 −

1

3!

x

2

+

1

5!

x

4

−

1

7!

x

6

+ · · ·

b

1

x + b

3

x

3

+ b

5

x

5

+ · · ·

wynika, ˙ze b

1

= −

2

3!

= −

1
3

, b

3

=

4

5!

+

1

3!

b

1

= −

1

45

. Mo˙zna wypisa´c bez trudu kilka

naste

,

pnych wzor´ow na kolejne wsp´o lczynniki b

5

, b

7

, . . . .

Zauwa˙zmy, ˙ze

ctg x −

1

x

= ln | sin x| − ln |x|

0

= ln

| sin x|

|x|

0

= ln

| sin x|

|x|

0

=

3

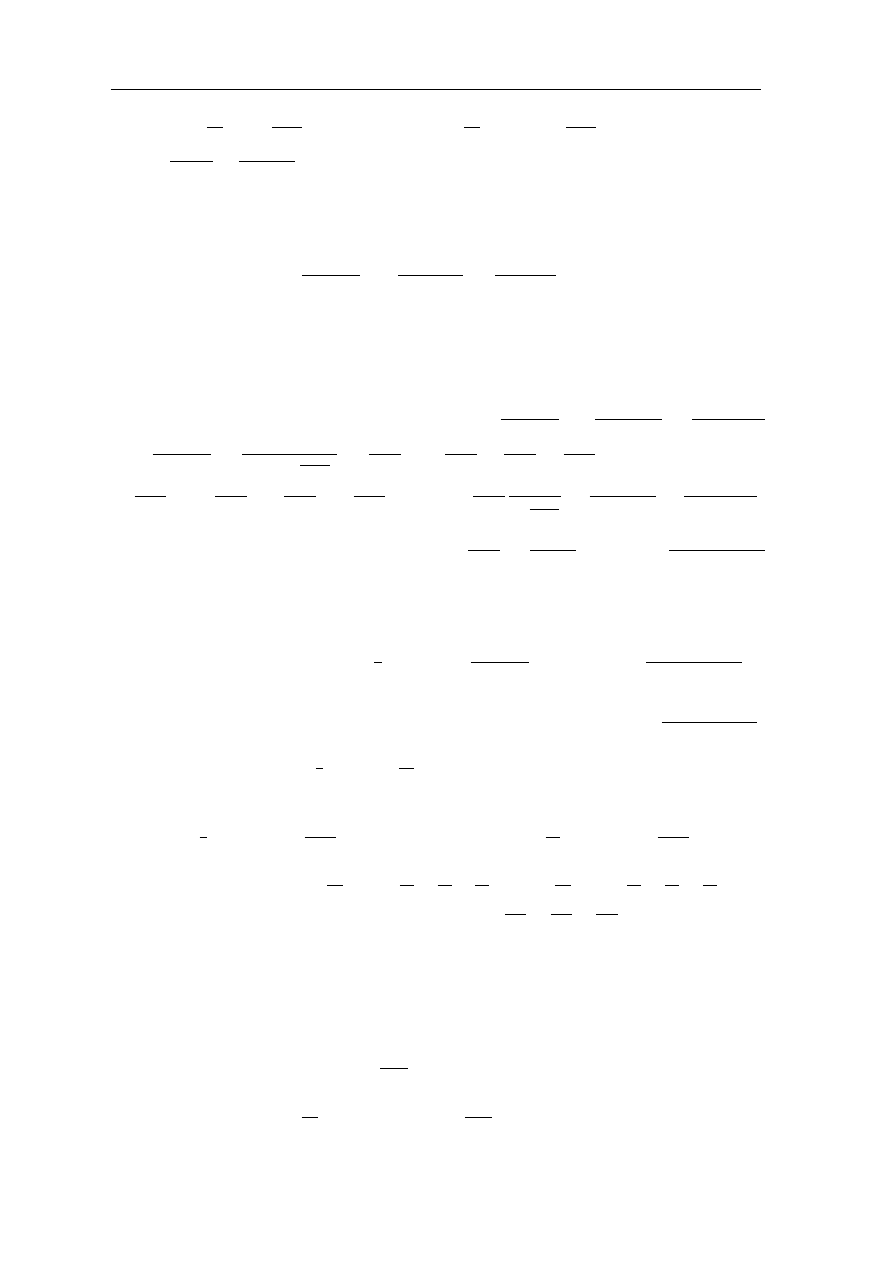
Funkcje analityczne — przyk lady

Micha l Krych

=

ln (1 −

x

2

π

2

)(1 −

x

2

2

2

π

2

) · . . .

0

=

ln(1 −

x

2

π

2

) + ln(1 −

x

2

2

2

π

2

) + . . .

0

=

= −2x

1

π

2

−x

2

+

1

2

2

π

2

−x

2

+ · · ·

.

Ostatni z wypisanych szereg´ow — jak udowodnimy ni˙zej — jest jednostajnie zbie˙z-

ny na ka˙zdym zbiorze zwartym K , kt´ory nie zawiera ani jednego spo´sr´od punkt´ow

±π , ±2π , . . . . Istnieje taka liczba dodatnia M , ˙ze je´sli x ∈ K , to |x| ¬ M . Je´sli

|n| > M i x ∈ K , to

1

n

2

π

2

−x

2

¬

1

n

2

π

2

−M

2

<

1

n

2

(π

2

−1)

. Teraz pozostaje powo la´c

sie

,

na kryterium Weierstrassa jednostajnej zbie˙zno´sci szeregu funkcyjnego. Wiedza

,

c,

˙ze szereg pochodnych jest jednostajnie zbie˙zny i ˙ze szereg funkcji jest zbie˙zny w co

najmniej jednym punkcie, stwierdzamy, ˙ze szereg funkcyjny jest zbie˙zny, a to w la´snie

chcieli´smy wykaza´c.

Niech 0 < r < 1 i |x| ¬ rπ . Mamy wtedy

1

n

2

π

2

−x

2

¬

1

n

2

π

2

−|x|

2

¬

1

n

2

π

2

−r

2

π

2

oraz

1

n

2

π

2

−x

2

=

1

n

2

π

2

(1−

x2

n2π2

)

=

1

n

2

π

2

1 +

x

2

n

2

π

2

+

x

4

n

4

π

4

+

x

6

n

6

π

6

+ · · ·

i wobec tego,

˙ze

1

n

2

π

2

1 +

x

2

n

2

π

2

+

x

4

n

4

π

4

+

x

6

n

6

π

6

+ · · ·

=

1

n

2

π

2

1

1−

|x2|

n2π2

=

1

n

2

π

2

−|x|

2

¬

1

n

2

π

2

−r

2

π

2

.

Wynika sta

,

d, ˙ze w szeregu podw´ojnym

∞

X

n=1

1

n

2

π

2

∞

X

k=0

x

2k

n

2k

π

2k

=

∞

X

n=1

∞

X

k=0

x

2k

n

2(k+1)

π

2(k+1)

mo˙zna zmienia´c kolejno´s´c sumowania w dowolny spos´ob zachowuja

,

c jego sume

,

. Mamy

wobec tego

b

1

x + b

3

x

3

+ b

5

x

5

+ · · · = ctg x −

1

x

= −2x

∞

X

n=1

1

n

2

π

2

−x

2

= −2x

∞

X

n=1

∞

X

k=0

x

2k

n

2(k+1)

π

2(k+1)

=

=

∞

X

k=0

x

2k+1

∞

X

n=1

−2

n

2(k+1)

π

2(k+1)

.

Przypomnijmy, ˙ze b

1

= −

1
3

, b

2

= −

1

45

. Por´ownuja

,

c wsp´o lczynniki przy x oraz x

3

po obu stronach r´owno´sci otrzymujemy

−

1
3

= b

1

=

∞

X

n=1

−2

n

2

π

2

,

oraz

−

1

45

= b

3

=

∞

X

n=1

−2

n

4

π

4

.

Z tych r´owno´sci wynika, ˙ze

π

2

6

= 1 +

1

2

2

+

1

3

2

+

1

4

2

+ · · · i

π

4

90

= 1 +

1

2

4

+

1

3

4

+

1

4

4

+ · · · .

Mo˙zemy w podobny spos´ob uzyska´c wzory na 1 +

1

2

2k

+

1

3

2k

+

1

4

2k

+ · · · dla dowolnej

liczby naturalnej k .

Lemat 12.3 Je´sli funkcja f jest analityczna w punkcie 0 , czyli ˜

f (x) =

∞

X

n=0

˜a

n

x

n

dla pewnych liczb ˜a

0

, ˜a

1

, . . . i wszystkich x spe lniaja

,

cych nier´owno´s´c |x| < r , gdzie

r > 0 , ˜a

0

6= 0 to r´ownie˙z funkcja

1

˜

f (x)

jest analityczna w punkcie 0 .

Dow´

od. Niech a

n

=

˜

a

n

˜

a

0

i niech f (x) =

˜

f (x)

˜

a

0

=

∞

X

n=0

a

n

x

n

= 1 +

∞

X

n=1

a

n

x

n

. Po-

4

Funkcje analityczne — przyk lady

Micha l Krych

niewa˙z

1

˜

f (x)

=

1

˜

a

0

f (x)

, wie

,

c wystarczy wykaza´c analityczno´s´c funkcji

1

f (x)

w punkcie

0 . Znajdziemy takie liczby b

1

, b

2

, . . . i liczbe

,

% > 0 , ˙ze

1

f (x)

= 1 +

∞

X

n=1

b

n

x

n

dla

ka˙zdego x ∈ (−%, %) . Z r´owno´sci 1 =

1 +

∞

X

n=1

a

n

x

n

!

1 +

∞

X

n=1

b

n

x

n

!

i twierdzenia

o mno˙zeniu szereg´ow, wynika, ˙ze musza

,

by´c spe lnione r´owno´sci:

a

1

+ b

1

= 0 , a

2

+ a

1

b

1

+ b

2

= 0 , a

3

+ a

2

b

1

+ a

1

b

2

+ b

3

= 0 , . . .

Sta

,

d wzory: b

1

= −a

1

, b

2

= −a

2

− a

1

b

1

, b

3

= −a

3

− a

2

b

1

− a

1

b

2

, . . . Mo˙zemy wie

,

c

wyliczy´c kolejne wsp´o lczynniki b

1

, b

2

, b

3

, . . . . Pozostaje kwestia zbie˙zno´sci otrzyma-

nego szeregu.

Niech c ∈ (0, r) . Szereg

P

a

n

c

n

jest zbie˙zny, zatem lim

n→∞

a

n

c

n

= 0 . Istnieje

wie

,

c taka liczba M > 1 , ˙ze dla ka˙zdego n = 1, 2, . . . spe lniona jest nier´owno´s´c

|a

n

c

n

| < M (cia

,

g o granicy sko´

nczonej jest ograniczony). Za pomoca

,

latwej indukcji

dowodzimy, ˙ze spe lnione sa

,

nier´owno´sci |b

n

| ≤ 2

n−1

M

n

c

−n

. Wynika sta

,

d, ˙ze szereg

P

b

n

x

n

jest zbie˙zny dla ka˙zdego x ∈ (−

c

2M

,

c

2M

) (by´c mo˙ze nie tylko dla tych x ),

wie

,

c ma dodatni promie´

n zbie˙zno´sci.

5