Funkcja wykÃladnicza, kosinus i sinus
Tekst poprawiony 15 lutego 2014, 0:35
W dalszej cze
,
´sci wyk ladu wygodnie jest u˙zy´c liczb zespolonych znanych ju˙z
studentom z wyk ladu algebry liniowej. Przypomnie´c wypada, ˙ze liczbami zespolo-
nymi nazywamy uporza
,
dkowane pary liczb rzeczywistych, kt´ore mo˙zna w naturalny
spos´ob identyfikowa´c z punktami p laszczyzny. Be
,
dziemy standardowo przyjmowa´c,
˙ze z = x + yi , z
n
= x
n
+ y
n
i zak ladaja
,
c, ˙ze x, y, x
n
, y
n
∈ R .
Przypomnie´c wypada, ˙ze je´sli z ∈ C i z = x + iy , x, y ∈ R , to piszemy
Re(z) = x oraz Im(z) = y . Piszemy te˙z |z| =
p
x
2
+ y
2
. Warto´s´c bezwzgle
,
dna to
tak jak w przypadku liczb rzeczywistych odleg lo´s´c punktu z od punktu 0 . Liczby
zespolone mo˙zna dodawa´c i mno˙zy´c. Sa
,
spe lnione wszystkie pewniki z listy podanej
dla liczb rzeczywistych z wyja
,
tkiem tych, w kt´orych wyste
,
puje nier´owno´s´c. W zbiorze
liczb zespolonych nier´owno´sci zgodnej z dzia laniami wprowadzi´c nie mo˙zna, bo gdyby
to sie
,
uda lo, to wszystkie niezerowe kwadraty okaza lyby sie
,
dodatnie, wie
,
c zar´owno
−1 = i
2
jak i 1 = 1
2
by lyby liczbami dodatnimi, ale ich suma, r´owna 0 , dodatnia
by nie by la.
Zachodzi natomiast nier´owno´s´c tr´ojka
,
ta: |z
1
+ z
2
| ≤ |z
1
| + |z
2
| dla dowolnych
liczb z
1
, z
2
∈ C .
Jej druga wersja to
|z
1
| − |z
2
|
≤ |z
1
− z
2
| . Tr´ojka
,
t, o kt´orym mo˙zna pomy´sle´c
(druga wersja) ma wierzcho lki z
1
, 0, z
2
. Nier´owno´s´c
|z
1
| − |z
2
|
≤ |z
1
− z
2
| jest
ostra chyba, ˙ze jeden z punkt´ow z
1
, z
2
le˙zy mie
,
dzy drugim z nich i punktem 0 . Nie
dowodzimy wszystkich tych stwierdze´
n bo ich latwe dowody pojawi ly sie
,
z pewno´scia
,
na zaje
,
ciach z algebry liniowej.
Przed podaniem naste
,
pnych przyk lad´ow i twierdze´
n zajmiemy sie
,
przez chwile
,
cia
,
gami i szeregami liczb zespolonych.
Twierdzenie 4.1 (granicy cia
,
gu liczb zespolonych)
Liczba zespolona z jest granica
,
cia
,
gu liczb zespolonych (z
n
) wtedy i tylko wtedy,
gdy dla ka˙zdej liczby ε > 0 istnieje liczba naturalna n
ε
taka, ˙ze je´sli n > n
ε
, to
|z
n
− z| < ε .
Jak wida´c definicja granicy jest dok ladnie taka sama jak w przypadku liczb
rzeczywistych. Jasne jest, ˙ze lim
n→∞
z
n
= z wtedy i tylko wtedy, gdy lim
n→∞
|z
n
− z| = 0 .
Nie mo˙zemy jednak m´owi´c o cia
,
gach monotonicznych, bo w zbiorze liczb zespolonych
nie da sie
,
zdefiniowa´c nier´owno´sci zgodnej z dodawaniem i mno˙zeniem. Twierdzenia,
definicje itp., kt´ore nie sa
,
zwia
,
zane z monotoniczno´scia
,
, mo˙zna przenie´s´c na og´o l bez
˙zadnych zmian na przypadek zespolony.
1
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
Stwierdzenie 4.2
Cia
,
g (z
n
) jest zbie˙zny do liczby z wtedy i tylko wtedy, gdy x = lim
n→∞
x
n
i jedno-
cze´snie y = lim
n→∞
y
n
.
Dow´
od. Zachodza
,
nier´owno´sci |z
n
− z| =
p
(x
n
− x)
2
+ (y
n
− y)
2
≥ |x
n
− x|
i |z
n
− z| =
p
(x
n
− x)
2
+ (y
n
− y)
2
≥ |y
n
− y| .* Wobec tego z twierdzenia o
trzech cia
,
gach wynika, ˙ze je´sli lim
n→∞
z
n
= z , to lim
n→∞
x
n
= x i lim
n→∞
y
n
= y , co
ko´
nczy dow´od stwierdzenia w jedna
,
strone
,
. Je´sli lim
n→∞
x
n
= x i lim
n→∞
y
n
= y , to
0 = lim
n→∞
p
(x
n
− x)
2
+ (y
n
− y)
2
= lim
n→∞
|z
n
− z| , wie
,
c lim
n→∞
z
n
= z .
Z nier´owno´sci |x
n
−x| ≤ |z
n
−z| , |y
n
−y| ≤ |z
n
−z| i |z
n
−z| ≤ |x
n
−x|+|y
n
−y|
wynika
Stwierdzenie 4.3
Cia
,
g (z
n
) spe lnia warunek Cauchy’ego wtedy i tylko wtedy, gdy oba cia
,
gi (x
n
) , (y
n
)
spe lniaja
,
warunek Cauchy’ego.
Wobec tego, podobnie jak w przypadku rzeczywistym, prawdziwe jest bardzo
wa˙zne
Stwierdzenie 4.4
Cia
,
g (z
n
) ma granice
,
(sko´
nczona
,
) wtedy i tylko wtedy, gdy spe lniony jest warunek
Cauchy’ego.
Z tego banalnie wygla
,
daja
,
cego stwierdzenia wynika, ˙ze twierdzenia o szeregach
bezwzgle
,
dnie zbie˙znych sa
,
prawdziwe r´ownie˙z w przypadku szereg´ow o wyrazach
zespolonych.
Przyk lad 4.1
Niech z oznacza dowolna
,
liczbe
,
zespolona
,
. Udowodnimy teraz
bezpo´srednio, ˙ze szereg
P
∞
n=0
z
n
n!
jest bezwzgle
,
dnie zbie˙zny. Zastosujemy kryterium
ilorazowe d’Alemberta do szeregu
P
∞
n=0
z
n
n!
w przypadku z 6= 0 , w przypadku
z = 0 nasz szereg ma wyrazy nieujemne: 1 + 0 + 0 + 0 + . . . , wie
,
c jest zbie˙zny
bezwzgle
,
dnie. Zachodzi wz´or
z
n+1
(n+1)!
.
z
n
n!
=
|z|
n+1
−−−−→
n→∞
0 < 1 , zatem szereg
P
∞
n=0
z
n
n!
jest zbie˙zny dla ka˙zdego z 6= 0 , co oznacza, ˙ze szereg
P
∞
n=0
z
n
n!
jest
zbie˙zny bezwzgle
,
dnie. Wyka˙zemy, ˙ze dla dowolnych liczb zespolonych z, w zachodzi
r´owno´s´c
P
∞
n=0
z
n
n!
·
P
∞
n=0
w
n
n!
=
P
∞
n=0
(z+w)
n
n!
. Zastosujemy oczywi´scie twierdzenie
Cauchy’ego o mno˙zeniu szereg´ow. Mamy
1 +
z
1!
+
z
2
2!
+
z
3
3!
+ . . .
·
1 +
w
1!
+
w
2
2!
+
w
3
3!
+ . . .
=
*
Odleg lo´s´
c mie,dzy rzutami na o´s nie przekracza odleg lo´sci mie,dzy rzutowanymi punktami.
2
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
= 1 +
z
1!
+
w
1!
+
z
2
2!
+
z
1!
·
w
1!
+
w
2
2!
+
z
3
3!
+
z
2
2!
·
w
1!
+
z
1!
·
w
2
2!
+
w
3
3!
+ · · · =
dwumian Newtona
=============1 +
z+w
1!
+
(z+w)
2
2!
+
(z+w)
3
3!
+ . . . .
Wypada stwierdzi´c, ˙ze w licznych podre
,
cznikach liczba e
x
jest definiowana jako
suma szeregu niesko´
nczonego
∞
X
n=0
x
n
n!
. Posta
,
pili´smy inaczej g l´ownie ze wzgle
,
du na to,
˙ze ta definicja, kt´ora
,
podali´smy wcze´sniej, e
x
= lim
n→∞
1 +
x
n
n
, mo˙ze by´c na tym po-
ziomie zaawansowania latwiej powia
,
zana z zastosowaniami i to w zrozumia ly spos´ob.
Nadmieni´c wypada, ˙ze po ostatnim przyk ladzie niewiele ju˙z zosta lo do zrobienia, by
otrzyma´c wszystkie w lasno´sci funkcji wyk ladniczej na drodze tu opisanej. Dobrym
i jednocze´snie prostym ´cwiczeniem by loby wykazanie nier´owno´sci
∞
X
n=0
x
n
n!
≥ 1 + x dla
ujemnych liczb rzeczywistych x za pomoca
,
operacji na szeregach.
Teraz zajmiemy sie
,
funkcja
,
wyk ladnicza o podstawie e i zespolonym wyk ladniku.
Lemat 4.5 (zespolony o granicach n -tych pote
,
g cia
,
g´
ow „szybko
zbie˙znych” do 1)
Je´sli lim
n→∞
n · z
n
= 0 , to lim
n→∞
(1 + z
n
)
n
= 1 .
Dow´
od. Wyka˙zemy, ˙ze zachodzi nier´owno´s´c |(1 + z)
n
− 1| ≤ (1 + |z|)
n
− 1 korzy-
staja
,
c z dwumianu Newtona i nier´owno´sci tr´ojka
,
ta. Zachodza
,
wzory:
|(1 + z)
n
− 1| =
1 +
n
1
z +
n
2
z
2
+ · · · +
n
n−1
z
n−1
+ z
n
− 1
≤
≤
n
1
|z| +
n
2
|z|
2
+ · · · +
n
n−1
|z|
n−1
+ |z|
n
= (1 + |z|)
n
− 1 .
Poniewa˙z za lo˙zyli´smy, ˙ze lim
n→∞
n · z
n
= 0 , wie
,
c lim
n→∞
n · |z
n
| = 0 i wobec tego, ˙ze
zachodzi nier´owno´s´c |(1 + z
n
)
n
− 1| ≤ (1 + |z
n
|)
n
− 1 , a to ostatnie wyra˙zenie ma
granice
,
0 przy n −→ ∞ , na mocy rzeczywistego lematu o pote
,
gach cia
,
g´ow szybko
zbie˙znych do 1 , wie
,
c lemat zespolony wynika natychmiast z twierdzenia o trzech
cia
,
gach.
Teraz czeka nas dow´od istnienia granicy lim
n→∞
(1 +
z
n
)
n
. Musi on sie
,
r´o˙zni´c od
dowodu w przypadku rzeczywistym, bo o ˙zadnej monotoniczno´sci tym razem m´owi´c
nie mo˙zemy, bo to poje
,
cie nie stosuje sie
,
do liczb nierzeczywistych. Zamiast niego wy-
korzystamy twierdzenie Cauchy’ego, wg. kt´orego cia
,
g liczbowy spe lniaja
,
cy warunek
Cauchy’ego ma granice
,
sko´
nczona
,
.
Lemat 4.6 (o zbie˙zno´sci cia
,
gu lim
n→∞
(1 +
z
n
)
n
)
Cia
,
g (1 +
z
n
)
n
spe lnia warunek Cauchy’ego, wie
,
c jest zbie˙zny.
Dow´
od. Zauwa˙zmy najpierw, ˙ze je´sli n > m ≥ k ≥ 0 , to
m
k
1
m
k
<
n
k
1
n
k
.Wynika
3
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
to natychmiast z tego, ˙ze
m
k
1
m
k
=
m(m−1)...(m−k+1)
m
k
k!
= 1 −
1
m
· 1 −
2
m
· . . . · 1 −
k−1
m
·
1
k!
,
wobec tego zaste
,
puja
,
c w tym wzorze m przez n > m zwie
,
kszamy mianowniki za-
chowuja
,
c liczniki bez zmian, co oczywi´scie powoduje wzrost mno˙zonych u lamk´ow.
Mamy zatem
1 +
z
n
n
− 1 +
z
m
m
=
1 +
n
1
z
n
+
n
2
z
n
2
+ · · · +
n
n−1
z
n
n−1
+
z
n
n
−
−
1 +
m
1
z
m
+
m
2
z
m
2
+ · · · +
m
m−1
z
m
m−1
+
z
m
m
≤
≤ [1 − 1]+
n
1
1
n
−
m
1
1
m
|z|+
n
2
1
n
2
−
m
2
1
m
2
|z|
2
+· · ·+
n
m
1
n
m
−
m
m
1
m
m
|z|
m
+
+
n
m+1
1
n
m+1
|z|
m+1
+ · · · +
n
n−1
1
n
n−1
|z|
n−1
+ |z|
n
=
1 +
|z|
n
n
−
1 +
|z|
m
m
.
Poniewa˙z cia
,
g
(1 +
|z|
n
)
n
jest zbie˙zny (liczba |z| jest rzeczywista!), wie
,
c spe lnia
on warunek Cauchy’ego, wobec tego r´ownie˙z cia
,
g (1 +
z
n
)
n
spe lnia warunek Cau-
chy’ego – wykazali´smy bowiem, ˙ze odleg lo´sci mie
,
dzy wyrazami tego ostatniego nie
przekraczaja
,
odleg lo´sci odpowiednich wyraz´ow cia
,
gu
(1 +
|z|
n
)
n
. Lemat zosta l do-
wiedziony.
Definicja 4.7 (zespolonej funkcji wyk ladniczej o podstawie e )
e
z
:= exp(z) := lim
n→∞
1 +
z
n
n
.
Twierdzenie 4.8 (o podstawowych w lasno´sciach funkcji zespolonej exp)
c1. Dla dowolnych liczb zespolonych z, w zachodzi r´owno´s´c
exp(z + w) = exp(z) · exp(w) .
c2. Dla dowolnego cia
,
gu (z
n
) liczb zespolonych r´o˙znych od 0 zbie˙znego do 0 za-
chodzi r´owno´s´c
lim
n→∞
exp(z
n
) − 1
z
n
= 1 .
Dow´
od. W lasno´s´c c1 wynika z lematu zespolonego o granicach n –tych pote
,
g
cia
,
g´ow szybko zbie˙znych do 1 w dok ladnie taki sam spos´ob jak w przypadku rze-
czywistym. Dla dowodu w lasno´sci c2 skorzystamy z w lasno´sci rzeczywistej funkcji
exp i wykazanej w dowodzie lematu o zbie˙zno´sci cia
,
gu
1 +
z
n
n
nier´owno´sci w
przypadku n > m = 1 zak ladaja
,
c, ˙ze |z| < 1 :
1 +
z
n
n
− (1 + z)
≤
1 +
|z|
n
n
− (1 + |z|) ≤ exp(|z|) − (1 + |z|) ≤
≤
1
1−|z|
− (1 + |z|) =
|z|
2
1 − |z|
4
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
Mamy wie
,
c
1 +
z
n
n
−(1 + z)
≤
|z|
2
1−|z|
. Sta
,
d przechodza
,
c do granicy przy n → +∞
otrzymujemy w przypadku 0 < |z| < 1 nier´owno´s´c | exp(z)−(1+z)| ≤
|z|
2
1−|z|
, z kt´orej
w lasno´s´c c2 wynika od razu:
exp(z)−1
z
− 1
=
exp(z)−(1+z)
z
≤
|z|
1−|z|
.
Wniosek 4.9 (o cia
,
g lo´sci funkcji exp)
Je´sli lim
n→∞
z
n
= z , to lim
n→∞
exp(z
n
) = exp(z) .
Dow´
od.
lim
n→∞
exp(z
n
) = exp(z) + exp(z) · lim
n→∞
(z
n
− z) · lim
n→∞
exp(z
n
−z)−1
z
n
−z
=
= exp(z) + exp(z) · 0 · 1 = exp(z).
Twierdzenie 4.10 (o jednoznaczno´sci funkcji zespolonej exp )
Je´sli funkcja f : C −→ C spe lnia warunki
c1 dla dowolnych liczb zespolonych z, w zachodzi r´owno´s´c f (z + w) = f (z)f (w) ,
c2 dla dowolnego cia
,
gu (z
n
) liczb zespolonych r´o˙znych od 0 zbie˙znego do 0 za-
chodzi r´owno´s´c lim
n→∞
f (z
n
)−1
z
n
= 1 ,
to dla ka˙zdej liczby zespolonej z zachodzi r´owno´s´c f (z) = exp(z) = lim
n→∞
1 +
z
n
n
.
Dow´
od. Mamy lim
n→∞
(1+
z
n
)
n
6= 0 . Dla dostatecznie du˙zych n mamy (1+
z
n
)
n
6= 0 .
Mamy te˙z f z
=
f
z
n
n
. Wobec tego
f (z)
lim
n→∞
(1 +
z
n
)
n
= lim
n→∞
1 +
f (
z
n
) − 1 −
z
n
1 +
z
n
n
= 1 ,
bo lim
n→∞
n · (f (
z
n
) − 1 −
z
n
) = lim
n→∞
z
f (
z
n
)−1
z
n
− z
= z · 1 − z = 0 , wie
,
c mo˙zemy
skorzysta´c z lematu o pote
,
gach cia
,
g´ow zespolonych szybko zbie˙znych do 1 , biora
,
c
pod uwage
,
te˙z to, ˙ze lim
n→∞
1 +
z
n
= 1 .
Uog´olnimy nieco twierdzenie o jednoznaczno´sci funkcji wyk ladniczej.
Twierdzenie 4.11 (o jednoznaczno´sci zespolonej funkcji wyk ladniczej)
Je´sli funkcja f : C −→ C spe lnia warunki
c1 dla dowolnych liczb zespolonych z, w zachodzi r´owno´s´c f (z + w) = f (z)f (w) ,
c2 dla dowolnego cia
,
gu (z
n
) liczb zespolonych r´o˙znych od 0 zbie˙znego do 0 za-
chodzi r´owno´s´c
lim
n→∞
f (z
n
)−1
z
n
= A ,
to dla ka˙zdej liczby zespolonej z zachodzi r´owno´s´c f (z) = exp(Az) = e
Az
.
Dow´
od. Mo˙zemy powt´orzy´c dow´od poprzedniej wersji twierdzenia, jednak posta
,
pi-
my nieco inaczej. Zdefiniujemy pomocnicza
,
funkcje
,
g(z) = f (
z
A
) , je´sli A 6= 0 . Mamy
g(z + w) = f (
z+w
A
) = f (
z
A
+
w
A
) = f (
z
A
) · f (
w
A
) = g(z) · g(w) .
5
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
Je´sli lim
n→∞
z
n
= 0 i z
n
6= 0 dla n ∈ N , to
lim
n→∞
g(z
n
)−1
z
n
=
1
A
· lim
n→∞
f (z
n
/A)−1
z
n
/A
=
1
A
· A = 1 .
Wobec tego dla ka˙zdej liczby zespolonej z zachodzi r´owno´s´c e
z
= g(z) . Sta
,
d wynika
od razu, ˙ze f (z) = f
Az
A
= g(Az) = e
Az
.
Pozosta l przypadek A = 0 . Niech z ∈ C \ {0} . Mamy lim
n→∞
z
n
= 0 i z
n
6= 0 dla
n ∈ N , wie
,
c lim
n→∞
f (
z
n
)−1
z
n
= A = 0 Z lematu zespolonego o granicach pote
,
g cia
,
g´ow
szybko zbie˙znych do 1 wynika, ˙ze f (z) =
f
z
n
n
=
1 +
f (
z
n
)−1
z
n
z
n
n
−−−−→
n→∞
1 , a to
oznacza, ˙ze dla ka˙zdej liczby zespolonej z zachodzi r´owno´s´c f (z) = 1 = e
0·z
.
Twierdzenie 4.12 (kilka naste
,
pnych w lasno´sci funkcji zespolonej exp)
c3. exp(z) = exp(z) dla ka˙zdej liczby zespolonej z .
c4. Je´sli y ∈ IR , to exp(iy) = exp (−iy) .
c5. Je´sli y ∈ IR , to | exp(iy)| = 1 .
c6. | exp(z)| = exp(Rez) ≤ exp(|z|) dla ka˙zdej liczby zespolonej z .
c7. Je´sli y ∈ IR , to | exp(iy) − 1| ≤ |y|
Dow´
od. Mamy
exp(z) = lim
n→∞
1 +
z
n
n
= lim
n→∞
1 +
z
n
n
= lim
n→∞
1 +
z
n
n
= exp(z) .
Wykazali´smy c3. Z tej w lasno´sci c4 wynika przez podstawienie, a naste
,
pna w lasno´s´c
wynika sta
,
d, ˙ze
| exp(iy)|
2
= exp(iy) · exp(iy) = exp(iy) · exp(−iy) = exp(iy + (−iy)) = exp(0) = 1 .
Je´sli x, y ∈ R i z = e
x+iy
, to |z| =
e
x+iy
=
e
x
·
e
iy
= e
x
; oznacza to, ˙ze warto´s´c
bezwzgle
,
dna pote
,
gi o wyk ladniku zespolonym i podstawie e zale˙zy jedynie od cze
,
´sci
rzeczywistej wyk ladnika, cze
,
´s´c urojona wyk ladnika ma wp lyw jedynie na argument
pote
,
gi. W lasno´s´c c6. zosta la udowodniona.
Wyka˙zemy c7. Mamy
| exp(ix) − 1| = | exp(i
x
n
)
n
− 1| =
=
exp(i
x
n
) − 1
·
exp
(n−1)
n
ix
+ exp
(n−2)
n
ix
+ · · · + exp
1
n
ix
+ 1
≤
≤
exp(i
x
n
) − 1
·
exp
(n−1)
n
ix
+
exp
(n−2)
n
ix
+ · · · +
exp
1
n
ix
+ 1
=
= n
exp(i
x
n
) − 1
=
ix
exp(i
x
n
) − 1
i
x
n
−−−−→
n→∞
|x|
W ostatnim przej´sciu granicznym skorzystali´smy oczywi´scie z w lasno´sci c2. W ten
spos´ob zako´
nczyli´smy dow´od.
Definicja 4.13 (funkcji sinus i kosinus)
Dla ka˙zdej liczby zespolonej z definiujemy
6
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
sin z =
1
2i
(exp(iz) − exp(−iz)) ,
cos z =
1
2
(exp(iz) + exp(−iz)) .
Twierdzenie 4.14 (wz´
or Eulera)
e
iz
= exp(iz) = cos z + i sin z dla ka˙zdego z ∈ C .
Wz´or ten jest natychmiastowa
,
konsekwencja
,
definicji sinusa i kosinusa.
Twierdzenie 4.15 (podstawowe w lasno´sci funkcji trygonometrycznych)
t0. cos y ∈ R oraz sin y ∈ R dla ka˙zedego y ∈ R .
t1. cos
2
z + sin
2
z = 1 dla ka˙zdej liczby zespolonej z .
t2. cos(z + w) = cos z cos w − sin z sin w dla dowolnych z, w ∈ C .
t3. sin(z + w) = sin z cos w + cos z sin w dla dowolnych z, w ∈ C .
t4.
lim
n→∞
sin z
n
z
n
= 1 dla ka˙zdego cia
,
gu (z
n
) liczb zespolonych r´o˙znych od 0 , zbie˙z-
nego do 0 .
Dow´
od. Poniewa˙z exp(iy) = exp(−iy) (w lasno´s´c c4), wie
,
c je´sli y jest liczba
,
rze-
czywista
,
, to cos y =
1
2
(exp(iy) + exp(−iy)) =
1
2
exp(iy) + exp(iy)
= Re(exp(iy))
oraz sin y =
1
2i
(exp(iy) − exp(−iy)) =
1
2i
exp(iy) − exp(iy)
= Im(exp(iy)) te˙z sa
,
liczbami rzeczywistymi. W lasno´s´c t0 jest udowodniona.
cos
2
z + sin
2
z =
1
2
(exp(iz) + exp(−iz))
2
+
1
2i
(exp(iz) − exp(−iz))
2
=
=
1
4
exp(2iz)+exp(−2iz)+2 exp(iz−iz)
−
1
4
exp(2iz)+exp(−2iz)−2 exp(iz−iz)
=
=
1
4
· 2 −
1
4
· (−2) = 1 . W lasno´s´c t1 jest udowodniona.
cos z cos w − sin z sin w =
1
2
(exp(iz) + exp(−iz)) ·
1
2
(exp(iw) + exp(−iw)) −
−
1
2i
(exp(iz) − exp(−iz)) ·
1
2i
(exp(iw) − exp(−iw)) =
=
1
4
exp(i(z + w)) + exp(i(z − w)) + exp(i(−z + w)) + exp(i(−z − w))
+
+
1
4
exp(i(z + w)) − exp(i(z − w)) − exp(i(−z + w)) + exp(i(−z − w))
=
=
1
2
exp(i(z + w)) + exp(i(−z − w))
= cos(z + w) . Udowodnili´smy w lasno´s´c t2.
sin z cos w + cos z sin w =
1
2i
(exp(iz) − exp(−iz)) ·
1
2
(exp(iw) + exp(−iw)) +
+
1
2
(exp(iz) + exp(−iz)) ·
1
2i
(exp(iw) − exp(−iw)) =
=
1
4i
exp(i(z + w)) + exp(i(z − w)) − exp(i(−z + w)) − exp(i(−z − w))
+
+
1
4i
exp(i(z + w)) − exp(i(z − w)) + exp(i(−z + w)) − exp(i(−z − w))
=
=
1
2i
exp(i(z + w)) − exp(i(−z − w))
= sin(z + w) . Udowodnili´smy w lasno´s´c t3.
Dowiedziemy prawdziwo´s´c w lasno´sci t4:
lim
n→∞
sin z
n
z
n
=
= lim
n→∞
exp(iz
n
)−exp(−iz
n
)
2iz
n
= lim
n→∞
1
2
exp(iz
n
)−1
iz
n
+
1
2
lim
n→∞
exp(−iz
n
)−1
−iz
n
=
1
2
+
1
2
= 1 .
Mo˙zna wykaza´c, ˙ze w lasno´sci t1 – t4 definiuja
,
pare
,
funkcji z lo˙zona
,
z kosinusa i si-
nusa. Zache
,
camy do samodzielnego udowodnienia tego stwierdzenia zar´owno w przy-
padku rzeczywistych jak i zespolonym.
7
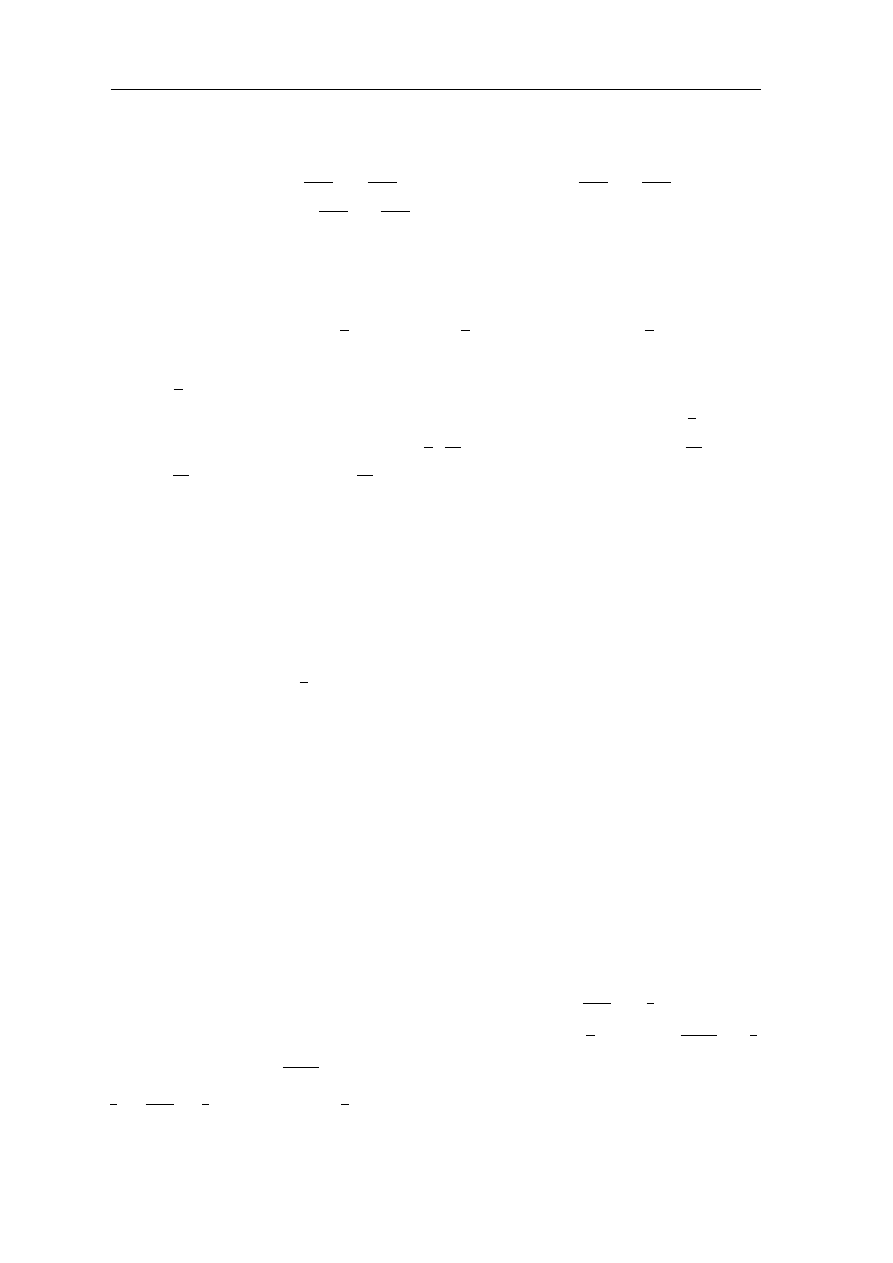
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
Twierdzenie 4.16 ( kilka naste
,
pnych w lasno´sci sinusa i kosinusa)
t5. cos(−z) = cos z , sin(−z) = − sin z dla ka˙zdej liczby zespolonej z .
t6. sin z ± sin w = 2 sin
z±w
2
cos
z∓w
2
, cos z + cos w = 2 cos
z+w
2
cos
z−w
2
,
cos z − cos w = −2 sin
z+w
2
sin
z−w
2
dla dowolnych z, w ∈ C .
t7. | sin x − sin y| ≤ |x − y| , | cos x − cos y| ≤ |x − y| dla dowolnych x, y ∈ R .
t8. Je´sli 0 < y ≤ 2 , to sin y > 0 . Je´sli 0 ≤ y ≤ 1 , to cos y > 0 i sin y < 1 i
0 < cos y < 1 .
t9. Istnieje liczba dodatnia
π
2
taka, ˙ze cos
π
2
= 0 i je´sli 0 < x <
π
2
, to sin x > 0
oraz cos x > 0 .
t10. sin
π
2
= 1 , na przedziale (0, π) funkcja sinus jest dodatnia, funkcja kosinus jest
na przedziale [0, π] maleja
,
ca, cos π = −1 , sin π = 0 , na przedziale [0,
π
2
] funkcja
sinus jest rosna
,
ca, na przedziale [
π
2
,
3π
2
] funkcja sinus maleje, sin
3π
2
= −1 ,
cos
3π
2
= 0 , na przedziale [
3π
2
, 2π] funkcja sinus ro´snie, sin 2π = 0 , cos 2π = 1 ,
na przedziale [π, 2π] funkcja kosinus ro´snie,
t11. Dla ka˙zdej liczby zespolonej z zachodza
,
r´owno´sci cos (z + 2π) = cos z oraz
sin(z + 2π) = sin z .
t12. Dla ka˙zdej pary liczb rzeczywistych x, y takiej, ˙ze x
2
+y
2
= 1 , istnieje dok ladnie
jedna liczba rzeczywista t ∈ [0, 2π) , taka ˙ze x = cos t i jednocze´snie y = sin t .
t13. sin t < t dla t ∈ (0, ∞) .
t14. t < tg t dla t ∈ 0,
π
2
.
Dow´
od. W lasno´s´c t5 to natychmiastowa konsekwencja definicji sinusa i kosi-
nusa, w lasno´s´c t6 mo˙zna wywnioskowa´c z definicji — obliczenia sa
,
bardzo proste
lub z w lasno´sci t2 i t3 dok ladnie tak, jak to czynia
,
autorzy podre
,
cznik´ow szkolnych,
a mo˙zna te˙z pos lu˙zy´c sie
,
wzorem Eulera.
W lasno´s´c t7 wywnioskujemy z nier´owno´sci wykazanej wcze´sniej: | exp(ix) − 1| ≤ |x|
dla x ∈ IR (c7). Wobec tego | sin x − sin y| ≤ | exp(ix) − exp(iy)| = | exp(iy)| ·
· | exp(ix − iy) − 1| = | exp(i(x − y)) − 1| ≤ |x − y| .
Dow´od drugiej nier´owno´sci jest analogiczny.
Dla ka˙zdego y ∈ R mamy 1 − cos y = | cos y − 1| = | cos y − cos 0| ≤ |y − 0| = |y| ,
zatem 1 − |y| ≤ cos y , wie
,
c je´sli |y| < 1 , to 0 < cos y . Mamy te˙z cos 1 ≥ 0 .
Istnieje taka liczba δ > 0 , ˙ze je´sli 0 < y < δ , to |1 −
sin y
y
| <
1
2
— gdyby nie
istnia la, to dla ka˙zdej liczby n ∈ N istnia loby takie y
n
∈ (0,
1
n
) , ˙ze |1 −
sin y
n
y
n
| ≥
1
2
,
wbrew temu, ˙ze lim
n→∞
sin y
n
y
n
= 1 , gdy˙z lim
n→∞
y
n
= 0 . Wobec tego, je´sli 0 < y < δ , to
1
2
<
sin y
y
<
3
2
, zatem sin y >
y
2
> 0 . Z tego, ˙ze 0 < sin y wynika, ˙ze cos y < 1 , wie
,
c
je´sli 0 < y < δ , to 0 < cos y < 1 . Z wzoru t3 wynika, ˙ze
8
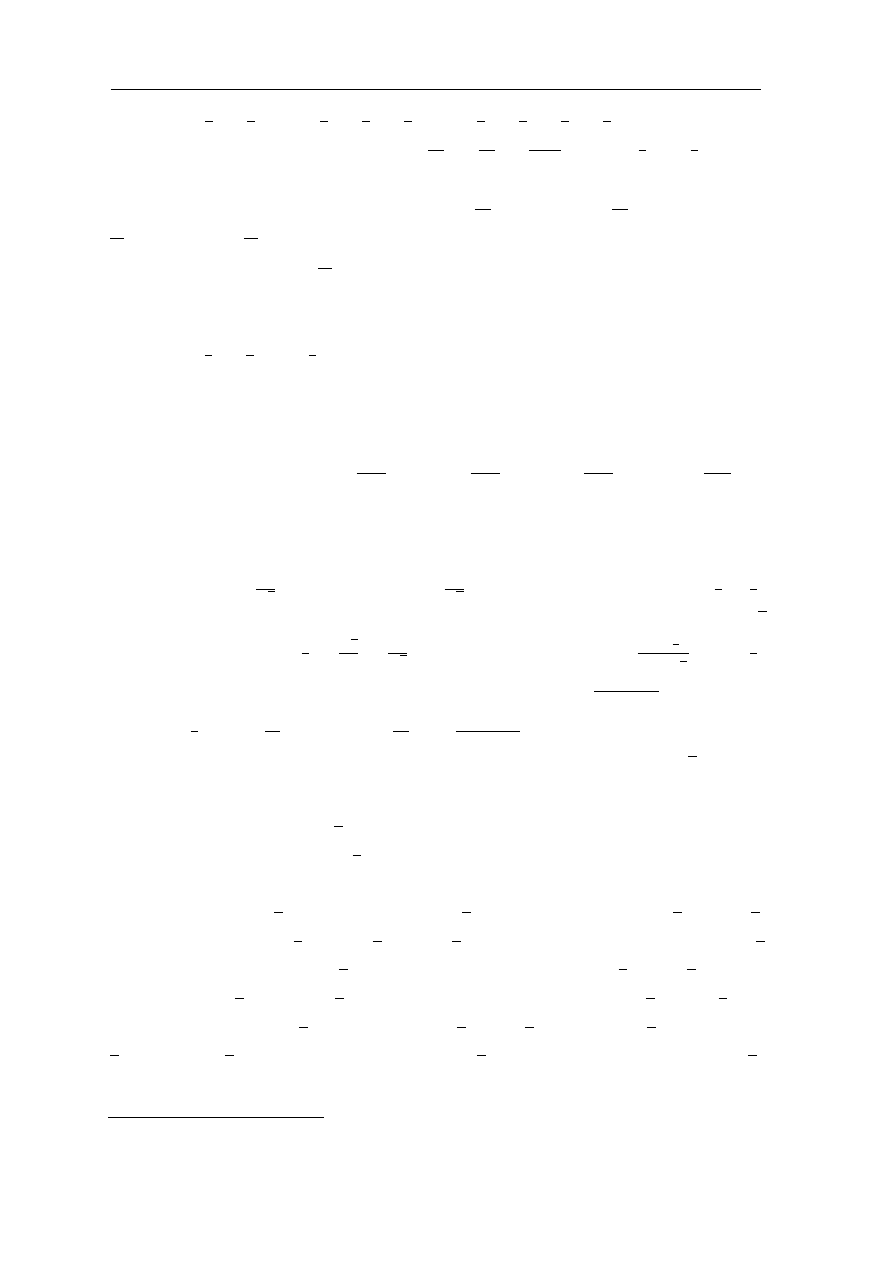
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
sin y = 2 sin
y
2
cos
y
2
= 4 sin
y
4
cos
y
4
cos
y
2
= 8 sin
y
8
cos
y
8
cos
y
4
cos
y
2
= . . . =
= 2
n
sin
y
2
n
cos
y
2
n
cos
y
2
n−1
· . . . · cos
y
4
· cos
y
2
(♠)
Z tego wzoru wynika, ˙ze je´sli 0 < y ≤ 2 , to sin y ≥ 0 , bo dla dostatecznie du˙zej
liczby naturalnej n zachodzi nier´owno´s´c 0 <
y
2
n
< δ , wie
,
c sin
y
2
n
> 0 i oczywi´scie
y
2
j
< 1 , wie
,
c cos
y
2
j
≥ 0 dla j = 1, 2, . . . , n .
W rzeczywisto´sci cos
y
2
j
> 0 dla j = 1, 2, . . . , n , gdy y < 2 lub gdy n > 1 .
Wyka˙zemy, ˙ze r´ownie˙z cos 1 > 0 , czyli ˙ze sin 1 < 1 .*
Z w lasno´sci t7 wynika, ˙ze sin y = | sin y − sin 0| ≤ |y| = y . Sta
,
d otrzymujemy
sin 1 = 2 sin
1
2
cos
1
2
≤ cos
1
2
< 1 , co ko´
nczy dow´od w lasno´sci t8.
Z w lasno´sci t7 i z nier´owno´sci (♠) wynika, ˙ze je´sli 0 < y ≤ 2 , to sin y < y ,
a poniewa˙z dla ka˙zdego rzeczywistego y mamy te˙z sin y ≤ 1 , wie
,
c sin y < y dla
ka˙zdego y > 0 . Udowodnili´smy w lasno´s´c t13.
Przypominamy, ˙ze tg z =
sin z
cos z
, ctg z =
cos z
sin z
, sec z =
1
cos z
i csc z =
1
sin z
dla
ka˙zdej liczby z ∈ C , dla kt´orej mianownik jest r´o˙zny od 0 . Dwie ostatnie funkcje,
tzn. sekans i kosekans, w Polsce sa
,
u˙zywane rzadko, ale sa
,
kraje, w kt´orych ich
popularno´s´c jest wie
,
ksza.
Je´sli 0 < α ≤
1
√
2
, to 0 < sin α < α ≤
1
√
2
, wie
,
c cos
2
α = 1 − sin
2
α > 1 −
1
2
=
1
2
,
zatem cos α > sin α > 0 , czyli tg α < 1 . Wobec tego z nier´owno´sci 0 < t <
√
2
wynika nier´owno´s´c 0 <
t
2
<
√
2
2
=
1
√
2
, a z niej nier´owno´s´c tg t =
2 tg
t
2
1−tg
2 t
2
> 2 tg
t
2
.
Sta
,
d (indukcja) oraz z r´owno´sci lim
n→∞
cos(t · 2
−n
) = 1 i lim
n→∞
sin(t·2
−n
)
t·2
−n
= 1 wynika
tg t > 2 tg
t
2
> 2
2
tg
t
2
2
> . . . > 2
n
tg
t
2
n
= t ·
sin(t·2
−n
)
t·2
−n
· cos(t · 2
−n
) −−−−→
n→∞
t · 1 · 1 = t ,
wie
,
c w lasno´s´c t14 jest prawie udowodniona, prawie bo tylko dla t ∈ (0,
√
2) .
W szczeg´olno´sci tg 1 > 1 , wie
,
c sin 1 > cos 1 , zatem cos 2 = cos
2
1 − sin
2
1 < 0 .
Teraz mo˙zemy zdefiniowa´c
π
2
= inf{t > 0:
cos t ≤ 0} . Z tego, co do tej pory
wykazali´smy, wynika, ˙ze 1 ≤
π
2
≤ 2 — zbi´or, kt´orego kres rozpatrujemy zawiera
liczbe
,
2 i z tego wynika prawa nier´owno´s´c, lewa nier´owno´s´c wynika z w lasno´sci t8 .
Udowodnimy, ˙ze cos
π
2
= 0 . Za l´o˙zmy, ˙ze cos
π
2
6= 0 . Z nier´owno´sci |t −
π
2
| < | cos
π
2
|
wynika, ˙ze | cos t − cos
π
2
| ≤ |t −
π
2
| < | cos
π
2
| . Sta
,
d wynika, ˙ze liczby cos t i cos
π
2
maja
,
ten sam znak. Je´sli cos
π
2
< 0 , to inf{t > 0:
cos t ≤ 0} ≤
π
2
− | cos
π
2
| , wbrew
definicji liczby
π
2
. Je´sli cos
π
2
> 0 , to inf{t > 0:
cos t ≤ 0} ≥
π
2
+ | cos
π
2
| , co
przeczy definicji liczby
π
2
. Wobec tego cos
π
2
= 0 .
π
2
6= 2 , bo cos
π
2
= 0 > cos 2 .
π
2
6= 1 , bo cos
π
2
= 0 < cos 1 . Wobec tego 2 >
π
2
> 1 . Jasne jest, ˙ze je´sli 0 < t <
π
2
,
to cos t > 0 i sin t > 0 . W lasno´s´c t9. zosta la
,
wykazana.
*
Wiemy ju˙z, ˙ze cos 1≥0 oraz cos
2
1+sin
2
1=1 , teraz chodzi o ostra, nier´owno´s´c.
9
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
Zajmiemy sie
,
w lasno´scia
,
t10. Poniewa˙z 1 = cos
2 π
2
+ sin
2 π
2
= sin
2 π
2
oraz
sin
π
2
> 0 , wie
,
c sin
π
2
= 1 . Je´sli 0 < x < π , to 0 <
x
2
<
π
2
, zatem — na mocy po-
przednio wykazanych w lasno´sci sinusa i kosinusa — mamy sin x = 2 sin
x
2
cos
x
2
> 0 .
Wynika sta
,
d, ˙ze je´sli 0 ≤ t < s ≤ π , to cos t − cos s = 2 sin
s−t
2
sin
s+t
2
> 0 .
Oznacza to, ˙ze funkcja kosinus maleje (´sci´sle) na przedziale [0, π] . Mamy r´ownie˙z
cos π = cos
2 π
2
− sin
2 π
2
= −1 i sin π = 2 sin
π
2
cos
π
2
= 0 . Wobec tego z nier´owno´sci
π
2
< x < π wynika, ˙ze 0 = cos
π
2
> cos x > cos π = −1 , wie
,
c kosinus przyjmuje
ujemne warto´sci na przedziale (
π
2
, π] . Je´sli wie
,
c 0 ≤ x < y ≤
π
2
, to sin y − sin x =
=2 sin
y−x
2
cos
x+y
2
> 0 , a zatem funkcja sinus jest rosna
,
ca na przedziale [0,
π
2
] .
Podobnie, je´sli
π
2
≤ x < y ≤ π , to 0 <
y−x
2
<
π
2
i
π
2
<
x+y
2
< π , zatem
sin y − sin x = 2 sin
y−x
2
cos
x+y
2
< 0 , zatem na przedziale [
π
2
, π] funkcja sinus maleje.
Zachowanie sie
,
obu funkcji kosinus i sinus na przedziale [π, 2π] badamy stosuja
,
c
wzory cos(x + π) = cos x cos π − sin x sin π = − cos x oraz sin(x + π) = sin x cos π +
+ cos x sin π = − sin x . To ko´
nczy sprawdzenie prawdziwo´sci w lasno´sci dziesia
,
tej.
Mamy cos
2 π
4
+ sin
2 π
4
= 1 i cos
2 π
4
− sin
2 π
4
= cos
π
2
= 0 . Dodaja
,
c te r´owno´sci
stronami otrzymujemy 2 cos
2 π
4
= 1 , a poniewa˙z cos
π
4
> 0 , wie
,
c cos
π
4
=
√
2
2
.
Sta
,
d sin
π
4
=
p
1 − cos
2 π
4
=
√
2
2
. Pozwala to stwierdzi´c, ˙ze rozumowanie, kt´ore
doprowadzi lo nas do stwierdzenia, ˙ze tg t > t , gdy 0 < t <
√
2 mo˙zna powt´orzy´c
przy zak ladaja
,
c, ˙ze 0 < t <
π
2
, bo istotne tam by lo jedynie to, ˙ze tg
t
2
< 1 , a tak
jest dla wszystkich t ∈ (0,
π
2
) .
W lasno´s´c jedenasta wynika natychmiast z wzor´ow cos(x + π) = − cos x oraz
sin(x + π) = − sin x , kt´ore ju˙z uzyskali´smy.
Udowodnimy teraz w lasno´s´c dwunasta
,
. Niech x
2
+ y
2
= 1 , x, y ∈ R . Oczywi´scie
zachodzi nier´owno´s´c −1 ≤ x ≤ 1 . Niech t = inf{α ∈ [0, π]:
cos α ≥ x} . Wyka˙zemy,
˙ze x = cos t . Za l´o˙zmy, ˙ze tak nie jest. Je˙zeli |t − α| < |x − cos t| , to z w lasno´sci t7.
wynika, ˙ze | cos t − cos α| ≤ |t − α| < |x − cos t| . Wynika sta
,
d, ˙ze liczby cos α
i cos t le˙za
,
po tej samej stronie punktu x . To jednak przeczy definicji liczby t .
Wobec tego x = cos t . Istnieje tylko jedna liczba t spe lniaja
,
ca ten warunek, bo je´sli
0 ≤ t
1
< t
2
≤ π , to cos t
1
> cos t
2
— w lasno´s´c t10.
Je´sli y ≥ 0 , to y =
√
1 − x
2
=
√
1 − cos
2
t =
√
sin
2
t = sin t , bo na przedziale
[0, π] funkcja sinus przyjmuje jedynie nieujemne warto´sci. Je´sli y < 0 , to definiujemy
τ = 2π − t ∈ (π, 2π] . Bez trudu przekonujemy sie
,
, ˙ze x = cos τ i y = sin τ .
Poniewa˙z cos(t + 2π) = cos t i jednocze´snie sin(t + 2π) = sin t , wie
,
c zmiana
argumentu t o 2π daje naste
,
pny argument τ , dla kt´orego spe lnione sa
,
r´owno´sci
x = cos τ i y = sin τ . Mo˙zemy wie
,
c znale´z´c liczbe
,
t w przedziale [0, 2π) . Je´sli y > 0 ,
10
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
to 0 < t < π , je´sli y < 0 , to π < t < 2π . Jedyno´s´c t w tym przedziale wynika
z tego, ˙ze na przedziale [0, π] funkcja kosinus jest ´sci´sle maleja
,
ca, a na przedziale
[π, 2π) — ´sci´sle rosna
,
ca. W ten spos´ob udowodnili´smy w lasno´s´c dwunasta
,
.
Mamy teraz exp(πi) = cos π + i sin π = −1 , zatem
e
πi
+ 1 = 0 .
Otrzymali´smy zatem wz´or, w kt´orym wyste
,
puja
,
pie
,
´c najwa˙zniejszych liczb w mate-
matyce.
Wyka˙zemy jeszcze jedno twierdzenie. Chodzi o to, by przekona´c sie
,
, ˙ze je´sli
t > 0 , to liczba ta mo˙ze by´c uwa˙zana za d lugo´s´c luku okre
,
gu jednostkowego, kt´ory to
luk zaczyna sie
,
w punkcie 1 = e
i·0
i ko´
nczy sie
,
w punkcie e
it
. Te
,
d lugo´s´c luku wypada
najpierw zdefiniowa´c. Rozsa
,
dnie jest przyja
,
´c, ˙ze jest ona r´owna kresowi g´ornemu
d lugo´sci lamanych wpisanych w ten luk.
Twierdzenie 4.17 (o d lugo´sci luku okre
,
gu)
Niech t > 0 . Wtedy
t = sup{
e
it
n
− e
it
n−1
+
e
it
n−1
− e
it
n−2
+ · · · +
e
it
2
− e
it
1
+
e
it
1
− e
it
0
: 0 = t
0
<
< t
1
< t
2
< . . . < t
n−2
< t
n−1
< t
n
= t, n ∈ N} .
Dow´
od. Dla dowolnego j ∈ {0, 1, 2, . . . , n − 1} mamy
e
it
j+1
− e
it
j
=
e
it
j
e
i(t
j+1
−t
j
)
− 1
=
e
i(t
j+1
−t
j
)
− 1
≤ (t
j+1
− t
j
) .
Sta
,
d od razu wynika, ˙ze
e
it
n
− e
it
n−1
+
e
it
n−1
− e
it
n−2
+ · · · +
e
it
2
− e
it
1
+
e
it
1
− e
it
0
≤
≤ (t
n
− t
n−1
) + (t
n−1
− t
n−2
) + · · · + (t
2
− t
1
) + (t
1
− t
0
) = t
n
− t
0
= t − 0 = t .
Wykazali´smy, ˙ze d lugo´s´c lamanej wpisanej w luk nie przekracza liczby t .
Zauwa˙zmy teraz, ˙ze je´sli dodamy do liczb t
0
< t
1
< t
2
< . . . < t
n−2
< t
n−1
< t
n
punkt τ ∈ (t
j
, t
j+1
) , to d lugo´s´c lamanej nie zmniejszy sie
,
, bo
e
it
j+1
− e
it
j
≤
e
it
j+1
− e
iτ
+
e
iτ
− e
it
j
.
Chca
,
c wykaza´c, ˙ze istnieja
,
lamane wpisane w luk, kt´orych d lugo´s´c jest tylko troche
,
mniejsza od t wystarczy zajmowa´c sie
,
jedynie lamanymi odpowiadaja
,
cymi jedynie
„drobnym” podzia lom odcinka [0, t] , tj. takim, ˙ze najwie
,
ksza z liczb t
j+1
− t
j
jest
„ma la”.
Niech ε ∈ (0, 1) . Wtedy (1 − ε)t < t . Wyka˙zemy, ˙ze istnieje taka liczba δ > 0 ,
˙ze je´sli 0 < τ < δ , to
e
iτ
− 1
≥ (1 − ε)τ . Gdyby nie by lo to prawda
,
, to dla ka˙zdej
liczby naturalnej m > 0 istnia laby taka liczba τ
m
∈ (0,
1
m
) , ˙ze
e
iτ
m
−1
< (1−ε)τ
m
.
Zachodzi laby wie
,
c nier´owno´s´c
e
iτ
m
− 1
iτ
m
< 1 − ε ,
11
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
co jednak nie jest mo˙zliwe ze wzgle
,
du na to, ˙ze lim
n→∞
iτ
m
= 0 i wobec tego by loby
1 =
lim
n→∞
e
iτ
m
− 1
iτ
m
= lim
n→∞
e
iτ
m
− 1
iτ
m
≤ 1 − ε .
Za l´o˙zmy teraz, ˙ze 0 = t
0
< t
1
< t
2
< . . . < t
n−2
< t
n−1
< t
n
= t i ˙ze dla
ka˙zdej liczby j ∈ {0, 1, 2, . . . , t
n−2
, t
n−1
} zachodzi nier´owno´s´c t
j+1
− t
j
< δ . Wtedy
e
it
n
− e
it
n−1
+
e
it
n−1
− e
it
n−2
+· · ·+
e
it
2
− e
it
1
+
e
it
1
− e
it
0
≥ (1−ε)(t
n
− t
n−1
) +
+ (1 − ε)(t
n−1
− t
n−2
) + · · · + (1 − ε)(t
2
− t
1
) + (1 − ε)(t
1
− t
0
) = (1 − ε)t .
Wobec dowolno´sci ε ∈ (0, 1) z udowodnionego stwierdzenia teza wynika natych-
miast.
Uwaga 4.18 Udowodnili´smy nieco wie
,
cej ni˙z obiecali´smy pisza
,
c teze
,
ostatniego
twierdzenia. Wykazali´smy nie tylko to, ˙ze liczba t jest kresem g´ornym lamanych
wpisanych w luk, ale te˙z, ˙ze ka˙zda lamana wpisana w ten luk odpowiadaja
,
ca dosta-
tecznie drobnemu podzia lowi odcinka [0, t] przybli˙za d lugo´s´c luku. Gdyby´smy nie
chcieli uzyska´c a˙z tyle, mogliby´smy w ostatniej cze
,
´sci dowodu rozwa˙za´c lamana
,
od-
powiadaja
,
ca
,
podzia lowi odcinka [0, t] na n r´ownych cze
,
´sci i skorzysta´c z tego, ˙ze
lim
n→∞
n ·
e
it/n
− 1
= t , co ju˙z wcze´sniej wykorzystywali´smy.
Lemat 4.19 (o lipschitzowsko´sci funkcji wyk ladniczej)
Je´sli t
1
< t
2
≤ w , to 0 < exp(t
2
) − exp(t
1
) ≤ exp(t
2
)(t
2
− t
1
) ≤ exp(w)(t
2
− t
1
) .
Dow´
od.
exp(t
2
) = exp(t
1
) exp(t
2
− t
1
) ≥ exp(t
1
)(1 + t
2
− t
1
) > exp(t
1
) — lewa
nier´owno´s´c jest udowodniona. Dalej exp(t
2
) − exp(t
1
) = exp(t
2
) 1 − exp(t
1
− t
2
)
≤
exp(t
2
) 1 − (1 + t
1
− t
2
)
= exp(t
2
)(t
2
− t
1
) ≤ exp(w)(t
2
− t
1
) . Wykazali´smy praw-
dziwo´s´c prawej nier´owno´sci.
Definicja 4.20 (warunku Lipschitza)
Funkcja f : A −→ R spe lnia warunek Lipschitza ze sta la
,
L ≥ 0 wtedy i tylko wtedy,
gdy dla dowolnych t
1
, t
2
∈ A ⊆ C zachodzi nier´owno´s´c |f (t
1
) − f (t
1
)| ≤ L|t
1
− t
2
| .
Uwaga 4.21 Wykazali´smy wie
,
c, ˙ze funkcja exp spe lnia warunek Lipschitza na
p´o lprostej (−∞, w] ze sta la
,
exp(w) .
Twierdzenie 4.22 (o zbiorze warto´sci funkcji exp)
1. Dla ka˙zdej liczby rzeczywistej w > 0 istnieje dok ladnie jedna taka liczba rze-
czywista x , ˙ze w = exp(x) .
2. Dla ka˙zdej liczby zespolonej w r´o˙znej od 0 istnieje taka liczba zespolona z , ˙ze
w = exp(z) .
3. Je´sli exp(z
1
) = exp(z
2
) , to istnieje taka liczba ca lkowita n , ˙ze z
2
− z
1
= 2nπi .
12
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
Dow´
od. Mamy exp(w) ≥ 1 + w > w oraz exp(
1
w
) ≥ 1 +
1
w
>
1
w
. Sta
,
d wynika,
˙ze exp(−
1
w
) < w < exp(w) . Zbi´or {t ∈ R:
exp(t) ≤ w} jest niepusty, bo zawiera
liczbe
,
−
1
w
. Jest ograniczony z g´ory liczba
,
w , bo je´sli t ≥ w , to e
t
≥ e
w
> w . Ma
wie
,
c sko´
nczony kres g´orny. Niech x = sup{t ∈ R:
exp(t) ≤ w} . Oczywi´scie x ≤ w .
Udowodnimy, ˙ze w = exp(x) . Za l´o˙zmy, ˙ze w 6= exp(x) . Wtedy je´sli t < w oraz
|t − x| < exp(−w)|w − exp(x)| , to | exp(t) − exp(x)| ≤ exp(w)|t − x| < |w − exp(x)| .
Z tej nier´owno´sci wynika, ˙ze liczby exp(t) i exp(x) le˙za
,
po tej samej stronie liczby w .
Je´sli wie
,
c exp(x) < w i x < t < x + exp(w)(t − x) , to exp(t) < w , wbrew temu, ˙ze
x jest ograniczeniem g´ornym zbioru {t ∈ R:
exp(t) ≤ w} . Je´sli za´s exp(x) > w i
x > t > x − exp(w)(t − x) , to exp(t) > w wbrew temu, ˙ze x jest najmniejszym
ograniczeniem g´ornym zbioru {t ∈ R:
exp(t) ≤ w} . Cze
,
´s´c pierwsza twierdzenia
jest udowodniona.
Je´sli w 6= 0 , to istnieje taka liczba y ∈ R , ˙ze
w
|w|
= exp(iy) — wynika to
z w lasno´sci t12 funkcji kosinus i sinus. Z poprzedniej cze
,
´sci dowodzonego twierdzenia
wynika istnienie takiej liczby x ∈ R , ˙ze |w| = exp(x) . Wobec tego w = |w| ·
w
|w|
=
= exp(x) · exp(iy) = exp(x + iy) , wie
,
c wystarczy przyja
,
´c z = x + yi . Zauwa˙zmy, ˙ze
| exp(z)| = exp(Re(z)) , zatem je´sli exp(z
1
) = exp(z
2
) , to Re(z
1
) = Re(z
2
) . Je´sli
y
1
, y
2
∈ R oraz exp(iy
1
) = exp(iy
2
) , to istnieje taka liczba n ∈ Z , ˙ze y
2
− y
1
= 2nπ
— wynika to z w lasno´sci t12. Dow´od zosta l zako´
nczony.
Kilka zada´
n
4. 01 Udowodni´c, ˙ze e = lim
n→∞
(1 +
1
1!
+
1
2!
+
1
3!
+ · · · + +
1
n!
) .
4. 02 Udowodni´c, ˙ze e 6∈ Q .
4. 03 Udowodni´c, ˙ze cos 3α = 4 cos
3
α − 3 cos α i sin 3α = 3 sin α − 4 sin
3
α .
4. 04 Wykaza´c, ˙ze dla dowolnej liczby naturalnej n > 0 istnieje taki wielomian w
stopnia 2n + 1 , ˙ze r´owno´s´c sin(2n + 1)α = w(sin α) zachodzi dla ka˙zdej liczby
α ∈ R . Znale´z´c wsp´o lczynnik kieruja
,
cy tego wielomianu (ten przy 2n + 1 –ej
pote
,
dze zmiennej).
4. 05 Wykaza´c, ˙ze dla ka˙zdej liczby zespolonej z 6= 0 i ka˙zdej liczby naturalnej n
istnieje dok ladnie n parami r´o˙znych liczb z
1
, z
2
, . . . , z
n
takich, ˙ze z
n
j
= z dla
j = 1, 2, . . . , n .
4. 06 Za l´o˙zmy, ˙ze cos α =
1
3
. Wykaza´c, ˙ze
α
π
/
∈ Q .
4. 07 Znale´z´c pierwiastki (wszystkie cztery) wielomianu z
4
+ z
3
− z
2
+ z + 1 i wykaza´c,
˙ze ˙zaden z nich nie jest pierwiastkiem z jedno´sci (˙zadnego stopnia).
4. 08 Udowodni´c, ˙ze dla ka˙zdej liczby zespolonej w istnieje taka liczba zespolona z ,
˙ze w = sin z .
13
Funkcja wyk ladnicza, kosinus i sinus
Micha l Krych
4. 09 Znale´z´c wz´or na sume
,
n
0
+
n
3
+
n
6
+ . . . — sumujemy dop´oki ma to sens.
4. 10 Udowodni´c, ˙ze je´sli a, b, c, d ∈ C oraz ad 6= bc i h(z) =
az+b
cz+d
dla z 6= −
d
c
, prze-
kszta lcenie H oznacza przeniesienie h na sfere
,
za pomoca
,
rzutu stereograficz-
nego, to H przekszta lca okre
,
gi na okre
,
gi. Oznacza to, ˙ze je´sli ϕ jest rzutem ste-
reograficznym „z bieguna p´o lnocnego” na p laszczyzne
,
, to H(p) = ϕ
−1
◦ h ◦ ϕ(p)
dla ka˙zdego p z wyja
,
tkiem bieguna p´o lnocnego (wtedy ϕ(p) nie jest w og´ole
okre´slone) oraz z wyja
,
tkiem punktu ϕ
−1
(−
d
c
) , definiujemy H ϕ
−1
(−
d
c
)
= P
N
,
gdzie P
N
oznacza biegun p´o lnocny, za´s H(P
N
) = P
N
, gdy c = 0 (i nie mo˙zna
m´owi´c o liczbie −
d
c
) oraz H(P
N
) = ϕ
−1
(
a
c
) , gdy c 6= 0 .
14