TERMODYNAMIKA
wszystkie paranoiczne wyprowadzenia
MIKROSTAN – dokładny opis położenia i pędu każdej cząstki układu w określonej chwili czasu
PRZESTRZEŃ FAZOWA – wszystkie mikrostany
Przestrzeń fazowa jest nieciągła, kwantyzacja wynika z zasady nieoznaczoności Heisenberga:
≥
∆
⋅
∆
≥
∆
⋅
∆
≥
∆
⋅
∆
h
p
r
h
p
r
h
p
r
z
z
y
y
x
x
1
,
1
,
1
,
1
,
1
,
1
,
3
h
- stała Plancka: max. dokładność, wymiar komórki w przestrzeni fazowej
W układzie makroskopowym o N cząstkach:
N
h
3
.
h
ma wymiar energii.
Wielkość obserwowana – średnia z zaobserwowanych stanów w pewnym czasie obserwacji
N
G
G
N
i
i
obs
∑
=
;
Ś
REDNIA STATYSTYCZNA :
∑
=
υ
υ
υ
G
p
G
- suma po wszystkich mikrostanach
υ
p - prawdopodobieństwo, że układ wystąpi w danym mikrostanie
przykładowa wielkość: energia
∑
=
υ
υ
υ
E
p
E
Znaczenie mają te stany, których prawdopodobieństwo jest największe.
_____________________________________________________________________
Możliwe warunki:
1. UKŁAD IZOLOWANY – nie ma wymiany energii ani cząstek z otoczeniem
ZESPÓŁ MIKROKANONICZNY - opis statystyczny takiego układu
const
V
N
E
=
,
,
;
Ω
=
=
1
const
p
υ
,
Ω
- liczba wszystkich możliwych stanów
2. UKŁAD NIEIZOLOWANY – dopuszczalne są fluktuacje energii, ale nie materii
ZESPÓŁ KANONICZNY:
const
V
N
=
,
;
wszechś
ukł
otoczenia
E
const
E
E
=
=
+
;
(
)
(
)
otoczenia
ukł
E
p
E
p
=
υ
υ
,
(prawdopodobieństwo znalezienia się układu w stanie o danej energii jest równe prawdopodobieństwu
znalezienia się otoczenia w stanie o energii odpowiadającej energii reszty wszechświata, gdy układ
jest w danym stanie)
3. UKŁAD OTWARTY – tylko objętość pozostaje stała, energia i materia fluktuują
ZESPÓŁ WIELKI KANONICZNY:
const
V
=
;
(
)
υ
υ
υ
N
E
p
,
________________________________________________________________________

ERGODYCZNOŚĆ UKŁADU – gdy wielkość obserwowana jest tożsama ze średnią statystyczną
G
G
obs
=
Po odpowiednio długim czasie układ przejdzie przez wszystkie mikrostany, i wówczas
υ
G
G
t
=
Przykład układu nieergodycznego: szkło – przez stulecia ulega powolnej krystalizacji
___________________________________________________________________________
ENTROPIA – definicja statystyczna:
Ω
=
ln
k
S
Stąd wynika termodynamiczna definicja temperatury:
∂
Ω
∂
=
∂
∂
=
E
k
E
S
T
ln
1
;
∂
Ω
∂
=
=
E
kT
ln
1
β
W zespole mikrokanonicznym mamy po prostu
Ω
=
1
υ
p
W zespole kanonicznym:
( )
(
)
υ
υ
E
E
p
E
p
otoczenia
ukł
−
=
,
gdzie E - całkowita energia wszechświata
Prawdopodobieństwo, że układ wystąpi w stanie o danej energii jest proporcjonalne do liczby stanów
o tej energii:
( )
( )
υ
υ
E
E
p
ukł
Ω
~
;
(
)
(
)
υ
υ
E
E
E
E
p
otoczenia
−
Ω
−
~
( )
(
)
υ
υ
E
E
p
E
p
otoczenia
ukł
−
=
→
( )
(
)
(
)
υ
υ
υ
E
E
ukł
e
E
E
E
p
−
Ω
=
−
Ω
ln
~
(
)
( )
( )
...
ln
ln
ln
+
∂
Ω
∂
−
Ω
=
−
Ω
E
E
E
E
E
E
υ
υ
, jednak
( )
β
=
∂
Ω
∂
E
E
ln
stąd:
β
υ
υ
E
E
ukł
e
p
−
Ω
)
(
ln
,
~
,
const
E
=
Ω
)
(
- liczba wszystkich mikrostanów wszechświata
a więc:
υ
β
υ
E
ukł
e
p
−
~
,
Normalizujemy sumę wszystkich prawdopodobieństw do 1:
1
=
∑
υ
P
∑
−
−
=
υ
β
β
υ
υ
υ
E
E
e
e
P
→ w mianowniku mamy sumę po wszystkich mikrostanach
Jest to SUMA STANÓW:
∑
−
=
υ
β
υ
E
e
Q
,
a jeśli występuje degeneracja:
∑
−
=
υ
β
υ
υ
E
e
g
Q
Jest ona potrzebna, aby policzyć średnią energię układu:
Q
E
e
E
e
e
E
P
E
E
E
E
∑
∑
∑
∑
−
−
−
=
=
=
υ
υ
β
υ
υ
υ
β
β
υ
υ
υ
υ
υ
υ
(
)
∑
∑
⋅
−
=
−
⋅
=
∂
∂
−
−
υ
υ
β
υ
υ
β
υ
υ
β
E
e
E
e
Q
E
E
;
stąd:
V
N
Q
Q
Q
E
,
ln
∂
∂
=
∂
∂
−
=
β
β
________________________________________________________________________________
Fluktuacje energii są przypadkowe, chwilowe, niekierunkowe. To one rządzą wszechświatem.
Ś
redni kwadrat fluktuacji energii:
( )
(
)
=
+
−
=
+
−
=
−
=
2
2
2
2
2
2
2
2
E
E
E
E
E
E
E
E
E
E
E
def
δ
2
2
2
2
2
2
2
2
2
E
E
E
E
E
E
E
E
E
−
=
+
−
=
+
−
=
(średnia kwadratu minus kwadrat średniej)
V
N
Q
E
,
ln
∂
∂
=
β
∑
∑
∑
∑
−
−
−
⋅
=
⋅
=
⋅
=
υ
β
υ
υ
υ
β
β
υ
υ
υ
υ
υ
υ
υ
E
E
E
e
E
Q
e
e
E
P
E
E
2
2
2
2
1
∑
−
−
=
∂
∂
υ
β
υ
υ
β
E
V
N
e
E
Q
,
∑
−
+
=
∂
∂
υ
β
υ
υ
β
E
V
N
e
E
Q
2
,
2
2
Stąd:
( )
=
⋅
−
⋅
=
−
=
∑
∑
−
−
2
2
2
2
2
Q
e
E
Q
e
E
E
E
E
E
E
υ
β
υ
υ
β
υ
υ
υ
δ
2
,
2
,
2
2
2
,
2
,
2
2
1
1
1
1
V
N
V
N
V
N
V
N
Q
Q
Q
Q
Q
Q
Q
Q
∂
∂
−
∂
∂
=
∂
∂
−
−
∂
∂
=
β
β
β
β
Jak to uprościć?
Po pierwsze:
(
)
V
N
V
N
V
N
V
N
E
E
Q
Q
,
,
,
,
2
2
ln
ln
∂
∂
−
=
−
∂
∂
=
∂
∂
∂
∂
=
∂
∂
β
β
β
β
β
Po drugie:
=
∂
∂
∂
∂
=
∂
∂
∂
∂
=
∂
∂
V
N
V
N
V
N
Q
Q
Q
Q
,
,
,
2
2
1
ln
ln
β
β
β
β
β
( )
2
,
2
2
2
1
1
E
Q
Q
Q
Q
Q
V
N
δ
β
β
β
=
∂
∂
+
∂
∂
∂
∂
−
=
A więc wychodzi na to, że:
( )
V
N
V
N
E
Q
E
,
,
2
2
2
ln
∂
∂
−
=
∂
∂
=
β
β
δ
Mamy więc związek fluktuacji z temperaturą:
( )
V
V
V
N
V
N
c
kT
c
k
T
k
T
E
k
T
T
E
E
E
2
2
2
2
,
,
2
1
=
=
∂
∂
+
=
∂
∂
∂
∂
−
=
∂
∂
−
=
β
β
β
δ
Uzyskujemy zależność pomiędzy fluktuacjami a pojemnością cieplną – im większa pojemność, tym
większe fluktuacje są możliwe.

Pojemność cieplna a przemiany fazowe:
PRZEMIANA FAZOWA II RODZAJU – fluktuacje energii dążą do nieskończoności, następuje
reorganizacja układu
PRZEMIANA FAZOWA I RODZAJU – również występuje skok fluktuacji, ale jest on skończony
V
N
V
T
E
c
,
∂
∂
=
→
dT
c
E
d
V
=
POJEMNOŚĆ CIEPLNA jest współczynnikiem proporcjonalności, określającym podatność układu na
zmiany temperatury.
________________________________________________________________________________
SUMA STANÓW DLA GAZU DOSKONAŁEGO:
STANY TRANSLACYJNE
Najprostsza cząstka – 1 atom (np. He): występują 3 translacyjne stopnie swobody.
Energia pojedyńczej cząstki:
m
p
p
p
E
E
z
y
x
kin
2
2
2
2
+
+
=
=
Suma stanów dla jednej cząstki: q (tzw. JEDNOCZĄSTKOWA SUMA STANÓW)
Suma stanów dla N cząstek (gaz doskonały):
- jeśli cząstki są rozróżnialne:
N
q
q
q
q
Q
⋅⋅
⋅
=
3
2
1
- jeśli cząstki są nierozróżnialne:
!
N
q
Q
N
=
W drugim przypadku zadanie sprowadza się do policzenia q :
(
)
∫ ∫ ∫
∑
+∞
∞
−
+∞
∞
−
+∞
∞
−
+
+
−
−
=
=
z
y
x
p
p
p
m
E
dp
dp
dp
e
e
q
z
y
x
2
2
2
2
β
υ
β
υ
(całki – bo pędy nie są skwantowane)
Po wprowadzeniu ograniczenia przestrzennego oraz nieoznaczoności:
∫
∫
∫
∫ ∫ ∫
+∞
∞
−
+∞
∞
−
+∞
∞
−
−
−
−
=
z
p
m
y
p
m
x
p
m
a
b
c
dp
e
dp
e
dp
e
dz
dy
dx
h
q
z
y
x
2
2
2
2
2
2
0
0
0
3
1
β
β
β
Korzystamy ze wzoru:
a
dx
e
ax
π
=
∫
+∞
∞
−
−
2
Stąd:
V
h
mkT
V
h
m
m
m
m
c
b
a
h
q
⋅
=
⋅
⋅
=
⋅
⋅
⋅
⋅
⋅
⋅
=
2
3
2
3
2
3
3
2
1
2
2
2
2
1
π
β
π
β
π
β
π
β
π
- jednocząstkowa suma stanów translacyjnych
Dla N cząstek:
!
1
2
)
(
2
3
2
N
V
h
mkT
N
Q
N
⋅
⋅
=
π
- jest to wzór prawdziwy dla cząsteczek bez struktury wewnętrznej
Cząsteczka 2-atomowa ma jeszcze oscylacyjne i rotacyjne stopnie swobody: może drgać i wirować.
Jeśli uwzględni się dodatkowo stany elektronowe:
el
rot
osc
tr
q
q
q
q
q
⋅
⋅
⋅
=

_____________________________________________________________________________
ROTACJA:
Stany rotacyjne wymagają spojrzenia kwantowego:
)
1
(
2
2
+
=
j
j
I
E
j
h
Występuje degeneracja, którą trzeba uwzględnić:
1
2
+
=
j
g
j
∑
∑
+
−
−
+
=
=
j
j
j
I
j
E
rot
e
j
e
g
q
j
)
1
(
2
2
)
1
2
(
h
β
β
υ
1. Przybliżenie dla niskich temperatur:
0
→
T
K – poziomy rotacyjne są daleko od siebie
...
)
1
1
2
(
)
1
0
2
(
)
1
1
(
1
2
)
1
0
(
0
2
2
2
+
+
⋅
+
+
⋅
=
+
⋅
⋅
−
+
⋅
⋅
−
I
I
rot
e
e
q
h
h
β
β
I
e
2
3
1
h
β
−
+
≈
- wystarczy uwzględnić tylko dwa człony rozwinięcia, następne szybko dążą do zera
2. Przybliżenie dla wysokich temperatur:
∞
→
T
– poziomy leżą bardzo blisko, zastępujemy
sumowanie całkowaniem:
=
+
=
∫
∞
+
−
0
)
1
(
2
2
)
1
2
(
dj
e
j
q
j
j
I
rot
h
β
dx
dj
j
x
j
j
=
+
=
+
)
1
2
(
)
1
(
:
ie
podstawien
=
=
∫
∞ −
0
2
2
dx
e
x
I
h
β
2
0
2
2
2
2
0
2
2
2
2
2
lim
2
2
2
2
h
h
h
h
h
h
h
β
β
β
β
β
β
β
I
e
I
e
I
e
I
I
x
I
x
x
I
=
⋅
+
⋅
−
=
⋅
−
=
⋅
−
−
∞
→
∞
−
Niestety, nie ma prostej metody policzenia
rot
q
dla temperatury pokojowej.
______________________________________________________________________________
OSCYLACJA
ω
h
+
=
2
1
n
E
n
...
2
5
2
3
2
1
2
1
+
+
+
=
=
=
−
−
−
+
−
−
∑
∑
ω
β
ω
β
ω
β
ω
β
β
h
h
h
h
e
e
e
e
e
q
n
n
n
E
osc
n
To nic innego, jak tylko szereg geometryczny:
q
1
0
−
=
a
S
( q < 1 )
ω
β
h
−
=
=
=
=
e
a
a
a
a
...
q
1
2
0
1
ω
β
ω
β
ω
β
ω
β
h
h
h
h
2
1
2
1
2
1
0
1
1
q
1
−
−
−
−
=
−
=
−
=
=
e
e
e
e
a
S
q
osc
_______________________________________________________________________________
POZIOMY ELEKTRONOWE
- leżą bardzo daleko od siebie, stąd po prostu
υ
υ
υ
P
E
q
el
∑
=
________________________________________________________________________________
FUNKCJE TERMODYNAMICZNE
FORMUŁA GIBBSA NA ENTROPIĘ:
∑
−
=
υ
υ
υ
P
P
k
S
ln
1. Zespół mikrokanoniczny – brak fluktuacji, stałe prawdopodobieństwo – stany są równocenne:
Ω
=
1
υ
p
;
Ω
+
=
Ω
Ω
Ω
−
=
Ω
Ω
−
=
∑
Ω
=
ln
1
ln
1
1
ln
1
1
k
k
k
S
υ
Przykład: układ dwustanowy – każda cząstka może być w jednym z dwóch stanów
(
)
!
!
!
n
N
n
N
n
N
−
=
=
Ω
2. Zespół kanoniczny:
prawdopodobieństwo zależy od energii mikrostanu:
Q
e
P
E
υ
β
υ
−
=
(
)
∑
∑
∑
∑
=
+
=
−
−
=
−
=
−
−
υ
υ
υ
υ
υ
υ
υ
β
υ
υ
β
υ
β
υ
υ
Q
P
k
E
P
k
Q
P
e
P
k
Q
e
P
k
S
E
E
ln
ln
ln
ln
Q
k
Q
T
P
Q
k
E
T
V
N
ln
ln
1
ln
1
,
+
∂
∂
−
=
⋅
+
=
∑
β
υ
υ
Mamy więc wzór na entropię jako funkcję sumy stanów:
V
N
Q
T
Q
k
S
,
ln
1
ln
∂
∂
−
=
β
ENERGIA SWOBODNA – część energii wewnętrznej, którą można manipulować
TS
U
F
−
=
; TS - część entropowa, związana z mikroskopową budową układu (nie do ruszenia)
Q
Q
kT
E
T
Q
k
T
E
TS
E
F
ln
1
ln
1
ln
β
−
=
−
=
−
−
=
−
=
- ten wzór pokazuje, czym tak naprawdę jest suma stanów
Parametry makroskopowe w funkcji sumy stanów: CIŚNIENIE
(
)
T
T
T
V
Q
V
Q
V
F
p
∂
∂
=
∂
−
∂
−
=
∂
∂
−
=
−
ln
1
ln
1
β
β
ENTALPIA SWOBODNA:
pV
F
G
+
=
ENTALPIA:
pV
E
H
+
=
3. Zespół wielki kanoniczny – stała tylko objętość
W tym wypadku sumę stanów oznaczamy wielką literą sigma (nie mylić ze znakiem sumowania):
(
)
∑
−
−
=
Σ
υ
βµ
β
υ
υ
N
E
e
prawdopodobieństwo:
(
)
(
)
∑
−
−
−
−
=
υ
βµ
β
βµ
β
υ
υ
υ
υ
υ
N
E
N
E
e
e
P
formuła Gibbsa:
(
)
(
)
(
)
∑
∑
∑
∑
=
Σ
−
=
−
=
−
=
−
−
−
−
−
−
υ
βµ
β
υ
υ
υ
βµ
β
βµ
β
υ
υ
υ
υ
υ
υ
υ
υ
υ
υ
N
E
N
E
N
E
e
P
k
e
e
P
k
P
P
k
S
ln
ln
ln
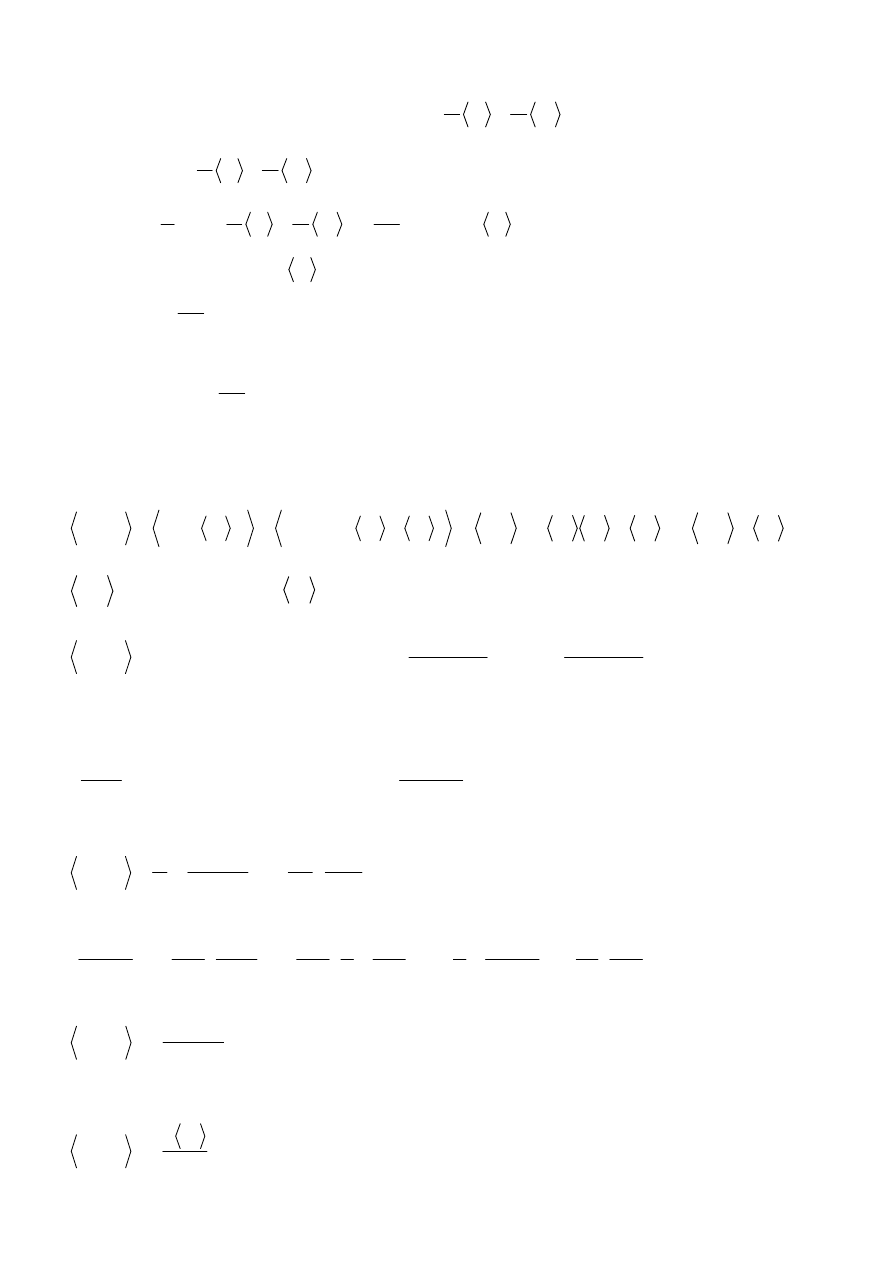
(
)
(
)
(
)
(
)
(
)
∑
∑
=
Σ
−
−
−
−
=
Σ
−
−
=
−
−
υ
υ
υ
υ
υ
υ
υ
βµ
β
υ
βµ
β
υ
υ
ln
ln
ln
P
N
E
P
k
P
e
P
k
N
E
∑
∑
∑
∑
⋅
Σ
+
−
=
Σ
+
−
+
=
υ
υ
υ
υ
υ
υ
υ
υ
υ
υ
µ
β
µ
β
P
k
N
T
E
T
P
k
N
P
k
E
P
k
ln
1
ln
Ostatecznie:
Σ
+
−
=
ln
1
k
N
T
E
T
S
µ
stąd:
(
)
E
G
TS
kT
N
T
E
T
S
k
−
+
=
+
−
⋅
=
Σ
1
1
1
ln
µ
jednocześnie mamy, że:
F
E
TS
−
=
−
a więc:
(
)
F
G
kT
−
=
Σ
1
ln
z kolei
pV
F
G
+
=
co nam daje:
pV
pV
kT
β
=
=
Σ
1
ln
Znając wielką kanoniczną sumę stanów możemy określić wszystkie funkcje termodynamiczne.
_____________________________________________________________________________
W układzie wielkim kanonicznym możemy mówić o średnim kwadracie fluktuacji liczby cząstek:
( )
(
)
=
+
−
=
−
=
2
2
2
2
2
N
N
N
N
N
N
N
def
δ
2
2
2
2
2
N
N
N
N
N
N
−
=
+
−
Z definicji:
∑
=
υ
υ
υ
P
N
N
2
2
∑
=
υ
υ
υ
P
N
N
( )
2
2
2
2
2
Σ
−
Σ
=
−
=
∑
∑
∑
∑
+
−
+
−
υ
βµ
β
υ
υ
βµ
β
υ
υ
υ
υ
υ
υ
υ
υ
υ
υ
υ
δ
N
E
N
E
e
N
e
N
P
N
P
N
N
∑
+
−
=
Σ
υ
βµ
β
υ
υ
N
E
e
∑
+
−
=
∂
Σ
∂
υ
βµ
β
υ
υ
υ
βµ
N
E
V
e
N
( )
∑
+
−
=
∂
Σ
∂
υ
βµ
β
υ
υ
υ
βµ
N
E
V
e
N
2
2
2
stąd:
( )
( )
2
2
2
2
2
1
1
V
V
N
∂
Σ
∂
Σ
−
∂
Σ
∂
⋅
Σ
=
βµ
βµ
δ
Jednocześnie mamy:
( )
( )
2
2
2
2
2
2
1
1
1
ln
ln
V
V
V
V
V
∂
Σ
∂
Σ
−
∂
Σ
∂
⋅
Σ
=
∂
Σ
∂
⋅
Σ
∂
∂
=
∂
Σ
∂
∂
∂
=
∂
Σ
∂
βµ
βµ
βµ
βµ
βµ
βµ
βµ
i uzyskujemy:
( )
( )
V
N
∂
Σ
∂
=
2
2
2
ln
βµ
δ
- kolejny przypadek ogólnej prawidłowości:
Ś
REDNI KWADRAT FLUKTUACJI DANEJ WIELKOŚCI JEST PROPORCJONALNY DO
POCHODNEJ ZE ŚREDNIEJ TEJ WIELKOŚCI PO WIELKOŚCI, KTÓRA SIĘ Z NIĄ SPRZĘGA
( )
∂
∂
ξ
δ
X
X
~
2

_________________________________________________________
Ś
redni kwadrat fluktuacji – wprost:
Rozpatrujemy gaz, na który nakładamy siatkę. Jeśli komórka jest zapełniona, przypisujemy jej 1, jeśli
pusta 0. W jednej komórce może być co najwyżej jedna cząstka.
=
0
1
i
n
jeden mikrostan:
(
)
m
n
n
n
n
,...,
,
,
3
2
1
Całkowitą liczbę cząstek można określić na podstawie jednego mikrostanu:
∑
=
i
i
n
N
Stąd:
( )
(
)
∑∑
=
=
−
=
−
=
m
i
m
j
j
i
j
i
n
n
n
n
N
N
N
1
1
2
2
2
δ
Pierwsze przybliżenie: brak oddziaływań:
j
i
j
i
j
i
ij
j
i
j
i
n
n
P
P
n
n
P
n
n
n
n
∑
∑
=
=
=
υ
υ
( )
=
−
+
−
=
∑ ∑
=
=
=
≠
m
i
i
j
j
i
j
i
m
j
i
j
j
i
j
i
n
n
n
n
n
n
n
n
N
1
1
2
'
δ
∑
∑ ∑
=
=
=
−
=
−
+
−
=
m
i
i
i
m
i
i
i
m
j
j
i
j
i
n
n
n
n
n
n
n
n
1
2
2
1
2
2
1
Dzięki temu, że
=
0
1
i
n
, mamy:
i
i
n
n
=
2
, ponieważ
=
0
1
2
i
n
W dodatku wszystkie komórki są identyczne:
m
n
n
n
=
=
=
...
2
1
W związku z tym:
( )
(
)
(
)
i
i
i
i
m
i
i
i
n
n
m
n
n
m
n
n
N
−
=
−
=
−
=
∑
=
1
2
1
2
2
2
δ
Ponieważ mamy do czynienia z gazem:
1
1
<<
n
(obsadzenie komórek jest niewielkie)
wówczas:
1
1
1
≈
−
n
( )
N
n
m
N
=
≈
1
2
δ
- średni kwadrat fluktuacji liczby cząstek jest proporcjonalny do średniej liczby cząstek
Z kolei sama, pojedyńcza fluktuacja:
( )
N
N
N
=
=
∆
2
δ
___________________________________________________________
Układ dość gęsty, np. roztwór, w którym zachodzą reakcje izomeryzacji
B
A
↔
Komórka może być obsadzona przez cząsteczkę A lub B.
Jeśli:
=
A
gdy
,
0
B
gdy
,
1
i
n
, to mamy ten sam model, co wcześniej:
( )
(
)
1
1
2
1
n
n
m
N
−
=
δ
jednak przybliżenie
1
1
1
≈
−
n
jest fałszywe, nie ma powodu sądzić, że B jest dużo mniej niż A.
B
x
n
≈
1
A
B
x
x
n
=
−
≈
−
1
1
1
stąd:
( )
B
A
x
mx
N
=
2
δ
Wcześniej doszliśmy do tego, że
( )
( )
V
V
N
N
∂
Σ
∂
∂
∂
=
∂
Σ
∂
=
=
βµ
βµ
βµ
δ
ln
ln
2
2
2
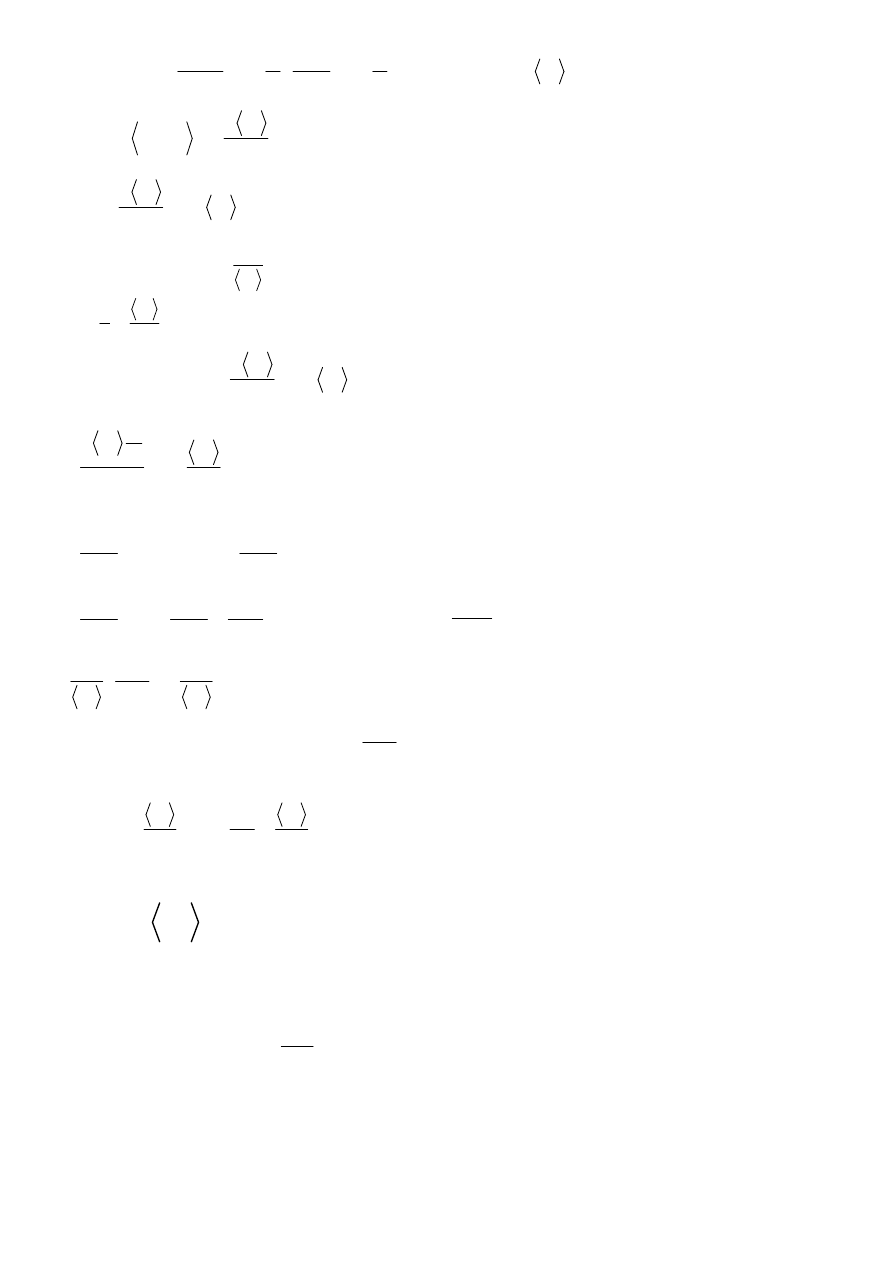
jednocześnie
N
e
N
N
E
V
V
=
Σ
=
∂
Σ
∂
Σ
=
∂
Σ
∂
∑
+
−
υ
βµ
β
υ
υ
υ
βµ
βµ
1
1
ln
co daje:
( )
V
N
N
∂
∂
=
βµ
δ
2
stąd:
N
N
V
=
∂
∂
βµ
Objętość molowa:
N
V
v
=
- odwrotność tego to coś w rodzaju gęstości, ale o wymiarze stężenia:
V
N
v
=
=
1
ξ
Dzielimy wyrażenie
N
N
V
=
∂
∂
βµ
przez V :
V
N
V
N
V
=
∂
∂
βµ
1
ξ
βµ
ξ
=
∂
∂
V
→
1
−
=
∂
∂
ξ
ξ
βµ
V
1
−
=
∂
∂
∂
∂
=
∂
∂
ξ
ξ
β
β
βµ
ξ
βµ
p
p
V
jednak
v
p
=
∂
∂
β
βµ
N
V
p
N
V
=
∂
∂
ξ
β
Dostajemy śmiesznie proste równanie:
1
=
∂
∂
ξ
β
p
ξ
β
d
p
d
=
V
N
p
=
=
ξ
β
V
N
kT
p
=
Z formuły fluktuacyjnej dostajemy RÓWNANIE CLAPEYRONA:
kT
N
pV
=
;
A
kN
R
=
→
nRT
pV
=
______________________________________________________________________
PODATNOŚĆ – współczynnik proporcjonalności pomiędzy zaburzeniem a odpowiedzią układu
ξ
χ
d
dX
=
warunki
ustalone
∂
∂
=
ξ
χ
X
Przyczyna i skutek (zaburzenie i odpowiedź) to wielkości sprzężone.
Zaburzenie powoduje obniżenie energii swobodnej, która determinuje równowagę termodynamiczną
(równowagę mechaniczną określa energia wewnętrzna przy ustalonej entropii).
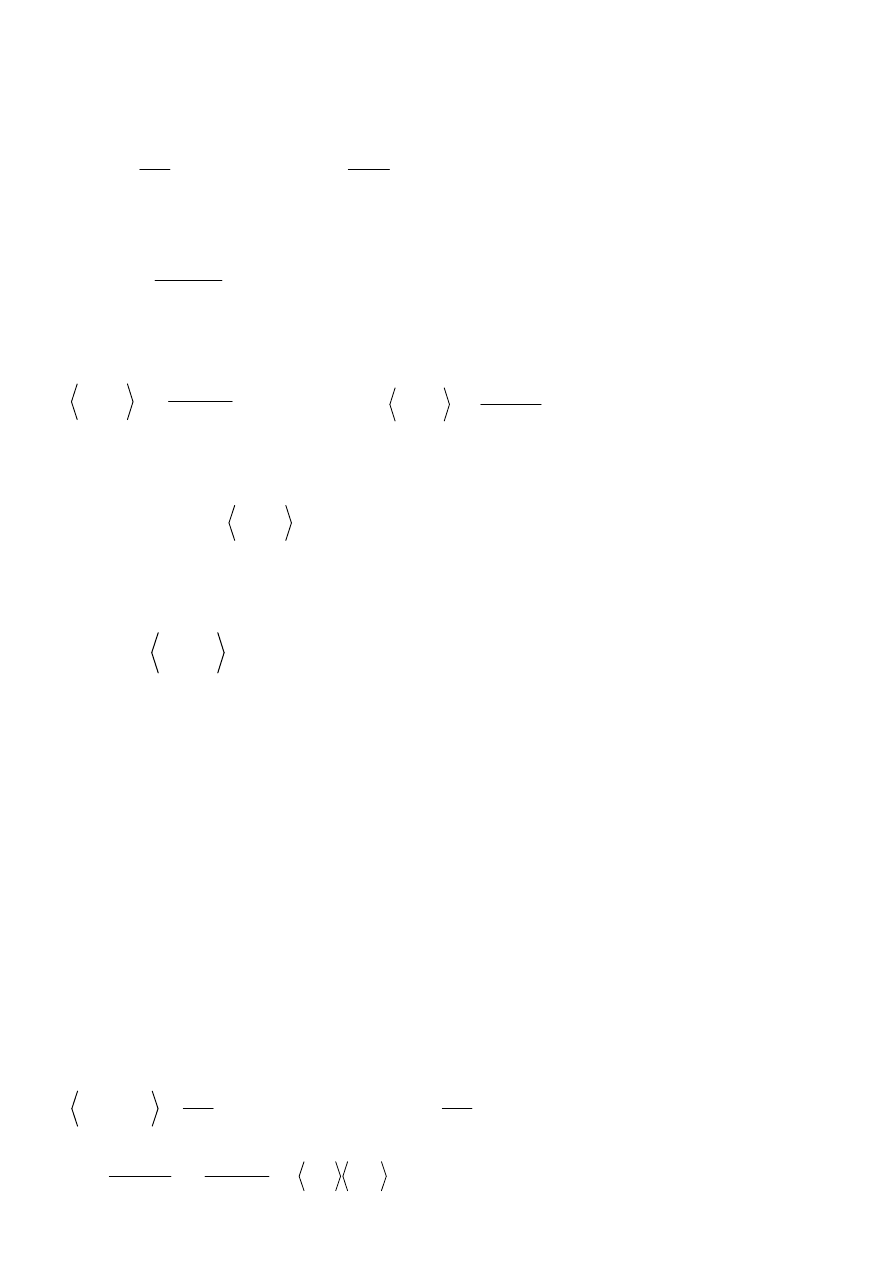
warunek równowagi termodynamicznej:
( )
0
,
=
V
T
F
δ
warunek równowagi mechanicznej:
( )
0
=
S
U
δ
Stąd:
warunki
ustalone
∂
∂
−
=
ξ
F
X
;
warunki
ustalone
2
2
∂
∂
−
=
ξ
χ
F
- podstawowa formuła podatności
Korzystamy ze wzoru:
Q
F
ln
1
−
−
=
β
warunki
ustalone
2
2
1
ln
∂
∂
=
−
ξ
β
χ
Q
Całkowita analogia:
ś
redni kwadrat fluktuacji energii:
ś
redni kwadrat fluktuacji liczby cząstek:
( )
V
N
Q
E
,
2
2
2
ln
∂
∂
=
β
δ
( )
( )
V
N
∂
Σ
∂
=
2
2
2
ln
βµ
δ
(parametr, który sprzęga się z liczbą cząstek –
- potencjał chemiczny – ilość energii wynikająca
z samej obecności cząstki)
Wynika stąd, że
( )
2
~
X
δ
χ
|
|
wielkość
fluktuacja
intensywna
wielkości ekstensywnej
( )
2
1
X
δ
β
χ
−
=
Podatność decyduje o stabilności układu. Jeśli
∞
→
χ
, mamy katastrofę (nieskończenie małe
zaburzenie powoduje nieskończenie dużą odpowiedź). Jest to sytuacja występująca w punktach
krytycznych układu, tam, gdzie następują przemiany fazowe. Zmiany podatności wynikają ze zmiany
wewnętrznej natury materii układu pod wpływem czynników zewnętrznych.
Jeśli zaburzenia są duże, mamy nieliniową odpowiedź:
...
3
)
3
(
2
)
2
(
+
+
+
=
ξ
χ
ξ
χ
χξ
X
___________________________________________________________________________
UKŁADY IDEALNE – drastyczne przybliżenie zakładające, że wszystkie cząstki są niezależne
W układach idealnych możliwa jest FAKTORYZACJA ENERGII – rozłożenie energii na sumę
składników zależnych od określonych parametrów:
)
2
(
)
1
(
)
,
(
m
n
E
E
m
n
E
+
=
υ
Wówczas suma stanów = iloczyn sum stanów podukładów powstałych po rozdzieleniu:
(
)
)
2
(
)
1
(
)
2
(
)
1
(
)
2
(
)
1
(
Q
Q
e
e
e
e
Q
m
n
m
n
E
E
E
E
E
⋅
=
⋅
=
=
=
∑
∑
∑
∑
−
−
+
−
−
υ
β
υ
β
υ
β
υ
β
υ
=
⋅
=
=
∑
∑
∑
−
−
−
−
υ
β
υ
β
β
β
)
2
(
)
1
(
)
2
(
)
1
(
)
2
(
)
1
(
2
,
)
2
(
)
1
(
2
)
2
(
)
1
(
1
1
m
n
m
n
E
m
E
n
m
n
E
E
m
n
e
E
e
E
Q
e
e
E
E
Q
E
E
)
2
(
)
1
(
)
2
(
)
1
(
ln
ln
E
E
Q
Q
=
∂
∂
−
∂
∂
−
=
β
β
- energie podukładów są nieskorelowane

Dla N nieskorelowanych stopni swobody:
)
(
)
2
(
)
1
(
)
(
N
Q
Q
Q
N
Q
⋅⋅
⋅
=
Gdy mamy N identycznych nieskorelowanych stopni swobody:
( )
N
Q
N
Q
)
1
(
)
(
=
Czyli wystarczy policzyć
)
1
(
Q
(jednocząstkowa suma stanów, często zapisywana jako q ).
Jeśli nie rozróżniamy cząstek:
N
q
N
N
Q
!
1
)
(
=
LICZBA OBSADZEŃ – ilość cząstek na danym poziomie energetycznym, opisuje dany mikrostan
Gdy mamy N nierozróżnialnych cząstek, liczba stanów jest determinowana liczbą obsadzeń.
W układach kwantowych:
2
2
1
1
φ
φ
ψ
υ
n
n
⋅
=
2
1
, n
n
- liczby obsadzeń (liczby cząstek w stanach o funkcjach falowych
2
1
,
φ
φ
)
Liczby obsadzeń są zmiennymi kolektywnymi – zależą od siebie i od całkowitej liczby cząstek.
Dany mikrostan jest opisany zbiorem liczb obsadzeń:
(
)
β
α
υ
n
n ,
;
∑
=
j
j
n
N
υ
j
n - liczba obsadzeń j-tego poziomu
∑
=
j
j
j
E
n
E
υ
j
E - energia j-tego poziomu
FERMIONY – na jednym poziomie może być tylko jedna cząstka
BOZONY – na jednym poziomie może być nieskończenie wiele cząstek
_______________________________________________________________
TERMODYNAMIKA POLA ELEKTROMAGNETYCZNEGO:
GAZ FOTONÓW
FOTON – kwant promieniowania EM, który można opisać tak jak oscylator harmoniczny, z tą
różnicą, że dla poziomu zerowego
0
≠
E
OSCYLATOR HARMONICZNY (klasycznie):
ω
h
n
E
n
=
(
...
2
,
1
,
0
=
n
)
∑
−
=
υ
β
υ
E
e
Q
∑
=
j
j
j
n
E
ε
υ
∑
∞
+
+
−
=
,..
,
...)
(
2
1
2
2
1
1
n
n
n
n
e
Q
ε
ε
β
- sumowanie od 0 do
∞
j
j
k
ω
ε
=
j
ω
- częstość kwantu promieniowania
∏
∏
∑
−
=
=
−
∞
−
j
j
n
n
n
j
j
j
e
e
Q
βε
ε
β
1
1
,..
,
2
1
↑
szereg geometryczny
Ś
rednia liczba obsadzeń każdego z poziomów:
(
)
(
)
1
,..
,
...)
(
,..
,
...)
(
1
ln
...
2
1
2
2
1
1
2
1
2
2
1
1
−
∞
+
+
−
∞
+
+
−
−
−
−
=
−
∂
∂
=
=
=
=
∑
∑
∑
∑
j
e
Q
e
e
n
e
e
n
n
j
n
n
n
n
n
n
n
n
j
E
E
j
j
βε
ε
ε
β
ε
ε
β
υ
β
υ
β
βε
υ
υ
- tzw. rozkład Plancka
______________________________________________________________________________

MODEL CIAŁA STAŁEGO:
POLE SPRĘŻYSTE – połączenie węzłów sieci za pomocą sprężyn, kwantami tego pola są FONONY
Liczba stopni swobody: N
3
translacyjnych + N
3
oscylacyjnych = N
6
gdzie N - liczba obsadzonych węzłów
WZBUDZENIA NORMALNE – 3 elementarne wzbudzenia pochodzące od trzech dolin w krajobrazie
potencjału, w których atomowi najłatwiej się poruszać. Pozornie chaotyczny ruch atomów można
złożyć z tych trzech podstawowych ruchów.
W sieci znajduje się N
3
oscylatorów kolektywnych. Energia jednego z nich = energia fononu.
Fonony: AKUSTYCZNE, OPTYCZNE, decydują o właściwościach mechanicznych.
Prędkość dźwięku w kierunku wektora falowego – określona przez współczynnik sprężystości
(nachylenie fononów akustycznych):
0
)
(
→
∂
∂
=
q
q
q
q
v
ω
STAŁA SIŁOWA -
γ
α
j
i
k
,
- macierz
N
3
x
N
3
, której wartości własne opisują drgania w danym
kierunku (wychylenie
i -tego atomu w kierunku
α
,
j -tego atomu w kierunku
γ
)
Energia potencjalna drgań:
(
)(
)
)
0
(
,
,
,
,
,
)
0
(
,
0
2
1
γ
γ
γ
α
α
α
γ
α
i
i
N
j
i
z
y
x
z
y
x
i
i
j
i
pot
s
s
s
s
k
U
E
−
−
+
=
∑ ∑
=
=
Zdiagonalizowanie
γ
α
j
i
k
,
da nam energie oscylatorów kolektywnych:
∑
+
=
N
j
j
j
pot
n
E
E
3
0
ω
h
;
energia zerowa:
∑
+
=
N
j
j
U
E
3
0
0
2
1
ω
h
Suma stanów dla zbioru oscylatorów – GAZU FONONOWEGO:
∑
∞
=
−
∑
=
0
,...
,
2
1
)
,
,
(
n
n
n
j
j
j
e
V
N
Q
ω
β
β
h
;
∑
=
=
N
j
j
Q
3
1
2
sinh
2
ln
ln
ω
β
h
___________________________________________________________________________
STATYSTYKI OBSADZENIA POZIOMÓW
Potrzebna jest DUŻA SUMA STANÓW:
(
)
(
)
∏
−
−
+
=
Σ
j
j
e
µ
ε
β
1
,
µ
- potencjał chem.
(
)
−
∂
∂
=
j
j
Q
n
βε
ln
(ogólna prawidłowość:
V
N ,
sprzega
się
która
wielkosc,
stanów
suma
ln
srednia
wartosc
∂
∂
=
)
Ś
rednia wartość obsadzenia j-tego poziomu w układzie fermionowym:
1
1
)
(
+
=
−
µ
ε
β
j
e
n
F
j
- ROZKŁAD FERMIEGO-DIRACA
W układzie bozonowym (bez ograniczeń w obsadzaniu):
1
1
)
(
−
=
−
µ
ε
β
j
e
n
B
j
- ROZKŁAD BOSEGO-EINSTEINA

___________________________________________________________________________
STATYSTYCZNA INTERPRETACJA STAŁEJ RÓWNOWAGI:
aA + bB = cC + dD
Współczynniki stechiometryczne: ujemne dla substratów, dodatnie dla produktów:
0
=
∑
i
i
i
x
ν
Zasady rządzące chemią: STECHIOMETRIA – proporcjonalność w zmianach liczby moli reagentów
B
A
n
b
a
n
∆
=
∆
Każda substancja wnosi do układu energię równą swojemu potencjałowi chemicznemu:
∑
=
i
i
i
n
E
δ
µ
δ
Fenomenologicznie:
0
=
∑
i
i
i
µ
ν
;
µ
µ
=
i
o
i
x
RT
ln
+
Statystycznie:
i
i
i
γ
ρ
βµ
ln
=
;
i
ρ
- gęstość (koncentracja):
V
N
i
i
=
ρ
i
γ
- stała, ukryta w potencjale standardowym
µ
o
W stanie równowagi:
( )
∏
∑
=
=
i
i
i
i
i
i
i
i
ν
γ
ρ
γ
ρ
ν
ln
ln
0
Stąd STAŁA RÓWNOWAGI:
( )
∏
∏
=
=
i
i
i
i
i
i
K
ν
ν
γ
ρ
1
prawo działania mas ↑
↑
statyst. interpretacja stałej równowagi
Czym jest
i
γ
?
Niech
i
q
oznacza sumę stanów dla cząstek i-tego rodzaju. Cząstek tych jest
i
N
. Z niezależności
oddziaływań i stopni swobody:
r
N
r
N
N
q
q
q
Q
⋅⋅
⋅
2
1
2
1
~
, gdzie r - liczba reagentów
Wykluczamy cząstki powtarzające się:
r
N
r
N
N
r
q
q
q
N
N
N
V
N
Q
⋅⋅
⋅
⋅
⋅⋅
⋅
⋅
=
2
1
2
1
2
1
!
1
!
1
!
1
)
,
,
(
β
Związek z energią swobodną:
(
)
∑
∏
−
=
−
=
−
=
i
i
i
i
i
N
i
i
q
N
N
q
N
Q
F
i
ln
!
ln
!
1
ln
ln
β
)
(
,
,
i
j
N
V
i
i
j
N
F
≠
∂
∂
=
β
β
βµ
Stąd:
i
i
i
q
N
ln
ln
−
=
βµ
Rozdzielamy sumę stanów na wewnętrzne stopnie swobody i stopnie translacyjne:
(int)
)
trans
(
i
i
i
q
q
q
⋅
=
, gdzie (int)
⊇
rot, osc, el
Cząstka w trójwymiarowym pudle:
3
)
trans
(
i
i
V
q
λ
=
gdzie
(
)
2
1
2
kT
m
h
i
i
π
λ
=
- DŁUGOŚĆ TERMICZNA (określenie wynikające z wymiaru)
=
−
+
−
=
−
−
=
(int)
3
(int)
3
ln
ln
ln
ln
ln
ln
ln
i
i
i
i
i
i
i
q
V
N
q
V
N
λ
λ
βµ

+
=
+
=
(int)
3
(int)
3
ln
ln
ln
ln
i
i
i
i
i
q
q
V
N
λ
ρ
λ
Korzystając z
i
i
i
γ
ρ
βµ
ln
=
mamy interpretację
i
γ
:
≡
(int)
3
i
i
i
q
λ
γ
Ostatecznie stała równowagi:
∏
=
i
i
i
i
q
K
ν
λ
3
(int)
(int)
i
q
zawiera w sobie rotacyjne i oscylacyjne stopnie swobody:
)
(
)
(
(int)
osc
i
rot
i
i
q
q
q
⋅
=
,
stopnie translacyjne są uwzględnione w
i
λ
, natomiast elektronowe niewiele wnoszą.
Możemy więc przewidzieć stałą równowagi na podstawie jednocząstkowej sumy stanów.
__________________________________________________________________________
KOLEKTYWNE ZJAWISKA FIZYCZNE
- np. przejścia fazowe, wymagają uwzględnienia oddziaływań między cząstkami
Cechy przejść fazowych:
- łamanie symetrii
- zmiana parametrów porządku
Symetria:
- geometryczna
- analityczna
Parametr porządku – wielkość, która w jednej fazie jest równa 0, w drugiej jest niezerowa
Podstawowy parametr porządku: gęstość względem punktu krytycznego:
c
c
ρ
ρ
ρ
−
Najprostszy model opisujący przejścia fazowe: MODEL ISINGA – sieć spinów
Każdy spin podlega działaniu dwóch zaburzeń:
- pole zewnętrzne:
∑
=
−
N
i
i
H
s
1
µ
- oddziaływanie z sąsiadami w sieci:
∑
=
⋅
⋅
−
N
j
i
ij
j
i
J
s
s
1
,
'
∑
∑
∑
∑
=
=
=
+
−
=
⋅
⋅
−
−
=
N
i
j
j
ij
i
N
j
i
ij
j
i
N
i
i
s
J
H
s
J
s
s
H
s
E
1
1
,
1
'
µ
µ
µ
Suma stanów:
∑
±
=
+
∑
∑
=
)
1
...
,
,
(
3
2
1
)
,
(
s
s
s
s
J
H
s
i
j
j
ij
i
e
N
Q
υ
µ
β
β
Metody rozwiązywania tego modelu:
- metoda pola średniego (cząstka widzi tylko uśrednione pole swoich sąsiadów, nie rozróżnia ich)
- metoda renormalizacyjna (oparta na skalowaniu)
- metody numeryczne, np. metoda symulacji Monte-Carlo, metoda dynamiki molekularnej (trajektorie)

Przybliżenia stosowane w modelu Isinga:
- metoda NN (najbliższych sąsiadów): parametr oddziaływania przybliżamy jedną liczbą:
J
J
ij
→
- redukcja liczby wymiarów
Największe możliwe uproszczenie: NN, 1D:
∑
∑
=
+
=
−
−
=
N
i
i
i
N
i
i
s
s
J
H
s
E
1
1
1
µ
µ
Zakładamy cykliczne warunki brzegowe:
1
1
s
s
N
≡
+
Parametr porządku: namagnesowanie
i
N
i
i
s
s
M
~
1
∑
=
=
µ
Suma stanów:
∑
±
=
+
∑
∑
=
+
)
1
...
,
,
(
3
2
1
1
)
,
(
s
s
s
s
s
J
s
H
i
i
i
i
i
e
N
Q
υ
β
βµ
β
0
=
H
: (brak pola zewn.)
(
)
( )
N
N
J
J
s
s
s
s
s
J
J
e
e
e
N
Q
i
i
i
β
β
β
β
υ
β
cosh
2
)
,
(
)
1
...
,
,
(
3
2
1
1
=
+
=
∑
=
−
±
=
∑
+
0
≠
H
:
niech
h
H
=
βµ
,
K
J
=
β
∑
±
=
+
+
∑
∑
=
+
+
)
1
...
,
,
(
2
3
2
1
1
1
)
,
(
s
s
s
s
s
K
s
s
h
i
i
i
i
i
i
e
N
Q
υ
β
Energia na jednym węźle w zależności od wzajemnej orientacji spinów:
i
i
s
s
\
1
+
-1
+1
-1
-h+K
-K
+1
-K
+h+K
Jednocząstkowa suma stanów:
=
+
−
−
+
−
)
(
)
(
K
h
K
K
K
h
e
e
e
e
q
Suma stanów:
(
)
N
K
h
K
h
N
e
e
q
N
Q
)
(
)
(
)
,
(
+
+
−
+
=
=
β
∑
=
=
N
i
i
s
M
1
µ
N
i
h
Q
N
s
,
ln
1
β
∂
∂
=
(wielkość sprzężona z
i
s - pole zewnętrzne)
Po podstawieniu
...
)
,
(
=
N
Q
β
otrzymamy:
( )
H
M
β
µ
tanh
=
TEMPERATURA KRYTYCZNA:
N
J
kT
c
=
WYKŁADNIKI KRYTYCZNE – opisują zależność parametrów porządku od temperatury
(
)
β
c
T
T
M
−
~
(
)
α
c
T
T
c
−
~
α
β
,
- wykładniki krytyczne: namagnesowania i ciepła wł.
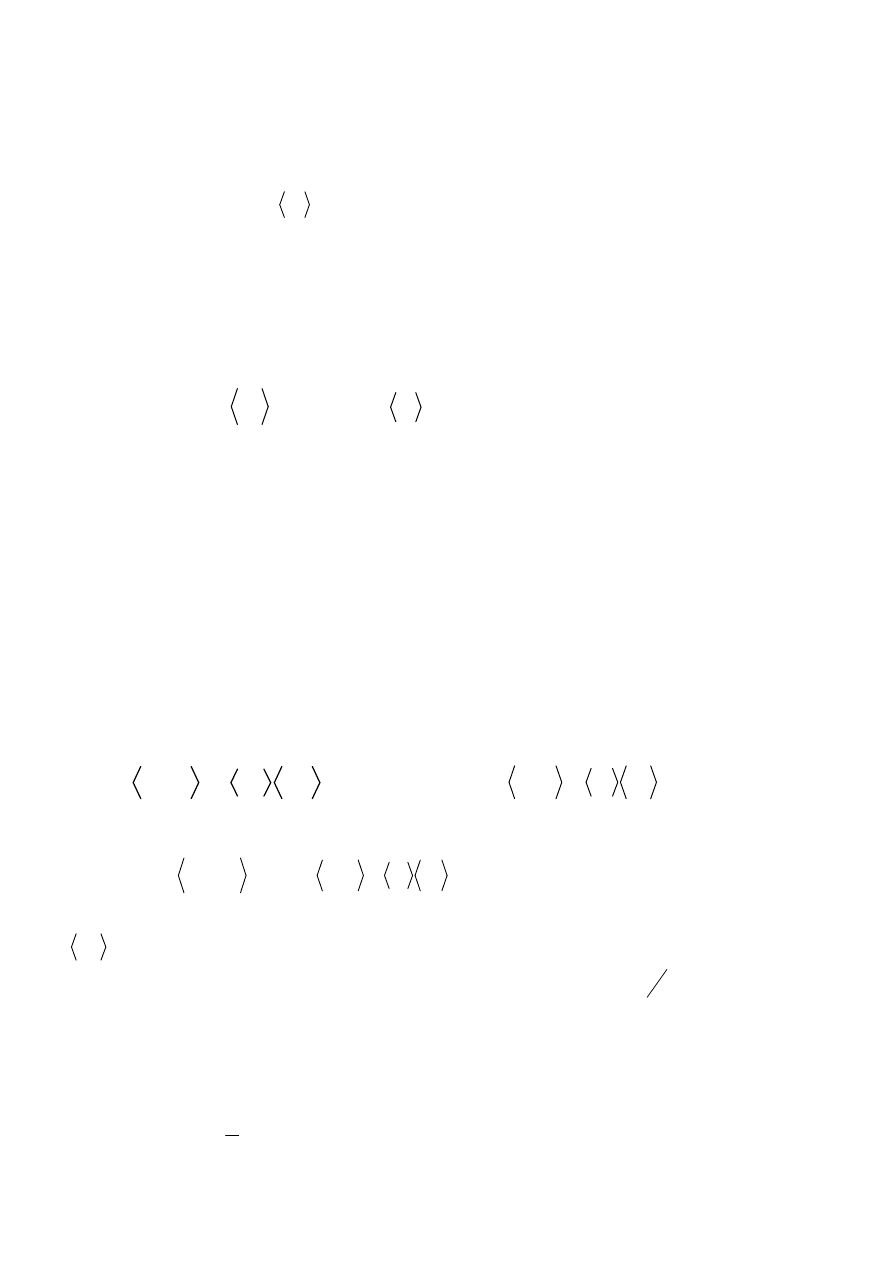
GAZ SIECIOWY:
{ }
1
,
0
=
i
n
- jest również modelem dwustanowym, powinien więc mieć identyczne
rozwiązanie co model Isinga ze spinami (prosta transformacja:
1
2
−
=
i
i
n
s
)
Hamiltonian w jawnej postaci:
∑
∑
=
−
N
i
j
i
j
i
i
n
n
n
1
,
'
ε
µ
Parametr porządku: gęstość:
ρ
~
i
n
Przejścia fazowe:
- z gazu do cieczy: gaz sieciowy
- ze stanu nieporządku do porządku: model Isinga
Opisanie trzech faz wymaga połączenia modeli (dwa parametry porządku: gęstość i uporządkowanie)
Potrzebna jest zmienna o trzech stanach:
{
}
1
,
0
±
=
i
s
{ }
1
,
0
2
=
i
s
- miara gęstości
Parametry porządku:
2
i
s
- gęstość
ρ
i
s
- namagnesowanie M
Hamiltonian:
H
(
)
∑
∑
∑
∑
∑
+
−
−
−
+
−
=
=
=
−
j
i
j
i
j
i
j
i
j
i
j
i
j
i
N
i
N
i
i
i
spin
s
s
s
s
K
s
s
s
s
J
s
s
H
,
2
2
,
2
2
,
1
1
2
1
'
'
'
ε
µ
|
|
|
oddziaływanie potencjał
dodatkowe oddziaływanie
z polem zewn. chemiczny
gdy sąsiadują ze sobą spiny
(1-szy człon (1-szy człon
uporządkowany i nieuporządkowany
modelu Isinga) gazu sieciowego)
___________________________________________________
ŁAMANIE SYMETRII
Mechanizm mikroskopowy: fluktuacja w obrębie mikroukładu stanowi dla układu rodzaj
zewnętrznego pola. Fluktuacje zwiększają swój zasięg aż do nieskończoności i układ się porządkuje.
Miara zasięgu fluktuacji – funkcja korelacyjna:
j
i
j
i
ij
s
s
s
s
c
−
=
, dla gazu sieciowego:
j
i
j
i
n
n
n
n
−
Ś
redni kwadrat fluktuacji – proporcjonalny do podatności (podatność w punkcie krytycznym rośnie do
nieskończoności):
( )
(
)
∑
∑
=
−
=
=
=
N
j
i
ij
N
j
i
j
i
j
i
c
s
s
s
s
M
N
,
1
,
2
)
,
(
β
β
δ
β
β
χ
Podatność jest współczynnikiem proporcjonalności pomiędzy odpowiedzią układu a zaburzeniem:
µ
β
χ
H
M
⋅
=
Szerokość obszaru o dużej zmienności namagnesowania jest proporcjonalna do
N
1
.
_______________________________________________________
MODEL POLA ŚREDNIEGO
Energia mikrostanu:
H
υ
µ
E
s
s
J
s
H
N
j
i
j
i
ij
N
i
i
=
−
−
=
∑
∑
=
,
1
2
1
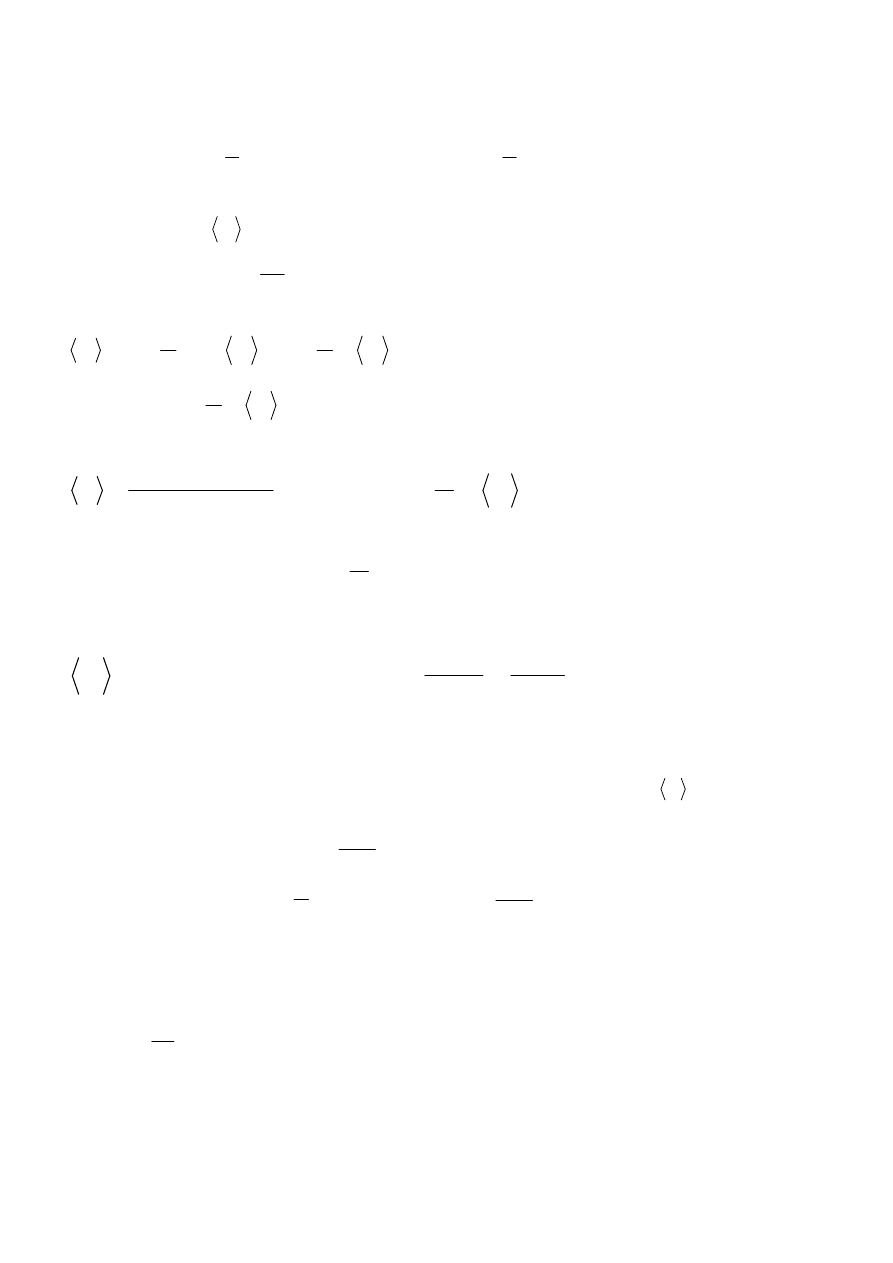
Postępowanie:
- zaniedbujemy fluktuacje
- wybieramy jeden konkretny spin
- analizujemy pole lokalne w zależności od konfiguracji otoczenia
H
∑
∑
∑ ∑
∑
−
−
=
−
−
=
=
=
i
j
i
i
N
i
i
i
j
j
ij
i
N
i
i
s
h
s
s
H
s
J
s
s
H
)
(
2
1
2
1
1
1
µ
µ
↑
pole lokalne
Przybliżenie:
j
j
s
s
→
Pole efektywne:
∑
+
=
∂
∂
−
=
j
ij
i
i
s
J
H
s
H
µ
µ
H
Uśrednienie pola efektywnego – przyjmujemy średnią konfigurację otoczenia:
j
j
ij
s
zJ
H
s
J
H
H
µ
µ
1
1
+
≅
+
=
∑
, gdzie z - liczba najbliższych sąsiadów
Fluktuacja:
j
s
zJ
H
µ
1
=
∆
(
)
(
)
+
=
=
∑
∑
±
=
∆
+
±
=
∆
+
j
s
s
H
H
s
s
H
H
s
zJ
H
e
e
s
s
µ
βµ
βµ
βµ
1
tanh
1
1
1
1
1
1
- równanie transcendentalne
Sytuacja krytyczna: dla
1
=
Jz
β
:
k
Jz
T
c
=
DJ
kT
c
2
=
, gdzie D - wymiar sieci (z wyjątkiem D =1)
Równanie transcendentalne prowadzi do równania Bragga-Williamsa:
(
)
m
m
Jzm
Jzm
m
s
j
−
+
=
→
=
≡
1
1
ln
2
1
tanh
β
β
Przeorientowanie spinów: rodzaj reakcji chemicznej:
.....↑.....
↔
....↓.....
ρ
−
1
ρ
Namagnesowanie: różnica między dwoma konfiguracjami:
(
)
1
1
2
1
s
=
−
=
−
−
ρ
ρ
ρ
Wyrażenie na stałą równowagi:
F
G
K
RT
∆
−
=
∆
−
=
ln
→
f
kT
∆
−
=
−
ρ
ρ
1
ln
- różnica energii
(
)
H
H
f
∆
+
=
∆
µ
µ
2
)
1
2
(
1
−
=
∆
ρ
µ
zJ
H
→
)
1
2
(
2
1
ln
−
−
=
−
ρ
ρ
ρ
Jz
kT
__________________________________________________________________
IDEA PRZESKALOWANIA – w kolejnych krokach postrzegamy układ z malejącą rozdzielczością,
wraz z tym zmienia się stała oddziaływania
Niech
kT
J
K
=
:
∑
±
=
+
+
+
=
1
...)
(
4
3
3
2
2
1
)
,
(
i
s
s
s
s
s
s
s
K
e
N
K
Q
Można przejść na sumowanie po parzystych spinach:
(
) (
)
)
,
'
(
)
,
(
1
...)
(
5
3
3
1
N
K
Q
e
N
K
Q
i
s
s
s
s
s
K
→
=
∑
±
=
+
+
+
+
Po pewnej liczbie kroków dojdziemy do układu z jednym elementem, będącym sumą stanów.
_______________________________________________________________________________
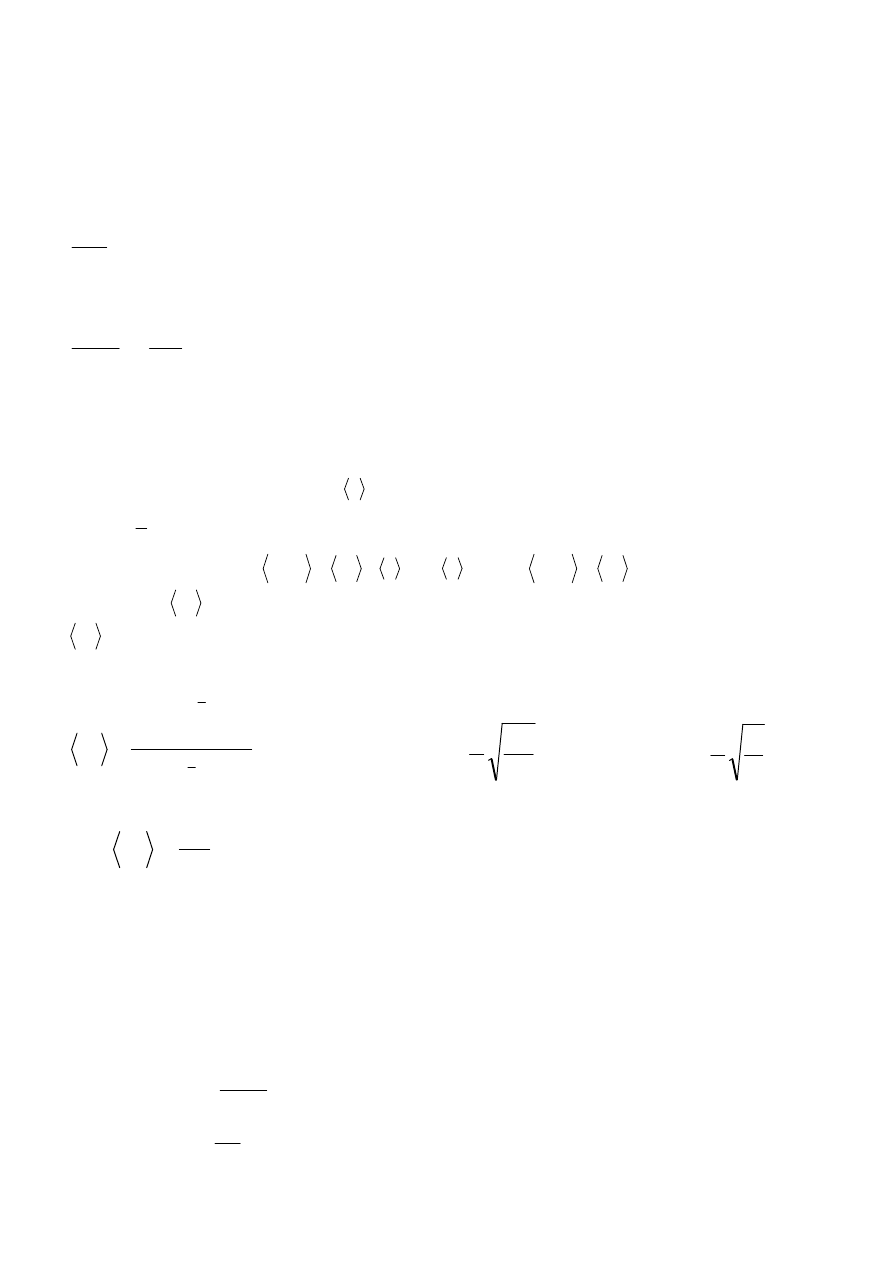
RÓWNANIE KINETYCZNE – zmiana prawdopodobieństwa obsadzenia danego mikrostanu w czasie
Kinetyka przejścia pomiędzy
υ
i
υ
’ zależy od prawdopodobieństwa tego przejścia
'
υυ
w
:
[
]
∑
+
−
=
•
'
'
'
'
υ
υ
υ
υ
υ
υυ
υ
P
w
P
w
P
Prawdopodobieństwa są zależne od bariery energetycznej (energii aktywacji):
'
'
υυ
β
υ
υ
E
e
P
P
∆
−
=
Stan równowagi: zmiana w czasie = 0:
'
'
'
'
υυ
β
υ
υ
υ
υ
υυ
E
e
P
P
w
w
∆
−
=
=
_________________________________________________________
PROCESY NIEODWRACALNE – nierównowagowe, nieliniowe, np. oscylator harmoniczny
Siła napędowa: fluktuacje:
x
x
x
−
=
δ
Energia:
2
2
1
Kx
Ś
redni kwadrat fluktuacji:
( )
2
2
2
x
x
x
−
=
δ
0
=
x
( )
2
2
x
x
=
δ
Oszacowanie
2
x
:
∑
=
υ
υ
P
x
x
i
2
2
Przybliżenie wysokotemperaturowe: przyjmujemy, że przestrzeń fazowa jest ciągła
∫
∫
∞
∞
−
−
∞
∞
−
−
=
dx
e
dx
e
x
x
Kx
Kx
2
2
2
1
2
1
2
2
β
β
3
2
2
1
2
A
dx
e
x
Ax
π
=
∫
∞
∞
−
−
A
dx
e
Ax
π
2
1
2
=
∫
∞
∞
−
−
Stąd:
K
kT
x
=
2
Fluktuacje termiczne – gdy energia termiczna >> energia drgań zerowych (
ω
h
>>
kT
).
Kryterium klasyfikacji procesu:
CZAS RELAKSACJI – czas potrzebny na powrót układu do stanu równowagi:
1
−
=
ω
τ
Procesy trwające znacznie dłużej niż
τ
- procesy nierównowagowe.
RÓWNANIE ONSAGERA (źródło entropii):
∑
=
k
k
ik
i
X
L
J
gdzie:
k
k
x
S
X
∂
∆
∂
=
)
(
- SIŁA TERMODYNAMICZNA (fluktuacja zmiany entropii)
dt
dx
J
i
i
=
:
- STRUMIEŃ ENERGII związany z fluktuacją
ik
L
- PARAMETRY ONSAGERA
W równaniu Onsagera mieszczą się równania szczegółowe, np. każde równanie kinetyczne:
( )
i
i
i
x
S
L
dt
dx
∂
∆
∂
=
W procesach nierównowagowych zawsze
0
≠
i
X
.
______________________________________________________________________
Wyszukiwarka
Podobne podstrony:
Fizyka wyprowadzenia wzorow
Elementy termodynamiki chemicznej
Sprawozdanie z Materiałoznawstwa--obróbka cieplno-chemiczna, Materialoznawstwo
Transformacja Laplace wyprowadzenie wzorów
1 3 Termodynamika chemiczna +Odpowiedzi
Obróbka cieplno-chemiczna, Materiałoznawstwo I i II
materialy ceramiczne cw 2 analiza ziarnowa, Technologia chemiczna, Materiały ceramiczne
materialy ceramiczne cw 3 prasowanie, Technologia chemiczna, Materiały ceramiczne
HIGIENA PRACY CZYNNIKI CHEMICZNE, materiały farmacja, Materiały 4 rok, epidemiologia, Higiena i epid
Definicje równoważnik chemiczny, Materiały - Biotechnologia
Podstawy termodynamiki chemicznej
iso-8859-2''Karta modu u Surowce Technologia chemiczna, Studia, Surowce mineralne i chemiczne, mater
higiena pracy czynniki chemiczne, materiały farmacja, Materiały 4 rok, farmacja 4 rok part 2, reszta
czynniki chemiczne, materiały farmacja, Materiały 4 rok, higiena, higiena2
Wyprowadzanie wzorów
ANOVA-AB-SS-wyprowadzenia wzorow, SWPS, ROK 2, Metodologia ze statystyką - Brzeziński
Zagadnienia cz 2 wyprowadzanie wzorów
TERMODYNAMIKA CHEMICZNA I TERMOCHEMIA
więcej podobnych podstron