
ZOFIA KUJAWA
ZBIÓR ZADAŃ DLA U C ZN IÓ W G IM N A Z JU M
Z B IÓ R
u w z g l ę d n i a
z m i a n y

1 . L I C Z B Y I W Y R A Ż E N I A A L G E B R A I C Z N E
■ 1 .1 . D Z I A Ł A N I A N A L I C Z B A C H
H
i
B g M m M M m
I 1. Ile razy większa jest liczba liczb trzycyfrowych niż liczb dwucyfrowych?
¡Za p isz o b iic
—
S f i ia.
...
;
!
i
i
|
!
i
I
i
^
!’
i
i
:
j
|
Odp.:
U 2. Członkowie kółka matematycznego
podali swój wzrost (zobacz rysu
nek). Oceń prawdziwość poniższych
zdań.
I. Wszyscy chłopcy użyli liczby wy
miernej.
□ PRAWDA
□ FAŁSZ
II. Rysunki ponumerowano w kolejności od chłopca najwyższego do najniższego.
□ PRAWDA
□ FAŁSZ
□ 3. Uzupełnij zdania.
I. Na niektórych budynkach znajdują się oznaczenia roku zakończenia ich budowy. Dom,
na którym umieszczono napis MCMVI powstał po
latach od wybudowa
nia domu z oznaczeniem MDCCCV.
II. W napisach końcowych filmu podano rok jego produkcji jako MCMLVIII. Po 44 la
tach nakręcono nową wersję tego filmu, którego zapis roku produkcji w systemie rzymskim
to
□ 4. Podaj dwie kolejne liczby naturalne, których suma jest równa 73.
Zapisz o b licze n ia .
i
j
_
Odp,
5

1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
O 5. O ile suma liczb 7,6 i - l | jest większa od ilorazu liczb 0,25 i l | ?
Zapisz o b lic z e n ia , i
O d p .: .......................................................................................................................
□ 6. Przy dodawaniu kilku liczb uczeń błędnie odczy
tał dwie cyfry. Cyfrę dziesiątek jednej z liczb: 5
odczytał jako 7, a cyfrę jedności którejś z liczb: 9
- jako 6 i otrzymał wynik równy 768. Podaj
właściwy wynik tego dodawania.
W ła ś c iw y w y n i k : ..................................................................................................
□ 7. O trzycyfrowej liczbie 78[? wiadomo, że dzie
li się przez 2 i 3. Podaj wszystkie możliwe cyfry,
które można wstawić w miejsce znaku zapytania.
O d p ,:
8. Wyznacz wszystkie cyfry x oraz y tak, aby licz
ba 23x75327)' była podzielna przez 36.
O d p .:
□ 9. Zaznacz zbiór, który zawiera wszystkie dzielniki liczby 48.
A. {2, 3, 4, 6, 8, 12,16, 24}
B. {1, 2, 3, 4, 6, 8, 12,16, 24}
C. {2, 3, 4, 6, 8, 12,16, 24, 48}
D. {1, 2, 3, 4, 6, 8, 12, 16, 24, 48}
Cf/D 10. Zaznacz fałszywe dokończenie zdania: Liczba 654 132
A. dzieli się przez 3 i dzieli się przez 4.
B. dzieli się przez 6 i nie dzieli się przez 9.
C. dzieli się przez 2 i dzieli się przez 6.
D. dzieli się przez 6 i dzieli się przez 9.
□ 11. Zaznacz parę liczb, których NWD {a, b) = 24 i NWW {a, b) = 144.
A. a = 48, b = 72
B. a = 144, b = 72
C. a = 24, b = 6
D. a = 24, b =72
Zapisz o b lic z e n ia .
|
Z a pisz o b lic z e n ia .
—
Z a pisz o b lic z e n ia .
6
1.1. D z i a ł a n i a n a l i c z b a c h
□ 12. Liczbę 9 804 można przedstawić w postaci
A. 9 • 1 003 + 8 • 102 + 1
B. 9 • 1 003 + 8 • 97 + 4
C. 9 • 1 003 + 8 • 102 + 4 • 10
D. 9 • 1 003 + 8 • 97 + 1
13. W wyrażeniach na rysunku postaw nawiasy tak, aby wynik był największą liczbą - wiek
dziadka oraz najmniejszą - wiek wnuczka. Jaka jest średnia wieku dziadka i wnuczka?
4 ■
12 + 18 : 6 + 3 !
O dp..
zapis? obliczenia.
....
Cfj □ 14. Podaj dziewięćdziesiątą dziewiątą cyfrę po prze-
13
•
cinku w rozwinięciu dziesiętnym ułamka —
Odpowiedź uzasadnij.
O dp.:
Zapisz o b lic z e n ia .
\
:
..... |..
i
1
□ 15. Zaznacz ^ liczby 54.
A. 5
B. 5
C. I 5
D. 4
□ 16. Zaznacz 1~ liczby 12,9.
A. 2,1
B. 2,15
C. 21,5
D. 215
□ 17. Zaznacz liczbę odwrotną do 3y.
A. - 3 j
B .3 J
□ 18. Zaznacz liczbę przeciwną do 1,15.
A 122.
115
b
- i s a
115
c —
23
C. 11,5
D. -1,15

U 19. Podaj podwojoną liczbę przeciwną do odwrotności
liczby 7.
OciD
......................................
1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
U 20. Uzasadnij, że liczba zapisana w postaci 212 + 48 + 2 ■
3 + 164 jest podzielna przez 5.
Zapisz o b lic z e n ia .
0 21. Budżet międzynarodowego kartelu wynosi siedem bilionów pięćset miliardów dolarów, czyli
A. 7,5 • 109 $.
B. 7,5 • 1010 $.
C. 7,5 • 1011 $.
D. 7,5 • 1012 $.
□ 22. Średnia odległość między Słońcem a najbliższą mu planetą - Merkurym równa iest oko
ło 57 900 000 km, czyli
A. 5 790 • 107 km.
B. 5,79 • 107 km.
C. 5 790 • 10“7 km.
D. 57,9 • 105 km.
□ 23. Objętość Ziemi równa jest 1,08321 • 1012km3, czyli
A. 1,08321 • 1015 m3.
B. 1,08321 • 1018m3.
C. 1,08321 • 1021 m3.
D. 1,08321 • 1025 m3.
□ 24. Przeciętna średnica atomu równa jest 0,00000008 cm, czyli
A. 8 - 0 , l 7 cm.
B. 0,8 • 0 ,l8cm.
C. 8 - 0 , l 8mm.
D. 0,8 • 0,19 mm.
;
z.
25. Rozpiętość rozmiarów komórek człowieka jest ogromna. Szczególnie jest to widoczne przy
porównaniu komórek rozrodczych - komórka jajowa ma około 0,2 mm, a plemnik jest od niej
85 000 razy mniejszy. Stosunek wielkości komórki jajowej do wielkości plemnika wyraża
się jako
104.
B. 85 • 103.
C. i • 102.
D. 85 • 104.
A
1.
■
85
26. Obok przedstawiono dane dotyczące średniej zawartości krwinek
czerwonych (erytrocytów) i białych (leukocytów) w 1 mm3 krwi psa.
a) W 1 cm3 krwi psa znajduje się średnio 650 000 000 erytrocytów.
□ T A K
□ N I E
b) Ile razy większa jest średnia liczba erytrocytów od średniej licz
by leukocytów w krwi psa?
8
1.1. D z i a ł a n i a n a l i c z b a c h
□ 27. Zaznacz rysunek przedstawiający zbiór liczb spełniających warunek x < i .
B
C
D
i
2
□ 28. Na osi liczbowej przedstawiono zbiór liczb spełniających warunek
A. x > 2,03.
B.x > 2,03.
C. x < 2,03.
D. x <2 , 0 3 .
2,03
U 29. Ile liczb naturalnych spełnia warunekx < 4 ?
A. nie ma takich liczb
B. cztery
C. pięć
D. nieskończenie wiele
U 30. Uzupełnij zdanie.
W zbiorze M = {-1, 0, ( ^ ) , 3, i/3} największą liczbą spełniającą warunekx < 1,69 jest
□ 31. Zaznacz na osi liczbowej wszystkie liczby spełniające warunek x > -2-|. Podaj najmniejszą
liczbę całkowitą spełniającą ten warunek.
!
1 1
0 32. Zaznacz na osi liczbowej zbiór liczb, które spełniają warunekx < l.W zbiorze tym wskaż
taką liczbę, żeby liczba do niej przeciwna także należała do tego zbioru.
i
1
■
i
i
!
i
i
j
i
i
i
l
i
i
!
i
i
i
i
i
i
!
i
!
i
:
:
i
1
........ L _ L J .........
j
;
J
33. Element x należący do zbioru zaznaczonego na osi liczbowej spełnia warunki
A. x > - 2 i x < 5 .
B . x > - 2 i x < 5 .
C. x > - 2 i x < 5 .
D . x ^ - 2 i x > 5 .
7?
□ 34. Maciej, wielbiciel komiksów, dostał 100 zł na zakupy w księgar
ni. Postanowił kupić powieść za 34 zł, a resztę chce przeznaczyć
na zeszyty z serii przygód swojego ulubionego komiksowego
superbohatera, w cenie 12 zł za sztukę. Ile co najwyżej komik
sów będzie mógł kupić Maciek?
A. 5
B. 6
C. 10
D. 12

1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
□ 35. Oblicz wartość wyrażenia.
L_-3
(2,2 +
1
•(
i) =
J '
J
--
-
□ 36. Oblicz wartość wyrażenia i podaj liczbę przeciwną oraz odwrotną do wyniku działania.
’ ~~j
T ' " { .....
j
V 4 2
+
2 a
[ 3 “ - j #
[‘...
i
]
|
......r.......
1
i
!
:
i
i
:
T
Liczba p r z e c iw n a :.............................
Liczba o d w ro tn a :
□ 37. Wyłącz wspólny czynnik przed nawias.
□ 38. Oblicz wartość wyrażenia.
□ 39. Oblicz wartość wyrażenia.
2
10,5 + [(?73-)
U-■(1,5) J]
-2,4)-' =
i ! !
1
1 f ■
..i... ”
i
1 0
1.1. D z i a ł a n i a n a l i c z b a c h
U
40. Oblicz wartość wyrażenia.
.... i..
o
5 ' [
8
( -
4-
(
5
I|
i"?
15
\
24
i l
• (
3
■)
... j-
3
4
j
|
|
....
U 41. Która z liczb m czy p jest większa i o ile?
m = 23 ■
[0,4 - 0 ,1
:
( - 0 ,4 ) ]
p = (i)3 -
0,8
: 2 - 2
Zapisz o b lic z e n ia .
i
i
0lip.: ..................... ........................... ............... - ................. .
................................... ...
□ 42. Oblicz obwód trójkąta o bokach:
38 • ( I ) 10 •
t
/3 • 35
a = 3 • (310 : 37)
b = - 36 • (0,25^36 - 5° ■
0,25 - 3 :1,5)
c = --------------------
V3
2 ? , 3 i 5 Z
>bUr* c:t' a.
Dc :
11
1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
□ 43. Wody zajmują 2 ' 19 ’ 10 2+
3 ’ 11 ’ 10 km2 powierzchni Ziemi, a lądy: 14,894 • 107 km2.
Oblicz powierzchnię Ziemi. Wynik podaj w kilometrach kwadratowych.
i
Sr
.......
! Z apis:
ib lic z e n ia .
'
T
j
______
~ 7 ~
_i _
i
...
-j
...... ..
.....
I
..... '[.....
| | |
l
j
[
i
i_
I
_
□ 44. Kasia zapisała się do rozpoczynającej działalność w Domu Kultury sekcji matematyków.
Dostała informację, że pierwsze spotkanie odbędzie się w sali, której numer jest trzycyfro
wą liczbą, gdzie cyfra setek równa jest 1 6 - ^ 3 ■
(V108 - V48 + V27), dziesiątek: 14 —
9 1,
44
a cyfra jedności: r—^ . Podaj numer sali.
o * 2
; Zapisz o b lic z e n ia . | j
]
]
|
]
|
M
|
I I
i
M
i i
i
!
1
|
|
i
!
i
i
|
i
j
|
;
1
|
|
|
1
1
1
i
!
!
!
i
i
i
1
!
i
|
i
|
I
M
|
|
|
|
....
..
□ 45. Pani Halina rozlała kompot do słoików o pojemności 0,6 1. Do ilu słoików nalała kompo
tu do pełna, jeżeli rozlała więcej niż 59 1 kompotu i mniej niż 61 1, a ilość kompotu
wyrażona jest liczbą naturalną?
Zapis
o b lic zen ia.
1
.....
i
O d p ,:
12
1.1. D z i a ł a n i a n a l i c z b a c h
O 47. Oblicz, w jakiej odległości jest burza, gdy pomiędzy wyładowaniem elektrycznym (błyskiem)
i grzmotem upłynęło 25 sekund. Wynik podaj w kilometrach. (Prędkość rozchodzenia się
dźwięku w powietrzu równa jest 340 ®).
Zapisz o b lic z e n ia .
" T....
— —
i
i
O d p .:
□ 48. Samochód w czasie 12 minut przejechał 19 km. Oblicz, ile kilometrów przejedzie ten
samochód w czasie 4 godzin, gdy będzie jechał dalej z tą samą średnią prędkością.
Z apisz o b lic z e n ia .!
i
O d p .:
□ 49. Janek wyszedł z domu o godzinie 8:00, a jego brat Tomek o godzinie 12:40 wyjechał
rowerem. Tomek, który jechał ze średnią prędkością 18
dogonił Janka po 1 godzinie
i 20 minutach. Oblicz, z jaką prędkością szedł Janek, przy założeniu, że poruszał się on ze
stałą prędkością i że obaj bracia tego dnia wybrali tę samą trasę.
Zapisz o b lic z e n ia .
—
.....
—
O d p .:
13
1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
□ 50. Na odcinku drogi o długości 800 m i szerokości 13 m wydzielono po obu jej stronach pas
dla rowerów o szerokości 2 m każdy. Na granicy pasa dla rowerów i jezdni dla samo
chodów co 2 metry umieszczono punktowe elementy odblaskowe.
a) Jaką część drogi stanowi wydzielony dla rowerów pas jezdni?
oburzę"5;}.
Od
b) Ile elementów odblaskowych znajduje się na tym odcinku drogi?
Zapisz o b lic z e n ia .
C-.V\
□ 51. Gęstość mleka równa jest 1 030
Oblicz, ile gramów mleka wypełnia szklankę o pojem
ności 250 ml.
Zapisz o b lic z e n ia .
i
0 €!(>.:
I n f o r m a c j a do z a d a ń 5 2 -5 6
Największą na świecie złotą monetę, 100-kilogramowy
„Mapie Leaf” (ang., „Klonowy Liść”) o nominale miliona do
larów kanadyjskich (CAD), sprzedano 25 czerwca 2010 roku
na aukcji w Wiedniu za 3,27 min euro, czyli równowartość
4,19 min CAD.
Królewska Mennica Kanadyjska wybiła w 2007 roku
pięć takich monet, aby zaprezentować swoje umiejętności
produkcyjne oraz uzyskać wpis do Księgi Rekordów
Guinnessa. „Mapie Leaf” o średnicy 53 cm i grubości 3 cm
jest wykonany z kruszcu o rekordowej czystości, zawie
rającego 99,999% złota.
□ 52. Masa innych metali stanowiących domieszkę w złocie, z którego zrobiono sprzedany
na aukcji „Mapie L eaf”, równa się
A. 0,01 g.
B. 0,1 g.
C. I g .
D. 10 g.
14
1.1. D z i a ł a n i a n a l i c z b a c h
□ 53. Oblicz kurs euro w dolarach kanadyj
skich z dnia 25 czerwca 2010 roku
Wynik zaokrąglij do 0,0001 CAD.
I 54. W dniu sprzedaży „Mapie Leaf” gram zło
ta kosztował średnio 148,13 zł. Oblicz
wartość kruszcu, z którego wykonana
jest ta unikatowa moneta. Wynik podaj
w PLN.
O d p . :
□ 55. Oblicz różnicę między wartością złota, z którego jest wykonany
„Mapie L eaf”, a ceną sprzedaży monety. Przyjmij podane śred
nie kursy z dnia aukcji. Wynik podaj w PLN.
j
|
i
|
OcJp :
J
56. Oblicz objętość monety „Mapie L eaf”, jeżeli gęstość złota równa jest 19 282
Podaj
wynik w cm3 z dokładnością do części tysięcznych.
0 a 0.:
Średni kurs 2010.06.25
d o la r k an a d y js k i:
1 CAD - 3,2348 PLN
euro:
1 EUR - 4,1405 PLN
Zapisz o b lic z e n ia .
.
v c
•"
■
•
•
Ą
.
:
i
-
, pp
2
t p ; ? ~
o b l i c z e n i a ,
'i
J_ 4
1 5

i L i c z b V i w y r a ż e n i a a l g e b r a i c z n e
I 1.2. P R O C E N T Y
□ 1. Adam na planowaną wraz z przyjaciółmi
wycieczkę przeznaczył 500 zł ze swoich
oszczędności. Wydatki zaplanował tak, jak
pokazano na diagramie. Uzupełnij dane
poprzez wpisanie odpowiednich kwot.
upom inki 2%
rezerwa
..........zł
tra nsf)o rt
15°4
□ 2. Uzupełnij zdania.
I. 20 minut to ok.
% godziny.
HI. 10 minut to
% kwadransa.
V 18 milimetrów to
% 18 centymetrów.
vn.
49 dekagramów to
% kilograma.
H. 5 minut to ok.
kwadransa.
IV 1,2 metra to
% 60 centymetrów.
VI. 250 decymetrów to
% kilometra.
VIII. 30 gramów to
% 3 dekagramów.
u 3. Klient wpłacił 150 zł zaliczki przy zamawianiu telewizora. Ile kosztuje telewizor, jeżeli
wpłacona zaliczka stanowi 15% jego wartości?
A. 650 zł
B. 800 zł
C. 1 000 zł
D. 1 150 zł
jf u 4. W pojemniku znajduje się 12 guzików czerwonych i 9 - niebieskich. O ile procent należy
zmniejszyć liczbę guzików czerwonych, aby stanowiły one 40% liczby wszystkich guzików
w pojemniku?
A. 10%
B. 20%
C. 50%
D. 100%
U
5. Sok malinowy rozcieńczono w proporcji 1:3 (1 część soku i 3 części wody). Jaki procent
soku znajduje się w szklance przyrządzonego napoju?
A. 25%
B. 30%
C. 50%
D. 75%
U 6.W koszyku znajduje się 50 cukierków, z czego 10% to cukierki truskawkowe. Jaki pro
cent cukierków owocowych stanowią cukierki truskawkowe, jeżeli w koszyku jest 20 cukier
ków owocowych, a reszta to krówki?
A. 5%
B. 10%
C. 20%
D. 25%
1 6
1.2. P r o c e n t y
□ 7. Ile kilogramów mąki otrzyma się ze 120 kg pszenicy, jeżeli masa mąki stanowi 65% masy
ziarna?
A. 58 kg
B. 70 kg
C. 78 kg
D. 80 kg
□ 8. Droga z Dobrego do Nowego ma 196 km, z czego tylko 49 km jest pokryte asfaltem. Jaki pro
cent tej drogi należy pokryć asfaltem, aby na caiej długości była asfaltowa?
A. 25%
B. 45%
C. 75%
D. 80%
□ 9. Wiek Kasi stanowi 32% wieku jej cioci, co stanowi 40% wieku taty Kasi. Oblicz, w jakim
wieku jest Kasia i jej tata, jeżeli ciocia ma 50 lat.
Zapisz o b lic z e n ia .
O d p .:
□ 10. Karol przeczytał w pierwszym dniu 20% książki liczącej 500 stron, drugiego dnia 40%
reszty, a trzeciego dnia skończył czytać książkę. Ile stron książki Karol przeczytał
w trzecim dniu?
i Zapisz o b lic z e n ia .
O d p .:
□ 11. Wśród uczniów pewnego gimnazjum przeprowadzono
ankietę na temat najchętniej czytanych książek. Wyniki
zilustrowano obok.
a) Oblicz, ilu uczniów brało udział w ankiecie, jeżeli ulu
bioną lekturą 45 spośród nich są książki przyrodnicze.
Za pisz o d lic z e n ia ."'
T"
i
j
i
]
]
|
O d p .:
b) O ilu uczniów więcej wybrało odpowiedź „komiksy” niż „książki historyczne”?
Zapisz o b lic z e n ia .
O dp.:
przyrodnicze
17
i . L i c z b
v
i w y r a ż e n i a a l g ę b r a i c z i i e
□ 12. W trakcie produkcji mydła poddaje się je procesowi suszenia, podczas którego traci 12%
masy. Oblicz masę produktu otrzymanego w wyniku suszenia 64 kg mydła.
' I m - s z
o b lic z e n ia .
|
.. j.
|
}
•
!
:
|
Udp
u
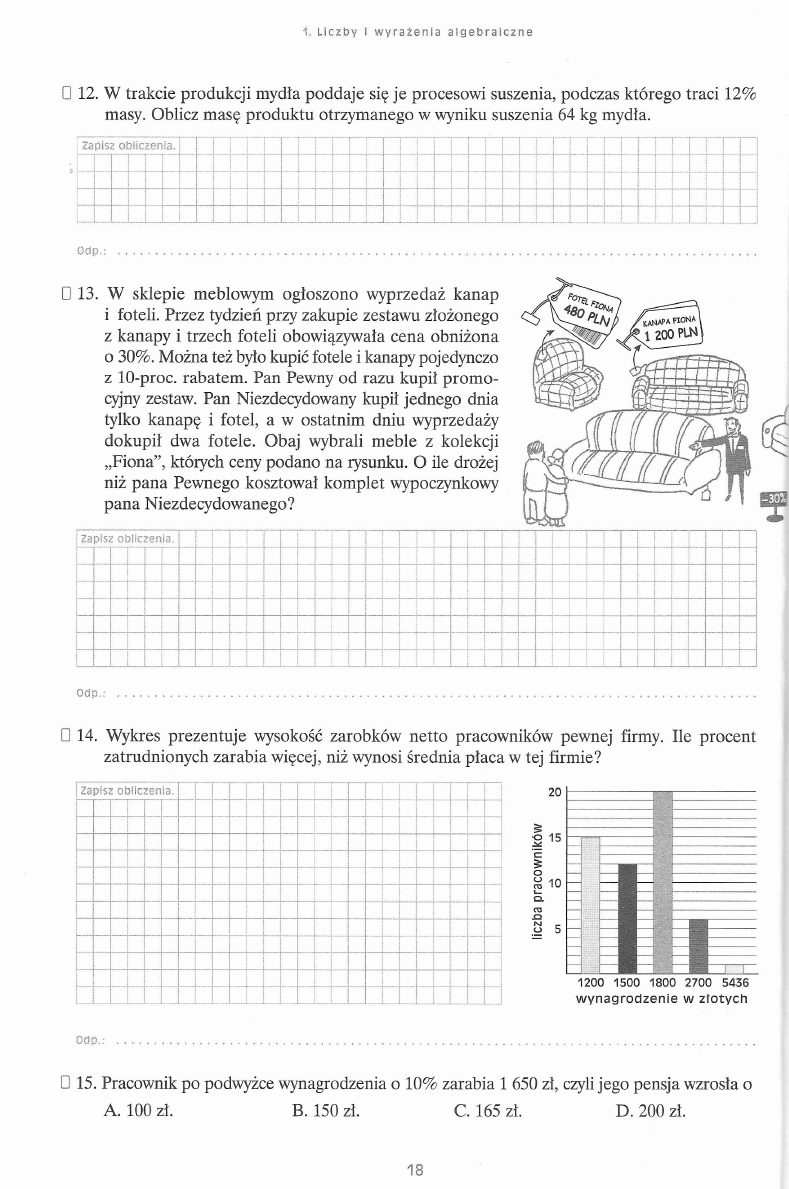
13. W sklepie meblowym ogłoszono wyprzedaż kanap
i foteli. Przez tydzień przy zakupie zestawu złożonego
z kanapy i trzech foteli obowiązywała cena obniżona
o 30%. Można też było kupić fotele i kanapy pojedynczo
z 10-proc. rabatem. Pan Pewny od razu kupił promo
cyjny zestaw. Pan Niezdecydowany kupił jednego dnia
tylko kanapę i fotel, a w ostatnim dniu wyprzedaży
dokupił dwa fotele. Obaj wybrali meble z kolekcji
„Fiona”, których ceny podano na rysunku. O ile drożej
niż pana Pewnego kosztował komplet wypoczynkowy
pana Niezdecydowanego?
Za
fisz ot
jHczersia.
1
l
i
I
0 0 f
U 14. Wykres prezentuje wysokość zarobków netto pracowników pewnej firmy. Ile procent
zatrudnionych zarabia więcej, niż wynosi średnia płaca w tej firmie?
Z a p i s u o b l i c z e n i a .
i
_
i
1
: i
1200 1500 1800 270 0 5436
w y n a g r o d z e n i e w z ło t y c h
□ 15. Pracownik po podwyżce wynagrodzenia o 10% zarabia 1 650 zł, czyli jego pensja wzrosła o
A. 100 zł.
B. 150 zł.
C. 165 zł.
D. 200 zł.
1 8

1.2. P r o c e n t y
J
16. Wynagrodzenie nowo zatrudnionego pracownika wynosi 1 100 zł miesięcznie, z podwyżką
co kwartał o stałą kwotę równą 10% pensji początkowej przez kolejne dwa lata. Oblicz
wysokość pensji pracownika po roku pracy.
Za pis: Ol)fic z e n ia .
~ ..;....
........
□ 17. Pan Zaradny pracuje w teatrze jako konserwator scenografii. Jego wynagrodzenie jest
obliczane w systemie godzinowym. Stawka podstawowa za godzinę pracy od poniedziałku
do piątku to 8,20 zł. Za pracę w sobotę pan Zaradny otrzymuje 25% więcej, a w niedzielę
50% więcej niż w dni robocze. Uzupełnij tygodniową kartę pracy pana Zaradnego.
Dzień tyg o d n ia
Czas pracy
Liczba godzin
W ynagrodzenie
[Zł]
podst.
25%
50%
Poniedziałek
dzień w o ln y
W to re k
5 .0 0 -1 3 .3 0
Środa
6 .3 0 - 1 3 .3 0
C zw artek
7 .0 0 -1 4 .0 0
Piątek
6 .0 0 - 1 3 .3 0
Sobota
1 4 .0 0 -2 2 .0 0
Niedziela
8 .3 0 -1 4 .3 0
Razem:
Zapisz o b lic z e n ia , i
.18. Pan Jan wpłacił 5 000 zł na lokatę Hit, której oprocentowanie równe jest 10% w stosunku
rocznym, a kapitalizacja odsetek odbywa się co kwartał. Jaka kwota pieniędzy będzie znaj
dowała się na lokacie pana Jana po pół roku od jej założenia? Wynik zaokrąglij do 1 gr.
¿a p is? obite
19
1. L i c z b y i w y r a ż e n i a
a l g e b r a i c z n e
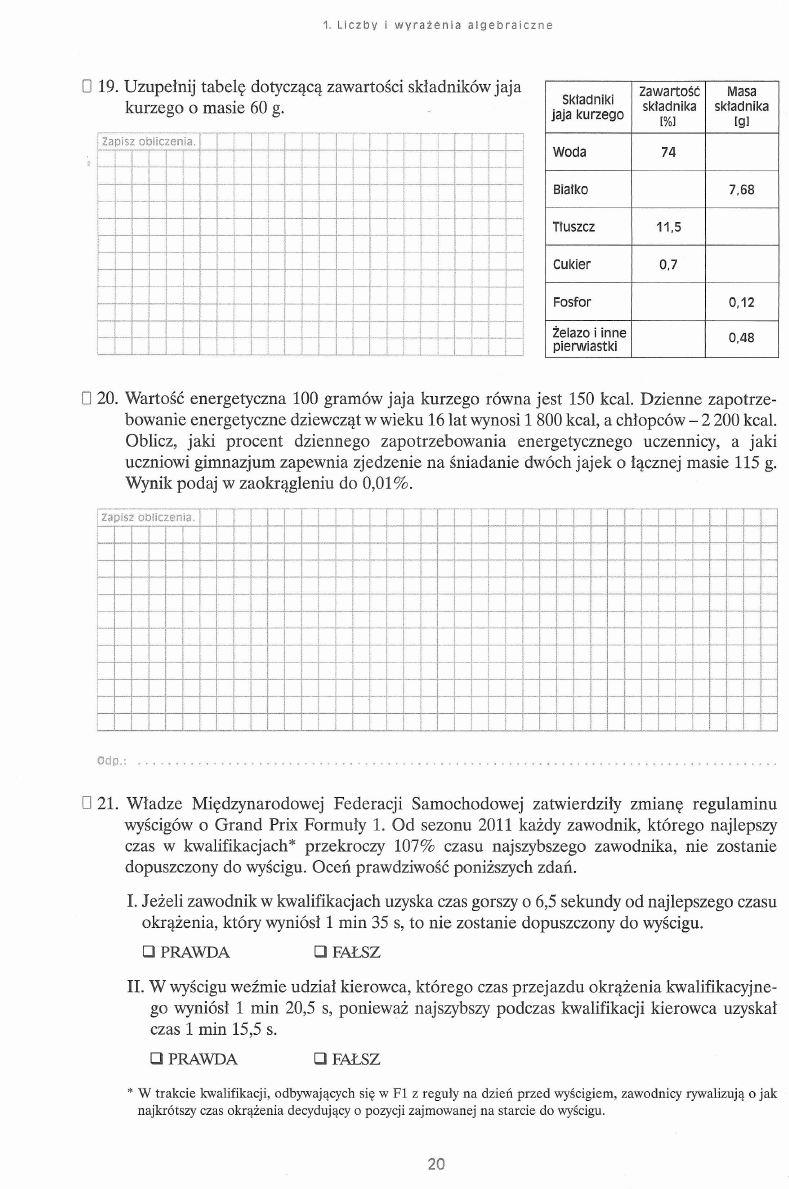
□ 19. Uzupełnij tabelę dotyczącą zawartości składników jaja
kurzego o masie 60 g.
Zapisz o b lic z e n i? .
Składniki
jaja kurzego
Zawartość
składnika
[%]
Masa
składnika
igi
Woda
74
Białko
7,68
Tłuszcz
11,5
Cukier
0,7
Fosfor
0,12
Żelazo i inne
pierwiastki
0,48
[J
20. Wartość energetyczna 100 gramów jaja kurzego równa jest 150 kcal. Dzienne zapotrze
bowanie energetyczne dziewcząt w wieku 16 lat wynosi 1 800 kcal, a chłopców - 2 200 kcal.
Oblicz, jaki procent dziennego zapotrzebowania energetycznego uczennicy, a jaki
uczniowi gimnazjum zapewnia zjedzenie na śniadanie dwóch jajek o łącznej masie 115 g.
Wynik podaj w zaokrągleniu do 0,01%.
Zapis? ODMczŁni;:
..................
□ 21. Władze Międzynarodowej Federacji Samochodowej zatwierdziły zmianę regulaminu
wyścigów o Grand Prix Formuły 1. Od sezonu 2011 każdy zawodnik, którego najlepszy
czas w kwalifikacjach* przekroczy 107% czasu najszybszego zawodnika, nie zostanie
dopuszczony do wyścigu. Oceń prawdziwość poniższych zdań.
I. Jeżeli zawodnik w kwalifikacjach uzyska czas gorszy o 6,5 sekundy od najlepszego czasu
okrążenia, który wyniósł 1 min 35 s, to nie zostanie dopuszczony do wyścigu.
□ PRAWDA
□ FAŁSZ
II. W wyścigu weźmie udział kierowca, którego czas przejazdu okrążenia kwalifikacyjne
go wyniósł 1 min 20,5 s, ponieważ najszybszy podczas kwalifikacji kierowca uzyskał
czas 1 min 15,5 s.
□ PRAWDA
□ FAŁSZ
* W trakcie kwalifikacji, odbywających się w F I z reguiy n a dzień przed wyścigiem, zawodnicy rywalizują o jak
najkrótszy czas okrążenia decydujący o pozycji zajmowanej na starcie do wyścigu.
2 0
1.2. P r o c e n t y
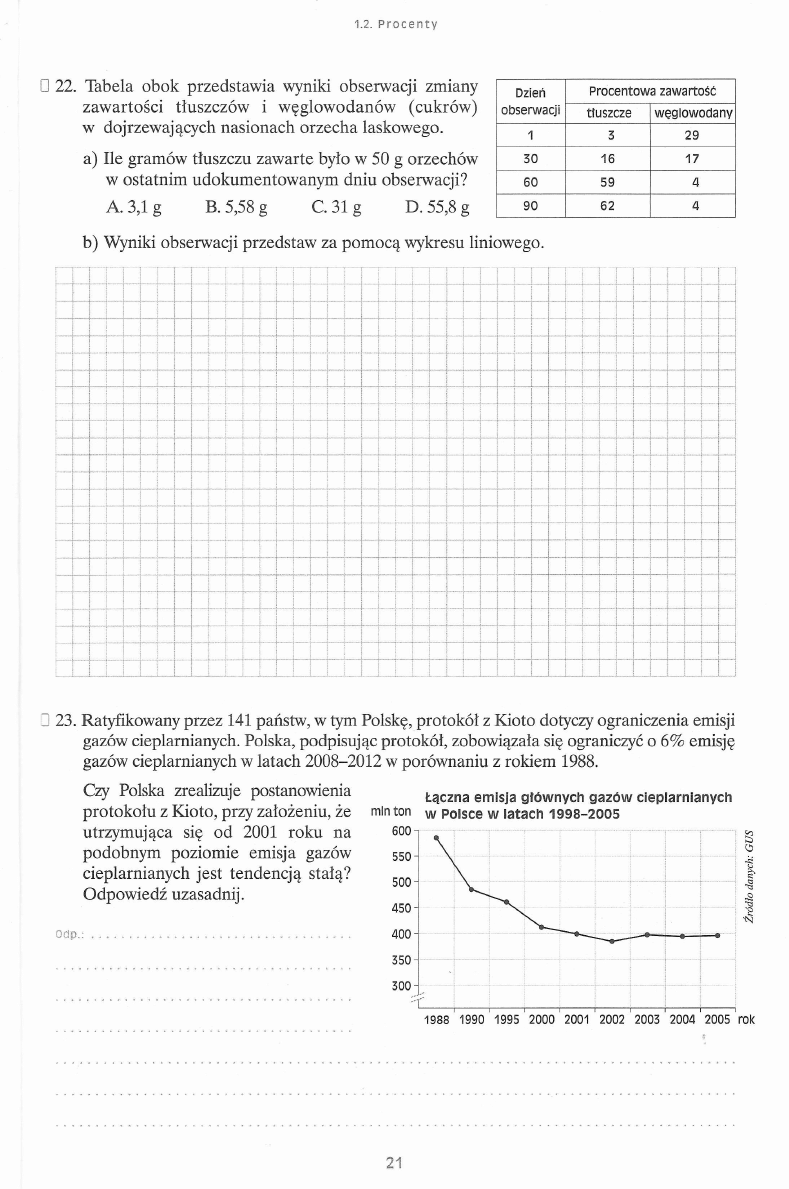
□ 22. Tabela obok przedstawia wyniki obserwacji zmiany
zawartości tłuszczów i węglowodanów (cukrów)
w dojrzewających nasionach orzecha laskowego.
a) Ile gramów tłuszczu zawarte było w 50 g orzechów
w ostatnim udokumentowanym dniu obserwacji?
A. 3,1 g
B. 5,58 g
C. 31 g
D. 55,8 g
Dzień
obserwacji
Procentowa zawartość
tłuszcze
węglowodany
1
3
29
30
16
17
60
59
4
90
62
4
b) Wyniki obserwacji przedstaw za pomocą wykresu liniowego.
23. Ratyfikowany przez 141 państw, w tym Polskę, protokół z Kioto dotyczy ograniczenia emisji
gazów cieplarnianych. Polska, podpisując protokół, zobowiązała się ograniczyć o 6% emisję
gazów cieplarnianych w latach 2008-2012 w porównaniu z rokiem 1988.
Czy Polska zrealizuje postanowienia
Łączna emisja głównych gazów cieplarnianych
protokołu z Kioto, przy założeniu, że
min ton
w p0 isce w latach 1998-2005
utrzymująca się od 2001 roku na
podobnym poziomie emisja gazów
cieplarnianych jest tendencją stałą?
Odpowiedź uzasadnij.
O i i p
..........................................................................
21
Źr
ód
ło
da
ny
ch
:
GUS
1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
□ 24. Latem 1988 roku w Górach Skalistych miały miejsce wielkie pożary. Spłonęło 323 tys. hekta
rów lasu znajdującego się w granicach Parku Narodowego Yellowstone. 36% parku zmieniło się
w pogorzelisko. Jednak już wiosną następnego roku zaobserwowano, że na zniszczonych przez
ogień terenach rosną liczne gatunki roślin zielnych. Oblicz powierzchnię Parku Narodowe
go Yellowstone. Podaj wynik w km2 w zaokrągleniu do drugiego miejsca po przecinku.
Zapisz o b lic z e n ia .
.
i
1
!
O d p .:
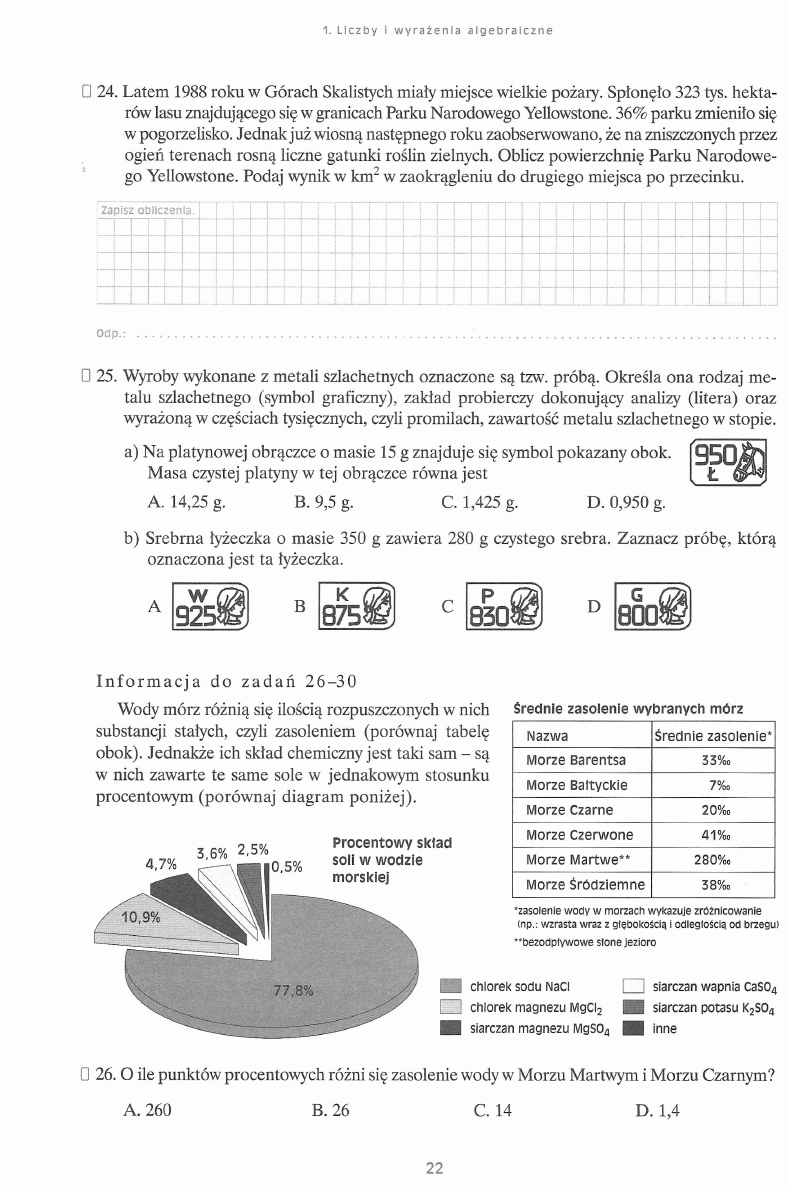
0 25. Wyroby wykonane z metali szlachetnych oznaczone są tzw. próbą. Określa ona rodzaj me
talu szlachetnego (symbol graficzny), zakład probierczy dokonujący analizy (litera) oraz
wyrażoną w częściach tysięcznych, czyli promilach, zawartość metalu szlachetnego w stopie.
a) Na platynowej obrączce o masie 15 g znajduje się symbol pokazany obok.
Masa czystej platyny w tej obrączce równa jest
A. 14,25 g.
B. 9,5 g.
9 5 0 ,
Ł
C. 1,425 g.
D. 0,950 g.
b) Srebrna łyżeczka o masie 350 g zawiera 280 g czystego srebra. Zaznacz próbę, którą
oznaczona jest ta łyżeczka.
A
W
9 2 5 $
B
K
8 7 5 ^
c
p
8 3 0 ^
D
8 0 0 ?
I n f o r m a c j a do z a d a ń 2 6 -3 0
Wody mórz różnią się ilością rozpuszczonych w nich
substancji stałych, czyli zasoleniem (porównaj tabelę
obok). Jednakże ich skład chemiczny jest taki sam - są
w nich zawarte te same sole w jednakowym stosunku
procentowym (porównaj diagram poniżej).
3 ,6 %
2 ,5 %
Procentowy skład
soli w wodzie
morskiej
Średnie zasolenie wybranych mórz
Nazwa
Ś rednie zasolenie*
M orze Barentsa
33%o
M orze B ałtyckie
7%o
M orze Czarne
20%o
M orze C zerw one
41%o
M orze M a rtw e **
280%o
M orze Ś ródziem ne
38%o
chlorek sodu NaCI
[ZH siarczan wapnia CaS04
I
I chlorek magnezu MgCI2
H I siarczan potasu K2S04
[_ J siarczan magnezu MgS04 H inne
'zasolenie wody w morzach wykazuje zróżnicowanie
(np.: wzrasta wraz z głębokością i odległością od brzegu)
•‘ bezodpływowe stone jezioro
□ 26. O ile punktów procentowych różni się zasolenie wody w Morzu Martwym i Morzu Czarnym?
A. 260
B. 26
C. 14
D. 1,4
22
1.2. P r o c e n t y
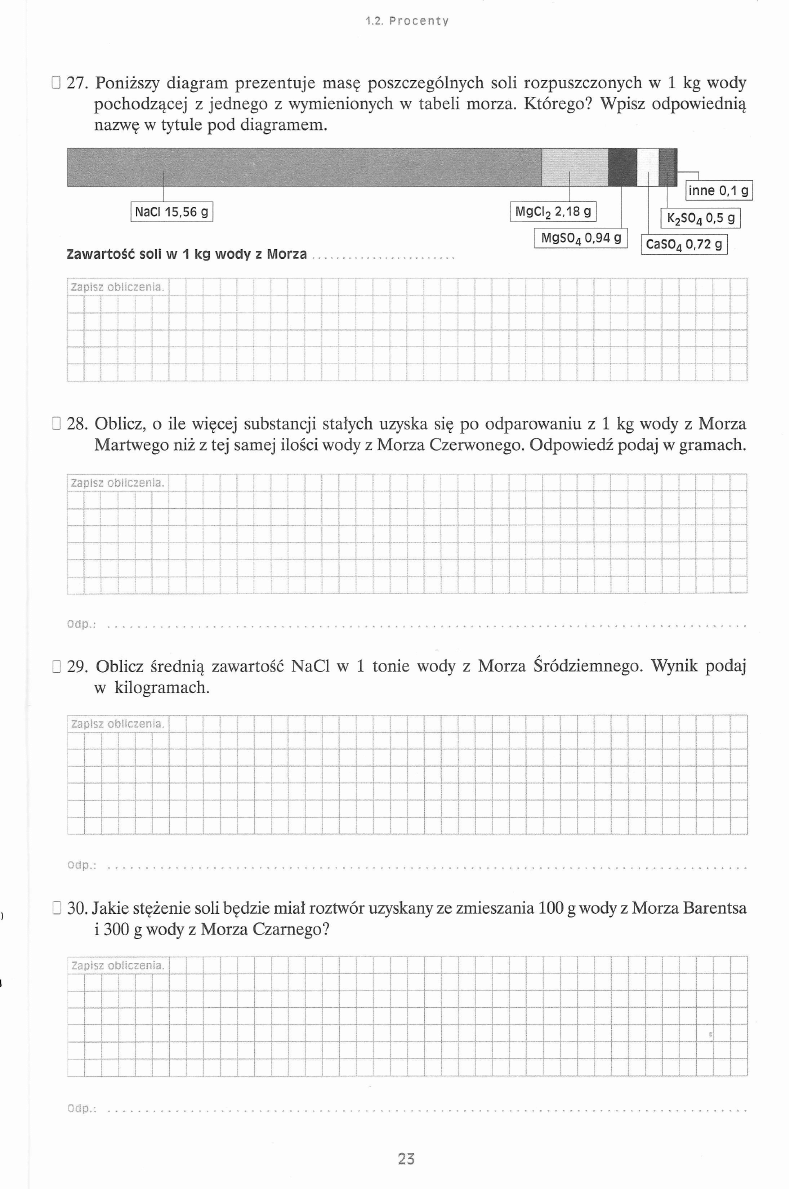
II 27. Poniższy diagram prezentuje masę poszczególnych soli rozpuszczonych w 1 kg wody
pochodzącej z jednego z wymienionych w tabeli morza. Którego? Wpisz odpowiednią
nazwę w tytule pod diagramem.
j 28. Oblicz, o ile więcej substancji stałych uzyska się po odparowaniu z 1 kg wody z Morza
Martwego niż z tej samej ilości wody z Morza Czerwonego. Odpowiedź podaj w gramach.
a
c
d
;; .
J:,'
□ 29. Oblicz średnią zawartość NaCl w 1 tonie wody z Morza Śródziemnego. Wynik podaj
w kilogramach.
ia p K z o D iic ie n ia
p
U 30. Jakie stężenie soli będzie miał roztwór uzyskany ze zmieszania 100 g wody z Morza Barentsa
i 300 g wody z Morza Czarnego?
Zapisz o b lic z e n ia .
:
23

1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
I 1.3. W Y R A Ż E N I A A L G E B R A I C Z N E
M B S B
□ 1. Zaznacz liczbę spełniającą warunek: a > 15.
A. a = -15
B. a = f
C a = f
□ 2. Wyłącz wspólny czynnik przed nawias.
I. 4ab2 - 8a2b —
II. 3a3x - 6abc + 15ox3 =
□ 3. Uzupełnij wyrażenie algebraiczne tak, aby równość była prawdziwa.
3x ■
= 15x2y
□ 4. Wyrażenie (2a - b)(2a + b) można zapisać w postaci
A. 4a - b.
B. 4a2 - b2.
C. 4a - lab - lab - b.
D. 4a2 - 4ab + b2.
□ 5. Dany jest zbiór wyrażeń: {lx, 3x,x - 1, lx - 1, lx + 6, lx + 1, 3x + 3,x,x + 1}. Wypisz z niego
te, które dla każdej całkowitej wartości x są:
I. parzyste
II. nieparzyste
DI. podzielne przez 3 .....................
□ 6. Zapisz za pomocą odpowiedniego wyrażenia algebraicznego iloczyn dowolnych trzech
kolejnych liczb nieparzystych.
0 7. Napisz liczbę trzycyfrową, której cyfra setek jest równa m, cyfra dziesiątek jest o 1 większa
od cyfry setek, a cyfra jedności jest dwa razy większa od cyfry setek. Uzasadnij, że zapisana
liczba jest podzielna przez 2.
U z a s a d n ie n ie :.......................................................................................................................................................................
0 8. Oblicz wartość liczbową wyrażenia V2x + 6 + V54 - 6x dl ax = 5.
D .a = 15
24
1.3. W y r a ż e n i a a l g e b r a i c z n e
□ 9. Wyrażenie Ą2x - 6 • Ą2 równe jest
A. V 4 x - 6 .
B. V4c - 12.
C. 4x - 6.
D. 4x - 12.
J 10. Oblicz wartość wyrażenia dla x = 1.
\x -1
("V-
f i
+ i) (3.
x
-
L)2 (3;c
-
_
z•)2 +
,2
o
1
n
«A
fil
¿j
\
2
' ^
4
|
|
|
j
I 11. Różnica sum algebraicznych (1,8m2 - 0,34m + 27,5) - (2,4m2 - 3,2m - 5,5) jest równa
A. -0,6m2 - 3,54m + 33.
B. -0,6m2 + 2,86m + 33.
C.
- 0 ,6 m 2
- 2,94m + 33.
D.
- 0 ,6 m 2
+ 24,3m + 22.
□ 12. Pole zacieniowanej części rysunku można zapisać w postaci
—
A. mk - 3 - 1 .
B. m k - 3 - 1 - 3 k.
m
C. (m - 3){k - 1).
D. (m - 3)(k + 1).
I
k
l
I] 13. O ile zwiększy się pole prostokąta o bokach a i b, gdy każdy z jego boków zwiększymy o 1,5?
A. 1,5ab + 2,25
B. ab + l,5a + 1,56 + 2,25
C. 1,5a + 1,5b + 2,25
D. l,5c + 1,56 + 22,5
II 14. Oblicz obwód trójkąta pokazanego obok. Odpowiedź
podaj w formie wyrażenia w najprostszej postaci.
Zapisz o b lic z e n ia .
■
25
1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
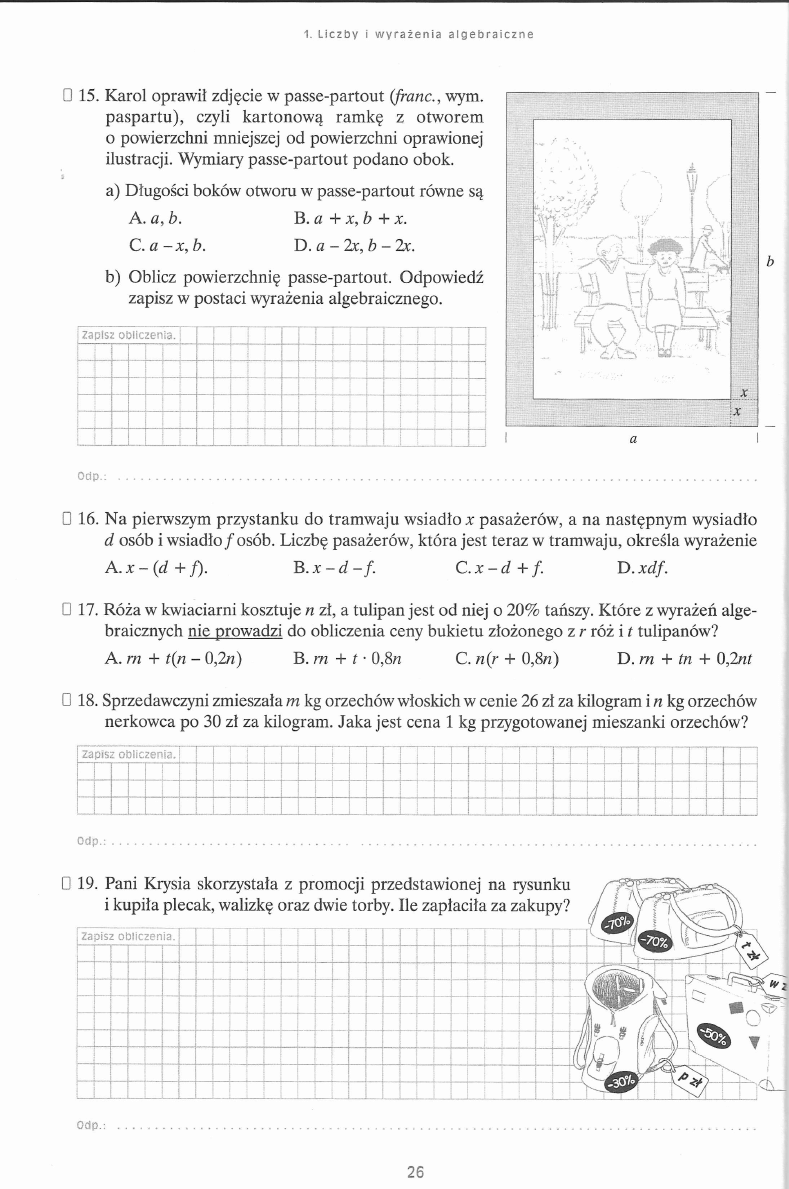
□ 15. Karol oprawił zdjęcie w passe-partout (franc., wym.
paspartu), czyli kartonową ramkę z otworem
o powierzchni mniejszej od powierzchni oprawionej
ilustracji. Wymiary passe-partout podano obok.
a) Długości boków otworu w passe-partout równe są
A. a, b.
B. a + x, b + x.
C. a - x , b .
D. a - 2x, b - 2x.
b) Oblicz powierzchnię passe-partout. Odpowiedź
zapisz w postaci wyrażenia algebraicznego.
Zapisz o b lic z e n ia .
Ocfp.
0 16. Na pierwszym przystanku do tramwaju wsiadło x pasażerów, a na następnym wysiadło
d osób i w siadło/osób. Liczbę pasażerów, która jest teraz w tramwaju, określa wyrażenie
A . x - ( d + f ) .
B , x - d - f .
C . x - d + f .
D. xdf.
□ 17. Róża w kwiaciarni kosztuje n zł, a tulipan jest od niej o 20% tańszy. Które z wyrażeń alge
braicznych nie prowadzi do obliczenia ceny bukietu złożonego z r róż i t tulipanów?
A. m + t(n - 0,2n)
B. m + t • 0,8n
C. n(r + 0,8«)
D , m + t n + 0,2nt
□ 18. Sprzedawczyni zmieszała m kg orzechów włoskich w cenie 26 zł za kilogram i n kg orzechów
nerkowca po 30 zł za kilogram. Jaka jest cena 1 kg przygotowanej mieszanki orzechów?
Za pisz o b lic z e n ia .
O d p .: . . . .
□ 19. Pani Krysia skorzystała z promocji przedstawionej na rysunku
i kupiła plecak, walizkę oraz dwie torby. Ile zapłaciła za zakupy?
Zapis
o t)iic zen ia.
_
-
: J 3 & \ !
'IÀ <*
\ A
...........
!.. > —
r=rt.—
...
l É É l Ê ) i \
F r C " '" '
•
r
1
A
M
^
U
*
l i s i
■ -
T
\ 7
O dp.
2 6
1.3. W y r a ż e n i a a l g e b r a i c z n e
□ 20. Przed sezonem w październiku 2009 roku sklep podwyższył cenę nart o 10%. Po sezonie
w kwietniu 2010 roku sklep ogłosił obniżkę ceny tych samych nart o 10%. Porównaj ceny nart
we wrześniu 2009 roku oraz w kwietniu 2010 roku. Która z cen była wyższa i o ile procent?
Zapisz o b lic z e n ia .
:;p
21. Wzór na objętość beczki do kisze
nia ogórków przedstawiono obok.
Przekształć podany wzór tak, aby
wyznaczyć średnicę beczki w naj
węższym punkcie jej przekroju.
V = ±
k
H ( 2D2 + d2)
H
D
- największa średnica
przekroju beczki
d
- najmniejsza średnica
u beczki
II
- wysokość beczki
¡¡i
.
J
22. Drogę przebytą przez ciało poruszające się ruchem ze wrastającą liniowo prędkością w sto
sunku do czasu, czyli ruchem jednostajnie przyspieszonym, opisuje wzór:
n t2
s = s0 + v0t +
,
gdzie ,s0 to droga początkowa ciała, v0 - prędkość początkowa ciała, t - czas trwania ruchu,
a - przyspieszenie. Wyznacz wartość przyspieszenia a.
Z a p iS i c o iic z e n ia
:
27
1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
» 1 . 4 . R
Ó
W
N
A
N
I A
H
^ H
B
^ H
H
B
H
K
a H
H
H
H
H
n n s n i
□ 1. Czy wartość poniższego wyrażenia jest pierwiastkiem równania: 1 - 3^--92 _ 2 X ?
..
■
> i
•
0
7
i T
V
i 1
n
i
, n
i
1
V3
2> \
3
*
i)
18
I 1
..
..
O d p .: ..........................................................................................................................................................................................................................................................
□ 2. Suma cyfr x iy dwucyfrowej liczby 10x + _y równa jest 9. Podaj wszystkie liczby spełniające
ten warunek.
O d p ,: ..........................................................................................................................................................................................................................................................
□ 3. Do liczby naturalnej x dopisano z prawej jej strony cyfrę 8. Teraz liczba jest o 251 większa
od x. Jaką liczbą jest x?
Zapisz o b lic z e n ia .
i
O d p .: ..........................................................................................................................................................................................................................................................
Cf/D 4. Liczbę 165 rozkładamy na sumę dwóch składników tak, aby jeden był o 30 większy od 35%
drugiego składnika. Te składniki to
A. 65 i 100.
B. 35 i 130.
C. 85 i 80.
D. 60 i 105.
□ 5. Na podstawie danych z rysunku obok oblicz wartość x.
Zapisz o b lic z e n ia .
!
)
!
28
1.4. R ó w n a n i a
-f/ J 6. Prostokątny karton o obwodzie 112 cm rozcięto na dwa identyczne prostokąty o obwodzie
86 cm każdy. Oblicz długości boków kartonu przed rozcięciem.
Zapisz o b lic z e n ia .
■dp........................................................................
...........................................................
j 7. Pola trzech działek mają się do siebie jak 2,5:3:4,5. Oblicz pole każdej działki, jeżeli
największa jest o 720 m2 większa od średniej.
Zapisz o b lic z e n ia .
0
D 9. Dwaj koledzy: Kamil i Alek mają pewną kwotę pieniędzy. Kamil ma tego, co ma Alek.
Gdyby Kamil wydał ^ swoich pieniędzy, a Alek dostał 120 zł, to razem mieliby 1 080 zł.
Jaką kwotę pieniędzy ma każdy z chłopców?
Za pis: o ttiic z e n ia .
i
i
i
i
!
!
i
j
]
j
■
¡i p
O d p .:
. . . .................................................................................... . . . . . . . . . . . . . .
.
8. Bukiet róż kosztuje dwa razy tyle, co bukiet tulipanów.
Bukiet z kwiatów mieszanych kosztuje trzy razy mniej
niż bukiet z róż. Zapisz ceny poszczególnych bukietów
na rysunku obok, jeżeli wartość wszystkich trzech to 33 zł.
Za )is: otoiic zenia.
1
29
1 L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
□ 10. Z mosiężnego pręta wykonano trzy wałki. Na pierwszy zużyto połowę pręta, na drugi | resz
ty, a trzeci ma masę 3 kg. Oblicz, jaką masę ma cały pręt.
O dp . . .
. . .
............................................................................................................
fW u 11. Woda przy maksymalnie odkręconym kranie wypełnia basen w ciągu 8 godzin, a odpływ
odprowadza z niego wodę w ciągu 12 godzin. Przez niedopatrzenie zaczęto napełniać
basen przy otwartym odpływie. Czy woda napełni basen? A jeśli tak, to po ilu godzinach
basen zostanie napełniony?
Zapisz o b lic z e ń
13-
: C . : ..
□ 12. Marysia ma 25% wieku swojego ojca, a jej brat Adam y wieku Marysi. Ile lat ma każda
z osób, jeżeli razem mają 64 lata?
Zapisz o b lic z e n ia .
Odp.:
0 13. Zwierzęta Tomka - hodowcy chomików i papug - mają razem 12 głów i 34 nogi. Zaznacz
równanie, które pozwoli obliczyć, ile chomików i ile papug ma Tomek.
A. x • 2 + (12 - x ) • 4 = 34
B. 2x • 4x = 34
C. (2 + 4>t = 34
D. 12x + (1 2 - x ) • 4 = 34
u 14. Ze zbiornika zawierającego 180 1 benzyny odlano taką jej ilość, że w zbiorniku pozostało
cztery razy tyle paliwa, co odlano. Ile paliwa zostało w zbiorniku?
A. 36 1
B. 45 1
C. 144 1
D. 180 1
30

1.4. R ó w n a n i a
13 15. Turysta pokonał trasę w ciągu 2 dni. W pierwszym przeszedł o 8 km więcej niż w drugim
i pokonał | całej trasy. Oblicz, ile kilometrów turysta przeszedł każdego dnia oraz podaj
długość całej trasy.
i
t
1
i
i
,:d p.
H 16. Pasażer płaci
5
złotych, gdy taksówkarz uruchomi taksometr. Za prze
jechanie 1 km taksometr wybija 3 zł. Które równanie pozwoli obliczyć,
ile kilometrów przejechał pan Jan, jeżeli za kurs zapłacił 61 zł?
A.
5 + 3 *
= 61
B.
3%
-
5
= 61
C . 3x =
61 +
5
D.
(5 + 3 > =
61
3 17. Taksówkarz miał kurs za miasto. W mieście trasę 7,2 km pokonał ze śred
nią prędkością 36
Z jaką średnią prędkością przejechał 40-kilo-
metrową trasę za miastem, jeżeli całą trasę pokonał w ciągu godziny?
Z apisz o b lic z e n ia .
dp.;
...............
□ 18. O godzinie 9.00 na trasę o długości 36 km wyjechał rowerzysta, który jedzie ze średnią pręd
kością 20
Pół godziny później w ślad za rowerzystą wyjechał motocyklista jadący ze
średnią prędkością 36
Oblicz, po jakim czasie motocyklista dogoni rowerzystę.
Z apisz o b lic z e n ia .
K ip
31
1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
K 1.5. U K Ł A D Y R Ó W N A Ń
□ 1. Obwód prostokąta ma 60 cm. Jeżeli jeden bok tego prostokąta zwiększy się o 5 cm, a drugi
zmniejszy o 2 cm, to jego pole się nie zmieni. Który z układów pozwoli obliczyć długości
boków tego prostokąta?
fx + y = 60
i 2x + 2y = 60
A. \
B. 1
x +5 = y - 2
[x + 5 + y - 2 = 60
2x + 2y = 60
1 2x + 2y = 60
(x + 5)(y - 2) = 60
{ (x + 5)(y - 2 ) - xy
□ 2. Obwód prostokąta jest równy 40 cm. Jeżeli długość jednego boku zwiększy się o 3 cm,
a drugiego zmniejszy o 3 cm, to otrzyma się kwadrat. Oblicz pole tego prostokąta.
Zapisz o b lic z e n ia .
O d p .: .........................................................................................................................................................................................................................................................
□ 3. Zmontowano rurociąg długości 344 m, złożony z 46 rur o dwóch długościach: 470 cm i 825 cm.
Uzupełnij równanie w układzie równań prowadzącym do obliczenia liczby rur krótszych
i dłuższych tworzących ten rurociąg.
k + d = 46
□
O d p .:
4. Dwie przyjaciółki zamówiły po porcji tortu; jedna wybrała śmietankowy, a druga - orze
chowy i zapłaciły razem 16 zł. Przy stoliku obok za zamówienie złożone z czterech
porcji tortu śmietankowego i dwóch - orzechowego zapłacono 52 zł.
Oblicz, ile kosztuje porcja tortu śmietankowego w tej kawiarni.
Zapisz o b lic z e n ia .
32

1.5. U k ł a d y r ó w n a ń
□ 5. Na podstawie układu równań uzupełnij dane w treści zadania.
x
+
y
= 40
Ile kilogramów cukierków dwóch rodzajów p o
zł i
złzakilo-
20x
+ 30_y = 24- 40
gram należy odważyć, aby otrzymać 40 kg mieszanki w cenie
zł?
I 6. Klientka kupiła rano tort owocowy oraz 15 ciastek i za
płaciła 54 zł. Po godzinie 18 cukiernia przecenia niesprze-
dane torty o 40%, a ciastka - o 60%. Klient, który
wieczorem kupował 2 torty i 20 ciastek zapłacił 44,80 zł.
Jaka była cena tortu, a jaka - ciastka przed przeceną?
; 2 ? p ś s z o d l e ż e n i a |
!
I
; ;
0<
I 7. Za trzy zeszyty i dwa długopisy zapłacono 26,20 zł. Po podwyżce ceny zeszytu o 10%, a ceny
długopisu o 20%, za tę samą liczbę zeszytów i długopisów zapłacono 30,42 zł. Oblicz cenę
zeszytu i długopisu po podwyżce cen.
z
O dp .:
I 8. W klasach 2a i 2b było razem 61 uczniów. W zorganizowanych zawodach sportowych brała
udział 29-osobowa drużyna złożona z 80% uczniów klasy 2a i 25% uczniów klasy 2b. Oblicz
liczbę uczniów każdej z klas.
zap ■
|
O dp .:
35
1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
□ 9. Drużyna za pięć meczów wygranych i cztery zremisowane otrzymała 29 punktów, a za cztery
wygrane i cztery zremisowane 24 punkty. Ile punktów drużyna otrzymuje za mecz wygrany,
a ile - za remis?
Li
10. Przed 10 laty ojciec był jedenaście razy starszy niż syn. Ile lat ma obecnie ojciec, a ile syn, jeżeli
za 10 lat będą mieli razem 64 lata? Wskaż układ równań pozwalający odpowiedzieć na pytanie.
A.
C.
[x = l l y
+ 10 + y + 10 = 64
f j c - 1 0 = l ( y — 1 0 )
[x + y — 64
B.
D.
J x - 1 0 = ll(y - 10)
jx + 10 + y + 10 = 64
|x = 11y
[x + y = 64
U
11. Zapisz w ramkach wiek Patryka i jego mamy.
i ZE
■■ ■ ' '
=r i
U 12. Teofil i młodsza od niego Agata mają razem 105 lat. Różnica ich wieku równa się połowie
liczby lat Agaty. Ile lat ma Agata, a ile - Teofil?
U
:
34
1.5. U k ł a d y r ó w n a ń
13. Suma cyfr liczby dwucyfrowej wynosi 12. Jeżeli odejmiemy od tej liczby liczbę otrzymaną
przez przestawienie cyfr w liczbie pierwotnej, to otrzymamy 54. Który z układów pozwoli
znaleźć tę liczbę?
fx + y = 12
fx + y — 12
A.
B-
[jcy = 54
[2xy = 54
^ J x + ; y = 12
J l 0 x + y = 12
| l(k + y - 10y - x = 54
[ 10x + y - 10y + x = 54
Z 14. Znajdź taką liczbę dwucyfrową, żeby suma jej cyfr wynosiła 14 i żeby po przestawieniu cyfr
otrzymać liczbę większą od liczby szukanej. Ile jest takich liczb? Podaj wszystkie
rozwiązania.
Z :
Odp : ...................... .............................. .. ........................................................................ .. . .................................................................... ..............................
I 15. Mianownik ułamka jest o 7 większy od jego licznika. Gdy od licznika i mianownika odję
to 8, to otrzymano ułamek równy
Jaki to ułamek?
zap
i
O dp .: ................................................................................ .. .....................................................................................................................................................................
16. Zaznacz układ równań prowadzący do znalezienia dwóch liczb, których suma równa jest 35.
Jeżeli pierwsza z liczb będzie większa o 20%, a druga mniejsza o 20%, to ich suma
zwiększy się o 3.
fx + y = 35
i x + y = 35
A.
B-
[20% -x + 20% -y = 35
[20% - x - 2 0 % - y = 35
c j x + y = 35
^ j x + y = 35
{120% • x - 2 0 % • y = 35 +3
'
1
120%-x + 8 0 % -y = 35 +3
55
1. L i c z b y i w y r a ż e n i a a l g e b r a i c z n e
tf/O 17. Gdyby turysta powiększył swoją prędkość o pewną liczbę kilometrów na godzinę,
to drogę 24 km przebyłby w ciągu 6 godzin. Gdyby zaś prędkość o tę samą liczbę
zmniejszył, to ową drogę przeszedłby w ciągu 8 godzin. Z jaką prędkością idzie turysta?
Zapisz o b lic z e n ia .
O d p .:
□ 18. Odległość między przystaniami A i B równa jest 36 km. Kurs statku z A do B odbywa
się pod prąd rzeki i trwa 3 godziny, a z B do A - 2 godziny. Jaka jest prędkość prądu
rzeki, a jaka - statku na wodzie stojącej?
Zapisz o b lic z e n ia .
i
i
—
1
....L
O dp.
□ 19. Krawcowa dostała 32,8 m materiału, z którego ma uszyć 11 kostiu
mów w dwóch rozmiarach. Ile kostiumów każdego z rozmiarów
uszyje, jeżeli na kostium w większym rozmiarze potrzebuje go 3,2 m,
a w mniejszym - 2,8 m i chce wykorzystać cały materiał?
1.5. U k f a d y r ó w n a ń
20. Zaznacz układ równań, który pozwoli obliczyć, ile trzeba zmieszać octu o stężeniu 6%
z octem o stężeniu 10%, żeby otrzymać 20 1 o stężeniu 7%.
A.
C.
+ y — 20
[ ó %- x + 10 % -y = 7% • 20
■
y = 20
\ ó %- x + 10% -y = 7% • 20
B.
D.
j"x
+ y
= 20
lo,6 -
jc
+ 10% -y =
20
fX + y = 10
l_0,06 • x - 0,01 •
y =
0,07 • 20
21. W 18 kontenerach dwóch rodzajów: o pojemności 4 1 i 6 1, znajduje się 88 ton kawy. Oblicz
liczbę kontenerów większych i mniejszych, zakładając, że są zapakowane do pełna.
zap
|
|
|
|
I
i
•
1
i
:
l
i
3 d p.:
I 22. Trzy skrzynki z towarem mają łącznie masę 250 kg. Trzecia skrzynka jest o 10 kg cięższa
niż pierwsza i druga razem, a druga z trzecią razem są cięższe o 110 kg od pierwszej. Jaką
masę ma każda skrzynka?
Zapisz o b lic z e n ia .
3 d p .: ........................................ ...............................................................................................................................................................................................................
_ 23. Uczestnikowi teleturnieju zadano 40 pytań. Za poprawną odpowiedź otrzymywał 10 punktów,
a tracił 5 punktów za błędną odpowiedź. Na ile pytań uczestnik odpowiedział błędnie, jeżeli
zdobył w sumie 340 punktów?
Zapisz o b lic z e n ia .
.i
...
O d p .; ................................................................................... .................. .. ......................................................................... .. ............................. .. ................................
37
2.
W Y CR , 5 “ F U N K C J I
■ 2.1. F UNKC J E m m m m m m m m m m m m m m m m m m M g&ff»t
£MR£g<1 »
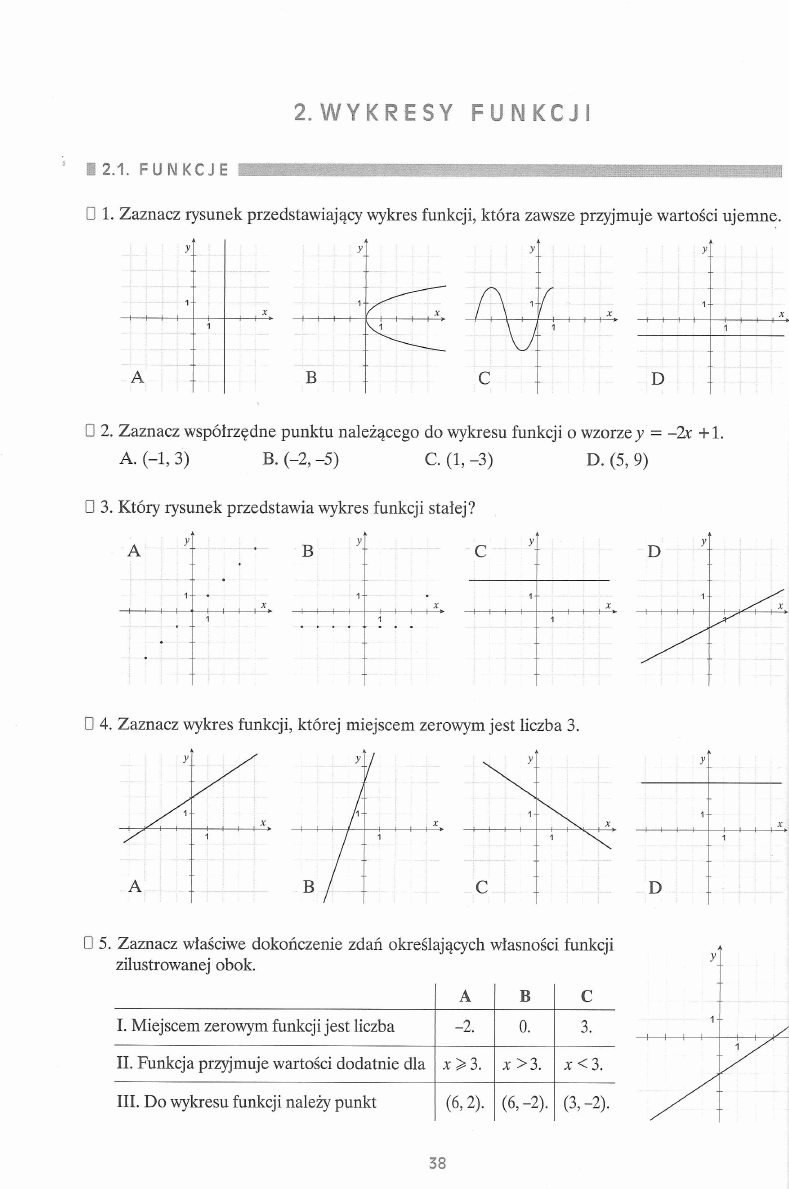
U 1. Zaznacz rysunek przedstawiający wykres funkcji, która zawsze przyjmuje wartości ujemne.
U 2. Zaznacz współrzędne punktu należącego do wykresu funkcji o wzorze y — -2x +1.
A. (-1 ,3 )
B. (-2, -5)
C. (1, -3)
D. (5, 9)
□ 3. Który rysunek przedstawia wykres funkcji stałej?
y
.
n
y
.
B
X
X
i
1
i-
:
X
1
D
L) 4. Zaznacz wykres funkcji, której miejscem zerowym jest liczba 3.
□ 5. Zaznacz właściwe dokończenie zdań określających własności funkcji
zilustrowanej obok.
A
B
C
I. Miejscem zerowym funkcji jest liczba
-2.
0.
3.
II. Funkcja przyjmuje wartości dodatnie dla
x > 3.
x >3.
x < 3.
III. Do wykresu funkcji należy punkt
(6, 2).
(6, -2).
(3,-2).
38
2.1. F u n k c j e
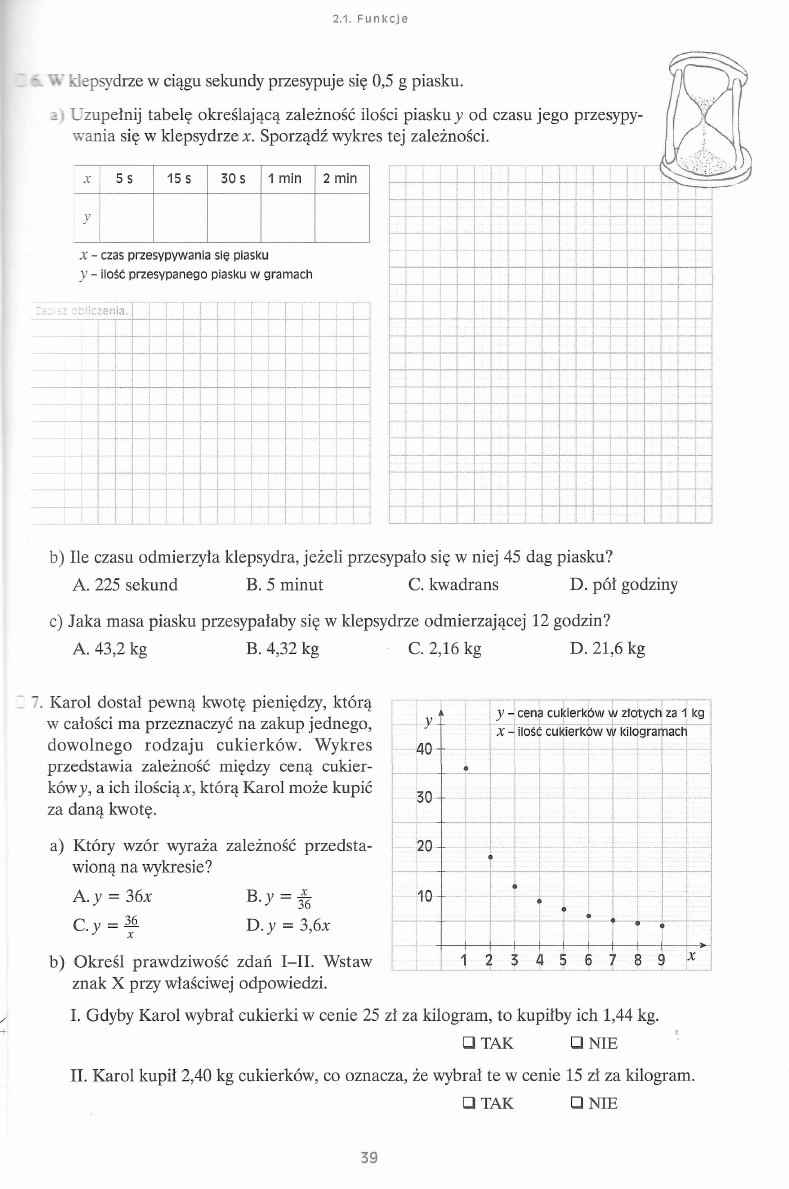
~ W klepsydrze w ciągu sekundy przesypuje się 0,5 g piasku.
a» Uzupełnij tabelę określającą zależność ilości p iask u j od czasu jego przesypy
wania się w klepsydrze x. Sporządź wykres tej zależności.
X
5 S
1 5 S
3 0 S
1 m in
2 m in
y
x
- czas przesypyw ania się piasku
y
- ilość przesypanego piasku w gram ach
b iic z e
b) Ile czasu odmierzyła klepsydra, jeżeli przesypało się w niej 45 dag piasku?
A. 225 sekund
B. 5 minut
C. kwadrans
D. pół godziny
c) Jaka masa piasku przesypałaby się w klepsydrze odmierzającej 12 godzin?
A. 43,2 kg
B. 4,32 kg
C. 2,16 kg
D. 21,6 kg
7. Karol dostał pewną kwotę pieniędzy, którą
w całości ma przeznaczyć na zakup jednego,
dowolnego rodzaju cukierków. Wykres
przedstawia zależność między ceną cukier
kowy, a ich ilością x, którą Karol może kupić
za daną kwotę.
a) Który wzór wyraża zależność przedsta
wioną na wykresie?
A. y = 36x
B .y =
C . y = f
D. y = 3,6x
b) Określ prawdziwość zdań I-II. Wstaw
znak X przy właściwej odpowiedzi.
I. Gdyby Karol wybrał cukierki w cenie 25 zł za kilogram, to kupiłby ich 1,44 kg.
□ TAK
□ NIE
II. Karol kupił 2,40 kg cukierków, co oznacza, że wybrał te w cenie 15 zł za kilogram.
□ TAK
□ NIE
v
y
- cen< cułcierków w złotych za 1 kg i
/i n
-
x
- ilość cukierków w kilogramach . V ,
I
7 0
.
. '
.. ..
..........
■... ■■■{.... ■
..
,.|
o n
. .
■
■■■ •
.
■
.......
;
........i........
4 0
•
►
1
2
3
LJ
3 i
X
39
2. W y k r e s y f u n k c j i
1
2 2
. o d c z y i y w a n i e w y k r e s ó w
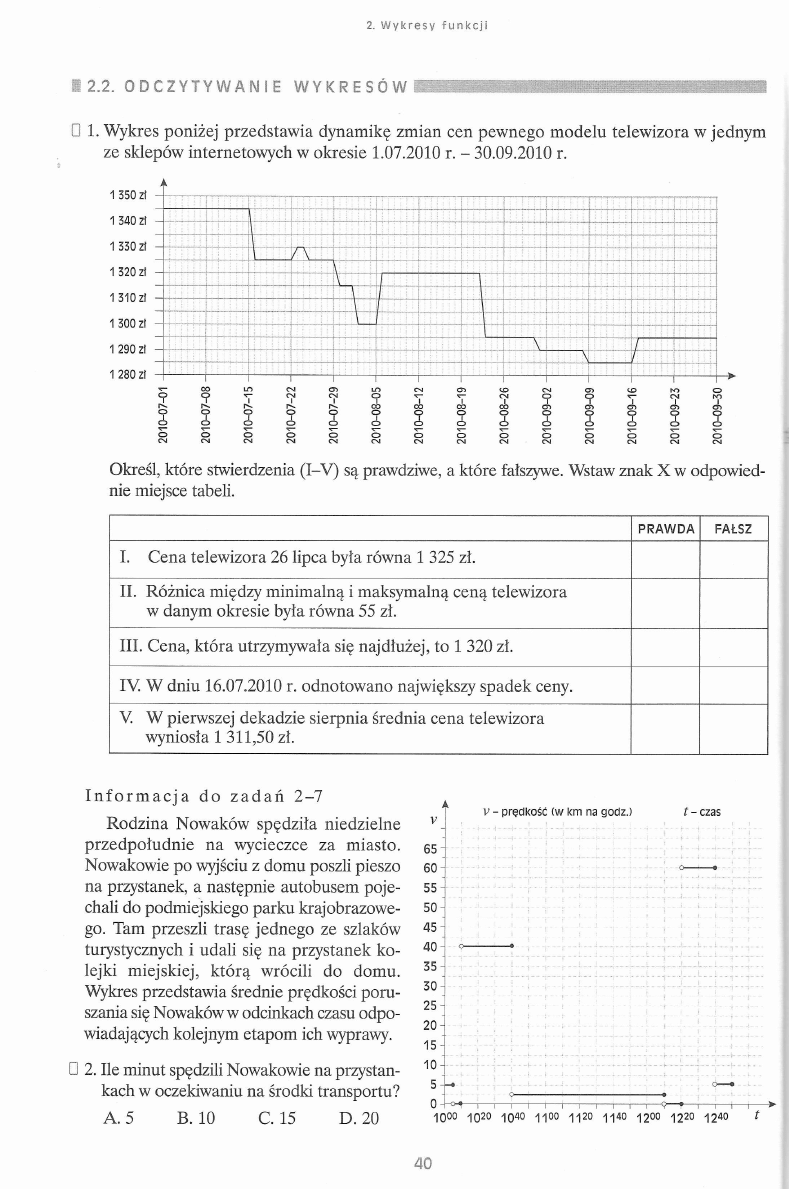
U 1. Wykres poniżej przedstawia dynamikę zmian cen pewnego modelu telewizora w jednym
ze sklepów internetowych w okresie 1.07.2010 r. - 30.09.2010 r.
Określ, które stwierdzenia (I-V) są prawdziwe, a które fałszywe. Wstaw znak X w odpowied
nie miejsce tabeli.
P R A W D A
FAŁSZ
I. Cena telewizora 26 lipca była równa 1 325 zł.
II. Różnica między minimalną i maksymalną ceną telewizora
w danym okresie była równa 55 zł.
III. Cena, która utrzymywała się najdłużej, to 1 320 zł.
IV. W dniu 16.07.2010 r. odnotowano największy spadek ceny.
V. W pierwszej dekadzie sierpnia średnia cena telewizora
wyniosła 1 311,50 zł.
I n f o r m a c j a d o z a d a ń 2 -7
Rodzina Nowaków spędziła niedzielne
przedpołudnie na wycieczce za miasto.
Nowakowie po wyjściu z domu poszli pieszo
na przystanek, a następnie autobusem poje
chali do podmiejskiego parku krajobrazowe
go. Tam przeszli trasę jednego ze szlaków
turystycznych i udali się na przystanek ko
lejki miejskiej, którą wrócili do domu.
Wykres przedstawia średnie prędkości poru
szania się Nowaków w odcinkach czasu odpo
wiadających kolejnym etapom ich wyprawy.
U 2. Ile minut spędzili Nowakowie na przystan
kach w oczekiwaniu na środki transportu?
A. 5
B. 10
C. 15
D. 20
65
60
55
50
45
40
35
30
25
20
15 J
10
5
0
v - prędkość (w km na godz.)
t - czas
—
i------- 1------- 1—
i------- i------- i—
i-------1------- 1—
i------- i—
y
t
—
i------- 1—
r
10°° 1020 1040 1100 1120 1140 1200 1220 1240
40
2.2. O d c z y t y w a n i e w y k r e s ó w
:
3
.
O dp .:
I 6. Oblicz, jaką długość miał szlak wybrany przez Nowaków, zakładając, że 10% czasu zajęła
im łączna droga z przystanku do szlaku oraz od szlaku do kolejki?
Zapisz o b lic z e n ia .
O dp .:
_ 7. Ile kilometrów łącznie pokonali Nowakowie podczas niedzielnej wycieczki?
Zapisz o b lic z e n ia .
O dp .:
i-c z a s (godz.)
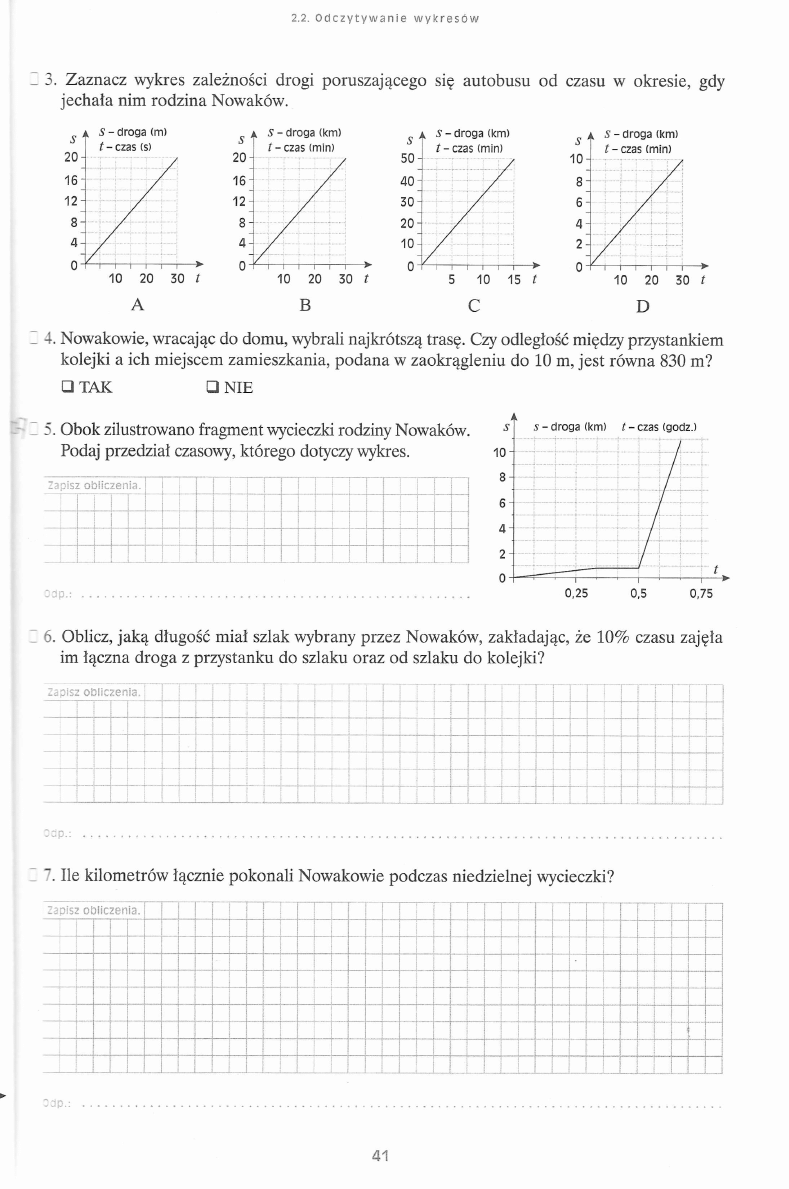
5. Obok zilustrowano fragment wycieczki rodziny Nowaków.
Podaj przedział czasowy, którego dotyczy wykres.
Zapisz o b lic z e n ia .
|
j
i
j
j
!
Zaznacz wykres zależności drogi poruszającego się autobusu od czasu w okresie, gdy
jechała nim rodzina Nowaków.
S - droga (m)
t - czas (s)
s - droga (km)
i - czas (min)
- droga (km)
■ czas (min)
a
s - droga (km)
t - czas (min)
i
i
i
i
i
i
10
20
3
4. Nowakowie, wracając do domu, wybrali najkrótszą trasę. Czy odległość między przystankiem
kolejki a ich miejscem zamieszkania, podana w zaokrągleniu do 10 m, jest równa 830 m?
□ TAK
□ NIE
41
2. W y k r e s y f u n k c j i
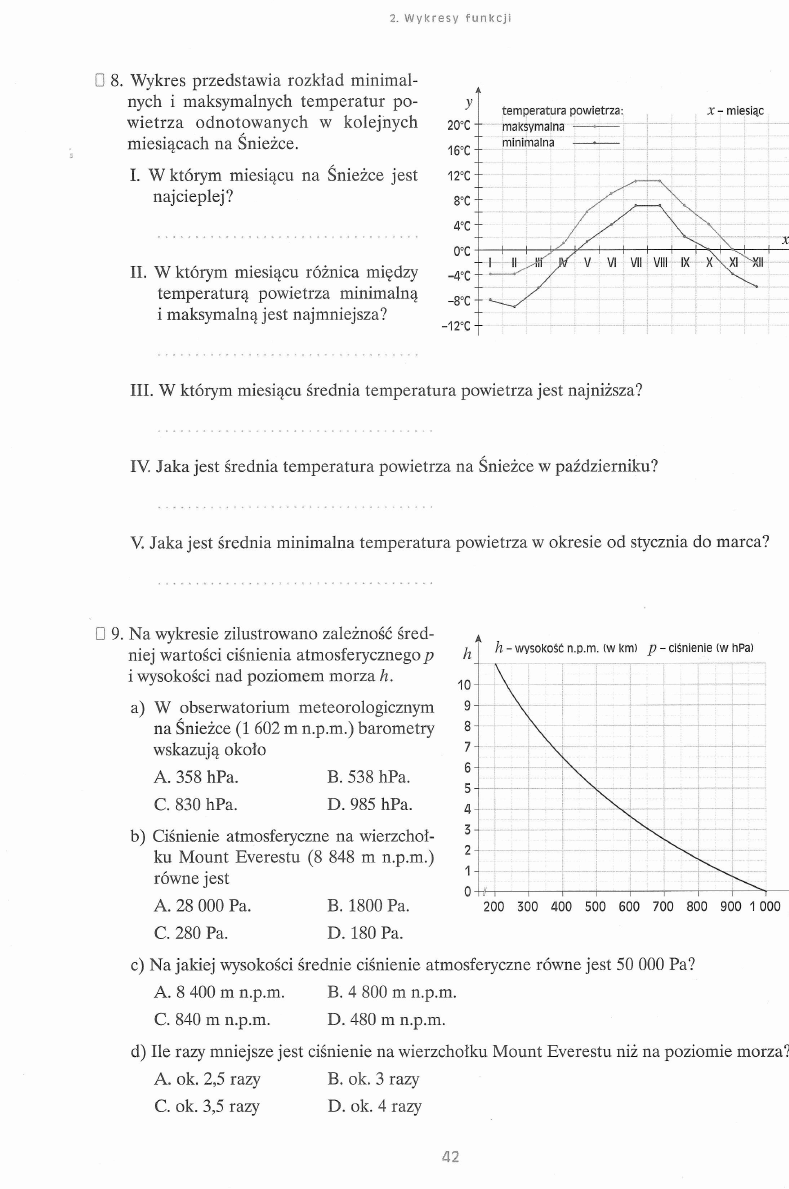
u 8. Wykres przedstawia rozkład minimal
nych i maksymalnych tem peratur po
wietrza odnotowanych w kolejnych
miesiącach na Śnieżce.
I. W którym miesiącu na Śnieżce jest
najcieplej?
II. W którym miesiącu różnica między
temperaturą powietrza minimalną
i maksymalną jest najmniejsza?
III. W którym miesiącu średnia temperatura powietrza jest najniższa?
IV. Jaka jest średnia temperatura powietrza na Śnieżce w październiku?
V. Jaka jest średnia minimalna temperatura powietrza w okresie od stycznia do marca?
0 9. Na wykresie zilustrowano zależność śred
niej wartości ciśnienia atmosferycznego p
i wysokości nad poziomem morza h.
a) W obserwatorium meteorologicznym
na Śnieżce (1 602 m n.p.m.) barometry
wskazują około
A. 358 hPa.
B. 538 hPa.
C. 830 hPa.
D. 985 hPa.
b) Ciśnienie atmosferyczne na wierzchoł
ku Mount Everestu (8 848 m n.p.m.)
równe jest
A. 28 000 Pa.
B. 1800 Pa.
C. 280 Pa.
D. 180 Pa.
c) Na jakiej wysokości średnie ciśnienie atmosferyczne równe jest 50 000 Pa?
A. 8 400 m n.p.m.
B. 4 800 m n.p.m.
C. 840 m n.p.m.
D. 480 m n.p.m.
d) Ile razy mniejsze jest ciśnienie na wierzchołku Mount Everestu niż na poziomie morza?
A. ok. 2,5 razy
B. ok. 3 razy
C. ok. 3,5 razy
D. ok. 4 razy
y
20°C
16°C
12°C
8°C
4°C
0°C
-4°C
-8°C
-12°C
temperatura powietrza:
maksymalna — •-------
minimalna
— *-------
x - miesiąc
h
- wysokość n.p.m. (w km)
p - ciśnienie (w hPa)
200 300 400 500 600 700 800 900 1 000
¿2
3.
E L E M E N T Y S T A T Y S T Y K I
i R A C H U N K U P R A W D O P O D O B I E Ń S T
1 3 . 1 .
S T A T Y S T Y K A O P I S O W A ! :
I n f o r m a c j a do z a d a ń 1-4
Do części matematyczno-przyrodniczej egzaminu gimnazjalnego, który odbył się 28 kwiet
nia 2010 roku, przystąpiło 444 115 uczniów. Poniżej przedstawiono dane dotyczące wyników
tej części egzaminu ogłoszone przez Centralną Komisję Egzaminacyjną.
□ 1. Uzupełnij zdania.
Do części matematyczno-przyrod
niczej egzaminu przystąpiło
uczniów. Wynik minimalny wyniósł
, a maksymalny -
Najwięcej zdających uzyskało wynik
. Maksymalną liczbę punktów
zdobyło ok.
% zdających.
I 2. Ilu uczniów zdobyło 28 punktów?
o
ź . a o i ^ a b ; c z ć ? r . i
2
.
;
:
3. Aby obliczyć, jaki procent zdających sta
nowili uczniowie szkół wiejskich, wystarczy
wykonać działanie:
A. 154 119 : 444 115.
B. (154 119 : 444 115) • 100%.
C. (444 115 • 100%) : 154 119.
D. 444 115 - 154 119 • 100%.
Wyniki części matematyczno-przyrodniczej egzaminu
gimnazjalnego a wielkość miejscowości
Wyszczególnienie
Liczba
uczniów
Średnia
Wieś
1 5 4 1 1 9
22,93
Miasto do 20 tys. mieszkańców
84 870
23,03
Miasto od 20 tys. do 100 tys. mieszkańców
90 769
24,18
Miasto powyżej 100 tys. mieszkańców
104 362
25,77
4. Czy Patrycja prawidłowo liczyła średnią punktów uzyskaną przez uczniów szkół w miastach?
W miejsce oznaczone jako I wpisz
T A K
lub
N I E ,
a w oznaczone jako II - wybrane uzasadnie
nie: A lub B.
(I)
, ponieważ (II)
A. Patrycja wyliczyła średnią arytmetycz
ną, a nie średnią ważoną.
B. Patrycja wyliczyła średnią ważoną, a nie
średnią arytmetyczną.
Obliczenie P atrycji:
23.03 + 24.18 + 25.17 _ 72.38 „
24,13
43

3. E l e m e n t y s t a t y s t y k i i r a c h u n k u p r a w d o p o d o b i e ń s t w a
□ 5. Grafika przedstawia zróżnicowanie plonów oraz udział poszczególnych województw w zbio
rach ziemniaków w 2008 roku.
a) Średnie plony z 1 ha w Polsce
w 2008 roku wynosiły
A. 1 910 kg.
B. 19 100 kg.
C. 1,91 tys. kg.
D. 191 tys. kg.
b) Najwyższe plony z hektara
odnotowano w województwie
A. mazowieckim.
B. dolnośląskim.
C. opolskim.
D. łódzkim.
165 185 205 225 245
*decytona - jednostka miary stosowana
w rolnictwie; 1 decytona Idtl = 0,1 tony Iti
c) Podaj nazwy województw, w których zebrano więcej niż 20,5 tony ziemniaków z hektara.
d) Podaj nazwy województw, których udział w zbiorach krajowych przekroczył 12%.
□ 6. Skład chemiczny ziemniaka uzależniony jest od jego odmiany.
Średnią zawartość składników odżywczych w ziemniakach
przedstawiono poniżej.
składniki mineralne -1 %
białko —1%~|—|
w 50 kg ziemniaków.
O d p .:
[błonnik -1 ,5 % ]
in n e -
woda - 78%
skrobia-1 7 ,5 %
J1
i
i
i
i
1
D
20
40
60
80
100 %
Z apisz o b lic z e n ia .
1
_
j
....
i
dostarcza średnio 30 g błonnika.
O d p .:
Zapisz o b lic z e n ia .
—
44
3.1. S t a t y s t y k a o p i s o w a
I n f o r m a c j a do z a d a ń 7 -1 0
W Polsce powierzchnia obszarów chronionych równa jest 104,2 tys. km2. Na 1 000 mieszkań
ców przypada 265 ha obszaru objętego ochroną. Główny element systemu ochrony to 23 parki
narodowe o łącznej powierzchni 3 145 km2. Równie ważne są inne formy ochrony przyrody,
w tym rezerwaty przyrody zajmujące obszar równy 1 736 km2, parki krajobrazowe - 25 138 km2,
a także obszary chronionego krajobrazu - 69 691 km2.
Dane liczbowe dotyczą roku 2008; źródło danych: „Mały rocznik statystyczny Polski 2009”, GUS, Warszawa 2009
_ 7. Powierzchnia Polski równa jest 322 575 km2. Jaki procent powierzchni naszego kraju stanowią
obszary objęte ochroną?
Zapisz o b lic z e n ia .
. J.. .
O dp .:
_ 8. Ile m2 obszaru chronionego przypada na jednego mieszkańca Polski?
Zapisz o b lic z e n ia . |
|
O dp .:
_ 9. Jaką część wszystkich obszarów chronionych w Polsce zajmują parki krajobrazowe?
ZapśS
2
o b lic z e n ia .!
i
|
l
i
1
O d p .: ..........................................................................................................................................................................................................................................................
_ 10. Zaznacz diagram, który poprawnie prezentuje obszary chronione z uwzględnieniem form
ochrony przyrody.
I
I - parki narodowe O - rezerwaty przyrody § H - parki krajobrazowe B - obszary chronionego krajobrazu H - inne
45
3. E l e m e n t y s t a t y s t y k i
i
r a c h u n k u p r a w d o p o d o b i e ń s t w a
H 11. Tabela obok przedstawia dane dotyczące wyna
lazków zgłoszonych w Urzędzie Patentowym
Rzeczypospolitej Polskiej.
a) W którym roku stosunek liczby wynalazków
zgłoszonych do liczby udzielonych patentów
był najwyższy?
A. 2000
B. 2005
b) Jaka była średnia udzielonych patentów
w latach 2007-2008?
Wyszczególnienie
2000
2005
2007
2008
Wynalazki:
zgtoszone
2 404
2 028
2 392
2 488
udzielone patenty
939
1 054
1 575
1451
C. 2007
D. 2008
'• 5b:
?enia.
!
c) Ile wynalazków w 2008 roku zgłosiły osoby fizyczne?
Wynalazki w 2008 r.
w edług podm iotów
zgłaszających
R ] - placówki naukowe
i I
- podmioty gospodarcze
[
i - osoby fizyczne
d) O ile punktów procentowych więcej
wynalazków zostało zgłoszonych przez
placówki naukowe niż osoby fizyczne?
Z a pisz o b lic z e n ia .
|
i
i
i
□ 12. Wykres przedstawia kurs euro w NBP obowiązujący w ostatnim dniu miesiąca.
I. Kiedy odnotowano najwyższy a kiedy naj-
zt
niższy kurs euro?
420
400
380
360
II. O ile złotych mniej płacono za 100 euro
340
we wrześniu 2000 roku w stosunku do
320
czerwca tegoż roku?
300
Kurs: 100 e u r o ------- 2000 ------- 2005 ..........2007 = 2 0 0 8
rLl EU. W którym kwartale, którego roku nastąpił najwyższy wzrost kursu euro, a w którym
wahania kursu były najmniejsze?
46
3.1. S t a t y s t y k a o p i s o w a
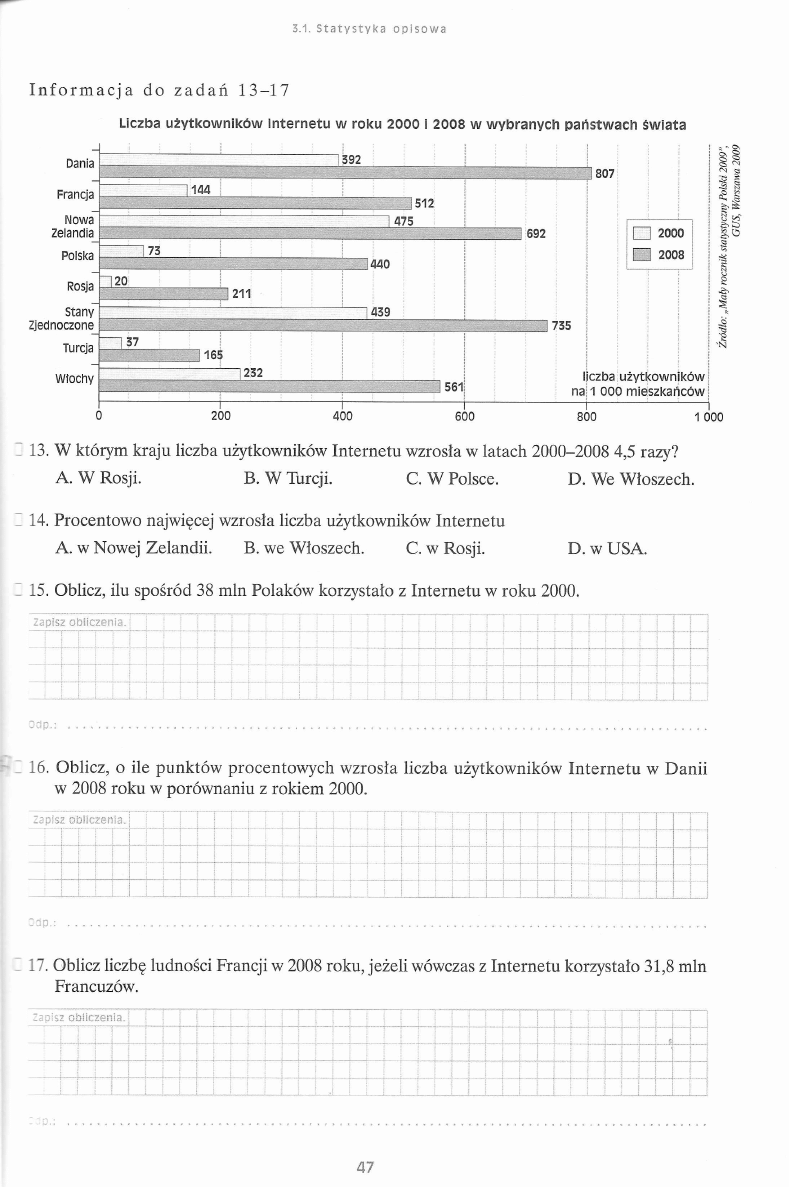
I n f o r m a c j a do z a d a ń 1 3 -1 7
Liczba użytkow ników Internetu w roku 2000 i 2008 w wybranych państwach świata
1392_______________________________________
807
2000
2008
Stany
Zjednoczone
liczba użytkow njków
n a ;i 000 mieszkańców
400
600
800
I
1 000
13. W którym kraju liczba użytkowników Internetu wzrosła w latach 2000-2008 4,5 razy?
A. W Rosji.
B. W Turcji.
C. W Polsce.
D. We Włoszech.
14. Procentowo najwięcej wzrosła liczba użytkowników Internetu
A. w Nowej Zelandii.
B. we Włoszech.
C. w Rosji.
D. w USA.
15. Oblicz, ilu spośród 38 min Polaków korzystało z Internetu w roku 2000.
Zap.i; r b r« e n :•
|
I
e s c
_ 16.
Oblicz, o ile punktów procentowych wzrosła liczba użytkowników Internetu w Danii
w 2008 roku w porównaniu z rokiem 2000.
Zapisz cl-)iic zen ¡3. i
.
.
.......
O dp.:
_ 17. Oblicz liczbę ludności Francji w 2008 roku, jeżeli wówczas z Internetu korzystało 31,8 min
Francuzów.
Zapis? obliczenia.
;
. ..
...
47
Ź
ró
d
ło
:
„M
ał
y
ro
cz
ni
k
st
at
ys
ty
cz
ny
P
ol
sk
i
2
0
0
9
”,
G
U
S,
W
ar
sz
aw
a
2009
3.
E l e m e n t y s t a t y s t y k i
i
r a c h u n k u
p r a w d o p o d o b i e ń s t w a
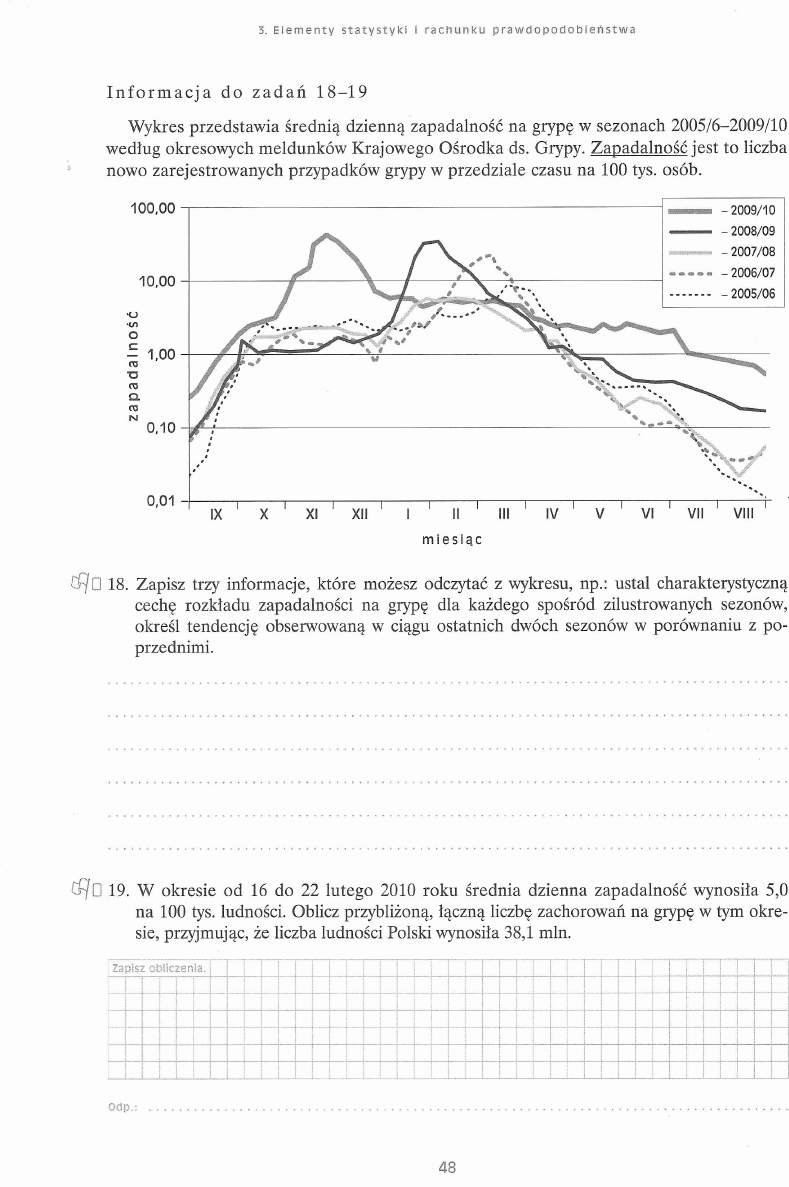
I n f o r m a c j a d o z a d a ń 1 8 -1 9
Wykres przedstawia średnią dzienną zapadalność na grypę w sezonach 2005/6-2009/10
według okresowych meldunków Krajowego Ośrodka ds. Grypy. Zapadalność jest to liczba
nowo zarejestrowanych przypadków grypy w przedziale czasu na 100 tys. osób.
Ci /U 18. Zapisz trzy informacje, które możesz odczytać z wykresu, np.: ustal charakterystyczną
cechę rozkładu zapadalności na grypę dla każdego spośród zilustrowanych sezonów,
określ tendencję obserwowaną w ciągu ostatnich dwóch sezonów w porównaniu z po
przednimi.
19. W okresie od 16 do 22 lutego 2010 roku średnia dzienna zapadalność wynosiła 5,0
na 100 tys. ludności. Oblicz przybliżoną, łączną liczbę zachorowań na grypę w tym okre
sie, przyjmując, że liczba ludności Polski wynosiła 38,1 min.
- o>:ik zer
:
48

3.2. W p r o w a d z e n i e d o r a c h u n k u p r a w d o p o d o b i e ń s t w a
3 .2 . W P R O W A D Z E N I E D O R A C H U N K U P R A W D O P O D O B I E Ń S T W A
1. Ile jest możliwych wyników dwukrotnego rzutu monetą?
O dp .: ...........................................................................................................
2. Sześcienna kostka ma jedną ściankę czer
woną, dwie - żółte, a trzy - niebieskie.
Uzupełnij drzewko przez pokolorowanie
pól zgodnie z możliwymi wynikami
zdarzenia polegającego na dwukrotnym
rzucie tą kostką.
3. Narysuj drzewko ilustrujące eksperyment
losowy polegający na trzykrotnym rzucie
monetą.
4. Eksperyment polega na dwukrotnym rzucie sześcienną kostką do gry ze ścianami ponu
merowanymi cyframi od 1 do 6.
I. Zapisz zbiór zdarzeń elementarnych tego eksperymentu.
II. Wypisz te zdarzenia, w których wypadała ta sama liczba oczek na obu kostkach.
5. W pudełku znajdują się trzy kartki oznaczone cyframi: 0, 1 i 2.
I. Wypisz wszystkie zdarzenia elementarne eksperymentu polegającego na losowaniu
kartek i układaniu ich w kolejności wylosowania.
II. Ile liczb trzycyfrowych uzyskano w tym eksperymencie?
49
3.
E l e m e n t y s t a t y s t y k i
i
r a c h u n k u p r a w d o p o d o b i e ń s t w a
□ 6. W pudełku znajdują się trzy kule: dwie oznaczone cyfrą 2 i jedna oznaczona cyfrą 1.
Losowano pojedynczo, i bez zwracania, trzy kule i zapisywano ich numery w kolejności
wylosowania. Ile liczb parzystych można otrzymać w wyniku opisanego zdarzenia?
Zapis: o b lic z e ń a.
|
[
o a p
................................................................
-
□ 7. Marcysia ma w szufladzie 9 różnych par kolczyków. Ile kolczyków musi wyciągnąć z szufla
dy (nie zaglądając do niej), aby mieć pewność, że skompletuje jedną parę.
O d p . . :
........................................................................................... ...........................................................................................................................................................................
■
. .
. ...................................................................................... .....
□ 8. Kajetan zabrał na wycieczkę trzy różne czapeczki, trzy koszulki - każda w innym kolorze
oraz trzy pary spodni o różnej długości nogawek. Ile maksymalnie różnych zestawów stro
ju może skomponować Kajetan z zabranych elementów garderoby?
Zapisz o b lic z e n ia .
i
s
j
i
l
On,;.;
............................
U 9. W szkolnym turnieju piłki siatkowej bierze udział 5 klasowych drużyn. Ile meczów należy
zaplanować, aby każda drużyna zagrała z każdą z drużyn?
Zapisz o b lic z e n ia . ]
i
|
i
|
i
__
!
J :ip .:
50

4. F I G U R Y P Ł A S K I E
4.1. T R Ó J K Ą T Y
1. Na podstawie rysunku wskaż równość fałszywą.
A . <£a = < 5
B. ^ a + <(3 = 180°
/
a U
C. <£p + <Xy = 180°
D . ^ y + < a = 180°
2. Rumb jest jednostką miary kąta stosowaną w nawigacji, służy m.in. do określania miejsc
na widnokręgu i zmiany kierunku wiatru. Jeden rumb to ^ kąta pełnego, czyli
A. 32°.
B. 11,25°.
C. 45°.
D. 16,25°.
3. Pod jakim kątem przetną się proste a i b z rysunku obok?
A. 60°
B. 35°
C. 40°
D. 25°
Ustal kolejność czynności podczas konstrukcji kąta o mierze 45°. Wstaw w kratki odpowied
nie numery.
] I.
Z wierzchołka kąta (O) kreślimy półprostą przechodzącą przez punkt wspólny
przecięcia okręgów.
n. Punkty przecięcia okręgu z ramionami kąta oznaczamy jako A i B.
] HI. Z wierzchołka kąta prostego oznaczonego jako O kreślimy okrąg o promieniu R
tak, aby przecinał ramiona kąta.
] IV Z punktował i B kreślimy okręgi o promieniach równych O A lub większym.
5. Długość odcinka BD na rysunku jest równa
A. 16 cm.
B. 8,5 cm.
C. 7,5 cm.
D. 7 cm.
6. Wskaż prawdziwą równość, dotyczącą trójkąta
na rysunku obok.
A
. k + m - p
B. p 2
=
k2
•
m 2
C. k
2 =
m 2
-I-
p 2
D . p 2 = k2 + m 2
a \\b
|£ B | = 2 4 cm
|
A B
| = 8 cm
\AC
| = 5 cm
51
4. F i g u r y p ł a s k i e
U 7. Oblicz długość boku trójkąta równobocznego, jeżeli jest ona o 2 cm większa niż wysokość
tego trójkąta.
Z;
; ■
■
'
;
1
0cip
........................
.
. .. .
U 8. Oblicz pole trójkąta równoramiennego o obwodzie równym 84 cm i podstawie równej 36 cm.
Z apisz o b lic z e n ia .
i
Od
D 10. Miara dwóch kątów wewnętrznych trójkąta równa jest 30° i 45°, a jego wysokość poprowa
dzona do najdłuższego boku ma 6 cm. Oblicz obwód trójkąta.
Z apisz o b lic z e n ia . |
i
i
i
i
1
f
1
i
i
j
Cc :
52
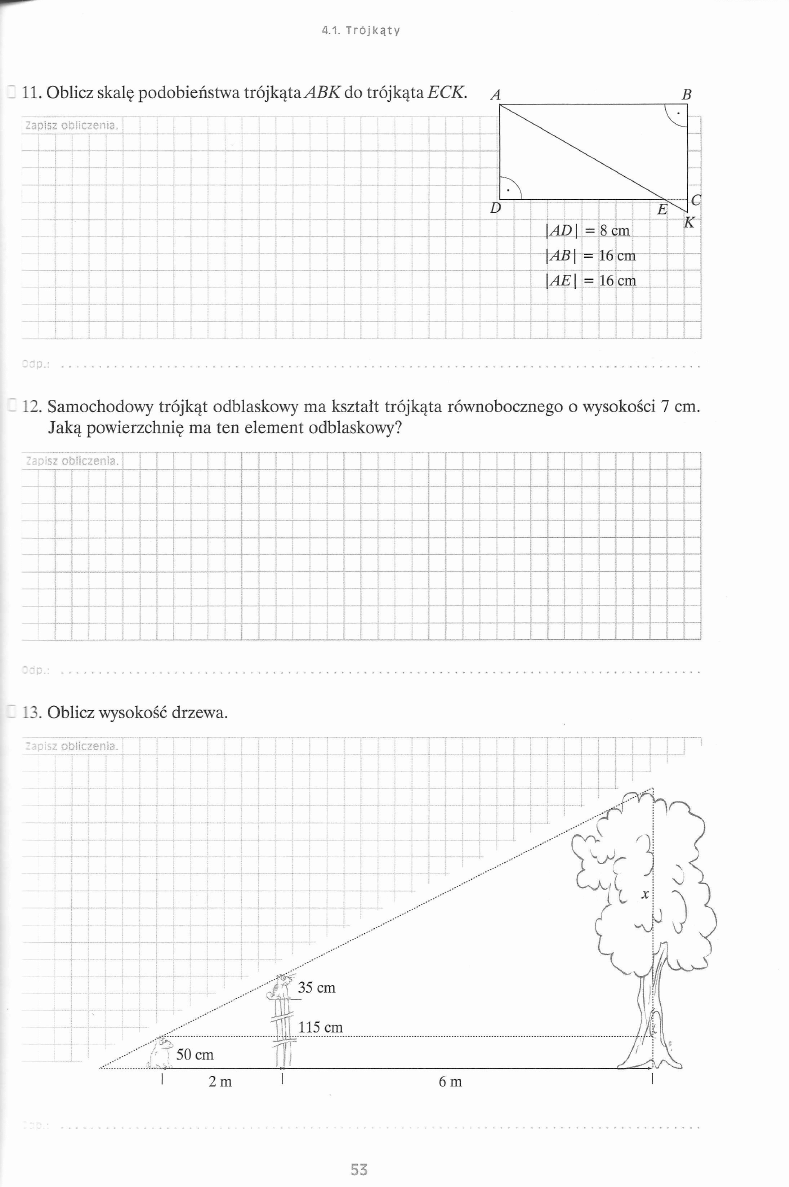
4.1. T r ó j k ą t y
11. Oblicz skalę podobieństwa trójkąta ARK do trójkąta ECK.
a
B
_ 12. Samochodowy trójkąt odblaskowy ma kształt trójkąta równobocznego o wysokości 7 cm.
Jaką powierzchnię ma ten element odblaskowy?
Zapisz o b licze n ia .
_ 13.
Oblicz wysokość drzewa.
53
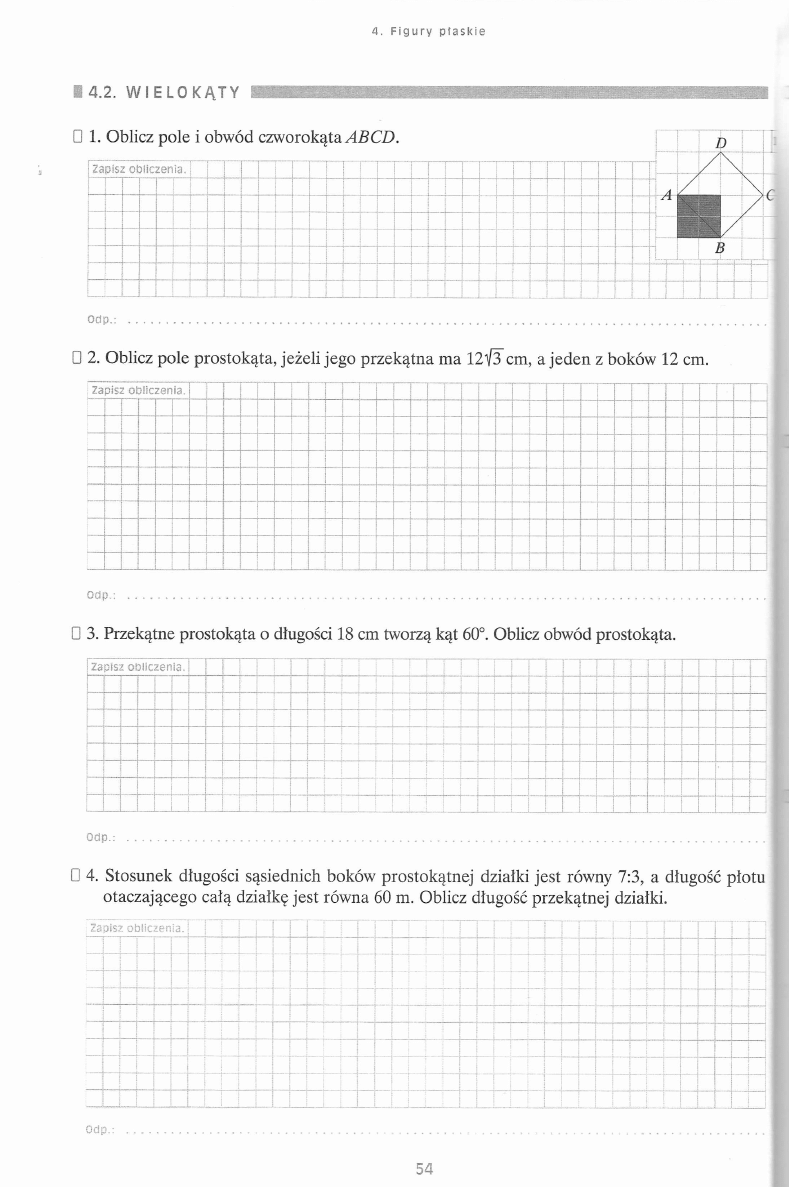
4 . F i g u r y p t a s k i e
B 4 .2 . W I E L O K Ą T Y H
B
1. Oblicz pole i obwód czworokąta
A B CD.
1
/
D
\
Zapisz o b licze n ia .
Z ,
\
' 1
■
/
i
1
k
o d p .
□ 2. Oblicz pole prostokąta, jeżeli jego przekątna ma
12^3
cm, a jeden z boków 12 cm.
Zapisz o b licze n ia .
Odp.
□ 3. Przekątne prostokąta o długości 18 cm tworzą kąt 60°. Oblicz obwód prostokąta.
Zapisz o b licze n ia .
1 i 1
1
;
i
O dp.:
□ 4. Stosunek długości sąsiednich boków prostokątnej działki jest równy 7:3, a długość płotu
otaczającego całą działkę jest równa 60 m. Oblicz długość przekątnej działki.
i Zapisz o b licze n ia .
—
!
_
1
|
I
Odp.
54
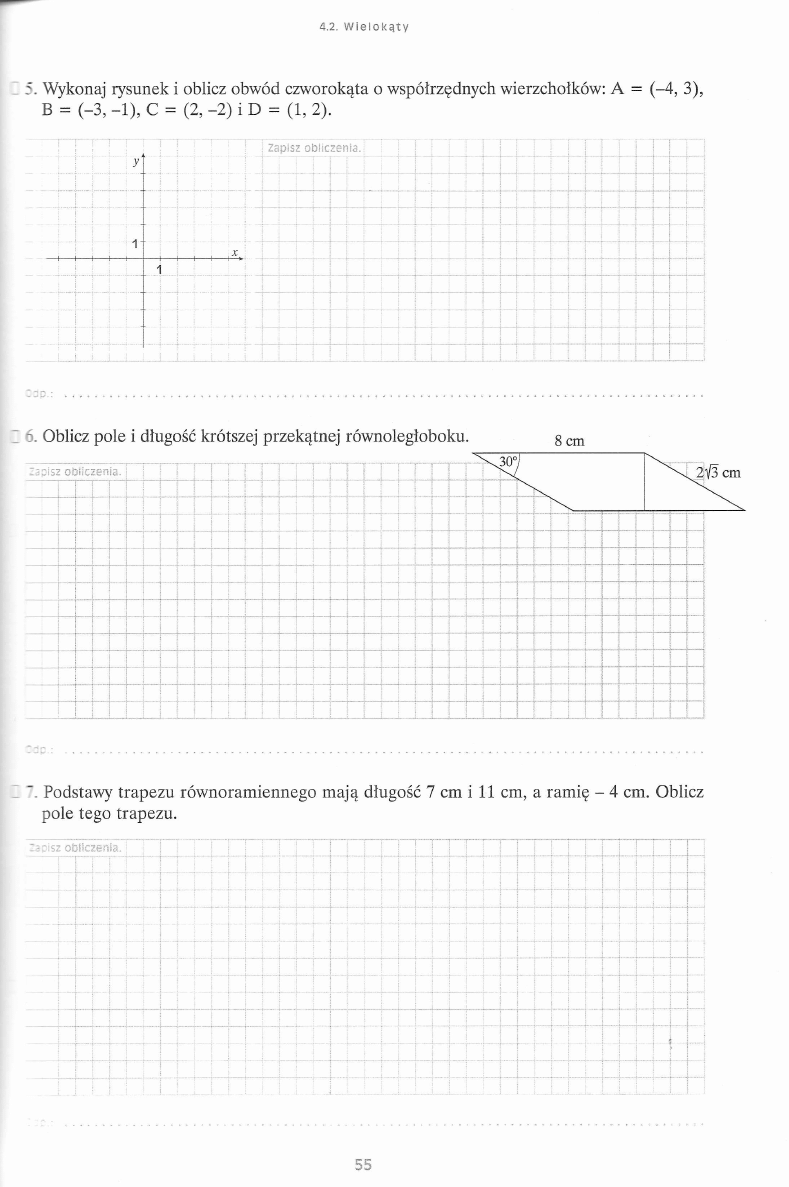
4.2. W i e l o k ą t y
_ 5. Wykonaj rysunek i oblicz obwód czworokąta o współrzędnych wierzchołków: A = (-4, 3),
B = (-3, -1), C = (2, -2) i D = (1, 2).
y
Zapisz o b licze n ia .
!!
|
|
i
.
.....r...~
i
1
:
X \
1
j
!
cap.
I 6. Oblicz pole i długość krótszej przekątnej równoległoboku.
:a p .:
", Podstawy trapezu równoramiennego mają długość 7 cm i 11 cm, a ramię - 4 cm. Oblicz
pole tego trapezu.
Zapisi
.
|
\
...
...
I
........................!...........
...:...
I
!
|
—
i
I
i
!
:
:
j
j
:
55
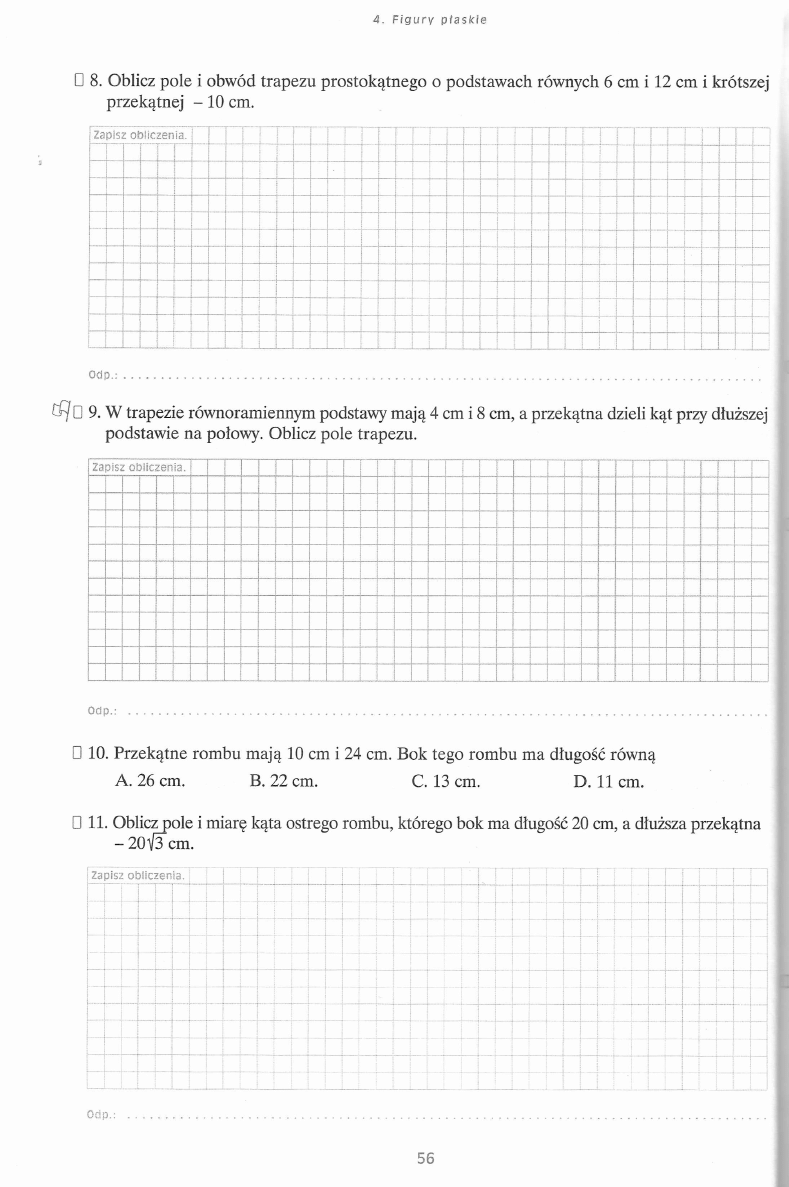
4 .
F i g u r y
p i a s f d e
□ 8. Oblicz pole i obwód trapezu prostokątnego o podstawach równych 6 cm i 12 cm i krótszej
przekątnej - 1 0 cm.
Zapisz ob'!Czenia.
O d p .: ...........................................................................................................................................................................................................................................
CfJU 9.
W trapezie równoramiennym podstawy mają 4 cm i 8 cm, a przekątna dzieli kąt przy dłuższej
podstawie na połowy. Oblicz pole trapezu.
Zapisz o b licze nia .
Odp.: ........................................................ ...............................................................................................................................................................................
□ 10. Przekątne rombu mają 10 cm i 24 cm. Bok tego rombu ma długość równą
A. 26 cm.
B. 22 cm.
C. 13 cm.
D. 11 cm.
□ 11. Oblicz pole i miarę kąta ostrego rombu, którego bok ma długość 20 cm, a dłuższa przekątna
- 201/3" cm.
Zapisz obliczenia.
■
Odp.:
56
<3.2. W i e l o k ą t y
_ 12. Oblicz obwód rombu, którego dłuższa przekątna ma długość
6 ^ cm,
a kąt ostry miarę 60°.
Zapisz o l 5liczema.
1
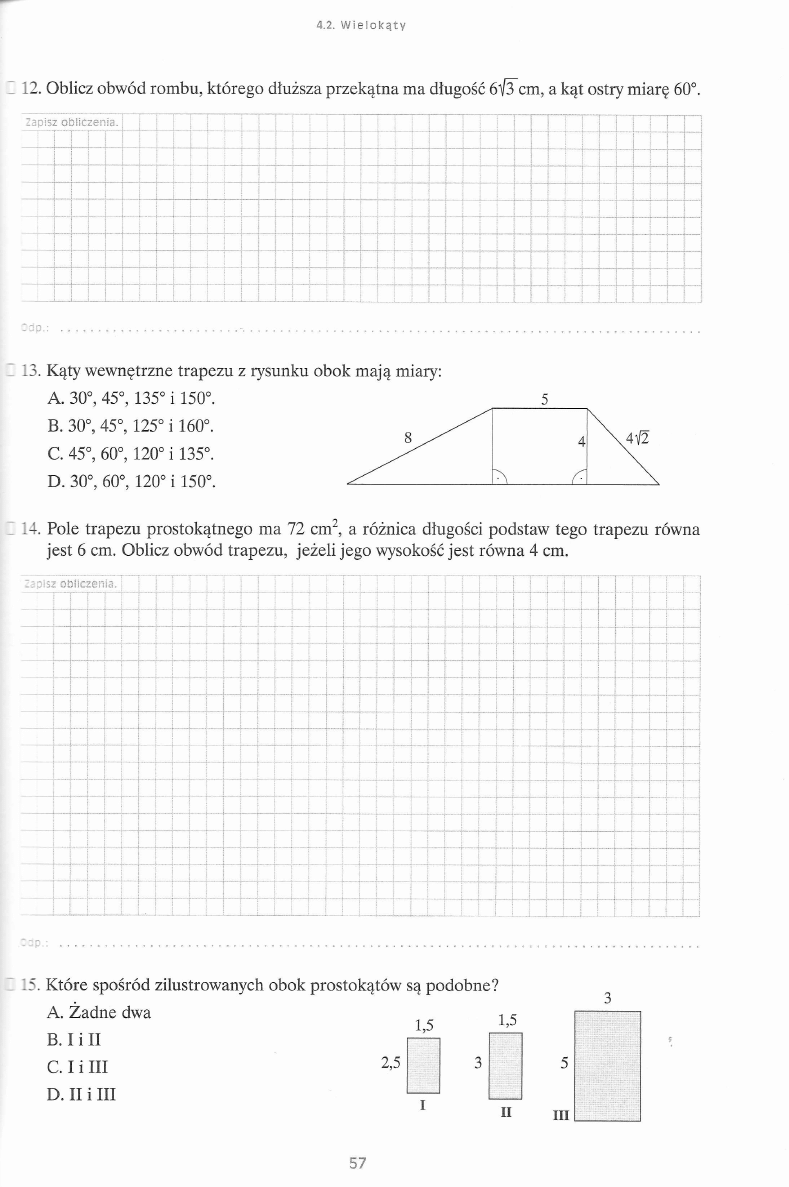
13. Kąty wewnętrzne trapezu z rysunku obok mają miary:
A. 30°, 45°, 135° i 150°.
B. 30°, 45°, 125° i 160°.
C. 45°, 60°, 120° i 135°.
D. 30°, 60°, 120° i 150°.
8
4
\ 4 V 2
^
r-
\
14. Pole trapezu prostokątnego ma 72 cm2, a różnica długości podstaw tego trapezu równa
jest 6 cm. Oblicz obwód trapezu, jeżeli jego wysokość jest równa 4 cm.
m s z
o D ii C z ę n ia
1,5
15. Które spośród zilustrowanych obok prostokątów są podobne?
A. Żadne dwa
B. I i II
C. I i III
2’5
D. II i III
1,5
I
II
I II
5 7
4. F i g u r y p i a s k i e
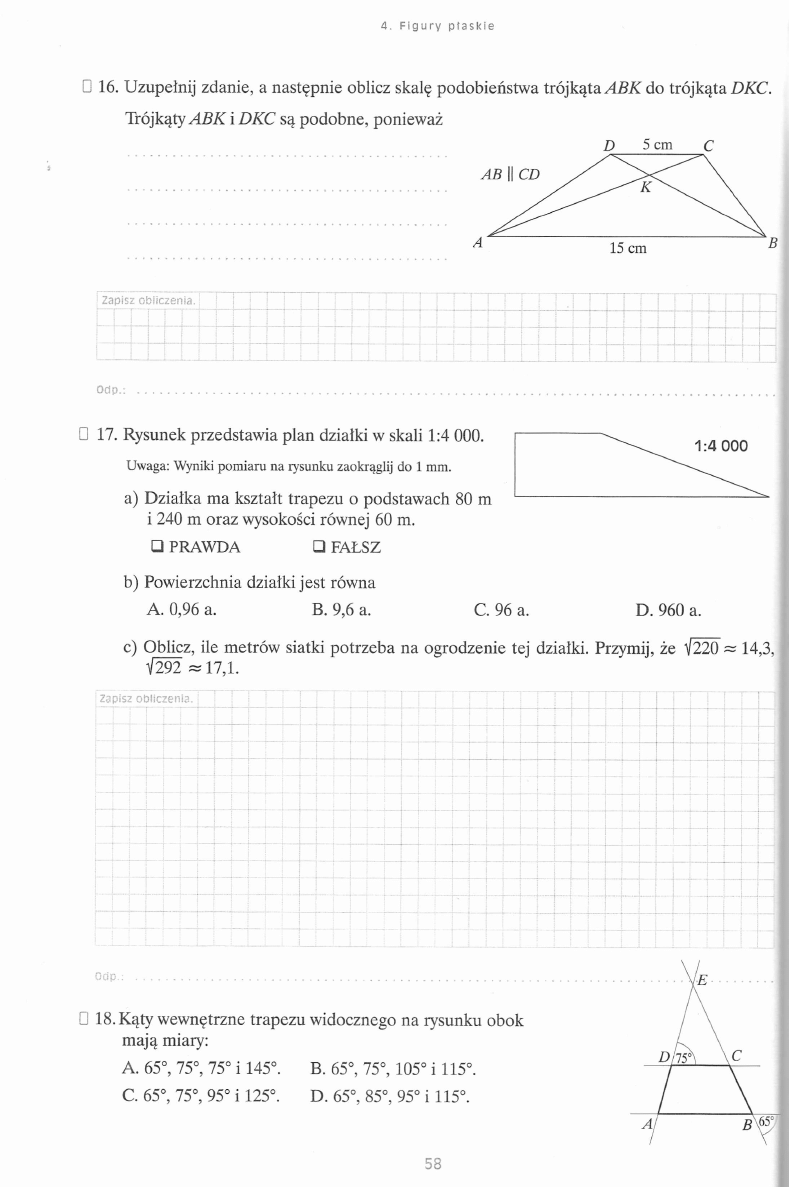
□ 16. Uzupełnij zdanie, a następnie oblicz skalę podobieństwa trójkąta
A B K
do trójkąta
DKC.
Trójkąty A B K
i
DKC
są podobne, ponieważ
D
5 cm
c
Zapisz obliczenia.
I
!
I
Ocip.: .................................................................................................................................
□ 17. Rysunek przedstawia plan działki w skali 1:4 000.
Uwaga: Wyniki pom iaru na rysunku zaokrąglij do 1 mm.
a) Działka ma kształt trapezu o podstawach 80 m
i 240 m oraz wysokości równej 60 m.
□ PRAW DA
□ FAŁSZ
b) Powierzchnia działki jest równa
A. 0,96 a.
B. 9,6 a.
C. 96 a.
D. 960 a.
c) Oblicz, ile metrów siatki potrzeba na ogrodzenie tej działki. Przymij, że V220 ~ 14,3,
l/292 -1 7 ,1 .
Zapisz obliczenia.
j
_
i
..L i
_i.
j
__
L
Odp.
□ 18. Kąty wewnętrzne trapezu widocznego na rysunku obok
mają miary:
A. 65°, 75°, 75° i 145°.
B. 65°, 75°, 105° i 115°.
C. 65°, 75°, 95° i 125°.
D. 65°, 85°, 95° i 115°.
58
4.2. W i e l o k ą t y
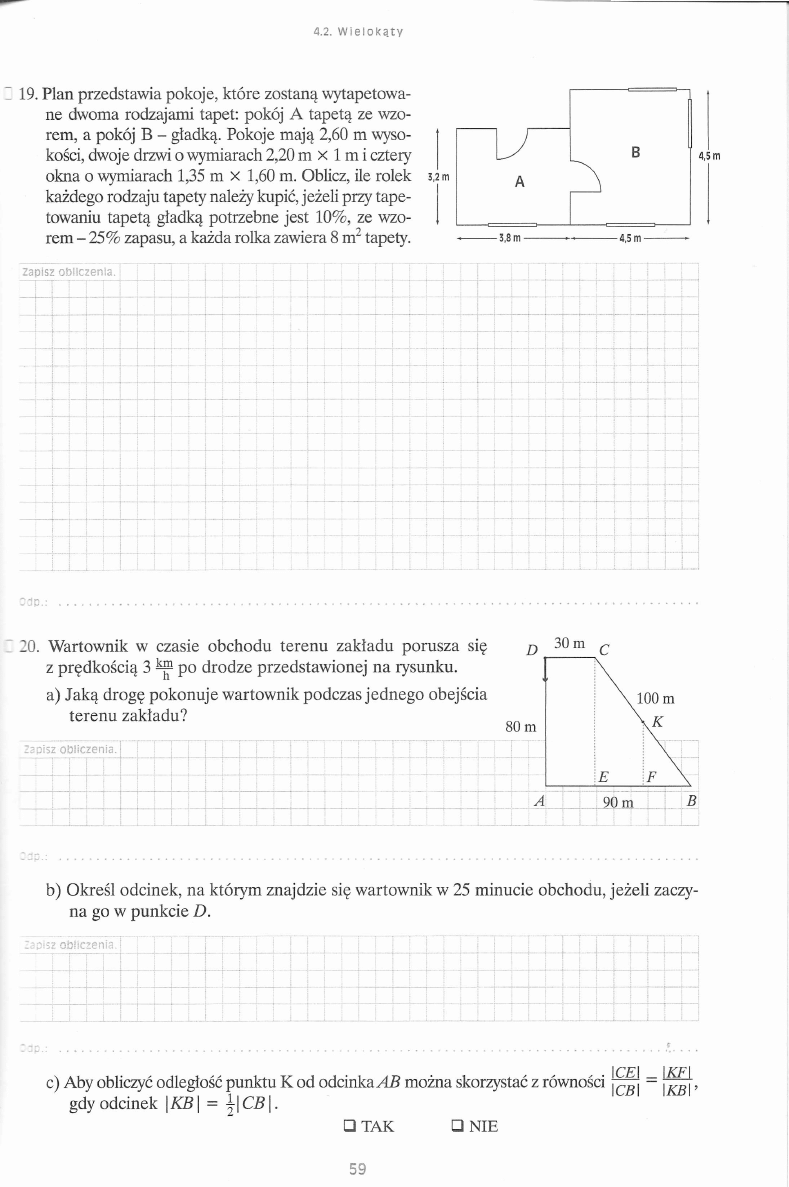
19. Plan przedstawia pokoje, które zostaną wytapetowa-
ne dwoma rodzajami tapet: pokój A tapetą ze wzo
rem, a pokój B - gładką. Pokoje mają 2,60 m wyso
kości, dwoje drzwi o wymiarach 2,20 m
X
1 m i cztery
okna o wymiarach 1,35 m x 1,60 m. Oblicz, ile rolek
każdego rodzaju tapety należy kupić, jeżeli przy tape
towaniu tapetą gładką potrzebne jest 10%, ze wzo
rem - 25% zapasu, a każda rolka zawiera 8 m2 tapety.
4,5 m
Zapisz o b licze n ia .
20. Wartownik w czasie obchodu terenu zakładu porusza się
z prędkością 3 ^ po drodze przedstawionej na rysunku.
a) Jaką drogę pokonuje wartownik podczas jednego obejścia
terenu zakładu?
D 30 m C
80 m
Zapisz o b licze n ia .
E
F
A
90 nr
B
b) Określ odcinek, na którym znajdzie się wartownik w 25 minucie obchodu, jeżeli zaczy
na go w punkcie
D.
Zapisz o b licze n ia .
I CE I
IKF |
c) Aby obliczyć odległość punktu K od odcinka AB można skorzystać z równości
~ \KBy.
gdy odcinek
\KB\ = \ \ C B \ .
□ TAK
□ N IE
59

4 . F i g u r y p ł a s k i e
I n f o r m a c j a d o z a d a ń 2 1 -2 4
Przedstawiony obok wzór ułożono z czterech rodzajów
drewna oznaczonych na rysunku jako I-IV.
□ 21. Rysunek wzoru wykonano w skali
A. 2:1.
B. 1:2.
C. 4:1.
D. 1:4.
□ 22. Ile osi symetrii ma pokazany obok wzór?
A. 1
B .2
C. 4
D. 8
10 cm
U 23. Oblicz powierzchnię poszczególnych rodzajów drewna, które tworzą pokazany wyżej
wzór.
: Zapisz oblicze n ia .
i
—
j
-
T
i
O tlp .:
.........................................................................................................................................................................................................................................................................
b) Powierzchnia dwóch rodzajów drewna mozaiki na kasetce będzie taka sama. Których?
A. I i II
B. II i III
C. III i IV
D. IV i I
Ile osi symetrii ma mozaika ułożona na wieczku kasetki?
A. 8
B. 4
C. 2
D. 1
6 0
a) Oblicz powierzchnię wieczka kasetki.
□ 24. Przedstawiony wyżej wzór jest fragmentem
mozaiki, która została ułożona na wieczku
kasetki pokazanej obok.
c)
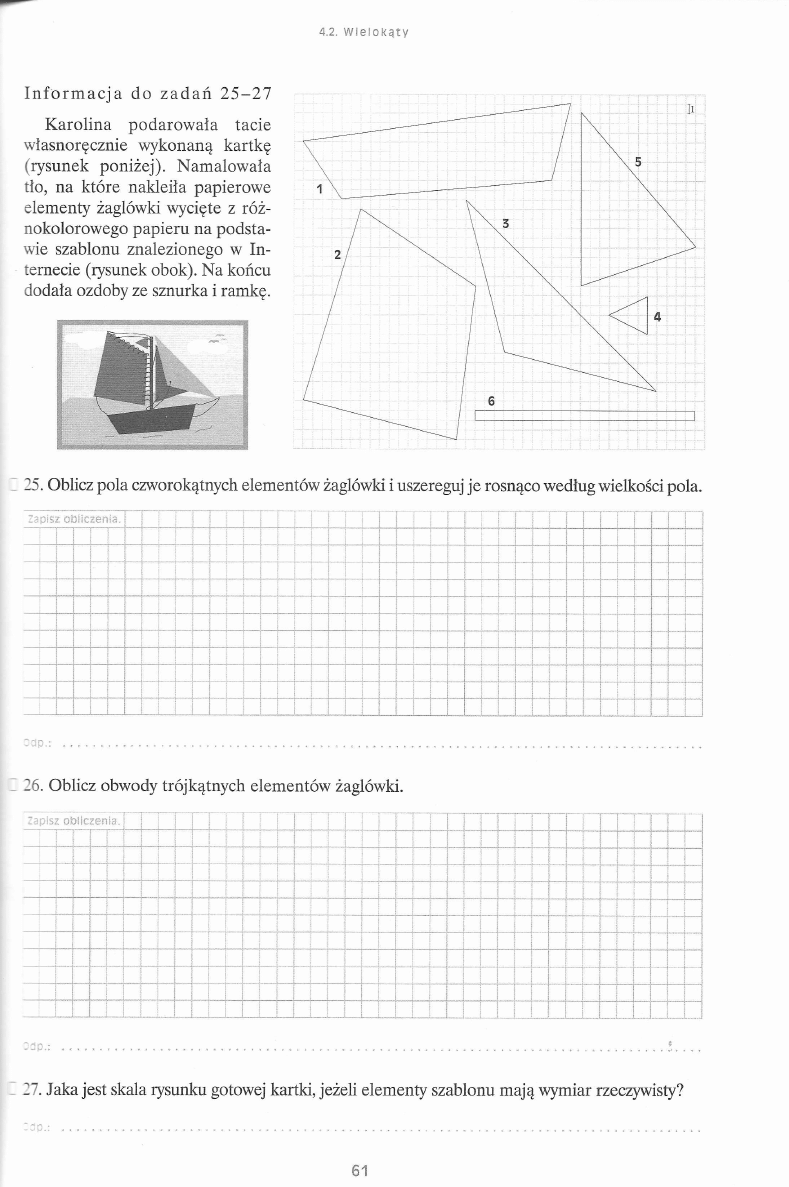
4.2. W i e l o k ą t y
I n f o r m a c j a do z a d a ń 2 5 -2 7
Karolina podarowała tacie
własnoręcznie wykonaną kartkę
(rysunek poniżej). Namalowała
tło, na które nakleiła papierowe
elementy żaglówki wycięte z róż
nokolorowego papieru na podsta
wie szablonu znalezionego w In
ternecie (rysunek obok). Na końcu
dodała ozdoby ze sznurka i ramkę.
_ 25. Oblicz pola czworokątnych elementów żaglówki i uszereguj je rosnąco według wielkości pola.
zac
.
C ip .:
_ 26. Oblicz obwody trójkątnych elementów żaglówki.
Zapisz o b licze n ia .
|
i
i
...
j
__
S
_ 27. Jaka jest skala rysunku gotowej kartki, jeżeli elementy szablonu mają wymiar rzeczywisty?
6 1
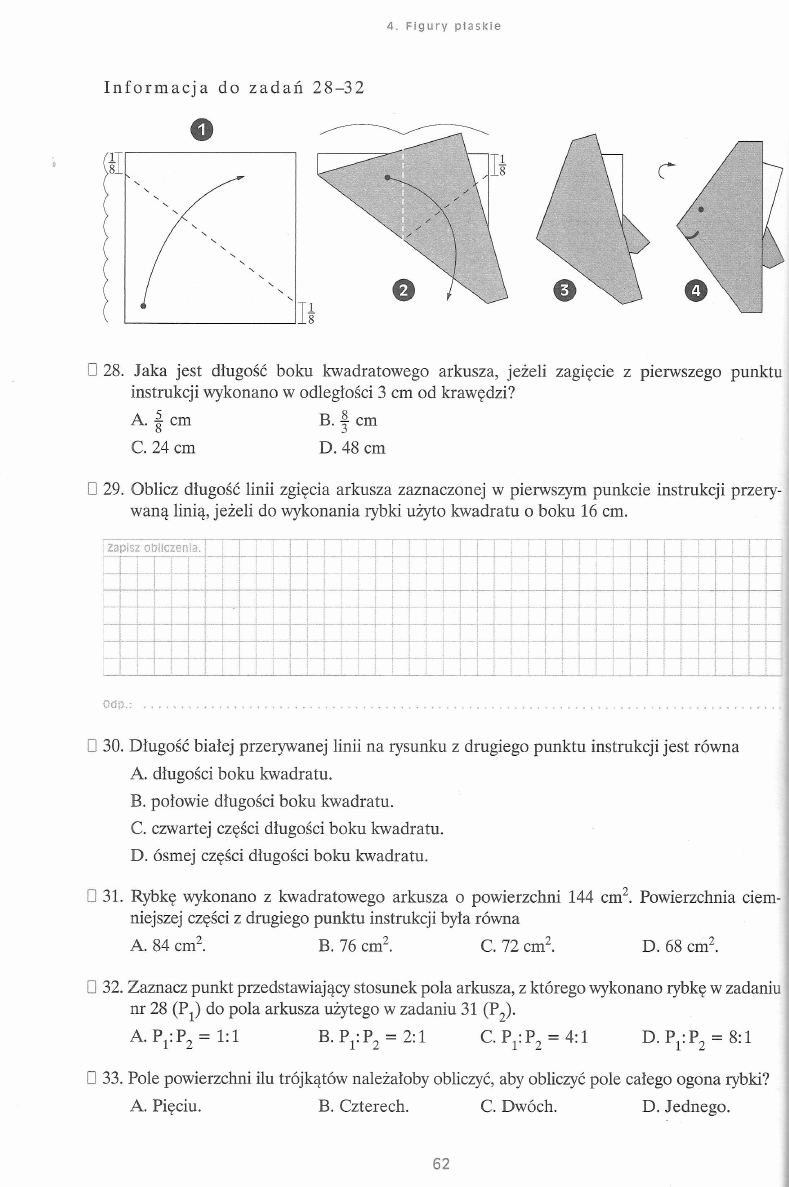
4.
f
; g u r y p t a s k i e
I n f o r m a c j a do z a d
O
U 28. Jaka jest długość boku kwadratowego arkusza, jeżeli zagięcie z pierwszego punktu
instrukcji wykonano w odległości 3 cm od krawędzi?
A. | cm
B. | cm
C. 24 cm
D. 48 cm
□ 29. Oblicz długość linii zgięcia arkusza zaznaczonej w pierwszym punkcie instrukcji przery
waną linią, jeżeli do wykonania rybki użyto kwadratu o boku 16 cm.
| Zapisz o b licze n ia .
i
j
I
Otu.:
.
.
. . .
.
.
□ 30. Długość białej przerywanej linii na rysunku z drugiego punktu instrukcji jest równa
A. długości boku kwadratu.
B. połowie długości boku kwadratu.
C. czwartej części długości boku kwadratu.
D. ósmej części długości boku kwadratu.
□ 31. Rybkę wykonano z kwadratowego arkusza o powierzchni 144 cm2. Powierzchnia ciem
niejszej części z drugiego punktu instrukcji była równa
A. 84 cm2.
B. 76 cm2.
C. 72 cm2.
D. 68 cm2.
u 32. Zaznacz punkt przedstawiający stosunek pola arkusza, z którego wykonano rybkę w zadaniu
nr 28 (P1) do pola arkusza użytego w zadaniu 31 (P9).
A . P
i
:P2 = 1 : 1
B .P
i
:P2 = 2:1
C .P i : P2 = 4 :l
D. P ^ P 2 = 8:1
□ 33. Pole powierzchni ilu trójkątów należałoby obliczyć, aby obliczyć pole całego ogona rybki?
A. Pięciu.
B. Czterech.
C. Dwóch.
D. Jednego.
a ń 2 8 -3 2
52
4.3. K o t a i o k r ę g i
1. Zaznacz rysunek, na którym odległość środków okręgów równa jest |r - r2.
2. Suma miar kątów wpisanego i środkowego, opartych na tym samym luku w okręgu, równa
jest 120°. Miary tych kątów to
A. 60° i 60°.
B. 20° i 100°.
C. 30° i 90°.
D. 40° i 80°.
3. Na rysunku podane są długości odcinków. Oblicz odległość środka okręgu od narysowa
nej cięciwy.
m
= 5 c m
Zapisz o c lirre n a
4. W okręgu o średnicy 10 cm poprowadzono cięciwę o długości 6 cm. Oblicz odległość cięciwy
od środka okręgu.
Zapis: ■
-------
5. Z p u n k tu j okręgu poprowadzono dwie prostopadłe cięciwy o długościach
2 f2
cm i 3"/2 cm
Oblicz pole koła.
Zapisz o b licze n ia .
!
53
4 . F i g u r y p ł a s k i e
U 6. Oblicz pole zacieniowanej figury na rysunku obok.
| Zapisz o b lic ze n ia .
1
.
|
i
1 -
□ 7. Oblicz pole zacieniowanej figury.
U
8. Koń chodzi w koło uwiązany na linie o długości 5 m. Jaką drogę pokona, jeżeli przejdzie
20 okrążeń?
■
0 9. Jaką drogę pokona w czasie jednego okrążenia samolot na uwięzi, ...
jeżeli porusza się zgodnie z danymi na rysunku obok?
Zapisz o b lic z e n ia .
1
6o°;
15
r
1
|
|
U 10. Równik ma długość 40 076 km. Równoleżnik 60° jest o połowę krótszy niż równik. Oblicz
promień tego równoleżnika.
:
i
1
1
i
64

4.3. K o t a i o k r ę g i
I n f o r m a c j a do z a d a ń 1 1 -1 4
Koło widokowe Singapore Flyer ma 150 m średnicy
i umożliwia obserwację panoramy w promieniu 45 km.
W przymocowanych na zewnętrznej obręczy koła 28 kapsu
łach turyści podróżują z prędkością 0,76
11. Singapurskie koło widokowe umożliwia obserwację
terenu o powierzchni równej
A. 635,85 km2.
B. 6358,5 km2.
C. 141,3 km2.
D. 1413 km2.
12. Oblicz kąt środkowy utworzony przez promienie dwóch
kolejnych kapsuł koła Singapore Flyer.
Zapisz obliczenia. I I I
I
I
!
I
F
T~ 1
13. Oblicz długość łuku koła Singapore Flyer, który wyznaczają dwie sąsiednie gondole.
Zapisz oblicze n ia .
.....j
:
|
|
|
{
|
I
.
i
|
|
i
1
|
:
;
i
1
!
i
1-. Po jakim najkrótszym czasie pasażer, który wsiadł do kapsuły koła Singapore Flyer, znaj
dzie się w tym samym miejscu? Wynik podaj z dokładnością do minuty.
iścisz obliczenia.
§•
|
65
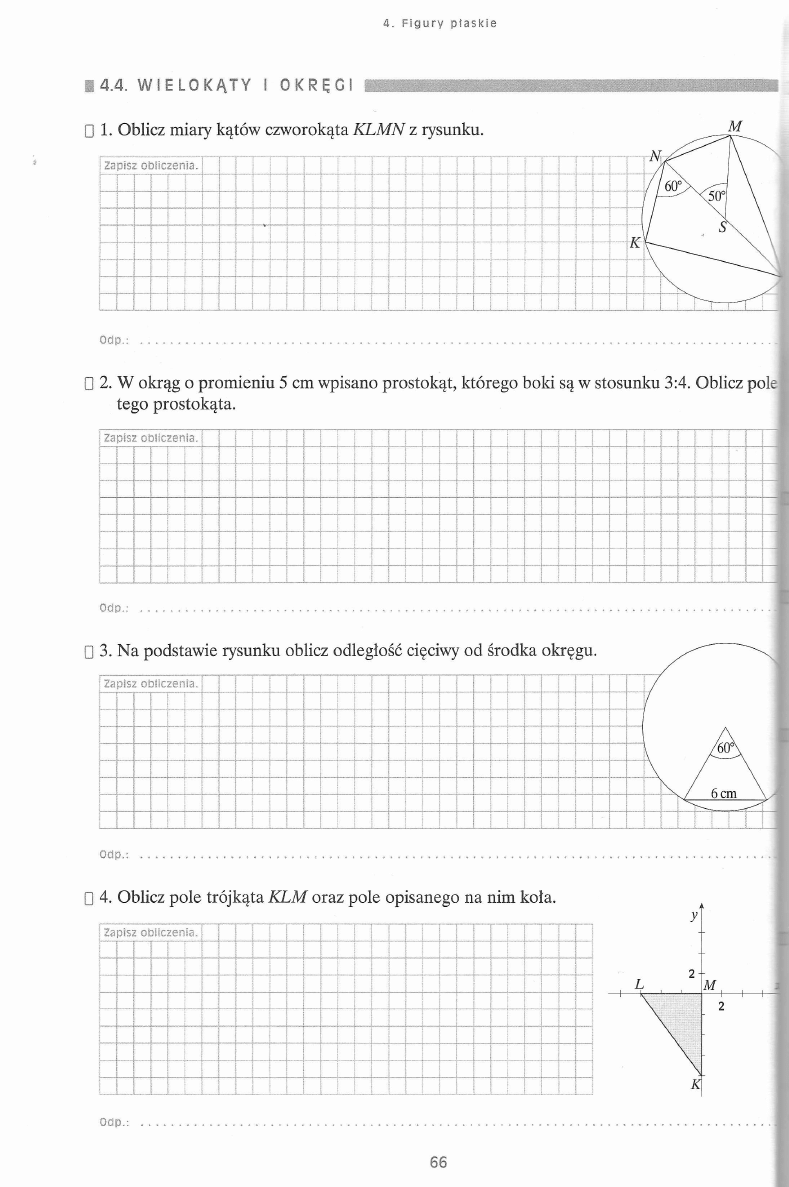
a. F i g u r y p i a s k i “
1 4.4. WI ELOKĄTY ! OKRĘGI
U 2. W okrąg o promieniu 5 cm wpisano prostokąt, którego boki są w stosunku 3:4. Oblicz pole
tego prostokąta.
Zapisz o b licze n ia .
I
Oc p.
6 6
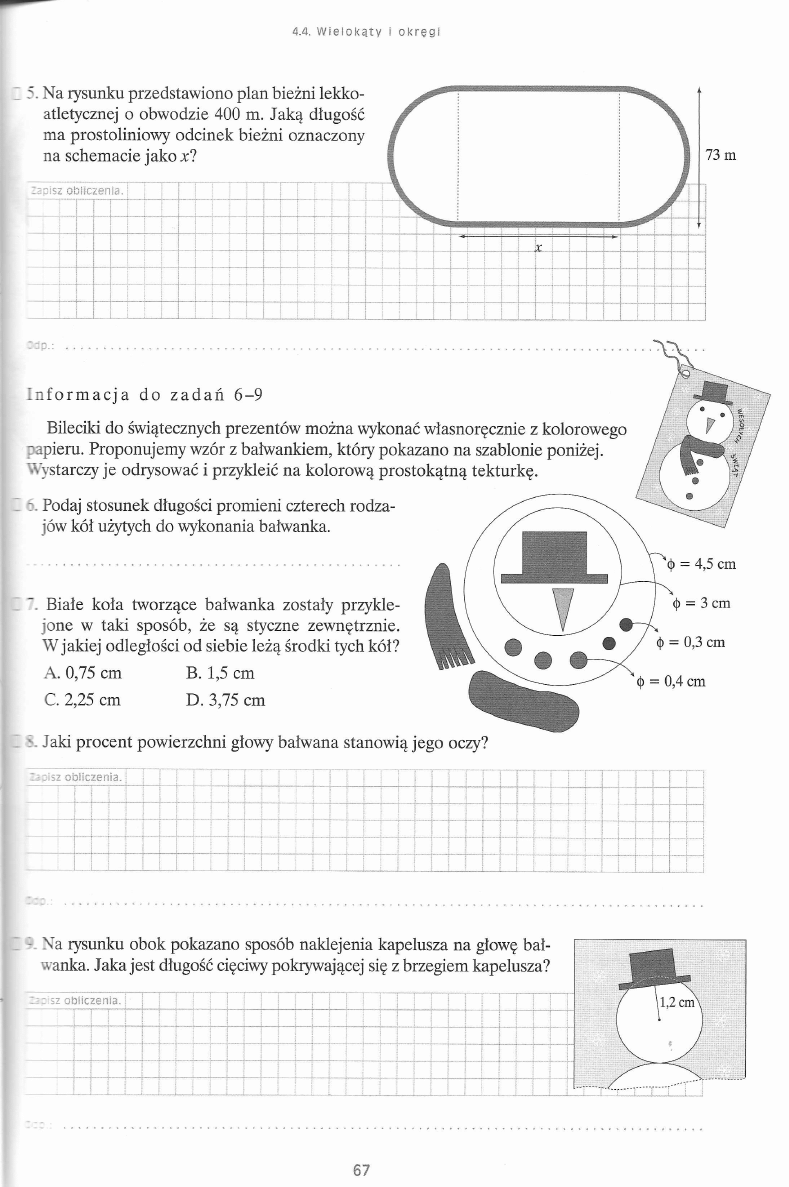
4.4, W ie lo k ą t y i o k r ę g i
. Na rysunku przedstawiono plan bieżni lekko
atletycznej o obwodzie 400 m. Jaką długość
ma prostoliniowy odcinek bieżni oznaczony
na schemacie jako
x l
m
_spisz o ::,:czen a.
<|) = 4,5 cm
(|> = 3 cm
<|) — 0,3 cm
= 0,4 cm
I n f o r m a c j a do z a d a ń 6-9
Bileciki do świątecznych prezentów można wykonać własnoręcznie z kolorowego
papieru. Proponujemy wzór z bałwankiem, który pokazano na szablonie poniżej.
Wystarczy je odrysować i przykleić na kolorową prostokątną tekturkę.
6. Podaj stosunek długości promieni czterech rodza
jów kół użytych do wykonania bałwanka.
Białe koła tworzące bałwanka zostały przykle
jone w taki sposób, że są styczne zewnętrznie.
W jakiej odległości od siebie leżą środki tych kół?
A. 0,75 cm
B. 1,5 cm
C. 2,25 cm
D. 3,75 cm
S. Jaki procent powierzchni głowy bałwana stanowią jego oczy?
Is o is i
i3.
!
: Na rysunku obok pokazano sposób naklejenia kapelusza na głowę bał
wanka. Jaka jest długość cięciwy pokrywającej się z brzegiem kapelusza?
: sz
67
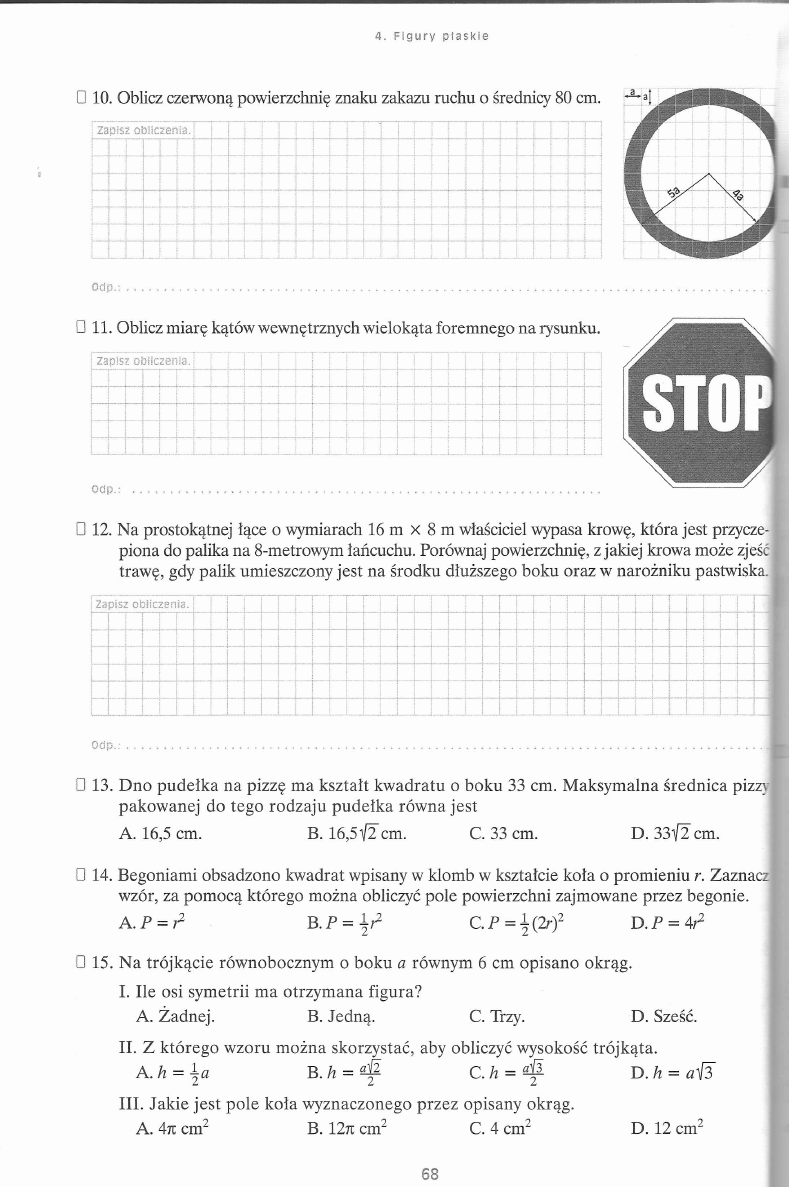
4 . F i g u r y p ł a s k i e
U 10. Oblicz czerwoną powierzchnię znaku zakazu ruchu o średnicy 80 cm.
l i i
i
:
■
U l i . Oblicz miarę kątów wewnętrznych wielokąta foremnego na rysunku.
:::
c u r c z e r i s .
f
Od
□ 12. Na prostokątnej łące o wymiarach 16 m x 8 m właściciel wypasa krowę, która jest przycze
piona do palika na 8-metrowym łańcuchu. Porównaj powierzchnię, z jakiej krowa może zjeść
trawę, gdy palik umieszczony jest na środku dłuższego boku oraz w narożniku pastwiska.
i
i
,
.
.....................................................................
□ 13. Dno pudełka na pizzę ma kształt kwadratu o boku 33 cm. Maksymalna średnica pizzy
pakowanej do tego rodzaju pudełka równa jest
A. 16,5 cm.
B. 16,5V^2cm.
C. 33 cm.
D. 3 3i2
cm.
J 14. Begoniami obsadzono kwadrat wpisany w klomb w kształcie koła o promieniu
r.
Zaznacz
wzór, za pomocą którego można obliczyć pole powierzchni zajmowane przez begonie.
A . P = r
B
.P = \ i 2
C .P = \ ( 2 r f
D .P = Ąr2
u 15. Na trójkącie równobocznym o boku
a
równym 6 cm opisano okrąg.
I. Ile osi symetrii ma otrzymana figura?
A. Żadnej.
B. Jedną.
C. Trzy.
D. Sześć.
II. Z którego wzoru można skorzystać, aby obliczyć wysokość trójkąta.
A.
h = \ a
B.
h =
C
. h = ^ -
D.
h = a i3
III. Jakie jest pole koła wyznaczonego przez opisany okrąg.
A.
4
k
cm2
B. 1271 cm2
C. 4 cm2
D. 12 cm2
6 8
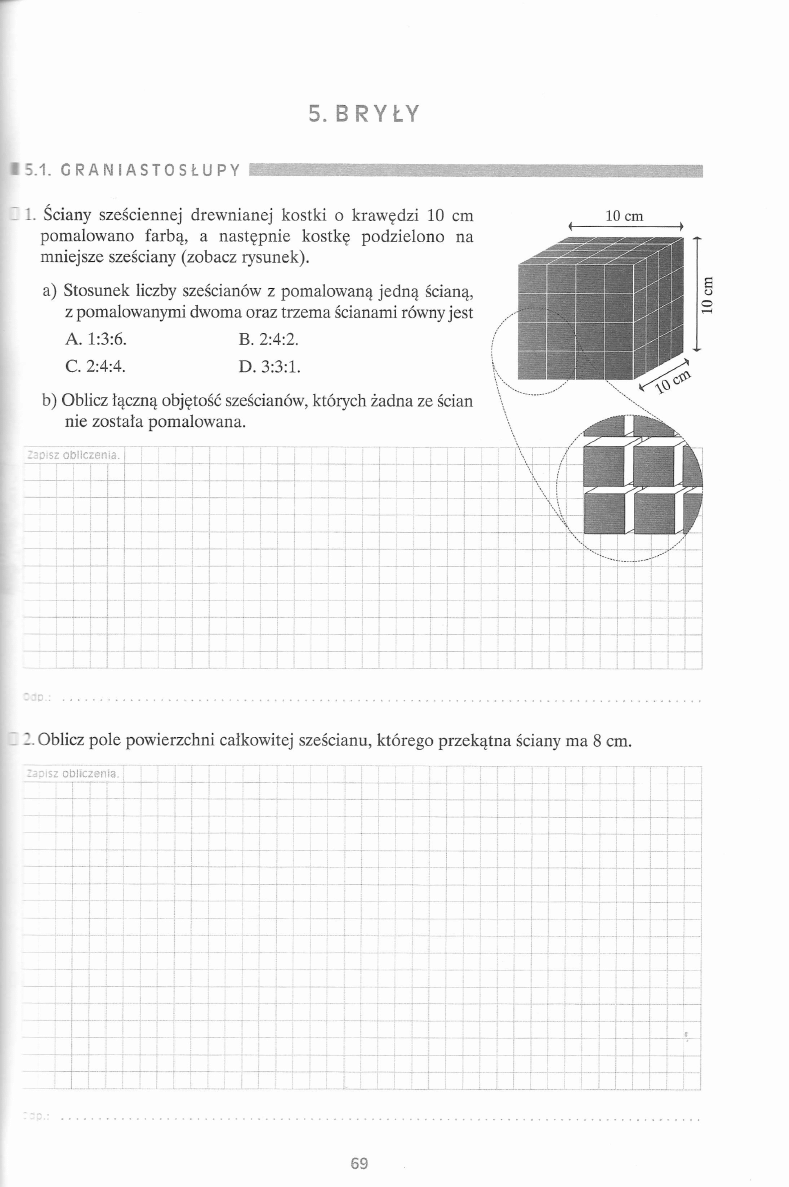
5. B R Y Ł Y
■ 5.1. G R A N I A S T O S Ł U P Y
Ściany sześciennej drewnianej kostki o krawędzi 10 cm
pomalowano farbą, a następnie kostkę podzielono na
mniejsze sześciany (zobacz rysunek).
a) Stosunek liczby sześcianów z pomalowaną jedną ścianą,
z pomalowanymi dwoma oraz trzema ścianami równy jest
A. 1:3:6.
B. 2:4:2.
C. 2:4:4.
D. 3:3:1.
b) Oblicz łączną objętość sześcianów, których żadna ze ścian
nie została pomalowana.
apisz o b licze n ia .
10 cm
_ 2. Oblicz pole powierzchni całkowitej sześcianu, którego przekątna ściany ma 8 cm.
Zapisz o b licze n ia .
1
.
-
|
_
!»
-
I
59
10
cm
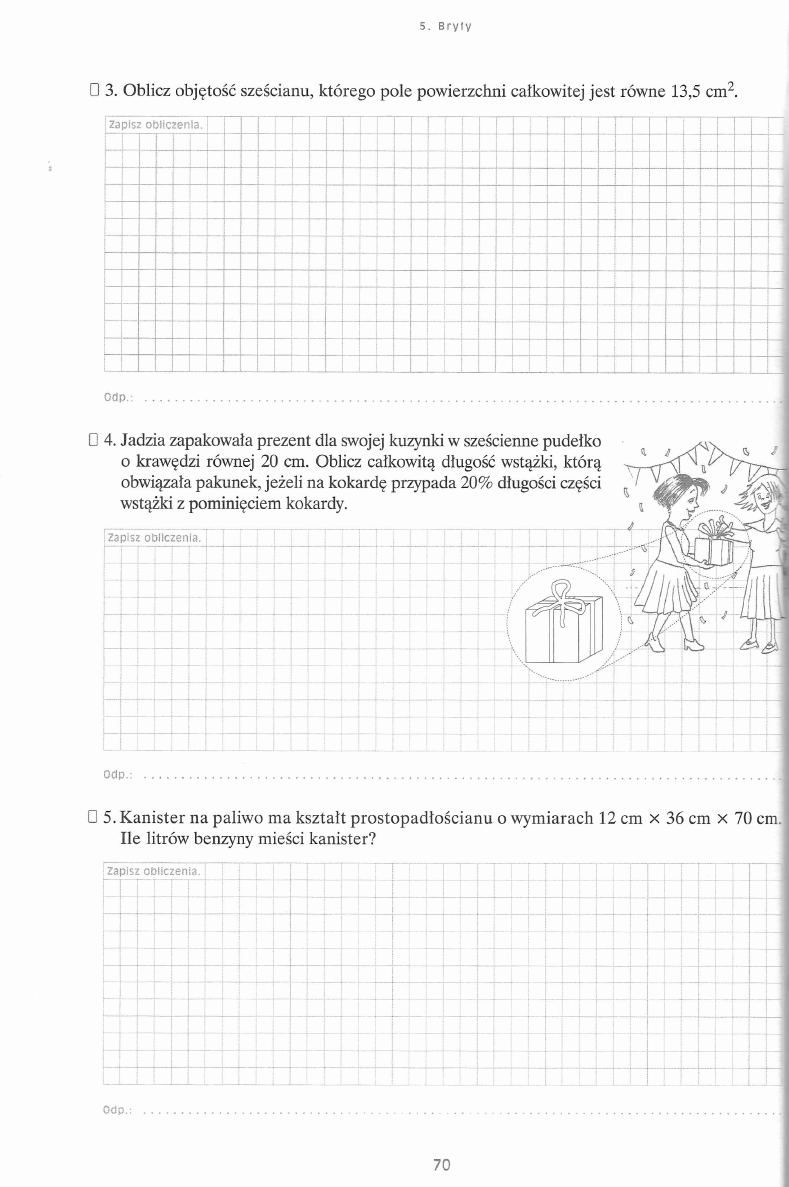
5. B r y ł y
□ 3. Oblicz objętość sześcianu, którego pole powierzchni całkowitej jest równe 13,5 cm2.
Zapisz o b licze n ia .
|
i
!
i
i
i
|
...i
!
!
|
O dp.:
□ 4. Jadzia zapakowała prezent dla swojej kuzynki w sześcienne pudełko
o krawędzi równej 20 cm. Oblicz całkowitą długość wstążki, którą
obwiązała pakunek, jeżeli na kokardę przypada 20% długości części
wstążki z pominięciem kokardy.
u
□ 5. Kanister na paliwo ma kształt prostopadłościanu o wymiarach 12 cm X 36 cm x 70 cm.
Ile litrów benzyny mieści kanister?
Zapisz o b licze n ia .
.... i
_
1
i
—
!
.......
O dp.:
70
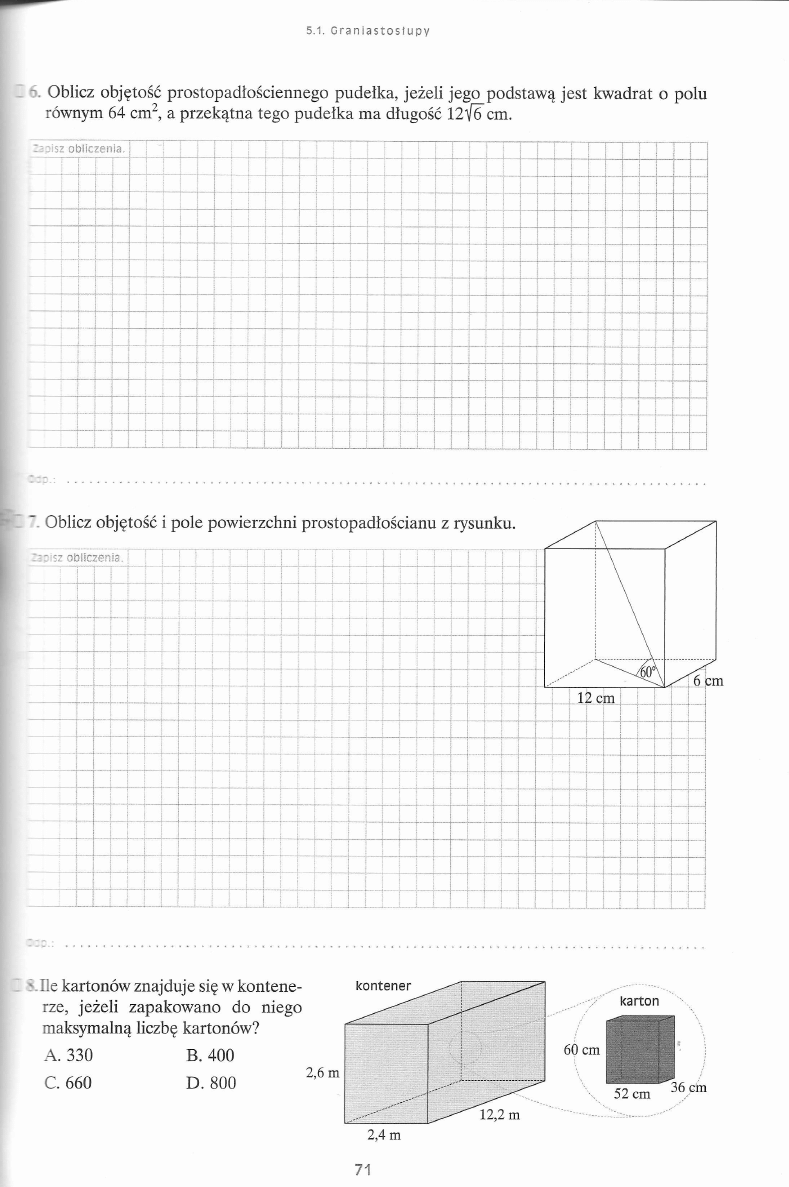
5.1. C r a n i a s t o s ł u p y
_
6
.
Oblicz objętość prostopadłościennego pudełka, jeżeli jego podstawą jest kwadrat o polu
równym 64 cm2, a przekątna tego pudełka ma długość 12^6" cm.
Zs.'2\SZ
0 )liczenia.
i
I 5-Ile kartonów znajduje się w kontene
rze, jeżeli zapakowano do niego
maksymalną liczbę kartonów?
A. 330
B. 400
C. 660
D . 800
12,2 m
kontener
karton
60 cm
71
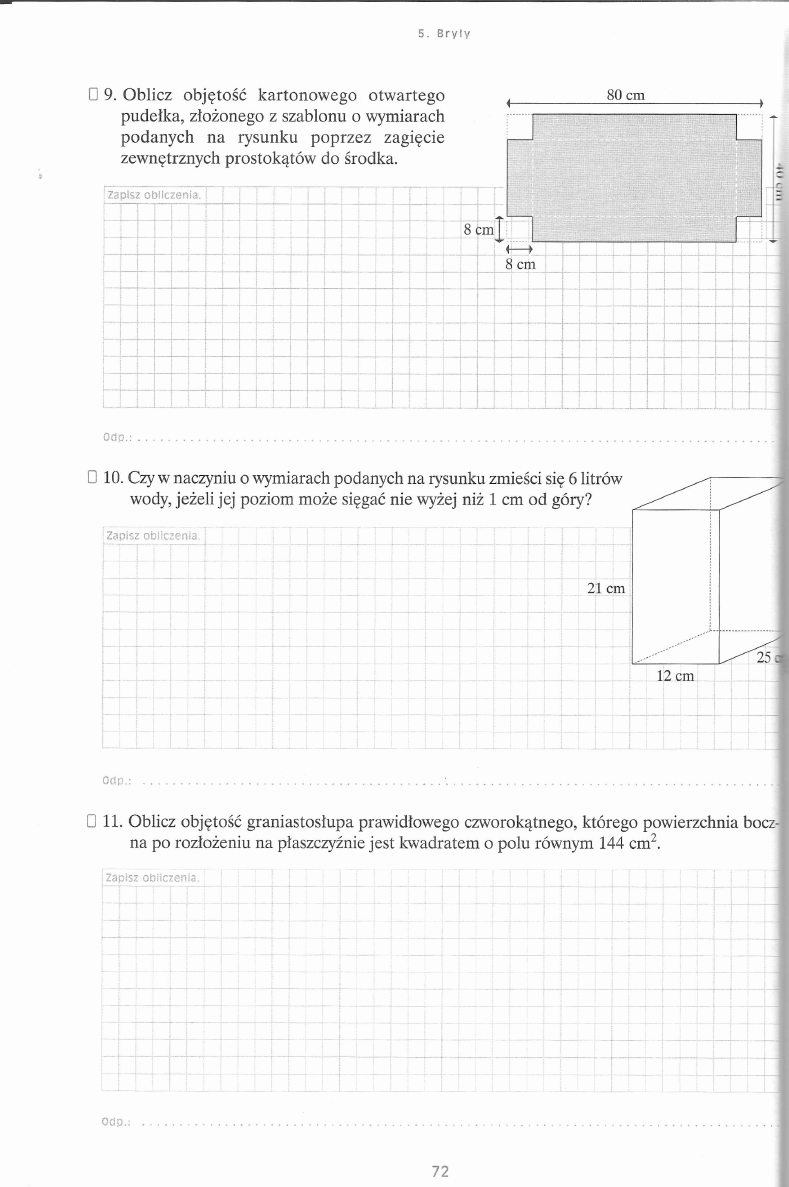
5. B r y t y
□ 9. Oblicz objętość kartonowego otwartego
i
___________
80 cm
pudełka, złożonego z szablonu o wymiarach
-------------------
podanych na rysunku poprzez zagięcie
—
zewnętrznych prostokątów do środka.
Zapisz o b licze n ia .
8 :m
| i
cr
i
n
- 1
]
Odp.:
72

5.1. G r a n i a s t o s t u p y
Zapisz o b licze n ia .
f
—
i
i
{
:
i *
Odp.:
73

5. B r y t y
□ 14. Podstawą graniastosłupa prostego jest trapez równoramienny o podstawach 6 cm i 12 cm,
którego ramię tworzy z dłuższą podstawą kąt 60°. Oblicz objętość graniastosłupa, jeżeli
przekątna największej ściany tworzy z krawędzią podstawy kąt 45°.
Zapisz o b licze n ia .
—
.....[---
i
O dp.:
□ 15. Oblicz masę jeżyn wypełniających maksymalnie pojemnik
1 0
Cm
O dp.: ................................................................................................................
74
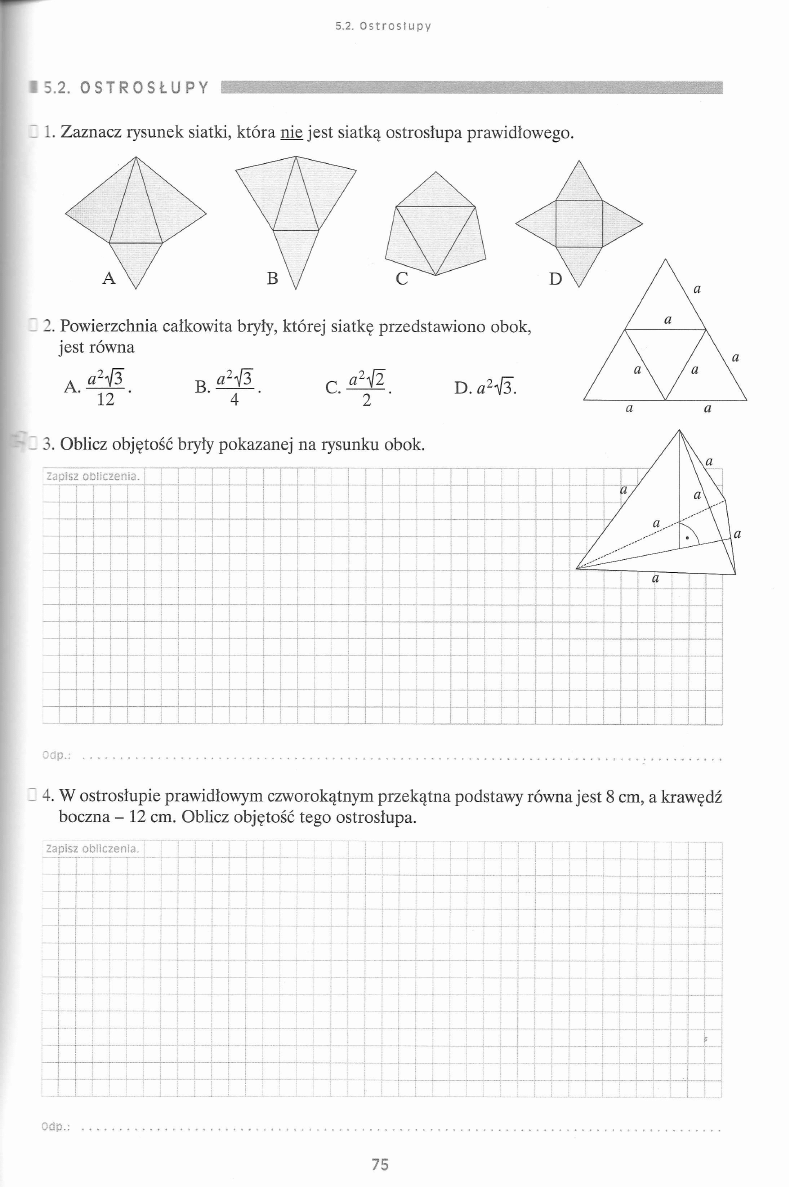
5.2. O s t r o s ł u p y
I 5.2. O S T R O S Ł U P Y
1. Zaznacz rysunek siatki, która nie jest siatką ostrosłupa prawidłowego.
2. Powierzchnia całkowita bryły, której siatkę przedstawiono obok,
jest równa
A .
12
B.
2V3
C.
l<2
D. a 2V3.
o
,
..........
..................
I 4. W ostrosłupie prawidłowym czworokątnym przekątna podstawy równa jest 8 cm, a krawędź
boczna - 12 cm. Oblicz objętość tego ostrosłupa.
Za pisz o b licze n ia .
—
—
75
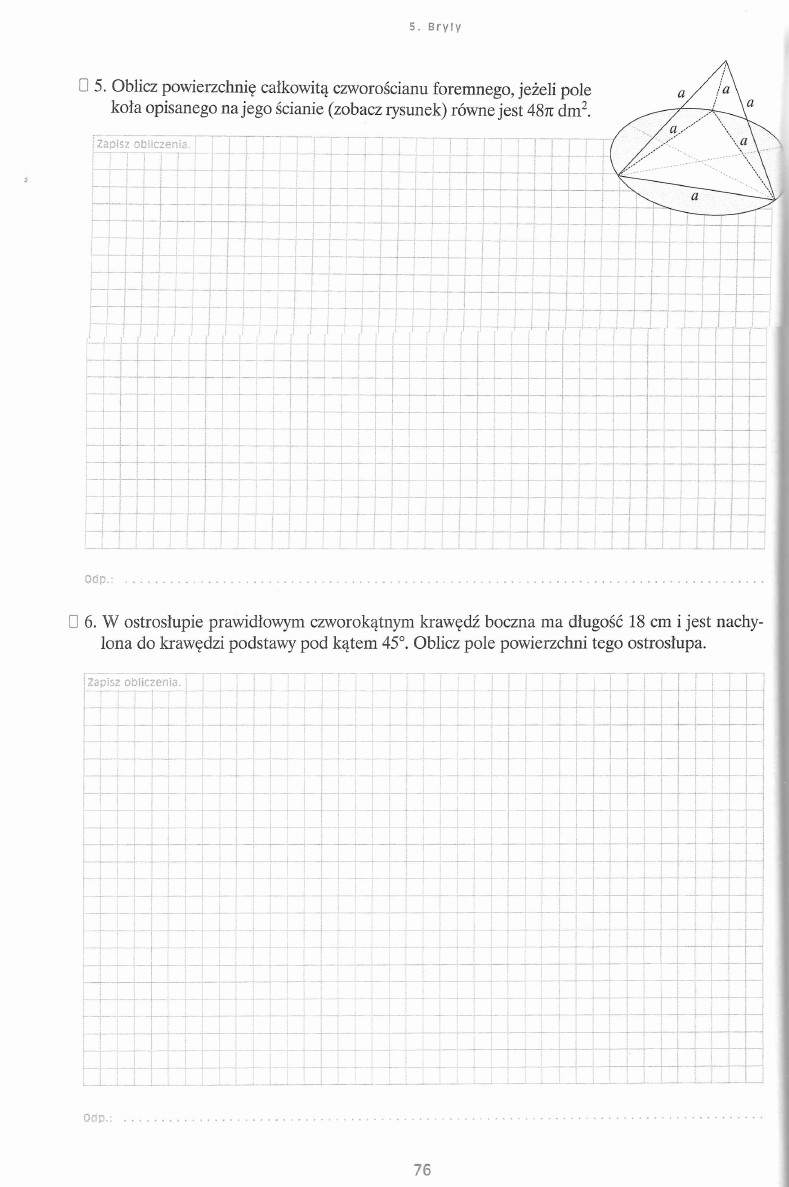
5. B r y t y
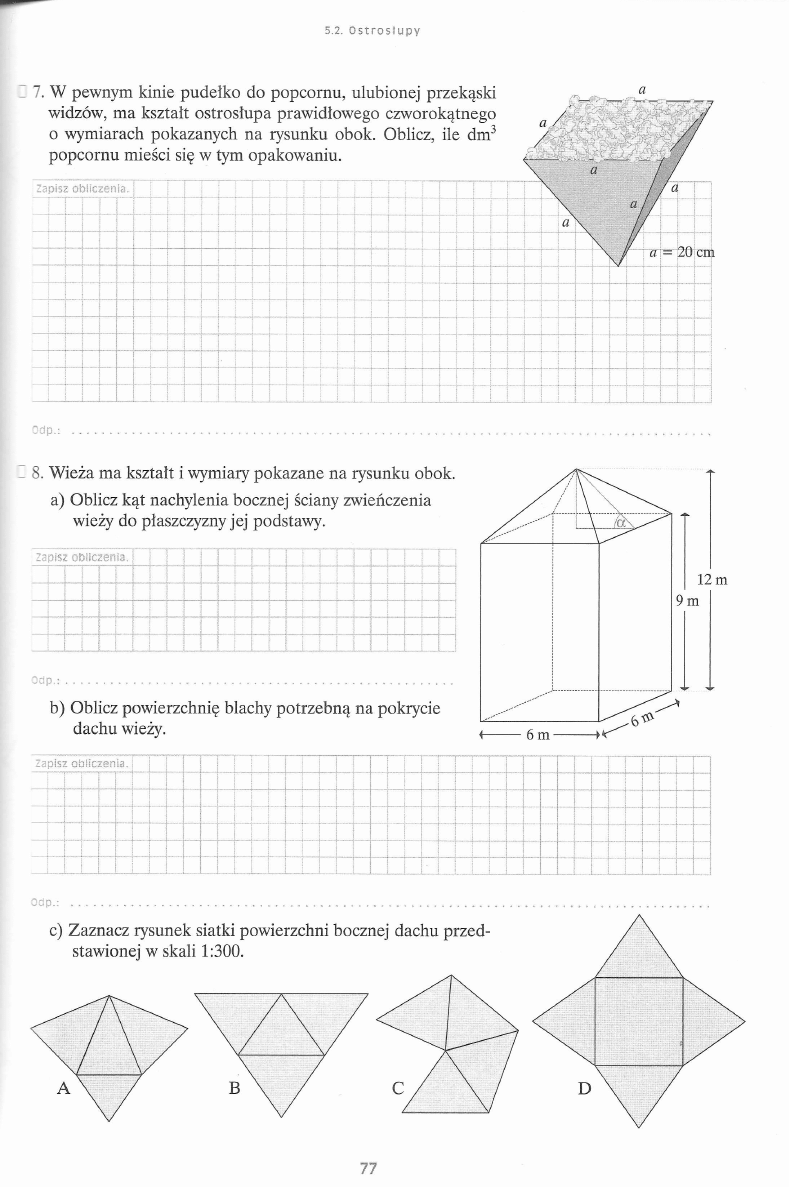
5.2. O s t r o s ł u p y
7. W pewnym kinie pudełko do popcornu, ulubionej przekąski
widzów, ma kształt ostrosłupa prawidłowego czworokątnego
o wymiarach pokazanych na rysunku obok. Oblicz, ile dm3
popcornu mieści się w tym opakowaniu.
Zapisz o b licze n ia .
i
;
]
/
/ a
!
¡1111H a t f
a
\
/ /
u
— 20 cm
Odp
8. Wieża ma kształt i wymiary pokazane na rysunku obok.
a) Oblicz kąt nachylenia bocznej ściany zwieńczenia
wieży do płaszczyzny jej podstawy.
Zap
i
j
3dp,:
b) Oblicz powierzchnię blachy potrzebną na pokrycie
dachu wieży.
6 m -
12 m
9 m
- 6 ^
Za;;
)
Odp,
c) Zaznacz rysunek siatki powierzchni bocznej dachu przed
stawionej w skali 1:300.
77
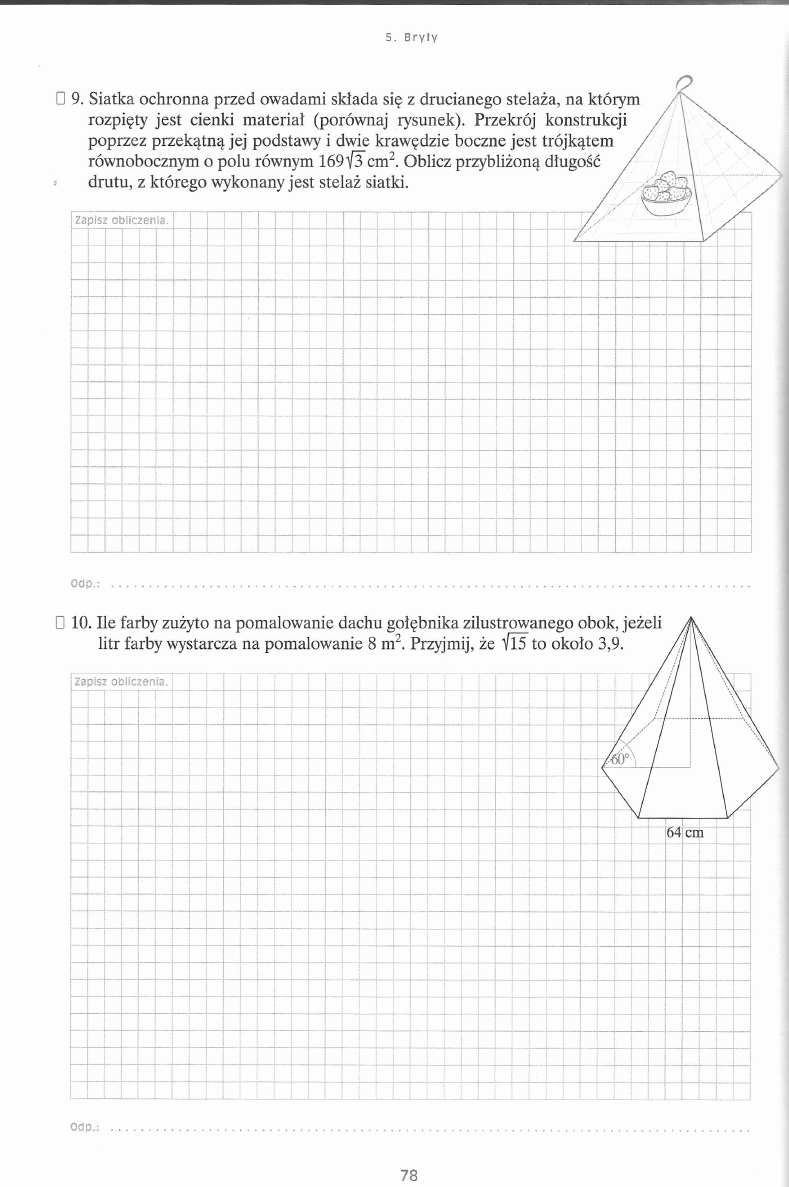
5 . B r y t y
78
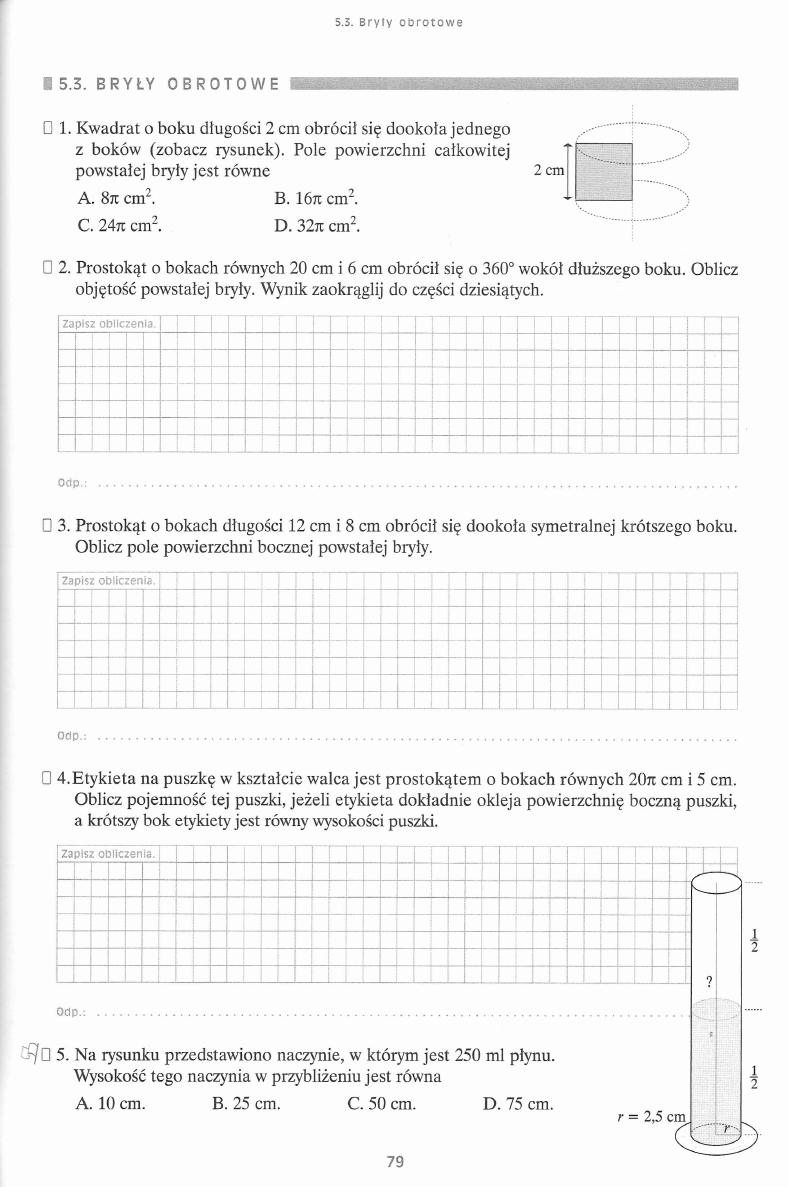
5.3. B r y t y o b r o t o w e
8 5.3. B R Y Ł Y O B R O T O W E
□ 1. Kwadrat o boku długości 2 cm obrócił się dookoła jednego
... .......
j
.....
z boków (zobacz rysunek). Pole powierzchni całkowitej
T K ...
powstałej bryły jest równe
2 cm
A. 871 cm2.
B. 1671 cm2.
---------
C.
24n
cm2.
D.
32n
cm2.
□ 2. Prostokąt o bokach równych 20 cm i 6 cm obrócił się o 360° wokół dłuższego boku. Oblicz
objętość powstałej bryły. Wynik zaokrąglij do części dziesiątych.
Zapisz oblicze n ia .
i
Ocip.: ............................................................................................................................................................................................................................................
□ 3. Prostokąt o bokach długości 12 cm i 8 cm obrócił się dookoła symetralnej krótszego boku.
Oblicz pole powierzchni bocznej powstałej bryły.
Zapisz o b licze n ia .
i
Odp.:
□ 4.Etykieta na puszkę w kształcie walca jest prostokątem o bokach równych
207C
cm i 5 cm.
Oblicz pojemność tej puszki, jeżeli etykieta dokładnie okleja powierzchnię boczną puszki,
a krótszy bok etykiety jest równy wysokości puszki.
Zapisz o b licze n ia .
j
9
O dp.: ........................................................................................................................................................................................................................
^fjo
5. Na rysunku przedstawiono naczynie, w którym jest 250 ml płynu.
Wysokość tego naczynia w przybliżeniu jest równa
A. 10 cm.
B. 25 cm.
C. 50 cm.
D. 75 cm.
r
= 2,5 cm
79
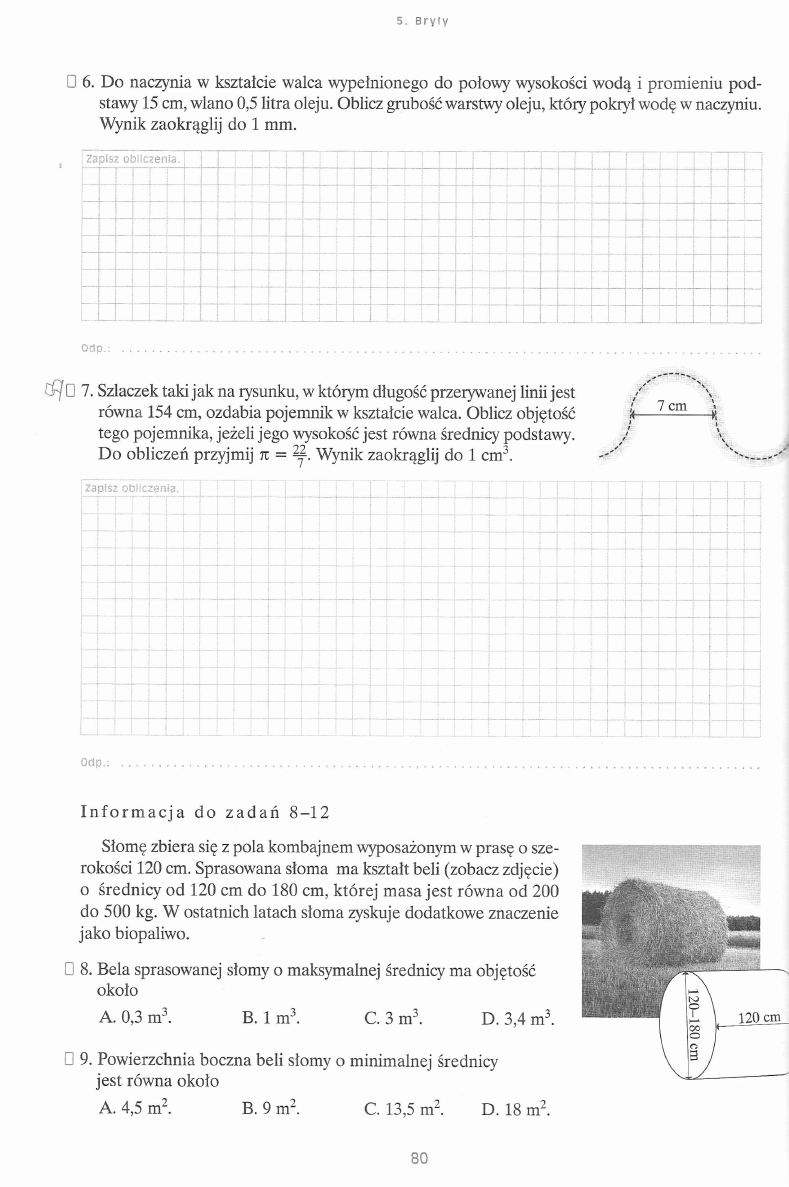
5. B r y t y
□ 6. Do naczynia w kształcie walca wypełnionego do połowy wysokości wodą i promieniu pod
stawy 15 cm, wlano 0,5 litra oleju. Oblicz grubość warstwy oleju, który pokrył wodę w naczyniu.
Wynik zaokrąglij do 1 mm.
Za pisz o b licze n ia .
1
i
1
O dp.: ...........................................................................................................................................................................................................................
irj
□ 7. Szlaczek taki jak na rysunku, w którym długość przerywanej linii jest
równa 154 cm, ozdabia pojemnik w kształcie walca. Oblicz objętość
i—
— £
tego pojemnika, jeżeli jego wysokość jest równa średnicy podstawy.
Do obliczeń przyjmij
n =
y . Wynik zaokrąglij do 1 cm3.
Zapisz o b licze n ia .
!
!
O dp.: ................................................................................................................................................................
I n f o r m a c j a d o z a d a ń 8 -1 2
Słomę zbiera się z pola kombajnem wyposażonym w prasę o sze
rokości 120 cm. Sprasowana słoma ma kształt beli (zobacz zdjęcie)
o średnicy od 120 cm do 180 cm, której masa jest równa od 200
do 500 kg. W ostatnich latach słoma zyskuje dodatkowe znaczenie
jako biopaliwo.
□ 8. Bela sprasowanej słomy o maksymalnej średnicy ma objętość
około
A. 0,3 m3.
B. 1 m3.
C. 3 m3.
D. 3,4 m3.
□ 9. Powierzchnia boczna beli słomy o minimalnej średnicy
jest równa około
A. 4,5 m2.
B. 9 m2.
C. 13,5 n r.
D. 18 n r.
80
5.3.
B r y f y o b r o t o w e
□ 10. Oblicz objętość 1 tony sprasowanej w bele słomy. Do obliczeń przyjmij średnią z danych
zawartych w tekście.
Zapisz o b licze n ia .
1
i
O dp.:
□ 11. Wydajność prasy to około 50 bel na godzinę. Przyjmij średnią wielkość oraz masę beli
i oblicz, ile czasu musi pracować prasa, aby sprasować objętość słomy równą 950 m3.
Wynik zaokrąglij do pełnej godziny.
Zapisz o b lic ze n ia , i
----------
j
i
____
___ -
O dp.:
12. Pan Witek kupił na zimę 5,6 tony słomy - ilość niezbędną do ogrzania domu jednorodzinnego
podczas całego sezonu grzewczego. Słoma sprasowana w bele o średnicy 120 cm i minimal
nej masie 200 kg będzie przechowywana w stodole o wymiarach 8 m x 16 m x 4,5 m. Oblicz,
jakim procentem kubatury stodoły jest sumaryczna objętość kupionych bel słomy.
5. B r y t y
□ 13. Podstawą walca i stożka jest koło o powierzchni 57t cm2. Wysokość stożka jest trzy razy
większa od wysokości walca, a więc objętość stożka jest
A. dziewięć razy mniejsza od objętości walca.
B. trzy razy mniejsza od objętości walca.
C. trzy razy większa od objętości walca.
D. równa objętości walca.
'■f i
□ 14. Pole podstawy bryły, której siatkę przedstawia rysunek obok,
8 cm
O dp.:
0 16. Trójkąt równoboczny o polu
16^3
cm2 obraca się o kąt 180° dookoła wysokości. Oblicz pole
powierzchni całkowitej powstałej bryły.
Zapisz o b licze n ia .
'
j
.. .
O dp.:
££/□ 17. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem 60°. Pole powierzch
ni całkowitej jest równe 4871 cm2. Oblicz objętość stożka.
Zapisz o b licze n ia .
i
i
i
—
|
—
Odp.:
5.3. B r y t y o b r o t o w e
□ 18. Podstawa stożka ma pole równe 25
n
cm2. Oblicz powierzchnię boczną stożka, jeżeli jego
tworząca jest nachylona do podstawy pod kątem 60°.
Zapisz oblicze n ia.
OuP.: ............................................................................................................................................................................................................................................
■f-Jii
19. Papierowe koło o promieniu 15 cm rozcięto na połowy i z każdej z nich zwinięto rożek,
przeznaczając wycinek o pwierzchni ^ półkola na zakładkę. Jaka jest objętość rożka?
Wynik zaokrąglij do 1 cm3.
Z a p i s z
o b lic z e n i
I
i
O dp.:
□ 20. Z 27 jednakowych ołowianych kulek o promieniu 2 cm po przetopieniu utworzono kulę.
Oblicz, ile razy powierzchnia tej kuli jest większa niż powierzchnia jednej z kulek,
z których powstała.
Zapisz o b licze n ia .
5
Odp.:
83
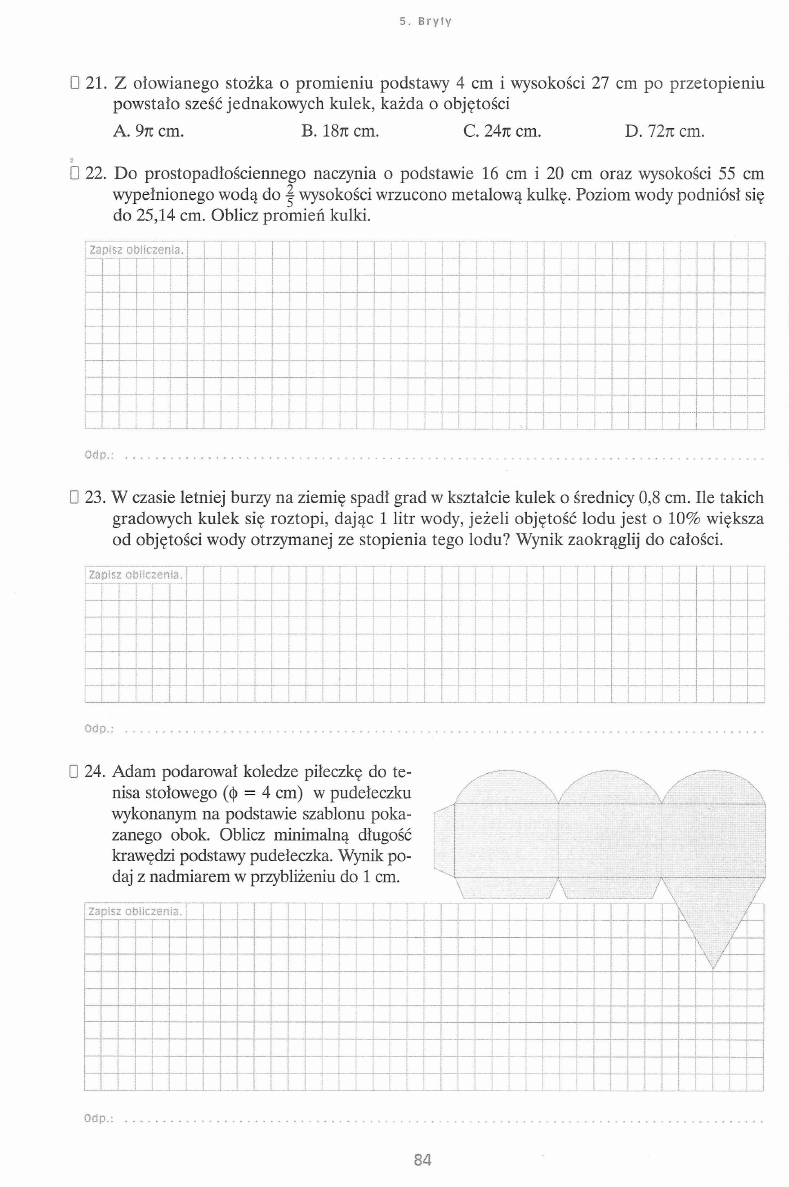
5. B r y f y
□ 21. Z ołowianego stożka o promieniu podstawy 4 cm i wysokości 27 cm po przetopieniu
powstało sześć jednakowych kulek, każda o objętości
A.
9
k
cm.
B. 1871 cm.
C. 24^ cm.
D. 72
n
cm.
i
□ 22. Do prostopadłościennego naczynia o podstawie 16 cm i 20 cm oraz wysokości 55 cm
wypełnionego wodą do | wysokości wrzucono metalową kulkę. Poziom wody podniósł się
do 25,14 cm. Oblicz promień kulki.
Zapisz o b licze n ia .
□ 23. W czasie letniej burzy na ziemię spadł grad w kształcie kulek o średnicy 0,8 cm. Ile takich
gradowych kulek się roztopi, dając 1 litr wody, jeżeli objętość lodu jest o 10% większa
od objętości wody otrzymanej ze stopienia tego lodu? Wynik zaokrąglij do całości.
Zapisz o b lic zenia.
]
i
i
i
|
0 ;■
;3.: ....................
U 24. Adam podarował koledze piłeczkę do te
nisa stołowego ((j) = 4 cm) w pudełeczku
wykonanym na podstawie szablonu poka
zanego obok. Oblicz minimalną długość
krawędzi podstawy pudełeczka. Wynik po
daj z nadmiarem w przybliżeniu do 1 cm.
Zapisz o b licze n ia .
—
—
—
..
.
|
i - .
/
|
'f ?
{
|
.
.
.
.
.
.
8 4
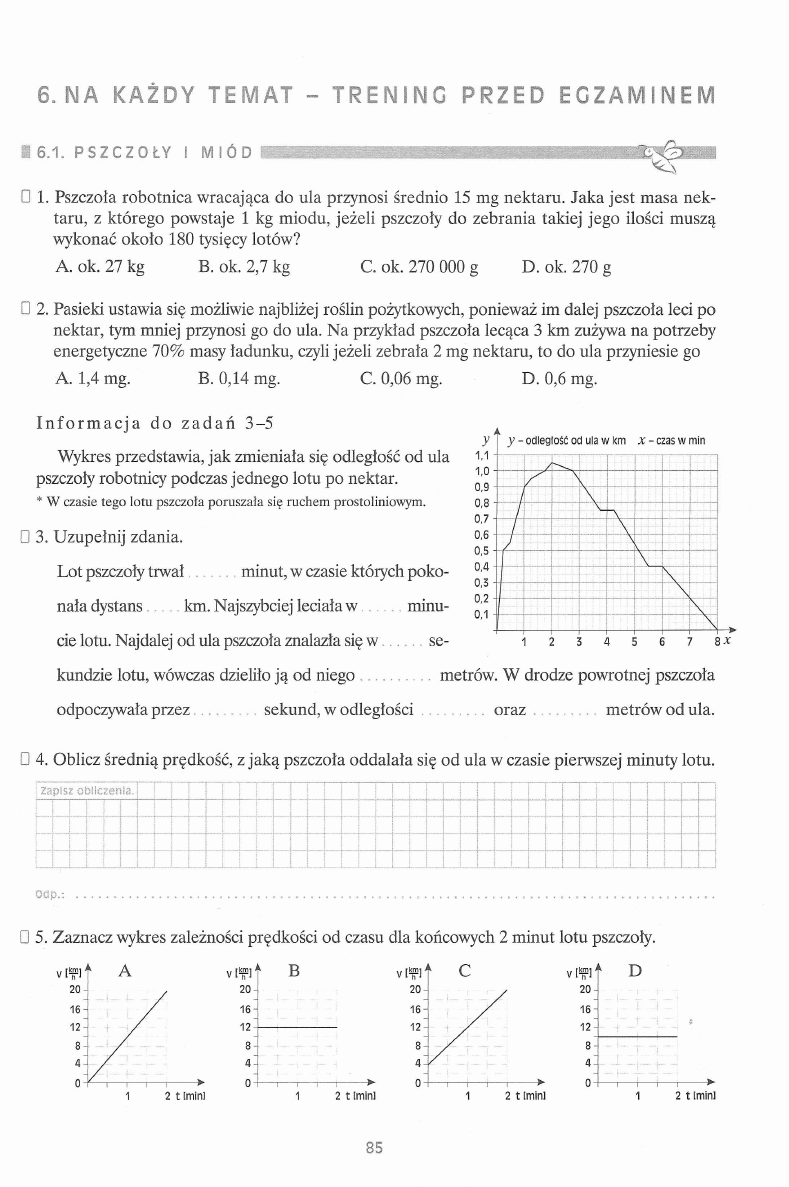
6
A K A Ż D Y T E M A T - T R E N I N G P R Z E D E G Z A M I N E M
fi i
DC 7 P 7 H Ł V
u> I . ■ O
w
U Ł Y
ó D
u
1. Pszczoła robotnica wracająca do ula przynosi średnio 15 mg nektaru. Jaka jest masa nek
taru, z którego powstaje 1 kg miodu, jeżeli pszczoły do zebrania takiej jego ilości muszą
wykonać około 180 tysięcy lotów?
A. ok. 27 kg
B. ok. 2,7 kg
C. ok. 270 000 g
D. ok. 270 g
U
2. Pasieki ustawia się możliwie najbliżej roślin pożytkowych, ponieważ im dalej pszczoła leci po
nektar, tym mniej przynosi go do ula. Na przykład pszczoła lecąca 3 km zużywa na potrzeby
energetyczne 70% masy ładunku, czyli jeżeli zebrała 2 mg nektaru, to do ula przyniesie go
A. 1,4 mg.
B. 0,14 mg.
I n f o r m a c j a do z a d a ń 3-5
C. 0,06 mg.
D. 0,6 mg.
Wykres przedstawia, jak zmieniała się odległość od ula
pszczoły robotnicy podczas jednego lotu po nektar.
* W czasie tego lotu pszczoła poruszała się ruchem prostoliniowym.
□ 3. Uzupełnij zdania.
Lot pszczoły trwał
minut, w czasie których poko
nała dystans
km. Najszybciej leciała w
minu
cie lotu. Najdalej od ula pszczoła znalazła się w
se
kundzie lotu, wówczas dzieliło ją od niego
metrów. W drodze powrotnej pszczoła
odpoczywała przez
sekund, w odległości
oraz
metrów od ula.
U 4. Oblicz średnią prędkość, z jaką pszczoła oddalała się od ula w czasie pierwszej minuty lotu.
-
.
U 5. Zaznacz wykres zależności prędkości od czasu dla końcowych 2 minut lotu pszczoły.
20
16-
12
4 -
0
B
2 t [min!
V iTfJ
20
16
12
8
4
0
D
i— i— i-----»-
1
2 t [mini
8 5
6. Na k a ż d y t e m a t - t r e n i n g p r z e d e g z a m i n e m
□ 6. W ciągu dnia pszczoła zbierająca nektar odwiedza 7 tys. kwiatów. Średnio ile razy dziennie
robotnica wylatuje po nektar, jeżeli podczas jednego lotu odwiedza około 140 kwiatów?
A. 5
B. 25
C. 50
D. 250
i
j 7. Nektar dostarczany do ula przez robotnice zawiera ok. 70% wody. Jednak w ciągu kolejnych
dni po złożeniu go w komórkach plastra pszczoły, wachlując skrzydłami, obniżają około
3,5 razy ilość zawartej w miodzie wody. Oblicz masę miodu, który powstaje z dziennych
zbiorów nektaru pszczelej rodziny równych 500 g.
■
U 8. Ile osi symetrii ma pojedyncza komórka plastra miodu?
A. 3
B. 4
C. 6
D. 12
□ 9. Pod zdjęciem przedstawiono obraz komórki plastra miodu
o boku
a
w przesunięciu o wektor. Oblicz długość tego wektora.
J / [] 10. Jaką powierzchnię na planie wykonanym w ska
li 1:5 000 zajmuje pasieka, której powierzchnia
równa jest 0,04 hektara. Odpowiedź podaj
w centymetrach kwadratowych.
•
.
~~r-~..
............
......
■
. . .
........ ........
:t ~
.
.
r : :
L 11. 720 ml miodu ma masę 1 kg.
a) Oblicz masę 11 miodu. Wynik podaj w przy
bliżeniu do 1 dag.
b) Gęstość miodu w zaokrągleniu do 0,01 rów
na jest
A. 1
,
3
0
B. 1,3 8 -^.
7
cm 3
7
c m 3
D. 1,40-
C. 1,39 -Ł;.
7
c m 3
c m 3*
8 6
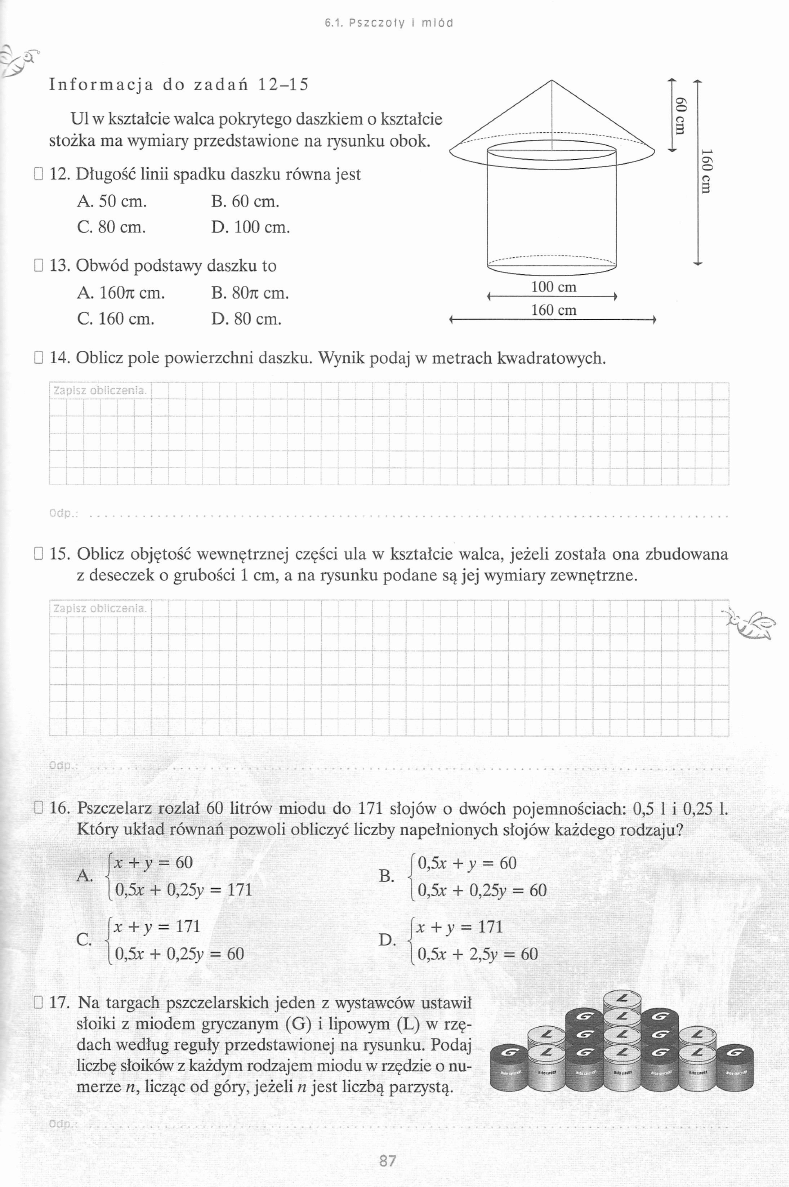
6.1. P s z c z o ł y i m i ó d
■ >
I n f o r m a c j a do z a d a ń 1 2 -1 5
Ul w kształcie walca pokrytego daszkiem o kształcie
stożka ma wymiary przedstawione na rysunku obok.
□ 12. Długość linii spadku daszku równa jest
A. 50 cm.
B. 60 cm.
C. 80 cm.
D. 100 cm.
□ 13. Obwód podstawy daszku to
A. 160
tt
cm.
B. 8071 cm.
C. 160 cm.
D. 80 cm.
100 cm
160 cm
O
n
O
G\
O
O
3
□ 14. Oblicz pole powierzchni daszku. Wynik podaj w metrach kwadratowych.
Zapisz ob licze n i,
O dp.:
□ 15. Oblicz objętość wewnętrznej części ula w kształcie walca, jeżeli została ona zbudowana
z deseczek o grubości 1 cm, a na rysunku podane są jej wymiary zewnętrzne.
Zapisz o b licze n ia . i
1...1"
16. Pszczelarz rozlał 60 litrów miodu do 171 słojów o dwóch pojemnościach: 0,5 1 i 0,25 1.
Który układ równań pozwoli obliczyć liczby napełnionych słojów każdego rodzaju?
A.
C.
jx
+ y
= 60
[ 0,5x + 0,25y = 171
\ x + y =
171
[ 0,5x +
0,25y
= 60
B.
D.
[ 0,5x +
y —
60
[ 0,5x + 0,2
5y =
60
jx
+ y = 171
[0,5x + 2
,5y —
60
D 17. Na targach pszczelarskich jeden z wystawców ustawił
słoiki z miodem gryczanym (G) i lipowym (L) w rzę
dach według reguły przedstawionej na rysunku. Podaj
liczbę słoików z każdym rodzajem miodu w rzędzie o nu
merze
n,
licząc od góry, jeżeli
n
jest liczbą parzystą.
87
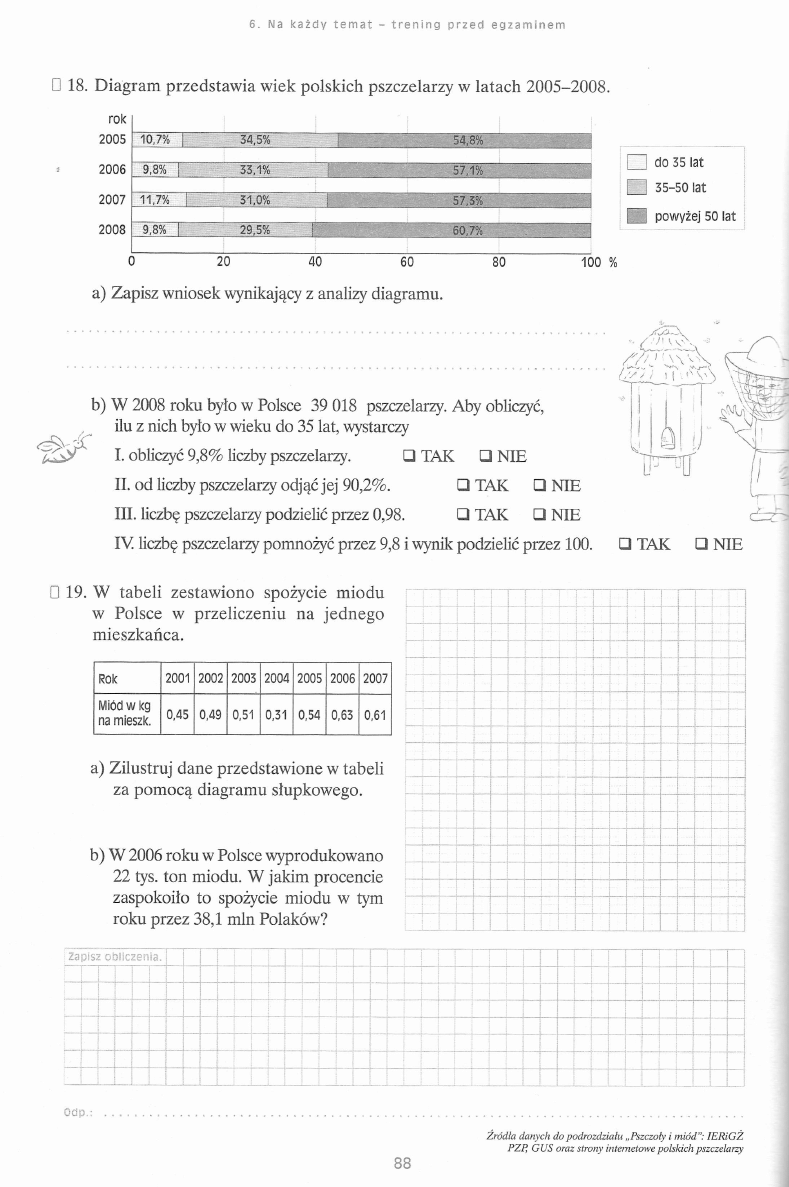
6. Ma k a ż d y t e m a t - t r e n i n g p r z e d e g z a m i n e m
O 18. Diagram przedstawia wiek polskich pszczelarzy w latach 2005-2008.
rok
2005
2006
2007
2008
10,7%
34,5%
54,!
9,8%
33,1%
"57,1%
11,7%
31,0%
57,3%
9,8
29,5%
H
60,7%
0
20
40
60
a) Zapisz wniosek wynikający z analizy diagramu.
80
100
■
do 35 lat
□
35-50 lat
E 3 powyżej 50 lat
b) W 2008 roku było w Polsce 39 018 pszczelarzy. Aby obliczyć,
ilu z nich było w wieku do 35 lat, wystarczy
I. obliczyć 9,8% liczby pszczelarzy.
□ TAK
□ NIE
II. od liczby pszczelarzy odjąć jej 90,2%.
□ TAK
□ NIE
III. liczbę pszczelarzy podzielić przez 0,98.
□ TAK
□ NIE
IV liczbę pszczelarzy pomnożyć przez 9,8 i wynik podzielić przez 100.
□ 19. W tabeli zestawiono spożycie miodu
w Polsce w przeliczeniu na jednego
mieszkańca.
Rok
2001 2002 2003 2004 2005 2006 2007
Miód w kg
na mieszk.
0,45 0,49 0,51 0,31 0,54 0,63 0,61
a) Zilustruj dane przedstawione w tabeli
za pomocą diagramu słupkowego.
b) W 2006 roku w Polsce wyprodukowano
22 tys. ton miodu. W jakim procencie
zaspokoiło to spożycie miodu w tym
roku przez 38,1 min Polaków?
■
Zapisz oblicze n ia .
|
Odp.
8 8
Źródła danych do podrozdziału „Pszczoły i miód”: IERiGŻ
PZP, GUS oraz strony internetowe polskich pszczelarzy

6.2. W p o d r ó ż y
□ 1. Zgodnie z definicją Światowej Organizacji Turystyki termin „turysta” dotyczy osób podróżu
jących w celach innych niż podjęcie pracy, głównie wypoczynkowych, i pozostających
poza miejscem stałego pobytu nie dłużej niż rok. Poniżej podano czasy pobytu za granicą
czterech osób. Który z wyjazdów według przytoczonej definicji można zaliczyć do wyjazdów
turystycznych?
A. 73 ■
22 • 3 • 5 godz.
B. 106 min
C. 6 • 107 s
D. 22 • 103 godz.
I 6.2. W P O D R Ó Ż Y
I n f o r m a c j a do z a d a ń 2- 4
Uczestnictwo Polaków w wieku 15 lat i więcej w wyjazdach turystycznych
W yszczególnienie
2 0 0 0
2005
2007
200 8
U czestnicy w y ja z d ó w w % badanej populacji*
W y je ż d ż a ją c y * * ........................................................
60
47
47
48
w kraju na okres: 2 - 4 d n i ....................................
37
24
23
20
5 dni i w i ę c e j ......................
34
29
28
29
za g r a n ic ę ...................................................................
15
12
15
17
IM iew yjeżdżający.......................................................
40
53
53
52
*w 2008 roku ankietowano 3,5 tys.
respondentów, tj. ok. 0,01% bada
nej populacji.
**W dalszym podziale uczestnik an
kiety może być wykazany więcej
niż jeden raz.
Na podstawie: „Mały rocznik statystyczny
Polski 2009”, GUS, Warszawa 2009
□ 2. Oblicz w przybliżeniu, ilu Polaków w roku 2008 było w wieku 15 lat i więcej oraz ilu z nich
wyjeżdżało w tymże roku w celach turystycznych.
Zapisz o b licze n ia .
—
—
OdP.:
0 3. Przedstaw graficznie za pomocą procento
wego diagramu słupkowego porównanie
liczby osób wyjeżdżających (bez względu na
rodzaj wyjazdu) i niewyjeżdżających w la
tach zestawionych w tabeli.
□ 4. Zapisz wnioski dotyczące turystycznych wy
jazdów Polaków w 2008 roku w porówna
niu z rokiem 2000.
89
6. Na k a ż d y t e m a t - t r e n i n g p r z e d e g z a m i n e m
□ 5. W 2008 roku w Polsce było 6 857 obiektów zbiorowego zakwaterowania, w tym 361 schronisk
młodzieżowych. Jaki procent wszystkich obiektów stanowiły schroniska młodzieżowe?
A. ok. 0,52%
B. ok. 0,53%
C. ok. 5,26%
D. ok. 52,60%
Ó 6. W hotelu jest łącznie 158 pokoi: cztero-, trzy- , dwu- i jednoosobowych, w których jest
329 miejsc. Oblicz, ile w tym hotelu jest pokoi każdego rodzaju, jeżeli pokoi czteroosobowych
jest tyle samo co trzyosobowych, a dwuosobowych tyle co jednoosobowych.
Zapisz o b licze n ia .
---
O dp.: ................................................................... , ......................................................................... ........................................................................................
□ 7. Opłata za pokój jednoosobowy wynosi 150 zł. W dwuosobowym pokoju nocleg dla jednej osoby
jest tańszy o 30 zł, w trzyosobowym stanowi 75% ceny „jedynki”, a w czteroosobowym równy
jest | ceny noclegu w „dwójce”. Oblicz cenę noclegu jednej osoby w każdym rodzaju pokoju.
Zapisz o b licze n ia .
O dp.:
□ 8. W 1841 roku Thomas Cook założył w Anglii pierwsze biuro podróży, którego pierwszą zorga
nizowaną wycieczką była podróż pociągiem na trasie Leicester - Loughborough. Jaka odległość
dzieli te miasta, jeżeli na mapie w skali 1:1 200 000 odległość między nimi równa jest 1,8 cm?
A. 216 km
B. 21,6 km
C. 18 km
D. 2,16 km
□ 9. W ofercie biura podróży lotnicza wycieczka do Paryża kosztuje 2 849 zł od osoby. Jednakże
osoby podróżujące bez pary są kwaterowane w pokoju jednoosobowym z dopłatą 252 zł.
Ile osób zamieszkało w pokojach jednoosobowych, jeżeli wycieczka liczyła 69 uczestników,
a łączny koszt wycieczki to 199 857 zł?
90
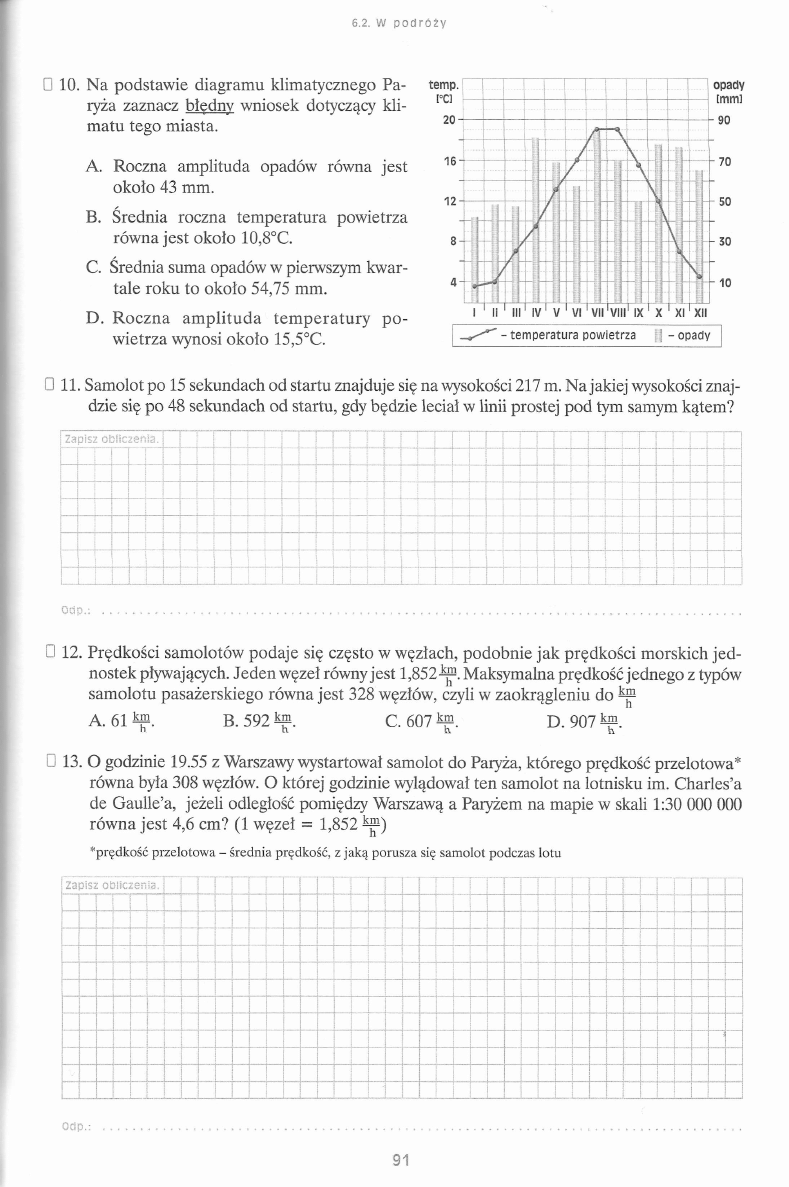
6
.
2
.
w
p o d r ó ż y
□ 10. Na podstawie diagramu klimatycznego Pa
ryża zaznacz błędny wniosek dotyczący kli
matu tego miasta.
A. Roczna amplituda opadów równa jest
około 43 mm.
B. Średnia roczna temperatura powietrza
równa jest około 10,8°C.
C. Średnia suma opadów w pierwszym kwar
tale roku to około 54,75 mm.
D. Roczna am plituda tem peratury p o
wietrza wynosi około 15,5°C.
■ tem peratura powietrza
■
opady
□ 11. Samolot po 15 sekundach od startu znajduje się na wysokości 217 m. Na jakiej wysokości znaj
dzie się po 48 sekundach od startu, gdy będzie leciał w linii prostej pod tym samym kątem?
O dp.:
U 12. Prędkości samolotów podaje się często w węzłach, podobnie jak prędkości morskich jed
nostek pływających. Jeden węzeł równy jest 1,852km Maksymalna prędkość jednego z typów
samolotu pasażerskiego równa jest 328 węzłów, czyli w zaokrągleniu do km
A. 61 km
B .592 km
C. 607 km
D. 907 km
n
ti
h.
h
□ 13. O godzinie 19.55 z Warszawy wystartował samolot do Paryża, którego prędkość przelotowa*
równa była 308 węzłów. O której godzinie wylądował ten samolot na lotnisku im. Charles’a
de Gaulle’a, jeżeli odległość pomiędzy Warszawą a Paryżem na mapie w skali 1:30 000 000
równa jest 4,6 cm? (1 węzeł = 1,852 km)
*prędkość przelotowa - średnia prędkość, z jaką porusza się samolot podczas lotu
Zapisz o b licze n ia .
i
i
Odp.:
91
6. Na k a ż d y t e m a t - t r e n i n g p r z e d e g z a m i n e m
[] 14. Bilet wstępu do parku rozrywki podparyskiego Disneylandu kosztuje 53 euro dla osoby
dorosłej i 45 euro dla dziecka do 11 lat. Ile osób dorosłych i ile dzieci wybrało się na wy
cieczkę do Disneylandu, jeżeli dzieci było trzy razy więcej niż dorosłych, a łączny koszt
biletów grupy w złotych - według kursu 4,05 zł za 1 euro - równy był 3 045,60 zł.
i
Z a p i s ;
w
-
< O D j l v
!
i
*Ą-;i ^
:
'
-•54
1' •
!
1
■
j
1
—
—
1
—
—
1
1 J g »
r
E
w
1
Ł
t
,
•
1
m
.... i.
“ 7*
—
....
;
m Ą
*
:
: "~i
k s
\
1
■
\
: V
| n —
r
! . .
> 3
" Ą
F
,
;
:;<vr
i-.< -,
r*r. 1
■H$ %i '
’
~
f t f {
!
m m
. ! ..
T i r
•
I S i -
ll
' 1
...
• J
r
t
i
.
h ..
- L ś
i
Ą
■
'
^
4
/ i J
>■
;
.../y
1
~ ~ r
"
F
' i
! . f
..
« :-=
. 1
i
odp.:....................................... ........ — , ....... ż; , ;. ..
n
□ 15. Uczestnicy wycieczki do Paryża kupili od ulicznego artysty malarza obraz na desce z wido
kiem bazyliki Sacré-Coeur na szczycie Montmartre. Czy obraz o wymiarach 90 cm x 42 cm
zmieści się na dnie walizki, której objętość równa jest 81 dm3, a długości jej boków są
do siebie w stosunku 1:3:8?
1
I
-
□ 16. Jaką odległość pokonali turyści, wchodząc na szczyt góry, jeżeli
na mapie w skali 1:50 000 odległość ta równa jest 2,4 cm, a róż
nica wysokości trasy odczytana z poziomic wynosi 500 m?
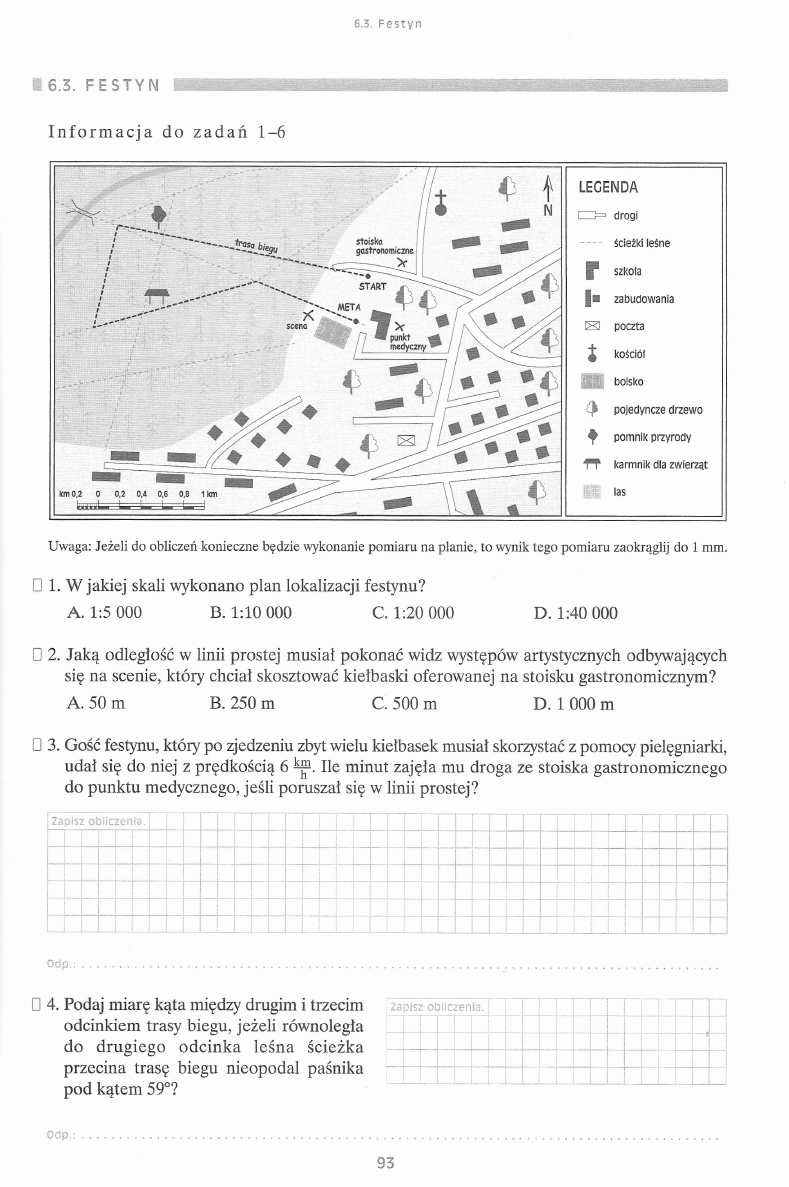
6.3. F e s t y n
1 6.3. F E S T Y N ■
«
—
—
I n f o r m a c j a do z a d a ń 1-6
Uwaga: Jeżeli do obliczeń konieczne będzie wykonanie pom iaru na planie, to wynik tego pom iaru zaokrąglij do 1 mm.
□ 1. W jakiej skali wykonano plan lokalizacji festynu?
A. 1:5 000
B. 1:10 000
C. 1:20 000
D. 1:40 000
□ 2. Jaką odległość w linii prostej musiał pokonać widz występów artystycznych odbywających
się na scenie, który chciał skosztować kiełbaski oferowanej na stoisku gastronomicznym?
A. 50 m
B. 250 m
C. 500 m
D. 1 000 m
□ 3. Gość festynu, który po zjedzeniu zbyt wielu kiełbasek musiał skorzystać z pomocy pielęgniarki,
udał się do niej z prędkością 6
Ile minut zajęła mu droga ze stoiska gastronomicznego
do punktu medycznego, jeśli poruszał się w linii prostej?
Zapisz o b licze n ia .
i
1
|
i
\
i
1
i
i
1
i
O d p . : ............................................................................................................................................................
0 4. Podaj miarę kąta między drugim i trzecim
odcinkiem trasy biegu, jeżeli równoległa
do drugiego odcinka leśna ścieżka
przecina trasę biegu nieopodal paśnika
pod kątem 59"?
Odp.: .............................................................................................................................................................
93
6 . N a
k
a ż ci y t e m a t - t r e r. i n g p r z e d e g z a m I n
.3
m
J
5. Dla uczestników biegu organizatorzy wydrukowali odpowiedni fragment planu, ustawiając
skalę powiększenia drukarki na 160%. W jakiej skali plan trasy biegu otrzymali zawodnicy?
A. 1:25
B. 1:250
C. 1:2 500
D. 1:25 000
U 6. Przedstaw za pomocą wykresu zależ
ność przebytej drogi od czasu dla
zawodnika, który całą trasę biegu
pokonał w 24 minuty. Z jaką średnią
prędkością biegł ten zawodnik?
Z?,alt.?, o o i k ¿s '!a.
I n f o r m a c j a do z a d a ń 7-9
Dla harcerzy festyn stał się okazją do dofinansowania zbliżającego się biwaku drużyny.
Dzień przed festynem zebrali w pobliskim lesie 12 kobiałek jagód. Owoce przesypali do włas
noręcznie wykonanych pojemników w kształcie rożków. Owoce sprzedawane na stoisku gastro
nomicznym rozeszły się w ciągu godziny.
□ 7. Oblicz objętość wszystkich owoców przygotowanych na festyn
przez harcerzy, jeżeli zbierali je, maksymalnie wypełniając
kobiałki o wymiarach podanych na rysunku obok.
'i52
0
j i k z e i r a .
....
/ / I /
z1
,
|
140 m m
94
110
m
m
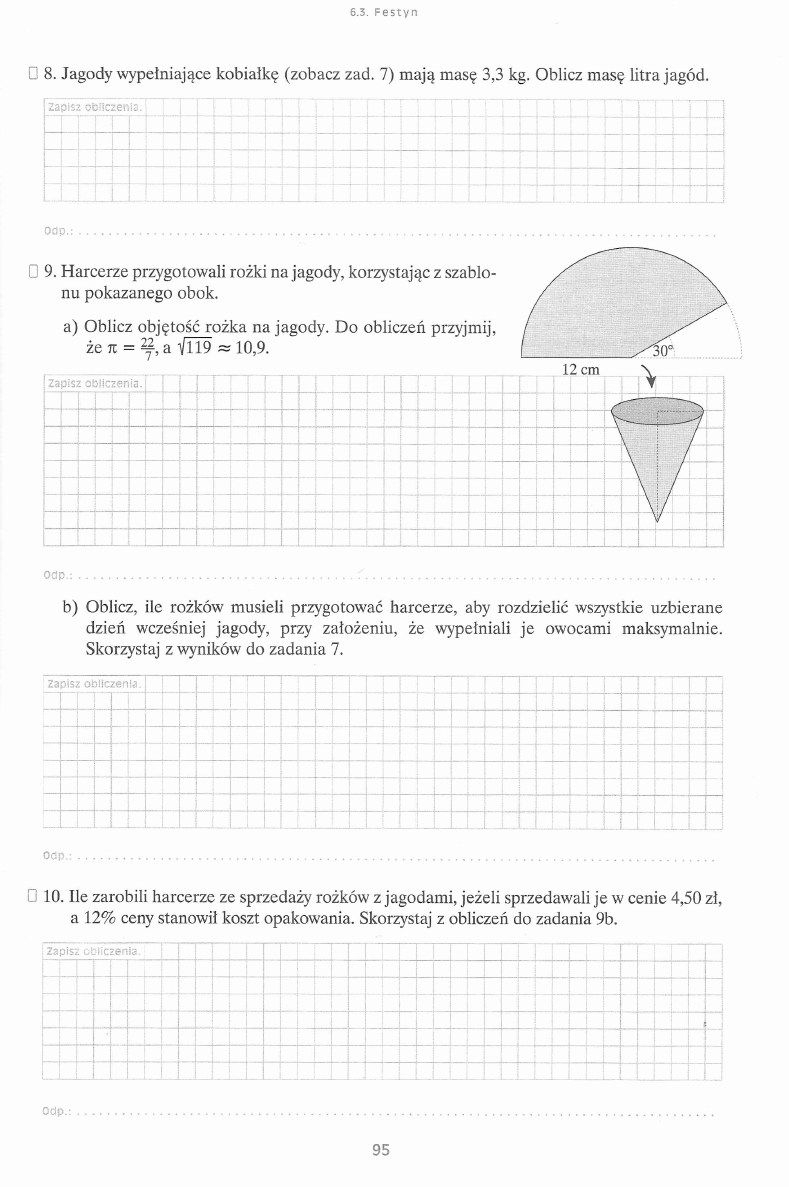
6.3. F e s t y n
□ 8. Jagody wypełniające kobiałkę (zobacz zad. 7) mają masę 3,3 kg. Oblicz masę litra jagód.
Zapisz o b licze n ia .
------
_
!
j
!
]
O dp.:
□ 9. Harcerze przygotowali rożki na jagody, korzystając z szablo-
nu pokazanego obok.
/
a) Oblicz objętość rożka na jagody. Do obliczeń przyjmij,
/
że
k
= y ,
a Vl 19 ~ 10,9.
(____________
^ 3 0 °
...............................................................................
12 cm
\
Zapisz ob licze n ia .
*
—
|
V
7
J
i
_
Odp.:
b) Oblicz, ile rożków musieli przygotować harcerze, aby rozdzielić wszystkie uzbierane
dzień wcześniej jagody, przy założeniu, że wypełniali je owocami maksymalnie.
Skorzystaj z wyników do zadania 7.
i Zapisz o b licze n ia .
. j _j.— j.
—
;
1
O dp.: . .
□ 10. Ile zarobili harcerze ze sprzedaży rożków z jagodami, jeżeli sprzedawali je w cenie 4,50 zł,
a 12% ceny stanowił koszt opakowania. Skorzystaj z obliczeń do zadania 9b.
Zapisz o b licze n ia .
i
—
..
—
i
—
—
1
-
Odp.:
95
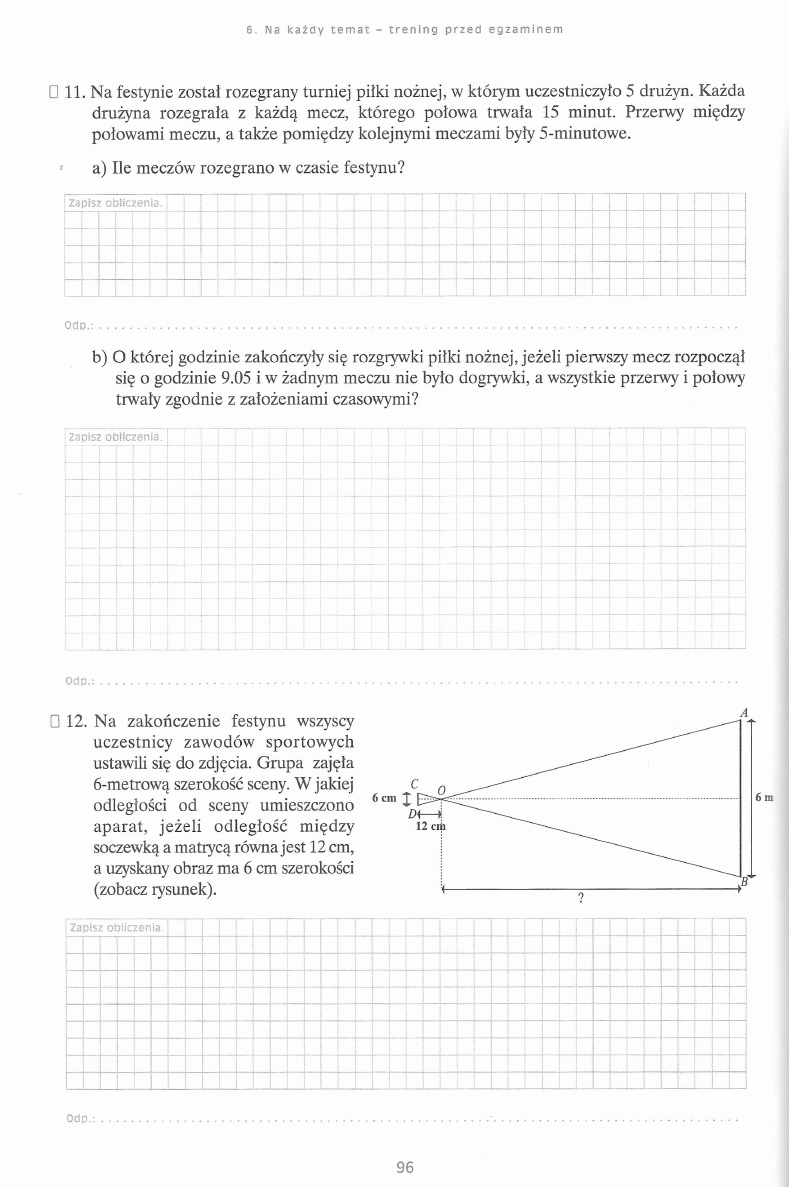
6. Na k a ż d y t e m a t - t r e n i n g p r z e d e g z a m i n e m
□ 11. Na festynie został rozegrany turniej piłki nożnej, w którym uczestniczyło 5 drużyn. Każda
drużyna rozegrała z każdą mecz, którego połowa trwała 15 minut. Przerwy między
połowami meczu, a także pomiędzy kolejnymi meczami były 5-minutowe.
a) Ile meczów rozegrano w czasie festynu?
Zapisz o b licze n ia .
O do.:
b) O której godzinie zakończyły się rozgrywki piłki nożnej, jeżeli pierwszy mecz rozpoczął
się o godzinie 9.05 i w żadnym meczu nie było dogrywki, a wszystkie przerwy i połowy
trwały zgodnie z założeniami czasowymi?
Zapisz o b licze n ia .
!
!
.....
1
i
i
1
I
!
i
i..... i___
O dp.:
□ 12. Na zakończenie festynu wszyscy
uczestnicy zawodów sportowych
ustawili się do zdjęcia. Grupa zajęła
6-metrową szerokość sceny. W jakiej
odległości od sceny umieszczono
aparat, jeżeli odległość między
soczewką a matrycą równa jest 12 cm,
a uzyskany obraz ma 6 cm szerokości
(zobacz rysunek).
Zapisz o b licze n ia .
O dp.:
96

6.4. M a t e m a t y k a o d k u c h n i
J 1. Koleżanki postanowiły zrobić biszkopt z galaretką i owoca
mi. Znalazły przepis na ciasto, w którym składniki są podane
w gramach. Podaj przepis zawierający przybliżone ilości skład
ników, przeliczone według poniższej tabeli tak, aby dziew
częta, które nie mają wagi kuchennej, mogły upiec biszkopt.
S 6 . 4. M A T E M A T Y K A O D K U C H N I
Produkt
spożywczy
Zawartość gramów produktu w:
szklance 250 ml
tyżce stołowej
łyżeczce do herbaty
Mąka pszenna
170
10,2
3,4
Cukier puder
200
12,0
4,0
Masfo
238
14,2
4,7
Proszek do pieczenia
-
-
5,1
|
□ 2. Na podstawie danych w tabeli do zadania 1 podaj masę 1 cm3 mąki pszennej.
A. 17 g
B. 0,68 g
C. l i ^ g
D. 25 g
J
3. Ile kilogramów cukru wsypano do 3 litrów wody, jeżeli uzyskano 25-proc. syrop - półprodukt
do przygotowania kompotu. Przyjmij, że litr wody ma masę 1 kg.
A. 0,5 kg
B. 0,75 kg
C. 1 kg
D. 1,25 kg
□ 4. Do ilu słoików o pojemności 500 ml rozlano 15 litrów kompotu, jeżeli nalewano do nich | ich
pojemności?
A. 18
B. 24
C. 25
D. 36
U 5. Pieczarki stanowią 18% sosu do spaghetti, sprzedawanego w słoikach o zawartości równej 0,5 kg.
a) Ile gramów pieczarek znajduje się w jednym słoiku?
A. 9
B. 18
C. 90
D. 180
b) Ile co najmniej słoików należy kupić, aby przygotować spaghetti dla 6 osób, jeżeli porcja
sosu ma zawierać około 27 000 mg pieczarek?
l
~ ~ r
..
i
i
i
i
S k ł a d n i k i n a b is z k o p t :
6 j
aj
3 0
d o g
m ąki p s z e n n e j
2 5 d a g c u k ru
p u d r u
1,7"
g p r o s z k u d o p i e c z e n ia
3 5
5
m a s ła
S^aaniKi n,s :
97
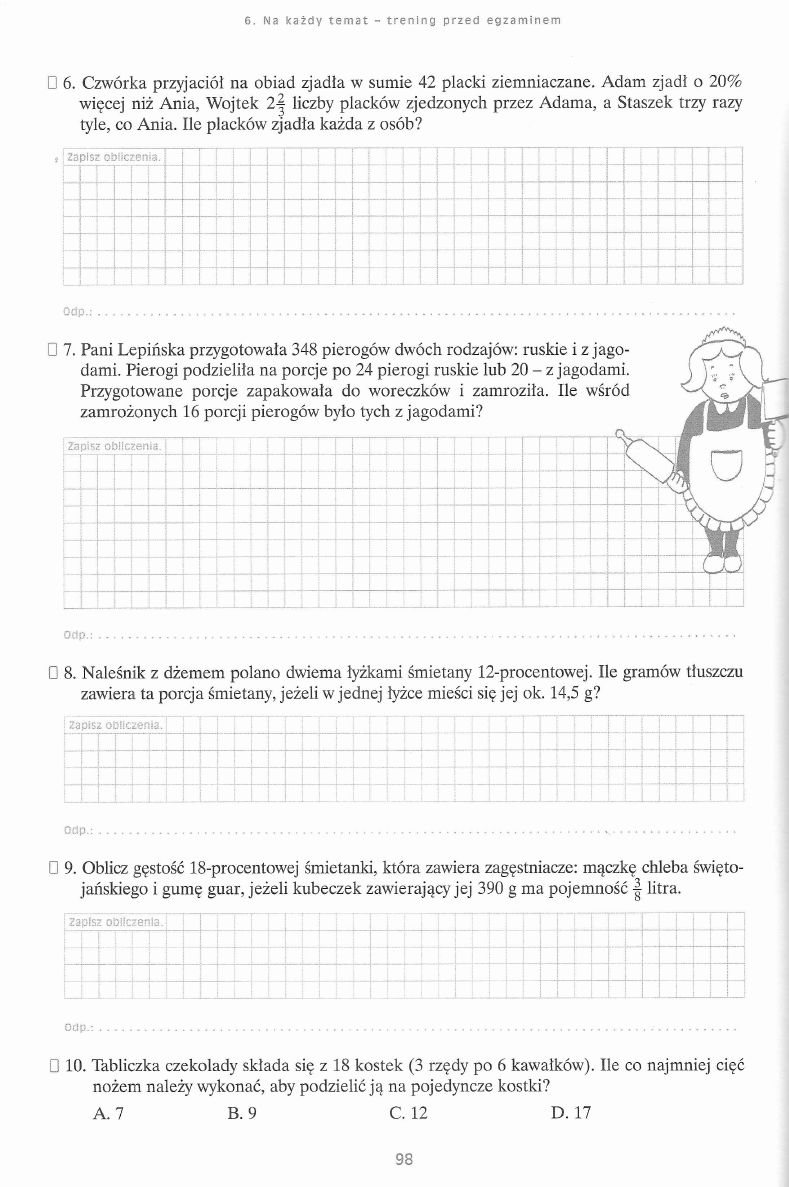
6. Na k a ż d y t e m a t - t r e n i n g p r z e d e g z a m i n e m
U
6. Czwórka przyjaciół na obiad zjadła w sumie 42 placki ziemniaczane. Adam zjadł o 20%
więcej niż Ania, Wojtek 2 | liczby placków zjedzonych przez Adama, a Staszek trzy razy
tyle, co Ania. Ile placków zjadła każda z osób?
.
j
1
1
i
i
J
U 8. Naleśnik z dżemem polano dwiema łyżkami śmietany 12-procentowej. Ile gramów tłuszczu
zawiera ta porcja śmietany, jeżeli w jednej łyżce mieści się jej ok. 14,5 g?
.
□ 9. Oblicz gęstość 18-procentowej śmietanki, która zawiera zagęstniacze: mączkę chleba święto
jańskiego i gumę guar, jeżeli kubeczek zawierający jej 390 g ma pojemność | litra.
CKi’."-.: .
.................
. . . . . . . .
. ■
................
..........
.
. . . .
u 10. Tabliczka czekolady składa się z 18 kostek (3 rzędy po 6 kawałków). Ile co najmniej cięć
nożem należy wykonać, aby podzielić ją na pojedyncze kostki?
A. 7
B. 9
C. 12
D. 17
7. Pani Lepińska przygotowała 348 pierogów dwóch rodzajów: ruskie i z jago
dami. Pierogi podzieliła na porcje po 24 pierogi ruskie lub 20 - z jagodami.
Przygotowane porcje zapakowała do woreczków i zamroziła. Ile wśród
zamrożonych 16 porcji pierogów było tych z jagodami?
98
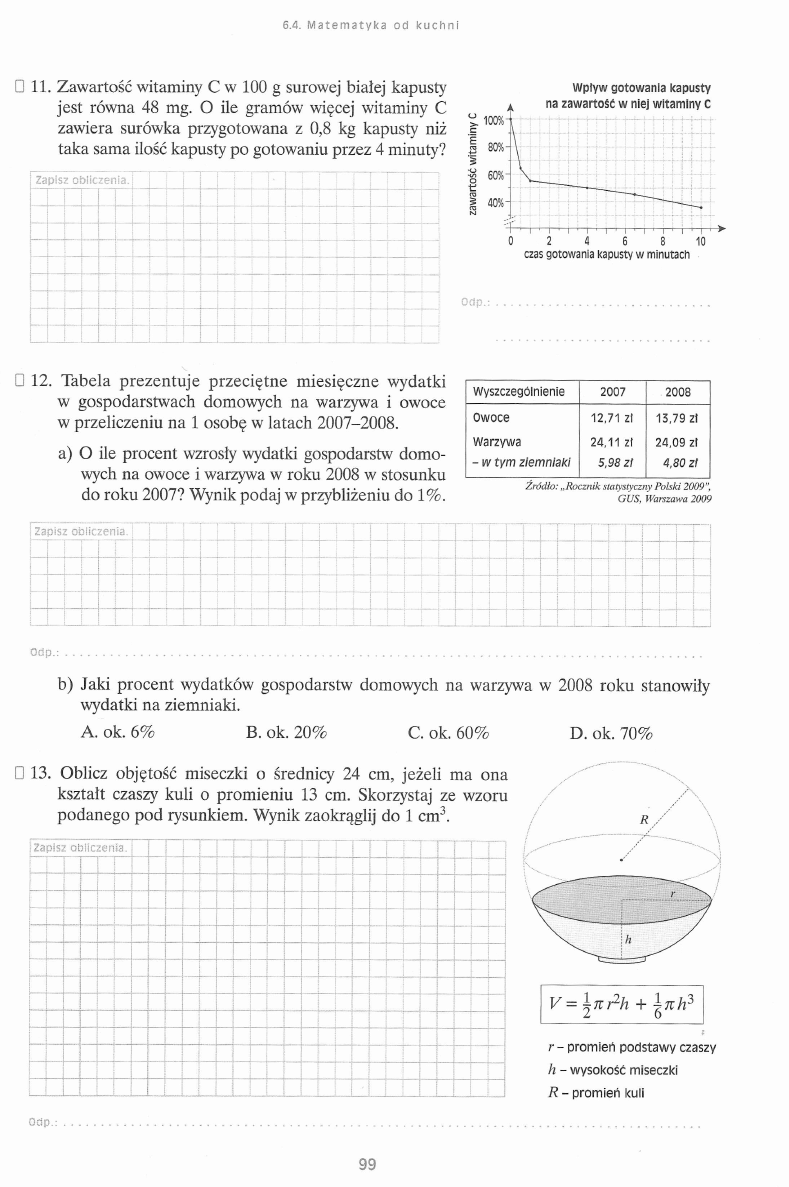
6.4. M a t e m a t y k a o d k u c h n i
□ 11. Zawartość witaminy C w 100 g surowej białej kapusty
jest równa 48 mg. O ile gramów więcej witaminy C
zawiera surówka przygotowana z 0,8 kg kapusty niż
e
taka sama ilość kapusty po gotowaniu przez 4 minuty?
g
Zapisz o b licze n ia .
_
□ 12. Tabela prezentuje przeciętne miesięczne wydatki
w gospodarstwach domowych na warzywa i owoce
w przeliczeniu na 1 osobę w latach 2007-2008.
a) O ile procent wzrosły wydatki gospodarstw domo
wych na owoce i warzywa w roku 2008 w stosunku
do roku 2007? Wynik podaj w przybliżeniu do 1%.
Wyszczególnienie
2007
2008
Owoce
W arzywa
-
i
/
i
/
ty m ziem niaki
12,71 zt
24,11 zl
5,98 Zt
13,79 zt
24,09 zt
4,80 Zl
Źródło: „Rocznik statystyczny Polski 2009”,
GUS, Warszawa 2009
Odp.
b) Jaki procent wydatków gospodarstw domowych na warzywa w 2008 roku stanowiły
wydatki na ziemniaki.
A. ok. 6%
B. ok. 20%
C. ok. 60%
D. ok. 70%
0 13. Oblicz objętość miseczki o średnicy 24 cm, jeżeli ma ona
kształt czaszy kuli o promieniu 13 cm. Skorzystaj ze wzoru
podanego pod rysunkiem. Wynik zaokrąglij do 1 cm3.
Zapisz o b licze n ia .
r~ “
—
—
r
/
r
- promień podstawy czaszy
h
- wysokość miseczki
R
- promień kuli
Odp.:
Wptyw gotowania kapusty
na zawartość w niej witam iny C
czas gotowania kapusty w minutach
99
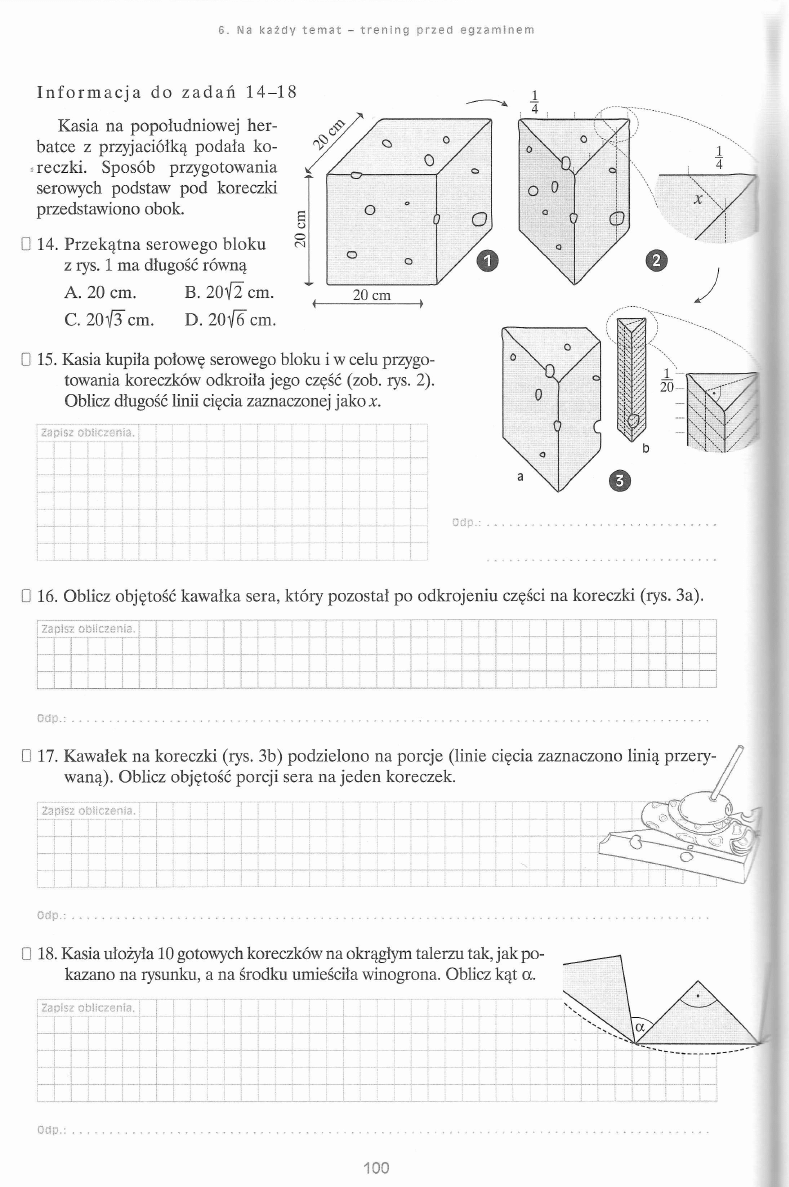
S. Na k a ż d y t e m a t - t r e n i n g p r z e d e g z a m i n e m
-
:
I n f o r m a c j a do z a d a ń 1 4 -1 8
Kasia na popołudniowej her
batce z przyjaciółką podała ko-
reczki. Sposób przygotowania
serowych podstaw pod koreczki
przedstawiono obok.
□ 14. Przekątna serowego bloku
z rys. 1 ma długość równą
A. 20 cm.
B.
2 0 f2
cm.
^
20 cm
>
C. 20^3"cm.
D.
2 0 f6
cm.
□ 15. Kasia kupiła połowę serowego bloku i w celu przygo
towania koreczków odkroiła jego część (zob. rys. 2).
Oblicz długość linii cięcia zaznaczonej jakox.
□ 16. Oblicz objętość kawałka sera, który pozostał po odkrojeniu części na koreczki (rys. 3a).
-
I
1
i
i
jci:)
...........................................
.................................... ......................................... ........................................
.......................................................................................
□ 17. Kawałek na koreczki (rys. 3b) podzielono na porcje (linie cięcia
waną). Oblicz objętość porcji sera na jeden koreczek.
Zapisz o lic z e n ia .
|
|
|
.
U 18. Kasia ułożyła 10 gotowych koreczków na okrągłym talerzu tak, jak po
kazano na rysunku, a na środku umieściła winogrona. Oblicz kąt
a.
:
zaznaczono
linią przery-
100
6.5. Z p a p i e r u
6.5. 2 p a p i e r u
□ 1. Dawne kroniki chińskie wymieniają jako wynalazcę papieru dostojnika na dworze cesarza
He Di z dynastii Han imieniem Caj Lun. On to miał wpaść około 105 r. n.e. na pomysł, aby
moczyć i gotować łyko drzewa morwowego, łodygi bambusa i szmaty jedwabne, a uzyskaną
w ten sposób masę odcedzać i suszyć na sicie. Do Europy wynalazek dotarł znacznie później
- pierwszą wytwórnię papieru otworzono w 1100 roku na Sycylii.
a) Ile lat upłynęło między wynalezieniem papieru a rozpoczęciem jego produkcji w Europie?
A. 95
B. 995
C. 1195
D. 1205
b) Ile dekad minęło od powstania pierwszej europejskiej papierni do dnia dzisiejszego?
A. 89
B. 90
C. 91
D. 92
0 2. Gramatura papieru jest to masa 1 m2 papieru wyrażona w gramach. Gramaturę oznacza się jed
nostką
jednak w krajach anglosaskich zwykle wyraża się ją w funtach (lb) na ryzę* papieru.
*ryza - tradycyjna jednostka liczby arkuszy papieru równa 500 arkuszy
a) Oblicz, jaką masę ma ryza papieru formatu 210 mm x 297 mm o gramaturze 90 -Ł.
b) Jeden kilogram jest równy 2,2046 funta. Jeden funt w zaokrągleniu do 1 g to
A. 4,53 kg.
B. 0,454 kg.
C. 0,45 kg.
D. 4,536 kg.
c) Na opakowaniu papieru jest oznaczenie 24,8 łb/ryza. Podaj gramaturę tego papieru w jed
nostkach stosowanych w Polsce. Wynik zaokrąglij do 1
U 3. Według danych Głównego Urzędu Statystycznego w Polsce w 2007 roku wyprodukowano
3 005 tys. ton papieru i tektury. Oblicz procentowy udział Polski w światowej produkcji papieru
i tektury, która wynosiła w 2007 roku 383 603 tys. ton. Wynik podaj w zaokrągleniu do 1
% o.
1 0 1
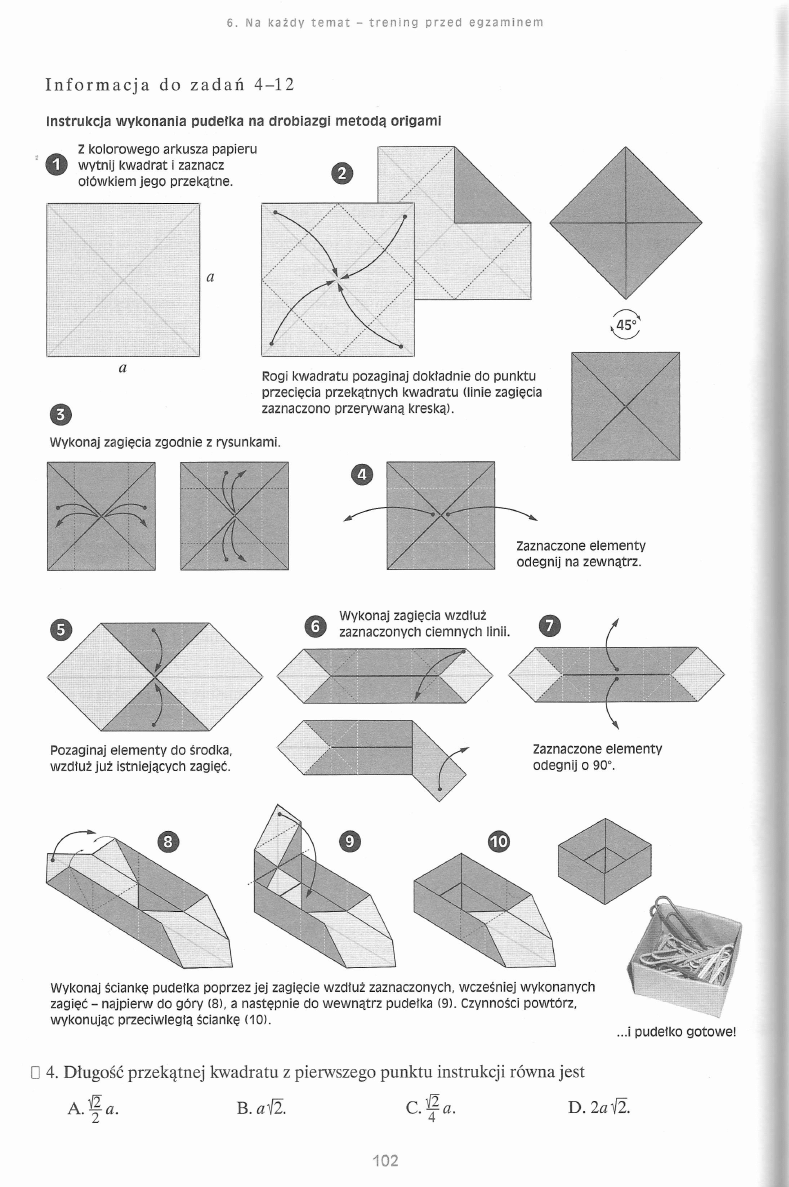
6
. Na k a ż d y t e m a t - t r e n i n g p r z e d e g z a m i n e m
I n f o r m a c j a do z a d a ń 4 -1 2
Instrukcja wykonania pudełka na drobiazgi m etodą origami
z kolorowego arkusza papieru
H H w ytnij kwadrat i zaznacz
otówkiem jego przekątne.
Zaznaczone elem enty
odegnij na zewnątrz.
Rogi kwadratu pozaginaj dokładnie do punktu
przecięcia przekątnych kwadratu (linie zagięcia
zaznaczono przerywaną kreską).
Wykonaj zagięcia zgodnie z rysunkami.
Wykonaj ściankę pudelka poprzez jej zagięcie wzdtuż zaznaczonych, wcześniej wykonanych
zagięć - najpierw do góry (8), a następnie do w ew n ątrz pudelka (9). Czynności powtórz,
wykonując przeciwiegtą ściankę (10).
...i pudełko gotowe!
Pozaginaj elem enty do środka,
wzdtuż już istniejących zagięć.
Wykonaj zagięcia wzdtuż
zaznaczonych ciemnych linii.
Zaznaczone elem enty
odegnij o 90°.
□ 4. Długość przekątnej kwadratu z pierwszego punktu instrukcji równa jest
A . f a .
B .a l2 .
C . f a .
D .2 a i2 .
102
6.5. Z p a p i e r u
□ 5 . 0 ile zmniejszy się powierzchnia kwadratu z pierwszego punktu instrukcji po wykonaniu za
gięcia pierwszego rogu w drugim punkcie?
A.
~ a 2
B.
—a2
C.
^ a 2
D. i « 2
□ 6. Bok kwadratu, który powstał po wykonaniu wszystkich zagięć rogów w drugim punkcie inst
rukcji, ma długość
a
Ą
u
.
b
M a.
c Ą a .
D.
a.
□ 7. Pole kwadratu, który powstał po wykonaniu drugiego punktu instrukcji, jest równe
A. 0,25
a.
B. 0,25
a2.
C. 0,5
a.
D. 0,5
a2.
□ 8. Podaj w postaci wyrażenia algebraicznego obwód sześciokąta z piątego punktu instrukcji.
Zapisz o b licze n ia .
i
i
i
I
I
Odp.:
□ 9. Podaj w postaci wyrażenia algebraicznego pole sześciokąta z piątego punktu instrukcji.
Zapisz
o b lic z e n ia .
i
!
...__L
....
i
....
...
Odp.:
U
10. Obwód sześciokąta z siódmego punktu instrukcji jest równy
B.
a
+
a f i .
C. a +
D. 2
a + a f l .
□ 11. Jaką częścią przekątnej kwadratu, z którego jest wykonane pudełko, jest odpowiednio kra
wędź podstawy i wysokość pudełka?
A _ L i i
16
8
C - i -
^ 4 1 2
D i i i
' 4 1 8
U 12. Oblicz objętość gotowego pudełka wykonanego z kwadratowego arkusza o boku 12 cm.
Zapisz o b licze n ia .
Odp.:
103
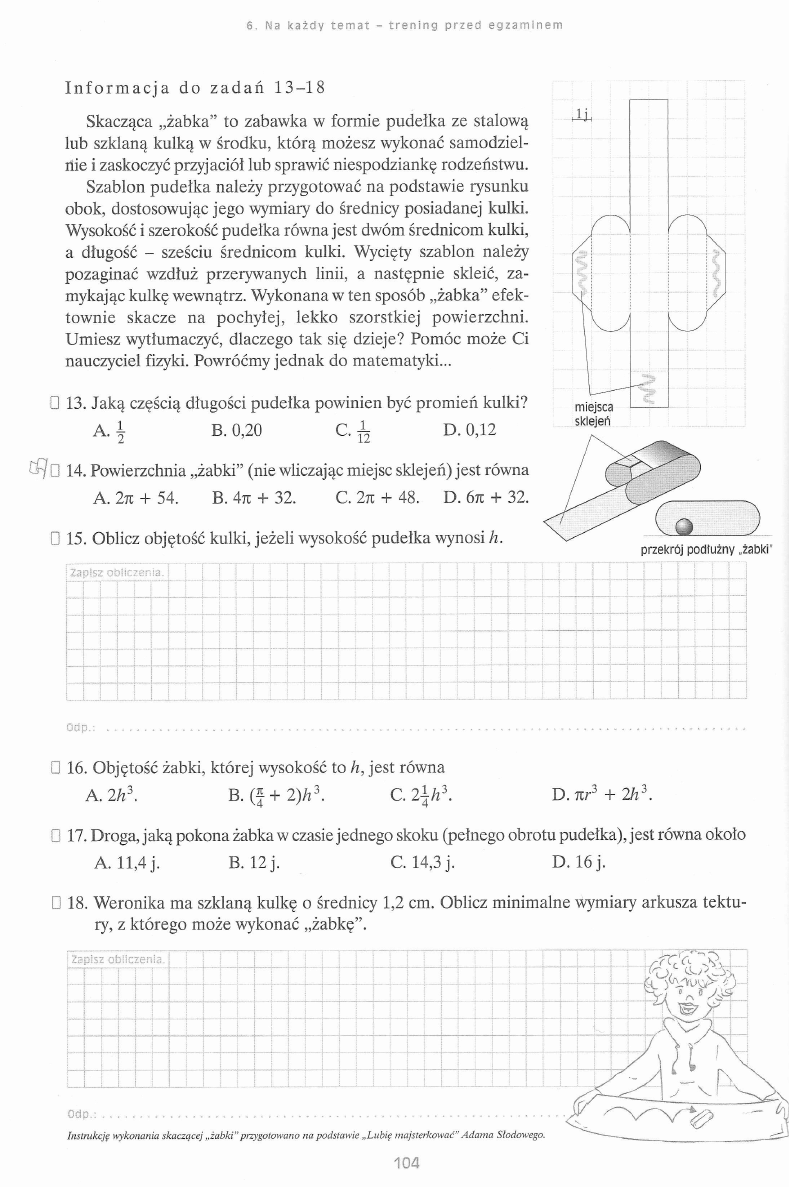
6
. Na k a ż d y t e m a t - t r e n i n g p r z e d e g z a m i n e m
I n f o r m a c j a do z a d a ń 1 3 -1 8
Skacząca „żabka” to zabawka w formie pudełka ze stalową
lub szklaną kulką w środku, którą możesz wykonać samodziel
nie i zaskoczyć przyjaciół lub sprawić niespodziankę rodzeństwu.
Szablon pudełka należy przygotować na podstawie rysunku
obok, dostosowując jego wymiary do średnicy posiadanej kulki.
Wysokość i szerokość pudełka równa jest dwóm średnicom kulki,
a długość - sześciu średnicom kulki. Wycięty szablon należy
pozaginać wzdłuż przerywanych linii, a następnie skleić, za
mykając kulkę wewnątrz. Wykonana w ten sposób „żabka” efek
townie skacze na pochyłej, lekko szorstkiej powierzchni.
Umiesz wytłumaczyć, dlaczego tak się dzieje? Pomóc może Ci
nauczyciel fizyki. Powróćmy jednak do matematyki...
□ 13. Jaką częścią długości pudełka powinien być promień kulki?
B. 0,20
C. i
D. 0,12
■'H
Q 14. Powierzchnia „żabki” (nie wliczając miejsc sklejeń) jest równa
A.
2n +
54.
B.
4n +
32.
C.
2n
+ 48.
D.
6n
+ 32.
□ 15. Oblicz objętość kulki, jeżeli wysokość pudełka wynosi
h.
T i
u
16. Objętość żabki, której wysokość to
h,
jest równa
A. 2/73.
B. (f +
2 )h
3.
C.
2 \ h \
D.
n r 3 +
2
h 3
.
j
17. Droga, jaką pokona żabka w czasie jednego skoku (pełnego obrotu pudełka), jest równa około
A. 11,4 j.
B. 12 j.
C. 14,3 j.
D. 16 j.
u 18. Weronika ma szklaną kulkę o średnicy 1,2 cm. Oblicz minimalne wymiary arkusza tektu
ry, z którego może wykonać „żabkę”.
przekrój podtużny „żabki"
Wyszukiwarka
Podobne podstrony:
Matematyka Zofia Kujawa (rozwiazania zadan)
Ćwiczenie 74, 74, ZOFIA KUJAWA
Kombinatoryka matematyka
WYKLAD ANALIZA MATEMATYCZNA
ZABAWA MATEMATYCZNA
Starożytni matematycy
MODEL MATEMATYCZNY TURBINY
Umiejętności matematyczne dzieci w przedszkolu
Matematyka wykład 1
Matematycy
operatory i funkcje matematyczne
Matematyka listopad 2009
Matematyka 2 Lekcje powtórzeniowe w gimnazjum
więcej podobnych podstron
