ZOFIA KUJAWA

ZBIÓR ZADAŃ DLA UCZNIÓW GIMNAZJUM

'•'■."■'I

Wydawni ct wo S E N E K A

R O Z W I Ą Z A M I A Z A D A Ń

W tabeli zestawione zostały rozwiązania wszystkich zadań ze zbioru: podano poprawne odpowiedzi

w zadaniach zamkniętych oraz przykładowe sposoby rozwiązania zadań otwartych. Dla tych drugich

podano także kryteria oceny poziomu rozwiązania zadania2, który określa, jakie zasadnicze trudności
zadania muszą zostać pokonane, aby zadanie zostało rozwiązane w sposób pełny. Jeżeli istnieje kilka
sposobów rozwiązania zadania, to wybrano te najczęściej stosowane, ale każde inne poprawne
rozwiązanie jest punktowane maksymalną liczbą punktów przyznawaną za dane zadanie.

Dodatkowo dla każdego zadania wskazano oznaczenia najważniejszych wymagań ogólnych i numery

wymagań szczegółowych określonych w podstawie programowej kształcenia ogólnego dla gimnazjum2.

Opis sprawdzanych w danym zadaniu wymagań znajdziecie na końcu zbioru3.

1 W ięcej in fo rm acji n a te m a t sp o so b u oceny z a d a ń n a eg zam in ie zaw iera In fo rm a to r o egzam inie gim nazjalnym o d roku szkolnego

2011/2012 d o stę p n y n a in te rn e to w e j stro n ie C e n tra ln e j K om isji E gzam inacyjnej o ra z w szkołach.

- P odstaw a p ro g ram o w a nie obejm uje d ziałań n a liczbach niewym iernych, d latego w ym agania szczegółowe dotyczące obliczeń, w których

o b o k liczb w ym iernych w ystępują liczby niew ym ierne, w ta b e li ozn aczo n o gw iazdką, np.: 2.4*.

3 Z a d a n ia m o g ą się o d n o sić ta k ż e d o w ym agań z z a k resu m a te m a ty k i p rzypisanych d o w cześniejszych e tap ó w edukacyjnych, czego

n ie u ję to szczegółow o w poniższej tab eli. W tak ich w y p ad k ach p o d a n o je d y n ie in fo rm ację w p o sta c i sk ró tu - SP.

1.

L ? C 2 B Y : W Y R A Ż E N I A A L C E B R A I C I IM

Si

1.1. D Z I A Ł A N I A N A L I C Z B A C H

Nr

Rozwiązanie zadania

Kryteria oceny

Suma

Wymagania

pkt

ogólne szczegot.

1.

99 - 9 = 90; 999 - 99 = 900
900 : 90 = 10
Odp.: Liczb trzycyfrowych jest 10 razy więcej niż dwucyfrowych.

• Obliczenie liczby liczb dwu­

cyfrowych i trzycyfrowych.

• Obliczenie, ile razy większa

jest liczba liczb trzycyfro­

wych niż dwucyfrowych.

2

IV

1.7
SP

2.

I.

FAŁSZ;

II.

FA ŁSZ

2

II

2.1

3.

I. 101; II. MMII

oznaczenia występujące w zdaniach: MCMVI = 1906;

MDCCCV

= 1805; MCMLVIII = 1958

• Odczytanie liczb naturalnych

zapisanych w systemie rzyms­
kim i wykonanie obliczeń.

2

II

1.1
SP

4.

mniejsza z liczb: (73 — 1 )

: 2 = 36

większa z liczb: 36

+ 1 = 37

Odp.: Dwie kolejne liczby naturalne, których suma jest
równa 73, to 36 i 37.

• Obliczenie mniejszej z liczb.
• Obliczenie większej z liczb.

2

IV

SP

5.

7,6 + ( - l § ) - ( 0 , 2 5 : l § ) = 5 i § i

Odp: Suma jest większa od ilorazu o 5 ^ |j •

• Zapisanie różnicy sumy

i ilorazu podanych liczb.

• Obliczenie różnicy.

3

IV

1.5

6. Uczeń 50 odczytał jako 70, czyli błąd wynikający z tej pomyłki

zawyża wynik o 20; 9 odczytał jako 6, co zaniża wynik o 3.

7 6 8 -2 0 + 3 = 751
Odp.: Właściwy wynik dodawania liczb to 751.

• Znalezienie błędu w zapisie

sumy.

• Obliczenie prawidłowej sumy.

2

IV

1.7
1.5

7.

Aby liczba dzieliła się przez 2, jej cyfra jedności musi być pa­
rzysta, czyli należy do zbioru {0, 2, 4, 6, 8}. Aby liczba dzieliła się
przez 3, suma jej cyfr musi być podzielna przez 3.

Cyfra jedności musi być parzysta i podzielna przez 3.
780 spełnia warunki zadania, ponieważ: 7 + 8 + 0 = 15 = 3- 5
781 nie spełnia warunków zadania 7 + 8 + 1 = 16 itd.
Odp.: W miejsce znaku zapytania można wstawić 0 (780)
lub 6 (786).

• Zastosowanie cech podziel­

ności liczb przez 2 i 3.

• Znalezienie liczb spełniają­

cych warunki zadania.

2

IV

1.5
SP

107

R o z w i ą z a n i a z a d a rt

8.

i

Liczba dzieli się przez 36, jeżeli dzieli się przez 4 i 9.

Aby liczba była podzielna przez 4, to liczba utworzona przez

cyfry w rzędzie dziesiątek i jedności musi być podzielna przez 4,
czylij należy do zbioru {2, 6}. Aby liczba była podzielna przez 9,
to suma jej cyfr musi dzielić się przez 9.
Odp.: Szukane pary to x = 5 i y = 2 oraz x = 1 i y = 6.

• Zastosowanie cech podziel­

ności liczb przez 4 i 9.

• Znalezienie liczb spełniają­

cych warunki zadania.

2

IV

SP
1.5

9.

D

1

IV

SP

10. D

1

IV

SP

11. A

1

IV

SP

12. D

1

IV

SP

13.

wiek dziadka: 4 • (12 + 18 : 6 +3) = 72
wiek wnuczka: (4 ■

12 + 18) : 6 +3 = 14

72 + 14 _ 43

2

Odp.: Średnia wieku dziadka i jego wnuczka równa jest 43 lata.

• Zastosowanie reguł dotyczą­

cych kolejności wykonywa­
nia działań.

• Obliczenie średniej

arytmetycznej.

3

IV

SP

9.4

14.

7 :13 = 0,538461538461... = 0,(538461)
99 : 6 = 16 r 3, czyli 99. cyfra po przecinku to trzecia cyfra

w 17. wystąpieniu okresu

Odp.: Szukaną cyfrą jest 8.

• Obliczenie ilorazu i ustalenie

okresu.

• Ustalenie 99. cyfry po prze­

cinku.

2

IV

V

1.5
1.3

15.

B

1

III

2.4

16.

C

1

III

1.3

17.

C

1

III

1.3

18.

D

1

III

SP

19.

2 ■ (-!) = - 2

Odp.: Liczba dwa razy większa niż liczba przeciwna do od­

wrotności liczby 7 to -%j.

• Obliczenie liczby dwa razy

większej niż liczba przeciwna

do odwrotności danej liczby.

1

III

SP

20. Liczba zapisana w postaci 212 + 48 + 2 ■

3 + 164 jest podzielna

przez 5, ponieważ suma cyfr (2 + 8 + 6 + 4) w rzędzie jedności

równa jest 0 (jest to cecha podzielności liczb przez 5).

• Zastosowanie cech podziel­

ności liczb przez 5 i uzasad­
nienie.

1

IV

SP

21. D

1

III

3.5

22. B

1

III

3.5

23.

C

1

III

3.5

24.

C

1

III

3.5

25.

B

1

III

3.5

26.

a) NIE

1

III

3.5

b) (6,5 ■

106) : (8 • 103) = 812,5

Odp.: W krwi psa średnia liczba erytrocytów jest
812,5 razy większa od średniej liczby leukocytów.

• Obliczenie, ile razy jedna

liczba jest większa od dru­

giej-

1

III

1.5

27.

A

1

III

2.2

28.

D

1

III

2.2

29.

B

1

III

2.2

30.

(_9_)2

W

• Wskazanie w zbiorze liczb

największej liczby spełniają­
cej podany warunek.

1

III

2.1

1 0 8

R o z w i ą z a n i a z a d a ń

31.

---------- A--------------- +—

*.

- 2§

0

Odp.: Najmniejszą liczbą całkowitą spełniającą warunek

x > - 2-= jest liczba - 2 .

• Zaznaczenie na osi liczbowej

zbioru liczb spełniających
podany warunek.

■ Wskazanie w zbiorze liczby

według warunków zadania.

2

II

2.1

32.

-----------1--------- ------------ ►

0

1

Odp.: Na przykład A i liczba do niej przeciwna - 1 .

• Zaznaczenie na osi liczbowej

zbioru liczb spełniających
podany warunek.

• Wskazanie w zbiorze liczby

według warunków zadania.

2

II

2.2

33.

A

1

III

2.1

34.

A

1

IV

1.6

35.

4
7

• Obliczenie wartości

wyrażenia.

2

II

1.2

36.

4

liczba przeciwna: -4 ; liczba odwrotna: 1

• Obliczenie wartości

wyrażenia.

• Podanie liczby przeciwnej

oraz odwrotnej do wyniku.

2

II

4.2

3.1

37.

5(5f2 + 3)

• Wyłączenie wspólnego

czynnika przed nawias.

1

II

2.4*

38.

212

20

• Obliczenie wartości

wyrażenia.

2

II

4.1
1.5

39.

18,1

• Obliczenie wartości

wyrażenia.

2

II

4.1

1.5

40.

-1,25

• Obliczenie wartości

wyrażenia.

2

II

3.4

1.5

41.

m = 14,95; p = -2,275
m - p = 17,225

Odp.: Liczba m jest większa od liczby p o 17,225.

• Obliczenie wartości

wyrażeń.

• Obliczenie różnicy wyników.

3

II

IV

1.5

1.7

42.

a = 81; b = 27; c = 81

81 + 27 + 81 = 189
Odp.: Obwód trójkąta jest równy 189.

• Obliczenie wartości

wyrażeń.

• Obliczenie sumy wyników.

4

II

3.1

1.5

4.1

43.

Wody zajmują 361 066 000 km2 powierzchni Ziemi, a lady -

148 940 000 km2.

361 066 000 km2 + 148 940 000 km2 = 510 006 000 km2
Odp.: Powierzchnia Ziemi jest równa 510 006 000 km2.

• Obliczenie wartości

wyrażeń.

• Obliczenie potęgi liczb wy­

miernych.

3

II

1.4

3.1

44.

cyfra setek: 1; cyfra dziesiątek: 5; cyfry jedności: 4

Odp.: Spotkanie odbędzie się w sali 154.

■ Obliczenie wartości

wyrażeń.

3

III

4.1
3.1

SP

45.

60 : 0,6 = 100
Odp.: Pani Halina napełniła 100 słoików.

• Obliczenie ilorazu i wskaza­

nie liczby w zbiorze liczb,

spełniającej warunki zadania.

2

V

1.5
1.2

46.

14 • 6 : 3 = 28 minut

1 500 s = 25 min
(28 min - 25 m in ): 2 = 3 min : 2 = 1 min 30 s

Odp.: Każdą relację należy skrócić o 1 min 30 s.

• Zastosowanie obliczeń

na liczbach w praktyce.

• Zamiana jednostek czasu.
• Obliczenie czasu według

warunków zadania.

3

III

1.7
1.5

109

R o :: w i ą z a n I a z a d a ń

47.

340 — • 25 s = 8 500 m = 8,5 km

s

Odp.: Burza jest w odległości około 8,5 km.

• Obliczenie odległości we­

dług warunków określonych

w zadaniu.

2

III

SP
1.7

48.

4 • 5 • 19 km = 380 km

Odp.: Samochód przejedzie 380 km.

• Obliczenie odległości we­

dług warunków określonych

w zadaniu.

1

III

1.7

49.

1 h 20 min • 18 ^ = 24 km - długość trasy

1240 + 1 h 20 min - 800 = 6 h - czas przejścia trasy

24 km : 6 h = 4 ^ 3

h

,

Odp.: Janek szedł ze średnią prędkością 4 ™ .

• Obliczenie długości, czasu

oraz średniej prędkości

według warunków określo­

nych w zadaniu.

3

III

SP

1.7

1.5

50.

a'!2 ' 2 - 4

> 13

13

Odp.: Pasy drogi dla rowerów stanowią ~ całej drogi.

• Zastosowanie obliczeń

w praktyce.

1

III

1.5
SP

b) (8 0 0 :2 + 1 )-2 = 802

Odp.: Na remontowanym odcinku drogi znajdują się 802
elementy odblaskowe.

• Zastosowanie obliczeń

w praktyce.

1

II

1.5

51.

1 030 ^4 = 1,03 -&T

mó

cmJ

1,03 -Ł - ■

250 cm3 = 257,5 g

cmj

Odp.: 250 ml mleka ma masę 257,5 g.

• Zamiana jednostek gęstości.

• Obliczenie masy według

warunków określonych

w zadaniu.

2

III

1.7

2.3

52.

C

1

II

5.2

53.

4,19 min : 3,27 min = 1,281345... = 1,2813 CAD
Odp.: Kurs euro w dolarach kanadyjskich z dnia 25 czerw­

ca 2010 roku równy był 1,2813 CAD.

• Zastosowanie obliczeń

w praktyce.

2

II

1.5

1.4

54.

100 000 ■

148,13 zł = 14 813 000 zł

Odp.: Wartość złota, z którego zrobiony jest „Mapie Leaf”,

w dniu jego sprzedaży równa była 14 813 000 zł.

• Zastosowanie obliczeń

w praktyce.

• Zamiana jednostek mone­

tarnych.

2

II

1.7

1.5

55.

3,27 min • 4,1405 zł = 13 539 435 zł

14 813 000 zł - 13 539 435 zł = 1 273 565 zł

Odp.: Różnica między wartością złota, z którego jest wykonany
„Mapie Leaf”, a ceną jego sprzedaży równa jest 1 273 565 zł.

• Zastosowanie obliczeń

w praktyce.

• Obliczenie różnicy według

warunków zadania.

2

II

1.7
1.5

56.

V

= 100kg: 19 2 8 2 ^ = 0,005186184005... m3 =

m 3

5 186,184005 cm3 = 5 186,184 cm3

Odp.: Objętość monety „Mapie Leaf” równa jest 5 186,184 cm3.

• Obliczenie objętości według

warunków zadania.

• Zamiana jednostek oraz

przybliżenie do 1 mm3.

2

II

1.7
1.5

1.2.

P

R 0

C E N

T ¥

Nr

Rozwiązanie zadania

Kryteria oceny

Suma

Wymagania

zad.

pkt

ogólne szczegół.

1. upominki: 2%

•

500

=

10 zł; rozrywki: 55 zł; telefon: 25 zł;

noclegi: 75 zł, wyżywienie: 225 zł, transport: 75 zł;
rezerwa: (100%

-

2% - 11%

-

5%

-

15%

-

45%

-

15%)

■

500

=

35 zł

•

Obliczenie procentu danej

liczby.

•

Obliczenie rezerwy.

2

II

5.2

9.3

2.

I. 33%; II. 33%, III. 6 6 |% ; IV. 200%, V. 10%, V I. 2,5%; V II. 49%;

V III. 100%

•

Obliczenie procentu danej

liczby.

4

II

5

:

3.

c

1

II

5.2

110

R o zw i ą za n i a zadań

4.

7.

C

D

wiek Kasi: 32% ■

50 = 16

wiek taty Kasi: 40%x = 16; x = 40

Odp.: Kasia ma 16 lat, a jej tata - 40.

' Obliczenie procentu danej

liczby.

' Zastosowanie obliczeń pro­

centowych w praktyce.

I I I

III

III

III

III

IV

5.4

5.4

5.4

5.4

5.4

5.2

5.3

10

.

pierwszy dzień: 20% • 500 = 100

drugi dzień: 40% ■

(500 - 1 0 0 ) = 160

trzeci dzień: 500 - 100 - 160 = 240

Odp.: Trzeciego dnia Karol przeczytał 240 stron książki.

1 Obliczenie procentu danej

liczby.

1 Obliczenie wartości wyraże­

nia.

IV

5.2

1.5

11

.

a) 9%x = 45; jc = 500

Odp.: W ankiecie brało udział 500 uczniów.

1 Obliczenie procentu danej

liczby.

II

5.2

b) (40% - 12%) • 500 = 140

Odp.: Odpowiedź „komiksy” wybrało o 140 uczniów więcej

niż odpowiedź „książki historyczne”.

Obliczenie procentu danej

liczby.

II

5.2

12

.

(100% - 12%) ■

64 kg = 56,32 kg

Odp.: Z 64 kg mydła poddanego procesowi suszenia otrzymuje się

56,32 kg gotowego produktu.

• Obliczenie procentu danej

liczby.

II

5.2

13.

pan Pewny: (1 200 zł + 3 • 480 zł) • 0,70 = 1 848 zł
pan Niezdecydowany: (1 200 zł + 480 zł) • 0,9 + 2 ■ 480 zł • 0,9

= 2 376 zł

2 376 zł - 1 848 zł = 528 zł
Odp.: Pan Pewny zapłacił za meble o 528 zł mniej

niż pan Niezdecydowany.

Zastosowanie obliczeń pro­

centowych w praktyce.

Obliczenie wartości wyraże­

nia.

IV

5.4

1.6

14.

(1 200 • 15 + 1 500 ■

12 + 1 800 • 20 + 2 700 • 6 + 5 436):

(15 + 12 + 20 + 6 + 1) = 1 734 [zł]
(20 + 6 + 1): (15 + 12 + 20 + 6 + 1) • 100% = 50%
Odp.: Płaca 50% pracowników jest wyższa od średniej płacy

w tej firmie.

Obliczenie średniej arytme­

tycznej.

Obliczenie, jakim procentem
jednej liczby jest druga licz­

ba.

IV

9.4
5.4

15.

D

IV

5.3

16.

0,1 • 1100 = 110 [zł]; 1100 + 4 • 110 = 1 540 [zł]

Odp.: Pracownik po roku pracy będzie zarabiał 1 540 zł.

■

Zastosowanie obliczeń pro­

centowych w praktyce.

IV

5.2

1.5

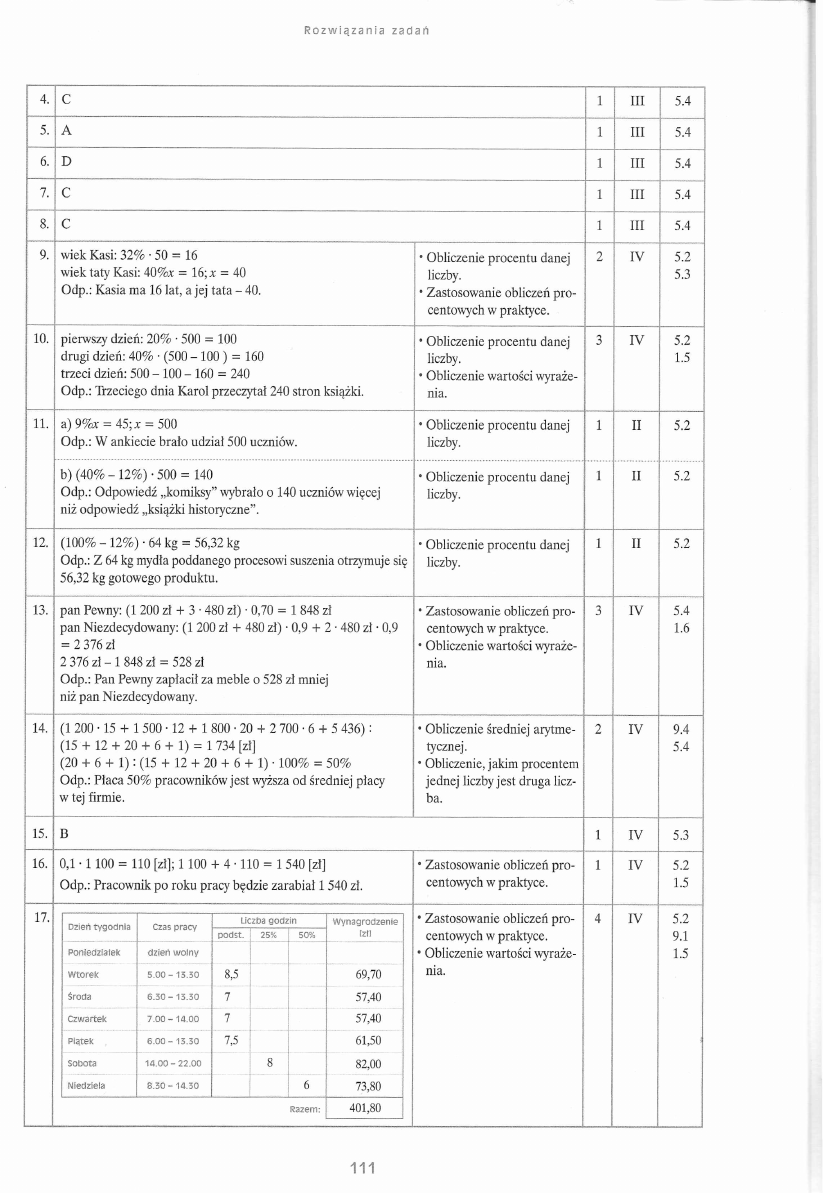
17.

Dzień tygodnia

Czas pracy

Liczba godzin

Wynagrodzenie

Ezłi

podst.

25%

50%

Poniedziałek

dzień wolny

Wtorek

5.00-13.30

8,5

69,70

Środa

6.30-13.30

7

57,40

Czwartek

7.00-14.00

7

57,40

Piątek

6.00-13.30

7,5

61,50

Sobota

14.00 - 22.00

8

82,00

Niedziela

8.30-14.30

6

73,80

Razem:

401,80

1 Zastosowanie obliczeń pro­

centowych w praktyce.

1 Obliczenie wartości wyraże­

nia.

IV

5.2

9.1

1.5

111

R o z w i ą za n i a zadań

18.

i • 0,1 • 5 000 + 5 000 = 5 125 [zł]

1 • 0,1 • 5 125 + 5 125 * 5 253,13 [zl]

Odp.: Po pół roku od założenia lokaty na koncie pana Jana

będzie się znajdowało 5 253,13 zł.

1 Zastosowanie obliczeń pro­

centowych w praktyce.

V

5.4
2.4

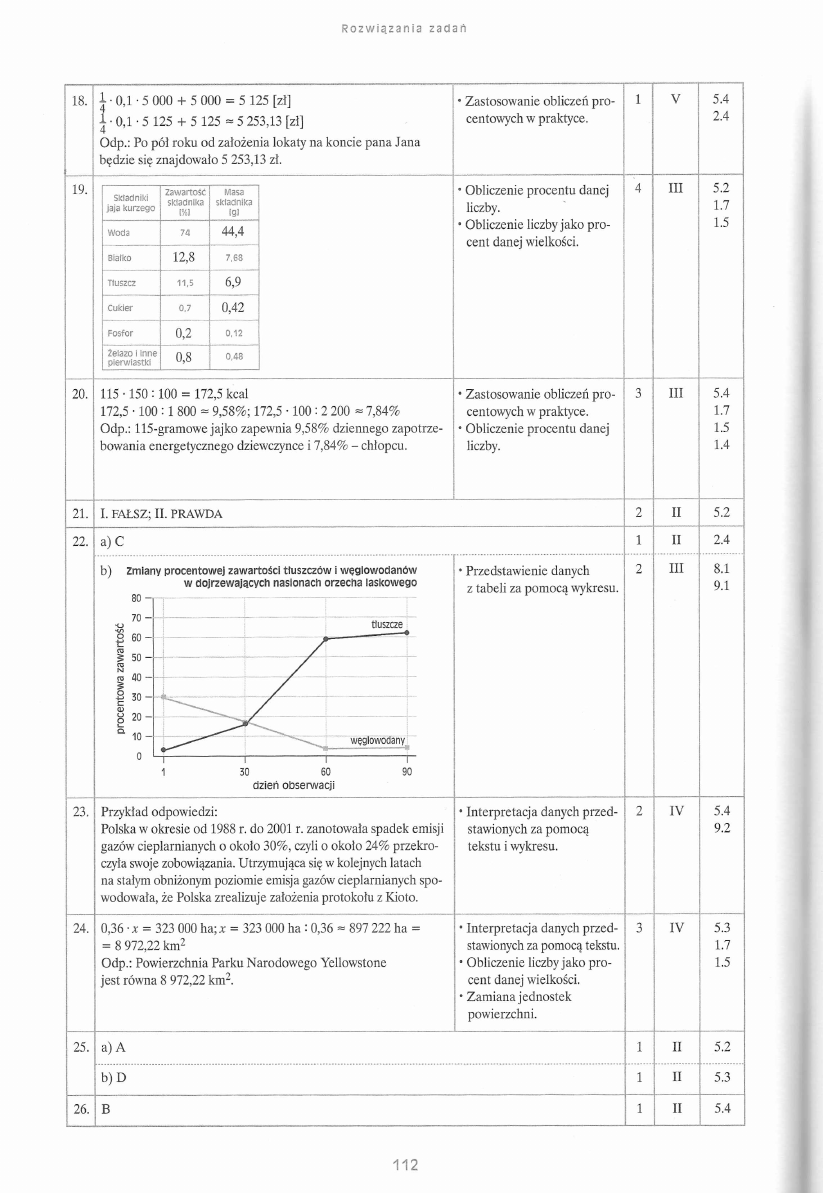
19.

Składniki

jaja kurzego

Zawartość

składnika

[%l

Masa

składnika

[gj

Woda

74

44,4

Biafko

12,8

7,68

Tłuszcz

11,5

6,9

Cukier

0,7

0,42

Fosfor

0,2

0,12

Żelazo i inne

pierwiastki

0,8

0,48

1 Obliczenie procentu danej

liczby.

1 Obliczenie liczby jako pro­

cent danej wielkości.

III

5.2

1.7
1.5

20

.

115 • 150 :100 = 172,5 kcal

172,5 • 100 :1 800 = 9,58%; 172,5 • 100 : 2 200 = 7,8
Odp.: 115-gramowe jajko zapewnia 9,58% dziennego zapotrze­

bowania energetycznego dziewczynce i 7,84% - chłopcu.

■

Zastosowanie obliczeń pro­

centowych w praktyce.

’ Obliczenie procentu danej

liczby.

III

5.4

1.7
1.5
1.4

21

.

I.

FAŁSZ;

II.

PRA W D A

II

5.2

22

.

a) C

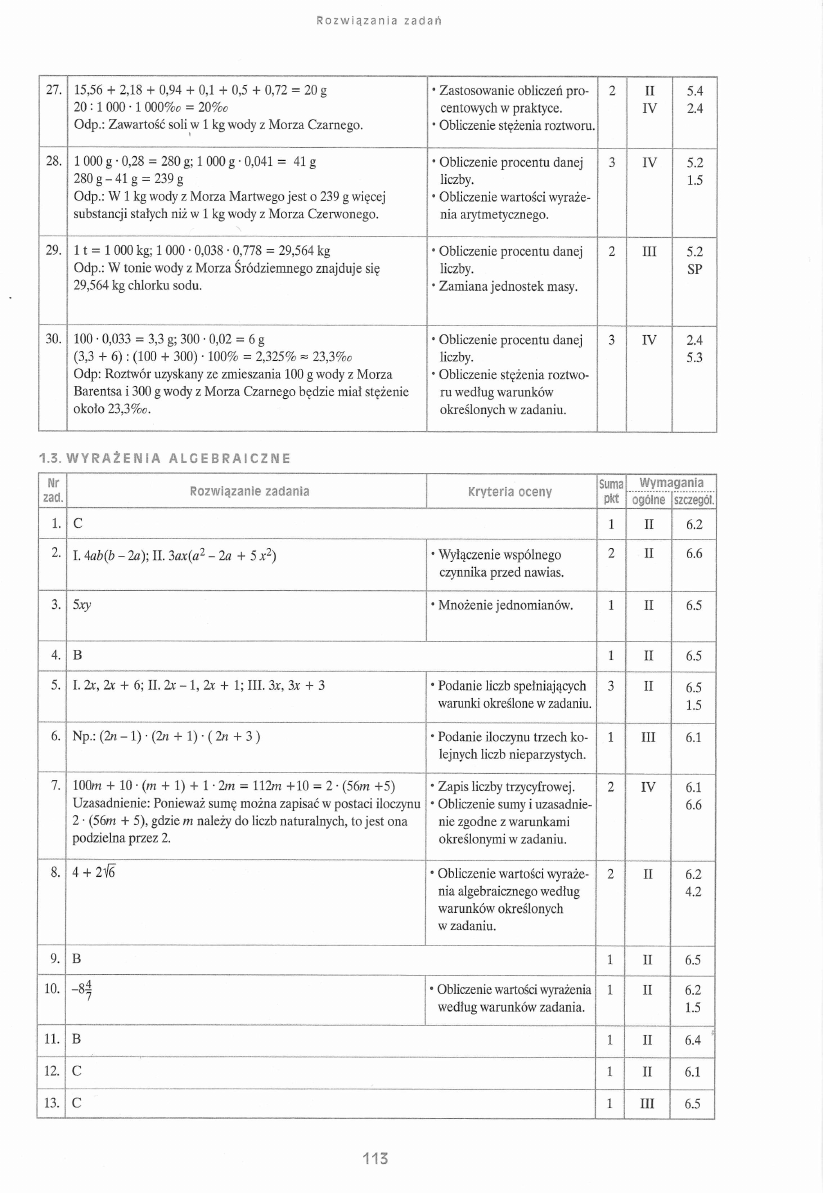
b)

Zmiany procentowej zawartości tłuszczów i węglowodanów

w dojrzewających nasionach orzecha laskowego

o

t

dzień obserwacji

1 Przedstawienie danych

z tabeli za pomocą wykresu.

II

III

2.4

8.1

9.1

23.

Przykład odpowiedzi:
Polska w okresie od 1988 r. do 2001 r. zanotowała spadek emisji

gazów cieplarnianych o około 30%, czyli o około 24% przekro­

czyła swoje zobowiązania. Utrzymująca się w kolejnych latach
na stałym obniżonym poziomie emisja gazów cieplarnianych spo­

wodowała, że Polska zrealizuje założenia protokołu z Kioto.

1 Interpretacja danych przed­

stawionych za pomocą
tekstu i wykresu.

IV

5.4
9.2

24.

25.

26.

0,36 • x = 323 000 ha; x = 323 000 ha : 0,36 = 897 222 ha

= 8 972,22 km2

Odp.: Powierzchnia Parku Narodowego Yellowstone

jest równa 8 972,22 km2.

a) A

b) D

B

’ Interpretacja danych przed­

stawionych za pomocą tekstu.

■

Obliczenie liczby jako pro­

cent danej wielkości.

■

Zamiana jednostek

powierzchni.

IV

II

II

II

5.3

1.7
1.5

5.2

5.3

5.4

1 1 2

R o zw i ą z a n i a zadań

27.

15,56 + 2,18 + 0,94 + 0,1 + 0,5 + 0,72 = 20 g

2 0 :1 000 • 1 000%c = 20%c

Odp.: Zawartość soli w 1 kg wody z Morza Czarnego.

• Zastosowanie obliczeń pro­

centowych w praktyce.

• Obliczenie stężenia roztworu.

2

II

IV

5.4
2.4

28.

1 000 g • 0,28 = 280 g; 1 000 g • 0,041 = 41 g

280 g - 41 g = 239 g

Odp.: W 1 kg wody z Morza Martwego jest o 239 g więcej

substancji stałych niż w 1 kg wody z Morza Czerwonego.

• Obliczenie procentu danej

liczby.

• Obliczenie wartości wyraże­

nia arytmetycznego.

3

IV

5.2

1.5

29.

1 1 = 1 000 kg; 1 000 • 0,038 ■

0,778 = 29,564 kg

Odp.: W tonie wody z Morza Śródziemnego znajduje się

29,564 kg chlorku sodu.

• Obliczenie procentu danej

liczby.

• Zamiana jednostek masy.

2

III

5.2

SP

30.

100 • 0,033 = 3,3 g; 300 • 0,02 = 6 g

(3,3 + 6) : (100 + 300) • 100% = 2,325% = 23,3%c

Odp: Roztwór uzyskany ze zmieszania 100 g wody z Morza
Barentsa i 300 g wody z Morza Czarnego będzie mial stężenie
około 23,3%e.

• Obliczenie procentu danej

liczby.

• Obliczenie stężenia roztwo­

ru według warunków
określonych w zadaniu.

3

IV

2.4
5.3

1.3.

W Y R A Ż E N I A

A L G E B R A I C Z N E

Nr

R o zw iązan ie

zadania

K ry te ria oceny

Suma

Wymagania

zad.

pkt

ogólne

szczegół.

1.

C

1

II

6.2

2. I. 4ab(b - 2a); II. 3ax(a2 - 2a + 5 x 2)

• Wyłączenie wspólnego

czynnika przed nawias.

2

II

6.6

3.

5xy

• Mnożenie jednomianów.

1

II

6.5

4.

B

1

II

6.5

5.

I. 2x, 2x + 6; ll.2 x - 1, 2x + 1; III. 3x, 3x + 3

• Podanie liczb spełniających

warunki określone w zadaniu.

3

II

6.5

1.5

6.

Np.: (2n - 1) • (2n + 1) • ( 2n + 3 )

• Podanie iloczynu trzech ko­

lejnych liczb nieparzystych.

1

III

6.1

7.

lOOm + 10 • (m + 1) + 1 • 2m = 112m +10 = 2 • (56m +5)

Uzasadnienie: Ponieważ sumę można zapisać w postaci iloczynu
2 • (56m + 5), gdzie w należy do liczb naturalnych, to jest ona
podzielna przez 2.

* Zapis liczby trzycyfrowej.

• Obliczenie sumy i uzasadnie­

nie zgodne z warunkami

określonymi w zadaniu.

2

IV

6.1
6.6

8. 4 + 21/6

• Obliczenie wartości wyraże­

nia algebraicznego według
warunków określonych

w zadaniu.

2

II

6.2
4.2

9.

B

1

II

6.5

10. -84

• Obliczenie wartości wyrażenia

według warunków zadania.

1

II

6.2

1.5

11. B

1

II

6.4

12.

C

1

II

6.1

13.

C

1

III

6.5

113

R o z w i ą za n i a zadań

14.

2 x - 3 + 5 - 2x + 4 * - 7 = 4 * - 5
Odp.: Obwód trójkąta równy jest 4* - 5.

• Obliczenie obwodu trójkąta.

2

III

6.4

10.9

15.

a) D

1

III

6.1

b) ab - (a - 2x) ■ (b - 2x) = 2ax + 2bx - 4*2
Odp.: Powierzchnia passe-partout równa jest 2ax + 2bx - 4*2.

• Obliczenie powierzchni

według warunków zadania.

3

III

6.5
6.3

16.

C

1

II

6.1

17.

C

1

II

6.1

18.

Odp.: Cena za kilogram mieszanki orzechów równa jest

(26m + 30n) : (m + n ) złotych.

• Opisanie związków między

wielkościami za pomocą
wyrażenia algebraicznego.

1

II

6.1

19.

(100% - 30%) • p + (100% - 50%) ■

w + 2(100% - 70%) • t =

= 10%p + 50%w + 2 • 30%i = 0,7p + 0,5w + 0,6ć

Odp.: Pani Krysia zapłaciła za zakupy (0,7p + 0,5w + 0,6i) zł.

• Opisanie związków między

wielkościami za pomocą
wyrażenia algebraicznego.

3

III

6.1
5.2
6.3

20. Cena we wrześniu 2009 roku:*; (100% + 10%) z i ; 1,1*

90% z 1,1*; 0,99*

x - 0,99* = 0,01*

Odp.: Cena w kwietniu 2010 roku była niższa od ceny

we wrześniu 2009 roku o 1%.

• Obliczenie procentu danej

liczby.

• Opisanie związków między

wielkościami za pomocą
wyrażenia algebraicznego.

" Sformułowanie odpowiedzi.

4

IV

5.2
6.1
6.3
5.4

21.

Odp.: Największą średnicę przekroju beczki można obliczyć

ze wzoru:

• Przekształcenie wzoru i wyz­

naczenie danej wielkości.

1

II

6.7

22. Odp.: Wartość przyspieszenia to:

a = 2 • (i -

+ Vgi): t2.

• Przekształcenie wzoru i wyz­

naczenie danej wielkości.

1

II

6.7

1.4. R Ó W N A N I A

Nr

zad.

Rozwiązanie zadania

Kryteria oceny

Suma

pkt

Wymagania

ogóirte

szczegół.

1. wartość wyrażenia: 12

L — 1 3 ' 12 - 9 2 - 9 ; p - 3 . 1 2 - 9 ; L —p

Odp.: Wartość wyrażenia jest pierwiastkiem równania.

• Obliczenie wartości wyrażenia.
• Podstawienie obliczonej

wartości do równania.

• Sprawdzenie, czy lewa strona

równania jest równa prawej.

3

III

1.5

7.2

2. Odp.: 18, 27,36,45, 54, 63, 72, 81, 90.

• Określenie liczb spełniają­

cych podane równanie.

1

II

7.2

3.

lOtc + 8 = x + 251; jc = 27

Odp.: Szukaną liczbą* jest 27.

• Ułożenie równania.

• Rozwiązanie równania.

2

III

7.1
7.3

4.

A

1

II

7.3

5.

5x - 1 = 3x +2; x = |

^

-i

Odp: Liczba* równa jest

• Zastosowanie własności

trójkąta równobocznego.

• Rozwiązanie równania.

2

III

10.22

7.3

6. 2- 8 6 - 2 - 6 = 112; b = 30 [cm]

2a + 2 • 30 = 112; a = 26 [cm]
Odp.: Boki prostokąta mają długość 30 cm i 26 cm.

• Ułożenie równania prowa­

dzącego do obliczenia jed­
nego z boków prostokąta.

• Rozwiązanie równania.
• Obliczenie drugiego boku

prostokąta.

3

III

7.1

10.9

7.3

114

R o zw i ą za n i a zadań

7.

Pj = 2,5x; P2 = 3jc; P3 - 4,5x
4,5x - 3x = 720; x = 480
P 1= 2,5 • 480 = 1 200 [m2]; P2 = 3 • 480 = 1 440 [m2];
p 3 = 4,5 • 480 = 2 160 [m2]

Odp: Działki mają powierzchnię równą: 1 200 m2, 1 440 m2
i 2 160 m2.

• Ułożenie równania.
• Rozwiązanie równania.
• Obliczenie pól powierzchni

według warunków zadania.

4

IV

10.9

7.1
7.3

8. cena bukietu róż:x + 0,5x +

= 33; x =18 [zł]

cena bukietu tulipanów: 0,5x = 9 [zł]

cena bukietu z kwiatów mieszanych:

= 6 [zł]

• Ułożenie równania pozwala­

jącego obliczyć jedną z szu­

kanych wielkości.

' Rozwiązanie równania.
• Obliczenie pozostałych

szukanych wielkości według

warunków zadania.

3

IV

7.1
7.3

6.3

9.

a - kwota Alka; k - kwota Kamila

2 f l - 2 - i « + t f + 1 2 0 = l 080; a = 640

4

4 3

k =

= 2 • 640 = 480

4

4

Odp.: Alek ma 640 zł, a Kamil 480 zł.

• Ułożenie równania.
• Rozwiązanie równania.
• Obliczenie pozostałych

szukanych wielkości według

warunków zadania.

3

IV

1.5

7.1
7.3

10. x - masa pręta

x - f y - 2 - ± x = 3;x = 18 [kg]

Odp.: Cały pręt ma masę 18 kg.

’ Ułożenie równania.
• Rozwiązanie równania.

2

IV

7.1
7.3

11. Kran w ciągu godziny napełnia 1 część basenu, a odpływ

opróżnia jL część basenu.

x - szukana liczba godzin

(5 ~

=

x =

24

Odp.: Tak, woda napełni basen w ciągu 24 godzin.

• Obliczenie wartości wyraże­

nia arytmetycznego.

• Ułożenie równania.

• Rozwiązanie równania.

3

IV

7.1
7.3

1.5

12. t - wiek ojca

25 %t + 1 • 25 %t + t = 64; t = 48

Marysia: i • 48 = 12; Adam: i • 12 = 4

Odp.: Ojciec ma 48 łat, Marysia 12 lat, a Adam 4 lata.

• Ułożenie równania.

0 Rozwiązanie równania.
• Obliczenie pozostałych

szukanych wielkości według

warunków zadania.

3

IV

7.1
7.3
5.2

13.

A

1

II

7.1

14.

C

1

III

7.3

15. x - długość trasy

(x - 8) : 2 + 8 =

x = 24

2- 2 4 = 16

Odp.: Pierwszego dnia turysta przeszedł 16 km, a drugiego -
8 km.

• Ułożenie równania.
• Rozwiązanie równania.
• Obliczenie szukanej wiel­

kości według warunków
zadania.

3

IV

7.1

7.3

1.5

16.

A

1

II

7.1

17.

1 - 7 ,2 :3 6 = 0,8 [h]

v = 40 : 0,8; v = 50 [b»i

h

Odp.: Samochód poza miastem jechał ze średnią prędkością
50 kilometrów na godzinę.

• Obliczenie wartości wyraże­

nia arytmetycznego.

• Zastosowanie wzoru

na średnią prędkość

w ruchu prostoliniowym.

3

IV

7.1
7.3

1.5

18.

0,5 • 20 = 10 [km]

10 + 20i = 36f; t = |

O

Odp: Motocyklista dogoni rowerzystę po upływie | godziny

od chwili wyjazdu.

• Obliczenie wartości wyraże­

nia arytmetycznego.

• Ułożenie równania.
• Rozwiązanie równania.

3

IV

7.1
7.3

1.5

115

R o z w ' ą z a n i a z a ci a ń

1.5. U K Ł A D Y R Ó W N A Ń

Nr

zad.

Rozwiązanie zadania

Kryteria oceny

Suma

pkt

'Wymagania

ogólne szczegół.

1. D

1

II

7.4

2. J2a

+ 26 = 40

«,

£> — długości boków prostokąta

j a

- 3

= b +3

a

= 13; b

=

7

P = a ■

b = 13 cm

• 7 cm = 91 cm2

Odp.: Pole prostokąta równe jest 91 cm2.

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.
• Obliczenie pola prostokąta.

3

IV

7.4

7.6

10.9

3.

4,70*

+ 8,25 d = 344

• Ułożenie równania.

1

III

7.4

4. j x + y = 16

x - cena porcji tortu śmietankowego

j 4x + 2y = 52

y - cena porcji tortu orzechowego

x = 10; y = 6

Odp.: Porcja tortu śmietankowego kosztuje 10 zł.

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.

2

IV

7.4

7.6

5.

Kolejno: 20, 30, 24

• Uzupełnienie danych.

1

III

7.4

6. j t + 15c = 54

t - pierwotna cena tortu

121 • 0,6 + 20c • 0,4 = 44,80

c - pierwotna cena ciastka

t = 24; c = 2

Odp: Tort przed obniżką kosztował 24 zł, a ciastko - 2 zł.

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.

2

IV

7.4
7.6

7.

f 3z + 2d = 26,20

z - pierwotna cena zeszytu

13z ■ 1,1 + 2d ■ 1,2 = 30,42

d - pierwotna cena długopisu

z = 3,4 i d = 8

3,4 • 1,1 = 3,74 zł; 8 • 1,2 = 9,60 zł
Odp.: Po podwyżce zeszyt kosztował 3,74 zł, a długopis - 9,60 zł.

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.
• Obliczenie pozostałych szu­

kanych wielkości.

3

IV

7.4
7.6
5.2

8.

f 0,8x + 0,25y = 29

x - liczba uczniów klasy 2a

1 x + y = 61

y - liczba uczniów klasy 2b

x = 25; y = 36

Odp.: W klasie 2a jest 25 uczniów, a w klasie 2b - 36 uczniów.

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.

2

IV

7.4

7.6

9.

j

5x + 4y = 29

x - liczba pkt za wygrany mecz

14x + 4y = 24

y - liczba pkt za remis

x = 5;y = 1

Odp.: Za mecz wygrany drużyna otrzymuje 5 punktów,

a za remis - 1 punkt.

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.

2

IV

7.4
7.6

10. B

1

II

7.4

11. Jx = y + 21

x - wiek mamy, y - wiek Patryka

|x + 10 + y +10 = 55

x = 28 - wiek mamy;y = 7 - wiek syna;

10 lat później: odpowiednio 38 i 17 lat

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.

2

IV

7.4

7.6

12. j x + y = 105

x - wiek Teofila, y - wiek Agaty

{ x - y = \y

x = 63 -,y = 42

Odp.: Agata ma 42 lata, a Teofil - 63.

• Ułożenie układu dwóch

równań.

■ Rozwiązanie układu równań.

2

IV

7.4
7.6

13.

C

1

II

7.4

14.

lx + y = 14

{ lOy + x > 10x + y

warunki spełniają: (5, 9); (6, 8)
95 > 59; 86 > 68

Odp.: Szukane liczby to 59 i 68, ponieważ zmiennex i y
oznaczające cyfry liczby 10x + y i lOy + x nie są równe.

• Ułożenie układu złożonego

z równania i nierówności.

• Rozwiązanie układu równań

i zapis rozwiązań.

• Analiza treści zadania i uza­

sadnienie rozwiązania.

3

IV

V

7.4
7.6

116

R o z w i ą z a n i a zadań

15.

iy = x + 7

x - licznik ułamka

1 * - 8 — A

y - mianownik ułamka

[ y - 8

12

* = 13 ;y = 20

Odp.: Szukanym ułamkiem jest

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.

2

IV

7.4

7.6

16.

D

1

IV

7.4

17.

i 6 (v + x) = 24

v - prędkość turysty

18 (v - x ) = 24

x - liczba km/h, o którą zmienia się prędkość

x = 0,5; v = 3,5

Odp.: Turysta poruszał się z prędkością 3,5

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.

2

IV

7.4

7.6

18.

i 3 (v - x ) = 36

v - prędkość statku

[2 (y + x) = 36

x - prędkość prądu rzeki

v = 15; x = 3

Odp.: Prędkość statku na wodzie stojącej równa jest 15
a prądu wody 3

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.

2

IV

7.4

7.6

19.

j x + y = 11

x - liczba większych kostiumów

13,2*4- 2,8>y

=

32,8

y - liczba mniejszych kostiumów

x = 5;y = 6

Odp.: Krawcowa z 32,8 m materiału uszyje 5 kostiumów

w większym rozmiarze i 6 w mniejszym.

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.

2

IV

7.4

7.6

20.

A

1

IV

7.4

21. Jx + y = 18

x - liczba mniejszych kontenerów

j 4x+ 6y = 88

y - liczba większych kontenerów

x

= 10; y = 8

Odp.: Kawę zapakowano do 10 kontenerów 4-tonowych
i 8 kontenerów 6-tonowych.

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu równań.

2

IV

7.4

7.6

22.

(x

+ y + z = 250

x - masa pierwszej skrzynki

\ z = V ) + x + y

y - masa drugiej skrzynki

[ y + z = 1 1 0 + x

z - masa trzeciej skrzynki

x

= 70; y = 50; z = 130

Odp.: Skrzynie z towarem mają masę 70 kg, 50 kg oraz 130 kg.

• Ułożenie układu trzech

równań.

• Rozwiązanie układu równań.

2

IV

7.4

7.6

23.

i 10x - 5y = 340

x - liczba poprawnych odpowiedzi

|x

+ y = 40

y - liczba błędnych odpowiedzi

x

= 36;y = 4

Odp.: Uczestnik teleturnieju udzielił 36 dobrych odpowiedzi

i 4 błędne.

• Ułożenie układu dwóch

równań.

* Rozwiązanie układu równań.

2

IV

7.4

7.6

2 . WYKRE S Y F UNKCJ I

2 .1 . F U N K C J E

Nr

zad.

Rozw iązanie zadania

Kryteria oceny

Suma

pkt

Wyms

ogólne

gania
szczegół.

1.

D

1

II

8.3

2.

A

1

II

8.5

3.

C

1

II

8.3

4.

C

1

II

8.3

5.

I. C, II. B, III. A

3

II

8.3

117

R o z w i ą z a n. i a zadań

b) I. TAK; II. TAK

.V

15 S

30 5

1 min

2 min

>

2,5

7,5

15

30

60

• Uzupełnienie tabeli przedsta­

wiającej zależność określoną
warunkami zadania.

• Sporządzenie wykresu

funkcji.

2.2. O D C Z Y T Y W A N I E W Y K R E S Ó W

Nr

zsd.

Rozwiązanie zadania

Kryteria oceny

Suma

pke

Wyme

ogólne

gania
szczegół

1.

I.

PRAW D A;

II.

FAŁSZ;

III.

PRA W D A ;

IV.

FAŁSZ;

V.

PRA W D A

5

I

8.4

2.

C

1

III

8.4

3.

B

1

I

8.4

4.

T A K

1

III

8.4

5.

Odp.: Przedział czasowy, którego dotyczy wykres,

to 11.50-12.30.

• Interpretacja danych

przedstawionych za pomocą

wykresu.

1

II

8.4

6.

czas przejścia całej trasy: 1 godz. 30 min

1,5 • 2,5 • 0,9 = 3,375 km

Odp.: Długość szlaku wybranego przez Nowaków równa jest

3,375 km.

• Odczytanie danych z wykre­

su.

• Obliczenie czasu i długości

według warunków zadania.

2

IV

8.4

1.7

7.

4 ' 5 +

• 40 + 1,5 • 2,5 +

• 60 + 12 • 5 = 45 km

12

60

60

60

Odp.: Nowakowie podczas niedzielnej wycieczki pokonali

trasę długości 45 km.

• Odczytanie danych z wykre­

su.

• Obliczenie drogi według

warunków zadania.

2

III

8.4

1.7

8.

I. w lipcu i sierpniu; II. w kwietniu; III. w lutym; IV. 2°C; V. -7 |°C

• Odczytanie danych z wykresu.

5

II

8.4

9.

a) C

1

II

8.4

b)

A

1

II

8.4

c) B

1

II

8.4

d) C

1

II

8.4

118

R o zw i ą z a n i a zadań

3 . E L E M E N T Y S T A T Y S T Y K I I R A C H U N K U P R A W D O P O D O B I E Ń S T W A

3.1. S T A T Y S T Y K A O P I S O W A

Nr

Ro zw iązanie zadania

Kry te ria oceny

Suma

Wymagania

zad.

pkt

ogólne szczegół.

1.

Kolejno: 444 115; 0 pkt, 50 pkt; 19; 0,5

" Odczytanie danych z diagra­

mu i uzupełnienie zdań.

2

II

8.4

2.

444 115 • 0,03 = 13 323
Odp.: Okoio 13 323 uczniów uzyskało wynik równy 28 punktów.

• Odczytanie danych z diagra­

mu i wykonanie obliczeń.

1

II

8.4

1.4

3.

B

1

II

5.4

4.

I. NIE; II. A

2

II

9.4

5.

a) B

1

II

1.7

b) C

1

II

9.1

c) pomorskie, zachodniopomorskie, dolnośląskie, opolskie,
śląskie

• Podanie nazw województw

zgodnie z warunkami zadania.

1

II

9.1

d) mazowieckie

* Podanie nazwy województwa

zgodnie z warunkami zadania.

1

II

9.1

6.

a) 50- ^

= 8,75 [kg]

Odp.: Średnia zawartość skrobi w 50 kg ziemniaków to 8,75 kg.

• Odczytanie danych z diagra­

mu i wykonanie obliczeń.

2

III

9.4

2.2

b) UK)'X = 30;x = 200° g = 2 k S

Odp.: Dwa kg ziemniaków dostarcza średnio 30 g błonnika.

• Odczytanie danych z diagra­

mu i ułożenie równania.

• Rozwiązanie równania.

3

III

9.1
7.1
7.3

7.

(104 200 : 322 575) • 100% * 32,3%
Odp.: Około 32,3% powierzchni kraju stanowią obszary chronione.

• Wykonanie obliczeń na pod­

stawie danych z tekstu.

1

III

5.4

8.

265 h a : 1 000 = 2 650 000 m2 :1 000 = 2 650 m2
Odp.: Na jednego mieszkańca Polski przypada 2 650 m2 obszaru
chronionego.

• Odczytanie danych z tekstu

i wykonanie obliczeń.

• Zamiana jednostek po­

wierzchni.

2

III

9.1
2.4

9.

25 138 : 104 200 = 0,24

Odp.: Powierzchnia parków krajobrazowych zajmuje 0,24

wszystkich obszarów chronionych.

• Odczytanie danych z tekstu

i wykonanie obliczeń.

2

III

9.1 1
2.4

1

10.

B

1

II

9.1

11.

a) A

1

III

2.3

b) (1 575 + 1 451): 2 = 1513
Odp.: W latach 2007-2008 udzielono średnio 1513 patentów rocznie.

* Odczytanie danych z tabeli

i obliczenie średniej.

1

III

9.4

i

|

c) (25,9 :100) • 2 488 = 644,392 = 644

Odp.: W 2008 roku osoby fizyczne zgłosiły 644 wynalazki.

• Odczytanie danych z tabeli

oraz diagramu i obliczenie

wyniku.

2

III

9.4 1
2.4 i

d) 43,6% - 25,9% = 17,7%

Odp.: Placówki naukowe w 2008 roku zgłosiły o 17,7 punktów
procentowych więcej wynalazków niż osoby fizyczne.

• Odczytanie danych z tabeli

oraz diagramu i obliczenie

wyniku.

1

III

5.4

s

12.

I. najwyższy kurs: kwiecień 2005 r., najniższy: w lipcu 2008 r.;
II. o 20 zł; III. najwyższy wzrost kursu: czwarty kwartał 2008 r.,

najmniejsze wahania kursu: trzeci kwartał 2007 r.

• Interpretacja danych przedsta­

wionych za pomocą wykresu.

1

II

9.1

119

R o z wi ą z a n i a zadań

13.

B

1

II

9.1

14.

C

1

III

5.4

}5.

(73 :1000) • 38 000 000 = 2 774 000
Odp.: W roku 2000 z Internetu korzystało 2 774 000 Polaków.

• Odczytanie danych z diagra­

mu i wykonanie obliczeń.

2

III

9.1
2.4

16.

80,7% -39,2% = 41,5%
Odp.: Liczba użytkowników Internetu w Danii w 2008 roku w po­
równaniu z rokiem 2000 wzrosła o 41,5 punktu procentowego.

• Odczytanie danych z diagra­

mu i wykonanie obliczeń.

2

III

9.1
5.4

17.

0,512* = 31 800 000;

x

= 62 109 375 = 62,1 min

Odp.: Liczba ludności Francji w 2008 roku wynosiła

około 62,1 min.

• Ułożenie równania.
• Rozwiązanie równania.

2

III

9.1
2.4

1.4

18.

Przykład odpowiedzi:
Grypa jest chorobą sezonową, której szczyt zachorowań notuje się
w okresie zimowym i trwa ok. 2 miesięcy, po czym liczba zachoro­
wań spada i w okresie letnim utrzymuje się na niskim poziomie.
W ostatnich latach obserwuje się stopniowe przesuwanie szczytu
zachorowań na wcześniejsze miesiące okresu zimowego.

• Interpretacja danych przedsta­

wionych za pomocą wykresu.

1

II

9.1

19.

38 100 000

: 100 000 = 381; 381 • 5 = 1 905; 1 905 • 7 = 13 335

Odp.: W okresie od 16 do 22 lutego 2010 r. na grypę zachoro­

wało w Polsce około 13 300 osób.

• Odczytanie danych dotyczą­

cych sposobu obliczenia
i wykonanie obliczenia.

2

III

2.4

1.4

3.2. W P R O W A D Z E N I E D O R A C H U N K U P R A W D O P O D O B I E Ń S T W A

Nr

Rozwiązanie zadania

Kryteria oceny

Suma

Wymagania

zad.

pkt

ogólne szczegół.

1.

możliwe wyniki: (R, R), (R, O), (O, R), (O, O)

Odp.: Są cztery możliwe wyniki dwukrotnego rzutu monetą.

• Analiza zdarzenia losowego

i podanie liczby jego wyników.

1

III

9.5

2.

_ CZ£rWOny

— f ń

[ z \

Pn] ~

IM

- niebieski

• Analiza zdarzenia losowego

i uzupełnienie rysunku.

1

III

9.5

3.

/ \

O

R

A

-

-

a

/ x r - R

R O

^

R 0

• Analiza zdarzenia losowego

i wykonanie rysunku.

1

III

9.5

4.

I. {(1,1), (1,2), (1,3), (1, 4), (1,5), (1, 6), (2,1), (2,2),..., (6, 6)}

- je s t 36 wyników zdarzenia;

II. (1,1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)

• Analiza doświadczenia loso­

wego i wypisanie jego zda­
rzeń elementarnych.

2

III

9.5

5.

I. 0-1-2, 0-2-1,1-0-2,1-2-0,2-0-1, 2-1-0; II. cztery

• Analiza zdarzenia losowego.

2

III

9.5

6.

wyniki:

{ ( 1 ,2, 2), (2 ,1, 2), ( 2 ,2 ,1)}

Odp.: Można otrzymać dwie liczby parzyste: 122 i 212.

• Analiza zdarzenia losowego.

2

III

9.5

7.

Odp.: Marcysia musi wyciągnąć z szuflady 10 kolczyków, aby
mieć pewność, że skompletuje jedną parę.

• Analiza zdarzenia losowego.

1

III

9.5

8.

3

• 3 • 3 = 27

Odp.: Kajetan może się ubrać na 27 sposobów.

• Analiza zdarzenia losowego.

1

III

9.5

9.

Sposób rozstawienia drużyn a, b, c, d, e: a-b b-c c-d d-e

5 • 4 : 2 = 10

a~c £-d c_e

a-d b-e

Odp.: Odbędzie się 10 meczów.

a-e

• Analiza zdarzenia losowego.

1

III

9.5

120

Ro z wi ą z a n i a z a d a ń

4. F I GURY P ŁAS KI E

4. 1. T R Ó J K Ą T Y

Nr

zad.

Rozwiązanie zadania

Kryteria oceny

Suma

pkt

Wymagania

ogólne szczegół

1.

D

1

II

10.1

2.

B

1

III

2.4

3.

C

1

III

SP

4.

I. 4; II. 2, III. 1, IV. 3

4

IV

10.20

5.

C

1

III

10.13

6.

D

1

II

10.7

7.

h

=

aM; a = h

+

2

a - a i

3 + 2; a - j ^ [ c m ]

Odp.: Długość boku trójkąta jest równa

cm.

• Obliczenie boku trójkąta.

3

IV

7.1
7.3

2.4*

8.

a

+ 2b

=

84; b = 24 cm

ń2 = 52 - (Aa)2; /z = 6l/7 [cm]

• Obliczenie wysokości trój­

kąta.

• Obliczenie pola trójkąta.

4

IV

7.1

10.9
10.7

P

= i • 36 • 6f7 = 108V7 [cm2j

a =

36 cm

Odp.: Pole trójkąta jest równe 108V7 cm2.

9.

ft = ib 2 - 6 2

=

21/3 [cm]

P

=

i • 12 • 2l/3 = 12l/3 [cm2]

Odp.: Pole trójkąta jest równe 12l/3 cm2.

" Obliczenie wysokości trój­

kąta.

• Obliczenie pola trójkąta.

2

IV

10.7
10.9

10. L = 61/2 + 12 + 6 + 6i3

cm

= 18 + 6i/2 + 6i/3 [cm]

\

6l/2 cm \

6V3 cm

Odp.: Obwód trójkąta

\ ~

j (

jest równv 18

+ 6V2 + 6l/3 cm.

W

m'v.

• Stosowanie własności trój­

kąta prostokątnego.

• Obliczenie długości boków

trójkąta.

• Obliczenie obwodu trójkąta.

4

V

10.20

10.9

10.15

2.4*

12 cm

11.

|D £ | = 1/I 62 - 82 = 8 f 3 ;|£ C | = I 6 - 81/3

AE C K -A A B K

L

_ 16-81/3 _ 2-1/3

16

2

Odp.: Trójkąt

jest podobny do trójkąta ARK w skali

• Obliczenie długości boku

trójkąta ADE.

‘ Obliczenie długości odcinka.
• Obliczenie skali podobień­

stwa trójkątów.

3

IV

10.7

2.4*

10.11

12.

h = d ź = l - , a = 14^-

p _ o M _ ( 1 4 f ) 2 -V3_ 49^

^

Odp.: Samochodowy trójkąt odblaskowy ma powierzchnię

równą yV 3 cm2.

• Obliczenie długości boku

trójkąta równobocznego.

• Obliczenie pola trójkąta.

3

IV

2.4*

10.7
10.9

13.

AOBA ~ AOLK w skali k = | = 4

|LX| = 35 + 115 - 50 = 100 [cm]

|AB | = k ■

\LK\ = 4 • 100 = 400 [cm] = 4 m

. . . . j

wysokość drzewa: 4 m + 0,5 m = 4,5 m

. - '

Odp.: Wysokość drzewa

•

j i- *i

1

jest równa

4,5 m.

■

(

'•'f « J

cfiL35cm

I*

O

_____ ............................................................

iM A

• Obliczenie skali podobień­

stwa trójkątów.

• Obliczenie boku trójkąta

powiększonego w skali.

• Obliczenie długości szuka­

nego odcinka.

4

IV

10.15

2.4

10.11

f

'

/ 'T 50cm

[|j

1

2 ni

1

6 m

1

121

R o zw i ą za n i a zadań

4 .2 . W I E L O K Ą T Y

Nr

zad.

Ro zw iązan ie zadania

K ryteria oceny

Suma

Wymagania

ogólne szczegół.

a = 2; b = 2l/2

P = b2 = (2l/2)2 = 8

L = 4 ■

2l/2 = 81/2

Odp.: Pole czworokąta A B CD jest równe 8, a obwód - 8l/2.

1 Obliczenie długości boku

kwadratu.

1 Obliczenie pola kwadratu.
1 Obliczenie obwodu kwadratu.

IV

10.7
10.9

2

.

x2 + 122 = ( 12V3)2; x = 12V2 cm

P = 12 • 12l/2 = 144i/2 [cm2]

Odp.: Pole prostokąta jest równe 144l/2 cm2.

12 cm

1 Obliczenie boku prostokąta.
1 Obliczenie pola prostokąta.

IV

10.7
10.9

3.

i è = 4,5 cm

i a = 4,5^3 cm

1 Obliczenie długości boków

prostokąta.

■

Obliczenie obwodu prostoką­

ta.

b = 9 cm; a = 9l/3 cm

L = 2 • 9 + 2 ■

9i/3 = 18(1 + V3) [cm]

Odp.: Obwód prostokąta jest równy 18(1 + i3) cm.

IV

10.15

2.4*

10.9

L = 2a -t- 2b = 60

2 - 7x + 2 • 3x = 60; x = 3;

a = 21 m, b = 9 m
¿2 = 212 + 92; d = 1/522 = 3l/58 [m]

Odp.: Długość przekątnej działki to 31/58 m.

b = 3x

a = lx

• Obliczenie długości boków

prostokąta.

1 Obliczenie długości przekąt­

nej prostokąta.

IV

10.9

7.1
7.3

10.7

5. a = \AD \ ; a2 = l 2 + 52; a = {26

b = \A B \;b 2 = \ 2 + 42-,b = f Ü
L = 2a + 2b = 2(i/26 + i/l7)

Odp.: Obwód czworokąta o podanych

współrzędnych jest równy 2(l/26 + l/Ï7).

■

Narysowanie czworokąta.

■

Obliczenie długości boków

czworokąta.

1 Obliczenie obwodu czworo­

kąta.

IV

10.7

2.4*

10.9

8.1

6

.

p = a • h = 8i/3 cm2

8 cm

x2 + 1/3^ = (2{3)2; x = 3 cm
y = 8 - 3 = 5 [cm]

¿2

=

52

+

t

/

32

=

28; d = 2

ff

[cm]

'

^

Odp.: Pole czworokąta jest równe 81/3 cm2,
a długość krótszej przekątnej - 2l/7 cm.

• Obliczenie pola powierzchni

czworokąta.

• Obliczenie długości boku

trójkąta.

• Obliczenie długości prze­

kątnej równoległoboku.

IV

10.9

10.7

2.4*

x =

7 = 2 [cm]

h2 + 22 = 42; h 2 = 1 2 ; h = 2^3 [cm]

^

P = 1(11 + 7) ■ 2l/3 = 18l/3 [cm2]

Odp.: Pole trapezu jest równe 18l/3 cm2.

7 cm

1 Obliczenie długości boku

trójkąta.

1 Obliczenie wysokości trape­

zu.

1 Obliczenie pola trapezu.

IV

10.9

10.7

2.4*

h 2 = 102 - 62 = 64; h = 8 cm

c = 10 cm, bo AABC jest równoramienny

6 cm

c

P = 6

+

12 8 = 72 [cm2]

L — 6 + 8 + 12 + 10 — 36 [cm]

Odp.: Pole trapezu jest równe 72 cm2,

a jego obwód - 36 cm.

12 cm

1 Obliczenie wysokości trape­

zu.

■

Obliczenie długości ramie­

nia trapezu.

■

Obliczenie pola trapezu.

■

Obliczenie obwodu trapezu.

IV

10.7

10.9

. _ 8 - 4 _

2 [cm]

4 cm

h 2 = 42 - 2 2 = 12; h = 2l/3 cm

p = ł ± J • 21/3 = 12l/3 [cm2]

Odp.: Pole powierzchni trapezu

jest równe 12l/3 cm2.

8 cm

' Obliczenie długości boku

trójkąta równoramiennego.

' Obliczenie wysokości trape­

zu.

1 Obliczenie pola trapezu.

IV

10.1

10.7

2.4*

10.9

122

R o zw i ą za n i a zadań

10.

C

1

III

10.7

11. x2 + (10i/3)2 = 202;x 2 = 100;x = 10[cm ]

z '

di = 20l/3cm; d2 = 20 cm

x

p = l . d r d2 = 1-20-201/3

= 2001/3 [cm2]

a = 2 ■ 30° = 60°

\ -

Odp.: Pole powierzchni rombu

jest równe 200 {3 cm2, a miara

10 cm

jego kąta ostrego to 60°.

-----------

6 0 ^ 2 0 cm

A

10i3 cm

• Obliczenie długości krótszej

przekątnej.

• Obliczenie pola rombu.

• Obliczenie miary kąta

ostrego.

5

IV

10.7

10.8

10.9

10.15

2.4*

12. L = 4 -6 = 24 [cm]

Odp.: Obwód rombu

x

jest równy 24 cm.

...............

3 cm

cm

^

i3 0 ^

3i3 cm

• Wykorzystanie własności

kątów w rombie.

• Obliczenie długości boku

rombu.

• Obliczenie obwodu rombu.

3

IV

10.15

10.8

10.9

13.

A

1

II

10.8

14.

a - b = 6; a = 6 + b

P = a i- — ■ h

4 cm

6 + b + b . 4 _ 72; b - 15 cm

a = 21 cm

42 + 62 = c2; c = 2l/l3 cm

L = 15 + 21 + 4 + 21/13 = 40 + 2l/

Odp.: Obwód trapezu równy jest 2(2

15 cm

s\

c

4 cm

15 cm

' 6 cm '

13 = 2(20 +1/I3) [cm]

3 + l/l3) cm.

• Obliczenie długości ramie­

nia trapezu.

• Obliczenie obwodu trapezu.

5

IV

10.7

7.1

7.4

10.9

15.

C

1

III

10.13

16.

T rójkąty^5iiiD iiC sąpodobne, ponieważ |st/C4.B| = \^D C K \

i \^ A B K \ = |<£CIU*r| (kąty naprzemianległe są równe),

\^D K C \ = \^HAKB\ (kąty wierzchołkowe).

\A B

\ _ 15 _ 3

\DC\

5

1

Odp.: Trójkąt A B K je st podobny do tró jk ą ta DKC

w skali 3:1.

• Podanie własności trójkątów

podobnych.

• Podanie skali podobieństwa.

3

V

10.1

2.4

17.

a ) PR A W D A

1

III

10.11

b) C

1

III

10.9

c) c = Vl602 + 602 = 101/292 =

= 10-17,1 = 171 [m]

L — 80 + 240 + 60 + 171

= 551 [m]

Odp.: Na ogrodzenie działki

potrzeba 551 m siatki.

160 m

• Obliczenie różnicy długości

podstaw trapezu.

• Obliczenie długości ramie­

nia trapezu.

• Obliczenie obwodu trapezu.

3

V

10.7
10.9

1.4

18.

B

1

III

10.8

19.

1,25 • [(3,2 ■

2 + 3,8 • 2) • 2,6 -1,35 • 1,6 - 2,20 • 2] = 37,3 [m2]

37,3 m2 : 8 m2 = 4,6625 ~ 5 rolek tapety wzorzystej

1,1 • (4,5 • 4 ■

2,6 - 3 • 1,35 • 1,6 - 2,2 • 1) = 41,932 [m2]

41,932 m2 : 8 m2 = 5,2445 “ 6 rolek tapety gładkiej

Odp.: Do wytapetowania pokojów należy kupić 5 rolek tapety

we wzory i 6 rolek tapety gładkiej.

• Obliczenie powierzchni

według warunków określo­

nych w zadaniu.

• Obliczenie wartości wyraże­

nia arytmetycznego.

4

IV

10.9

2.4

1.4

123

R o

2

: w i ą z a n i a z a d a ń

20.

i

a) L = 80 + 90 + 100 + 30 = 300 [m]
Odp.: Wartownik podczas jednego obejścia terenu zakładu

pokonuje drogę równą 300 m.

• Obliczenie obwodu trapezu.

1

III

10.9

b) 25 min =

3 ^ = 3 000 ®

7

60

h

h

S

= H • 3 000 = 1 250 [m]

1 250 : 300 = 4 r 50, czyli wartownik obejdzie teren cztery razy

i jeszcze 50 metrów

Odp.: W 25 minucie obchodu wartownik znajdzie się na odcinku

oznaczonym ja k o ^D .

• Zamiana jednostek czasu

i jednostek prędkości.

• Obliczenie drogi według

warunków określonych

w zadaniu.

• Sformułowanie odpowiedzi.

1

IV

V

SP

1.7

2.4

c) TAK

1

II

10.11

21. B

1

III

10.11

22. C

1

II

10.16

23.

I. 4 • 22 = 16 [cm2]; II. 4 • 2 ■

6 = 48 [cm2];

III. 4 • 1 • 3 • 3 = 18 [cm2]; IV. ± • 62 = 18 [cm2]

Odp.: Wzór tworzy 16 cm2 drewna oznaczonego jako I,
48 cm2 - II, oraz po 18 cm2 drewna - III i IV

• Obliczenie powierzchni pól

według warunków określo­

nych w zadaniu.

4

IV

SP

10.9

24.

a) 10 + 10 - 2 = 18 [cm]; 2 • 10 + 10 - 2 = 28 [cm]

p = 18 • 28 = 504 [cm2]

Odp.: Powierzchnia wieczka kasetki jest rówma 504 cm2.

• Obliczenie poła zgodnie

z warunkami zadania.

3

IV

1.7

10.9

b) C

1

II

10.9

c) C

1

II

SP

25.

1 . 2 8 - 1 0 - 1 - 4 - 2 8 - 1 - 6 - 4 - 1 - 2 2 - 2 - 1 ( 2 + 10) -2 = 178

2.18 - 2 4 - 1 - 4 - 1 4 - 1 - 2 0 - 6 - 1 - 1 0 - 8 - 1 - 2 - 6 = 276

6 . 1 - 2 3 = 2 3

Odp.: 6 - 2 3 ,1 - 1 7 8 , 2 -2 7 6 .

• Obliczenie pól powierzchni

czworokątów.

• Porównanie wielkości pól

czworokątów.

4

V

10.9

2.4

26.

3. 42 + 162 = rnr; m = 4Vl7

202 + 202 = k 2; k = 20{2

L = 2 • 4l/l7 + 201/2 =

= 8Vl7 + 20V2

K i

4. 42 + 22 = c2; c = 2{5

\ \

k

¿ = 4 + 2- 2^5 = 4 + 41/5

Ą

\

5. 122 + 4 2 = b2;b = 4i/l0

\

142 + i 22 = d2;d = 2{85

L = 18 + 41/IO + 2V85

\ 5

ą

d

b

4

• Obliczenie długości boków

trójkątów.

• Obliczenie obwodów

trójkątów.

6

V

10.7

10.9

27.

Odp.: Rysunek gotowej kartki jest przedstawiony w skali 1:3.

• Podanie skali rysunku.

1

II

SP

28.

C

1

III

2.4

29.

1 - 1 6 = 2 [cm]

■

162 + 122 = x2; x = 20 cm

Odp.: Linia pierwszego zagięcia

arkusza ma długość 20 cm.

16 cm

X' N

2 cm

12 cm

• Obliczenie długości boków

trójkąta.

• Obliczenie długości przeciw-

prostokątnej.

3

III

2.4

10.7

30.

B

-

■

1

II

SP

31.

C

1

III

10.9

32.

C

1

III

10.12

33.

B

1

II

SP

124

R o zw i ą za n i a zadań

4 .3 . K O Ł A

S

O K R Ę G !

Nr

zad.

Rozw iązanie zadania

Kryteria oceny

Suma

pkt

Wytru

ogólne

igania

szczegół

1.

A

1

II

10.3

2.

D

1

II

10.4

3. *2 + 2,52 = 72;x 2 = m ; x = M 2 c m

Odp.: Odległość środka okręgu od cięciwy

jest równa

cm.

j

ni

—

5 cm

/

x

j

\

r—

7 cm\

.V'

• Obliczenie odległości z wy­

korzystaniem twierdzenia
Pitagorasa.

3

IV

10.7

4.

52 - 32

= x 2; x

=

4 cm

Odp.: Odległość cięciwy od środka okręgu

jest równa 4 cm.

|

/ ''-x

J

• Zastosowanie twierdzenia

Pitagorasa.

• Obliczenie długości według

warunków określonych
w zadaniu.

3

III

10.7

5.

4r2 =

(2V2)2 + (31/2)2; r2 = ~

P = jtr2 = 12-71 [cm2l

2

i-,

,

21/2 cir|

Odp.: Pole koła jest równe -yTt cm .

\

>

• Zastosowanie twierdzenia

Pitagorasa.

• Obliczenie długości promie­

nia koła.

• Obliczenie pola koła.

4

IV

10.7

6. Ą 7 = l j t - 2 2 = 7t;PA = l - 2 - 2 = 2

P = n - 2

Odp.: Powierzchnia pola figury jest równa n - 2.

• Obliczenie pola wycinka

kołowego.

• Obliczenie pola trójkąta.
• Obliczenie pola figury.

3

IV

10.6
10.9

2.4*

7.

r; = 1,5 cm; r2 = 1 cm; r3 =

= 2,5 [cm];

P = n ■

2,52 - 7t • l 2 - Tc • 1,52 = 3n cm2

Odp.: Zacieniowana figura ma pole równe 37t cm2.

• Obliczenie długości promieni.
• Obliczenie pól kół.
• Obliczenie pola figury.

4

IV

2.4*

10.6

8.

20 • 2nr = 20 ■ 2 ■ 71 • 5 = 20071 = 628 [m]
Odp.: Koń pokona drogę około 628 m.

• Obliczenie obwodu okręgu.

• Obliczenie drogi.

2

IV

10.5

2.4*

9.

152 = 7,52 + r2;r = 7,5^3 m

L = 2 • 7,5V3 • 7t = 151/3 • 7t » 80,07 [m]

Odp.: W czasie jednego okrążenia samolot na uwięzi pokona

drogę około 80,07 m.

• Zastosowanie własności trój­

kąta prostokątnego i oblicze­

nie długości promienia.

• Obliczenie długości okręgu.

3

IV

10.5

10. L = 40 076 : 2 = 20 036 [km]

2tir - 20 038; r - 20_038 - 3 1 90,764 km

2n

Odp.: Długość promienia koła przekroju kuli ziemskiej, którego

obwodem jest równoleżnik 60°, jest równa 3 190,764 km.

• Obliczenie długości równo­

leżnika.

• Obliczenie długości promie­

nia.

4

IV

2.4*

10.5

7.1

1.4

11.

B

1

III

10.6

12.

360° : 28 = 12^°

Odp.: Kąt środkowy utworzony przez promienie dwóch

kolejnych kapsuł koła Singapore Flyer ma miarę 12^°.

• Obliczenie miary kąta środ­

kowego.

2

III

10.4

2.4

13.

i • 27ir » 16,82 [m]

Odp.: Długość łuku koła Singapore Flyer, który wyznaczają
dwie sąsiednie gondole, wynosi około 16,82 m.

• Obliczenie długości luku

okręgu.

2

III

10.5

2.4*

1.4

14.

(27tr): 0,76 ^ = (2 • 3,14 • 75): (0,76 ■

i f f i ) = 37 [min]

Odp.: Pasażer, który wsiadł do kapsuły koła Singapore Flyer,
znajdzie się w tym samym miejscu po 37 minutach.

• Obliczenie obwodu okręgu.

• Obliczenie czasu okrążenia.
• Zamiana jednostek pręd­

kości.

3

V

10.5

1.7
1.4

125

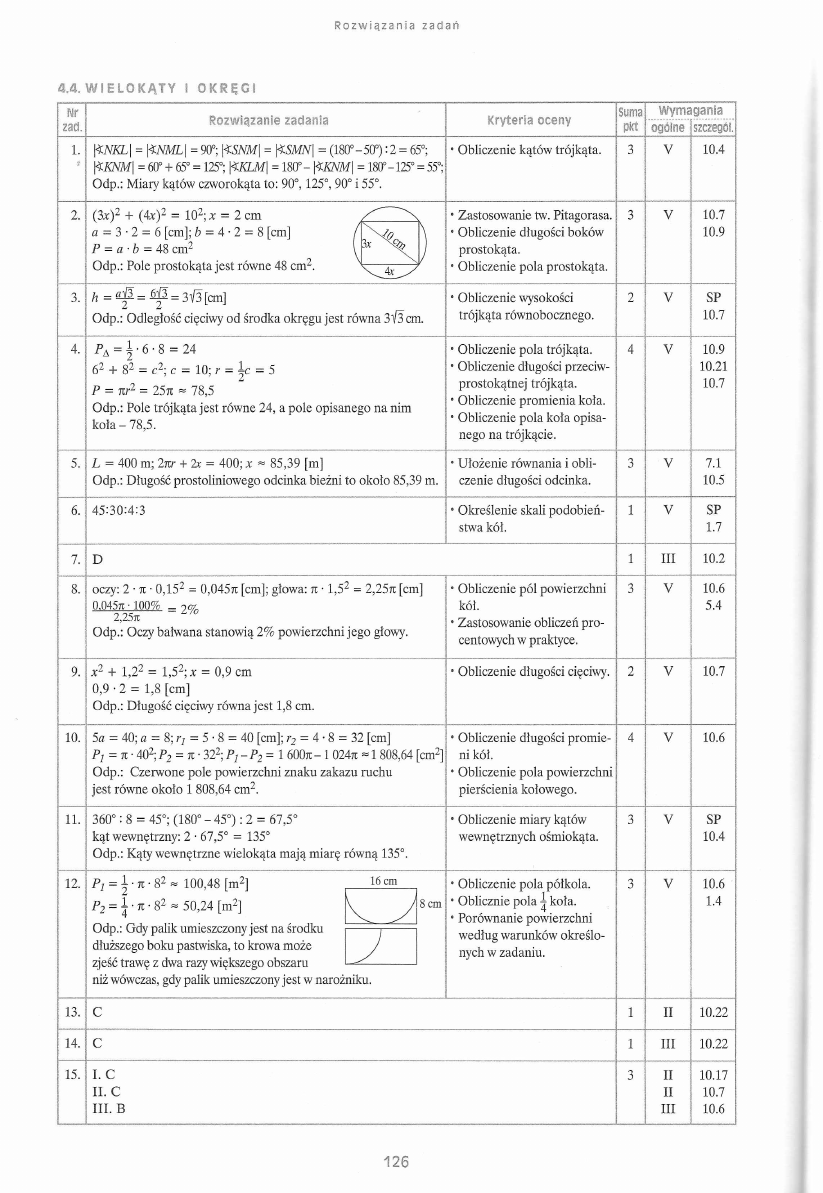
R o z w I ą z a n i a z a d a ń

4.4. W I E L O K Ą T Y ! O K R Ę G !

Nr

zad.

Rozwiązanie zadania

Kryteria oceny

Suma

pkt

Wyni i

ogólne

gania

szczegół.

1.

s

|<WKL|

= |<EJVML| = 90°;

\<SNM\

= |<SMV| = (180°-50°): 2 = 65°;

\<KNM\

= 60° + 65° = 125°;

\<KLM\

= 180°-

\<KNM\

= 180° -125° = 55°;

Odp.: Miary kątów czworokąta to: 90°, 125°, 90° i 55°.

• Obliczenie kątów trójkąta.

3

V

10.4

2.

('3x')2

+ (4x)2 = 102;x = 2 cm

a

=

3 -2 = 6 [cm]; b

=

4

■

2

= S

[cm]

P

= a

■

b

= 48 cm2

( 3x

Odp.: Pole prostokąta jest równe 48 cm-.

4v

,

• Zastosowanie tw. Pitagorasa.
• Obliczenie długości boków

prostokąta.

• Obliczenie pola prostokąta.

3

V

10.7
10.9

3.

h = s M = M = 31/3[cm]

Odp.: Odległość cięciwy od środka okręgu jest równa 3^3 cm.

• Obliczenie wysokości

trójkąta równobocznego.

2

V

SP

10.7

4.

PA = i • 6 • 8 = 24

62 + 82 = c2; c = 10; r = i-c = 5

p = nr2 = 25

k

« 78,5

Odp.: Pole trójkąta jest równe 24, a pole opisanego na nim
k o ła -7 8 ,5 .

• Obliczenie pola trójkąta.
• Obliczenie długości przeciw-

prostokątnej trójkąta.

• Obliczenie promienia kola.

• Obliczenie pola koła opisa­

nego na trójkącie.

4

V

10.9

10.21

10.7

5.

L = 400 m; 2nr + 2x = 400; x = 85,39 [m]

Odp.: Długość prostoliniowego odcinka bieżni to około 85,39 m.

• Ułożenie równania i obli­

czenie długości odcinka.

3

V

7.1

10.5

6.

45:30:4:3

• Określenie skali podobień­

stwa kół.

1

V

SP
1.7

7.

D

1

III

10.2

8.

oczy: 2 ■

7t • 0,152 = 0,045ti [cm]; głowa:

k

■ 1,52 = 2,25ti [cm]

0.04571 ■

100% - w .

2,25

ti

Odp.: Oczy bałwana stanowią 2% powierzchni jego głowy.

• Obliczenie pól powierzchni

kół.

• Zastosowanie obliczeń pro­

centowych w praktyce.

3

V

10.6

5.4

9. x2 + 1,22 = l,5 2;x = 0,9 cm

0,9 • 2 = 1,8 [cm]
Odp.: Długość cięciwy równa jest 1,8 cm.

■ Obliczenie długości cięciwy.

2

V

10.7

10.

5a = 40; a = 8; rj = 5 • 8 = 40 [cm]; r2 = 4 • 8 = 32 [cm]

P , = 7t • 402;P2 = n ’ 322; P1- P 2 = 1 600ti- 1 024tt = 1 808,64 [cm2]

Odp.: Czerwone pole powierzchni znaku zakazu ruchu

jest równe około 1 808,64 cm2.

• Obliczenie długości promie­

ni kół.

• Obliczenie pola powierzchni

pierścienia kołowego.

4

V

10.6

11.

360°: 8 = 45°; (180° - 45°): 2 = 67,5°
kąt wewnętrzny: 2 • 67,5° = 135°
Odp.: Kąty wewnętrzne wielokąta mają miarę równą 135°.

• Obliczenie miary kątów

wewnętrznych ośmiokąta.

3

V

SP

10.4

12.

P1 = 1 • 7t • 82 = 100,48 [m2]

p 2 = i • 7i • 82 = 50,24 [m2]

Odp.: Gdy palik umieszczony jest na środku
dłuższego boku pastwiska, to krowa może
zjeść trawę z dwa razy większego obszaru
niż wówczas, gdy palik umieszczony jest w naroż

16 cm

niku.

8 cm

• Obliczenie pola półkola.
• Oblicznie pola i kola.

• Porównanie powierzchni

według warunków określo­

nych w zadaniu.

3

V

10.6

1.4

13.

C

1

II

10.22

14.

C

1

III

10.22

15.

I.

c

II.

c

III. B

3

II
II

III

10.17

10.7

10.6

126

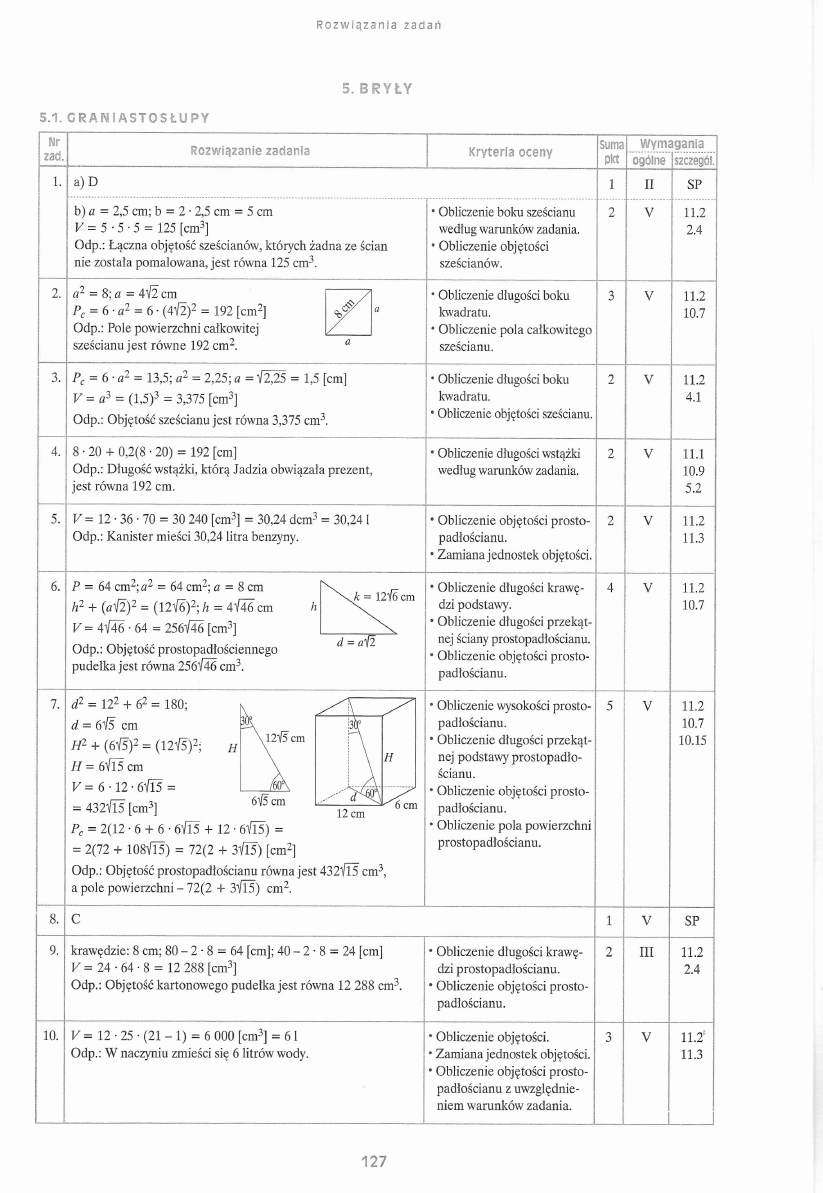
R o z w i ą za n i a zadań

5. B R Y Ł Y

5.1. G R A N I A S T O S Ł U P Y

Nr

zad.

Rozwiązanie zadania

Kryteria oceny

Suma

pkt

Wymi

ogólne

jgania

szczegół.

1.

a) D

1

II

SP

b)

a =

2,5 cm; b

=

2

•

2,5 cm

=

5 cm

V

=

5

•

5

■

5

=

125 [cm3]

Odp.: Łączna objętość sześcianów, których żadna ze ścian

nie została pomalowana, jest równa 125 cm3.

• Obliczenie boku sześcianu

według warunków zadania.

• Obliczenie objętości

sześcianów.

2

V

11.2

2.4

2. a2 = 8; a =

4i/2 cm

Pc =

6-a2 = 6-

(4i/2)2

=

192 [cm2]

Odp.: Pole powierzchni całkowitej

sześcianu jest równe 192 cm2.

^

a

a

•

Obliczenie długości boku

kwadratu.

•

Obliczenie pola całkowitego

sześcianu.

3

V

11.2

10.7

3. p c =

6-a2

= 13,5;

a

2 = 2,25;

a

= l/2^5 = 1,5 [cm]

V = a3 = (1,5)3 = 3,375 [cm3]

Odp.: Objętość sześcianu jest równa 3,375 cm3.

• Obliczenie długości boku

kwadratu.

• Obliczenie objętości sześcianu.

2

V

11.2

4.1

4.

8 • 20 + 0,2(8 • 20) = 192 [cm]
Odp.: Długość wstążki, którą Jadzia obwiązała prezent,

jest równa 192 cm.

• Obliczenie długości wstążki

według warunków zadania.

2

V

11.1
10.9

5.2

5.

V = 12 • 36 • 70 = 30 240 [cm3] = 30,24 dcm3 = 30,241
Odp.: Kanister mieści 30,24 litra benzyny.

• Obliczenie objętości prosto­

padłościanu.

* Zamiana jednostek objętości.

2

V

11.2

11.3

6.

P

= 64 cm2;«2 = 64 cm2;

a

=

8

cm

h 2 +

(a{2)2

= (121/6)2; h = 41/46 cm

h

V = 4i/46 ■

64 = 2561/46 [cm3]

Odp.: Objętość prostopadłościennego

pudełka jest równa 256^46 cm3.

SSN\ sf c ^ l2 ^ c m

d = ai2

• Obliczenie długości krawę­

dzi podstawy.

• Obliczenie długości przekąt­

nej ściany prostopadłościanu.

• Obliczenie objętości prosto­

padłościanu.

4

V

11.2

10.7

7.

d 2 = 122 + 62 = 180;

d = 6V5 cm

H 2 + (6i/5)2 = (121/5)2;

H

H

=

6il5

cm

V = 6 ■

12 • 6l/l5 =

■

432i/l5 [cm3]

Pc

= 2(12 • 6 + 6 • 6l/l5 + 12 •

= 2(72 + 1081/15) = 72(2 + 3

Odp.: Objętość prostopadłości;
a pole powierzchni - 72(2 + 3"!

I\

• Obliczenie wysokości prosto­

padłościanu.

• Obliczenie długości przekąt­

nej podstawy prostopadło­
ścianu.

• Obliczenie objętości prosto­

padłościanu.

• Obliczenie pola powierzchni

prostopadłościanu.

5

V

11.2
10.7

10.15

\ 1 21/5 cm

m \

H

óV5 cm

6l/l5) =

/l5 ) [cm2]

mu równa jest
^15) cm2.

12 cm

4321/15 cm3

^ 6cir

8.

C

1

V

SP

9.

krawędzie: 8 cm; 80 - 2 ■

8 = 64 [cm]; 40 - 2 ■

8 = 24 [cm]

V = 24 • 64 ■

8

= 12 288 [cm3]

Odp.: Objętość kartonowego pudełka jest równa 12 288 cm3.

• Obliczenie długości krawę­

dzi prostopadłościanu.

• Obliczenie objętości prosto­

padłościanu.

2

III

11.2

2.4

10.

V = 12 ■ 25 • (21 - 1) = 6 000 [cm3] = 61

Odp.: W naczyniu zmieści się 6 litrów wody.

• Obliczenie objętości.
• Zamiana jednostek objętości.
• Obliczenie objętości prosto­

padłościanu z uwzględnie­
niem warunków zadania.

3

V

1

11.2’
11.3

1

127

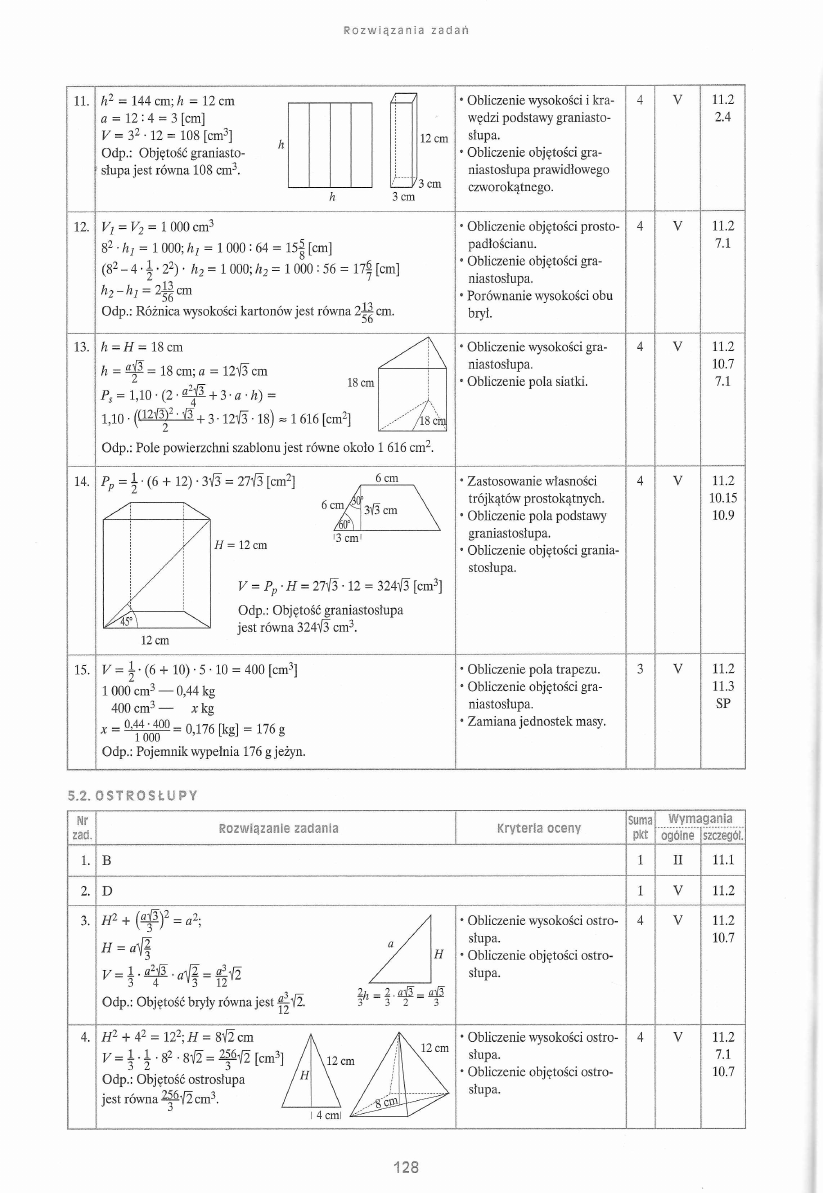
R o z w i ą z a n i a z a ci a ń

11.

h 2 = 144 cm; h = 12 cm
a = 12 : 4 = 3 [cm]

j/ = 32 • 12 = 108 [cm3]
Odp.: Objętość graniasto-
słupa jest równa 108 cm3.

/

7l

12 cm

'3 cm

3 cm

Obliczenie wysokości i kra­

wędzi podstawy graniasto-

siupa.

Obliczenie objętości gra-

niastoslupa prawidłowego
czworokątnego.

V

11.2

2.4

12

.

Vi = V2 = 1 000 cm3

82 • h j = 1 000; hj = 1 000 : 64 = 1 5 | [cm]

(82 - 4 • i • 22) • h2 = 1 000; h 2 = 1 000 : 56 = 17^ [cm]

h 2 - hq = 2 ^ | cm

Odp.: Różnica wysokości kartonów jest równa 2 ^ cm.

Obliczenie objętości prosto­

padłościanu.

Obliczenie objętości gra-

niastostupa.

Porównanie wysokości obu

brył.

V

11.2

7.1

13.

h = H = 18 cm

h =

= 18 cm; a = 12l/3 cm

Ps = l , 1 0 - ( 2 - ^ S + 3 -fl-/!) =

1,10 ■

((12^ )2' ^ + 3 • 121/3 • 18)

18 cm

1 616 [cm2]

Obliczenie wysokości gra-

niastoslupa.

Obliczenie pola siatki.

Odp.: Pole powierzchni szablonu jest równe około 1 616 cm2.

V

11.2

10.7

7.1

14. Pp = \ • (6 + 12) • 3Í3 = 271/3 [cm2]

6 cm

3Í3 cm

H = 12 cm

' 3

c m

1

12 cm

y = P p . H = 21{3 ■

12 = 3241/3 [cm3]

Odp.: Objętość graniastoslupa

jest równa 324{3 cm3.

1 Zastosowanie własności

trójkątów prostokątnych.

1 Obliczenie pola podstawy

graniastoslupa.

1 Obliczenie objętości grania-

stosłupa.

V

11.2

10.15

10.9

15.

V = i • (6 + 10) • 5 • 10 = 400 [cm3]

1 000 cm3 — 0,44 kg

400 cm3 —

x kg

X = 5f o T O ^ ° ’176[kg] =

176g

Odp.: Pojemnik wypełnia 176 g jeżyn.

1 Obliczenie pola trapezu.
1 Obliczenie objętości gra-

niastosłupa.

1 Zamiana jednostek masy.

V

11.2

11.3

SP

5,2. O S T R O S Ł l P Y

Nr

zad.

Rozwiązanie zadania

Kryteria oceny

Suma

pkt

Wy mi

ogóine

gania

SiCzegoi.

1.

B

1

II

11.1

2.

D

1

V

11.2

3.

H 2 +

= a 2;

/

H = a j |

a /

y — 1 . a2{3 . a- J I = s L f i

/

3

4

"3

12

z -------- ——

3 i—

27. _ 2 . a i3 —

Odp.: Objętość bryły równa jest

^ v 2 .

3

3

2

H

d 3

3

• Obliczenie wysokości ostro­

słupa.

• Obliczenie objętości ostro­

słupa.

4

V

11.2
10.7

4. H 2 + 42 = 122\ H =

8 V 2 c m

/

j / = 1 . 1 . 8 2 - 8i / 2 = ^ 6 V 2 [ c m 3]

/

Odp.: Objętość ostrosłupa

jest równa

22i>V2 c m 3.

/

\ 12 cm

/

\ /

4 cml

12 cm

• Obliczenie wysokości ostro­

słupa.

• Obliczenie objętości ostro­

słupa.

4

V

11.2

7.1

10.7

1 28

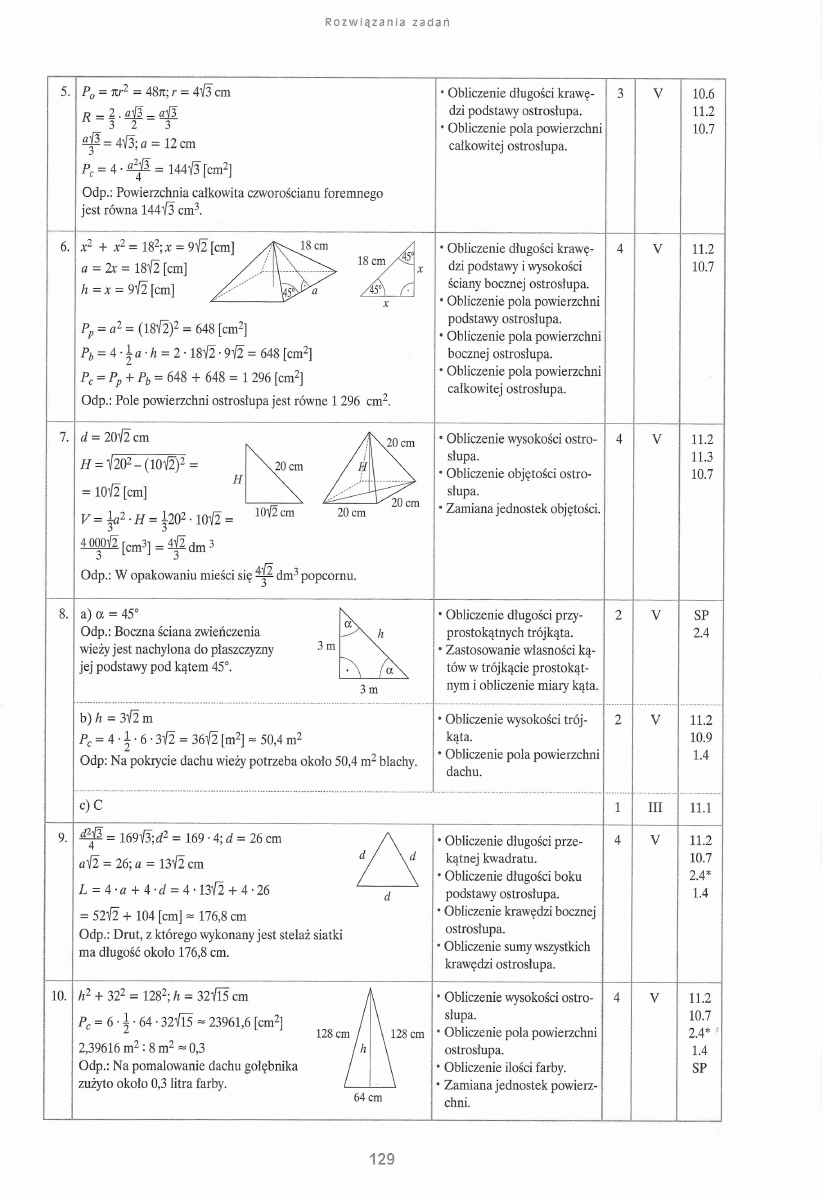
R o zw i ą z a n i a zadań

Pa = nr2 = 48ji; r = 4l/3 cm

d _ 2 . a f i _ a j_3

3

2

3

«£ = 4 1 /3 ; a = 12 cm

p c = 4 . ¿¡M = 144y3 fcm2]

Odp.: Powierzchnia całkowita czworościanu foremnego

jest równa 1441/3 cm3.

1 Obliczenie długości krawę

dzi podstawy ostrosłupa.

1 Obliczenie pola powierzchni

całkowitej ostrosłupa.

V

10.6

11.2

10.7

x 2 + x 2 = 182;jc = 9l/2 [cm]

a = 2x = I 81/2 [cm]

h = x = 9l/2 [cm]

Pp = a2 = (18i/2)2 = 648 [cm2]

p b = 4 • 1 « -/j = 2 • 18l/2 • 91/2 = 648 [cm2]

Pc = Pp + Pb = 648 + 648 = 1 296 [cm2]

Odp.: Pole powierzchni ostrosłupa jest równe 1 296 cm2.

1 Obliczenie długości krawę­

dzi podstawy i wysokości

ściany bocznej ostrosłupa.

Obliczenie pola powierzchni

podstawy ostrosłupa.

Obliczenie pola powierzchni
bocznej ostrosłupa.

Obliczenie pola powierzchni

całkowitej ostrosłupa.

V

11.2

10.7

d = 20V2 cm

20 cm

H = i2 0 2 - ( 1 0 i2 ) 2 =

= 10V2 [cm]

V = ^a2 -H = i-202 • IO1/2 =

4 0 f fli2 [cm3] = 4 i2 d m 3

Odp.: W opakowaniu mieści się ^

dm3 popcornu.

20 cm

1 Obliczenie wysokości ostro­

słupa.

Obliczenie objętości ostro­

słupa.

Zamiana jednostek objętości.

V

11.2

11.3

10.7

a) a = 45°

Odp.: Boczna ściana zwieńczenia

wieży jest nachylona do płaszczyzny

jej podstawy pod kątem 45°.

3 m

Obliczenie długości przy-

prostokątnych trójkąta.

Zastosowanie własności ką­

tów w trójkącie prostokąt­

nym i obliczenie miary kąta.

V

SP

2.4

b) h = 31/2 m

P c

= 4 • I • 6 • 31/2 = 36l/2 [m2] * 50,4 m2

Odp: Na pokrycie dachu wieży potrzeba około 50,4 m2 blachy.

Obliczenie wysokości trój­
kąta.

Obliczenie pola powierzchni

dachu.

c) C

V

III

11.2

10.9

1.4

11.1

= 169l/3;d2 = 169 • 4; d = 26 cm

a i l = 26; a = 13{2 cm

L = 4 -a + 4 - d = 4- 13l/2 + 4- 26

= 52i2 + 104 [cm] ~ 176,8 cm

Odp.: Drut, z którego wykonany jest stelaż

ma długość około 176,8 cm.

siatki

• Obliczenie długości prze­

kątnej kwadratu.

• Obliczenie długości boku

podstawy ostrosłupa.

• Obliczenie krawędzi bocznej

ostrosłupa.

• Obliczenie sumy wszystkich

krawędzi ostrosłupa.

11.2
10.7

2.4*

1.4

10

.

h2 + 322 = 1282; h = 32l/l5 cm

P c

= 6 • i • 64 • 32l/l5 = 23961,6 [cm2]

2,39616 m2 : 8 m2 = 0,3

Odp.: Na pomalowanie dachu gołębnika

zużyto około 0,3 litra farby.

128 cm

128 cm

64 cm

• Obliczenie wysokości ostro­

słupa.

• Obliczenie pola powierzchni

ostrosłupa.

• Obliczenie ilości farby.

• Zamiana jednostek powierz­

chni.

V

11.2

10.7

2.4*

1.4

SP

129

R o z wi ą z a n i a zadań

5 .3 . B R Y Ł Y O B R O T O W E

Nr

zad.

Ro zw iązanie zadania

K ry te ria oceny

Suma

pkt

Wymagania

ogólne szczegół.

1.

B

1

III

11.2

2.

V = nr2 ■

H = TC ■

62 • 20 = 720tc = 2 260,8 [cm3]

Odp.: Objętość powstałej bryiy

jest równa około 2 260,8 cm3.

„

1

H = 20 cm

r = 6 cm

H

r '■

• Obliczenie objętości walca.

2

IV

11.2

2.4*

1.4

3.

Pb = 2nr ■

H = 2 • 4 • tc • 12 = 9Ó7c = 301,44 [cm2]

Odp.: Pole powierzchni bocznej bryły

jest równe około 301,44 cm2.

H = 12 cm
r = 4 cm

H

r

• Obliczenie pola powierzchni

bocznej walca.

2

IV

11.2

2.4*

1.4

4.

2jcr • H = 20tc • 5; r = 10 cm

K = OT-2 ■

H = it ■

102 ■

5 = 500tc = 1 570 [cm3] =

1,57 dm3 = 1,571

Odp.: Pojemność puszki jest równa około 1,57 litra.

• Obliczenie promienia koła.

• Obliczenie objętości walca.
• Zamiana jednostek objętości.

4

V

11.2
11.3

7.1

1.4

5.

B

1

IV

11.2

6.

0,51 = 0,5 dm3 = 500 cm3

nr2 ■

h = 500; h =

= 0,71 [cm] ~ 0,7 cm

Odp.: Grubość warstwy oleju, który pokrył wodę w naczyniu

jest równa około 0,7 cm.

•

Zamiana jednostek objętości.

• Obliczenie wysokości walca.

3

V

11.2

11.3

7.1

1.4

7.

154 cm

=

n

■

2tc

■

3,5; n

=

7;

7

•

14 cm

=

98 cm; 2mp

~

98; rp

=

4 ^ [cm]; dp

=

^

[cm]

V = Ter2 ■

H ~

1

■

( ^ ) 2 •

= 5 764|01 „ 2 3 821 [cm3]

Odp.: Pojemność pojemnika jest równa około 23 821 cm3.

• Ustalenie sposobu oblicze­

nia długości promienia pod­
stawy i wysokości walca.

• Obliczenie liczby półokręgów.

•

Obliczenie objętości walca.

3

V

11.2

2.4*

10.5

7.1

1.4

8.

C

1

IV

11.2

9.

A

1

IV

11.2

10.

(200

+

500)

:

2

=

350 [kg]; (120

+

180)

:

2

=

1,50 [m], r

=

0,75 m

F =Tt - 0 , 7 5 2 - 1,2

=

2,1195 [m3]

2,1195 m3 — 350 kg

x

m3

—

1 000 kg

x = 6,0557...

~

6 [m3]

Odp.: Objętość 1 tony sprasowanej w bele słomy jest równa

około 6 m3.

•

Obliczenie powierzchni koła.

•

Obliczenie średniej arytme­

tycznej.

•

Obliczenie objętości według

warunków określonych
w zadaniu.

5

V

11.2

9.4

2.4*

7.1

1.4

11.

V =

2,1195 [m3]

950

:

2,1195

=

448; 448

:

50

=

8,96

=

9

[h]

Odp.: Aby sprasować objętość słomy równą 950 m3,
prasa musi pracować przez około 9 godzin.

•

Obliczenie czasu i zaokrą­

glenie wyniku.

2

V

11.2

1.4

12.

objętość beli:

V =

7t

•

0,62

•

1,2

~

1,35648 [m3]

masa beli: 200 kg; liczba bel: 5 600

:

200

=

28

objętość stodoły zajęta przez bele: 28

■

1,35648

=

37,98144 [m3]

objętość stodoły: V

=

8

■

1,6

•

4,5

=

576 [m3]

(37,98144

:

576)

■

100%

=

6,6%

Odp.: Bele słomy zajmują 6,6% kubatury stodoły.

•

Obliczenie objętości walca.

•

Obliczenie objętości prosto­

padłościanu.

•

Obliczenie, jaki procent

jednej liczby stanowi druga

liczba.

5

V

11.2

5.1

2.4*

1.4

13.

D

1

III

11.2

14.

D

1

III

11.2

130

R o zw i ą za n i a zadań

15.

H 2 + 22 = 82;H = 2Vl5 cm

K = l - 7 i - r 2 - / / = i - j f 4 - 2 f i 5 = | 7iVl5 [cm3]

/

Odp.: Objętość bryły jest równa

/

| j i i l 5 cm3.

/ __

\ 8 cm

• Obliczenie długości stożka.
• Obliczenie objętości stożka.

4

V

11.2

10.7

16. Pa = 16{3 cm;

= 16i/3; a = 8 cm, o = Z,

P = 7trZ + 7tr2 = 7t • 4 • 8 + 7t • 42 = 4871 “ 150,72 [cm2]

Odp.: Pole powierzchni powstałej bryły jest równe 150,72 cm2.

• Obliczenie długości boku

trójkąta.

• Obliczenie pola powierzchni

stożka.

5

V

11.2
11.3

7.4

10.7

17.

Kri

+

n r

2

= 48tc;

r

= 4 cm; Z = 8 cm; / i = 4i/3 cm

/

F = i - 7 t - ? ' 2 - / / = i ' 7 t ' 1 6 - 4l/3 =

2r z'

= y jili3 [cm3]

//

Odp.: Objętość stożka jest

zWYr

równa y-7tV3 cm3.

-------

r { 3 \

• Obliczenie długości promie­

nia podstawy, tworzącej
i wysokości stożka.

• Obliczenie objętości stożka.

5

V

11.2
11.3

7.4

18.

7tr2 = 25tc; r = 5 cm; Z = 10 cm

/ '

p b = Krl = 507t [cm2]

10 cm

Odp.: Pole powierzchni bocznej stożka

/

jest równe 50

tc

cm2.

.........

5 cm

5{3ćm

• Obliczenie długości promie­

nia podstawy i wysokości

stożka.

• Obliczenie pola powierzchni

bocznej stożka.

5

V

11.2

7.4

10,15

19.

im . .

_

oc

• Obliczenie długości promie­

nia podstawy i wysokości

stożka.

• Obliczenie objętości stożka.
• Zaokrąglenie wyniku.

6

V

11.2
10.9

7.4

10.7

1.5

^ a u = ¿nr; r = ^ cm

i

V^50>¥

h 2 + (22)2 = 152; h = |V li9 cm

V

V = ^ - n ■ r2 ■ h = j - n ■

(25)2 • |VTl9 =

3 I25?! ~ 51 [cm3]

/

15 cm /

Odp.: Objętość rożka jest równa

/

około 51 cm3.

/-r~ "

h \

20. |t i R 3= 27 • | 7tr3; P 3 = 27 • 23;P = 6 cm

47tR2 _ 62 _ n

471T2

22

Odp.: Powierzchnia kuli jest 9 razy większa niż powierzchnia

jednej z kulek, z których powstała.

• Obliczenie promienia dużej

kuli.

• Obliczenie stosunku pól kul.

5

V

11.2

2.4
4.1

21. C

1

III

11.2

22. poziom wody przed wrzuceniem kulki:

^

i

55 = 22 [cm]

różnica poziomów przed i po wrzucę-

55 cm

niu kulki: 25,14-22 = 3,14 [cm]

V = 16-20-3, 14 = 1 004,8 [cm3]

| j t r 3= 1 004,8; r3 - 240; r - 2l/30 cm

3,—

16 cm

Odp.: Promień kulki jest równy 21/30 cm.

2t

22 cm

cm

• Obliczenie wysokości słupa

wody przed wrzuceniem

kulki.

• Obliczenie, 0 ile podniósł się

poziom wody po wrzuceniu
kulki.

• Obliczenie objętości wody

wypartej przez kulkę.

• Obliczenie promienia kuli.

6

V

11.2

2.4*

4.1

23.

r = 0,4 cm; | Ttr3 = | n ■

0,43 == 0,27 [cm3]

1,11 = 1100 cm3; 1100 cm3 : 0,27 cm3 = 4 074

Odp.: Litr wody powstanie po roztopieniu około 4 074 kulek.

• Obliczenie promienia kuli.
• Obliczenie objętości kuli.
• Obliczenie liczby według

warunków zadania.

• Zamiana jednostek objętości.

4

V

11.2
11.3

2.4*

24.

r = i h = 1 ^

= a l i - a i I = 2;a = 4l/3 [cm] = 7 cm

Odp.: Minimalna długość krawędzi podstawy pudełeczka

jest równa około 7 cm.

• Obliczenie promienia piłki.
• Obliczenie długości boku

trójkąta równobocznego
opisanego na okręgu.

4

V

10,7

2.4*

131

Rozwiązania zadań

6. h A K A D Y

E M P- ' - i 5 E N I IM C P R E I

E C Z A IV1!

N E M

6.1. P S Z C Z O Ł Y i MI ÓD

Nr

zad.

Rozwiązanie zadania

Kryteria oceny

Suma

pKt

Wymagania

ogólne szczegół.

1.

B

1

II

1.7

2.

D

1

II

5.2

3.

Kolejno: 8; 2,1; pierwszej, 120; 1 050; 60; 750; 400.

• Odczytanie danych z wykre­

su i uzupełnienie zdań.

3

I

8.4

4.

0,9 km

: 1 min = 0,9 km : ¿ r h = 54 ^

60

h

Odp.: W czasie pierwszej minuty lotu pszczoła oddalała się
od ula z prędkością 54 t a

• Odczytanie danych z wykre­

su i zamiana jednostek czasu.

• Obliczenie prędkości.

2

III

8.4
1.7

5.

B

1

V

8.4

6.

C

1

II

1.2

7.

(500 g • 70% ): 100% = 350 g; 500 g - 350 g = 150 g
350 g : 3,5 = 100 g

150 g + 100 g = 250 g

Odp.: Masa miodu, która powstaje z 500 g nektaru,

jest równa 250 g.

• Obliczenie procentu danej

liczby.

2

V

5.2
5.4
2.4

8.

C

1

II

10.17

9.

(la )1 = a2 + x2; x = a i 3
Odp.: Wektor ma długość równą a{3.

• Obliczenie długości

odcinka.

1

IV

10.7

10.

0,04 ha = 4 000 000 cm2

4 000 000 cm2 : 5 0002 = 0,16 cm2
Odp.: Na planie w skali 1:5 000 pasieka zajmuje 0,16 cm2.

• Zamiana jednostek po­

wierzchni.

• Obliczenie powierzchni

w skali.

2

III

10.11
10.12

11.

a) 720 cm3 — 100 dag

1 000 cm3 — x

x = 138,88... dag = 1,3888... kg = 1,39 kg

Odp.: Litr miodu ma masę około 1,39 kg.

• Obliczenie masy według

warunków zadania.

• Zam iana jednostek masy

i przybliżenie.

2

II

1.7
SP
1.4

b ) C

1

II

1.7

12.

D

1

II

10.7

13.

A

1

II

10.5

14.

Z2 = H 2 + r2 = 602 + 802 = 100 cm

z ''

p b

= %rl * 3,14 • 80 • 100 =

H

= 25 120 [cm2] = 2,512 m2

/ /

\

H =

60 cm

X . /

/ = ioo cm

\ r = 80 cm

• Zastosowanie twierdzenia

Pitagorasa.

• Obliczenie pola powierzchni

stożka i zamiana jednostek
powierzchni.

1

IV

10.7
11.2

Odp.: Pole powierzchni daszku

r

to w przybliżeniu 2,512 m2.

15.

V = nr2H =

7t(50 - 1)2 • 100 = 0,75 [m3]

Odp.: Objętość wewnętrznej części ula równa jest
około 0,75 m3.

• Obliczenie objętości walca

z uwzględnieniem warun­

ków określonych w zadaniu.

1

IV

11.2

16.

C

1

IV

7.4

17.

Jeśli n

jest liczbą parzystą, to w rzędzie o numerze n

będzie n

słoików z miodem gryczanym i n - 1 słoików

z miodem lipowym.

• Zbudowanie modelu mate­

matycznego zilustrowanej

sytuacji.

1

V

6.1

152

R o zw i ą za n i a zadań

18.

a) Przykłady odpowiedzi:

Z upływem lat jest coraz więcej starszych pszczelarzy, a coraz

mniej młodych.

b) I - T A K , I I - T A K , I I I - N IE , I V - T A K

’ Analiza diagramu i zapisa­

nie wniosku.

I I

9.1

19.

a)

0,8

: 0,7

0,6

0,5

0,4

i 0,3 -

0,2

0,1 H

0,0

Spożycie miodu w Polsce
w latach 2001-2007

2001 2002 2003 2004 2005 2006 2007 rok

' Sporządzenie diagramu

słupkowego na podstawie
danych podanych w tabeli.

9.3

b) 38,1

min

• 0,63 kg = 24 003 000 kg = 24 003 t

(22 0001 : 24 003 t) • 100% = 92%

Odp.: Produkcja miodu w naszym kraju w 2006 roku zaspokoiła

spożycie miodu przez Polaków w około 92%.

■

Odczytanie danych z tabeli

i wykonanie obliczeń zgod­

nie z warunkami zadania.

■

Zamiana jednostek masy.

1 Zastosowanie obliczeń

procentowych w praktyce.

I I

6.1

SP

5.4

6.2. W P O D R Ó Ż Y

Nr

zad.

Rozwiązanie

zadania

K ry te ria oceny

Suma

pkt

Wyrm

ogólne

igania

szczegół.

1.

A

1

I I

3.3

2.

3 500 = 0,01%

jc

;

x

= 35 000 000;

0,48 • 35 000 000 = 16 800 000

Odp.: Polaków w wieku 15 lat i więcej w 2008 roku było 35 min,
z czego 16,8 min wyjeżdżało w celach turystycznych.

• Odczytanie danych z wy­

kresu i wykonanie obliczeń

zgodnie z warunkami zada­

nia.

• Obliczenie procentu danej

liczby.

4

I I I

9.2

5.2

7.1

1.5

3.

Porć
1 nie

60%

50%

40%

30%

20%

10%

0

>wnar
wyje;

iie

dż£

iczby o<

ijących

□

ób w wiek

w celach tu

-wyjeżdżając

li

15 lat

i w

rystycznyc

y

8 - nie

Ięcej wyjeżdżających

h

wyjeżdżający

* Sporządzenie diagramu

słupkowego na podstawie

danych podanych w tabeli.

1

I

9.3

2000

2005

2007

2008

4.

Przykład odpowiedzi: Liczba wyjazdów turystycznych w stosunku
do 2000 roku spadła, przy czym znacznie obniżyła się liczba osób

wypoczywających w kraju, ale zanotowano wzrost liczby osób wy­

bierających wypoczynek za granicą.

• Analiza danych zapisanych

w tabeli i z własnoręcznie

wykonanego diagramu oraz

sformułowanie wniosków.

2

I

9.1

133

Rozwiązania zadań

5.

C

1

II

5.2

6.

liczba pokoi: czteroosobowych -x , trzyosobowych - x,
dwuosobowych -v , jednoosobowych - y

¡2x + 2 y = 158
[4x + 3x + 2y + y = 329

x = 23; y = 56

Odp.: Pokoi dwu- i jednoosobowych jest po 56, a cztero-
i trzyosobowych po 23.

• Zapisanie zależności między

wielkościami według warun­

ków określonych w zadaniu.

• Ułożenie układu równań.
• Rozwiązanie układu

równań.

3

IV

7.4

7.5

7.

cena noclegu w pokoju:

jednoosobowym: 150 zł

dwuosobowym: 150 zł - 30 zł = 120 zł

trzyosobowym: 75% • 150 zł = 112,50 zł
czteroosobowym: | ■

120 zł = 80 zł

Odp.: Koszt noclegu jednej osoby w pokojach jedno-, dwu-,

trzy- i czteroosobowym równy jest kolejno: 150 zł, 120 zł,

112,50 zł oraz 80 zł.

• Obliczenie procentu danej

liczby.

• Obliczenie ułamka danej

liczby.

• Obliczenie kosztów według

warunków określonych
w zadaniu.

3

IV

SP
1.5
1.2

5.2

8.

B

1

II

SP

9. x - liczba osób zakwaterowanych w pokojach dwuosobowych

y - liczba osób zakwaterowanych w pokojach jednoosobowych

i x + y = 69

[2 849x + 3 lOly = 199 857

y = 13; x = 56

Odp.: W pokojach jednoosobowych zakwaterowano 13 uczest­

ników wycieczki.

• Ułożenie układu równań.

• Rozwiązanie układu równań.

2

IV

7.4
7.5

10.

C

1

II

9.1

11.

4§ = ~jy;x = 694,4 m

Odp.: Samolot po 46 sekundach

A

• Zastosowanie podobieństwa

trójkątów.

• Obliczenie długości boku

trójkąta.

3

IV

10.13

7.1
7.2

kości 694,4 m.

|

48

1

12.

C

1

II

7.5

13.

4,6 cm • 30 000 000 cm = 138 000 000 cm = 1 380 km =

308 węzłów = 570,416 t a

1 380 : 570,416 * 2,42 [h] = 2 h 24 min
1955 + 2 h 24 min = 2219

Odp.: Samolot wylądował w Paryżu około godziny 22.19.

• Przeliczenie jednostek dłu­

gości.

• Obliczenie długości odcinka

na podstawie skali.

• Obliczenie czasu według

warunków zadania.

4

IV

1.7
SP

14.

3 045,6 : 4,05 = 752 [euro]

x - liczba osób dorosłych, y - liczba dzieci

fy = 3x

[53x + 45- y = 752

x = 4-y = l2

Odp.: Na wycieczkę wybrało się 12 dzieci i 4 osoby dorosłe.

• Zamiana jednostek mone­

tarnych.

• Ułożenie układu równań.
• Rozwiązanie układu równań.

3

IV

SP

7.4

7.6

15.

ix ■

3x • & = 81; 24x3 = 81; x = 1,5 [dm]

1,5 dm x 4,5 dm x 12 dm -w ym iary walizki

Odp.: Obraz zmieści się do walizki.

• Ułożenie równania.
• Rozwiązanie układu równań.
• Obliczenie objętości prosto­

padłościanu.

4

IV

V

7.3

11.2

4.1

16.

skala: 1:50 000; odległość: 2,4 cm

x

różnica wysokości: 500 m

500 m

9 4 ■

^0 0^0 —

000 cm - 1 ^>0^ m

• Zastosowanie twierdzenia

Pitagorasa.

• Obliczenie odległości według

warunków zadania.

2

IV

10.7

SP

x2 = 1 2002 + 5002; x = 1 300 [m]

1 200 m

Odp.: Turyści pokonali 1 300 m.

1 3 4

Rozwiązania zadań

6.3. F E S T Y N

Nr

zad.

Rozwiązanie zadania

Kryteria oceny

Suma

pkt

Wym

ogólne

agania

szczegół.

1.

D

1

II

SP

2.

D

1

II

SP

3.

=

ioo

-4 -

n

mm

0,6 cm

= 600 m; 600 m : 100 - S - = 6 min

mm

Odp.: Droga ze stoiska gastronomicznego do punktu medycz­

nego zajęła gościowi festynu 6 minut.

• Zamiana jednostek pręd­

kości.

• Zastosowanie obliczeń na

liczbach wymiernych.

3

II

1.7

4.

Odp.: Kąt między drugim i trzecim odcinkiem trasy biegu
ma miarę 59°.

• Wykorzystanie związków

między kątami utworzonymi
przez prostą przecinającą

dwie proste równoległe.

1

II

10.1

5.

D

1

II

5.2

6.

24 min

=

h

s [km]

1,1

60

i

6-

6 k m : i h

= 1 5 t a

5n

60

h

4 .

Odp.: Zawodnik biegł ze średnią

3.

prędkością 15

2

0-

V

—

>

6 12 18 241 Imin]

• Przedstawienie zależności

drogi od czasu za pomocą

wykresu.

• Zamiana jednostek prędkości.
• Obliczenie prędkości.

3

IV

8.1

1.7

2.3

7.

110 mm

=

11 cm; 370 mm

=

37 cm; 140 mm

=

14 cm

V =

11

•

37

•

14= 5 698 [cm3]

12

•

5 698 cm3

=

68 376 cm3

=

68,41

Odp.: Owoce przygotowane na festyn mają objętość
równą 68,4 1.

• Zamiana jednostek długości.

•

Obliczenie objętości prosto­

padłościanu.

• Obliczenie objętości według

warunków zadania.

3

IV

I.7

II.2

8.

11 = 1 000 cm3

3,3

•

1 000

:

5 698

=

0,5791...

=

0,579 kg

Odp.: Litr jagód ma masę 0,579 kg.

• Zamiana jednostek objętości.
• Obliczenie masy i zaokrągle­

nie wyniku.

2

IV

1.7
1.5
1.4

9.

a) r : 12 = 150°: 360°; r = 5 [cm]

H 2 = r2 + 122; H = VTl9 [cm]

V = 1 ■

n ■

r2 • H = 1 • n ■

52 • iU 9 * 285,216 [cm3] = 0,29 1

Odp.: Objętość rożka na jagody równa jest 0,291.

• Obliczenie objętości stożka.
• Zaokrąglenie rozwinięcia

dziesiętnego liczby.

2

IV

11.2

1.4

b) 68,4 1: 0,29 1 - 235

Odp.: Harcerze przygotowali 235 rożków z jagodami.

• Zastosowanie obliczeń na

liczbach wymiernych.

• Zaokrąglenie rozwinięcia

dziesiętnego liczb.

2

IV

1.7
1.4

10.

0,12 • 4,50 = 0,54 [zł]; 4,50 - 0,54 = 3,96 [zł]
3,96 • 235 = 930,60 [zł]

Odp.: Harcerze na sprzedaży rożków z jagodami

zarobili 930 zł 60 gr.

• Obliczenie procentu danej

liczby.

• Zastosowanie obliczeń na

liczbach wymiernych.

2

IV

5.2

1.7

11.

a) 5 • 4 : 2 = 10
Odp.: Odbędzie się 10 meczów.

• Obliczenie liczby rozegra­

nych meczów.

1

III

9.5

b) 10 • 2 • 15 + 10 • 5 + 9 • 5 = 395 min = 6 h 35 min

905 + 6 godz. 35 min = 1540
Odp.: Rozgrywki zakończyły się o godzinie 15.40.

• Obliczenie czasu i godziny

według warunków określo­

nych w zadaniu.

2

IV

1.7

ę

12.

AABO ~ AOCD w skali k = 6 m •’ 6 cm = 100

x = 12 cm ■ 100 = 1 200 cm = 12 m

Odp.: A parat umieszczono w odległości 12 m od sceny.

• Obliczenie skali podobień­

stwa trójkątów.

• Obliczenie odległości.

3

III

IV

10.13
10.11

2.4

135

R o z w i ą za n i a zadań

6 .4 . M A T E M A T Y K A OD K U C H N I

Nr

zad.

R o zw iązanie zadania

K ryteria oceny

Suma

pkt

Wymagania

ogólne szczegół.

1.

i

Np.: 6 jaj; 1 szklanka i 13 łyżek mąki; 1 szklanka i 4 łyżki cukru

pudru; i łyżeczki proszku do pieczenia; 7 łyżeczek masła

• Przeliczenie jednostek masy

na niestandardowe.

2

II

1.2

2.

B

1

II

1.7

3.

C

1

II

5.3

4.

D

1

II

1.2

5.

a) C

1

II

5.4

b) 27 000 mg = 27 g

6 - 2 7 : 9 0 = 1,8 = 2

Odp.: Do przygotowania sześciu porcji spaghetti należy kupić
dwa słoiki sosu.

• Obliczenie liczby na podsta­

wie danego jej procentu.

• Zaokrąglenie rozwinięcia

dziesiętnego liczby.

2

IV

1.2
1.4

6. x - liczba placków zjedzonych przez Anię

1,2* + x + • \,2x + 3x = 42; x = 5

1,2 • 5 = 6; | • 1,2 • 5 = 16; 3 • 5 = 15

Odp.: Adam zjadł 6 placków, Ania - 5, Wojtek -1 6 ,
a Staszek -1 5 .

• Ułożenie równania.
• Rozwiązanie równania.

• Obliczenie pozostałych

szukanych danych.

3

IV

1.2

7.1
7.3

7.

liczba porcji pierogów: ruskich - x , z jagodam i- y

fx + y = 16

124x + 2Dy = 348

x = 1-y = 9

Odp.: Pani Lepińska przygotowała 9 porcji pierogów z jagodami.

• Ułożenie układu dwóch

równań.

• Rozwiązanie układu

równań.

2

IV

7.4

7.6

8.

0,12 • 2 • 14,5 = 3,48 g
Odp.: Dwie łyżki 12-procentowej śmietany zawierają

3,48 g tłuszczu.

• Obliczenie procentu danej

liczby.

2

IV

5.2

1.2

9.

1 1 = 375 cm3

390 g : 375 cm3 = 1,04 -Ł j

cm

Odp.: Śmietana ma gęstość równą 1,04

• Zamiana jednostek masy.
• Obliczenie gęstości.

2

IV

11.3

1.2

10.

A

1

V

9.5

11.

0,8 : 0,1 • 0,5 • 48 = 192 [mg]

Odp.: Surówka z kapusty zawiera o 192 mg więcej witaminy C

niż taka sama ilość kapusty po gotowaniu przez 4 minuty.

• Obliczenie procentu danej

liczby.

• Zastosowanie obliczeń

na liczbach wymiernych.

2

III

IV

5.2

1.2

12.

12,71 + 24,11 = 36,82 [zł]; 13,79 + 24,09 = 37,88 [zl]

(37,88 - 36,82): 36,82 ■

100% = 2,88% = 3%

Odp.: Wydatki na owoce i warzywa wzrosły o około 3%.

• Odczytanie danych z tabeli

i obliczenie kosztów według

warunków zadania.

• Obliczenie, jakim procentem

jednej liczby jest druga liczba.

• Zaokrąglenie rozwinięcia

dziesiętnego liczby.

3

III

1.2

5.1

1.4

b) B

1

II

5.1

13. x2 = 132 - 122;x = 5 cm; h = 13 - 5 = 8 [cm]

V = 0,5tc • 122 • 8 + ±ti83 = 2 076,59 = 2 077 [cm3]

Odp.: Miseczka ma objętość równą 2 077 cm3.

• Obliczenie objętości czaszy.
• Zaokrąglenie rozwinięcia

dziesiętnego liczby.

2

II

11.2

1.4

136

R o z w i ą za n i a zadań

14.

C

1

IV

10.7

15.

(0,25 • 20)2 + (0,25 ■

20)2 = x2

x = 5{2

cm

Odp.: Linia, wzdłuż której przecięto ser, ma długość
równą 5f2 cm.

• Zastosowanie twierdzenia

Pitagorasa.

• Obliczenie długości odcinka.

2

IV

10.7

1.2

16.

1 ■ 203 = 4 000 [cm3] - objętość połowy sera

• 4 000 = 250 [cm3] - objętość kawałka sera n a koreczki

4 0 0 0 -2 5 0 = 3 750 [cm3]

Odp.: Objętość pozostałej części sera jest równa 3 750 cm3.

• Obliczenie objętości gra-

niastosłupa.

2

IV

11.2

1.2

17.

V = 250: 20 = 12,5 [cm3]

Odp.: Jeden koreczek ma 12,5 cm3 objętości.

• Obliczenie objętości gra-

niastosłupa.

2

IV

11.2

1.2

18.

360°: 10 = 36°
(180° - 36°): 2 = 72°; 2 • 72° = 144°

±oc = 0,5 • 144° - 45°= 72° - 45° = 27°

a = 2 • 27° = 54°

Odp.: Kąt między dwoma koreczkami ma 54°.

• Obliczenie miary kąta środ­

kowego dziesięciokąta.

* Obliczenie miary kąta dzie­

sięciokąta.

3

III
IV

1.2

5.1

1.4

10.4

6.5.

Z P A P I E R U

Nr

Rozwiązanie zadania

Kryteria oceny

Suma

Wymagania

zad.

pkt

ogólne szczegół.

1.

a) B

1

III

SP

b) C

1

II

SP

2.

a) 210 mm • 297 mm • 90 Ą ; = 5,6133 g

m2

500 • 5,6133 g = 2 806,65 g = 2,8 kg

Odp.: Ryza papieru form atu 210 mm x 297 mm

o gram aturze 90 ^ m a m asę równą 2,8 kg.

• Zamiana jednostek długości.
• Obliczenie masy według

warunków określonych
w zadaniu.

2

V

1.7
1.2

b) B

1

III

1.2

r \

24,8

lb _

24.8

-

0.454

S

>

ryza

500-0,21-0,297

m2

Odp.: G ram atura papieru to około 361 Ą^.

• Przeliczenie jednostek grama­

tury papieru według warun­

ków określonych w zadaniu.

• Zaokrąglenie wyniku.

2

V

1.7
1.4

3.

(3 005 tys. t

: 383 603 tys. ton) • 100% = 0,783% * 0,8% = 8%o

Odp.: Papier wyprodukowany w Polsce w 2007 roku stanowił
8%o

światowej produkcji papieru w tymże roku.

• Obliczenie, jakim procentem

jednej liczby jest druga liczba.

• Zaokrąglenie rozwinięcia

dziesiętnego liczby.

2

III

5.2

1.4

4.

B

1

III

10.7

5.

B

1

IV

10.9

6.

A

1

IV

10.7

7.

D

1

IV

10.9

8.

4 - i a + 2 - ^ = 2 a + a i 2

Odp.: Obwód sześciokąta jest równy 2a

+ a f l .

• Obliczenie obwodu sześcio­

kąta.

• Zastosowanie działań na

wyrażeniach algebraicznych.

3

IV

10.9

6.3

6.5

1 3 7

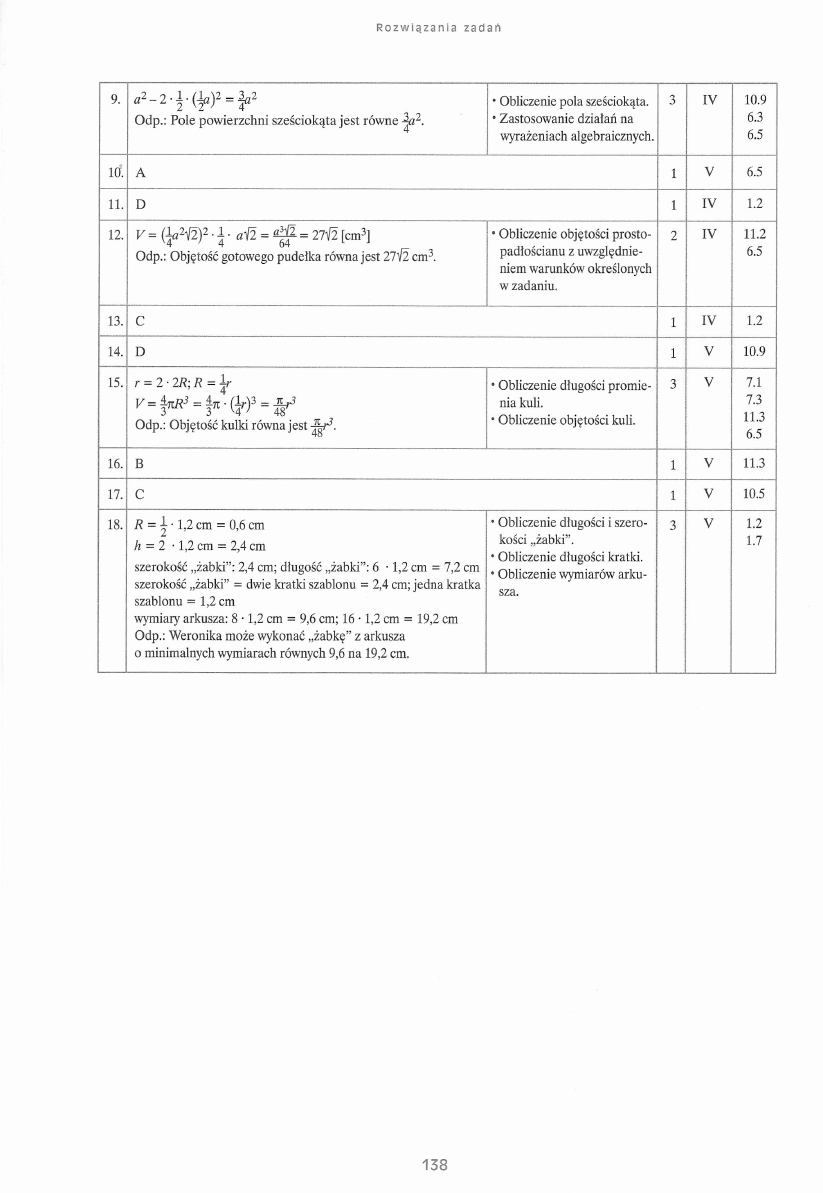
R o zw i ą za n i a zadań

9.

a2 - 2 - l - ( j a ) 2 = f e 2

Odp.: Pole powierzchni sześciokąta jest równe -2a2.

• Obliczenie pola sześciokąta.
• Zastosowanie działań na

wyrażeniach algebraicznych.

3

IV

10.9

6.3

6.5

id1. A

1

V

6.5

11. D

1

IV

1.2

12.

V = (ifl2V2)2 • 1 • a{2 = 3^2- = 21 f i [cm3]

Odp.: Objętość gotowego pudełka równa jest 21 f i cm3.

• Obliczenie objętości prosto­

padłościanu z uwzględnie­
niem warunków określonych

w zadaniu.

2

IV

11.2

6.5

13.

C

1

IV

1.2

14.

D

1

V

10.9

15.

r = 2 • 2R; R = ±r

V = \ n R 3 =

= ^

Odp.: Objętość kulki równa jest jg 3 .

• Obliczenie długości promie­

nia kuli.

• Obliczenie objętości kuli.

3

V

7.1
7.3

11.3

6.5

16.

B

1

V

11.3

17.

C

1

V

10.5

18.

R = 1 • 1,2 cm = 0,6 cm

h = 2 • 1,2 cm = 2,4 cm

szerokość „żabki”: 2,4 cm; długość „żabki”: 6 • 1,2 cm = 7,2 cm
szerokość „żabki” = dwie kratki szablonu = 2,4 cm; jedna kratka
szablonu = 1,2 cm

wymiary arkusza: 8 • 1,2 cm = 9,6 cm; 16 • 1,2 cm = 19,2 cm

Odp.: Weronika może wykonać „żabkę” z arkusza
o minimalnych wymiarach równych 9,6 na 19,2 cm.

• Obliczenie długości i szero­

kości „żabki”.

• Obliczenie długości kratki.
• Obliczenie wymiarów arku­

sza.

3

V

1.2
1.7

138

W Y M A G A N I A OG ÓL N E I

S Z C Z E G Ó Ł O W E

Z MA T E MA T Y K I

Z A WA R T E W P OD S T A WI E P R O G R A M O W E J K S Z T A Ł C E N I A

O G Ó L N E G O DL A G I M N A Z J U M

Cele kształcenia - wymagania ogólne

I. Wykorzystanie i tworzenie informacji.

Uczeń interpretuje i tworzy teksty o charakterze mate­

matycznym, używa języka matematycznego do opisu
rozumowania i uzyskanych wyników.

II. Wykorzystywanie i interpretowanie reprezentacji.

Uczeń używa prostych, dobrze znanych obiektów

matematycznych, interpretuje pojęcia matematyczne

i operuje obiektami matematycznymi.

III. Modelowanie matematyczne.

Uczeń dobiera model matematyczny do prostej sytuacji,

buduje model matematyczny danej sytuacji.

IV. Użycie i tworzenie strategii.

Uczeń stosuje strategię jasno wynikającą z treści zada­

nia, tworzy strategię rozwiązania problemu.

V. Rozumowanie i argumentacja.

Uczeń prowadzi proste rozumowania, podaje argumen­

ty uzasadniające poprawność rozumowania.

Treści nauczania - wymagania szczegółowe

1. Liczby wymierne dodatnie. Uczeń:

1) odczytuje i zapisuje liczby naturalne dodatnie

w systemie rzymskim (w zakresie do 3000);

2) dodaje, odejmuje, mnoży i dzieli liczby wymierne

zapisane w postaci ułamków zwykłych lub roz­

winięć dziesiętnych skończonych zgodnie z własną

strategią obliczeń (także z wykorzystaniem kalku­
latora);

3) zamienia ułamki zwykłe na ułamki dziesiętne

(także okresowe), zamienia ułamki dziesiętne

skończone na ułamki zwykłe;

4) zaokrągla rozwinięcia dziesiętne liczb;

5) oblicza wartości nieskomplikowanych wyrażeń

arytmetycznych zawierających ułam ki zwykłe
i dziesiętne;

6) szacuje wartości wyrażeń aiytmetycznych;

7) stosuje obliczenia na liczbach wymiernych do roz­

wiązywania problemów w kontekście praktycz­
nym, w tym do zamiany jednostek (jednostek

prędkości, gęstości itp.).

2. Liczby wymierne (dodatnie i niedodatnie). Uczeń:

1) inteipretuje liczby wymierne na osi liczbowej,

oblicza odległość między dwiema liczbami na osi
liczbowej;

2) wskazuje na osi liczbowej zbiór liczb spełnia­

jących warunek typu: x ^ 3 , x<5;

3) dodaje, odejmuje, mnoży i dzieli liczby wymierne;

4) oblicza wartości nieskomplikowanych wyrażeń

aiytmetycznych zawierających liczby wymierne.

3. Potęgi. Uczeń:

1) oblicza potęgi liczb wymiernych o wykładnikach

naturalnych;

2) zapisuje w postaci jednej potęgi: iloczyny i ilorazy

potęg o takich samych podstawach, iloczyny i ilo­

razy potęg o takich samych wykładnikach oraz

potęgę potęgi (przy wykładnikach naturalnych);

3) porównuje potęgi o różnych wykładnikach natu­

ralnych i takich samych podstawach oraz

porównuje potęgi o takich samych wykładnikach

naturalnych i różnych dodatnich podstawach;

4) zamienia potęgi o wykładnikach całkowitych

ujemnych na odpowiednie potęgi o wykładnikach

naturalnych;

5) zapisuje liczby w notacji wykładniczej, tzn. w p o ­

staci a ■

10^, gdzie l ^ a < 1 0 oraz k jest liczbą

całkowitą.

4

.

Pierwiastki. Uczeń:

1) oblicza wartości pierwiastków drugiego i trzeciego

stopnia z liczb, które są odpowiednio kwadratami
lub sześcianami liczb wymiernych;

2) wyłącza czynnik przed znak pierwiastka oraz włą­

cza czynnik p o d znak pierwiastka;

3) mnoży i dzieli pierwiastki drugiego stopnia;

4) mnoży i dzieli pierwiastki trzeciego stopnia.

5

.

Procenty. Uczeń:

1) przedstawia część pewnej wielkości jako procent

lub promil tej wielkości i odwrotnie;

2) oblicza procent danej liczby;

3) oblicza liczbę na podstawie danego jej procentu;

4) stosuje obliczenia procentowe do rozwiązywania

problemów w kontekście praktycznym, np. oblicza

ceny po podwyżce lub obniżce o dany procent,

wykonuje obliczenia związane z VAT, oblicza
odsetki dla lokaty rocznej.

6. Wyrażenia algebraiczne. Uczeń:

1) opisuje za pom ocą wyrażeń algebraicznych

związki między różnymi wielkościami;

2) oblicza wartości liczbowe wyrażeń algebraicznych;

3) redukuje wyrazy podobne w sumie algebraicznej;

4) dodaje i odejmuje sumy algebraiczne;

5) mnoży jednomiany, mnoży sumę algebraiczną

przez jednomian oraz, w nietrudnych przykładach,

mnoży sumy algebraiczne;

139

P od s t a w a p r og r a m o w a ( f r a g m e n t !

6) wyłącza wspólny czynnik z wyrazów sumy alge­

braicznej poza nawias;

7) wyznacza wskazaną wielkość z podanych wzorów,

w tym geometrycznych i fizycznych.

i

7. Równania. Uczeń:

1) zapisuje związki między wielkościami za pomocą

równania pierwszego stopnia z jedną niewia­
domą, w tym związki między wielkościami wprost

proporcjonalnymi i odwrotnie proporcjonalnymi;

2) sprawdza, czy dana liczba spełnia równanie stop­

nia pierwszego z jedną niewiadomą;

3) rozwiązuje równania stopnia pierwszego z jedną

niewiadomą;

4) zapisuje związki między nieznanymi wielkościami

za pomocą układu dwóch równań pierwszego
stopnia z dwiema niewiadomymi;

5) sprawdza, czy dana para liczb spełnia układ

dwóch równań stopnia pierwszego z dwiema
niewiadomymi;

6) rozwiązuje układy równań stopnia pierwszego

z dwiema niewiadomymi;

7) za pomocą równań łub układów równań opisuje

i rozwiązuje zadania osadzone w kontekście prak­
tycznym.

8. Wykresy funkcji. Uczeń:

1) zaznacza w układzie współrzędnych na płaszczyź­

nie punkty o danych współrzędnych;

2) odczytuje współrzędne danych punktów;

3) odczytuje z wykresu funkcji: wartość funkcji dla

danego argumentu, argumenty dla danej wartości

funkcji, dla jakich argumentów funkcja przyjmu­

je wartości dodatnie, dla jakich ujemne, a dla ja ­

kich zero;

4) odczytuje i interprettije informacje przedstawione

za pomocą wykresów funkcji (w tym wykresów

opisujących zjawiska występujące w przyrodzie,

gospodarce, życiu codziennym);

5) oblicza wartości funkcji podanych nieskom­

plikowanym wzorem i zaznacza punkty należące

do jej wykresu.

9

.

Statystyka opisowa i wprowadzenie do rachunku

prawdopodobieństwa. Uczeń:

1) interpretuje dane przedstawione za pomocą tabel,

diagramów słupkowych i kołowych, wykresów;

2) wyszukuje, selekcjonuje i porządkuje informacje

z dostępnych źródeł;

3) przedstawia dane w tabeli za pomocą diagramu

słupkowego łub kołowego;

4) wyznacza średnią arytmetyczną i medianę zestawu

danych;

5) analizuje proste doświadczenia losowe (np. rzut

kostką, rzut monetą, wyciąganie losu) i określa

prawdopodobieństwa najprostszych zdarzeń

w tych doświadczeniach (prawdopodobieństwo

wypadnięcia orła w rzucie monetą, dwójki lub
szóstki w rzucie kostką, itp.).

10

.

Figury płaskie. Uczeń:

1) korzysta ze związków między kątami utworzonymi

przez prostą przecinającą dwie proste równoległe;

2) rozpoznaje wzajemne położenie prostej i okręgu,

rozpoznaje styczną do okręgu;

3) korzysta z faktu, że styczna do okręgu jest

prostopadła do promienia poprowadzonego do
punktu styczności;

4) rozpoznaje kąty środkowe;

5) oblicza długość okręgu i łuku okręgu;

6) oblicza pole koła, pierścienia kołowego, wycinka

kołowego;

7) stosuje twierdzenie Pitagorasa;

8) korzysta z własności kątów i przekątnych w pros­

tokątach, równoległobokach, rombach i w trape­

zach;

9) oblicza pola i obwody trójkątów i czworokątów;

10) zamienia jednostki pola;

11) oblicza wymiary wielokąta powiększonego łub

pomniejszonego w danej skali;

12) oblicza stosunek pó l wielokątów podobnych;

13) rozpoznaje wielokąty przystające i podobne;

14) stosuje cechy przystawania trójkątów;

15) korzysta z własności trójkątów prostokątnych

podobnych;

16) rozpoznaje pary figur symetrycznych względem

prostej i względem punktu. Rysuje pary figur

symetrycznych;

17) rozpoznaje figury, które mają oś symetńi, i figury,

które mają środek symetrii. Wskazuje oś symetrii
i środek symetrii figury;

18) rozpoznaje symetralną odcinka i dwusieczną

kąta;

19) konstruuje symetralną odcinka i dwusieczną

kąta,

20) konstruuje kąty o miarach 60°, 30°, 45°;

21) konstruuje okrąg opisany na trójkącie oraz okrąg

wpisany w trójkąt;

22) rozpoznaje wielokąty foremne i korzysta z ich

podstawowych własności.

11

.

Bryły. Uczeń:

1) rozpoznaje graniastosłupy i ostrosłupy prawidłowe;

2) oblicza pole powierzchni i objętość graniastosłupa

prostego, ostrosłupa, walca, stożka, kuli (także

w zadaniach osadzonych w kontekście prakty­
cznym);

3) zamienia jednostki objętości.

140