Wojciech Pacho Szkoła Główna Handlowa

1

Kącik dla ciekawskich

☺

Wybór optymalnego koszyka dóbr. Przykład liczbowy.

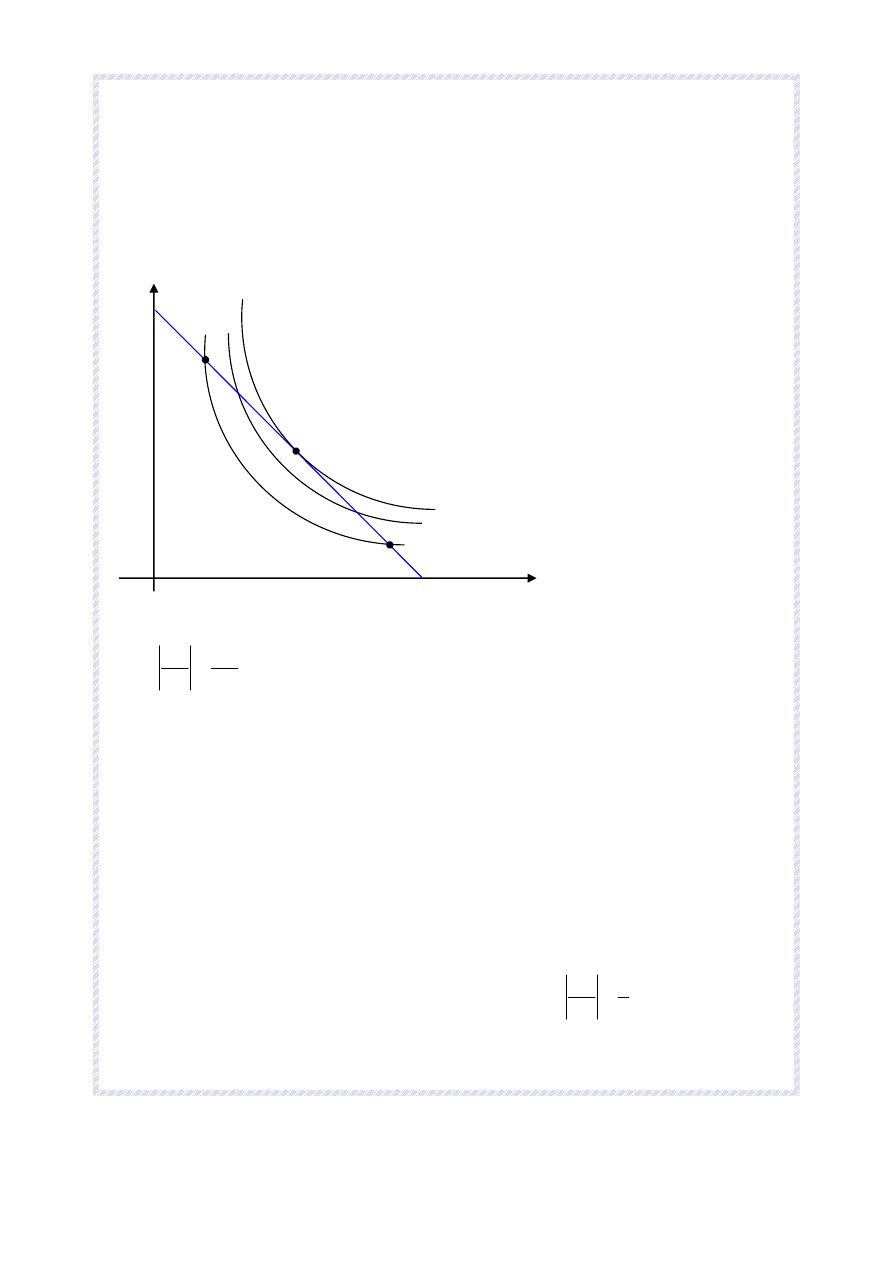
Rysunek przedstawia mapę gustu konsumenta w stosunku do dóbr X i Y. Dobro X kosztuje
P

X

=1, natomiast Y P

Y

=2. Załóżmy, iż początkowo konsument posiada koszyk w punkcie A

na krzywej obojętności I. Przyjmijmy, że w tym punkcie krańcowa stopa substytucji MRS jest

równa

100

1

=

∆

∆

Y

X

. Oznacza to, iż utrzymanie się na krzywej obojętności I przy wzroście Y o

1 jednostkę wymagałoby ubytku X o 0,01 jednostki. Większy ubytek jest niedopuszczalny,
gdyż wiązałoby się to ze spadkiem użyteczności. Ze stosunku cen wynika, iż aby zwiększyć
Y o 1 należy zrezygnować z 2X, czyli z ilości większej niż dopuszczalna dla utrzymania się
na tej samej krzywej obojętności. Zatem gdybyśmy chcieli zrealizować powiększenie koszyka
o 1 Y, to użyteczność spadnie.

Natomiast gdybyśmy chcieli powiększyć koszyk o 1X, to jest to korzystne, gdyż rośnie
użyteczność. Aby powiększyć koszyk o 1X i nie pogorszyć użyteczności (pozostać na
krzywej obojętności I), możemy pozbyć się 100Y. Ze stosunku cen wynika, iż gdybyśmy
pozbyli się 100Y, to moglibyśmy zakupić dodatkowo aż 200X, czyli zdecydowanie więcej niż
wymagane dla utrzymania niezmienionej użyteczności. Zyskalibyśmy aż 199 jednostek X na
powiększenie użyteczności (na rysunku oznaczałoby to przejście na wyżej położona krzywą
obojętności na przykład II). Zmiana koszyka A poprzez powiększanie X kosztem ubytków Y
jest zatem korzystne nabywcy. Dodatkowe korzyści będą rosły aż do punktu E, w którym

krańcowa stopa substytucji zrównuje się ze stosunkiem cen

1

2

=

∆

∆

Y

X

. W tym punkcie po

dodaniu 1X utrzymanie tej samej użyteczności (pozostanie na krzywej obojętności III) wiąże
się z ubytkiem ½ Y. Pozbywając się ½ Y możemy kupić dodatkowo tylko 1X, czyli dokładnie
tyle ile potrzeba, aby użyteczność nie zmieniła się (pozostajemy na krzywej obojętności III).

Y

X

A

B

I

II

III

E

Wojciech Pacho Szkoła Główna Handlowa

2

Przyjmijmy teraz, że konsument posiada koszyk w punkcie B, gdzie krańcowa stopa

substytucji jest równa

1

100

=

∆

∆

Y

X

. Wzorując się na poprzednim rozumowaniu, spróbuj

samodzielnie przeprowadzić dowód, iż opłacalne jest pozbywanie się z koszyka dobra X na
rzecz dobra Y.