M

M

M

M

ETODA

ETODA

ETODA

ETODA

3

3

3

3-

---

CH

CH

CH

CH

M

M

M

M

OMENTÓW

OMENTÓW

OMENTÓW

OMENTÓW

I

I

I

I

M

M

M

M

ETODA

ETODA

ETODA

ETODA

P

P

P

P

RZEMIESZCZEŃ

RZEMIESZCZEŃ

RZEMIESZCZEŃ

RZEMIESZCZEŃ

W U

W U

W U

W UKŁADACH

KŁADACH

KŁADACH

KŁADACH

B

B

B

B

ELKOWYCH

ELKOWYCH

ELKOWYCH

ELKOWYCH

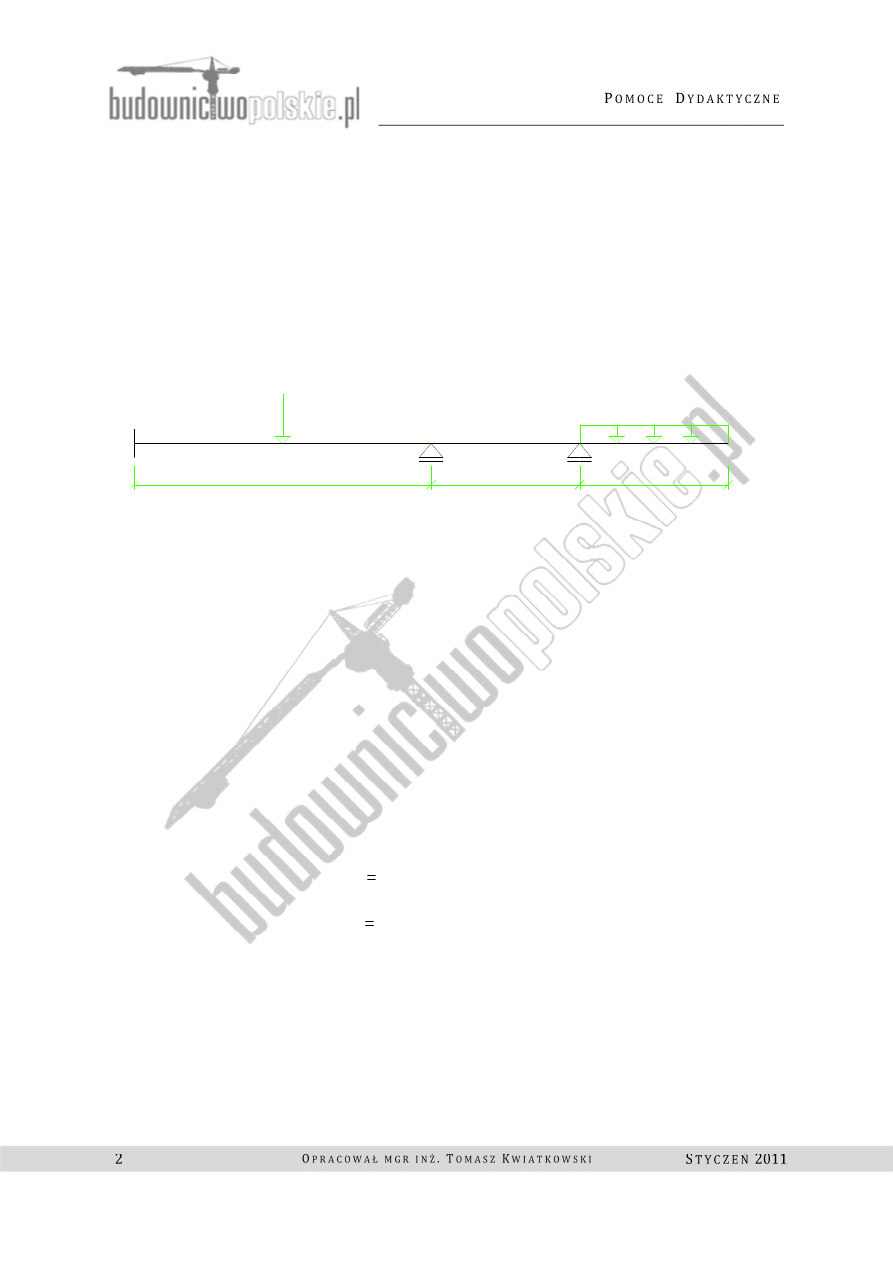
Przykład nr 1.1

Wyznaczyć wykresy sił wewnętrznych w belce przedstawionej na rysunku 1.1

(EJ = const.) metodą 3-ch momentów. Otrzymane wyniki zweryfikować metodą
przemieszczeń.

4

2

2

6 kN/m

10 kN

2 EJ

EJ

3 EJ

2

Rys.1.1 Belka statycznie niewyznaczalna dla przykładu 1.1

(długości przęseł podane są w metrach ).

Metoda 3-ch Momentów.

Na początku musimy obliczyć statyczną niewyznaczalność układu.

S = 2

Dany układ jest dwukrotnie statycznie niewyznaczalny.

W celu rozwiązania układu metodą 3-ch momentów sporządzam układ równań, który

w naszym przypadku wygląda następująco:

Kolejnym krokiem jest wyznaczenie długości sprowadzonych „l`” (długości zastępczych)
wg następującego wzoru:

l`= l

k

· EJ`/EJ

k

gdzie:

x0 l'1

⋅

2 x1

⋅

l'1

l'2

+

(

)

⋅

+

x2 l'2

⋅

+

N 1p

x1 l'2

⋅

2 x2

⋅

l'2

l'3

+

(

)

⋅

+

x3 l'3

⋅

+

N2p

l

k

to długość rzeczywista przęsła,

EJ

k

to sztywność rzeczywista przęsła,

EJ` to sztywność porównawcza.

Przyjmuję że EJ`= 2EJ i wg wzoru na obliczenie długości sprowadzonych otrzymuję:

l`

1

= 0 m

l`

2

= 4 m

l`

3

= 4 m

L`2

10 kN

2 EJ

EJ

L`3

X0

X1

X2

X3 = -12

L`1

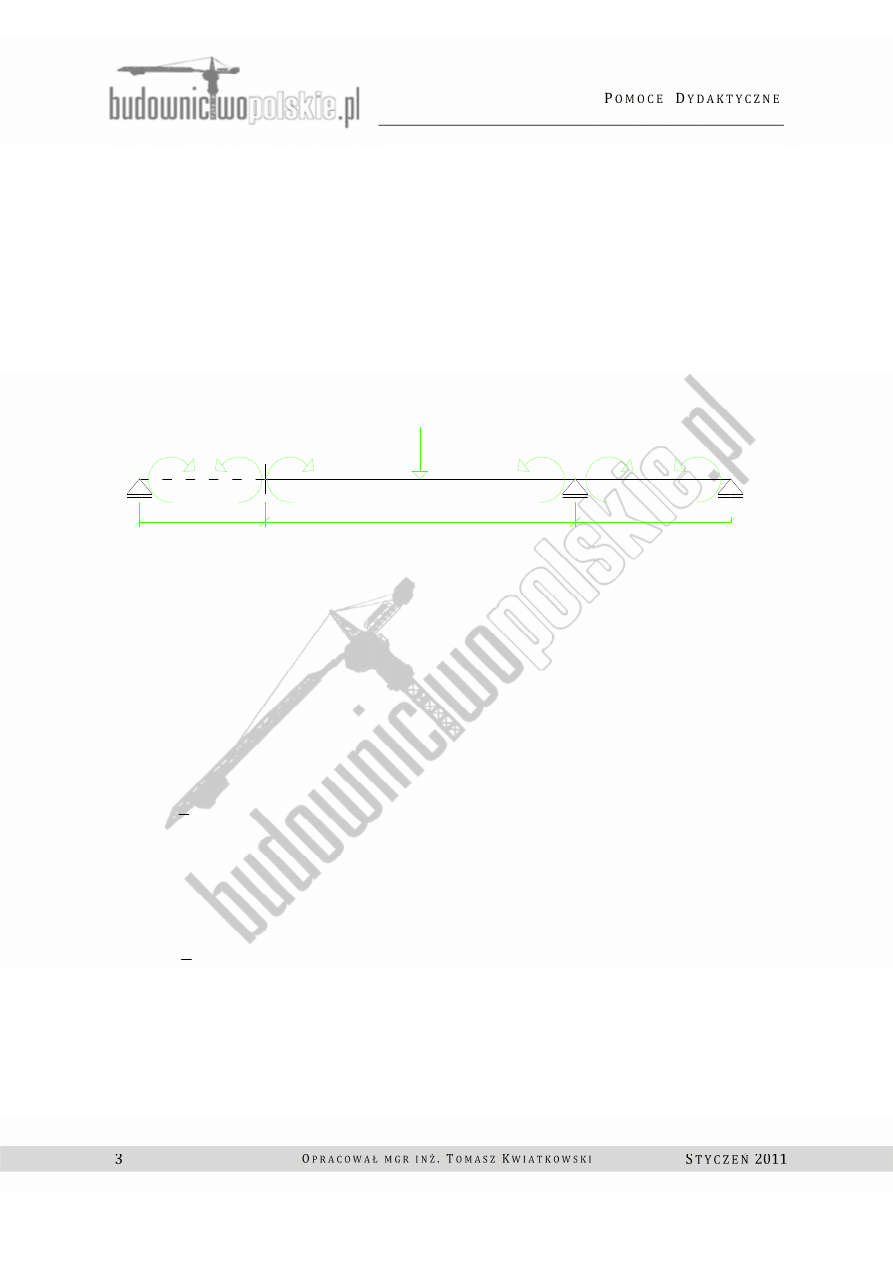
Rys. 1.2 Model zastępczy belki.

Następnie przystępuje do obliczeń niewiadomych N

1p

i N

2p

korzystają ze wzorów

transformacyjnych . Jak widać z Rys. 1.2 momenty skrajne tj. X0 = 0 i X3 = -12 kNm.

Dla k =1

dla k = 2

N1p

3

8

−

P

⋅

l'2

⋅

l2

⋅

=

N1p

60

−

kN m

2

⋅

⋅

=

N 2p

3

8

−

P

⋅

l'2

⋅

l2

⋅

=

N2p

60

−

kN m

2

⋅

⋅

=

Rozwiązujac układ równań otrzymujemy szukane niewiadome:

X1 = -8,143 kNm,

X2 = 1,286 kNm

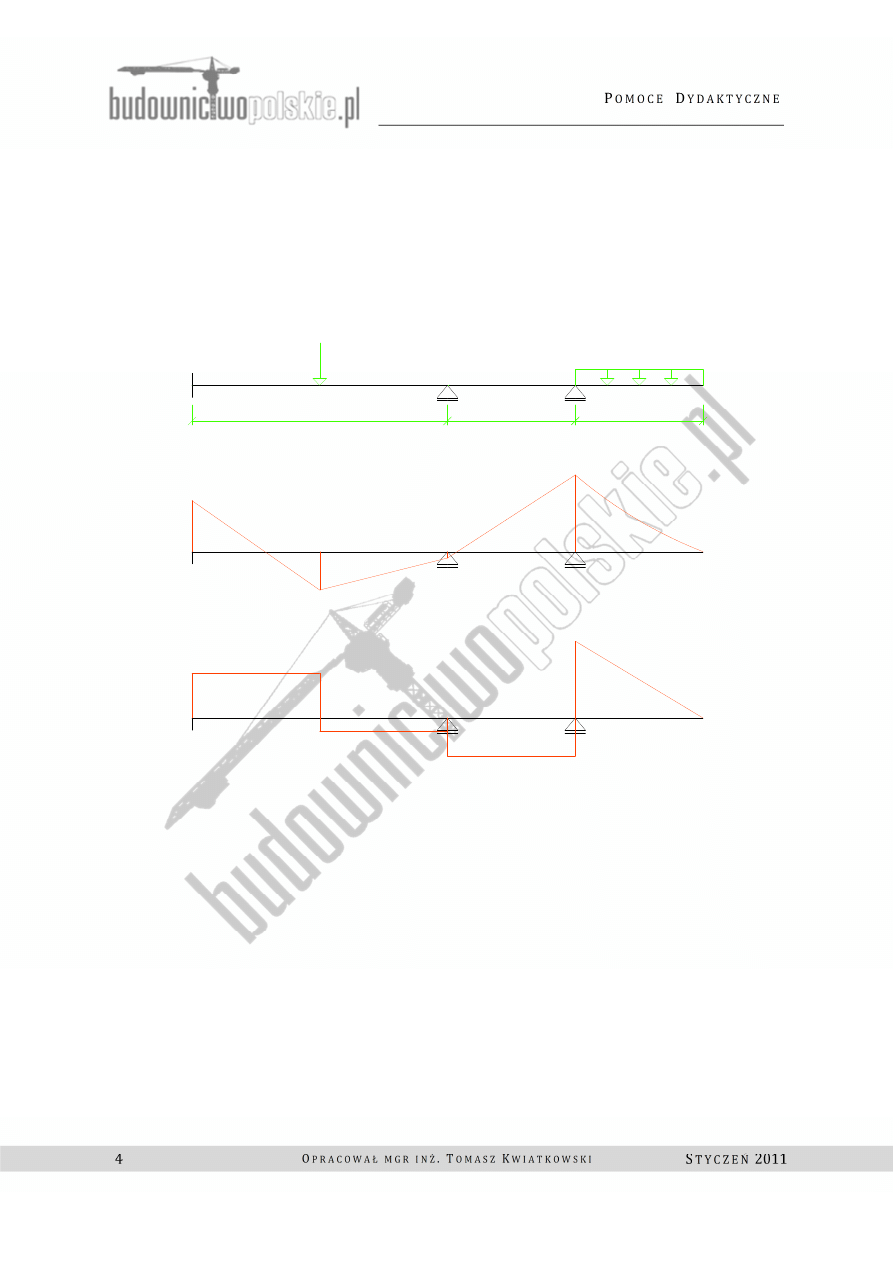
Mając szukane wielkości momentów przywęzłowych obliczamy reakcje i sporządzamy
wykresy momentów i sił tnących.

a)

4

2

2

6 kN/m

10 kN

2 EJ

EJ

3 EJ

2

-8,143

6,571

1,286

-12

b)

7,357

-2,643

-12

-6,643

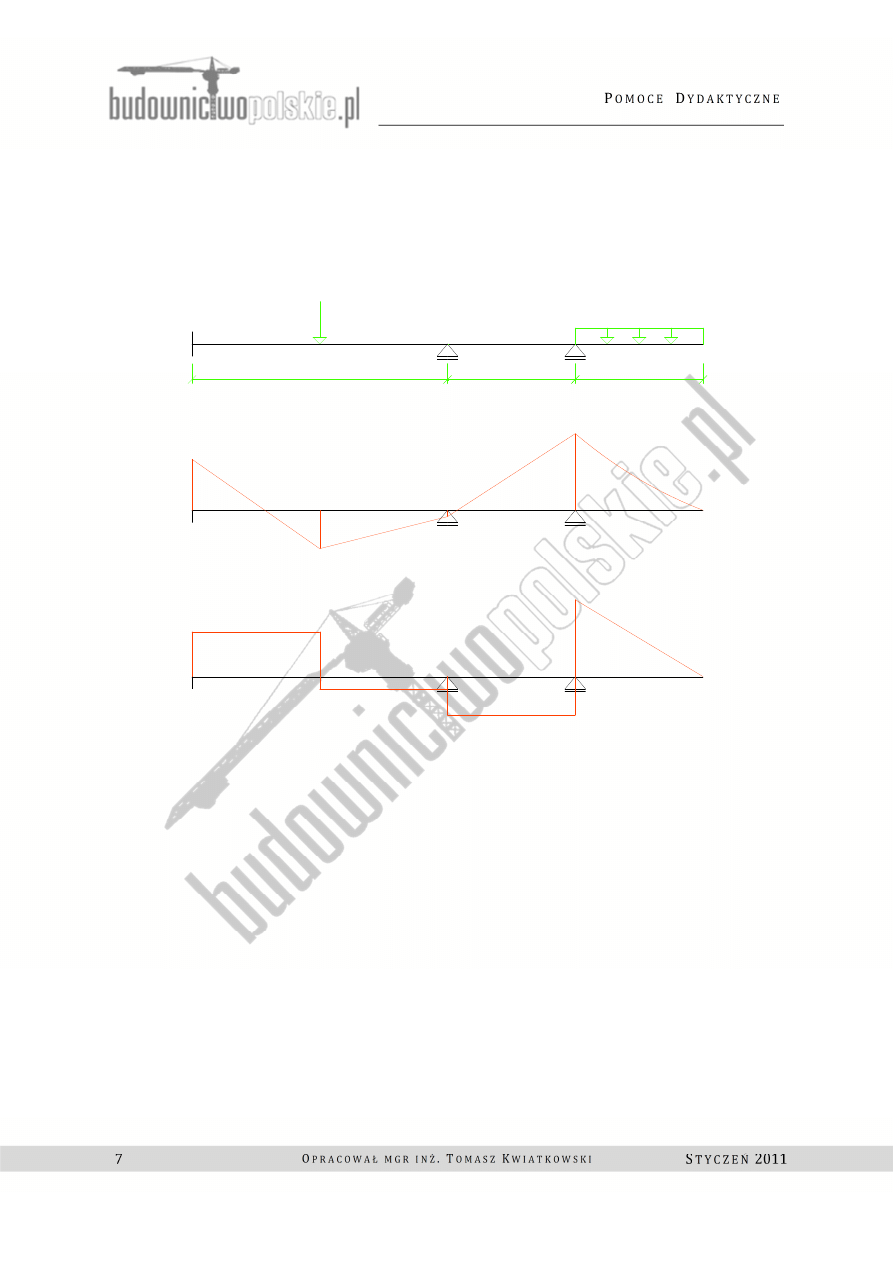
Rys.1.3 Belka a) wykres momentów [kNm], b) wykres sił tnących [kN].

Metoda Przemieszczeń.

Metodę przemieszczeń zaczynamy od przyjęcia układu podstawowego, dla którego

tworzymy układ równań kanonicznych. I tak:

4

2

2

6 kN/m

10 kN

2 EJ

EJ

3 EJ

2

φ

4

2

2

6 kN/m

10 kN

2 EJ

EJ

3 EJ

2

Rys.2.1 Belka a) układ rzeczywisty b) układ podstawowy.

Dla układu obciążonymi siłami zewnętrznymi układ kanoniczny ma postać:

r

11

· φ + R

1p

= 0

W celu wyznaczenia współczynników r

11

, R

1p

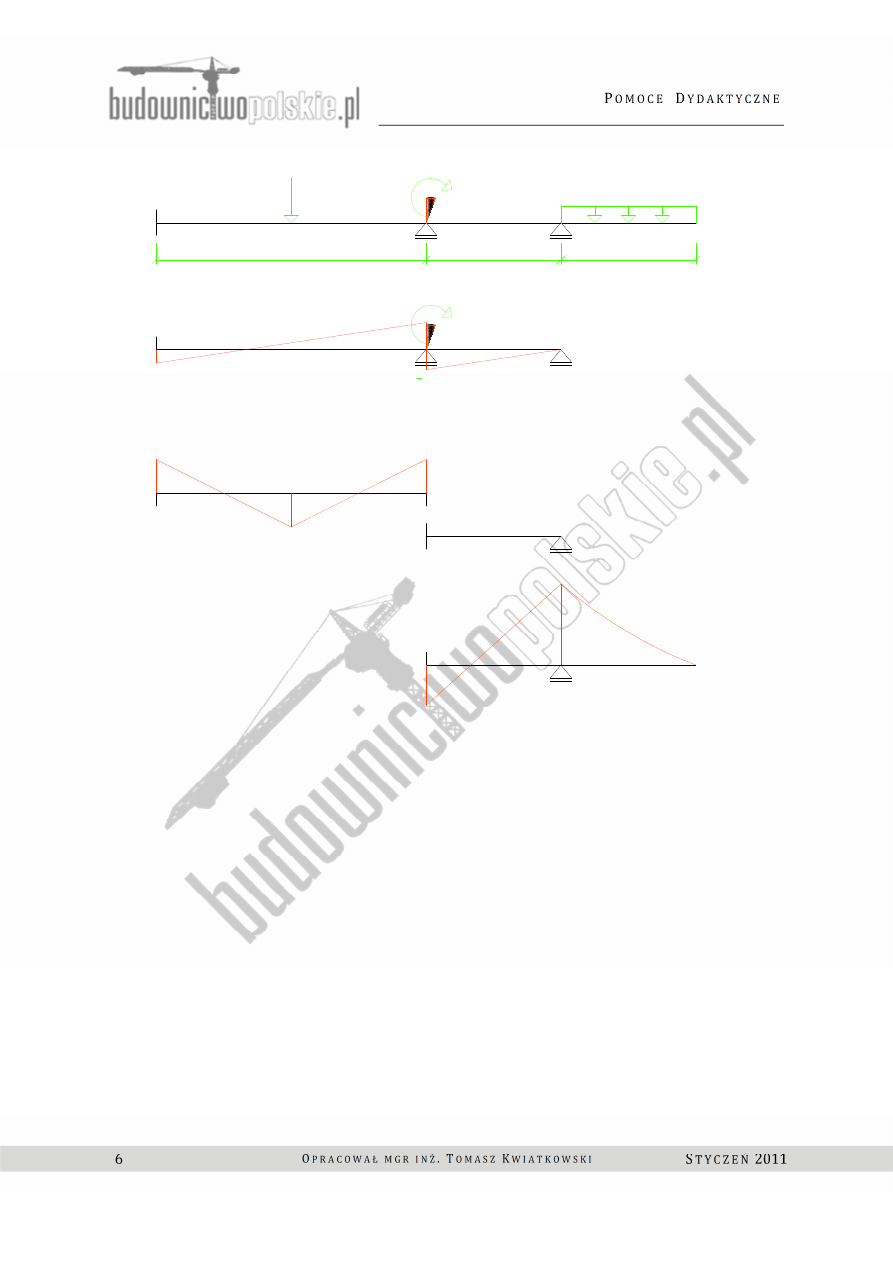
wykonujemy wykresy momentów

zgodnie z poznanymi wzorami transformacyjnymi przy φ = 1 oraz od obciążenia siłami
zewnętrznymi.

4

2

2

6 kN/m

10 kN

2 EJ

EJ

3 EJ

2

φ

φ

EJ

2 EJ

3
2

EJ

5

5

-12

6

a)

b)

Rys.2.2 Belka a) od φ = 1 b) od obciążeń zewnętrznych.

Poszczególne współczynniki wyznaczamy z równowagi węzłów:

r

11

= 2EJ + 3/2EJ = 3,5EJ

R

1p

= 5 + 6 = 11

Rozwiązując układ równań otrzymujemy:

φ

=

−

R

1p

/ r

11

=>

φ

=

−

3,143· 1/EJ

wartości te wstawiamy do wzoru:

M

ik

= M

φ

· φ +M

p

otrzymując końcowe wartości momentów na poszczególnych końcach prętów.
Wykresy momentów przedstawiono na poniższym rysunku.

a)

4

2

2

6 kN/m

10 kN

2 EJ

EJ

3 EJ

2

-8,143

6,571

1,286

-12

b)

7,357

-2,643

-12

-6,643

Rys.2.3 Belka a) wykres momentów [kNm], b) wykres sił tnących [kN].