Piotr Łukowski, Wykład dla studentów pedagogiki

1

Logika

WYKŁAD 11: rozumowania

Piotr Łukowski, Wykład dla studentów pedagogiki

2

Jan Gregorowicz, Zarys logiki dla prawników, Grand Gamma, Łódź 1995.

Piotr Łukowski, Wykład dla studentów pedagogiki

3

PRZYPOMNIENIE:

Definicja wynikania

Zdanie W wynika ze zdania Z, jeśli implikacja

Z

W

jest zdaniem prawdziwym na mocy związku jaki zachodzi między tym o czym orzeka
zdanie W a tym o czym orzeka zdanie Z.

Z nazywamy racją, a W następstwem.

Z definicji wynikania wnioskujemy, iż istnieją różne rodzaje wynikania W z Z w
zależności od rodzaju związku będącego podstawą prawdziwości implikacji Z W.

Piotr Łukowski, Wykład dla studentów pedagogiki

4

Związek zachodzący między Z i W, będący podstawą prawdziwości Z W może być:

- przyczynowo-skutkowy (ze względu na wiedzę o rzeczywistości)

Jeśli zaleję herbatę zimną wodą, to jej nie zaparzę.

- strukturalny (w sensie czasu lub przestrzeni)

Jeśli wczoraj był poniedziałek, to jutro jest środa. (także analityczny)
Jeśli obraz a wisi nad obrazem b, to obraz b wisi pod obrazem a. (także analityczny)
Jeśli stoję twarzą na północ, to po prawej ręce mam wschód.

- tetyczny (ze względu na obowiązywanie pewnych norm)

Jeśli w sklepie płacę za towar, to część mojej zapłaty jest przeznaczona na podatek.

- analityczny (ze względu na sens słów - węższe rozumienie analityczności)

Jeśli ta figura jest kwadratem, to [ta figura] ma cztery boki równe.

- logiczny (ze względu na budowę zdań - nieprecyzyjne określenie, patrz wcześniejsze
wykłady)

Jeśli Jan jest łysym adwokatem, to Jan jest adwokatem.
(Jeśli Jan jest łysy i Jan jest adwokatem, to Jan jest adwokatem.)

KONIEC PRZYPOMNIENIA

Piotr Łukowski, Wykład dla studentów pedagogiki

5

Rozumowanie to myślenie uzasadniające, czyli takie, w którym przyjmujemy jakieś
zdanie (zdania) za prawdziwe i dochodzimy do przeświadczenia o prawdziwości
jakichś innych zdań.

Ogólniej:

Rozumowanie to myślenie uzasadniające, w którym przyjmujemy określone wartości
pewnych zdań i dochodzimy do przeświadczenia o określonych wartościach
logicznych innych zdań.

Rozumowanie niezawodne to takie, które od prawdziwych przesłanek zawsze prowadzi
do prawdziwych wniosków.

Piotr Łukowski, Wykład dla studentów pedagogiki

6

UWAGA:

Wynikanie to relacja

, która zachodzi między zdaniami.

Rozumowanie to

czynność wykonywana przez człowieka.

Piotr Łukowski, Wykład dla studentów pedagogiki

7

Uwaga:
Dotychczas, słowo „dedukcja” oznaczało wnioskowanie, w którym wniosek wynika
logicznie z przesłanek. Miało więc ono formalno-logiczne znaczenie.

Obecnie, słowa „dedukcja” będziemy używali w znaczeniu ogólniejszym.

Piotr Łukowski, Wykład dla studentów pedagogiki

8

Dedukcja i redukcja jako czynność.

Dedukcja

1

(rozumowanie dedukcyjne) to rozumowanie, w którym racja jest znana jako

prawdziwa, a następstwo jako prawdziwe nieznane.
Redukcja

1

(rozumowanie redukcyjne) to rozumowanie, w którym następstwo jest znane jako

prawdziwe, a racja jako prawdziwa nieznana.


Dedukcja

1

jest rozumowaniem (niezawodnym) bazującym na wynikaniu (logicznym).

Przykład

{Jeśli deszcz pada to ulice są mokre, Deszcz pada} | Ulice są mokre

Redukcja

1

jest rozumowaniem zawodnym bazującym na wynikaniu (logicznym).

Przykład

{Jeśli deszcz pada to ulice są mokre, Ulice są mokre} | Deszcz pada

p

q

p

q

p

q

q

p

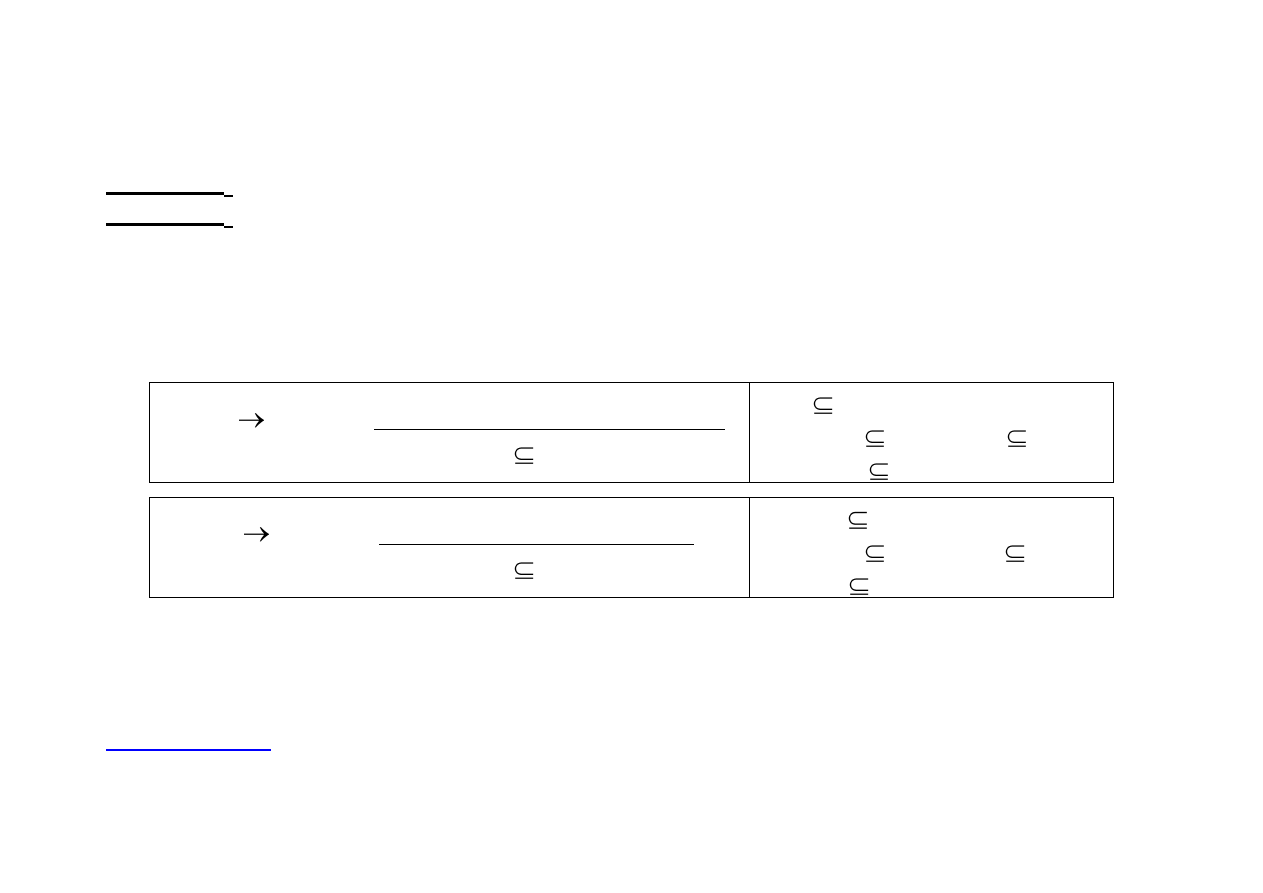
Piotr Łukowski, Wykład dla studentów pedagogiki

9

Dedukcja i redukcja jako stan.

Dedukcja

2

to funkcja reprezentująca poszerzenie zbioru przekonań.

Redukcja

2

to funkcja reprezentująca zmniejszenie zbioru przekonań.

Przykładem dedukcji

2

jest operacja konsekwencji logicznej, zaś redukcji

2

operacja eliminacji

logicznej.

C:

P(L) P(L) jest operacją konsekwencji logicznej

wtw dla dowolnych zbiorów X,Y L

1. X C(X)
2. jeśli X Y, to C(X) C(Y)
3. CC(X) C(X)

E:

P(L) P(L) jest operacją eliminacji logicznej

wtw dla dowolnych zbiorów X,Y L

1. E(X) X
2. jeśli X Y, to E(X) E(Y)
3. E(X) EE(X)

L jest zbiorem wszystkich zdań języka.
P(L) jest zbiorem wszystkich podzbiorów zbioru L.

Prosta uwaga

: Z 1 i 3 wynika, że C(X) = CC(X) oraz E(X) = EE(X).

Piotr Łukowski, Wykład dla studentów pedagogiki

10

W dalszym ciągu wykładu, słowa „dedukcja” i „redukcja” będą oznaczały dedukcję i
redukcję w pierwszym znaczeniu, czyli jako czynność myślenia. Zatem:

dedukcja = dedukcja

1

i redukcja = redukcja

1

.

Piotr Łukowski, Wykład dla studentów pedagogiki

11

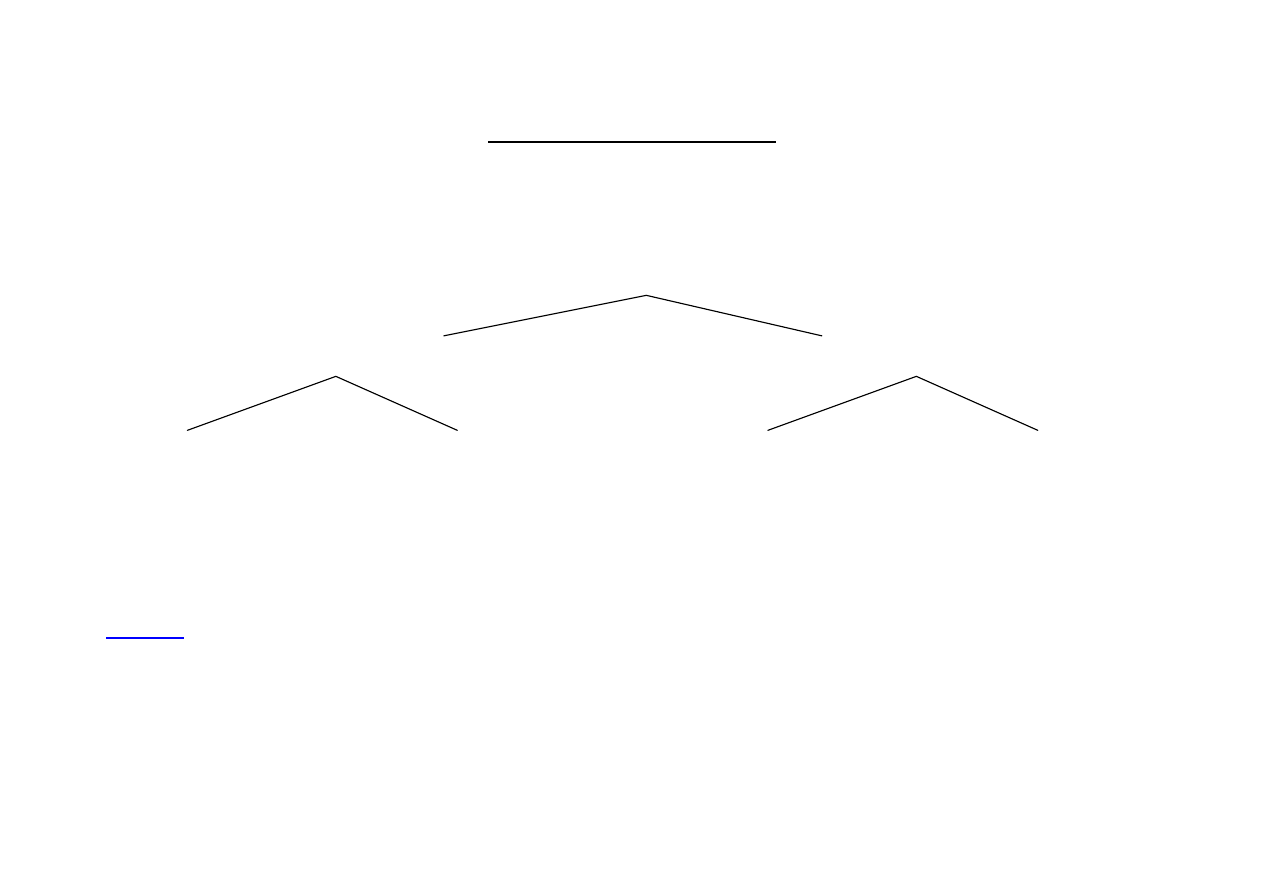
Podział rozumowań

Uwaga:
Naturalnie, w tym schemacie zarówno rozumowanie dedukcyjne jak i redukcyjne jest
pojmowane jako czynność.

rozumowanie

dedukcyjne

redukcyjne

wnioskowanie

dowodzenie

tłumaczenie

sprawdzanie

Piotr Łukowski, Wykład dla studentów pedagogiki

12

Wnioskowanie,
to dobieranie następstwa do racji znanej skądinąd jako prawdziwa.

1 1

R

N

m sz

(m = mamy, sz = szukamy)

Zatem, wnioskuje ten, kto uznaje prawdziwość następstwa na mocy prawdziwości
racji. Innymi słowy, poszukuje (różnych) skutków/konsekwencji danej racji.

Uwaga

: Niezawodność (wartość) wnioskowania zależy od niezawodności (wartości) związku

wynikania. Wnioskowanie oparte na wynikaniu logicznym jest niezawodne.

[na pewno?]

Piotr Łukowski, Wykład dla studentów pedagogiki

13

Przykłady wnioskowania:

1.

Wiem, że prawdą jest zdanie A = „Liście herbaty zostały zalane wrzątkiem”. Czy prawdziwe będzie zdanie
B = „Otrzymaliśmy napar herbaty”? Jeśli tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku przyczynowo-skutkowego uznaję, że prawdą jest implikacja A

B.

Zatem jeśli prawdą jest A, to prawdą jest także B. Wiem więc, że B jest prawdziwe na mocy wnioskowania.

2.

Wiem, że Jan prowadzi samochód będąc w stanie upojenia alkoholowego (A). Czy prawdą jest, że Jan
popełnia przestępstwo (B)? Jeśli tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku tetycznego wiem, że prawdą jest implikacja A

B.

Zatem jeśli prawdą jest A, to prawdą jest także B. Wiem więc, że B jest prawdziwe na mocy wnioskowania.

3.

Wiem, że Marek został osadzony w więzieniu (A). Czy prawdą jest, że Markowi udowodniono popełnienie
przestępstwa (B)? Jeśli tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku tetycznego wiem, że prawdą jest implikacja A

B.

Zatem jeśli prawdą jest A, to prawdą jest także B. Wiem więc, że B jest prawdziwe na mocy wnioskowania.

Piotr Łukowski, Wykład dla studentów pedagogiki

14

4.

Wiem, że wczoraj był poniedziałek, więc na mocy związku strukturalnego wnioskuję, że jutro będzie środa.

5.

Wiem, że ulice nie są mokre (A). Czy prawdą jest, że deszcz nie pada (B)? Jeśli tak to na mocy jakiego
rozumowania?

Odp.

Na mocy związku przyczynowo-skutkowego wiem, że prawdą jest implikacja B

A. Ta zaś, na mocy

krz, jest równoważna implikacji A

B. Zatem jeśli prawdą jest A, to prawdą jest także B.

Wiem więc, że B jest prawdziwe na mocy wnioskowania. Naturalnie, wywnioskuję także, że ani nie jeździła
polewaczka, ani nie było awarii wodociągowej.

6.

Wiem, że prawdziwe są zdania A ( A B) oraz A. Czy prawdą jest zdanie A B? Jeśli tak to na
mocy jakiego rozumowania?

Odp.

Wiem, że prawdą logiczną krz jest implikacja ((A ( A B)) A) ( A B). Zatem, zdanie A B
wynika logicznie na mocy krz, z dwóch zdań A

( A

B) oraz A. Skoro one są prawdziwe, to wnioskuję,

że prawdziwe jest A B.

Piotr Łukowski, Wykład dla studentów pedagogiki

15

7.

Tytus jest poza kręgiem osób podejrzanych o popełnienie zbrodni.
Wiem, że prawdą jest zdanie A = „Na miejscu zbrodni znaleziono odciski palców Tytusa”. Czy prawdziwe
będzie zdanie B = „Tytus był na miejscu zbrodni”? Jeśli tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku przyczynowo-skutkowego uznaję, że prawdą jest implikacja A

B.

Zatem jeśli prawdą jest A, to prawdą jest także B. Wiem więc, że B jest prawdziwe na mocy wnioskowania.
[Pytanie: A co z Kramerem z Vabanku?
Odpowiedź: Spoko, spoko, mała blaszka, to nie miejsce zbrodni.



]

Piotr Łukowski, Wykład dla studentów pedagogiki

16

Dowodzenie

,

to dobieranie racji znanej skądinąd jako prawdziwa do danego nieznanego
jeszcze jako prawdziwe następstwa.

1 1 ?

R

N

sz m

Zatem, dowodzi ten, kto chce przekonać się o prawdziwości następstwa przez
znalezienie prawdziwej dla niego racji.

Uwaga

: Niezawodność (wartość) dowodzenia zależy od niezawodności (wartości) związku

wynikania. Dowodzenie oparte na wynikaniu logicznym jest niezawodne.

[na pewno?]

Piotr Łukowski, Wykład dla studentów pedagogiki

17

Przykłady dowodzenia:

1.

Kasjusz jest głównym podejrzanym o popełnienie zbrodni.
Zastanawiam się, czy prawdziwe jest zdanie B = „Kasjusz był na miejscu zbrodni”. Po pewnym czasie
dowiaduję się jednak, że prawdą jest zdanie A = „Na miejscu zbrodni znaleziono odciski palców Kasjusza”.
Czy mogę uznać prawdziwość zdania B? Jeśli tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku przyczynowo-skutkowego uznaję, że prawdą jest implikacja A

B.

Zatem jeśli prawdą jest A, to prawdą jest także B. Ale A jest prawdą, udowodniłem więc, że B jest
prawdziwe.

2.

Agrypa jest podejrzanym o popełnienie w Łodzi zbrodni a.
Zastanawiam się, czy prawdziwe jest zdanie A = „Agrypa popełnił w Łodzi zbrodnię a”. Po pewnym czasie
dowiaduję się jednak, że prawdą jest zdanie B = „W chwili popełnienia w Łodzi zbrodni a, wiarygodny
świadek X widział Agrypę w Krakowie”.
Czy mogę uznać fałszywość zdania A (czyli prawdziwość zdania A)? Jeśli tak to na mocy jakiego
rozumowania?

Odp.

Na mocy związku strukturalnego uznaję, że prawdą jest implikacja B

A.

Zatem jeśli prawdą jest B (a to zależy od wiarygodności świadka X), to udowodniłem, że prawdą jest także

A, czyli że A jest fałszem.

Piotr Łukowski, Wykład dla studentów pedagogiki

18

3.

Są wakacje i straciłem rachubę czasu. Zastanawiam się czy dziś jest wtorek. Przypomniałem sobie jednak, że
przedwczoraj byłem na niedzielnym obiedzie u rodziców, więc na mocy związku strukturalnego
udowodniłem samemu sobie, że faktycznie dziś jest wtorek.
[ale czy na pewno dobrze sobie przypomniałem?]

4.

Zastanawiam się, czy prawdziwe jest zdanie A.
Zauważam jednak, że prawdziwe są zdania B i (¬A ¬B). Wiem też, że prawdą logiczną jest implikacja
(¬A ¬B) (B A). Na mocy związku logicznego krz udowodniłem zatem prawdziwość zdania A.
[a co z paradoksami logiki klasycznej?]

Piotr Łukowski, Wykład dla studentów pedagogiki

19

Sprawdzanie

,

to dobieranie następstwa znanego skądinąd jako prawdziwe do nieznanej jako
prawdziwa racji.

? 1 1

R

N

m sz

Zatem, sprawdza ten, kto chce wzmocnić swoją wiarę w prawdziwość racji (czyli
uprawdopodobnić prawdziwość racji) znajdując dla niej prawdziwe następstwo.
Pozytywny wynik sprawdzania danej tezy, zwiększa szansę na jej prawdziwość, ale nie
dowodzi jej prawdziwości.

Uwaga

: Każde sprawdzanie jest zawodne, także to oparte na wynikaniu logicznym:

jeśli A B oraz B są prawdziwe, to A nie musi być prawdziwe.

Zatem, wartość sprawdzania, które z natury rzeczy jest zawodne może jeszcze być pomniejszona
przez niską wartość (czyli niepewność) implikacji R N.

Piotr Łukowski, Wykład dla studentów pedagogiki

20

Przykłady sprawdzania

1.

Leżąc jeszcze w łóżku, zastanawiam się, czy wczorajsza prognoza pogody mówiąca, że rano będą opady
deszczu się sprawdziła. Innymi słowy, zastanawiam się, czy prawdziwe jest zdanie A = „Rano padał deszcz”.
W tym celu wyglądam przez okno i widzę, że moja ulica jest mokra, czyli prawdziwe jest zdanie B = „Moja
ulica jest [rano] mokra”.
Czy na tej podstawie mogę uznać prawdziwość zdania A? Jeśli tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku przyczynowo-skutkowego uznaję, że prawdą jest implikacja A

B.

Zatem jeśli prawdą jest B, to prawdą może być także A. Jednak A nie musi być prawdą, nawet jeśli prawdą
jest B. Prawdziwość A stała się dla mnie bardziej prawdopodobna, gdyż jeśli A jest prawdą, to prawdą jest i
B. Jednak prawdziwość zdania A zaledwie sprawdziłem: deszcz mógł padać, gdyż ulica jest mokra.

2.

Zastanawiam się, czy Marek jest na wolności, czy może jest osadzony w więzieniu. Interesuje mnie
prawdziwość zdania A = „Marek został osadzony w więzieniu”. Po pewnym czasie dowiaduję się, że Marek
miał proces, w wyniku którego udowodniono mu winę. Zatem, prawdą jest B = „Markowi udowodniono
popełnienie przestępstwa”.
Czy na tej podstawie mogę uznać prawdziwość zdania A? Jeśli tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku tetycznego wiem, że prawdą jest implikacja A

B.

Zatem jeśli prawdą jest B, to prawdą może być, choć nie musi, także A. Oznacza to, że jedynie sprawdziłem,
iż Marek może być w więzieniu, bo udowodniono mu, że popełnił przestępstwo.

Piotr Łukowski, Wykład dla studentów pedagogiki

21

3.

Zastanawiam się, czy prawdziwe jest zdanie A = „Pan X o godz. Y spotkał się w parku z panią Z”.
Dowiaduję się (sprawdzam), że prawdziwe jest zdanie B = „O godz. Y pan X był nieobecny w pracy”.
Czy na tej podstawie mogę uznać prawdziwość zdania A? Jeśli tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku strukturalnego uznaję, że prawdą jest implikacja A

B.

Zatem jeśli prawdą jest B, to prawdą może być także A. Jednak A nie musi być prawdą, nawet jeśli prawdą
jest B. Prawdziwość A stała się dla mnie bardziej prawdopodobna, gdyż jeśli A jest prawdą, to prawdą jest i
B. Jednak prawdziwość zdania A zaledwie sprawdziłem: pan X mógł o godz. Y spotkać się w parku z panią
Z.

[przykład jest nieprecyzyjny, bo nie jest w nim wykluczone, że pan X pracuje w parku]

Piotr Łukowski, Wykład dla studentów pedagogiki

22

Tłumaczenie,
to dobieranie racji do znanego skądinąd jako prawdziwe następstwa.

? 1 1

R

N

sz m

Zatem, tłumaczy ten, kto chce znaleźć przyczynę prawdziwego następstwa przez
znalezienie jakiejś dla niego racji. Ponieważ, dana teza może wynikać z różnych racji
(dane zjawisko może mieć różne przyczyny), każde tłumaczenie jest zawodne.

Uwaga

: Każde tłumaczenie jest jedynie próbą znalezienia przyczyny zajścia danego

zjawiska.

Piotr Łukowski, Wykład dla studentów pedagogiki

23

Przykłady tłumaczenia

1.

Wyglądając rano przez okno widzę, że moja ulica jest mokra, innymi słowy, prawdziwe jest zdanie B =
„Moja ulica jest [rano] mokra”. Zastanawiam się, czemu jest mokra.
Czy na podstawie prawdziwości zdania B mogę uznać prawdziwość zdania A = „Rano padał deszcz”? Jeśli
tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku przyczynowo-skutkowego uznaję, że prawdziwa jest implikacja A

B.

Zatem skoro prawdą jest B, to prawdą może być także A. Jednak A nie musi być prawdą, nawet jeśli prawdą
jest B. Zdarzenie opisane zdaniem A jest jedną, lecz nie jedyną możliwą przyczyną zajścia zdarzenia
opisanego zdaniem B.
Zatem zdarzenie wyrażone przez B (prawdziwość zdania B) tłumaczę w jeden z możliwych sposobów, czyli
w tym przypadku przyjmując prawdziwość zdania A: moja ulica jest mokra, ponieważ rano padał deszcz.

Piotr Łukowski, Wykład dla studentów pedagogiki

24

2.

Zastanawiam się, dlaczego pan X był nieobecny w pracy w godz. Y. Czyli zastanawiam się jak wytłumaczyć
prawdziwość zdania B = „O godz. Y pan X był nieobecny w pracy”.
Czy na tej podstawie mogę uznać prawdziwość zdania A = „Pan X o godz. Y spotkał się w parku z panią Z”?
Jeśli tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku strukturalnego uznaję, że prawdą jest implikacja A

B.

Zatem jeśli prawdą jest B, to prawdą może być A. Jednak A nie musi być prawdą.
Zatem zdarzenie wyrażone przez B (prawdziwość zdania B) tłumaczę w jeden z możliwych sposobów, czyli
w tym przypadku przyjmując prawdziwość zdania A: pan X był w godz. Y nieobecny w pracy, bo spotkał się
z panią Z w parku. Osoba życzliwsza panu X wytłumaczyłaby jego nieobecność w pracy np. chorobą, jakimś
przypadkiem losowym, etc.

3.

Zastanawiam się, dlaczego budynek X postrzegamy jako mniejszy od Y, czyli zastanawiam się dlaczego (jak
wytłumaczyć) prawdziwość zdania B = „Budynek X postrzegamy jako mniejszy od Y”.
Czy na tej podstawie mogę uznać prawdziwość zdania A = „Budynek X stoi dalej od nas niż budynek Y”?
Jeśli tak to na mocy jakiego rozumowania?

Odp.

Na mocy związku strukturalnego uznaję, że prawdą jest implikacja A

B.

Zatem jeśli prawdą jest B, to prawdą może być A. Jednak A nie musi być prawdą.
Zatem zdarzenie wyrażone przez B (prawdziwość zdania B) tłumaczę w jeden z możliwych sposobów, czyli
w tym przypadku przyjmując prawdziwość zdania A: budynek X postrzegamy jako mniejszy od Y, bo X stoi
dalej od nas niż Y.

Piotr Łukowski, Wykład dla studentów pedagogiki

25

Przypomnienie

Entymemat, to przesłanka niewypowiedziana z powodu oczywistości jej prawdziwości.

Przykład
Zamiast wypowiedzieć na głos argumentację:
A. Każdy człowiek jest śmiertelny. Sokrates jest człowiekiem. Zatem, Sokrates jest śmiertelny.

Można powiedzieć krócej:
B. Sokrates jest człowiekiem. Zatem, Sokrates jest śmiertelny.

W rozumowaniu B, oczywista przesłanka „Każdy człowiek jest śmiertelny” została pominięta
jako prawdziwa w sposób oczywisty.

[jest to przykład rozumowania opartego na związku przyczynowo-skutkowym]

Koniec przypomnienia

Piotr Łukowski, Wykład dla studentów pedagogiki

26

Rozumowanie indukcyjne (indukcja) to szczególny przypadek tłumaczenia -
tłumaczenie uogólniające. Polega ono na tym, że na podstawie szeregu zdań
szczegółowych formułuje się zdanie ogólne.

Przykład
Ten wróbel jest szary.
I ten wróbel jest szary.
I tamten wróbel także jest szary.
...
Zatem,
każdy wróbel jest szary.

Komentarz:

Indukcja ta jest tłumaczeniem, bo związkiem logicznym jaki uznajemy za prawdziwy jest ten,
wyrażony przez implikację:

„Jeśli każdy wróbel jest szary, to ten wróbel jest szary”

Zatem, rozumując indukcyjnie dobieramy rację do znanego skądinąd jako prawdziwe następstwa.

Piotr Łukowski, Wykład dla studentów pedagogiki

27

1. Indukcja przez wyliczenie (enumeracyjna) polega na tym, że sprawdza się
prawdziwość szeregu zdań szczegółowych podpadających pod pewien ogólny schemat
i na tej podstawie formułuje się zdanie ogólne odpowiadające temu schematowi.

Ponieważ,

S

1

jest P

i S

2

jest P

i S

3

jest P

i S

4

jest P

i S

5

jest P

i S

6

jest P,

więc,

Każde S jest P.

Jeśli wykorzystane w rozumowaniu indukcyjnym zdania szczegółowe wyczerpują
wszystkie przypadki spełnienia zdania ogólnego, będącego wnioskiem tego
rozumowania, to indukcję taką nazwiemy wyczerpującą (zupełną). W przeciwnym
razie, indukcja jest niewyczerpująca (niezupełna).

Oczywiście, indukcja wyczerpująca jest rozumowaniem niezawodnym, zaś
niewyczerpująca, zawodnym.

Piotr Łukowski, Wykład dla studentów pedagogiki

28

Podany wcześniej przykład z wróblami, ilustruje indukcję niewyczerpującą - nie jesteśmy w
stanie sprawdzić koloru upierzenia wszystkich wróbli - a więc zawodną.

Przykład indukcji wyczerpującej:

Pierwsza osoba siedząca w tej sali ma mniej niż 80 lat.
Druga osoba siedząca w tej sali ma mniej niż 80 lat.
Trzecia osoba siedząca w tej sali ma mniej niż 80 lat.
...
Dwudziesta ósma osoba siedząca w tej sali ma mniej niż 80 lat.
...

Wypowiadanie zdań szczegółowych dotyczących osób znajdujących się w auli podczas naszego
wykładu z logiki kończymy wówczas, gdy wypowiemy się na temat każdej osoby przebywającej
w auli podczas wykładu. Zatem, zdania szczegółowe wyczerpują wszystkie możliwe przypadki
spełnienia zdania ogólnego „Każda osoba przebywająca w auli ma mniej niż 80 lat”. Zatem,
zdanie „Każda osoba przebywająca w auli ma mniej niż 80 lat” jest wnioskiem wyciągniętym na
mocy indukcji wyczerpującej z wszystkich zdań szczegółowych.
Naturalnie, wniosek ten jest niezawodny chociaż trywialny, jałowy, nieciekawy, nieistotny.

Piotr Łukowski, Wykład dla studentów pedagogiki

29

2. Indukcja matematyczna bazuje na dwóch przesłankach:
- sprawdzającej czy dana własność W jest spełniona w przypadku pierwszym z całej
serii przypadków
oraz
- indukcyjnej, stwierdzającej dziedziczenie własności W, czyli stwierdzającej że jeśli
którykolwiek z przypadków ma własność W, to własność W ma przypadek
bezpośrednio po nim następujący.

Zatem, istotną rolę w indukcji matematycznej odgrywa uporządkowanie wszystkich
możliwych przypadków. Standardowo, w celu uporządkowania tych przypadków
wykorzystuje się zbiór liczb naturalnych.

Piotr Łukowski, Wykład dla studentów pedagogiki

30

Przykłady tez dowodzonych w oparciu o indukcję matematyczną:

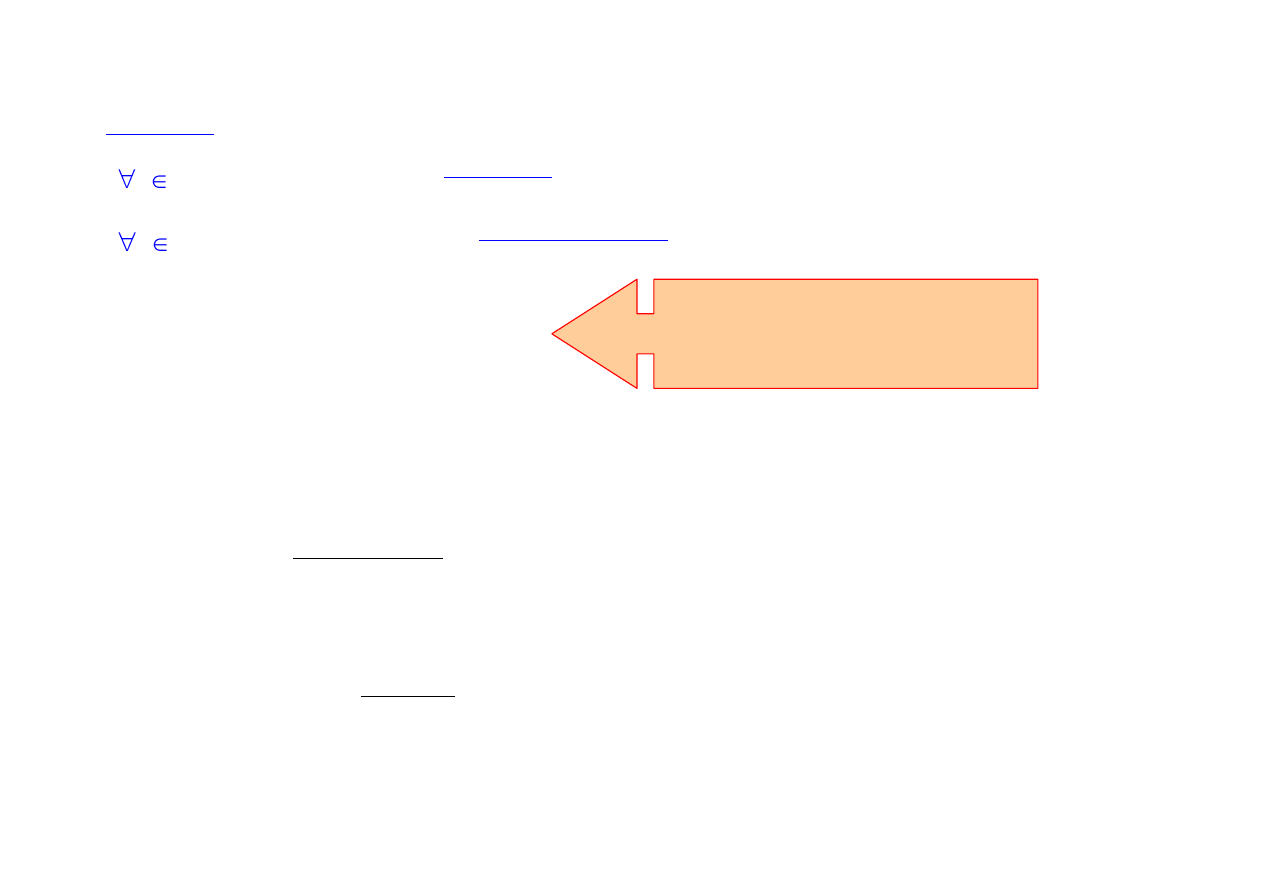
n N 1 + 2 + 3 + ... + n =

n(n + 1)

2

n N 1

2

+ 2

2

+ 3

2

+ ... + n

2

=

n(n + 1)(2n + 1)

6

Każdy człowiek jest łysy.
Każdy człowiek jest niełysy.
Każdy człowiek jest staruszkiem.
Każdy człowiek jest noworodkiem.

Jest to dość poważny problem logiczno-filozoficzny, który wiąże się ściśle z tak zwaną
tolerancyjnością wyrażeń języka naturalnego.

Wyrażenie jest tolerancyjne, jeśli z faktu jego zastosowania w danym przypadku P
wynika, że może ono być zastosowane w przypadku zbliżonym do P.

Z konieczności wszystkie pozamatematyczne wyrażenia języka naturalnego są
tolerancyjne. Zatem, niestety, każde z nich daje się wykorzystać w rozumowaniu przez
indukcję matematyczną, co w konsekwencji prowadzi do paradoksu sorites.

Czy zatem, indukcja

ma

tematyczna może być

stosowana poza matematyką?

Piotr Łukowski, Wykład dla studentów pedagogiki

31

3. Indukcja eliminacyjna to rozumowanie uogólniające, którego celem jest wykrycie
związków jakie zachodzą między faktami, przy czym, uogólnienie to jest typu:

„Zawsze ilekroć jest (względnie zmienia się w określony sposób) A,
to jest (względnie zmienia się w określony sposób) B.”

John Stuart Mill

(1806 - 1873)

Przykładami indukcji eliminacyjnej są Kanony Milla (A System of Logic, 1843):

- kanon jedynej zgodności
- kanon jedynej różnicy
- kanon zgodności i różnicy
- kanon zmian towarzyszących
- kanon reszt

(dawno temu odrzucony - i bardzo dobrze)

Piotr Łukowski, Wykład dla studentów pedagogiki

32

Kanon jedynej zgodności

Jeśli okoliczność O stale towarzyszy występowaniu zjawiska Z mimo, iż inne
okoliczności nie zachodzą stale, to między O i Z zachodzi związek przyczynowo-
skutkowy:

albo O jest przyczyną Z,
albo O jest skutkiem Z,
albo O jest niezbędną częścią przyczyny wywołującej Z,
albo Z jest niezbędną częścią przyczyny wywołującej O.

Schemat kanonu jedynej zgodności:

jest A,B,C - jest Q

jest A,C,D - jest Q

jest A,B,D - jest Q

Zatem, ilekroć jest A, to jest i Q

Oczywiście, rozumowanie bazujące na kanonie jedynej zgodności jest zawodne, gdyż
np. nie zawsze jesteśmy w stanie uwzględnić (rozpoznać) wszystkie istotne
okoliczności zajścia danego zjawiska.

Piotr Łukowski, Wykład dla studentów pedagogiki

33

Przykład trafnego zastosowania kanonu jedynej zgodności

1. Jest (A) ukąszenie przez zakażoną wesz, (B) brud, (C) głód - jest (Q) tyfus plamisty.
2. Jest (A) ukąszenie przez zakażoną wesz, (C) głód, (D) złe warunki mieszkaniowe - jest (Q)
tyfus plamisty.
3. Jest (A) ukąszenie przez zakażoną wesz, (B) brud, (D) złe warunki mieszkaniowe - jest (Q)
tyfus plamisty.
Zatem, jedynym czynnikiem stale poprzedzającym (Q) zachorowanie na tyfus plamisty jest (A)
ukąszenie przez zarażoną wesz.

Piotr Łukowski, Wykład dla studentów pedagogiki

34

Przykład 1 nietrafnego zastosowania kanonu jedynej zgodności

1. Jest (A) herbata zielona, (B) nieświeża wędlina, (C) stary ser - są (Q) problemy.
2. Jest (A) herbata zielona, (C) stary ser, (D) przeterminowany jogurt - są (Q) problemy.
3. Jest (A) herbata zielona, (B) nieświeża wędlina, (D) przeterminowany jogurt - są (Q) problemy.
Zatem, jedynym czynnikiem stale poprzedzającym (Q) problemy układu pokarmowego jest (A) herbata
zielona.

Przykład 2 nietrafnego zastosowania kanonu jedynej zgodności

1. Jest (A) herbata zielona, (B) wędlina, (C) ser - są (Q) problemy układu pokarmowego.
2. Jest (A) herbata zielona, (C) ser, (D) owoce - są (Q) problemy układu pokarmowego.
3. Jest (A) herbata zielona, (B) wędlina, (D) owoce - są (Q) problemy układu pokarmowego.
Zatem, jedynym czynnikiem stale poprzedzającym (Q) problemy układu pokarmowego jest (A) herbata
zielona.

Przykład 3 nietrafnego zastosowania kanonu jedynej zgodności

1. Mając na sobie (A) niebieską koszulę w kratkę zjadłem (B) wędlinę - (Q) zatrułem się.
2. Mając na sobie (A) niebieską koszulę w kratkę zjadłem (C) ser - (Q) zatrułem się.
3. Mając na sobie (A) niebieską koszulę w kratkę zjadłem (D) jogurt - (Q) zatrułem się.
Zatem, jedynym czynnikiem stale poprzedzającym zatrucie pokarmowe (Q) jest to, że (A) mam na sobie
niebieską koszulę w kratkę.

Piotr Łukowski, Wykład dla studentów pedagogiki

35

Kanon jedynej różnicy

(Mill uważał ten kanon za najważniejszy)

Jeśli okoliczność Q zachodzi, gdy występuje zjawisko A i Q nie zachodzi, gdy A nie
występuje, przy czym wszystkie inne okoliczności zachodzą stale, to między Q i A
zachodzi związek przyczynowo-skutkowy.


Schemat kanonu jedynej różnicy:

jest A,B,C - jest Q

nie ma A, jest B,C - nie ma Q

Zatem, ilekroć jest A, to jest i Q

Oczywiście, rozumowanie bazujące na kanonie jedynej różnicy jest zawodne.

Piotr Łukowski, Wykład dla studentów pedagogiki

36

Przykład trafnego/nietrafnego zastosowania kanonu jedynej różnicy

1. Zjadłem (A) pomidory, (B) ser pleśniowy, (C) saszimi - miałem wysypkę.
2. Zjadłem (B) ser pleśniowy, (C) saszimi - nie miałem wysypki.
Zatem, jedyną spośród A, B i C potrawą, na którą jestem uczulony są (A) pomidory.



Przykład nietrafnego zastosowania kanonu jedynej różnicy

Załóżmy, że na niezakłóconą pracę silnika ma wpływ jednoczesne funkcjonowanie trzech
elementów systemu: A, B i C.
1. Elementy A, B i C systemu działają - silnik pracuje.
2. Elementy B i C systemu działają, a element A systemu nie działa - silnik nie pracuje.
Zatem, jedynym czynnikiem mającym wpływ na działanie silnika jest element A systemu.

Piotr Łukowski, Wykład dla studentów pedagogiki

37

Kanon zgodności i różnicy

Kanon powstały z połączenia kanonu jedynej zgodności z kanonem jedynej różnicy.
Ma zdaniem Milla większą wartość niż każdy z tych dwóch kanonów zastosowany
oddzielnie. W praktyce, najczęściej stosuje się najpierw jeden kanon, potem drugi.

Piotr Łukowski, Wykład dla studentów pedagogiki

38

Kanon zmian towarzyszących

Jeśli w zaobserwowanych przypadkach odpowiednim zmianom A towarzyszą
odpowiednie zmiany Q, gdy pozostałe czynniki nie ulegają zmianie, to między A i Q
zachodzi związek przyczynowo-skutkowy.

Schemat kanonu jedynej różnicy:

jest A

1

,B,C - jest Q

1

jest A

2

,B,C - jest Q

2

jest A

3

,B,C - jest Q

3

jest A

4

,B,C - jest Q

4

jest A

5

,B,C - jest Q

5

Zatem, ilekroć w określony sposób zmienia się A,
to w określony sposób zmienia się Q.

Oczywiście, rozumowanie bazujące na kanonie zmian towarzyszących jest zawodne.

Kanon zmian towarzyszących bazuje na zasadzie jedyności przyczyn - dla każdego
zjawiska istnieje jego nieodłączna przyczyna.

(odrzucona - i bardzo słusznie)

Piotr Łukowski, Wykład dla studentów pedagogiki

39

Przykłady trafnego zastosowania kanonu zmian towarzyszących

Przekręcam gałką ściemniacza (A) - zwiększa się jasność świecenia żarówek w żyrandolu (Q).
Przekręcam gałką grzejnika (A), inny sprzęt elektryczny pracuje bez zmian - zwiększa się

obserwowany na liczniku pobór prądu (Q).



Przykład nietrafnego zastosowania kanonu zmian towarzyszących

Postępujące zmiany klimatyczne są wywołane rosnącą liczbą latających samolotów. (przykład

autentyczny, bo podsłuchany w tramwaju)

Obserwowany od pewnego czasu stały spadek wagi swojego ciała Jan tłumaczy jakąś

nierozpoznaną jeszcze poważną chorobą i zaczyna podejrzewać, że ma nowotwór. Tymczasem,
stały spadek wagi jest wywołany rosnącym stresem w pracy, spowodowanym wdrażaniem
nowych metod funkcjonowania firmy.

Świadomość nietrafnego wnioskowania opartego na obserwacji zakazuje stosowania pewnych

leków w pewnych sytuacjach, gdyż ich przyjmowanie może przez jakiś czas likwidować objawy
chorobowe wywołane np. nowotworem.

Piotr Łukowski, Wykład dla studentów pedagogiki

40

Kanon reszt

(dziś uważany za szczególnie kontrowersyjny)

Jeśli jakaś całość AB jest przyczyną całości ab i B jest przyczyną b, to A jest przyczyną
a.

Wadą tego rozumowania jest sztuczne (czysto spekulatywne) rozdzielanie całości na
części, które samodzielnie nie powinny być brane pod uwagę.

Jeśli

procesy górotwórcze, erozja spowodowana wiatrami, osadnictwo europejskie w
Ameryce, śluby pradziadków Johna, śluby dziadków Johna, ślub rodziców Johna, ...
, zepsucie się dachu, złe samopoczucie Johna i deszcz

spowodowały, że

John kupił ziemię, wybudował dom, robotnicy wadliwie wykonali dach, John nie był
w pracy z powodu złego samopoczucia, stracił życie (bo wchodził na drabinę
postawioną na śliskiej od wody skale, na której stał dom),

to jak tu przyporządkować oddzielne skutki do oddzielnie pojmowanych przyczyn?

Piotr Łukowski, Wykład dla studentów pedagogiki

41

Analogia

(wyjątkowo inspirujące, a przez to twórcze rozumowanie)

to rozumowanie, w którym na zasadzie wspólności kilku cech dwóch lub więcej
przedmiotów domyślamy się wspólności innych cech tych przedmiotów. Analogia nie
jest ani rozumowaniem dedukcyjnym, ani redukcyjnym.

Konkretnie:
Jeśli przedmiot A jest podobny do przedmiotu B o tyle, że cechom a, b, c przedmiotu A
odpowiadają cechy a, b, c przedmiotu B, a ponadto przedmiot A posiada cechę d, to
przypuszczamy, że przedmiot B także posiada cechę d.

Przykłady

Jeśli Tuluza jest dużym miastem Unii Europejskiej i nie ma dziurawych ulic, to skoro Łódź

także jest dużym miastem Unii Europejskiej, to Łódź też nie ma dziurawych ulic. 

Jeśli Drezno jest miastem Unii Europejskiej i nie ma na ulicach psich kup w ilościach

statystycznych, to skoro Łódź także jest miastem Unii Europejskiej, to Łódź też nie ma na
ulicach psich kup w ilościach statystycznych. 

Wartość analogii polega nie na uzasadnianiu, bo do tego analogia się raczej nie nadaje, lecz na
roli inspirującej poszukiwania trafnych rozwiązań. Analogia nie uzasadnia tez, lecz naprowadza
na nowy trop, podpowiada gdzie szukać nowych rozwiązań.