Piotr Łukowski, Wykład dla studentów pedagogiki

1

Logika

- 3 -

nazwa

Piotr Łukowski, Wykład dla studentów pedagogiki

2

Piotr Łukowski, Logika praktyczna z elementami wiedzy o manipulacji, Wolters
Kluwer Polska, Warszawa 2012.

Kazimierz Ajdukiewicz, Logika pragmatyczna, PWN, Warszawa 1965.

Edward Nieznański, Logika, Wydawnictwo C.H. Beck, Warszawa 2006

Zygmunt Ziembiński, Logika praktyczna, PWN, Warszawa, [1959-] 2006.

i wiele innych książek

Piotr Łukowski, Wykład dla studentów pedagogiki

3

Składniki zdań - kategorie syntaktyczne - nazwa

znaczeniowo samodzielne

znaczeniowo niesamodzielne

kategorie składniowe

nazwy

zdania

funktory

operatory

Piotr Łukowski, Wykład dla studentów pedagogiki

4

Nazwą nazywamy wyrażenie mogące wystąpić w zdaniu jako podmiot lub orzecznik
orzeczenia imiennego.

Orzeczenie imienne to orzeczenie stwierdzające o podmiocie, że jest taki a taki.

Zatem, jeśli mamy zdanie „a jest b”, to a jest w tym zdaniu podmiotem, a b
orzecznikiem orzeczenia imiennego.

Piotr Łukowski, Wykład dla studentów pedagogiki

5

Oznaczanie Nazwa oznacza, przy pewnym swym znaczeniu, każdy i tylko taki
przedmiot, o którym można zgodnie z prawdą tę nazwę orzec. Oznaczanie, to stosunek
jaki zachodzi między nazwą a jej desygnatem.

Desygnat
Przedmiot oznaczony przez nazwę jest jej desygnatem.

Zakres nazwy (denotacja, ekstensja, ekstensja pozytywna) Zbiór wszystkich
desygnatów nazwy jest jej zakresem.

Denotowanie, to stosunek zachodzący między nazwą a jej zakresem.

Równoważność nazw Nazwy mające ten sam zakres są równoważne
(równozakresowe).

Znaczenie nazwy generalnej (konotacja), to przyjęty w języku sposób jej rozumienia,
zwany też pojęciem, ustalony przez treść nazwy generalnej.

Patrz dalej.

Piotr Łukowski, Wykład dla studentów pedagogiki

6

Klasyfikacje nazw

1. ze względu na budowę

2. ze względu na oznaczanie (desygnaty/zakres)

2.1. ze względu na ilość desygnatów
2.2. ze względu na kategorię desygnatów
2.3. ze względu na strukturę desygnatu
2.4. ze względu na rozpoznawalność desygnatu

3. ze względu na znaczenie (treść nazwy)

3.1. ze względu na posiadanie znaczenia

3.1.1. ze względu na rodzaj korelatu semantycznego (supozycję)
3.1.2. ze względu na ilość znaczeń
3.1.3. ze względu na intencję znaczeniową
3.1.4. ze względu na rozpoznawalność znaczenia
3.1.5. ze względu na zmienność znaczenia

Piotr Łukowski, Wykład dla studentów pedagogiki

7

1. ze względu na budowę (postać zewnętrzną, czyli ilość wyrazów tworzących
nazwę):
- prosta, to nazwa składająca się z jednego wyrazu (np. „psycholog”)
- złożona, to nazwa składająca się z więcej niż jednego wyrazu, czyli taka która nie jest
prosta (np. „koszmarny sen studenta w sesji poprawkowej”)

Piotr Łukowski, Wykład dla studentów pedagogiki

8

2. ze względu na oznaczanie (desygnaty/zakres)

2.1. ze względu na ilość desygnatów:
- pusta, to nazwa bez desygnatu (np. „krasnoludek”). Szczególnym przypadkiem nazw
pustych są nazwy sprzeczne (np. „żonaty kawaler”, „drewniane żelazo”, „kwadratowe
koło”)
- jednostkowa, to nazwa mająca jeden desygnat (np. „najwyższa góra na świecie”)
- ogólna, to nazwa mająca więcej niż jeden desygnat (np. „student”)



Nazwa sprzeczna to taka nazwa, dla której założenie istnienia jej desygnatu prowadzi
do sprzeczności.

Sprzecznością jest koniunkcja dwóch zdań, z których jedno jest negacją
(zaprzeczeniem) drugiego:

A i nie-A.

Piotr Łukowski, Wykład dla studentów pedagogiki

9

Przykład (nie na egzamin, ale dla zainteresowanych) „Żonaty kawaler” jest nazwą sprzeczną,
ponieważ założenie, iż nie jest nazwą pustą prowadzi do sprzeczności. Wprowadźmy
oznaczenia:

ŻK(x) - „x jest żonatym kawalerem”
Ż(x) - „x jest żonaty”
K(x) - „x jest kawalerem”
mŻ(x) - „x ma żonę”
a należy do zbioru wszystkich mężczyzn

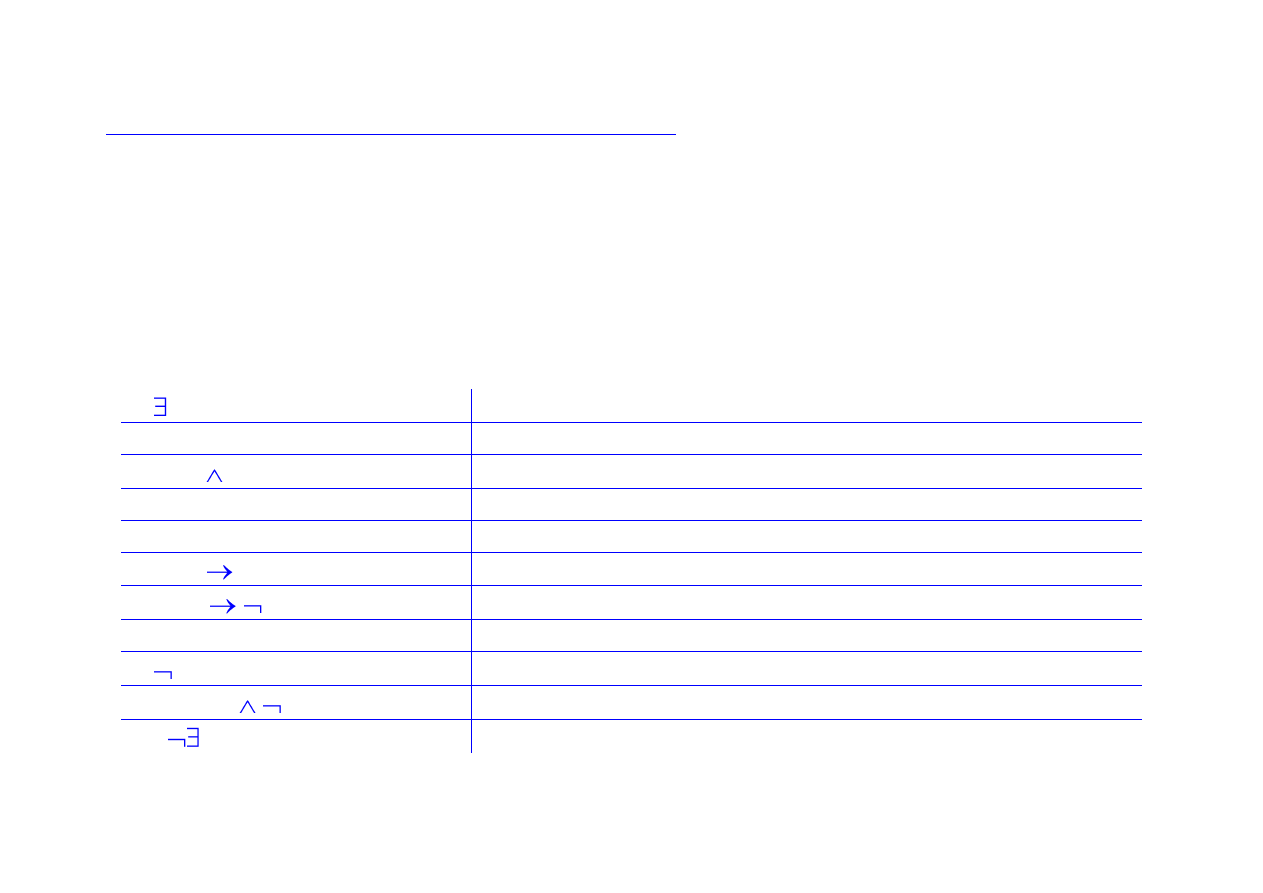
1. x ŻK(x)

założenie istnienia żonatego kawalera

2. ŻK(a)

opuszczanie kwantyfikatora szczegółowego, 1

3. Ż(a) K(a)

interpretacja predykatu ŻK, 2

4. Ż(a)

odłączanie koniunkcji, 3

5. K(a)

odłączanie koniunkcji, 3

6. Ż(a)

mŻ(a)

teza pomocnicza

7. K(a)

mŻ(a)

teza pomocnicza

8. mŻ(a)

odrywanie następnika implikacji (Modus Ponens), 4, 6

9. mŻ(a)

odrywanie następnika implikacji (Modus Ponens), 5, 7

10. mŻ(a) mŻ(a)

dołączanie koniunkcji, 8, 9 - prowadzi do

sprzeczności

11.

x ŻK(x)

1-10

Piotr Łukowski, Wykład dla studentów pedagogiki

10

Sprzeczność bywa nazywana absurdem - wyrażenie absurdalne ma znaczenie, ale
generuje sprzeczność. Nonsens, to wyrażenie, które nie ma znaczenia.

Zatem,

absurd nonsens.

Piotr Łukowski, Wykład dla studentów pedagogiki

11

2.2. ze względu na kategorię desygnatów (czy odnoszą się do obiektów materialnych
lub ich wyobrażeń, czy nie):
- konkretna, to nazwa oznaczająca osobę lub rzecz lub wyobrażenie osoby lub
wyobrażenie rzeczy (np. „pedagog”, „łamigłówka” (jako rzecz), „nieomylny
psycholog”)
- abstrakcyjna, to nazwa, która nie jest konkretna

(dychotomiczne, ścisłe, eleganckie

definiowanie)

(np. „przyjaźń”, „łamigłówka” (jako problem), „zboczenie”)

Błąd hipostazowania polega na takim rozumieniu nazwy abstrakcyjnej jakby była ona
konkretną. Np. „To są ofiary stalinizmu” - stalinizm nikogo nie zamordował, to
konkretni ludzie mordowali innych ludzi.
Trik erystyczny „ucieczka w abstrakcję” wykorzystuje właśnie błąd hipostazowania.

Piotr Łukowski, Wykład dla studentów pedagogiki

12

2.4. ze względu na rozpoznawalność desygnatu:
- ostra, to nazwa, dla której zawsze możemy bez wątpliwości i jednoznacznie
stwierdzić, czy dany, dowolnie wybrany obiekt jest jej desygnatem, czy nie jest. Np.
„kwadrat”, „koło”, funkcja monotoniczna”, „zbiór liczb wymiernych”, „byt”, „niebyt”,
„ruch”, „bezruch”, „spoczynek”.
- nieostra, to nazwa która nie jest ostra. Nieostrymi są wszystkie nazwy i predykaty
języka naturalnego z wyjątkiem takich nazw jak „byt”, „niebyt”, „ruch”, „bezruch”,
„spoczynek” oraz odpowiadających im predykatów.

Kryterium rozpoznawania nieostrości dostarcza rozumowanie zwane paradoksem
stosu. Każde wyrażenie nieostre cechuje się właśnie tym, że zastosowana do niego
argumentacja stosu prowadzi do sprzeczności.

Piotr Łukowski, Wykład dla studentów pedagogiki

13

Problem nieostrości

Eubulides z Miletu (IV w. p.n.e.) uczeń Euklidesa z Megary (ok. 400 p.n.e.), twórcy
erystyki.

Bertrand Arthur William Russell (1872-1970)
[1923] Vagueness - artykuł będący zapisem referatu wygłoszonego w Jowett Society w
Oxfordzie 25 listopada 1922.

Piotr Łukowski, Wykład dla studentów pedagogiki

14

Bertrand Arthur William Russell (1872-1970):
[1922] Umieranie jest procesem polegającym na wygaszaniu wielu funkcji
życiowych. Funkcje te ustają w wyniku trwającego w czasie procesu. W którym
momencie można stwierdzić wyraźnie, że nie mamy do czynienia z człowiekiem, lecz
ze zwłokami?

Brak możliwości jednoznacznego i zadowalającego wszystkich rozwiązania tego problemu ma swoje
konsekwencje w fakcie, iż w konkretnych przypadkach nie jest jasne, czy można odłączyć kogoś od
aparatury podtrzymującej życie, czy należy to podtrzymywanie kontynuować - nie ma możliwości jasnego
sprecyzowania tego co się określa mianem „uporczywej terapii”.

Czy n-minutowy płód jest człowiekiem? Jeśli tak, to (n-1)-minutowy płód też jest
człowiekiem. Zatem, każdy płód jest człowiekiem - z człowiekiem mamy do
czynienia od chwili poczęcia.
Czy n-minutowy płód jest nie-człowiekiem (czyli nie jest człowiekiem)? Jeśli tak, to
(n+1)-minutowy płód też jest nie-człowiekiem. Zatem, każdy płód, do samej chwili
narodzin jest nie-człowiekiem, czyli nie jest człowiekiem - człowieczeństwo pojawia
się więc nagle w chwili narodzin.

Brak możliwości jednoznacznego i zadowalającego wszystkich rozwiązania tego problemu ma swoje
konsekwencje w fakcie, iż aborcja jest i (chyba zawsze) będzie problemem prowokującym dyskusję.

Piotr Łukowski, Wykład dla studentów pedagogiki

15

Leon Chwistek (1884-1944):
[1934] Czy matką człowieka może być nie-człowiek? Oczywiście, że nie. Matką
każdego człowieka jest człowiek. Wybierzmy więc dowolnego człowieka i zacznijmy
podróż w czasie w przeszłość podążając tropem jego przodkiń: matki, matki

2

,

matki

3

,..., matki

n

,... itd. (matka

1

= matka oraz matka

n+1

= matka matki

n

, dla dowolnej

liczby naturalnej n 1). Jeśli wędrówka ta będzie trwała odpowiednio długo, to okaże
się że, dla pewnej liczby naturalnej k, matka

k

nie jest już człowiekiem lecz jakimś

drobnym ssakiem pierwotnym, a dla jakiejś większej od k liczby naturalnej m, nie
sposób już mówić o płci matki

m

. Jeśli jednak pierwszą przodkinię, niewątpliwie będącą

człowiekiem, nazwaliśmy człowiekiem, to posługując się konsekwentnie naszym
oczywistym założeniem, jakiś pierwotny, jednokomórkowy organizm również musimy
nazwać człowiekiem.

Nazwa „człowiek” reprezentuje tu nazwę dowolnej istoty żywej. Zatem,
r

ozumowanie to można powtórzyć, dla każdej innej nazwy istoty żywej.

Piotr Łukowski, Wykład dla studentów pedagogiki

16

Max Black (1909-1988):
[1937] Wyobraźmy sobie niezwykłą wystawę w niezwykłym Muzeum Logiki
Stosowanej, przedstawiającą szereg złożony z tysięcy przedmiotów. Każde dwa
sąsiadujące ze sobą przedmioty różnią się w możliwie najmniejszy, prawie
niedostrzegalny sposób. Na jednym końcu tego długiego szeregu stoi pierwszy obiekt
będący doskonale wykonanym krzesłem Chippendale'a. Drugim obiektem jest idealna
kopia pierwszego obiektu, która jednak uległa bardzo nieznacznemu uszkodzeniu -
różni się od niego drobnym ledwo dostrzegalnym ubytkiem. Trzeci obiekt różni się od
poprzedniego podobnie ledwie dostrzegalnym ubytkiem, itd. Na drugim końcu tego
niezwykle długiego szeregu tak określonych obiektów spoczywa mały, bliżej
nieokreślony kawałek drewna, będący fragmentem nogi idealnej kopii wspomnianego
krzesła. Jeśli więc, pierwszy obiekt nazwiemy krzesłem, to każdy następny musimy
nazwać krzesłem, a zatem konsekwentnie, także kawałek nogi krzesła również będzie
musiał być przez nas nazwany krzesłem. Przecież, tak maleńki, jak tu rozważany
ubytek z żadnego krzesła nie uczyni nie-krzesło. Podobnie, jeśli kawałek nogi krzesła
nazwiemy nie-krzesłem, to każdy poprzedzający obiekt musimy nazwać nie-krzesłem,
a więc w szczególności i doskonały wytwór Chippendale’a.

Nazwa „krzesło” reprezentuje tu nazwę dowolnego obiektu materialnego. Zatem,
r

ozumowanie to można powtórzyć, dla każdej innej nazwy obiektu materialnego.

Piotr Łukowski, Wykład dla studentów pedagogiki

17

Roy Sorensen:
[1990] Czy pozbawienie kogoś jednej kropli krwi jest zabójstwem? Nie.
Czy pozbawienie kogoś o jedną kroplę krwi więcej niż ilość, której pozbawienie nie
jest zabójstwem, jest zabójstwem? Nie.
Itd.

A przecież Czy pozbawienie kogoś takiej ilości kropel krwi, która odpowiada jej
czterem litrom jest zabójstwem.

Zatem, nie ma wyraźnej granicy między zabójstwem a nie-zabójstwem.

Piotr Łukowski, Wykład dla studentów pedagogiki

18

Ekstensja pozytywna nazwy nieostrej (ekstensja), to kolekcja (nie zbiór w sensie
matematycznym!) tych obiektów (przypadków), o których orzekanie tej nazwy jest
prawdą. Innymi słowy, są to te obiekty które bez wątpienia są desygnatami tej nazwy.
Ekstensja negatywna nazwy nieostrej (antyekstensja), to kolekcja (nie zbiór w sensie
matematycznym!) tych obiektów (przypadków), o których orzekanie tej nazwy jest
fałszem. Innymi słowy, są to te obiekty które bez wątpienia nie są desygnatami tej
nazwy.
Obszar nieostrości nazwy nieostrej tworzą te obiekty (przypadki), które nie należą, ani
do ekstensji pozytywnej, ani do ekstensji negatywnej tej nazwy.

Dla zdecydowanej większości nazw nieostrych, żadna z ekstensji, a więc i obszar
nieostrości nie jest zbiorem, czyli nie jest wyznaczona w jednoznaczny sposób przez
swoje elementy (przypadki). Mówi się o nich, że są zbiorami rozmytymi, czyli
zbiorami o niewyraźnych granicach.

Błąd nieostrości polega na stosowaniu nazwy nieostrej poza jej ekstensjami:
pozytywną i negatywną. Pragmatyczne podejście do nieostrości to koncepcja
zakładająca stosowanie terminów nieostrych jedynie w sytuacjach, które nie budzą
wątpliwości, czyli w zakresie wyznaczonym przez sumę ekstensji pozytywnej i
negatywnej. Naturalnie, koncepcja ta jest stosowana od zawsze.