
Teoria miary i całki
Spis treści
1
Wstęp
3
2
Algebra zbiorów
5
3
Pierścienie, ciała, σ
−ciała zbiorów.
7
3.1
Definicja pierścienia ciała i σ
−ciała . . . . . . . . . . . . . . .
7
3.2
Pierścień, ciało i σ
−ciało generowane przez rodzinę zbiorów. . 10
3.3
Rodziny monotoniczne zbiorów . . . . . . . . . . . . . . . . .
10
4
Półpierścienie
13
4.1
Definicja półpierścienia . . . . . . . . . . . . . . . . . . . . . .
13
4.2
Pierścień generowany przez półpierścień . . . . . . . . . . . .
13
4.3
Iloczyn kartezjański półpierścieni . . . . . . . . . . . . . . . .
15
5
Funkcje addytywne i miary.
17
5.1
Pojęcie funkcji addytywnej
. . . . . . . . . . . . . . . . . . .
17
5.2
Miary na σ
−ciele . . . . . . . . . . . . . . . . . . . . . . . . . 18
5.3
Zupełność miary . . . . . . . . . . . . . . . . . . . . . . . . .
21
6
Funkcje addytywne i miary na półpierścieniach
23
6.1
Funkcje addytywne i miary na dowolnej rodzinie zbiorów . . .
23
6.2
Przedłużanie funkcji addytywnych i miar z półpierścienia na
pierścień . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
7
Funkcja addytywna na iloczynie kartezjańskim półpierścieni 26
7.1
Miara Jordana generowana przez funkcję addytywną . . . . .
27
8
Miara zewnętrzna
28
8.1
Definicja i własności miary zewnętrznej
. . . . . . . . . . . .
28
8.2
Twierdzenie Caratheodyr’ego . . . . . . . . . . . . . . . . . .
28
8.3
Ogólna metoda konstrukcji miary zewnętrznej . . . . . . . . .
33
8.4
Miara zewnętrzna generowana przez funkcję addytywną na
półpierścieniu . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
1

9
Miara Lebesque’a w
R
k
35
9.1
Przedziały k
−wymiarowe, figury elementarne . . . . . . . . . 35
9.2
Objętość figur elementarnych . . . . . . . . . . . . . . . . . .
38
9.3
Miara zewnętrzna Lebesque’a w
R
k
. . . . . . . . . . . . . . .
40
9.4
Zbiory mierzalne w sensie Lebesque’a . . . . . . . . . . . . . .
41
9.5
Zbiory borelowskie . . . . . . . . . . . . . . . . . . . . . . . .
46
9.6
Miara wewnętrzna Lebesque’a . . . . . . . . . . . . . . . . . .
47
9.7
Miara Jordana
. . . . . . . . . . . . . . . . . . . . . . . . . .
48
9.8
Jedyność miary Lebsque’a . . . . . . . . . . . . . . . . . . . .
50
10 Funkcje mierzalne
52
10.1 Definicja funkcji mierzalnych, podstawowe własności . . . . .
52
10.2 Ciągi funkcji mierzalnych
. . . . . . . . . . . . . . . . . . . .
57
10.3 Funkcje proste
. . . . . . . . . . . . . . . . . . . . . . . . . .
58
10.4 Funkcje mierzalne względem σ
−ciała zbiorów mierzalnych w
sensie Lebesque’a . . . . . . . . . . . . . . . . . . . . . . . . .
60
11 Zbieżność prawie wszędzie i zbieżność według miary
63
12 Całka Lebesque’a
65
12.1 Całka funkcji nieujemnych . . . . . . . . . . . . . . . . . . . .
65
12.2 Funkcje całkowalne . . . . . . . . . . . . . . . . . . . . . . . .
68
13 Całka Lebesque’a a całka Riemanna
72
14 Iloczyn kartezjański miar
73
14.1 Iloczyn kartezjański półpierścieni . . . . . . . . . . . . . . . .
73
14.2 Miara na iloczynie kartezjańskim półpierścieni . . . . . . . . .
74
14.3 Iloczyn kartezjański przestrzeni z miarą . . . . . . . . . . . .
74
15 Miary zespolone
76
2

1
Wstęp
Problem. Czy istnieje funkcja µ : 2
R
k
→ [0, ∞] taka, że
(i) µ(
∅) = 0,
(ii) µ(
∞
∪
n=1
A
n
) =
∞
∑
n=1
µ(A
n
),
(iii) µ(P ) =
|P | dla dowolnego przedziału k−wymiarowego P,
(iv) µ(A + x) = µ(A) dla dowolnego zbioru A
⊂ R
k
i dowolnego x
∈ R
k
.
Twierdzenie 1.1 Nie istnieje funkcja µ : 2
R
→ [0, ∞] spełniająca warunki
(i), (ii), (iii), (iv).
Dowód. Załóżmy, że funkcja µ : 2
R
k
→ [0, ∞] spełnia warunki (i), (ii), (iii).
Zauważmy, że z warunku (ii) wynika, że dla dowolnych zbiorów A, B
∈ R,
jeżeli A
⊂ B, to µ(A) 6 µ(B).
Zdefiniujmy zbiór V
⊂ [0, 1] w następujący sposób. Zdefiniujmy relację
∼ w zbiorze [0, 1] w sposób następujący: x ∼ y ⇔ x − y ∈ Q. Łatwo spraw-
dzić, że relacja
∼ jest relacją równoważności w [0, 1]. Jak wiadomo dowolna
relacja w zbiorze rozbija ten zbiór na sumę rodziny podzbiorów niepustych
i parami rozłącznych mianowicie na sumę klas abstrakcji tej relacji. Niech
V będzie zbiorem zawierającym po dokładnie jednym elemencie każdej kla-
sy abstrakcji relacji
∼ . Ustawmy dalej wszystkie liczby wymierne odcinka
[
−1, 1] w ciąg q
1
, q
2
, ... i niech V
n
= q
n
+ V. Wówczas z warunku (iv) mamy
µ(V
n
) = µ(V ). Zauważmy, że V
n
∩ V
m
=
∅ gdy n ̸= m. Mogą zajść dwa
przypadki. Albo µ(V ) = 0 albo µ(V ) > 0. Rozpatrzmy najpierw pierwszy
przypadek. Jeżeli x
∈ [0, 1], to zbiór V zawiera dokładnie jeden element v
klasy abstrakcji [x]. Z definicji relacji
∼ mamy x−v ∈ Q. Ale x−v ∈ [−1, 1]
więc istnieje takie n, ze x
− v = q
n
, zatem x = v + q
n
, stąd zaś wynika, że
x
∈ V
n
. Pokazaliśmy więc, że [0, 1]
⊂
∞
∪
n=1
V
n
, więc
1 = µ([0, 1])
6 µ(
∞
∪
n=1
V
n
) =
∞
∑
n=1
µ(V
n
) = 0.
Zatem przypadek µ(V ) = 0 jest niemożliwy. Stąd wynika, że musi być
µ(V ) > 0. Zauważmy, że dla dowolnego n
∈ N mamy V
n
⊂ [−1, 2] więc
∞
∪
n=1
V
n
⊂ [−1, 2]. Stąd wynika, że µ(
∞
∪
n=1
V
n
)
6 3 ale to prowadzi do sprzecz-
ności, bo
µ(
∞
∪
n=1
V
n
) =
∞
∑
n=1
µ(V
n
) =
∞
∑
n=1
µ(V ) =
∞.
3

Tak więc nie możliwe jest zdefiniowanie miary zdefiniowanej na wszyst-
kich podzbiorach
R tak aby spełniała ona naturalne warunki (i) - (iv).
Zbiór V zdefiniowany w dowodzie powyższego twierdzenia nazywa się
zbiorem Vitaliego.
4

2
Algebra zbiorów
Definicja 2.1 Niech A będzie podzbiorem ustalonego zbioru X. Wówczas
dla ε
∈ {−1, 1} przez A
ε
oznaczamy zbiór zdefiniowany następująco:
A
ε
=
{
A
jeżeli ε = 1
A
′
jeżeli ε =
−1
Lemat 2.1 Niech A
1
, ..., A
n
będą podzbiorami zbioru X. Wówczas dla do-
wolnego i = 1, ..., n mamy:
A
i
=
∪
ε
i
=1
A
ε
1
1
∩ ... ∩ A
ε
n
n
Dowód. Inkluzja
⊃ jest oczywista. Aby uzasadnić inkluzję ⊂ wystarczy
zauważyć, że jeżeli x
∈ A
i
, to x
∈ A
ε
1
1
∩ . . . ∩ A
ε
n
n
, gdzie
ε
j
=
{
1
jeżeli i = j;
0
jeżeli i
̸= j.
Definicja 2.2 Mówimy, że rodzina zbiorów parami rozłącznych
S jest roz-
biciem rodziny
R jeżeli:
(a) dowolny zbiór rodziny
S jest zawarty w pewnym zbiorze rodziny R;
(b) dla dowolnego zbioru A
∈ R istnieje skończona podrodzina S
0
⊂ S
taka, że
∪
S
0
= A.
Z lematu 2.1 wynika:
Twierdzenie 2.1 Niech
R = {A
1
, ..., x
n
} będzie dowolną skończoną rodzi-
nę podzbiorów zbioru X. Niech
S będzie rodziną składająca się z wszystkich
zbiorów postaci
A
ε
1
1
∩ ... ∩ A
ε
n
n
gdzie ε
1
, ..., ε
n
∈ {−1, 1} są takie, że co najmniej jeden z wskaźników ε
i
nie jest równy
−1. Wówczas rodzina S jest rozbiciem rodziny R.
Z definicji granicy górnej i dolnej wynika, że
x
∈ lim sup
n
→∞
A
n
⇔ x ∈ A
n
dla nieskończenie wielu n,
oraz
x
∈ lim inf
n
→∞
A
n
⇔ x ∈ A
n
dla prawie wszystkich n.
Zatem mamy zawsze
lim inf
n
→∞
A
n
⊂ lim sup
n
→∞
A
n
.
5

Definicja 2.3 Mówimy, że ciąg zbiorów (A
n
) jest zbieżny do zbioru A (albo,
że A jest granicą ciągu (A
n
), jeżeli
lim inf
n
→∞
A
n
= lim sup
n
→∞
A
n
= A.
Zauważmy, że jeżeli (A
n
) jest ciągiem zstępującym zbiorów (to znaczy gdy
A
n+1
⊂ A
n
dla dowolnego n
∈ N, to dla dowolnego m ∈ N mamy
∞
∪
m=n
A
m
= A
n
,
∞
∩
m=n
A
m
=
∞
∩
n=1
A
n
,
zatem
lim inf
n
→∞
A
n
= lim sup
n
→∞
A
n
=
∞
∩
n=1
A
n
.
Analogicznie, jeżeli (A
n
) jest ciągiem wstępującym zbiorów to
lim inf
n
→∞
A
n
= lim sup
n
→∞
A
n
=
∞
∪
n=1
A
n
.
Definicja 2.4 Mówimy, że ciąg zbiorów (A
n
) jest ciągiem monotonicznym,
jeżeli jest wstępującym, albo zstępującym.
Tak więc dowolny ciąg monotoniczny zbiorów ma granicę.
6

3
Pierścienie, ciała, σ
−ciała zbiorów.
3.1
Definicja pierścienia ciała i σ
−ciała
Niech X będzie niepustym zbiorem a M rodziną podzbiorów zbioru X.
Definicja 3.1 Mówimy, że niepusta rodzina zbiorów M jest pierścieniem,
jeżeli spełnione są następujące warunki:
(a)
∅ ∈ M;
(b) A, B
∈ M ⇒ A ∪ B ∈ M;
(c) A, B
∈ M ⇒ A \ B ∈ M.
Zauważmy, że jeśli założyć warunek (b) powyższej definicji to warunek (a)
jest równoważny temu, że M jest rodziną niepustą.
Uwaga 3.1 Z warunku (b) powyższej definicji poprzez indukcję matema-
tyczną dowodzimy, że A
1
∪ ... ∪ A
n
∈ M dla dowolnych A
1
, ..., A
n
∈ M.
Przykład 3.1 (a) Rodzina wszystkich podzbiorów skończonych zbioru X
jest pierścieniem.
(b) Jeżeli A jest dowolnym podzbiorem X, to rodzina dwuelementowa
{∅, A} jest pierścieniem.
(c) Niech
P będzie rodziną wszystkich przedziałów ograniczonych (bie-
rzemy przedziały wszystkich możliwych typów, to znaczy przedziały otwarte,
domknięte, i oba typy przedziałów domknięto otwartych, przyjmujemy, że
zbiór pusty jest przedziałem (x, x).) Łatwo udowodnić, że rodzina
M =
{P
1
∪ ... ∪ P
n
: P
1
, ..., P
n
in
P}
jest pierścieniem.
(d) Wszystkie podzbiory
R
k
mierzalne w sensie Jordana tworzą pierścień.
Uwaga 3.2 Jeżeli M jest pierścieniem zbiorów, to A
∩ B ∈ M dla dowol-
nych zbiorów A, B
∈ M.
Dowód Mamy A
∩ B = A \ (A \ B) ∈ M.
Poprzez indukcję matematyczną podobnie jak w przypadku sumy dowo-
dzimy, że A
1
∩ ... ∩ A
n
∈ M dla dowolnych A
1
, ..., A
n
∈ M.
Definicja 3.2 Mówimy, że rodzina M jest ciałem podzbiorów zbioru X
jeżeli spełnione są następujące warunki:
(a)
∅ ∈ M,
(b) A, B
∈ M ⇒ A ∪ B ∈ M,
(c) A
∈ M ⇒ A
′
∈ M.
7

Ponieważ
∅ = (A ∪ A
′
)
′
więc przy założeniach (a) i (b) warunek (a)
jest równoważny niepustości rodziny M. Z warunków (a) i (c) definicji ciała
zbiorów wynika, że X
∈ M dla dowolnego ciała podzbiorów zbioru X.
Przykład 3.2 (a) Rodzina 2
X
wszystkich podzbiorów zbioru X jest ciałem
zbiorów.
(b) Rodzina
{∅, X} jest ciałem podzbiorów X.
(c) Niech M będzie rodziną tych podzbiorów zbioru X które są skoń-
czone, lub których dopełnienia są skończone. Łatwo sprawdzić, że M jest
ciałem podzbiorów X.
Twierdzenie 3.1 Dowolne ciało zbiorów jest pierścieniem.
Dowód. Jeżeli M jest ciałem podzbiorów X, to dla dowolnych A, B
∈ M
mamy A
∩ B
′
= (A
′
∪ B)
′
więc z warunków (b) i (c) definicji 3.2 mamy
A
\ B ∈ M.
Jak łatwo zauważyć, pierścień podzbiorów zbioru X jest ciałem wtedy i
tylko wtedy gdy zawiera X.
Definicja 3.3 Mówimy, że M jest σ
−ciałem podzbiorów zbioru X, jeżeli
spełnione są następujące warunki:
(a)
∅ ∈ M,
(b) jeżeli A
n
∈ M dla dowolnego n ∈ N, to
∞
∪
n=1
A
n
∈ M,
(c) A
∈ M ⇒ A
′
∈ M.
Przykład 3.3 (a) Dowolne skończone ciało zbiorów jest σ
−ciałem.
(b) Rodzina 2
X
wszystkich podzbiorów zbioru X jest σ
−ciałem.
(c) Niech M =
{A ⊂ X : A − przeliczalny lub A
′
− przeliczalny}. Sprawdza
się łatwo, że M jest σ
−ciałem podzbiorów zbioru X.
Ciało zbiorów zdefiniowane w punkcie (c) przykładu 3.2 w przypadku
gdy zbiór X jest nieskończony jest ciałem ale nie jest σ
−ciałem podzbiorów
zbioru X.
Twierdzenie 3.2 Dowolne σ
−ciało jest ciałem.
Dowód Niech M będze σ
−ciałem podzbiorów zbioru X i weźmy dwa do-
wolne dwa zbiory A, B
∈ M. Zdefiniujmy ciąg zbiorów (A
n
) w sposób na-
stępujący:
A
1
= A, A
2
= B, A
n
=
∅ gdyn 3.
Wówczas A
n
∈ M dla dowolnego n zatem
A
∪ B =
∞
∪
n=1
A
n
∈ M.
8

Ponieważ dla dowolnego ciągu zbiorów (A
n
) zachodzą wzory de Morgana:
∞
∩
n=1
A
n
= (
∪
n=1
A
′
n
)
′
,
∞
∪
n=1
A
n
= (
∩
n=1
A
′
n
)
′
więc mamy następujące twierdzenie
Twierdzenie 3.3 M jest σ
−ciałem wtedy i tylko wtedy gdy spełnia warunki
(a) i (c) definicji 3.3 oraz
A
n
∈ M dla dowolnego n ∈ N ⇒
∞
∩
n=1
A
n
∈ M.
Następujące dwa twierdzenia pokazują, że w przypadku gdy rodzina M
jest ciałem warunek (b) w definicji σ
−ciała można osłabić. Pierwsze z tych
twierdzeń mówi, że wystarczy zakładać aby suma ciągu zbiorów parami
rozłącznych należała do M, a drugie że suma ciągu wstępującego należy do
M.
Twierdzenie 3.4 Ciało M podzbiorów zbioru X jest σ
−ciałem jeżeli speł-
nia następujący warunek:
A
n
∈ M, A
n
∩ A
m
=
∅ (n, m ∈ N, n ̸= m) ⇒
∞
∪
n=1
A
n
∈ M.
Dowód. Niech B
n
będzie ciągiem dowolnych zbiorów należących do ciała M
i niech zbiory A
n
będą zdefiniowane w następujący sposób A
1
= B
1
, A
n
=
B
n
\ (B
1
∪ ... ∪ B
n
−1
) gdy n > 1. Wówczas (A
n
) jest takim ciągiem zbio-
rów rozłącznych, że
∪
∞
n=1
A
n
=
∪
∞
n=1
B
n
. Ponieważ M jest ciałem podzbio-
rów X więc A
n
∈ M dla dowolnego n. Stąd na podstawie założenia mamy
∪
∞
n=1
B
n
∈ M.
Twierdzenie 3.5 Na to aby ciało zbiorów było σ
−ciałem wystarcza aby
spełniony był następujący warunek:
A
n
∈ M, A
n
⊂ A
n+1
(n
∈ N) ⇒
∞
∪
n=1
A
n
∈ M.
Twierdzenie to dowodzimy podobnie jak poprzednie przyjmując B
n
= A
1
∪
...
∪ A
n
.
Twierdzenie 3.6 Na to aby ciało zbiorów było σ
−ciałem wystarcza aby
spełniony był następujący warunek:
A
n
∈ M, A
n+1
⊂ A
n
(n
∈ N) ⇒
∞
∩
n=1
A
n
∈ M.
Twierdzenie 3.7 Przekrój dowolnej ilości pierścieni, podzbiorów zbioru X
jest pierścieniem podzbiorów X. Analogicznie przekrój dowolnej ilości ciał
(σ
−ciał) podzbiorów zbioru X jest ciałem (σ-ciałem).
9

3.2
Pierścień, ciało i σ
−ciało generowane przez rodzinę zbio-
rów.
Twierdzenie 3.8 Jeżeli
R jest dowolną rodziną podzbiorów X, to istnieje
najmniejszy pierścień, najmniejsze ciało i najmniejsze σ
−ciało podzbiorów
zbioru X zawierające
R.
Dowód. Jak łatwo zauważyć iloczyn
∩
{M ; M pierścień podzbiorów X, R ⊂ M}
jest najmniejszym pierścieniem zawierającym
R.
Definicja 3.4 Najmniejszy pierścień zawierający rodzinę
R nazywamy pier-
ścieniem generowanym przez rodzinę
R i oznaczamy przez P (R). Analogicz-
nie najmniejsze ciało (σ
−ciało) podzbiorów zbioru X zawierające rodzinę
R nazywamy ciałem (σ−ciałem) generowanym przez R. Ciało generowane
przez rodzinę
R oznaczamy F (R), natomiast przez Σ(R) oznaczamy σ−ciało
generowane przez
R.
Bezpośrednio z powyższej definicji i z tego, że pierścień jest ciałem a
σ
−ciało ciałem dostajemy inkluzję:
P (
R) ⊂ F (R) ⊂ Σ(R).
3.3
Rodziny monotoniczne zbiorów
Twierdzenie 3.9 Załóżmy, że N jest ciałem podzbiorów zbioru X i niech
M będzie najmniejszą rodziną podzbiorów zbioru X taką, że
(a) N
⊂ M,
(b) A
∈ M ⇒ A
′
∈ M,
(c) A
n
∈ M, A
n
⊂ A
n+1
, dla n
∈ N ⇒
∞
∪
n=1
A
n
∈ M.
Wówczas M = Σ(
R).
Dowód. Na podstawie twierdzenia 3.5 wystarczy pokazać, że M jest ciałem
zbiorów. Dla dowolnego A
∈ M niech:
M(A) :=
{B ∈ M : A ∪ B, A \ B, B \ A, A ∩ B ∈ M}.
Z definicji M(A) wynika, że
A
∈ M(B) ⇔ B ∈ M(A).
(1)
Udowodnimy, że dla dowolnego A
∈ M rodzina M(A) spełnia warunki (b) i
(c) dowodzonego twierdzenia. Niech B
∈ M(A) wówczas
A
∪ B
′
= (B
\ A)
′
∈ M,
10

A
\ B
′
= A
∩ B ∈ M,
B
′
\ A = (B ∪ A)
′
∈ M,
A
∩ B
′
= A
\ B ∈ M.
Załóżmy dalej, że (B
n
) jest ciągiem wstępującym zbiorów należących do
M(A). Wówczas
A
∪
∞
∪
n=1
B
n
=
∞
∪
n=1
(A
∪ B
n
)
∈ M,
A
∩
∞
∪
n=1
B
n
=
∞
∪
n=1
(A
∩ B
n
)
∈ M,
A
\
∞
∪
n=1
B
n
= A
∩ (
∞
∪
n=1
B
n
)
′
= A
∩ (
∞
∩
n=1
B
′
n
) =
∞
∩
n=1
(A
∩ B
′
n
) =
∞
∩
n=1
(B
n
∪ A
′
)
′
= (
∞
∪
n=1
B
n
∪ A
′
)
′
∈ M,
∞
∪
n=1
B
n
\ A =
∞
∪
n=1
(B
n
\ A) ∈ M.
Zauważmy, że jeżeli A
∈ N, to N ⊂ M(A) zatem z (1) mamy N ⊂ M(A) dla
dowolnego A
∈ M. Zatem M(A) spełnia warunki (i), (ii), (iii). Stąd wynika,
że M = M(A), dla dowolnego A
∈ M zatem M jest ciałem zbiorów.
Definicja 3.5 Mówimy, że rodzina N podzbiorów zbioru X jest rodziną
monotoniczną, jeżeli granica dowolnego ciągu monotonicznego zbiorów na-
leżących do N należy do N.
Oczywiście dowolne σ
−ciało zbiorów jest rodziną monotoniczną. Z praw
de Morgana wynika, że ciało M jest rodziną monotoniczną wtedy i tyl-
ko wtedy gdy dla dowolnego ciągu (A
n
) zbiorów należących do M mamy
∪
∞
n=1
A
n
∈ M. Z twierdzenia 3.5, wynika, że ciało jest σ−ciałem wtedy i
tylko wtedy gdy jest rodziną monotoniczną.
Podobnie jak w twierdzeniu 3.8 dowodzimy, że dla dowolnej rodziny
R
podzbiorów zbioru X istnieje najmniejsza rodzina monotoniczna zawierają-
ca
R. Najmniejszą rodzinę monotoniczną zawierającą rodzinę R będziemy
oznaczać przez M (
R).
Twierdzenie 3.10 Niech N będzie dowolnym ciałem podzbiorów zbioru X.
Wówczas σ
−ciało generowane przez rodzinę N pokrywa się z najmniejszą
rodziną monotoniczną zawierającą N, to znaczy mamy równość Σ(N) =
M (N).
11

Dowód. Niech
M =
{A ∈ M(N) : A
′
∈ M(N)}.
Wówczas M jest rodziną monotoniczną zawierającą N i zawartą w M (
R).
Stąd wynika, że M = M (M). Ale z definicji M wynika, że M wraz z każdym
zbiorem zawiera dopełnienie tego zbioru. Inaczej mówiąc jeżeli A
∈ M(N),
to A
′
∈ M(N). Na podstawie twierdzenia 3.9 mamy M(N) = Σ(N).
12

4
Półpierścienie
4.1
Definicja półpierścienia
Definicja 4.1 Mówimy, że niepusta rodzina
R jest półpierścieniem jeżeli
(a) jeżeli A, B
∈ R to A ∩ B ∈ R,
(b) dla dowolnych zbiorów A, B
∈ R istnieją zbiory C
1
, ..., C
n
∈ R
parami rozłączne takie, że
A
\ B = C
1
∪ ... ∪ C
n
.
Z niepustości półpierścienia warunku (b) wynika, że
∅ ∈ R.
Przykład 4.1 Jeżeli
P jest rodziną zbiorów parami rozłącznych, zawiera-
jącą zbiór pusty, to
P jest półpierścieniem.
Podstawowy przykład półpierścienia stanowi rodzina wszystkich prze-
działów w
R.
Definicja 4.2 Przedziałem w
R nazywamy jeden ze zbiorów postaci
(a, b), [a, b), [a, b], (a, b],
gdzie a
6 b. Rodzinę wszystkich przedziałów w R będziemy oznaczać przez
I.
Zauważmy, że w definicji przedziału zakładamy tylko, że zachodzi słaba
nierówność a
6 b, zatem zbiór pusty i zbiór jednopunktowy są również
przedziałami.
Twierdzenie 4.1 Rodzina
I wszystkich przedziałów w R jest półpierście-
niem.
Dowód. Iloczyn dwóch przedziałów jest przedziałem. Natomiast różnica
P
1
− P
2
dwóch przedziałów jest sumą co najwyżej dwóch przedziałów.
4.2
Pierścień generowany przez półpierścień
Twierdzenie 4.2 Niech
R będzie taką niepustą rodziną podzbiorów zbioru
X, że dla dowolnych zbiorów A, B
∈ R istnieją zbiory C
1
, ..., C
n
∈ R
takie, że
A
\ B = C
1
∪ ... ∪ C
n
.
(2)
Wówczas
P (
R) = {C
1
∪ ... ∪ C
n
: C
1
, C
2
, ..., C
n
∈ R}.
(3)
13

Dowód. Oznaczmy przez M rodzinę zbiorów występującą po prawej stronie
równości (3). Oczywiście
R ⊂ M oraz M ⊂ P (R). Aby pokazać równość
wystarczy pokazać, że M jest pierścieniem. Ponieważ z definicji rodziny M
wynika, że jest to rodzina zamknięta na sumy skończone, więc wystarczy
pokazać, że A
\ B ∈ M dla dowolnych A, B ∈ M.
Udowodnimy najpierw przez indukcję względem n, że jeżeli A
∈ R, oraz
B = B
1
∪ ... ∪ B
n
, gdzie B
1
, ..., B
n
∈ R, to A \ B ∈ M. Inaczej mówiąc,
że A
\ B ∈ M, gdy A ∈ R, oraz B ∈ M. W przypadku n = 1 dostajemy
A
\ B ∈ M na podstawie założenia. Przypuśćmy, że dowodzone wynikanie
jest prawdziwe dla pewnego n
∈ N. Załóżmy, że A, B
1
, ..., B
n+1
∈ R, B =
B
1
∪ ... ∪ B
n+1
. Wówczas:
A
\ B = [A \ (B
1
∪ ... ∪ B
n
)]
\ B
n+1
.
Z założenia indukcyjnego zbiór A
\ (B
1
∪ ... ∪ B
n
) daje się przedstawić w
postaci sumy C
1
∪ ... ∪ C
m
, zatem
A
\ B = (C
1
\ B
n+1
)
∪ ... ∪ (C
m
\ B
n+1
).
Ponieważ każdy ze zbiorów C
i
\ B
n+1
∈ M i rodzina M jest zamknięta na
sumy skończone, więc A
\ B ∈ M.
Rozpatrzmy teraz przypadek ogólny gdy oba zbiory A, B należ do M.
Załóżmy, że A = A
1
∪ ... ∪ A
n
, wówczas
A
\ B = (A
1
\ B) ∪ ... ∪ (A
n
\ B)
a ponieważ A
i
\ B ∈ M dla i = 1, ..., n więc A \ B ∈ M.
Twierdzenie 4.3 Jeżeli rodzina
R jest półpierścieniem, to
P (
R) = {C
1
∪ ... ∪ C
n
: C
i
∈ R, C
i
∩ C
j
=
∅ (i ̸= j)}
Dowód. Oznaczmy przez M rodzinę występującą po prawej stronie równości
Jak łatwo zauważyć, rodzina ta jest zamknięta na iloczyny skończone. Na
podstawie twierdzenia 4.2 wystarczy pokazać, ze C
1
∪ ... ∪ C
n
∈ M dla
dowolnych zbiorów C
1
, ..., C
n
∈ M. Dowód przeprowadzamy przez indukcję
względem n. Dla n = 1 dowodzone wynikanie wynikanie jest oczywiste.
Załóżmy, że jest prawdziwe dla pewnego n
∈ N, i weźmy dowolne zbiory
C
1
, ...., C
n+1
∈ R. Z założenia indukcyjnego istnieją parami rozłączne
zbiory D
1
, ..., D
m
∈ R takie, że C
1
∪ ... ∪ C
n
= D
1
∪ ... D
m
. Wówczas
sumę C
1
∪ ... ∪ C
n+1
można przedstawić w postaci sumy A
∪ B gdzie:
A = C
1
∪ ... ∪ C
n
, B = C
n+1
\ (C
1
∪ ... ∪ C
n
)
Ponieważ zbiory A, B są rozłączne więc wystarczy pokazać, że B
∈ M.
Mamy
B = (C
n+1
\ C
1
)
∩ ... ∩ (C
n+1
\ C
n
).
14

Z założenia, ze
R jest półpierścieniem wynika, że każdy ze zbiorów C
n+1
\C
i
należy do M dla dowolnego i = 1, ..., n. Ponieważ rodzina M jest zamknięta
na iloczyny skończone więc B
∈ M.
Twierdzenie 4.4 Niech
P będzie półpierścieniem i załóżmy, że mamy skoń-
czoną rodzinę
R = {A
1
, ..., A
n
} zbiorów należących do P. Wówczas istnieją
zbiory B
1
, ...., B
m
∈ P takie, że rodzina {B
1
, ..., B
m
} jest rozbiciem R.
Dowód. Jeżeli
P jest pierścieniem to rodziną tą jest rodzina zdefiniowana
w twierdzeniu 2.1. W przypadku ogólnym oznaczmy przez M pierścień ge-
nerowany przez
P, i niech rodzina {B
1
, ..., B
m
} elementów pierścienia M
będzie rozbiciem rodziny
R. Z twierdzenia 4.3 wynika, że każdy ze zbiorów
B
i
można zapisać w postaci sumy zbiorów rozłącznych:
B
i
= C
i1
∪ ... ∪ C
in
i
,
gdzie C
ij
i
∈ P dla i = 1, ..., n oraz j = 1, ..., n
i
. Jak łatwo zauważyć
rodzina
{C
ij
: i = 1, ..., n, j = 1, ..., n
i
}
jest rozbiciem rodziny
R.
4.3
Iloczyn kartezjański półpierścieni
Twierdzenie 4.5 Załóżmy, że
P
1
,
P
2
są półpierścieniami.
P = {A × B : A ∈ P
1
, B
∈ P
2
}.
(4)
Wówczas
P jest również półpierścieniem.
Dowód Mamy
(A
× B) ∩ (C × D) = (A ∩ C) × (B ∩ D)
oraz
(A
× B) \ (C × D) = (A × B) ∩ (C × D) = [(A \ C) × B] ∪ [A × (B \ D)] =
= [(A
\ C) × (B ∩ D)] ∪ [(A \ C) × (B \ D)] ∪ [(A ∩ C) × (B \ D)]
Zauważmy, że wszystkie trzy zbiory występujące w ostatniej sumie są parami
rozłączne. Wystarczy więc pokazać, że każdy z nich jest sumą rozłącznych
zbiorów należących do rodziny
P. Załóżmy, że
A
\ C =
∪
i=1
E
i
, B
\ D =
m
∪
j=1
F
j
,
15

gdzie zbiory E
i
, F
j
należą odpowiednio do
P
1
,
P
2
. Wówczas
(A
\ C) × (B ∩ D) =
n
∪
i=1
[E
i
× (C ∩ D)],
(A
\ C) × (B \ D) =
n
∪
i=1
m
∪
j=1
(C
i
× D
j
),
(A
∩ C) × (B \ D) =
m
∪
j=1
[(A
∩ C) × D
j
].
Jak łatwo zauważyć wszystkie zbiory występujące po prawej stronie w trzech
ostatnich równościach należą do
P i są parami rozłączne. .
Wykorzystując poprzednie twierdzenie poprzez indukcję matematyczną
dowodzimy:
Twierdzenie 4.6 Jeżeli
P
1
, ...,
P
n
są półpierścieniami to rodzina
P = {A
1
× ... × A
n
: A
i
∈ P
i
dla i = 1, ..., n
}
jest półpierścieniem.
16

5
Funkcje addytywne i miary.
5.1
Pojęcie funkcji addytywnej
Definicja 5.1 Niech X będzie dowolnym zbiorem a M pierścieniem pod-
zbiorów X. Mówimy, że funkcja µ : M
→ [0, ∞] jest funkcją addytywną,
jeżeli
(i) µ(
∅) = 0;
(ii) µ(A
∪ B) = m(A) + m(B) dla dowolnych zbiorów A, B ∈ M takich,
że A
∩ B = ∅.
Przykład 5.1 (a) Załóżmy, że M = 2
X
i niech: µ(A) = ilość elementówA
gdy A jest podzbiorem skończonym A i µ(A) =
∞ dla nieskończonych pod-
zbiorów X. Funkcja µ jest funkcją addytywną na M.
(b) Niech Ω będzie zbiorem skończonym n elementowym i niech dla do-
wolnego zbioru A
⊂ Ω :
µ(A) =
ilość elementów zbioru A
n
.
Indukcyjnie dowodzimy
Uwaga 5.1 Jeżeli µ jest funkcją addytywną na pierścieniu M, to
µ(A
1
∪ ... ∪ A
n
) = µ(A
1
) + ... + µ(A
n
)
dla dowolnych zbiorów A
1
, A
2
, ..., A
n
∈ M parami rozłącznych.
Twierdzenie 5.1 Jeżeli µ jest funkcją addytywną na na pierścieniu M, to
(a) jeżeli A, B
∈ M oraz B ⊂ A, to µ(B) ¬ µ(A).
(b) µ(A
\ B) = µ(A) \ µ(B) dla dowolnych A, B ∈ M takich, że B ⊂ A,
oraz µ(B) <
∞.
(c) µ(A
∪B) = µ(A)+µ(B)\µ(A∩B) dla dowolnych A, B ∈ M takich,
że µ(A
∩ B) < ∞.
(d) µ(A
∪ B) ¬ µ(A) + µ(B) dla dowolnych A, B ∈ M.
Dowód. (a), (b) wynikają z równości A = B
∪ (A \ B).
(c) Mamy
µ(A
∪ B) = µ(A ∪ (B \ A)) = µ(A) + µ(B \ A) = µ(A) + µ(B \ (A ∩ B)) =
µ(A) + µ(B)
\ µ(A ∩ B).
(d) µ(A
∪ B) = µ((A \ B) ∪ B) = µ(A \ B) + µ(B) ¬ µ(A) + µ(B).
Definicja 5.2 Funkcje określone na pewnym pierścieniu M i spełniającą
warunek (a) twierdzenia 5.1 nazywamy funkcjami monotonicznymi. Nato-
miast funkcje spełniające warunek (d) tego twierdzenia nazywamy funkcjami
podaddytywnymi (albo skończenie podaddytywnymi).
17

Przez indukcję matematyczną dowodzimy, że dowolna funkcja podaddy-
tywna spełnia warunek
µ(A
1
∪ ... ∪ A
n
)
¬ µ(A
1
) + ... + µ(A
n
)
dla dowolnych A
1
, ..., A
n
∈ M.
Twierdzenie 5.2 Jeżeli µ jest funkcją addytywną na pierścieniu M, to
µ(
∞
∪
n=1
A
n
)
∞
∑
n=1
µ(A
n
)
dla dowolnego ciągu (A
n
) parami rozłącznych zbiorów należących do σ
−ciała
takiego, że
∞
∪
n=1
A
n
∈ M.
Dowód. Z punktu (a) twierdzenia 5.1 i uwagi 5.1 dla dowolnego m
∈ N
mamy:
µ(
∞
∪
n=1
A
n
)
µ(
m
∪
n=1
A
n
) =
m
∑
n=1
µ(A
n
).
Przechodząc z m do
∞ dostajemy dowodzoną nierówność.
5.2
Miary na σ
−ciele
Definicja 5.3 Niech X będzie zbiorem niepustym a M dowolnym σ
−ciałem
podzbiorów X. Mówimy, że funkcja µ : M
→ [0, ∞] jest miarą jeśli:
(i) µ(
∅) = 0,
(ii) Dla dowolnego ciągu (A
n
) zbiorów parami rozłącznych należących
do M zachodzi równość:
µ(
∞
∪
n=1
A
n
) =
∞
∑
n=1
µ(A
n
).
Jeżeli µ(X) <
∞ to mówimy, że miara µ jest miarą skończoną, a jeżeli
µ(X) = 1 to miarę nazywamy miarą probabilistyczną. Jeżeli istnieją takie
zbiory A
n
∈ M, że µ(A
n
) <
∞ oraz X =
∞
∪
n=1
A
n
, to mówimy, że miara µ
jest miarą σ
−skończoną.
Uwaga 5.2 Dowolna miara jest funkcją addytywną.
Dowód. Załóżmy, że A, B
∈ M są zbiorami rozłącznymi i niech
A
1
= A, A
2
= B, A
n
=
∅ gdy n 3.
Ponieważ zbiory A
n
są parami rozłączne więc:
m(A
∪ B) = m(
∞
∪
n=1
A
n
) =
∞
∑
n=1
m(A
n
) = m(A) + m(B).
18

Przykład 5.2 (a) Niech (ε
n
) będzie ciągiem liczb nieujemnych. Zdefiniuj-
my funkcję
µ : 2
N
→ [0, ∞]
wzorem:
µ(A) =
∑
n
∈A
ε
n
Łatwo sprawdzić, że µ jest miarą na 2
N
.
(b) Niech X będzie zbiorem niepustym a x dowolnym punktem zbioru
X. Funkcja δ
x
: 2
X
→ {0, 1} określona wzorem
δ
x
(A)) =
{
0,
gdy x
∈ A;
1,
gdy x
̸∈ A.
jest miarą. Miarę tą nazywamy miarą Diraca.
Twierdzenie 5.3 Jeżeli µ jest miarą na σ
−ciele M, to
µ(
∞
∪
n=1
A
n
)
¬
∞
∑
n=1
µ(A
n
)
(5)
dla dowolnych zbiorów A
n
∈ M.
Dowód. Niech B
n
będą zbiorami zdefiniowanymi w następujący sposób:
B
1
= A
1
, B
n
= A
n
\ (A
1
∪ ... ∪ A
n
−1
).
Zbiory B
n
są parami rozłączne, należą do M oraz
∪
∞
n=1
A
n
=
∪
∞
n=1
B
n
.
Ponieważ B
n
⊂ A
n
, więc
µ(
∞
∪
n=1
A
n
) = µ(
∞
∪
n=1
B
n
) =
∞
∑
n=1
µ(B
n
)
¬
∞
∑
n=1
µ(A
n
).
Definicja 5.4 Funkcję określoną na σ
−ciele M o wartościach w [0, ∞] i
spełniającą dla dowolnych zbiorów A
n
∈ M warunek (5) nazywamy funkcją
przeliczalnie podaddytywną.
Twierdzenie 5.4 Funkcja µ określona na σ
−ciele M jest miarą wtedy i
tylko wtedy gdy jest funkcją addytywną i przeliczalnie podaddytywną.
Dowód. Konieczność wynika z twierdzenia 5.3, natomiast wystarczalność z
twierdzenia 5.2.
Twierdzenie 5.5 Jeżeli µ jest miarą na σ
−ciele M, to
µ(
∞
∪
n=1
A
n
) = lim
n
→∞
µ(A
n
)
(6)
dla dowolnego ciągu wstępującego ciągu zbiorów (A
n
).
19

Dowód. Zdefiniujmy ciąg zbiorów (B
n
) w następujący sposób:
B
1
= A
1
, B
n
= A
n
\ A
n
−1
gdy n > 1.
Oczywiście B
n
∈ M dla dowolnego n ∈ N, ponadto zbiory B
n
są parami
rozłączne, oraz
∪
∞
n=1
B
n
=
∪
∞
n=1
A
n
. Stąd
µ(
∞
∪
n=1
A
n
) = µ(
∞
∪
n=1
B
n
) =
∞
∑
n=1
µ(B
n
) = lim
m
→∞
m
∑
n=1
µ(B
n
) =
lim
m
→∞
µ(
m
∪
n=1
B
n
) = lim
m
→∞
µ(B
m
).
Twierdzenie 5.6 Jeżeli µ jest funkcją addytywną na σ
−ciele M spełnia-
jącą warunek (6) z tezy poprzedniego twierdzenia, to µ jest miarą na M.
Dowód. Jeżeli (A
n
) jest ciągiem zbiorów parami rozłącznych, to
∪
∞
n=1
A
n
=
∪
∞
n=1
B
n
, gdzie B
n
= A
1
∪ ... ∪ A
n
. Mamy więc ponieważ, ciąg zbiorów
(B
n
) jest ciągiem wstępującym więc:
µ(
∞
∪
n=1
A
n
) = µ(
∞
∪
n=1
B
n
) = lim
m
→∞
µ(B
m
) = lim
m
→∞
m
∑
n=1
µ(A
n
) =
∞
∑
n=1
µ(A
n
).
Twierdzenie 5.7 Jeżeli µ jest miarą na σ
−ciele M, to
µ(
∞
∩
n=1
A
n
) = lim
n
→∞
µ(A
n
)
(7)
dla dowolnego ciągu (A
n
) zbiorów należących do M, takiego, że µ(A
n
0
) <
∞
dla pewnego n
0
∈ N.
Dowód. Dla dowolnego n
n
0
niech B
n
= A
n
0
\ A
n
. Tak zdefiniowane
zbiory B
n
tworzą ciąg wstępujący więc z twierdzenia 5.5 mamy
µ(
∞
∪
n=1
B
n
) =
lim
n
→∞
µ(B
n
) = lim
n
→∞
µ(A
n
0
\ A
n
) = lim
n
→∞
[µ(A
n
0
)
− µ(A
n
)] =
µ(A
n
0
)
− lim
n
→∞
µ(A
n
).
Ale
µ(
∞
∪
n=1
B
n
) = µ(A
n
0
\
∞
∩
n=1
A
n
) = µ(A
n
0
)
− µ(
∞
∩
n=1
A
n
).
Stąd dostajemy dowodzoną równość.
Uwaga 5.3 Z dowodu twierdzenia 5.7 wynika, że jeżeli µ jest taką funkcją
addytywną, że µ(X) <
∞ to spełnianie warunku 7 twierdzenia 5.7 jest
równoważne spełnianiu warunku 6 twierdzenia 5.5.
20

Twierdzenie 5.8 Jeżeli µ jest funkcją addytywną na σ
−ciele M taką, że
µ(X) <
∞ i spełniającą dla dowlnego ciągu zstępującego (A
n
) dowarunek
(7), to µ jest miarą na M.
Szczególną rolę w teorii miary odgrywają zbiory miary zero.
Uwaga 5.4 Załóżmy, że µ jest miarą na σ
−ciele M. Wówczas
(a) jeżeli A, B
∈ M, B ⊂ A, µ(A) = 0, to µ(B) = 0,
(b) jeżeli A
n
∈ M oraz µ(A
n
) = 0 to µ(
∪
∞
n=1
A
n
) = 0.
Punkt (a) wynika z monotoniczności miar, a punkt (b) z przeliczalnej po-
daddytywności.
Definicja 5.5 Mówimy, że zbiór A
∈ M jest atomem miary µ, jeżeli
(a) µ(A) > 0,
(b) jeżeli B
∈ M i B ⊂ A, to albo µ(B) = 0 albo µ(B) = µ(A).
Jeżeli żaden zbiór A
∈ M nie jest atomem miary µ to mówimy, że miara
µ jest miarą bezatomową.
Przykład 5.3 Niech δ
x
będzie miarą Diraca zdefiniowaną w przykładzie 5.2
punkt (b). Jak łatwo zauważyć dowolny zbiór A
⊂ X jest atomem miary δ
x
.
5.3
Zupełność miary
Definicja 5.6 Mówimy, że miara µ określona na σ
−ciele M jest miara zu-
pełną, jeżeli z tego, że A
∈ M oraz µ(A) = 0 wynika, że B ∈ M dla
dowolnego zbioru B
⊂ A.
Uwaga 5.5 Miara µ jest miarą zupełną wtedy i tylko wtedy gdy:
[A
∈ M i A ÷ B ⊂ C, gdzie C ∈ M, oraz µ(C) = 0] ⇒ B ∈ M.
(8)
Dowód. Załóżmy, że spełniony jest warunek (8). Jeżeli A
∈ M, µ(A) = 0
oraz B
⊂ A, to B ÷ ∅ ⊂ A więc z (8) wynika, że B ∈ M. Zatem miara µ jest
miarą zupełną.
Załóżmy, że µ jest miarą zupełną i załóżmy, że zbiory A, B spełniają
warunki z (8). Wówczas
B = [(A
÷ B) \ A] ∪ (A ∩ B) = [(A ÷ B) \ A] ∪ [A \ (A \ B)].
(9)
Zgodnie założeniem zbiór A
÷ B należy do M i miarę równą 0. Z zupełności
miary również zbiory (A
÷B)\A oraz A\B należą do M. Zatem na podstawie
równości (9) również B
∈ M.
21
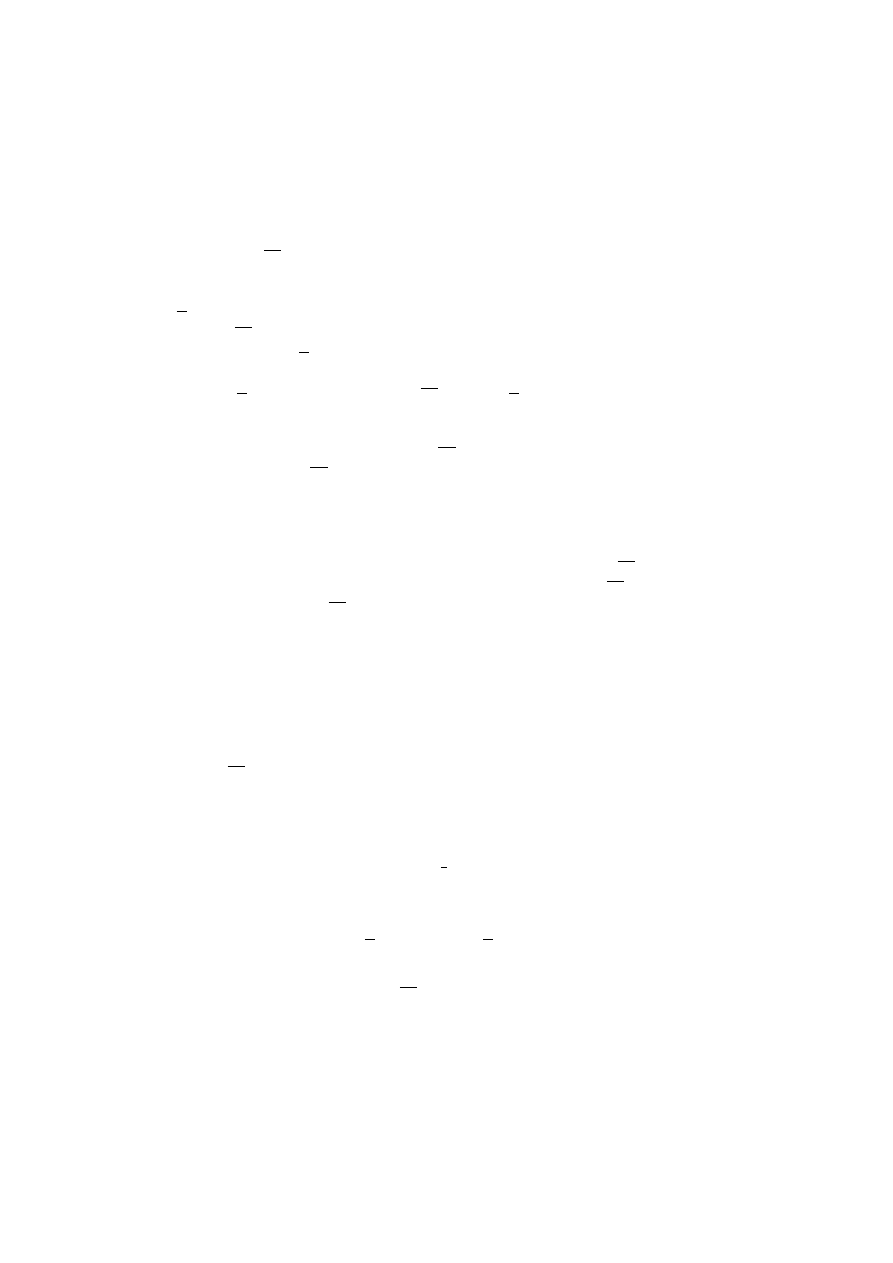
Twierdzenie 5.9 Załóżmy, że µ jest miarą na σ
−ciele M podzbiorów zbio-
ru X. Niech
M =
{B ∪ C : B ∈ M, ∃
D
∈M
µ(D) = 0, C
⊂ D}.
Jeżeli A = B
∪ C gdzie B ∈ M, C ⊂ D, D ∈ M, µ(D) = 0 to przyjmujemy
µ(A) = µ(B). Wówczas
(a) M jest σ
−ciałem podzbiorów zbioru X zawierającym M,
(b) definicja µ(A) nie zależy od przedstawienia zbioru A w postaci sumy
B
∪ C,
(c)
µ jest miarą zupełną na M taką, że µ(A) = µ(A) dla dowolnego
A
∈ M.
Dowód. Udowodnimy najpierw, że M jest σ
−ciałem zbiorów. Weźmy do-
wolny zbiór A
∈ M i niech A = B ∪ C gdzie A ∈ M, C ⊂ D, D ∈
M, µ(D) = 0. Wówczas
A
′
= B
′
∩C
′
= B
′
∩[D\(D\C)]
′
= B
′
∩[D
′
∪(D\C)] = (B
′
∩D
′
)
∪B
′
∩(D\C).
Oczywiście B
′
∩ D
′
∈ M, oraz B
′
∩ (D \ C) ⊂ D, zatem A
′
∈ M.
Załóżmy dalej, że mamy ciąg zbiorów (A
n
) należących do M. Niech A
n
=
B
n
∪ C
n
, gdzie B
n
∈ M, C
n
⊂ D
n
D
n
∈ M, µ(D
n
) = 0. Wówczas
∞
∪
n=1
A
n
=
∞
∪
n=1
A
n
∪
∞
∪
n=1
C
n
,
∞
∪
n=1
C
n
⊂
∞
∪
n=1
D
n
,
oraz
∞
∪
n=1
D
n
∈ M, µ(
∞
∪
n=1
D
n
) = 0.
Zatem M jest σ
−ciałem zbiorów zawierającym M.
Aby pokazać punkt (b) twierdzenia załóżmy, że B
1
∪C
1
= B
2
∪C
2
, gdzie
C
1
⊂ D
1
, C
2
⊂ D
2
, oraz µ(D
1
) = µ(D
2
) = 0. Wówczas B
1
⊂ B
2
∪ C
2
⊂
B
2
∪D
2
, więc µ(B
1
) = µ(B
2
) + µ(D
2
) = µ(B
2
). Analogicznie µ(B
2
)
¬ µ(B
1
)
zatem µ(B
1
) = µ(B
2
).
Jeżeli A
∈ M, to A = A ∪ ∅ więc (µ)(A) = µ(A).
Udowodnimy dalej, że
µ(
∞
∪
n=1
A
n
) =
∞
∑
n=1
µ(A
n
)
dla dowolnych zbiorów A
n
∈ M parami rozłącznych. Załóżmy, że A
n
=
B
n
∪ C
n
, gdzie A
n
∈ M, C
n
⊂ D
n
, D
n
∈ M, µ(D
n
) = 0. Wówczas
∞
∪
n=1
A
n
=
∞
∪
n=1
B
n
∪
∞
∪
n=1
C
n
,
22

oraz
∞
∪
n=1
B
n
∈ M,
∞
∪
n=1
C
n
⊂
∞
∪
n=1
D
n
, oraz
∞
∪
n=1
D
n
∈ M, i µ(
∞
∪
n=1
D
n
) = 0.
Zatem
µ(
∞
∪
n=1
A
n
) =
∞
∪
n=1
µ(B
n
),
a ponieważ zbiory B
n
są parami rozłączne więc
µ(
∞
∪
n=1
A
n
) =
∞
∑
n=1
µ(B
n
) =
∞
∑
n=1
µ(A
n
).
6
Funkcje addytywne i miary na półpierścieniach
6.1
Funkcje addytywne i miary na dowolnej rodzinie zbiorów
Dalej będzie wygodniej rozpatrywać pojęcie funkcji addytywnej nie tylko
dla funkcji określonych na pierścieniu zbiorów, ale dla funkcji określonej na
dowolnej rodzinie zbiorów zawierającej zbiór pusty.
Definicja 6.1 Niech
R będzie dowolną rodziną zbiorów zawierającą zbiór
pusty. Wówczas mówimy, że funkcja µ :
R → [0, ∞] jest
(a) µ jest funkcją addytywną jeżeli
µ(A) = µ(A
1
) + ... + µ(A
n
)
dla dowolnych A, A
1
, ..., A
n
∈ R takich, że A = A
1
∪ .... ∪A
n
, oraz zbiory
A
i
(i = 1, ..., n) są parami rozłączne,
(b) µ jest miarą jeżeli
µ(A) =
∞
∑
n=1
µ(A
n
),
dla dowolnego ciągu (A
n
) zbiorów parami rozłącznych takiego, że A
n
∈ R,
oraz A =
∞
∪
n=1
A
n
∈ R.
(c) µ jest funkcją monotoniczną jeżeli µ(B)
6 µ(A), dla dowolnych
A, B
∈ R takich, że B ⊂ A.
(d) µ jest funkcją podaddytywną jeżeli:
µ(A)
6 µ(A
1
) + ... + µ(A
n
)
dla dowolnych dla dowolnych A, A
1
, ..., A
n
∈ R takich, że A = A
1
∪ .... ∪
A
n
.
23

(e) µ jest funkcją przeliczalnie podaddytywną jeżeli:
µ(A)
6
∞
∑
n=1
µ(A
n
)
przy założeniu, że A
n
∈ R dla dowolnego n ∈ N, oraz A =
∞
∪
n=1
A
n
∈ R.
Zauważmy, że jeżeli rodzina
R jest pierścieniem, to definicje pojęć po-
danych w punktach (a), (c), (d) pokrywają się z wcześniejszymi definicjami
tych pojęć. Analogiczna uwaga dotyczy punktów (b), (e) w przypadku gdy
R jest σ−ciałem.
Zupełnie analogicznie jak twierdzenie 5.3 dowodzimy:
Lemat 6.1 Dowolna miara określona na pierścieniu jest funkcją przeliczal-
nie podaddytywną.
6.2
Przedłużanie funkcji addytywnych i miar z półpierście-
nia na pierścień
Twierdzenie 6.1 Załóżmy, że
P jest półpierścieniem podzbiorów zbioru X.
Niech µ
0
:
P → [0, ∞) będzie funkcją addytywną. Niech M będzie pier-
ścieniem generowanym przez
P (patrz twierdzenie ??). Jeżeli A ∈ M oraz
A = C
1
∪ ... ∪ C
n
, gdzie zbiory C
i
są parami rozłączne, to przyjmijmy
µ(A) = µ
0
(C
1
) + ... + µ
0
(C
n
).
Wówczas:
(a) funkcja µ jest poprawnie określona; to znaczy jej definicja nie zależy
od przedstawienia zbioru z M w postaci sumy zbiorów parami rozłącznych
należących do M,
(b) µ jest funkcją addytywną na M.
Dowód. (a) Załóżmy, że
C
1
∪ ... ∪ C
n
= D
1
∪ .. D
m
gdzie zbiory C
i
(i = 1, ..., n) oraz D
j
(j = 1, ..., m) są parami rozłączne.
Wówczas dla dowolnego i = 1, ..., n mamy
C
i
=
m
∪
j=1
C
i
∩ D
j
zatem
µ
0
(C
i
) =
m
∑
j=1
µ
0
(C
i
∩ D
j
).
24

Analogicznie
µ
0
(B
j
) =
n
∑
i=1
µ
0
(D
i
∩ D
j
).
Zatem
n
∑
i=1
µ
0
(C
i
) =
n
∑
i=1
m
∑
j=1
µ
0
(C
i
∩ D
j
) =
m
∑
j=1
n
∑
i=1
µ
0
(C
i
∩ D
j
) =
m
∑
j=1
µ
0
(D
j
).
Punkt (b) twierdzenia jest oczywisty.
Ponieważ funkcje addytywne na półpierścieniach są podaddytywne (twier-
dzenie 5.1) więc z twierdzenia 6.1 wynika:
Twierdzenie 6.2 Dowolna funkcja addytywna na półpierścieniu jest funk-
cją monotoniczną i podaddytywną.
Twierdzenie 6.3 Załóżmy, że µ
0
jest miarą określoną na półpierścieniu
P.
Niech M będzie pierścieniem generowanym przez
P, a µ funkcją addytywną
będącą przedłużeniem µ
0
na M (zdefiniowanym tak jak w twierdzeniu 6.1).
Wówczas µ jest miarą na M.
Dowód. Załóżmy, że A
∈ M oraz A =
∪
∞
n=1
A
n
gdzie A
n
∈ M są parami
rozłączne. Załóżmy najpierw, że A
∈ P. Jeżeli
A
n
= A
n1
∪ ... A
nk
n
,
gdzie A
ni
, i = 1, ..., k
n
są zbiorami parami rozłącznymi należącymi do
P,
to
A =
∞
∪
n=1
k
n
∪
i=1
A
nk
i
,
(10)
i wszystkie zbiory występujące w sumie po prawej (10) stronie są parami
rozłącznymi zbiorami z półpierścienia
P. Ponieważ µ
0
jest miarą na
P, więc
µ(A) = µ
0
(A) =
∞
∑
n=1
k
n
∑
i=1
µ
0
(A
nk
i
) =
∞
∑
n=1
µ(A
n
).
Weźmy teraz dowolny zbiór A
∈ M i załóżmy, że A = C
1
∪ ... ∪ C
k
, gdzie
zbiory C
i
∈ P są parami rozłączne. Wówczas µ(A) = µ
0
(C
1
) + ... + µ
0
(C
k
),
oraz
C
i
= C
i
∩ A =
∞
∪
n=1
(C
i
∩ A
n
),
zatem ponieważ C
i
∈ P oraz C
i
∩ A
n
∈ P dla dowolnego i = 1, ..., k, oraz
n
∈ N, więc
µ(C
i
) =
∞
∑
n=1
µ(C
i
∩ A
n
).
25

Stąd dostajemy równość:
µ(A) =
k
∑
i=1
µ(C
i
) =
k
∑
i=1
∞
∑
n=1
µ(C
i
∩ A
n
) =
∞
∑
n=1
k
∑
i=1
µ(C
i
∩ A
n
) =
∞
∑
n=1
µ(
k
∪
i=1
(C
i
∩ A
n
)) =
∞
∑
n=1
µ((
k
∪
i=1
C
i
)
∩ A
n
) =
∞
∑
n=1
µ(A
∩ A
n
) =
∞
∑
n=1
µ(A
n
).
Twierdzenie 6.4 Niech
P będzie półpierścieniem. Funkcja addytywna µ na
P jest miarą jest miarą wtedy i tylko wtedy, gdy jest funkcją przeliczalnie
podaddytywną.
Dowód. Niech M będzie pierścieniem generowanym przez
P, a ν funkcją
addytywną na M będącą przedłużeniem µ.
Aby udowodnić wystarczalność podanego warunku załóżmy, że (A
n
) jest
ciągiem zbiorów parami rozłącznych takim, że A =
∪
∞
n=1
A
n
∈ P. Z twier-
dzenia 5.2 wynika, że
∞
∑
n=1
µ(A
n
) =
∞
∑
n=1
ν(A
n
)
> ν(A) = µ(A).
Nierówność w przeciwną stronę wynika z przeliczalnej podaddytywności.
Do dowodu konieczności zauważmy, że z twierdzenia 6.3 wynika, że ν jest
miarą na M, więc z lematu 6.1 wnioskujemy, że ν jest funkcją przeliczalnie
podaddytywną na M a więc również na
R.
7
Funkcja addytywna na iloczynie kartezjańskim
półpierścieni
Definicja 7.1 Załóżmy, że
P
1
,
P
2
są półpierścieniami a µ
1
, µ
2
funkcjami
addytywnymi odpowiednio na
P
1
,
P
2
. Niech
P = {A × B : A ∈ P
1
, B
∈ P
2
}
Zdefiniujmy funkcję µ na
P przyjmując
µ(A
× B) = µ
1
(A)µ
2
(B),
przy czym przyjmujemy, że iloczyn po prawej stronie jest równy 0, gdy jeden
z czynników jest równy 0, a drugi jest
∞.
26

Dowód. Załóżmy, że A
∈ P
1
, B
∈ P
2
oraz, że
A
× B =
∪
i=1
(A
i
× B
i
)
gdzie A
i
∈ P
1
oraz B
i
∈ P
2
dla i = 1, ..., n, oraz zbiory A
i
× B
i
są parami
rozłączne. Na mocy twierdzenia 4.4 istnieje rodzina zbiorów
{C
1
, ..., C
k
} ⊂
P
1
będąca rozbiciem
{A
1
, ..., A
n
} oraz rodzina {D
1
, ..., D
m
} ⊂ P
2
będąca
rozbiciem
{B
1
, ..., B
n
}. Oczywiście możemy zakładać, że wszystkie zbiory
C
i
i wszystkie zbiory D
j
są zbiorami niepustymi. Mamy
µ(A
×B) = µ
1
(A)µ
2
(B) =
n
∑
j=1
µ
1
(C
j
)
(
m
∑
l=1
µ
2
(D
l
)
)
=
k
∑
i=1
m
∑
j=1
µ
1
(C
j
)µ
2
(D
l
).
Oznaczmy
M
i
=
{(j, l) : C
j
× D
l
⊂ A
i
× B
i
}.
dla i = 1, ..., n. Wówczas M
i
są zbiorami parami rozłącznymi takimi, że
∪
(j, l)
∈M
i
(C
j
× D
l
) = A
i
× B
i
.
7.1
Miara Jordana generowana przez funkcję addytywną
Twierdzenie 7.1 Niech N będzie pierścieniem podzbiorów zbioru X, a µ
skończoną funkcją addytywną na N. Dla dowolnego zbioru A
⊂ X zdefiniuj-
my dwie funkcje m
w
, m
z
: 2
X
→ [0, ∞] w następujący sposób:
m
w
(A) = sup
{µ(B) : B ∈ N, B ⊂ A},
m
z
(A) = inf
{µ(B) : C ∈ N, A ⊂ C}.
Niech
M =
{A ⊂ X : m
w
(A) = m
z
(A) <
∞}.
Dla zbiorów A
∈ M przez m(A) oznaczamy wspólną wartość funkcji m
w
, m
z
na zbiorze A. Wówczas M jest pierścieniem zawierającym pierścień N. Funk-
cja m funkcją addytywną na X będącą przedłużeniem µ. Jeżeli µ jest miarą,
to m jest miarą na pierścieniu M.
Uwaga 7.1 Przy założeniach twierdzenia jeżeli A jest dowolnym podzbio-
rem X, to A
∈ M ⇔ dla dowolnego ε > 0 istnieją zbiory B, C ∈ N takie, że
B
⊂ A ⊂ C, oraz µ(C \ B) < ε.
Dowód twierdzenia Weźmy dowolne zbiory A
1
, A
2
⊂ X takie, że A, B ∈
M.
27

8
Miara zewnętrzna
8.1
Definicja i własności miary zewnętrznej
Definicja 8.1 Niech X będzie dowolnym zbiorem niepustym. Mówimy, że
funkcja µ
∗
: 2
X
→ [0, ∞] jest miarą zewnętrzną, jeżeli spełnia następujące
warunki:
(a) µ
∗
(
∅) = 0,
(b) A
⊂ B ⊂ X ⇒ µ
∗
(A)
¬ µ
∗
(B),
(c) µ
∗
(
∞
∪
n=1
A
n
)
¬
∞
∑
n=1
µ
∗
(A
n
) dla dowolnego ciągu (A
n
) podzbiorów zbio-
ru X.
Jak łatwo zauważyć jeśli założymy, że funkcja µ
∗
: 2
X
→ [0, ∞] spełnia
warunek (a) powyższej definicji, to warunki (b) i (c) można sformułować
równoważnie w postaci jednego warunku:
(c’) A
⊂
∞
∪
n=1
A
n
⇒ µ(A) ¬
∞
∑
n=1
µ
∗
(A
n
) dla dowolnego zbioru A
⊂ X i
dowolnego ciągu (A
n
) podzbiorów zbioru X.
Inaczej mówiąc miara zewnętrzna na zbiorze X, jest to funkcja monoto-
niczna i przeliczalnie podaddytywna określona na σ
−ciele wszystkich pod-
zbiorów zbioru X. W szczególności dowolna miara zewnętrzna jest również
funkcją skończenie podaddytywną, to znaczy dla dowolnej skończonej ilości
zbiorów A
1
, A
2
, ..., A
n
⊂ X zachodzi nierówność:
µ
∗
(A
1
∪ A
2
∪ ... ∪ A
n
)
¬ µ
∗
(A
1
) + µ
∗
(A
2
) + ... + µ
∗
(A
n
).
Z twierdzenia 5.3 wynika, że dowolna miara określona na 2
X
jest mia-
rą zewnętrzną na X, ponadto z twierdzenia 5.4 wnioskujemy, że miara ze-
wnętrzna jest miarą wtedy i tylko wtedy gdy jest funkcją addytywną. Co
więcej możemy sformułować następujące twierdzenie.
Twierdzenie 8.1 Jeżeli µ
∗
jest miarą zewnętrzną, M jest takim σ
−ciałem
podzbiorów zbioru X, że µ
∗
jest funkcją addytywną na M, to µ
∗
jest miarą
na M.
8.2
Twierdzenie Caratheodyr’ego
Definicja 8.2 Niech µ
∗
będzie miarą zewnętrzną na zbiorze X. Mówimy, że
zbiór A
⊂ X spełnia warunek Caratheodory’ego względem miary zewnętrz-
nej µ
∗
jeśli dla dowolnego zbioru Z
⊂ X zachodzi równość:
µ
∗
(Z) = µ
∗
(Z
∩ A) + µ
∗
(Z
∩ A
′
).
(11)
28

Ponieważ miara zewnętrzna jest funkcją podaddytywną, więc na to aby
zbiór A
⊂ X spełniał warunek Caratheodory’ego, wystarcza aby dla dowol-
nego zbioru Z
⊂ X zachodziła nierówność:
µ
∗
(Z)
µ
∗
(Z
∩ A) + µ
∗
(Z
∩ A
′
).
(12)
Lemat 8.1 Niech µ
∗
będzie miarą zewnętrzną na zbiorze X. Jeśli A
⊂ X
jest takim zbiorem, że µ
∗
(A) = 0 to A spełnia warunek Caratheodory’ego
względem µ
∗
.
Dowód. Weźmy dowolny zbiór Z
⊂ X. Wówczas z warunku (b) w definicji
8.1 miary zewnętrznej, mamy µ
∗
(A
∩ Z) = 0, oraz µ
∗
(Z)
µ
∗
(Z
∩ A
′
). Stąd
µ
∗
(Z)
µ
∗
(A
∩ Z) + µ
∗
(A
∩ Z
′
).
Nierówność przeciwna wynika z podaddytywności miary zewnętrznej.
Twierdzenie 8.2 (Caratheodorye’go) Niech µ
∗
będzie miarą zewnętrzną na
zbiorze X. Oznaczmy przez M klasę wszystkich podzbiorów X spełniających
warunek Caratheodory’ego względem µ
∗
. Wówczas:
(a) M jest σ
−ciałem podzbiorów zbioru X,
(b) µ
∗
jest miarą na M.
Dowód. Dowodzimy najpierw, że M jest ciałem zbiorów. Oczywiście
∅ ∈ M, oraz jeśli A ∈ M to A
′
∈ M bo prawa strona w równości (11) nie
zmienia się gdy zbiór A zastąpić zbiorem A
′
. Wystarczy więc udowodnić,
że suma dwóch zbiorów spełniających warunek Caratheodory’ego również
spełnia ten warunek. Aby to pokazać weźmy dwa dowolne zbiory A, B
∈ M
i dowolny zbiór Z
⊂ X. Ponieważ zbiór A spełnia warunek Caratheodory’ego
to biorąc w równości (11) zamiast zbioru Z kolejno zbiory Z
∩ B i Z ∩ B
′
otrzymujemy równości:
µ
∗
(Z
∩ B) = µ
∗
(Z
∩ B ∩ A) + µ
∗
(Z
∩ B ∩ A
′
)
(13)
µ
∗
(Z
∩ B
′
) = µ
∗
(Z
∩ B
′
∩ A) + µ
∗
(Z
∩ B
′
∩ A
′
)
(14)
Ponieważ zbiór B spełnia warunek Caratheodory’ego więc mamy rów-
ność:
µ
∗
(Z) = µ
∗
(Z
∩ B) + µ
∗
(Z
∩ B
′
),
zatem wykorzystując równości (13) i (14) dostajemy:
µ
∗
(Z) = µ
∗
(Z
∩B∩A)+µ
∗
(Z
∩B∩A
′
)+µ
∗
(Z
∩B
′
∩A)+µ
∗
(Z
∩B
′
∩A
′
) (15)
29

Oznaczmy przez I, II, III, IV kolejne składniki sumy po prawej stronie
równości (15). Ponieważ miara zewnętrzna jest funkcją podaddytywną, więc
zachodzi nierówność
I +II +III
µ
∗
((Z
∩B ∩A)∪(Z ∩B ∩A
′
)+(Z
∩B
′
∩A)) = µ
∗
(Z
∩(A∪B)),
(16)
bo
(Z
∩ B ∩ A) ∪ (Z ∩ B ∩ A
′
) + (Z
∩ B
′
∩ A) = Z ∩ (A ∪ B).
Ponadto mamy B
′
∩ A
′
= (A
∪ B)
′
więc:
IV = µ
∗
(Z
∩ (A ∪ B))
(17)
Z (15), (16) i (17) otrzymujemy nierówność:
µ
∗
(Z)
µ
∗
(Z
∩ (A ∪ B)) + µ
∗
(Z
∩ (A ∪ B)
′
),
dla dowolnego zbioru Z
⊂ X. Z nierówności tej wynika, że zbiór A∪B spełnia
warunek Caratheodory’ego. Udowodniliśmy więc, że rodzina M wszystkich
zbiorów spełniających warunek Caratheodory’ego jest ciałem podzbiorów X.
W następnym kroku dowodu udowodnimy indukcyjnie że dla dowolne-
go m
∈ N, dowolnych zbiorów parami rozłącznych A
1
, A
2
, ..., A
m
∈ M i
dowolnego zbioru Z
⊂ X, zachodzi równość:
µ
∗
(Z
∩
m
∪
n=1
A
n
) =
m
∑
n=1
µ
∗
(Z
∩ A
n
).
(18)
Dla m=1 równość (18) jest oczywista. Załóżmy że jest prawdziwa dla
pewnego m
∈ N i weźmy m+1 zbiorów parami rozłącznych A
1
, A
2
, ..., A
m+1
∈
M i dowolny zbiór Z
⊂ X. Ponieważ zbiór A
m+1
spełnia warunek Carathe-
odory’ego więc biorąc w (11) zamiast Z zbiór Z
∩
∪
m+1
n=1
A
n
a zamiast A
zbiór A
m+1
otrzymujemy równość:
µ
∗
(Z
∩
m+1
∪
n=1
A
n
) = µ
∗
((Z
∩
m+1
∪
n=1
A
n
)
∩A
m+1
) + µ
∗
((Z
∩
m+1
∪
n=1
A
n
)
∩A
′
m+1
) (19)
Ponieważ wszystkie zbiory A
n
są parami rozłączne, więc mamy równości:
(Z
∩
m+1
∪
n=1
A
n
)
∩ A
m+1
= Z
∩ A
m+1
(20)
oraz
(Z
∩
m+1
∪
n=1
A
n
)
∩ A
′
m+1
= Z
∩
m
∪
n=1
A
n
.
(21)
Zatem z założenia indukcyjnego i z (21) mamy
µ
∗
((Z
∩
m+1
∪
n=1
A
n
)
∩ A
′
m+1
) =
m
∑
n=1
µ
∗
(Z
∩ A
n
)
(22)
30

Z (19), (20) i (22) otrzymujemy więc równość:
µ
∗
(Z
∩ (
m+1
∪
n=1
A
n
)) =
m+1
∑
n=1
µ
∗
(A
n
)
kończącą dowód indukcyjny równości (18)
Dalej pokażemy że w równości (18) zamiast skończonej sumy zbiorów
parami rozłącznych, można wziąć sumę nieskończoną. Dokładniej mówiąc
udowodnimy, że jeśli (A
n
) jest ciągiem zbiorów parami rozłącznych takim,
że A
n
∈ M dla dowolnego n ∈ N to dla dowolnego zbioru Z ⊂ X zachodzi
równość:
µ
∗
(Z
∩
∞
∪
n=1
A
n
) =
∞
∑
n=1
µ
∗
(Z
∩ A
n
).
(23)
Zauważmy, że nierówność:
µ
∗
(Z
∩
∞
∪
n=1
A
n
)
¬
∞
∑
n=1
µ
∗
(Z
∩ A
n
),
(24)
wynika bez żadnych założeń o zbiorach A
n
z warunku (c) w definicji 8.1
miary zewnętrznej. Wystarczy więc pokazać nierówność przeciwną.
Ponieważ miara zewnętrzna jest funkcją monotoniczną (warunek (b) w
definicji miary zewnętrznej) więc dla dowolnego m
∈ N mamy nierówność:
µ
∗
(Z
∩
∞
∪
n=1
A
n
)
µ
∗
(Z
∩
m
∪
n=1
A
n
)
(25)
Wykorzystując powyższą nierówność i równość (18) widzimy, że dla dowol-
nego m
∈ N zachodzi nierówność:
µ
∗
(Z
∩
∞
∪
n=1
A
n
)
m
∑
n=1
µ
∗
(Z
∩ A
n
).
Przechodząc z m do
∞ dostajemy nierówność
µ
∗
(Z
∩
∞
∪
n=1
A
n
)
∞
∑
n=1
µ
∗
(Z
∩ A
n
).
(26)
Nierówności (24), (26) dają nam równość (23).
Udowodnimy dalej, że M jest σ
−ciałem podzbiorów zbioru X. Ponie-
waż udowodniliśmy wcześniej, że M jest ciałem zbiorów więc na podstawie
twierdzenia 3.4 wystarczy pokazać, że jeśli (A
n
) jest ciągiem zbiorów parami
rozłącznych takim że A
n
∈ M dla dowolnego n ∈ N to
∪
∞
n=1
A
n
∈ M.
Weźmy dowolny zbiór Z
⊂ X. Ponieważ M jest ciałem zbiorów więc dla
dowolnego m
∈ N mamy nierówność:
µ
∗
(Z) = µ(Z
∩
m
∪
n=1
A
n
) + µ
∗
(Z
∩ (
m
∪
n=1
A
n
))
′
)
(27)
31

Ponieważ miara zewnętrzna jest funkcją monotoniczną więc:
µ
∗
(Z
∩ (
m
∪
n=1
A
n
)
′
)
µ
∗
(Z
∩ (
∞
∪
n=1
A
n
)
′
)
(28)
Z równości (18) oraz z (28) i (27) otrzymujemy dla dowolnego m
∈ N
nierówność:
µ(Z)
m
∑
n=1
µ
∗
(Z
∩ A
n
) + µ
∗
(Z
∩ (
∞
∪
n=1
A
n
)
′
)
Przechodząc w ostatniej nierówności z m do
∞ dostajemy nierówność:
µ(Z)
∞
∑
n=1
µ
∗
(Z
∩ A
n
) + µ
∗
(Z
∩ (
∞
∪
n=1
A
n
)
′
)
Na koniec wykorzystując równość (23) otrzymujemy nierówność:
µ
∗
(Z)
µ
∗
(Z
∩
∞
∪
n=1
A
n
) + µ
∗
(Z
∩ (
∞
∪
n=1
A
n
)
′
)
dla dowolnego zbioru Z
⊂ X. To zaś oznacza, że zbiór
∪
∞
n=1
A
n
spełnia
warunek Caratheodory’ego, a więc należy do M.
Udowodniliśmy więc, że M jest σ
−ciałem podzbiorów zbioru X. Aby
pokazać że µ
∗
jest miarą na M weźmy dowolny ciąg zbiorów (A
n
) parami
rozłącznych takich, że A
n
∈ M dla dowolnego n ∈ N. Biorąc w równości
(23) Z = X, dostajemy równość:
µ
∗
(
∞
∪
n=1
A
n
) =
∞
∑
n=1
µ
∗
(A
n
)
dowodzącą, że µ
∗
jest miarą na M i kończącą dowód twierdzenia.
Definicja 8.3 Jeżeli µ
∗
jest miarą zewnętrzną na zbiorze X, to σ
−ciało zło-
żone z wszystkich zbiorów spełniających warunek Caratheodory’ego wzglę-
dem tej miary zewnętrznej będziemy nazywać σ
−ciałem generowanym przez
miarę zewnętrzną µ
∗
, a miarę będącą obcięciem miary zewnętrznej do σ
−ciała
generowanego przez µ
∗
, nazywamy miarą generowaną przez miarę zewnętrz-
ną µ
∗
.
Z lematu 8.1 otrzymujemy.
Twierdzenie 8.3 Miara generowana przez miarę zewnętrzną jest miarą zu-
pełną.
32

Twierdzenie 8.4 Załóżmy, że µ
∗
jest miarą zewnętrzną na zbiorze X. Niech
M będzie σ
−ciałem generowanym przez miarę zewnętrzną µ
∗
. Jeśli A jest
takim podzbiorem X, że dla dowolnego ε > 0 istnieją zbiory B, C
∈ M takie,
że B
⊂ A ⊂ C, oraz µ(C \ B) ¬ ε, to A ∈ M.
Dowód.Z założenie dla dowolnego n
∈ N istnieją zbiory B
n
, C
n
∈ M takie,
że B
n
⊂ A ⊂ C
n
oraz µ
∗
(C
n
\ B
n
) < 1/n. Niech
B =
∞
∪
n=1
B
n
, C =
∞
∩
n=1
C
n
.
Wówczas B
⊂ A ⊂ C, B, C ∈ M, oraz dla dowolnego n ∈ N zachodzi
nierówność µ
∗
(C
\ B) ¬ 1/n, zatem µ
∗
(C
\ B) = 0. Ponieważ A \ B ⊂ C \ B
więc również µ
∗
(A
\ B) = 0. Z lematu 8.1 wynika więc, że A \ B ∈ M a
ponieważ B
∈ M oraz A = B ∪ (A \ B) więc A ∈ M.
8.3
Ogólna metoda konstrukcji miary zewnętrznej
Następujące twierdzenie podaje ogólną metodę konstrukcji miary zewnętrz-
nej.
Twierdzenie 8.5 Niech X będzie dowolnym zbiorem niepustym, a
R rodzi-
ną podzbiorów X. Załóżmy, że ν :
R → [0, ∞] jest taką funkcją, że
inf
{ν(A) : A ∈ R} = 0
(29)
Dla dowolnego zbioru A
⊂ X niech
µ
∗
(A) = inf
{
∞
∑
n=1
ν(A
n
) : A
⊂
∞
∪
n=1
A
n
, A
n
∈ R dla dowolnego n ∈ N} (30)
(przyjmujemy, że inf zbioru pustego jest równe
∞.) Wówczas µ
∗
jest miarą
zewnętrzną na X.
Dowód. Funkcja zdefiniowana wzorem
8.4
Miara zewnętrzna generowana przez funkcję addytywną
na półpierścieniu
Uwaga 8.1 Jeżeli
P jest półpierścieniem σ−skończonym a ν funkcją addy-
tywną ma
P. Wówczas funkcja µ
∗
: 2
X
→ [0, ∞] określona wzorem (30) jest
miarą zewnętrzną na X.
Jeżeli M jest pierścieniem generowanym przez
P a nu : M → [0, ∞]
funkcją addytywną będącą przedłużeniem funkcji ν, to
µ
∗
(A) = inf
{
∞
∑
n=1
ν(A
n
) : A
⊂
∞
∪
n=1
A
n
, A
n
∈ M}
33

Twierdzenie 8.6 Niech
P będzie półpierścieniem −sigma skończonym pod-
zbiorów zbioru X, a µ
∗
: 2
X
→ [0, ∞] miarą zewnętrzną zdefiniowaną tak
jak w twierdzeniu 8.5. Wówczas:
(a) dowolny zbiór A należący do
P spełnia warunek Caratheodory’ego;
(b) µ
∗
(A)
¬ ν(A) dla dowolnego A ∈ P;
(c) jeżeli ν jest miarą na
P, to µ
∗
(A) = ν(A) dla dowolnego A
∈ P.
Dowód. Na podstawie uwagi 8.1 możemy zakładać, że
P jest pierścieniem.
Aby udowodnić (a) weźmy dowolny zbiór A
∈ P i Z ⊂ X. Aby pokazać
nierówność (12) można zakładać, że µ
∗
(Z) <
∞. Weźmy dowolne ε > 0 i
dobierzmy takie ciągi zbiorów (C
n
), że C
n
∈ P dla dowolnego n ∈ N, oraz:
Z
⊂
∞
∪
n=1
C
n
oraz
∞
∑
n=1
ν(C
n
) < µ
∗
(A) + ε.
Zauważmy, że Z
∩ A ⊂
∞
∪
n=1
(C
n
∩ A), oraz Z ∩ A
′
⊂
∞
∪
n=1
(C
n
∩ A
′
), oraz dla
dowolnego n
∈ N. Ponieważ C
n
∩ A, C
n
∩ A
′
∈ P, więc Stąd
µ
∗
(Z
∩ A) + µ
∗
(Z
∩ A
′
)
¬
∞
∑
n=1
ν(C
n
∩ A) +
∞
∑
n=1
ν(C
n
∩ A
′
) =
∞
∑
n=1
[ν(C
n
∩ A) + ν(C
n
∩ A
′
)] =
∞
∑
n=1
ν(C
n
)
¬ µ
∗
(Z) + ε.
Ze względu na dowolność ε mamy nierówność µ
∗
(Z
∩A)+µ
∗
(Z
∩A
′
)
¬ µ
∗
(Z).
Ponieważ we wzorze (30) możemy przyjąć A
1
= A, oraz A
n
=
∅ dla n > 1
więc mamy nierówność µ
∗
(A)
¬ ν(A).
Aby pokazać punkt (b) twierdzenia wystarczy udowodnić, że ν(A)
¬
µ
∗
(A) gdy A
∈ N. Można zakładać, że µ
∗
(A) <
∞. Weźmy dowolne ε > 0 i
niech (A
n
) będzie takim ciągiem zbiorów z N, że
A
⊂
∞
∪
n=1
A
n
oraz
∞
∑
n=1
ν(A
n
) < µ
∗
(A) + ε.
Wówczas A =
∞
∪
n=1
(A
n
∩ A) więc
ν(A)
¬
∞
∑
n=1
ν(A
n
∩ A) ¬
∞
∑
n=1
ν(A
n
)
¬ µ
∗
(A) + ε.
Ze względu na dowolność ε dostajemy dowodzoną nierówność.
34

9
Miara Lebesque’a w
R
k
9.1
Przedziały k
−wymiarowe, figury elementarne
Przez
R
k
oznaczamy przestrzeń euklidesową k
− wymiarową, to znaczy
R
k
=
{(x
1
, ..., x
k
) : x
i
∈ R (i = 1, ..., k)}
W przestrzeni tej będziemy rozpatrywać zwykłą metrykę euklidesową
d
k
(x, y) =
(
n
∑
i=1
|x
i
− y
i
|
2
)
1
2
,
jeżeli x = (x
1
, x
2
, ..., x
k
), y = (y
1
, y
2
, ..., y
k
). W stosunku do tej przestrze-
ni będziemy używać wszystkich pojęć wprowadzanych w teorii przestrzeni
metrycznych i w topologii; jak pojęcia kuli, zbiorów otwartych, zbiorów do-
mkniętych, wnętrza i domknięcia zbioru, zbiorów zwartych i.t.d.
Definicja 9.1 (a) Przedziałem w
R nazywamy dowolny ze zbiorów postaci
(a, b), [a, b], [a, b), (a, b],
gdzie a, b
∈ R oraz a ¬ b. W szczególności zbiór pusty i zbiór jednopunktowy
jest przedziałem.
(b) Przedziałem k
−wymiarowym nazywamy dowolny zbiór w R
k
postaci
P
1
× P
2
× ... × P
k
(31)
gdzie P
i
jest przedziałem jednowymiarowym dla i = 1, 2, ..., k.
Rodzinę wszystkich przedziałów k
−wymiarowych będziemy oznaczać przez
P
k
.
Jeżeli conajmniej jeden z przedziałów P
i
jest zbiorem jednopunktowym
lub zbiorem pustym, to mówimy, że przedział jest przedziałem zdegenero-
wanym.
Jeżeli wszystkie przedziały P
i
są przedziałami domkniętymi (otwartymi)
to przedział (31) nazywamy przedziałem domkniętym (otwartym).
Definicja 9.2 Dla dowolnych a, b
∈ R
k
takich, że a = (a
1
, a
2
, ..., a
k
), b =
(b
1
, b
2
, ..., b
k
) przyjmujemy, że a
¬ b jeżeli a
i
¬ b
i
dla dowolnego i = 1, .., k,
oraz a < b jeżeli a
i
< b
i
dla dowolnego i = 1, ..., k.
Jeżeli a, b
∈ R
k
i a
¬ b to przyjmujemy
[a, b] =
{x ∈ R
k
: a
¬ x ¬ b}
[a, b) =
{x ∈ R
k
: a
¬ x < b}
(a, b] =
{x ∈ R
k
: a < x
¬ b}
35

[a, b] =
{x ∈ R
k
: a < x < b
}
Jeżeli a, b są dowolnymi liczbami rzeczywistymi takimi, że a
6 b, to definiu-
jemy [a, b]
k
jako przedział k
−wymiarowy [a, b] gdzie a = (a, ..., a), b =
(b, ...., b).
Analogicznie definujemy przedziały (a, b)
k
, [a, b)
k
, (a, b]
k
.
Uwaga 9.1 Jeżeli P jest dowolnym przedziałem k
−wymiarowym postaci
(31) to
¯
P = ¯
P
1
× ¯
P
2
× ... × ¯
P
k
,
oraz
int(P ) = int(P
1
)
× int(P
2
)
× ... × int(P
k
).
Twierdzenie 9.1 Dowolny zbiór otwarty można zapisać w postaci sumy
przeliczalnej ilości przedziałów otwartych.
Dowód. Udowodnimy najpierw, że dla dowolnego x
∈ U istnieją takie
punkty a, b
∈ Q
k
, że a < x < b, oraz (a, b)
⊂ U. Weźmy dowolny punkt
x = (x
1
, ..., x
k
)
∈ U i niech ε > 0 będzie takie, że K(x, ε) ⊂ U. Weź-
my δ > 0 takie, że δ <
ε
√
k
. Niech a
i
, b
i
będą takimi liczbami wymierny-
mi, że a
i
< x
i
< b
i
, oraz x
i
− a
i
, b
i
− x
i
< δ dla i = 1, ..., k. Niech
a = (a
1
, ..., a
k
), b = (b
1
, ..., b
k
) i załóżmy, że y = (y
1
, ..., y
k
)
∈ U.
Wówczas
d
k
(x, y) =
(
n
∑
i=1
(x
i
− y
i
)
2
)
1
2
<
(
n
∑
i=1
δ
2
)
1
2
=
√
kδ < ε.
Niech teraz dla dowolnego x
∈ U, a
x
, b
x
∈ Q
k
będą takie, że a
x
< x <
b
x
, (a
x
, b
x
)
⊂ U. Wówczas
∪
x
∈U
(a
x
, b
x
) = U
oraz rodzina
{(a
x
, b
x
) : x
∈ U}
jest rodziną przeliczalną (bo Q
k
× Q
k
jest zbiorem przeliczalnym).
Twierdzenie 9.2 Dowolny zbiór otwarty można zapisać w postaci sumy
przeliczalnej ilości przedziałów parami rozłącznych.
Uwaga 9.2 Dowolny zbiór otwarty w
R można zapisać w postaci sumy
przeliczalnej ilości przedziałów otwartych (ograniczonych albo nieograniczo-
nych) parami rozłącznych.
36

Lemat 9.1 Niech X będzie ośrodkową przestrzenią topologiczną. Jeżeli
R
jest rodziną podzbiorów niepustych, parami rozłącznych otwartych w X, to
R jest rodziną przeliczalną.
Dowód lematu. Niech A będzie dowolnym podzbiorem przeliczalnym i
gęstym w X. Niech f :
R → A będzie taką funkcją, że f(U) ∈ U ∩ A dla
dowolnego zbioru U
∈ R. Funkcja f jest funkcją przeliczalną więc A 6 ℵ
0
.
Dowód twierdzenia. Niech U będzie dowolnym zbiorem otwartym w
R.
Dla dowolnego x
∈ U, niech
a
x
= inf
{a : (a, x] ⊂ U}, b
x
= sup
{b : [x, b) ⊂ U}.
Jak łatwo zauważyć, mamy x
∈ (a
x
, b
x
)
⊂ U, zatem
∪
x
∈U
(a
x
, b
x
) = U.
(32)
Z definicji przedziałów (a
x
, b
x
) wynika, że dla dowolnych punktów x, y
∈ U
zbiory (a
x
, b
x
) są albo identyczne albo rozłączne, zatem na podstawie lematu
9.1 rodzina
{(a
x
, b
x
) : x
∈ U}
jest rodziną przeliczalną, stąd z (32) dostajemy tezę twierdzenia.
Definicja 9.3 Mówimy, że zbiór A
⊂ R
k
jest k
−wymiarową figurą elemen-
tarną jeżeli A można przedstawić w postaci
A = P
1
∪ P
2
∪ ... ∪ P
n
(33)
gdzie P
i
dla i = 1, 2, ..., n jest przedziałem k
−wymiarowym.
Zbiór wszystkich k
−wymiarowych figur elementarnych będziemy ozna-
czać przez
E
k
.
Definicja 9.4 Mówimy, że figura elementarna jest figurą zdegenerowaną je-
żeli daje się przedstawić w postaci sumy skończonej ilości przedziałów zde-
generowanych.
Mówimy, że dwie figury elementarne A, B są prawie rozłączne, jeżeli ich
iloczyn A
∩ B jest figurą elementarną zdegenerowaną.
Twierdzenie 9.3 Rodzina
P
k
wszystkich przedziałów k
− wymiarowych jest
półpierścieniem.
Dowód. Dla k = 1 twierdzenie jest oczywiste a dla dowolnego k wynika z
twierdzenia 14.2.
Z twierdzenia 9.3 wynika
37

Twierdzenie 9.4 Rodzina
E
k
wszystkich figur elementarnych k
−wymiarowych
jest pierścieniem. Dowolną figurą elementarną można przedstawić w postaci
sumy
P
1
∪ ... ∪ P
n
,
gdzie P
i
są przedziałami k
−wymiarowymi parami rozłącznymi.
Wniosek 9.1 Jeżeli A jest figurą elementarną domkniętą to A można przed-
stawić w postaci skończonej sumy przedziałów dotkniętych prawie rozłącz-
nych.
9.2
Objętość figur elementarnych
Definicja 9.5 Dla dowolnego przedziału k
−wymiarowego P = P
1
× P
2
×
...
× P
k
definiujemy uogólnioną objętość tego przedziału jako
|P |
k
=
|P
1
| × |P
2
| × ... × |P
k
|.
gdzie dla dowolnego przedziału jednowymiarowego P
i
, przez
|P
i
| oznaczyli-
śmy długość tego przedziału.
Przedział k
−wymiarowy P jest przedziałem zdegenerowanym wtedy i tylko
wtedy gdy jego objętość jest równa 0. Jak łatwo zauważyć, mamy
|P |
k
=
|P |
k
=
|int(P
k
)
|
k
(34)
dla dowolnego przedziału k
−wymiarowego P. Tak więc dla dowolnego prze-
działu k
−wymiarowego P istnieje przedział otwarty zawarty w tym prze-
dziale i istnieje przedział domknięty zawierający P taki, że objętości obu
przedziałów są równe
|P |
k
.
Lemat 9.2 Dla dowolnego przedziału k
−wymiarowego P i dla dowolnego
ε > 0 istnieje przedział domknięty K i przedział otwarty Q takie, że K
⊂
P
⊂ Q oraz
|K|
k
>
|P |
k
− ε, |Q|
k
<
|P |
k
+ ε.
Definicja 9.6 Mówimy, że dwa przedziały k
−wymiarowe P i Q są prawie
rozłączne jeżeli ich iloczyn jest przedziałem k
− wymiarowym zdegenerowa-
nym, to znaczy gdy int(P
∩ Q) = ∅ albo równoważnie gdy |P ∩ Q|
k
= 0.
Dalej będziemy używać następującego oczywistego choć trudnego tech-
nicznie w dowodzie lematu
38
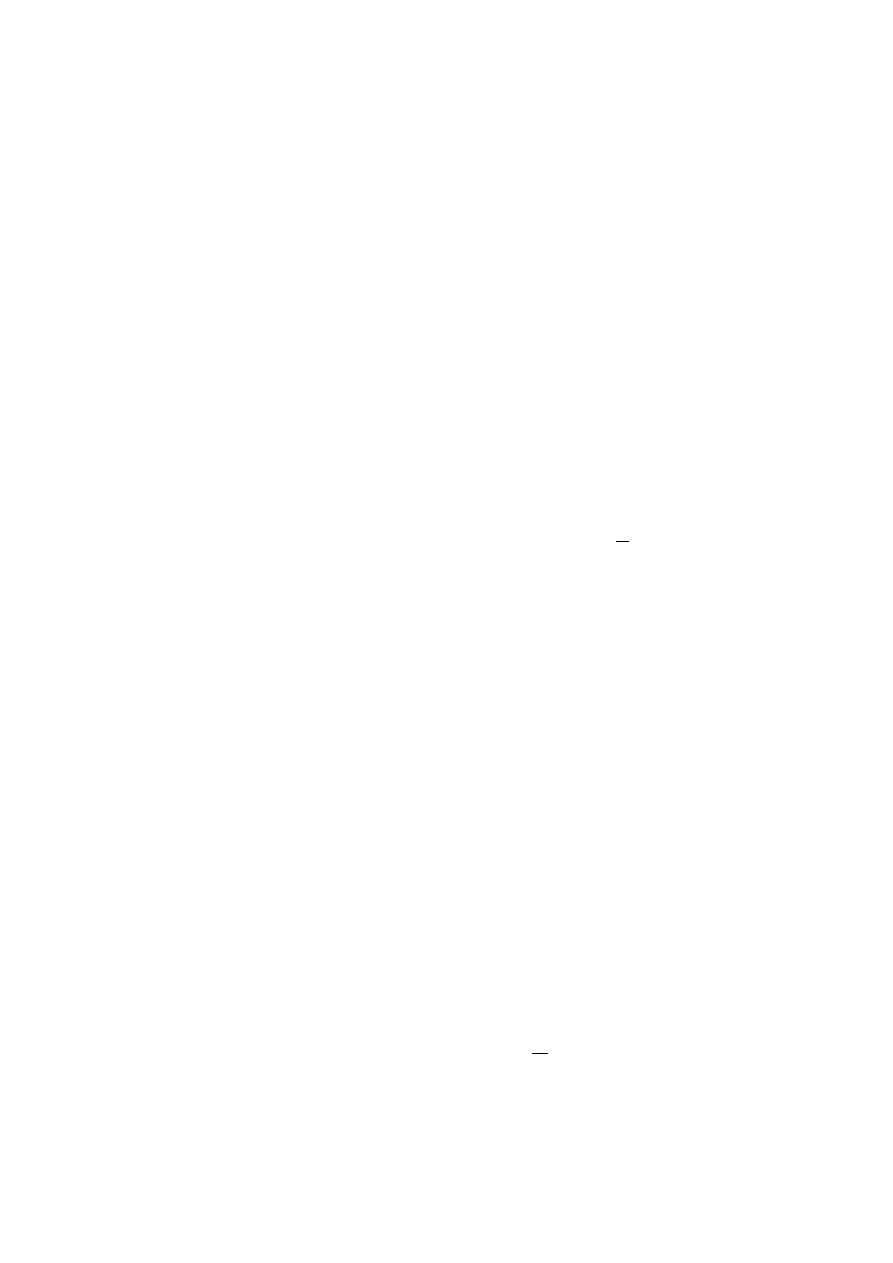
Lemat 9.3 Jeżeli dowolny przedział k
−wymiarowy P przedstawić w posta-
ci skończonej sumy rozłącznych przedziałów k
− wymiarowych
P = P
1
∪ P
2
∪ ... ∪ P
k
to
|P |
k
=
|P
1
|
k
+
|P
2
|
k
+ ... +
|P
k
|
k
Inaczej mówiąc funkcja
| · |
k
jest funkcją addytywną na
P
k
.
Ponieważ pierścieniem generowanym przez
P
k
jest rodzina wszystkich
k
−wymiarowych figur elementarnych więc na podstawie twierdzenia 6.1 mo-
żemy zdefiniować objętość k
−wymiarowych figur elementarnych przyjmując,
że
|E|
k
=
|P
1
|
k
+ ... +
|P
n
|
k
gdy E = P
1
∪ ... ∪P
n
gdzie P
i
∩P
j
=
∅ gdy i ̸= j. W ten sposób przedłużamy
| · |
k
do funkcji addytywnej na pierścień
E
k
.
Lemat 9.4 (a) Jeżeli E jest figurą elementarną to int(E) i E są figurami
elementarnymi o takiej samej objętości co E.
(b)
Dla dowolnej figury elementarnej E i dowolnego ε > 0 istnieją
domknięta figura elementarna F oraz otwarta G takie, że F
⊂ E ⊂ G oraz
|F |
k
>
|E|
k
− ε, |G|
k
<
|E|
k
+ ε.
Wykorzystując lemat 9.3 udowodnimy.
Twierdzenie 9.5 Funkcja
| · |
k
jest miarą na
P
k
.
Dowód. Na podstawie twierdzenia 9.3
P jest półpierścieniem. Z lematu 9.3
wynika, że
| · |
k
jest funkcją addytywną na
P. Z twierdzenia 6.4 wystar-
czy pokazać, że jeżeli P jest dowolnym przedziałem k
−wymiarowym a (P
n
)
takim ciągiem przedziałów, że P
⊂
∪
∞
n=1
P
n
to,
|P |
k
¬
∞
∑
n=1
|P
n
|
k
.
(35)
Załóżmy najpierw, że P jest przedziałem domkniętym. Weźmy dowolne ε >
0. Wówczas dla dowolnego n istnieje przedział otwarty Q
n
taki, że P
n
⊂ Q
n
oraz
|Q
n
|
k
<
|P
n
|
k
+ ε/2
n
. Ponieważ P
⊂
∪
∞
n=1
Q
n
i P jest zbiorem zwartym
więc istnieje takie m
∈ N, że P ⊂
∪
m
n=1
Q
n
. Ponieważ
| · |
k
jest funkcją
addytywną na P więc
|P |
k
¬
m
∑
i=1
|Q
n
|
k
¬
∞
∑
n=1
|Q
n
|
k
¬
∞
∑
n=1
|P
n
|
k
+
ε
2
n
=
∞
∑
n=1
|P
n
|
k
+ ε.
39

Ze względu na dowolność ε mamy nierówność (35). Załóżmy teraz, że P
jest dowolnym przedziałem. Weźmy dowolne ε > 0 i niech P
0
będzie takim
przedziałem domkniętym zawartym w P, że
|P
0
|
k
>
|P |
k
− ε. Ponieważ
P
0
⊂
∪
∞
n=1
P
n
więc
|P
0
|
k
¬
∑
∞
n=1
|P
n
|
k
stąd dostajemy nierówność
|P |
k
<
ε +
∑
∞
n=1
|P
n
|
k
a ze względu na dowolność ε dowodzoną nierówność.
9.3
Miara zewnętrzna Lebesque’a w
R
k
.
Definicja 9.7 Miarę zewnętrzną Lebesque’a w przestrzeni
R
k
określamy
wzorem
l
∗
k
(A) = inf
{
∞
∑
n=1
|P
n
|
k
: A
⊂
∞
∪
n=1
P
n
, P
n
− przedziały w R
k
}.
(36)
Twierdzenie 9.6 l
∗
k
jest miarą zewnętrzną w
R
k
.
Dowód. Wystarczy wykorzystać twierdzenie 8.5 biorąc zamiast
R rodzinę
wszystkich przedziałów k
−wymiarowych i przyjmując, że Φ(P ) jest objęto-
ścią przedziału k
−wymiarowego P.
Z drugiej części uwagi 8.1 dostajemy:
Lemat 9.5 Dla dowolnego A
⊂ R
k
, mamy
l
∗
k
(A) = inf
{
∞
∑
n=1
|E
n
|
k
: E
n
∈ E
k
, A
⊂
∞
∪
n=1
E
n
}
(37)
Z twierdzeń 8.6 i 9.5 wynika
Lemat 9.6 Dla dowolnego zbioru A
⊂ R
k
mamy:
l
∗
k
(A) = inf
{
∞
∑
n=1
|P
n
|
k
: A
⊂
∞
∪
n=1
P
n
, P
n
− przedziały otwarty w R
k
}. (38)
Dowód. Oznaczmy przez I prawą stronę równości (38). Nierówność l
∗
k
(A)
¬
I jest oczywista, wystarczy więc udowodnić nierówność przeciwną. Można
więc zakładać, że l
∗
k
(()A) <
∞. Weźmy dowolne ε > 0. Z definicji kresu
górnego istnieje taki ciąg przedziałów (P
n
), że A
⊂
∞
∪
n=1
P
n
, oraz
∞
∑
i=1
|P
n
|
k
< l
∗
k
(A) +
ε
2
.
40

Z lematu 9.2 istnieją otwarte przedziały k
−wymiarowe Q
n
takie, że P
n
⊂ Q
n
oraz
|Q
n
|
k
− |P
n
|
k
< ε/2
n+1
. Mamy A
⊂
∞
∪
n=1
Q
n
, więc
I
¬
∞
∑
n=1
|Q
n
|
k
<
∞
∑
n=1
(
|P
n
|
k
+
ε
2
n+1
)
=
∞
∑
n=1
|P
n
|
k
+
ε
2
< l
∗
k
(A) + ε.
Ze względu na dowolność ε mamy dowodzoną nierówność I
¬ l
∗
k
(A).
9.4
Zbiory mierzalne w sensie Lebesque’a
Definicja 9.8 Miarę generowaną przez k
−wymiarową miarę zewnętrzną
Lebesque’a nazywamy k
−wymiarową miarą Lebesque’a, oznaczamy ją przez
l
k
(.) Przez
L
k
oznaczamy σ
−ciało zbiorów spełniających warunek Carathe-
odory’ego względem l
∗
k
. O zbiorach należących do
L
k
mówimy, że są mierzal-
ne w sensie Lebesque’a. Miarę wewnętrzną generowaną przez k
−wymiarową
miarę zewnętrzną Lebesque’a
Ponieważ na podstawie twiedzenia 8.3 dowolna miara generowana przez
miarę zewnętrzną jest miarą zupełną jest więc:
Twierdzenie 9.7 Miara Lebesque’a jest miarą zupełną.
Twierdzenie 9.8 Dowolny przedział k
−wymiarowy P jest zbiorem mierzal-
nym w sensie Lebesque’a. Ponadto
l
k
(P ) =
|P |
k
.
Twierdzenie 9.9 Miara Lebesque’a nie jest miarą skończoną, ale jest mia-
rą σ
−skończoną.
Dowód. Mamy
l
k
(R
k
)
l
k
([
−n, n]
k
) = 2
k
n
k
dla dowolnego n
∈ N więc l
k
(R
k
) =
∞. Ponadto
R
k
=
∞
∪
n=1
[
−n, n]
k
oraz l
k
([
−n, n]
k
) = 2
k
n
k
<
∞.
Definicja 9.9 Niech µ będzie miarą określoną na σ
−ciele M podzbiorów
zbioru X. Mówimy, że zbiór A
∈ M jest atomem miary µ jeżeli, µ(A) > 0 i
dla dowolnego zbioru B
∈ M takiego, że B ⊂ A mamy
µ(B) = 0 lub µ(B) = µ(A).
41

Twierdzenie 9.10 Miara Lebesque’a jest miarą bezatomową. Dokładniej
jeżeli A
∈ L
k
jest takim zbiorem, że l
k
(A) > 0, to dla dowolnego c
∈
(0, l
k
(A)) istnieje taki zbiór B
⊂ A taki, że B ∈ R oraz l
k
(B) = c.
Dowód. Zdefiniujmy funkcję f : [0,
∞) → [0, ∞) w następujący sposób
f (x) = l
k
(A
∩ [−x, x]
k
).
Łatwo zauważyć, że f jest funkcją ciągłą na [0,
∞) taką, że f(0) = 0, oraz
lim
x
→∞
f (x) = µ(A). Z twierdzenia Darboux wynika, że istnieje takie x
∈
(0,
∞), że f(x) = c. Wystarczy więc przyjąć B = A ∩ [−x, x]
k
.
Ponieważ dla dowolnego przedziału P i dowolnego x
∈ R
k
zbiór x + P
jest przedziałem o takiej samej objętości co przedział P więc mamy:
Twierdzenie 9.11 Dla dowolnego zbioru A
⊂ R
k
i dowolnego x
∈ R
k
ma-
my
l
∗
k
(A + x) = l
∗
k
(A).
Definicja 9.10 Niech X będzie przestrzenią liniową, M σ
−ciałem podzbio-
rów zbioru X a µ : M
→ [0, ∞] miarą. Mówimy, że µ jest miarą niezmienni-
czą jeżeli dla dowolnego zbioru A
∈ M mamy:
A + x
∈ M, µ(A + x) = µ(A).
Twierdzenie 9.12 Miara Lebesque’a jest miarą niezmienniczą.
Dowód. Na podstawie twierdzenia wystarczy pokazać, że jeżeli zbiór A
spełnia warunek Caratheodory’ego, to również dla dowolnego x
∈ R
k
zbiór
A + x również spełnia ten warunek. Weźmy dowolny zbiór Z
⊂ R
k
. Jeżeli
zbiór A spełnia warunek Caratheodory’ego, to z twierdzenia 9.4 mamy:
l
∗
k
(Z) = l
∗
k
(Z
− x) = l
∗
k
((Z
− x) ∩ A) + l
∗
k
((Z
− x) ∩ A
′
)
= l
∗
k
((Z
∩ (A + x)) − x)) + l
∗
k
((Z
∩ (A
′
+ x))
− x))
= l
∗
k
(Z
∩ (A + x)) + l
∗
k
(Z
∩ (A + x)
′
)
Ponieważ dowolny zbiór jednopunktowy jest przedziałem o objętości rów-
nej 0 więc jako wniosek z twierdzenia 9.8 dostajemy
Twierdzenie 9.13 Dowolny zbiór przeliczalny jest zbiorem mierzalnym i
ma miarę Lebesque’a równą zero.
Z twierdzenia DZOJSP wnioskujemy, że dowolny zbiór otwarty jest sumą
przeliczalnej ilości przedziałów otwartych. Ponieważ przedziały są zbiorami
mierzalnymi w sensie Lebesque’a więc wnioskujemy:
42

Twierdzenie 9.14 Dowolny podzbiór otwarty
R
k
jest zbiorem mierzalnym
w sensie Lebesque’a.
Z twierdzenia 9.1 i lematu 9.6 dostajemy
Twierdzenie 9.15 Dla dowolnego zbioru A
⊂ R
k
mamy:
l
∗
k
(A) = inf
{l
k
(U ) : A
⊂ U, U otwarty w R
k
}.
Ponieważ dopełnieniami zbiorów otwartych są zbiory domknięte więc z
twierdzenia 9.14 dostajemy.
Twierdzenie 9.16 Dowolny podzbiór domknięty
R
k
jest zbiorem mierzal-
nym w sensie Lebesque’a.
Uwaga 9.3 Zbiór Cantora jest zbiorem mierzalnym o mocy c i mierze rów-
nej 0. Ponieważ miara Lebesque’a jest miarą zupełną więc istnieje 2
c
zbiorów
mierzalnych w sensie Lebesque’a.
Definicja 9.11 Niech (X,
G) będzie dowolną przestrzenią topologiczną.
Mówimy, że zbiór A
⊂ X jest zbiorem typu G
δ
jeżeli A daje się przedstawić
w postaci
A =
∞
∩
n=1
U
n
,
gdzie U
n
są zbiorami otwartymi dla dowolnego n
∈ N.
Mówimy, że zbiór A jest zbiorem typu F
σ
w X jeżeli A można zapisać w
postaci
A =
∞
∪
n=1
F
n
,
gdzie wszystkie zbiory F
n
są zbiorami domkniętymi.
Uwaga 9.4 (a) Zbiór A jest zbiorem typu G
δ
wtedy i tylko wtedy gdy A
′
jest zbiorem typu F
σ
.
(b) Zbiory otwarte są zbiorami typu G
δ
a zbiory domknięte zbiorami
typu F
σ
.
Twierdzenie 9.17 Niech (X, d) będzie dowolną przestrzenią metryczną. Wów-
czas dowolny zbiór domknięty w X jest zbiorem typu G
δ
, a więc dowolny
zbiór otwarty jest zbiorem typu F
σ
.
Dowód. Jeżeli A jest dowolnym podzbiorem X, to dla dowolnego ε > 0
zbiór
A
ε
=
{x ∈ X : d(x, A) < ε}
43

jest podzbiorem otwartym X. Ponadto
∞
∩
n=1
A
1
n
= A.
Zatem jeżeli A jest podzbiorem domkniętym X, to
∩
∞
n=1
A
1
n
= A, zatem A
jest zbiorem typu G
δ
.
Twierdzenie 9.18 Dla dowolnego zbioru A
⊂ R
k
następujące warunki są
równoważne:
(a) A jest zbiorem mierzalnym w sensie Lebesque’a,
(b) Dla dowolnego ε > 0 istnieje zbiór otwarty U w
R
k
taki, że
A
⊂ U oraz l
∗
k
(U
− A) < ε,
(c) Dla dowolnego ε > 0 istnieje zbiór domknięty F w
R
k
taki, że
F
⊂ E oraz l
∗
k
(A
− F ) < ε,
(d) Istnieje zbiór H taki, że H jest zbiorem typu G
δ
w
R
k
oraz
A
⊂ H, l
∗
k
(H
− A) = 0,
(e) Istnieje zbiór E taki, że E jest zbiorem typu F
σ
w
R
k
oraz
E
⊂ A, l
∗
k
(A
− E) = 0.
Dowód. (a)
⇒(b). Załóżmy, najpierw, że A jest zbiorem mierzalnym w sensie
Lebesque’a i że l
k
(A) <
∞. Z lematu 9.6 istnieje ciąg przedziałów otwartych
(P
n
) taki, że
∑
∞
n=1
|P
n
|
k
< l
k
(A) + E oraz A
⊂
∪
∞
n=1
P
n
. Zbiór U =
∪
∞
n=1
P
n
jest zbiorem otwartym zawierającym A. Mamy
l
∗
k
(U
− A) = l
k
(U
− A) = l
k
(U )
− l
k
(A)
¬
∞
∑
n=1
|P
n
|
k
− l
k
(A) < ε.
(b)
⇒(d) Dla dowolnego nN istnieje taki zbiór otwarty U
n
, zawierający
zbiór A, że l
∗
k
(U
n
− A) < 1/n. Niech H =
∩
∞
n=1
U
n
. Zbiór H jest zbiorem
typu G
δ
zawierającym zbiór A oraz dla dowolnego n
∈ N mamy nierówność
l
∗
k
(H
− A) < l
∗
k
(U
n
− A) <
1
n
zatem l
∗
k
(H
− A) = 0.
(d)
⇒(a) Zbiór H jako zbiór typu G
δ
jest zbiorem mierzalnym w sensie
Lebesque’a. Ponieważ l
∗
k
(H
− A) = 0 więc z zupełności miary Lebesque’a
zbiór H
−A jest zbiorem mierzalnym. Ponieważ A = H −(H −A) więc zbiór
A jest również zbiorem mierzalnym.
44

Udowodniliśmy więc równoważność warunków (a), (b), (d). Ponieważ jak
łatwo zauważyć zbiór A spełnia warunek (c) wtedy i tylko wtedy gdy zbiór A
′
spełnia warunek (b) i analogicznie spełnianie przez zbiór A warunku (c) jest
równoważne spełnianie przez A
′
warunku (e) więc dostajemy równoważność
wszystkich warunków.
Definicja 9.12 Mówimy, że miara µ na σ
−ciele M jest miarą ośrodkową,
jeżeli istnieje przeliczalna rodzina
R ⊂ M taka, że dla dowolnego zbioru
A
∈ M takiego, że µ(A) < ∞ i dla dowolnego ε > 0 istnieje zbiór B ∈ R
taki, że µ(A
÷ B) < ε.
Twierdzenie 9.19 Niech M będzie σ
−ciałem podzbiorów zbioru X, a µ
miarą skończoną. Oznaczmy przez M
0
rodzinę tych zbiorów należących do
M które mają miarę skończoną. Wprowadźmy w M
0
relację
∼ w następujący
sposób:
A
∼ B ⇔ µ(A ÷ B) = 0.
Wówczas
∼ jest relacją równoważności w M
0
. Niech
M będzie zbiorem
wszystkich klas abstrakcji relacji
∼ . Określmy funkcję d : M × M → [0, ∞)
w następujący sposób:
d([A], [B]) = µ(A
÷ B).
Wówczas
(a)
Defincja funkcji d jest poprawna to znaczy nie zależy od wyboru
reprezentantów klas abstrakcji,
(b) (
M, d) jest przestrzenią metryczną,
(c)
Przestrzeń ta jest przestrzenią ośrodkową
⇔ miara µ jest miarą
ośrodkową.
Wniosek 9.2 Miara µ jest miarą ośrodkową wtedy i tylko wtedy gdy do-
wolna rodzina
R ⊂ M
0
taka, że µ(A
÷B) > 0 dla dowolnych różnych zbiorów
A, B
∈ R jest rodziną przeliczalną.
Twierdzenie 9.20 Miara Lebesque’a jest miarą ośrodkową.
Dowód. Rodzina
R wszystkich sum skończonych postaci:
(a
1
, b
1
)
∪ ... ∪ (a
n
, b
n
)
gdzie a
i
, b
i
∈ Q
n
, oraz a
i
< b
i
dla dowolnego i = 1, ..., n, jest rodziną
przeliczalną. Weźmy dowolny zbiór A
∈ L
k
taki, że l
k
(A) <
∞, oraz ε > 0.
Udowodnimy, że istnieje zbiór B
∈ R taki, że l
k
(A
÷ B) < ε. Z twierdzenia
9.15 istnieje taki zbiór otwarty U
⊂ R
k
, że A
⊂ U oraz l
k
(U
− A) <
ε
2
.
Ponieważ przedziały otwarte postaci (a, b) gdzie a, b
∈ Q
k
tworzą bazę
45

przestrzeni
R
k
, więc zbiór U można przedstawić w postaci przeliczalnej sumy
∪
∞
n=1
(a
n
, b
n
) przedziałów tego typu. Mamy więc
l
k
(U ) = l
k
(
∞
∪
n=1
(a
n
, b
n
)) = lim
m
→∞
l
k
(
m
∪
n=1
(a
n
, b
n
)).
Stąd istnieje takie m
∈ N, że
l
k
(U ) < l
k
(
m
∪
n=1
(a
n
, b
n
)) +
ε
2
(39)
Zbiór B =
∪
m
n=1
(a
n
, b
n
) jest zbiorem należącym do rodziny
R zawartym w
zbiorze U i na podstawie nierówności (39) spełniającym warunek l
k
(U
−B) <
ε/2. Stąd dostajemy nierówność
l
k
(A
÷ B) = l
k
((A
÷ U) ÷ (U ÷ B)) ¬ l
k
((A
÷ U) ∪ (U ÷ B)) =
l
k
((U
− A) ∪ (U − B)) ¬ l
k
(U
− A) + l
k
(U
− B) < ε.
9.5
Zbiory borelowskie
Definicja 9.13 Niech X będzie przestrzenią topologiczną. σ
−ciało pod-
zbiorów X generowane przez rodzinę wszystkich podzbiorów otwartych X
nazywamy σ
−ciałem zbiorów borelowskich tej przestrzeni i oznaczamy je
przez
B(X). Elementy tego σ−ciała nazywamy zbiorami borelowskimi.
Twierdzenie 9.21 (o klasyfikacji zbiorów borelowskich) Załóżmy, że X
jest przestrzenią metryczną. Niech ω
1
będzie pierwszą liczbą porządkową nie-
przeliczalną. Dla dowolnego α < ω
1
zdefiniujmy rodziny
G
α
oraz
F
α
w na-
stępujący sposób.
(a)
G
0
=
G, F
0
=
F,
(b) jeżeli α jest liczbą parzystą to
G
α
= (
∪
β<α
G
β
)
σ
,
F
α
= (
∪
β<α
F
β
)
δ
,
(b) jeżeli α jest liczbą nieparzystą to
G
α
= (
∪
β<α
G
β
)
δ
,
F
α
= (
∪
β<α
F
β
)
σ
.
Wówczas
B(X) =
∪
α<ω
1
G
α
=
∪
α<ω
1
F
α
.
46

Dowód. Zauważmy najpierw że jeżeli β < α < ω
1
, to
G
β
⊂ G
α
F
β
⊂ F
α
.
Udowodnimy, że dla dowolnego α < ω
1
mamy:
(i) A
∈ G
α
⇔ A
′
∈ F
α
(ii)
F
α
⊂ G
α+1
,
G
α
⊂ F
α+1
.
Twierdzenie 9.22 Jeżeli przestrzeń topologiczna X spełnia II aksjomat
przeliczalności to moc(
B(X)) ¬ c. W sczególności taka nierówność zachodzi
w dowolnej przestrzeni metrycznej ośrodkowej.
Twierdzenie 9.23 Dowolny zbiór borelowski w
R
k
jest zbiorem mierzalnym
w sensie Lebesque’a. Istnieje c zbiorów borelowskich w
R
k
, zatem istnieją
zbiory mierzalne w sensie Lebesque’a które nie są zbiorami borelowskimi.
Dowód. Zbiory otwarte w
R
k
są mierzalane w sensie Lebesque’a, więc σ
−
ciało
L
k
zbiorów mierzalnych w sensie Lebesque’a zawiera σ
−ciało genero-
wane przez rodzinę wszystkich zbiorów otwartych w
R
k
, to znaczy zawiera
B(R
k
). Z ośrodkowości
R
k
ilość zbiorów borelowskich w tej przestrzeni nie
jest większa od c. Ponieważ wszystkie przedziały są mierzalne i jest ich c,
więc moc(
B(R
k
) = c.
Z twierdzenia 9.18 wynika:
Twierdzenie 9.24 Miara Lebesque’a jest uzupełnieniem miary Lebesque’a
obciętej do zbiorów borelowskich w R
k
.
9.6
Miara wewnętrzna Lebesque’a
Definicja 9.14 Dla dowolnego zbioru A
⊂ R
k
definujemy k
− wymiarową
miarę wewnętrzną Lebesque’a zbioru A w następujący sposób:
l
w
k
(A) = sup
{l
k
(B) : B
∈ L
k
, B
⊂ A}.
Oczywiście dla dowolnego zbioru A
⊂ R
k
mamy l
w
k
(A)
¬ l
∗
k
(A). Jest również
oczywiste, że jeżeli zbiór A jest mierzalny w sensie Lebesque’a, to l
w
k
(A) =
l
k
(A).
Z twierdzenia ?? wynika:
Twierdzenie 9.25 Jeżeli A
⊂ R
k
jest takim zbiorem, że l
∗
k
(A) <
∞ to A
jest zbiore mierzalnym w sensie Lebesque’a wtedy i tylko wtedy gdy l
w
k
(A) =
l
∗
k
(A).
47

9.7
Miara Jordana
Definicja 9.15 Dla dowolnego zbioru ograniczonego A
⊂ R
k
definiujemy
miarę wenętrzną Jordana zbioru A
j
w
k
(A) = sup
{|E|
k
: E
∈ E
k
, E
⊂ A}
oraz miarę zewnętrzną Jordana:
j
z
k
(A) = sup
{|E|
k
: E
∈ E
k
, E
⊂ A}
jeżeli j
w
k
(A) = j
z
k
(A) to mówimy, że zbiór A jest zbiorem mierzalnym w
sensie Jordana i wspólną wartość miary zewnętrznej i wewnętrznej Jordana
zbioru A oznaczamy j
k
(A) i nazywamy miarą Jordana zbioru A. Przez
J
k
oznaczamy rodzinę wszystkich podzbiorów R
k
mierzalnych w sensie Jordana.
W przypadku k = 1 w ozanaczeniach pomijamy wskaźnik k.
Z definicji miary Jordana i z definicji kresów dostajemy.
Lemat 9.7 Zbiór A
⊂ R
k
jest zbiorem mierzalnym w sensie Jordana wtedy
i tylko wtedy gdy dla dowolnego ε > 0 istnieją figury elementarne F, E
∈ E
k
takie, że P
⊂ A ⊂ Q i |Q|
k
− |P |
k
< ε.
Ponieważ figury elementarne są zbiorami mierzalnymi w sensie Jordana
to dla dowolnego zbioru ograniczonego A
⊂ R
k
mamy oczywiste nierówności:
j
w
k
(A)
¬ l
w
k
(A)
¬ l
∗
k
(A)
¬ j
z
k
(A).
Z tych nierówności zaś wynika:
Twierdzenie 9.26 Jeżeli zbiór A
⊂ R
k
jest mierzalny w sensie Jordana,
to A jest mierzalny w sensie Lebesque’a i l
k
(a) = j
k
(A).
Przykład 9.1 Zbiór W wszystkich liczb wymiernych odcinka [0, 1] jest
zbiorem przeliczalnym więc na podstawie twierdzenia 9.13 jest zbiorem mie-
rzalnym w sensie Lebesque’a. Pokażemy, że zbiór ten nie jest zbiorem mie-
rzalnym w sensie Jordana. Ponieważ każdy przedział niezdegenerowany za-
wiera liczbę niewymierną więc jeżeli figura elementarna zawiera się w W
to jest figurą zdegenerowaną. Stąd j
w
(A) = 0. Oczywiście j
z
(A)
¬ 1, bo
W
⊂ [0, 1]. Jeżeli mamy skończoną ilość P
1
, P
2
, ..., P
n
przedziałów pokry-
wających zbiór W, to musi być
|P
1
| + ... + |P
n
| ¬ 1. Inaczej zbiór
K = [0, 1]
− (P
1
∪ ... ∪ P
n
)
jest figurą elementarną taką, że
|K| > 0. Stąd K musi zawierać przedział
niezdegenerowany a więc liczbę niewymierną. To zaś jest niemożliwe bo W
∩
K =
∅.
Analogiczny przykład można podać w
R
2
biorąc zamiast W zbiór wszyst-
kich punktów kwadratu [0, 1]
×[0, 1] które obie współrzędne mają wymierne.
48

Twierdzenie 9.27 Rodzina
J
k
wszystkich podzbiorów
R
k
mierzalnych w
sensie Jordana jest pierścieniem. Miara Jordana jest funkcją addytywną.
Dowód. Załóżmy, że A, B
∈ J
k
Niech F
1
, E
1
, F
2
, E
2
będą takimi k
− wy-
miarowymi figurami elementarnymi, że
F
1
⊂ A ⊂ E
1
, F
2
⊂ B ⊂ E
2
,
|E
1
− F
1
|
k
<
ε
2
,
|E
2
− F
2
|
k
<
ε
2
.
(40)
Wówczas
F
1
∪ F
2
⊂ A ∪ B ⊂ E
1
∪ E
2
oraz
|(E
1
∪ E
2
)
− (F
1
∪ F
2
)
|
k
=
|[E
1
− (F
1
∪ F
2
)]
∪ [E
2
− (F
1
∪ F
2
)]
|
k
¬
|(E
1
− F
1
)
∪ (E
2
− F
2
)
|
k
¬ |E
1
− F
1
|
k
+
|E
2
− F
2
|
k
¬
ε
2
+
ε
2
= ε.
Ponieważ ε było dobrane dowolnie, więc zbiór A
∪B jest zbiorem mierzalnym
w sensie Jordana. Aby udowodnić, że różnica A
−B jest zbiorem mierzalnym
dobierzmy dla ustalonego ε figury elementarne E
1
, E
2
, F
1
, F
2
spełniające
(40). Wówczas
F
1
− E
2
⊂ A − B ⊂ E
1
− F
2
,
oraz
(E
1
− F
2
)
− (F
1
− E
2
) = (E
1
∩ F
′
2
)
∩ (F
1
∩ E
′
2
)
′
= (E
1
∩ F
′
2
)
∩ (F
′
1
∪ E
2
)
= [(E
1
∩ F
′
2
)
∩ F
′
1
]
∪ [(E
1
∩ F
′
2
)
∩ E
2
]
⊂ [(E
1
− F
1
)
∪ (E
2
− F
2
)].
Stąd
|(E
1
−F
2
)
−(F
1
−E
2
)
|
k
< ε więc ze względu na dowolność ε dostajemy
mierzalność w sensie Jordana zbioru A
− B.
Twierdzenie 9.28 Zbiór ograniczony A
⊂ R
k
jest zbiorem mierzalnym w
sensie Jordana wtedy i tylko wtedy gdy brzeg tego zbioru to znaczy zbiór
∂A = A
− int(A)
jest zbiorem o mierze Jordana równej 0.
Załóżmy, że A jest zbiorem mierzalnym w sensie Jordana. Wówczas dla do-
wolnego ε > 0 znajdziemy dwie figury elementarne E, F takie, że E
⊂ A ⊂
F oraz
|F |
k
−|E|
k
< ε. Na mocy lematu 9.4 zbiory E
0
= int(E) oraz F
0
= F
są takimi figurami elementarnymi, że
|E
0
|
k
=
|E|
k
oraz
|F
0
|
k
=
|F |
k
. Mamy
E
0
⊂ intA, oraz A ⊂ F
0
. Stąd
j
z
k
(A) <
|F
0
− E
0
|
k
=
|F
0
|
k
− |E
0
|
k
=
|F |
k
− |E|
k
< ε.
Ze względu na dowolność ε dostajemy, że j
z
k
(A) = 0.
49

Ustalmy dowolnw ε > 0. Z drugiej części lematu 9.4 istnieje otwarta
figura elementarna G taka, że ∂(A)
⊂ G oraz |G|
k
< ε. Z twierdzenia ??
istnieje ciąg (P
n
) przedziałów otwartych taki, że
int(A) =
∞
∪
n=1
P
n
.
Wówczas
A
⊂ G ∪
∞
∪
n=1
P
n
,
więc ze zwartości zbioru A istnieje takie m
∈ N, że
A
⊂ G ∪ P
1
∪ ... ∪ P
m
.
Niech F = P
1
∪ ... ∪ P
m
oraz E = F
∪ G. Wówczas F i E są figurami
elementarnymi takimi, że
F
⊂ int(A) ⊂ A ⊂ A ⊂ E
oraz E
− F ⊂ G więc |E|
k
− |F |
k
=
|E − F |
k
¬ |G|
k
< ε. Dostajemy więc
mierzalność w sensie Jordana zbioru A.
Twierdzenie 9.29 Jeżeli N jest pierścieniem podzbiorów
R
k
takim, że
P
k
⊂
N
⊂ J
k
, a µ : N
→ [0, ∞) jest funkcją addyttywną na N taką, że µ(P ) =
|P |
k
dla dowolnego P
∈ P
k
, to µ(A) = l
k
(A) dla dowolnego A
∈ N.
9.8
Jedyność miary Lebsque’a
Twierdzenie 9.30 Niech M będzie σ
−ciałem podzbiorów R
k
zawierającym
wszystkie przedziały k
−wymiarowe a µ : M → [0, ∞] dowolną miarą taką,
że
µ(P ) =
|P |
k
dla dowolnego przedziału P. Wówczas
µ(A) = l
k
(A)
dla dowolnego A
∈ M ∩ L
k
.
Dowód. Oczywiście σ
−ciało M zawiera wszystkie zbiory borelowskie. Niech
U będzie dowolnym podzbiorem otwartym R
k
. Z twierdzenia 9.2 wynika, że
isntnieje ciąg (P
n
) k
−wymiarowcyh przedziałów parami rozłącznych taki, że
U =
∪
∞
n=1
P
n
. Mamy
µ(U ) = µ(
∞
∪
n=1
P
n
) =
∞
∑
n=1
µ(P
N
) =
∞
∑
n=1
|P
n
|
k
=
∞
∑
n=1
l
k
(P
n
) = l
k
(
∞
∪
n=1
P
n
) = l
k
(U ).
50

Udowodniliśmy więc, że miara µ pokrywa się z miarą Lebesque’a na zbiorach
otwartych. Udowodnimy dalej, że obie miary przyjmują równe wartości na
zbiorach typu G
δ
. Załóżmy, najpierw, że H jest zbiorem ograniczonym typu
G
δ
Wówczas zbiór H można przedstawić w postaci H =
∪
∞
n=1
U
n
gdzie (U
n
)
jest ciągiem zstępującym zbiorów otwartych. Możemy zakładać, że wszystkie
zbiory U
n
są ograniczone w więc w szczególności mają miarę skończoną
względem obu miar. Z twierdzenia 5.7 wynika więc, że
µ(H) = µ(
∞
∩
n=1
U
n
) = lim
n
→∞
µ(U
n
) = lim
n
→∞
l
k
(U
n
) = l
k
(
∞
∪
n=1
U
n
) = l
k
(H)
Jeżeli H jest dowolnym zbiorem typu G
δ
to weźmy ciąg wstępujący (P
n
)
przedziałów otwartych taki, że
∪
∞
n=1
P
n
=
R
k
. Wówczas na podstawie twier-
dzenia 5.5 mamy:
µ(H) = µ(
∞
∪
n=1
(H
∩ P
n
)) = lim
n
→∞
µ(H
∩ P
n
) = lim
n
→∞
l
k
(H
∩ P
n
) = l
k
(H).
Niech teraz A będzie dowolnym zbiorem należącym do M i mierzalnym w
sensie Lebesque’a. Z twierdzenia 9.18 istnieje zbiór H
⊂ R
k
będący zbiorem
typu G
δ
taki, że A
⊂ H oraz l
k
(H
− A) = 0. Wówczas H ∈ M zatem
H
− A ∈ M oraz
µ(A) = µH
− µH − A = l
k
(H)
− µH − A.
(41)
Z twierdzenia 9.15 dla dowolnego ε > 0 istnieje taki zbiór otwarty U, że
H
−A ⊂ U oraz l
k
(U ) < ε. Ponieważ jak udwodniliśmy miara µ pokrywa się z
miarą Lebesque’a na zbiorach otwartych więc µ(H
−A) ¬ µ(U) ¬ l
k
(U ) < ε.
Stąd µ(H
− A) = 0 zatem z (41) dostajemy
µ(A) = l
k
(H) = l
k
(A) + l
k
(H
− A) = l
k
(A).
Uwaga 9.5 Można pokazać, że zbiór A jest zbiorem mierzalnym w sensie
Lebesque’a wtedy i tylko wtedy gdy gdy dowolna miara określona na σ
−ciele
zawierającym wszystkie przedziały i zbiór A przyjmuje na zbiorze A wartość
równą l
∗
k
(A).
Twierdzenie 9.31 Niech µ będzie miarą niezmienniczą określoną na pew-
nym σ
−ciele M podzbiorów R
k
zawierającym wszystkie przedziały k
−wymiarowe.
Wówczas istnieje taka liczba rzeczywista α, że
µ(A) = cl
k
(A).
51
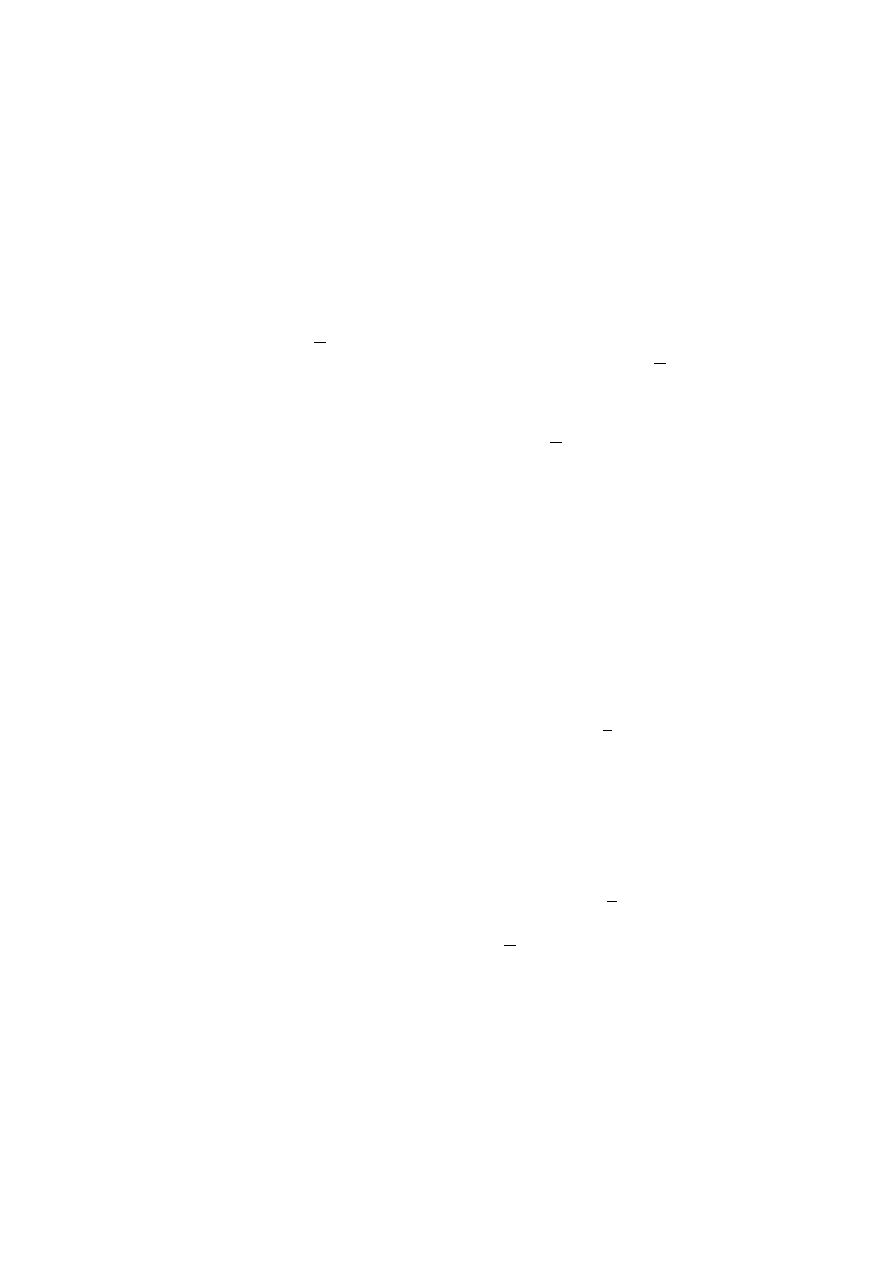
10
Funkcje mierzalne
10.1
Definicja funkcji mierzalnych, podstawowe własności
W całym rozdziale zakładamy, że jest zbiorem niepustym, a M σ
−ciałem
podzbiorów X, oraz A
∈ M. O podzbiorach zbioru X należących do M
będziemy mówili, że są zbiorami mierzalnymi. Jeżeli dodatkowo na M jest
określona miara µ to trójkę uporządkowaną (X, M, µ) nazywamy przestrze-
nią z miarą. Przez R oznaczamy zbiór R
∪ {−∞, ∞}. Mówiąc o funkcjach
na A mamy na myśli funkcje określone na zbiorze A i o wartościach R. Przez
M
A
oznaczamy rodzinę wszystkich podzbiorów A które są mierzalne. M
A
jest σ
−ciałem podzbiorów A,
Twierdzenie 10.1 Dla dowolnej funkcji f : A
→ R następujące warunki
są równoważne:
(a)
∀
a
∈R
{x ∈ A : f(x) > a} ∈ M
(b)
∀
a
∈R
{x ∈ A : f(x) ¬ a} ∈ M
(c)
∀
a
∈R
{x ∈ A : f(x) < a} ∈ M
(d)
∀
a
∈R
{x ∈ A : f(x) a} ∈ M.
Dowód. (a)
⇒(b) wynika z równości
{x ∈ A : f(x) ¬ a} = A − {x ∈ A : f(x) > a}.
Implikacja (b)
⇒(c) wynika z równości
{x ∈ A : f(x) < a} =
∞
∪
n=1
{x ∈ A : f(x) ¬ a +
1
n
}.
Implikacja (c)
⇒(d) zachodzi na mocy wzoru:
{x ∈ A : f(x) a} = A − {x ∈ A : f(x) < a}.
Wreszcie implikacja (d)
⇒(a) wynika z równości:
{x ∈ A : f(x) > a} =
∞
∪
n=1
{x ∈ A : f(x) a +
1
n
.
Definicja 10.1 Mówimy, że funkcja f : X
→ R jest funkcją mierzalną jeżeli
spełnia jeden z równoważnych warunków twierdzenia 10.1.
Przykład 10.1 (a) Jak łatwo zauważyć funkcja stała jest funkcją mierzalną
gdyż zbiory występujące w twierdzeniu 10.1 są albo zbiorami pustymi albo
pokrywają się ze zbiorem A.
52

(b) Niech B będzie dowolnym podzbiorem zbioru A. Niech χ
B
oznacza
funkcję charakterystyczną zbioru B (na zbiorze A). Wówczas:
{x ∈ A : χ
B
(x) > a) =
∅,
gdy a
∈ [1, ∞);
B,
gdy a
∈ [0, 1);
X
gdy a
∈ (−∞, 0).
Stąd wynika, że funkcja χ
B
jest funkcją mierzalną wtedy i tylko wtedy gdy
B
∈ M.
(c) Załóżmy, że X jest przestrzenią topologiczną i niech M będzie σ
−ciałem
podzbiorów zbioru X i A
∈ M. Wówczas dowolna funkcja ciągła f : A → R
jest funkcją mierzalną. Wynika to z tego, że dla dowolnego a
∈ R zbiór
{x ∈ A : f(x) < a} = f
−1
((
−∞, a))
jako przeciwobraz zbioru otwartego w
R jest zbiorem otwartym w A, to
znaczy jest przecięciem zbioru otwartego w X ze zbiorem A, a więc jest
zbiorem borelowskim.
Definicja 10.1 Mówimy, że dwie funkcje f, g : A
→ R są równe prawie
wszędzie, jeżeli zbiór
{x ∈ A : f(x) ̸= g(x)}
jest zbiorem mierzalnym i ma miarę równą 0
Uwaga 10.1 Załóżmy, że miara µ jest miarą zupełną. Dwie funkcje f, g
określone na zbiorze A są równe prawie wszędzie wtedy i tylko wtedy, gdy
istnieje zbiór C
∈ M
A
taki, że µ(C) = 0 i f (x) = g(x) gdy x
∈ A \ C.
Twierdzenie 10.2 Załóżmy, że miara µ jest miarą zupełną. Jeżeli funkcja
f : A
→ R jest funkcją mierzalną a g : A → R jest równa prawie wszędzie
funkcji f, to g jest funkcją mierzalną.
Dowód. Załóżmy, że f (x) = g(x) dla x
∈ A \ C, gdzie µ(C) = 0. Wówczas
dla dowolnego c
∈ R, mamy
g
−1
((
−∞, c)) = f
−1
((
−∞, c)) ∩ (A \ C) + g
−1
((
−∞, c)) ∩ C.
Pierwszy ze zbiorów jest zbiorem mierzalnym, bo funkcja f jest mierzalna
a drugi jest mierzalny bo µ(C) = 0 więc z zupełności miary jego dowolny
podzbiór jest mierzalny.
Twierdzenie 10.3 Jeżeli f : A
→ R jest funkcją mierzalną, to dla dowol-
nego zbioru borelowskiego B
⊂ R mamy f
−1
(B)
∈ M.
53

Dowód. Niech
M =
{B ⊂ R : f
−1
(B)
∈ M}.
Jak łatwo sprawdzić M jest σ
−ciałem podzbiorów R. Dla dowolnych a, b ∈
R takich, że a < b mamy (a, b) = (−∞, b) ∩ (a, ∞) więc
f
−1
((a, b)) = f
−1
((
−∞, b) ∩ (a, ∞)) = f
−1
((
−∞, b)) ∩ f
−1
((a,
∞)).
Zatem przeciwobraz dowolnego przedziału otwartego w R należy do σ
−ciała
M. Stąd wynika, że σ
−ciało to zawiera wszystkie zbiory borelowskie.
Twierdzenie 10.4 Jeżeli f : A
→ R jest funkcją mierzalną,to dla dowol-
nego c
∈ R zbiór
B =
{x ∈ A : f(x) = c}
jest zbiorem mierzalnym.
Dowód. W przypadku c
∈ R zbiór B jest przeciwobrazem zbioru jednoele-
mentowego a więc zbioru borelowskiego, zatem z poprzedniego twierdzenia
jest zbiorem mierzalnym. Jeżeli c =
∞, to
B =
∞
∩
n=1
{x ∈ A : f(x) > n}.
Podobnie przedstawiamy zbiór B w przypadku gdy a =
−∞.
Definicja 10.2 Mówimy, że zbiór B
⊂ R jest zbiorem borelowskim w R,
jeżeli B
∩ R jest zbiorem borelowskim w R.
Z twierdzeń 10.3 i 10.4 wynika, że przeciwobraz zbioru borelowskiego w
R jest zbiorem mierzalnym.
Twierdzenie 10.5 Niech f, g : A
→ R będą funkcjami mierzalnymi. Wów-
czas każdy ze zbiorów
A
1
=
{x ∈ A : f(x) > g(x)},
A
2
=
{x ∈ A : f(x) g(x)},
A
3
=
{x ∈ A : f(x) < g(x)},
A
4
=
{x ∈ A : f(x) ¬ g(x)},
A
5
=
{x ∈ A : f(x) = g(x)}
A
6
=
{x ∈ A : f(x) ̸= g(x)}
jest zbiorem mierzalnym
54

Ustawmy w ciąg q
1
, q
2
, ... wszystkie liczby wymierne. Mamy
A
1
=
∞
∪
n=1
{x ∈ A : g(x) < q
n
< f (x)
} =
∞
∪
n=1
(
{x ∈ A : g(x) < q
n
} ∩ {x ∈ A : f(x) > q
n
}) ∈ M.
Podobnie dowodzimy, że A
3
∈ M a ponieważ zbiory A
2
i A
4
są dopełnieniami
do A odpowiednio A
1
i A
3
więc A
2
, A
4
∈ M. Zbiór A
5
jest przecięciem
zbiorów A
1
i A
3
a zbiór A
6
dopełnieniem zbioru A
5
.
Twierdzenie 10.6 Jeżeli f : A
→ R jest funkcją mierzalną to dla dowol-
nego zbioru B
⊂ A funkcja g = f
|B
jest funkcją mierzalną.
Dowód.
{x ∈ B : g(x) > c} = B ∩ {x ∈ A : f(x) > c}.
Twierdzenie 10.7 Załóżmy, że A =
∞
∪
n=1
A
n
i funkcje f
n
= f
|A
n
są mie-
rzalne. Wówczas funkcja f jest funkcją mierzalną.
Dowód.
{x ∈ A : f(x) > c} =
∞
∪
n=1
{x ∈ A
n
: f (x) > c
} =
∞
∪
n=1
{x ∈ A
N
: f
n
(x) > c
} ∈ M.
W następnym twierdzeniu przyjmujemy, że 0
· ∞ = 0 · (−∞) = 0.
Twierdzenie 10.8 Jeżeli funkcja f : X
→ R jest funkcją mierzalną, to dla
dowolnego c
∈ R funkcja cf jest funkcją mierzalną.
Twierdzenie 10.9 Niech f, g : A
→ R będą funkcjami mierzalnymi. Wów-
czas funkcje
f + g, f
− g, fg
są mierzalne.
Dowód. Jeżeli g jest funkcją mierzalną to dla dowolnego c
∈ R funkcja g +c
jest również funkcją mierzalną. Ponieważ
{x ∈ A : f(x) − g(x) < c} = {x ∈ A : f(x) < g(x) + c}
więc na podstawie twierdzenia 10.5 funkcja f
− g jest funkcją mierzalną.
Na podstawie poprzedniego twierdzenia również funkcja f + g jest funkcją
55

mierzalną. Aby udowodnić, że iloczyn dwóch funkcji mierzalnych jest funk-
cją mierzalną udowodnimy najpierw, że jeżeli h jest funkcją mierzalną, to
funkcja h
2
jest również funkcją mierzalną. Niech c
∈ R i niech
A =
{x ∈ A : h
2
(x) < c
}.
Jeżeli c
¬ 0 to A = ∅, a inaczej
A =
{x ∈ A : h(x) <
√
c
} ∩ {x ∈ A : h(x) > −
√
c
}.
Udowodniliśmy więc, że kwadrat funkcji mierzalnej jest funkcją mierzalną.
Dalej zauważmy, że dla dowolnych funkcji mierzalnych f i g mamy:
f
· g =
1
4
[(f + g)
2
− (f − g)
2
]
więc f
· g jest funkcją mierzalną.
Twierdzenie 10.10 Jeżeli g : A
→ R jest funkcją mierzalną taką, że
g(x)
̸= 0 dla dowolnego x ∈ A, to
1
g
jest funkcją mierzalną.
Twierdzenie 10.11 Jeżeli f, g są funkcjami mierzalnymi na zbiorze A to
funkcje
max
{f, g}, min{f, g}
są również mierzalne.
Dowód.
{x ∈ A : max{f, g}(x) a} = {x ∈ A : f(x) a} ∪ {x ∈ A : g(x) a},
oraz
{x ∈ A : min{f, g}(x) a} = {x ∈ A : f(x) a} ∩ {x ∈ A : g(x) a}.
Twierdzenie 10.12 Jeżeli f jest funkcją mierzalną na zbiorze A, to funk-
cja
|f| jest również funkcją mierzalną.
Dowód. Mamy
|f| = max{f, −f}.
Definicja 10.3 Dla dowolnej funkcji f : A
→ R określamy część dodatnią
f
+
i część ujemną f
−
funkcji f przyjmując
f
+
(x) = max
{f(x), 0}, f
−
(x) = min
{f(x), 0}.
Z twierdzenia 10.11 wynika, że jeżeli f jest funkcją mierzalną to f
+
, f
−
są
funkcjami mierzalnymi. Ponieważ jak łatwo zauważyć mamy f = f
+
+ f
−
=
f
+
− (−f
−
) więc mamy:
Twierdzenie 10.13 Dowolną funkcję mierzalną można przedstawić w po-
staci różnicy dwóch funkcji mierzalnych nieujemnych.
Uwaga 10.2 Z twierdzenia 10.9 wynika, że jeżeli f jest funkcją o warto-
ściach skończonych to z mierzalności funkcji f
+
, f
+
są funkcjami mierzal-
nymi to f jest funkcją mierzalną.
56

10.2
Ciągi funkcji mierzalnych
Twierdzenie 10.14 Jeżeli (f
n
) jest dowolnym ciągiem funkcji mierzalnych
na zbiorze A, to funkcje
sup
n
∈N
f
n
,
inf
n
∈N
f
n
są funkcjami mierzalnymi.
Dowód. Dla dowolnego a
∈ R mamy:
{x ∈ A : sup
n
∈N
f
n
> a
} =
∞
∪
n=1
{x ∈ A : f
n
(x) > a
},
oraz
{x ∈ A : inf
n
∈N
f
n
(x) < a
} =
∞
∪
n=1
{x ∈ A : f
n
(x) < a
}.
Twierdzenie 10.15 Dla dowolnego ciągu (f
n
) funkcji mierzalnych na zbio-
rze A fnkcja
lim sup
n
→∞
f
n
lim inf
n
→∞
f
n
są funkcjami mierzalnymi.
Dowód. Wynika to z poprzedniego twierdzenia i z tego, że
lim inf
n
→∞
f
n
= sup
n
∈N
inf
m
n
f
m
oraz
lim sup
n
→∞
f
n
= inf
n
∈N
sup
m
n
f
m
.
Wniosek 10.1 Jeżeli (f
n
) jest takim ciągiem funkcji mierzalnych na zbiorze
A i dla dowolnego x
∈ A ciąg (f
n
(x)) jest zbieżny to funkcja
f (x) = lim
n
→∞
f
n
(x)
jest funkcją mierzalną na zbiorze A.
Twierdzenie 10.16 (Jegorowa) Niech (X, M, µ) będzie przestrzenią z
miarą. Załóżmy, że (f
n
) jest ciągiem funkcji mierzalnych na zbiorze A
∈ M
takim, że µ(A) <
∞ zbieżnym punktowo do funkcji skończonej f, Wówczas
dla dowolnego ε > 0 istnieje zbiór F
⊂ A taki, że µ(A − F ) < ε, oraz ciąg
(f
n
|F
) jest zbieżny jednostajnie do f
|F
.
57

Dowód. Ustalmy dowolne ε > 0. Niech
A
mn
=
{x ∈ A : ∀
i
n
|f
i
(x)
− f(x)| <
1
m
.
Wówczas dla dowolnego m, n
∈ N zbiór A
mn
jest zbiorem mierzalnym, oraz
∞
∪
n=1
A
nm
= A,
a ponieważ A
mn
⊂ A
m n+1
więc z twierdzenia 5.5 mamy:
µ(A) = lim
n
→∞
µ(A
mn
).
Stąd dla dowolnego n
∈ N istnieje taki wskaźnik n
m
, że
µ(A)
− µ(A
mn
m
) <
ε
2
m
.
Niech F =
∞
∩
m=1
A
mn
m
. Wówczas jeżeli x
∈ F to dla i n
m
mamy
|f
i
(x)
− f(x)| <
1
m
.
Stąd ciąg (f
n
) jest zbieżny jednostajnie do f na zbiorze F. Ponadto
µ(A
− F ) = µ(A −
∞
∩
m=1
A
mn
m
) = µ(
∞
∪
m=1
(A
− A
mn
m
))
¬
∞
∑
m=1
µ(A
− A
mn
m
) <
∞
∑
m=1
ε
2
m
= ε.
Uwaga 10.3 W przypadku gdy X = R
k
a µ = l
k
, to przy założeniach
twierdzenia Jegorowa możemy znaleźć zbiór domknięty F spełniający tezę
twierdzenia.
10.3
Funkcje proste
Definicja 10.4 Funkcją prostą nazywamy dowolną funkcję mierzalną f :
A
→ R przyjmującą skończoną ilość wartości.
Twierdzenie 10.17 Funkcja f : A
→ R jest funkcją prostą wtedy i tylko
wtedy gdy isnieje skończona ilość zbiorów A
1
, ..., A
n
∈ M zawartych w
zbiorze A, oraz liczby rzeczywiste λ
1
, ..., λ
n
takie, że
f =
n
∑
i=1
λ
i
χ
A
i
.
(42)
Można przy tym zakładać, że zbiory A
i
są parami rozłączne i w sumie dają
cały zbiór A.
58
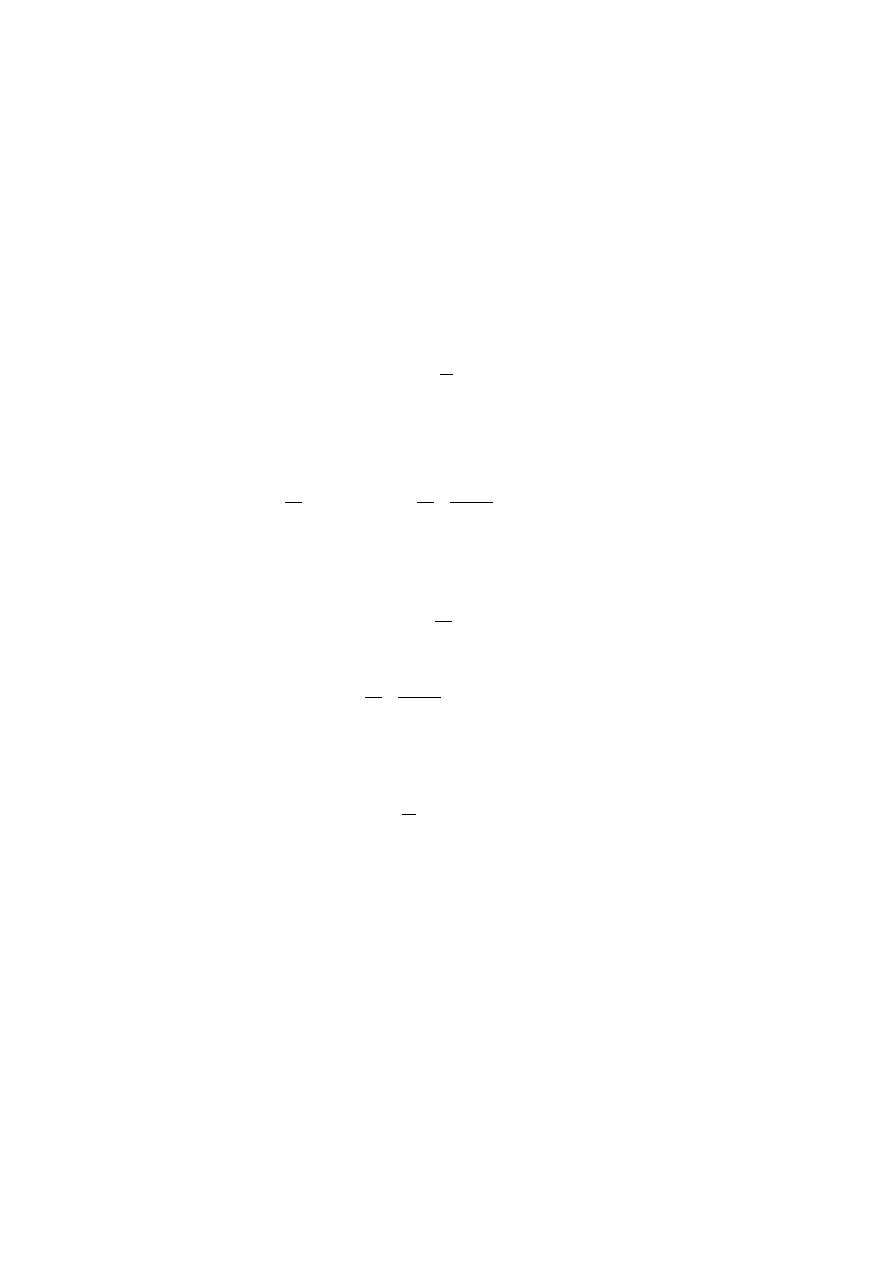
Dowód. Załóżmy, że f jest funkcją charkterystyczną i niech λ
1
, ..., λ
n
bę-
dąą wszystkimi (różnymi) wartościami funkcji prostej f. Niech A
i
=
{x ∈ A :
f (x) = λ
i
}. Wówczas zbiory A
i
są parami rozłącznymi zbiorami mierzalnymi
i w sumie dają cały zbiór A. Jak łatwo zauważyć mamy f =
∑
n
i=1
λ
i
χ
A
i
.
Załóżmy teraz że f spełnia (42). Każda z funkcji χ
A
i
jest funkcją mie-
rzalną (patrz przykład 10.1- punkt (b) ) więc z twierdzeń 10.8, 10.9 funkcja f
jest funkcją mierzalną. Ponieważ każda z funkcji λ
i
χ
A
i
przyjmuje skonczoną
ilość wartości, więc również funkcja f przyjmuje skończoną ilość wartości.
Twierdzenie 10.18 Niech f : A
→ R będzie funkcją mierzalną nieujemną.
Wówczas istnieje ciąg (f
n
) funkcji prostych taki, że f
n
¬ f
n+1
oraz f
n
(x)
→
f (x) dla dowolnego x
∈ A.
Dowód. Niech
f
n
(x) =
m
2
n
,
gdy f (x)
∈
[
m
2
n
,
m + 1
2
n
)
m = 0, 1, ..., n2
n
− 1;
n,
gdy f (x)
n.
Funkcje f
n
są funkcjami mierzalnymi bo
f
n
=
n2
n
−1
∑
m=0
m
2
n
χ
A
n
+ nχ
A
,
gdzie
A
n
= f
−1
([
m
2
n
,
m + 1
2
n
))
, A = f
−1
([n,
∞)) ,
a zbiory A
n
, A są mierzalne jako przeciwobrazy poprzez funkcję mierzalną
zbiorów borelowskich.
Udowodnimy, że f
n
→ f (punktowo). Jeżeli f(x) = ∞, to f
n
(x) = n
dla dowolnego n
∈ N, zatem f
n
(x)
→ ∞. W przeciwnym wypadku jeżeli
n > [f (x)], to
|f(x) − f
n
(x)
| <
1
2
n
.
Twierdzenie 10.19 (Zasad indukcji dla funkcji mierzalnych) Niech Ω
⊂
[0,
∞]
A
będzie taką rodziną funkcji mierzalnych, że
(a) jeżeli B
∈ M oraz B ⊂ A, to χ
B
∈ Ω,
(b) dla dowolnych f, g
∈ Ω i dowolnych α, β > 0 mamy αf + βg ∈ Ω,
(c) jeżeli (f
n
) jest dowolnym ciągiem niemalejącym funkcji należących do
Ω, a f : A
→ [0, ∞] funkcją mierzalną taką, że f
n
→ f (punktowo),
to f
∈ Ω,
Wówczas dowolna funkcja mierzalna nieujemna f : A
→ [0, ∞] należy do Ω.
59

Dowód. Z warunku (a) wynika, że funkcje charakterystyczne zbiorów mie-
rzalnych należą do Ω, z warunku (b), że funkcje proste nieujemne a z wa-
runku (c) i twierdzenia 10.18 dowolna funkcja mierzalna należy do Ω.
Analogicznie dowodzimy:
Twierdzenie 10.20 Jeżeli Ω
⊂ [0, ∞)
A
jest rodziną funkcji mierzalnych
spełniającą warunki (a), (b) poprzedniego twierdzenia, oraz warunek
(c’) jeżeli (f
n
) jest dowolnym ciągiem niemalejącym funkcji należących do
Ω, a f : A
→ [0, ∞) funkcją mierzalną taką, że f
n
→ f (punktowo),
to f
∈ Ω,
to Ω = [0,
∞)
A
.
Wówczas dowolna funkcja mierzalna nieujemna f : A
→ [0, ∞) należy do Ω.
Ponieważ dowolną funkcję mierzalną f : [0,
∞) można przedstawić w
postaci różnicy dwóch funkcji mierzalnych nieujemnych, więc
Twierdzenie 10.21 Niech Ω
⊂ R
A
będzie rodziną funkcji mierzalnych speł-
niającą warunek (a) twierdzenia 10.19, warunek (b) tego twierdzenia dla do-
wolnych α, β
∈ R. Jeżeli rodzina Ω jest zamknięta na zbieżność punktową,
to dowolna funkcja mierzalan f : A
→ R należy do Ω.
10.4
Funkcje mierzalne względem σ
−ciała zbiorów mierzal-
nych w sensie Lebesque’a
Niech A
⊂ R
k
będzie dowolnym zbiorem mierzalnym w sensie Lebesque’a.
Twierdzenie 10.22 Dowolna funkcja ciągła f : A
→ R jest funkcją mie-
rzalną.
Twierdzenie 10.23 Jeżeli zbiór punktów nieciągłości funkcji f : A
→ R
jest zbiorem o mierze Lebesque’a równej 0, to f jest funkcją mierzalną.
Twierdzenie 10.24 Dowolna funkcja f : [a, b]
→ R całkowalna w sensie
Riemanna jest funkcją mierzalną.
Twierdzenie 10.25 Jeżeli f :
R → R jest funkcją monotoniczną, to jest
funkcją mierzalną.
Jako zastosowanie Zasady indukcji dla funkcji mierzalnych (twierdze-
nie 10.19) udowodnimy następujące twierdzenie opisujące funkcje mierzalne
względem σ
−ciała zbiorów mierzalnych względem σ−ciała zbiorów mierzal-
nych w sensie Lebesque’a.
60

Twierdzenie 10.26 (Łuzina) Niech A
⊂ R
k
będzie zbiorem mierzalnym w
sensie Lebesque’a. Jeżeli funkcja f : A
→ R jest funkcją mierzalną, to dla
dowolnego ε > 0 istnieje zbiór domknięty F
⊂ A taki, że l
k
(A
−F ) < ε, oraz
f
|F
jest funkcją ciągłą.
Dowód.
⇒ . Niech Ω będzie rodziną wszystkich funkcji mierzalnych f :
A
→ R spełniających tezę twierdzenia dla dowolnego ε > 0. Niech B ⊂ A
będzie dowolnym zbiorem mierzalnym w sensie Lebesque’a i niech f = χ
A
.
Z twierdzenia 9.18 istnieją zbiory domknięte F
1
⊂ B, F
2
⊂ A − B takie, że
l
k
(B
− F
1
) <
ε
2
, l
k
(A
− B − F
2
) <
ε
2
.
Niech F = F
1
∪ F
2
. Wówczas F jest domkniętym podzbiorem A takim, że
l
k
(A
− F ) < ε, oraz f
|F
jest funkcją ciągłą. Pokazaliźmy więc, że dowolna
funkcja charakterystyczna zbioru mierzalnego B
⊂ A należy do Ω.
Jeżeli f, g
∈ Ω, α, β ∈ R, oraz F
1
, F
2
są zbiorami spełniającymi tezę
twierdzenia dla funkcji f i g gdy zamiast ε wziąć
ε
2
, to zbiór F = F
1
∪ F
2
spełnia tezę twierdzenia dla funkcji αf + βg ze stałą ε.
Wreszcie załóżmy, że f
n
∈ Ω, oraz f : A → R jest taką funkcją, że
f
n
→ f (punktowo). Weźmy dowolne ε > 0 i niech F
n
będzie takim zbiorem
domkniętym, że
l
k
(A
− F
n
) <
ε
2
n+1
,
oraz f
|F
n
jest funkcją ciągłą. Wówczas zbiór B =
∩
∞
n=1
F
n
jest zbiorem
domkniętym (a więc mierzalnym w sensie Lebesque’a) takim, że l
k
(A
−B) <
ε
2
. Z twierdzenia Jegorowa (10.16) istnieje zbiór domknięty F
⊂ B taki, że
l
k
(B
− F ) <
ε
2
oraz f
n
→ f jednostajnie na F. Wówczas l
k
(A
− F ) < ε, a
ponieważ F
⊂ F
n
więc dla dowolnego n funjcja f
n
|F
jest ciągła. Ponieważ
granica jednostajnie zbieżnego ciągu funkcji ciągłych jest funkcją ciągłą więc
funkcja f
|F
jest ciągła.
Uwaga 10.4 Warunek z tezy poprzedniego twierdzenia jest warunkiem ko-
niecznym i wystarczającym na to żeby funkcja f : A
→ R była funkcją
mierzalną.
Dowód. Konieczność wynika z poprzedniego twierdzenia, aby wystarczal-
ność zauważmy, że z rozważanego warunku wynika, że istnieje ciąg (F
n
)
zbiorów domkniętych takich, l
k
(A
− F
n
) <
1
n
, oraz f
n
= f
|F
n
jest funkcją
ciągłą. Niech
B =
∞
∪
n=1
F
n
, C = A
− B.
Wówczas B, C są mierzalnymi podzbiorami A takimi, że A = B
∪ C, oraz
l
k
(C) = 0. Dla dowolnego c
∈ R mamy
{x ∈ A : f(x) 6 c} = {x ∈ B : f(x) 6 c} ∪ {x ∈ C : f(x) 6 c},
61

wystarczy więc udowodnić mierzalność obu zbiorów po prawej stronie rów-
ności. Zbiór
{x ∈ C : f(x) 6 c}
jest zbiorem mierzalnym jako podzbiór zbioru miary 0. Natomiast
{x ∈ B : f(x) 6 c} =
∞
∪
n=1
{x ∈ F
n
: f (x)
6 c} =
∞
∪
n=1
{x ∈ F
n
: f (x)
6 c} =
∞
∪
n=1
f
−1
n
([c,
∞))
Każdy ze zbiorów f
−1
n
([c,
∞)) jako przeciwobraz zbioru zbioru domkniętego
poprzez funkcją ciągłą jest domkniętym podzbiorem zbioru F
n
a więc zbio-
rem domkniętym w
R
k
zatem zbiorem mierzalnym. Stąd dostajemy mierzal-
ność zbioru
{x ∈ B : f(x) 6 c}.
Definicja 10.5 Niech X będzie dowolną przestrzenią metryczną. Mówimy,
że funkcja f : X
→ R jest funkcją I−klasy Baire’a jeżeli istnieje ciąg (f
n
)
funkcji ciągłych na X taki, że f
n
→ f (punktowo).
Twierdzenie 10.27 Niech A
⊂ R
k
będzie dowolnym zbiorem mierzalnym
w sensie Lebesque’a. Jeżeli f : A
→ R jest dowolną funkcją mierzalną, to
istnieje funkcja I
−klasy Baire’a g : A → R taka, że f = g (p.w.)
62

11
Zbieżność prawie wszędzie i zbieżność według
miary
W tym rozdziale zakładamy, że (X, M, µ) jest przestrzenią z miarą, A jest
zbiorem należącym do M i że f
n
: A
→ R są funkcjami mierzalnymi dla
dowolnego n
∈ N.
Definicja 11.1 Mówimy, że ciąg (f
n
) o jest zbieżny według miary do funkcji
mierzalnej f : A
→ R, jeżeli dla dowolnego ε > 0 mamy
lim
n
→∞
µ(
{x ∈ A : |f
n
(x)
− f(x)| ε}) = 0.
Definicja 11.2 Mówimy, że ciąg (f
n
) jest zbieżny prawie wszędzie do funk-
cji f jeżeli istnieje taki zbiór B
∈ M, że µ(B) = 0, oraz
f
n
(x)
→ f(x) dla dowolnego x ∈ A − B.
Twierdzenie 11.1 Jeżel f
n
→ f (prawie wszędzie), to f jest funkcją mie-
rzalną.
Twierdzenie 11.2 Jeżeli µ(A) <
∞, to
f
n
→ f (prawie wszędzie) ⇒ f
n
→ f (według miary).
Twierdzenie 11.3 Dowolny ciąg zbieżny według miary do f zawiera pod-
ciąg zbieżny prawie wszędzie do f.
Dowód. Istnieje taki ciąg liczb (α
n
), że dla dowolnego k
α
n
mamy
µ(
{x ∈ A : |f
k
(x)
− f(x)|
1
n
}) <
1
2
n
.
Niech
A
n
=
{x ∈ A : |f
α
n
(x)
− f(x)| <
1
2
n
}.
Mamy µ(A
− A
n
) < 2
−n
. Niech
C =
∞
∪
n=1
∞
∩
m=n
A
m
Mamy
A
− C =
∞
∩
n=1
(A
− A
m
).
Więc µ(A
− C) = 0. Jeżeli x ∈ C to f
α
n
(x)
→ 0.
63

Twierdzenie 11.4 Niech A będzie dowolnym podzbiorem mierzalnym w sen-
sie Lebesque’a R
k
. Jeżeli f : A
→ R jest dowolną funkcją mierzalną, to
istnieje ciąg (f
n
) funkcji prostych na A taki, że f
n
→ f prawie wszędzie.
Dowód. Na podstawie twierdzenia Łuzina (twierdzenie 10.26) dla dowolne-
go n
∈ N istnieje zbiór domknięty F
n
⊂ A, że f
|F
n
jest funkcją ciągłą oraz
l
k
(A
− F
n
) < 2
−n
. Z twierdzenia Tietzego wynika, że istnieje funkcja ciągła
f
n
: A
→ R taka, że f
|F
n
= f
n
|F
n
. Niech
B =
∞
∩
m=1
∞
∪
n=m
(A
\ F
n
).
Zauważmy, że dla dowolnego m
∈ N mamy
l
k
(B)
6 l
k
(
∞
∪
n=m
F
m
)
6
∞
∑
n=m
l
k
(A
\ F
n
)
6
∞
∑
n=m
2
−n
= 2
−m+1
.
Stąd dostajemy, że l
k
(B) = 0. Ponadto jeżeli x
̸∈ B, to istnieje takie m ∈ N,
że x
∈ F
n
dla n
> m. Zatem f
n
(x) = f (x) dla p.w.n
64

12
Całka Lebesque’a
12.1
Całka funkcji nieujemnych
W całym rozdziale zakładamy, że (X, M, µ) jest przestrzenią z miarą i że
A
∈ M.
Definicja 12.1 Dla dowolnej funkcji prostej nieujemnej g : A
→ R takiej,
że
g =
m
∑
k=1
λ
k
χ
B
k
,
(43)
gdzie B
k
∈ M są zbiorami parami rozłącznymi a λ
k
dowolnymi stałymi
nieujemnymi, definiujemy
∫
A
f =
m
∑
k=1
λ
k
µ(B
k
).
Uwaga 12.1 Jeżeli g, h są dowolnymi nieujemnymi funkcjami prostmi, to
(a) jeżeli g
6 h, to
∫
A
g
6
∫
A
h;
(b)
∫
A
(g + h) =
∫
A
+
∫
A
h.
Dalej przez
P będziemy oznaczać rodzinę wszystkich funkcji prostych na A.
Definicja 12.2 Dla dowolnej funkcji mierzalnej i nieujemnej f : A
→ R
definiujemy całkę z funkcji f po zbiorze A względem miary µ jako:
∫
A
f dµ = sup
{∫
A
g; g
∈ P, g 6 f
}
Z punktu (a) uwagi 12.1 wynika, że dla funkcji prostych podana definicja
całki pokrywa się z podaną wcześniej.
Twierdzenie 12.1 Niech f : A
→ R będzie dowolną funkcją mierzalną
nieujemną.
(a)
∫
A
f = 0 wtedy i tylko wtedy gdy f = 0 prawie wszędzie na A;
(b) jeżeli
∫
A
f <
∞, to f < ∞ prawie wszędzie na A.
Dowód. (a) Załóżmy, że zbiór
B =
{x ∈ A : f(x) > 0}
ma miarę dodatnią. Zauważmy, że B =
∪
∞
n=1
B
n
, gdzie
B
n
=
{x ∈ A : f(x) > 1/n},
65

zatem jeden ze zbiorów B
n
ma miarę dodatnią. Ale ponieważ
1
n
χ
B
n
6 f,
więc
∫
A
f
>
1
n
µ(B
n
) > 0.
(b) Załóżmy, że zbiór
B =
{x ∈ A : f(x) = ∞}
ma miarę dodatnią. Ponieważ nχ
b
6 f dla dowolnego n ∈ N więc
∫
A
f
>
nµ(A). Stąd wynika, że
∫
A
f =
∞.
Kolejne dwa twierdzenia wynikają bezpośrednio z definicji całki.
Twierdzenie 12.2 Jeżeli f, g : A
→ R są dowolnymi funkcjami mierzalny-
mi nieujemnymi takimi, że f
¬ g, to
∫
A
f dµ
¬
∫
A
gdµ.
Twierdzenie 12.3 Dla dowolnej funkcji mierzalnej nieujemnej i mierzal-
nej f : A
→ R zachodzi nierówność:
inf f (A)µ(A)
¬
∫
A
f dµ
¬ sup f(A)µ(A).
Twierdzenie 12.4 Jeżeli f
n
jest ciągiem nieujemnych funkcji prostych ta-
kim, że f
n
↗ f, to
∫
A
f
n
→
∫
A
f.
Dowód. Granica ciągu
∫
A
f
n
istnieje, bo jest to ciąg rosnący. Ponadto na
podstawie twierdzenia 12.2 mamy
lim
n
→∞
∫
A
f
n
6
∫
A
f.
Wystarczy więc udowodnić nierówność przeciwną. Weźmy dowolną funkcję
prostą postaci (43) taką, że g
6 f. Niech
Definicja 12.1 Dalej przez M
A
będziemy oznaczać σ
−ciało podzbiorów
zbioru A złożone ze wszystkich podzbiorów mierzalnych zbioru A. Inaczej
mówiąc
M
A
=
{B ⊂ A : B ∈ M}
Twierdzenie 12.5 Załóżmy, że f : A
→ R jest dowolną nieujemną funkcją
mierzalną. Wówczas funkcja ν określona na M
A
A wzorem
ν(B) =
∫
B
f dµ
jest miarą na M
A
..
66
Dowód. Udowodnimy najpierw, że ν jest funkcją przeliczalnie podaddytyw-
ną. Niech (B
n
) będzie ciągiem parami rozłacznych, mierzalnych podzbiorów
zbioru A i niech B =
∪
∞
n=1
B
n
. Jeżeli dla pewnego n mamy ν(A
n
) =
∞, to
jak łatwo zauważyć mamy również ν(B) =
∞. Możemy więc zakładać, że
dla dowolnego n mamy µ(B
n
) <
∞. Weźmy dowolne ε > 0. Dla dowolnego
n
∈ N niech
Π
n
=
{B
nm
: m
∈ N}
będzie takim podziałem zbioru B
n
, że
S
Π
n
(f ) < ν(B
n
) +
ε
2
n
.
Rodzina Π =
{B
nm
: n, m
∈ N} jest podziałem zbioru B zatem
∫
B
f dµ
¬ S
Π
(f ) =
∑
n,m
∈N
sup f (B
nm
)µ(B
nm
) =
∞
∑
n=1
∞
∑
m=1
sup f (B
nm
)µ(B
nm
) =
∞
∑
n=1
S
Π
n
(f )
¬
∞
∑
n=1
(ν(A
n
+
ε
2
n
) =
∞
∑
n=1
µ(A
n
) + ε.
Ze względu na dowolność ε dostajemy podaddytywność ν.
Wystarczy dalej pokazać, że µ jest funkcją skończenie addytywną. Ze
względu na podaddytywność ν wystarczy udowodnić, że jeżeli zbiory B, C
⊂
A są mierzalne i rozłączne, to ν(B
∪ C) ν(B) + ν(C). Można zakładać,
że ν(B
∪ C) < ∞. Weźmy dowolne ε > 0 i niech Π = {A
n
} będzie takim
podziałem zbioru B
∪ C, że S
Π
(f ) < ν(B
∪ C) + ε. Zauważmy, że Π
1
=
{B ∩ A
n
} oraz Π
2
=
{C ∩ A
n
} są podziałami zbiorów B i C zatem
ν(A) + ν(B)
¬ S
Π
1
(f ) + S
Π
2
(f ) =
∑
n=1
sup f (B
∩ A
n
)µ(B
∩ A
n
) +
∞
∑
n=1
sup f (C
∩ A
n
)µ(C
∩ A
n
)
¬
¬
∞
∑
n=1
sup f (A
n
)µ(B
∩ A
n
) +
∞
∑
n=1
sup f (A
n
)µ(C
∩ B
n
) =
∞
∑
n=1
sup f (A
n
)[µ(B
∩ A
n
) + µ(C
∩ B
n
)]
∞
∑
n=1
sup f (A
n
)µ(A
n
) = S
Π
(f )
¬ ν(B ∪ C) + ε.
Ze względu na dowolność ε dostajemy dowodzoną nierówność.
Twierdzenie 12.6 Niech f będzie funkcją mierzalną i nieujemną na zbio-
rze A
∈ M. Jeżeli
∫
A
f dµ = 0 to f = 0 prawie wszędzie w A.
67

Dowód. Załóżmy nie wprost, że zbiór B =
{x ∈ A : f(x) > 0 ma miarę
nieujemną. Niech
B
n
=
{
x
∈ B : f(x)
1
n
}
.
Twierdzenie 12.7 (Lebesque’a) Jeżeli (f
n
) jest ciągiem rosnącym funk-
cji mierzalnych i nieujemnych zbieżnym punktowo do funkcji f, to
∫
A
f dµ = lim
n
→∞
∫
A
f
n
dµ.
(44)
Dowód. Z twierdzenia 12.2 wynika, że granica po prawej stronie równości
44 istnieje i jest nie większa od prawej strony. Aby udowodnić nierówność
przeciwną załóżmy najpierw, że f (x) <
∞ dla dowolnego x ∈ A i weźmy
dowolną liczbę η
∈ (0, 1). Niech
A
n
=
{x ∈ A : f
n
(x) > ηf (x)
}.
Mamy
∫
A
f
n
dµ
∫
A
n
f
n
dµ
∫
A
n
ηf dµ = η
∫
A
n
f dµ.
(45)
Ale ciąg (A
n
) jest ciągiem wstępującym takim, że
∞
∪
n=1
A
n
= A więc na
podstawie twierdzenia 12.5 mamy
∫
A
n
f dµ
→
∫
A
f dµ.
Na podstawie (45) dostajemy więc:
lim
n
→∞
∫
A
f
n
dµ
> η lim
n
→∞
∫
A
n
f dµ
> η
∫
A
f dµ.
a ze względu na dowolność η dostajemy dowodzoną nierówność.
Twierdzenie 12.8 Jeżeli f, g : A
→ R są dowolnymi funkcjami mierzalny-
mi nieujemnymi, to dla dowolnych liczb α, β
0 mamy:
∫
A
(αf + βg)dµ = α
∫
A
f dµ + β
∫
A
gdµ.
12.2
Funkcje całkowalne
Definicja 12.3 Dla dowolnej funkcji f : A
→ R przyjmujemy,
f
+
(x) = max
{f(x), 0}, f
−
(x) = max
{−f(x), 0}.
Mówimy, że funkcja f : A
→ R jest funkcją całkowalną w sensie Lebesque’a,
jeżeli
∫
A
f
+
dµ <
∞, oraz
∫
A
f
−
dµ <
∞.
68

Jeżeli f jest funkcją całkowalną to przyjmujemy
∫
A
f dµ =
∫
A
f
+
dµ
−
∫
A
f
−
dµ
Uwaga 12.2 Funkcja mierzalna nieujemna f : A
→ R jest całkowalna w
sensie Lebesque’a wtedy i tylko wtedy, gdy
∫
A
f dµ <
∞.
Twierdzenie 12.9 Jeżeli f : A
→ R jest funkcją mierzalną i istnieje funk-
cja całkowalna g : A
→ R taka, że |f| < g, to f jest funkcją całkowalną.
Dowód. Mamy f
+
<
|f|, więc z naszych założeń wynika, że
∫
A
f
+
dµ <
∞,
oraz analogicznie
∫
A
f
−
dµ <
∞, więc f jest funkcją całkowalną.
Twierdzenie 12.10 Jeżeli f : A
→ R jest dowolną funkcją mierzalną to
całkowalność funkcji f jest równoważna całkowalności funkcji
|f|. Zachodzi
przy tym nierówność
∫
A
f dµ
¬
∫
A
|f|dµ.
Dowód. Mamy
|f| = f
+
+ f
−
, więc z całkowalności funkcji f wynika całko-
walność funkcji
|f|. Odwrotna implikacja wynika z twierdzenia 12.9.
Twierdzenie 12.11 Jeżeli f, g są funkcjami całkowalnymi na zbiorze A i
f (x)
¬ g(x) na zbiorze A to
∫
A
f dµ
¬
∫
A
gdµ.
Twierdzenie 12.12 Funkcja całkowalna na zbiorze A jest na tym zbiorze
prawie wszędzie skończona.
Dowód. Załóżmy, że funkcja f : A
→ R jest funkcją całkowalną i załóżmy,
że zbiór B =
{x ∈ A : |f(x)| = ∞} ma miarę dodatnią. Ponieważ I
B
6
|f| więc z poprzedniego twierdzenia ∞ =
∫
A
I
B
dµ
6
∫
A
f dµ, co prowadzi
do sprzeczności, bo na podstawie twierdzenia 12.10 funkcja
|f jest funkcją
całkowalną.
Twierdzenie 12.13 Jeżeli f jest funkcją całkowalną na zbiorze A to dla
dowolnego zbioru mierzalnego B
⊂ A funkcja f
|B
jest również funkcją cał-
kowalną.
Twierdzenie 12.14 Jeżeli A =
∪
∞
n=1
A
n
, gdzie A
n
są zbiorami parami roz-
łącznymi, to dla dowolnej funkcji całkowalnej f : A
→ R mamy równość:
∫
A
f dµ =
∞
∑
n=1
∫
A
n
f dµ.
69

Twierdzenie 12.15 Jeżeli funkcje f, g są całkowalne na zbiorze A to funk-
cja f + g jest funkcją całkowalną i
∫
A
(f + g)dµ =
∫
A
f dµ +
∫
A
gdµ.
(46)
Dowód. Całkowalność funkcji f + g wynika z nierówności
|f +g| 6 |f|+|g|,
oraz z twierdzenia 12.9. Aby udowodnić równość (46) zauważmy, że mamy
f + g = (f + g)
+
− (f + g)
−
,
a z drugiej strony f = f
+
− f
−
, oraz g = g
+
− g
−
, więc
(f + g)
+
+ f
−
+ g
−
= f
+
+ g
+
+ (f + g)
−
,
zatem z twierdzenia 12.8 dostajemy dowodzoną równość.
Twierdzenie 12.16 Jeżeli funkcja f : A
→ R jest funkcją całkowalną, to
dla dowolnego λ
∈ R funkcja λf jest funkcją całkowalną i
∫
A
λf dµ = λ
∫
f dµ.
Twierdzenie 12.17 (lemat Fatou) Jeżeli f
n
jest ciągiem funkcji mierzal-
nych i nieujemnych na A, to
∫
A
lim inf
n
→∞
f
n
dµ
¬ lim inf
n
→∞
∫
A
f
n
dµ.
Dowód. Niech
g
n
(x) = inf
{f
m
(x) : m
n}.
Wówczas g
n
jest rosnącym ciągiem funkcji mierzalnych takim, że
lim
n
→∞
g
n
(x) = lim inf f
n
(x)
dla dowolnego x
∈ A Stąd na podstawie twierdzenia 12.7 mamy
∫
A
lim inf
n
→∞
f
n
dµ =
∫
A
lim
n
→∞
g
n
dµ = lim
n
→∞
∫
A
g
n
¬ lim inf
n
→∞
∫
A
f
n
.
Twierdzenie 12.18 (Lebesque’a o zmajoryzowanej zbieżności) Jeżeli funk-
cje f
n
są całkowalne na zbiorze A, oraz
|f
n
| ¬ g gdzie g : A → R jest funkcją
całkowalną, to
∫
A
lim inf
n
→∞
f
n
dµ
¬ lim inf
n
→∞
∫
A
f
n
dµ
¬ lim sup
n
→∞
∫
A
f
n
dµ
¬
∫
A
lim sup
n
→∞
f
n
dµ.
Dowód. Zauważmy, że dla dowolnego x
∈ A mamy f
n
(x)
−g(x) więc
f
n
(x) + g(x)
0. Możemy więc do ciągu f
n
+ g zastosować lemat Fatou.
70

Twierdzenie 12.19 (Lebesque’a o zmajoryzowanej zbieżności) Załóżmy,
że (f
n
) jest ciągiem funkcji mierzalnych na A takim, że
|f
n
(x)
| < g(x),
gdzie g jest funkcją całkowalną na A. Jeżeli f
n
(x)
→ f(x) dla dowolnego
x
∈ A, to f jest funkcją całkowalną na A, oraz
∫
A
f
n
→
∫
A
f.
71
13
Całka Lebesque’a a całka Riemanna
Jeżeli Π =
{x
0
, x
1
, . . . x
k
} jest dowolnym podziałem przedziału [a, b], to dla
dowolnej funkcji ograniczonej f : [a, b]
→ R definiujemy funkcje g
Π
, h
π
w
następujący sposób
g
Π
=
k
∑
i=1
m
i
χ
[x
i
−1
,x
i
]
,
h
Π
=
k
∑
i=1
M
i
χ
[x
i
−1
,x
i
]
.
gdzie
m
i
= inf f ([x
i
−1
, x
i
]), M
i
= sup f ([x
i
−1
, x
i
])
funkcje te są oczywiście całkowalne w sensie Lebesque’a i
∫
[a,b]
g
Π
dl = S(f, Π),
∫
[a,b]
h
Π
dl = S(f, Π).
Lemat 13.1 Jeżeli (Π
n
) jest normalnym ciągiem podziałów takim, że Π
n
⊂
Π
n+1
to ciąg (h
Π
n
) jest malejącym ciągiem zbieżnym punktowo do pewnej
funkcji h całkowalnej w sensie Lebesque’a na [a, b] takiej, że
∫
[a,b]
hdl =
∫
[a,b]
f.
Analogicznie ciąg h
Π
n
jest ciągiem malejącym zbieżnym punktowo do takiej
funkcji całkowalnej h, że
∫
[a,b]
gdl =
∫
[a,b]
f.
Zachodzi nierówność g
¬ f ¬ h.
Twierdzenie 13.1 Dowolna funkcja f : [a, b]
→ R całkowalną w sensie
Riemanna, jest funkcją całkowalną w sensie Lebesque’a i
∫
b
a
f (x)dx =
∫
[a, b]
f dl.
Dowód. Niech Π
n
będzie wstępującym ciągiem normalnym podziałów [a, b].
72

14
Iloczyn kartezjański miar
W tym rozdziale przyjmujemy, że 0
· ∞ = 0.
14.1
Iloczyn kartezjański półpierścieni
Twierdzenie 14.1 Jeżeli
P
1
,
P
2
są półpierścieniami podzbiorów zbiorów
X i Y, to rodzina
P = {A × B : A ∈ P
1
, B
∈ P
2
}
jest półpierścieniem podzbiorów X
× Y.
Uwaga 14.1 Jeżeli A
∈ P (P
1
), B
∈ P (P
2
), to iloczyn A
× B daje się
przedstawić w postaci sumy zbiorów parami rozłącznych należących do
P.
Dowód (uwagi) Jeżeli
A =
n
∪
i=1
A
i
, B =
m
∪
j=1
B
j
,
to
A
× B =
n
∪
i=1
m
∪
j=1
(A
i
× B
j
).
Łatwo zauważyć, że zbiory A
i
× B
j
są parami rozłączne.
Dowód. Mamy
(A
1
× B
1
)
∩ (A
2
× B
2
) = (A
1
∩ A
2
)
× (B
1
∩ B
2
).
Ponadto:
(A
2
× B
2
)
′
= (X
× B
′
2
)
∪ (A
′
2
× Y ).
zatem
(A
1
× B
1
)
− (A
2
× B
2
) = [A
1
× (B
1
− B
2
)]
∪ [(A
1
− A
2
)
× B
1
].
Dalej
A
1
× (B
1
− B
2
) = [(A
1
∩ A
2
)
× (B
1
− B
2
)] + [(A
1
− A
2
)
× (B
1
− B
2
)],
(A
1
− A
2
)
× B
1
= [(A
1
− A
2
)
× (B
1
∩ B
2
)] + [(A
1
− A
2
)
× (B
1
− B
2
)],
zatem
(A
1
× B
1
)
− (A
2
× B
2
) = [(A
1
∩ A
2
)
× (B
1
− B
2
)] + [(A
1
− A
2
)
× (B
1
− B
2
)]
+(A
1
− A
2
)
× (B
1
∩ B
2
).
Zauważmy, że trzy zbiory występujące po prawej stronie ostatniej równości
są parami rozłączne, ponadto każdy z nich na mocy uwagi 14.1 daje się
przedstawić w postaci sumy zbiorów parami rozłącznych należących do
P.
73

Twierdzenie 14.2 Jeżeli
P
1
, ....,
P
n
są półpierścieniami, i
P = {A
1
× .... × A
n
: A
i
∈ P
i
(i = 1, ..., n)
},
to
P jest półpierścieniem.
14.2
Miara na iloczynie kartezjańskim półpierścieni
Twierdzenie 14.3 Załóżmy, że
P
1
,
P
2
są półpierścieniami a µ
1
, µ
2
funk-
cjami addytywnymi odpowiednio na
P
1
,
P
2
. Niech pierścień
P będzie zdefi-
niowany tak jak w twierdzeniu 14.1). Zdefiniujmy funkcje µ :
P → [0, ∞] w
następujący sposób:
µ(A
× B) = µ
1
(A)µ
2
(B)
Wówczas µ jest funkcją addytywną na
P. Jeżeli µ
1
, µ
2
są miarami, to µ
jest miarą.
Dowód Załóżmy, że A
i
∈ P
1
, B
i
∈ P
2
, (A
i
× B
i
)
∩ (A
j
× B
j
) =
∅, dla
i, j = 1, ..., n oraz, że
A
× B =
n
∪
i=1
(A
i
× B
i
)
∈ P.
Na podstawie twierdzenia 4.4 istnieją zbiory parami rozłączne
C
1
, ..., C
m
, D
1
, ..., D
k
∈ P
i istnieją zbiory M
i
⊂ {1, ..., m} oraz K
i
⊂ {1, ..., k} dla i = 1, ..., n
takie, że
A
i
=
∪
s
∈M
i
C
s
, B
i
=
∪
s
∈K
i
D
s
.
Mamy
A
i
× B
i
=
∪
(s,t)
∈M
i
×K
i
(C
s
× D
t
).
14.3
Iloczyn kartezjański przestrzeni z miarą
Twierdzenie 14.4 Niech (X
1
, N
1
, µ
1
), (Y, N
2
, µ
2
) będą przestrzeniami
z miarą. Niech M będzie σ
−ciałem podzbiorów X × Y generowanym przez
rodzinę
{A × B : A ∈ M
1
, B
∈ M
2
}.
Istnieje dokładnie jedna miara µ : M
→ [0, ∞] taka, że
µ(A
× B) = µ
1
(A)µ(B).
74

Twierdzenie 14.5 Niech
P
1
,
P
2
będą pierścieniami podzbiorów odpowied-
nio X i Y. Załóżmy, że µ
i
:
P
i
→ [0, ∞] funkcjami addytywnymi na tych
pierścieniach. Niech
P będzie półpierścieniem podzbiorów X ×Y zdefiniowa-
nym tak jak w twierdzeniu 14.1. Zdefiniujmy funkcję µ :
P → [0, ∞ przyj-
mując
µ(A
× B) = µ(A)µ(B)
(47)
dla dowolnego A
∈ P
1
i B
∈ P
2
, Wówczas µ jest funkcją addytywną na
półpierścieniu
P.
Definicja 14.1 Przestrzeń z miarą (X
× Y, M, µ), gdzie M i µ są zde-
finiowane tak jak w twierdzeniu 14.5 nazywamy iloczynem kartezjańskim
przestrzeni z miarą (X, M
1
, µ
1
), (Y, M
2
, µ
2
) a miarę µ nazywamy produk-
tem miar µ
1
i µ
2
.
Twierdzenie 14.6 Przy założeniach definicji jeżeli C
∈ M, to dla dowol-
nego x
∈ X mamy
C
x
=
{y ∈ Y : (x, y) ∈ C} ∈ M
2
,
oraz dla dowolnego y
∈ Y :
C
y
=
{x ∈ X : (x, y) ∈ C} ∈ M
1
.
Dowód. Niech
R = {C ⊂ X × Y : C
x
∈ M
2
}.
Jak łatwo zauważyć rodzina
R zawiera wszystkie zbiory postaci A×B, gdzie
A
∈ M
1
, B
∈ M
2
. Jak łatwo zauważyć mamy
(
∞
∪
n=1
A
n
)
x
=
∞
∪
n=1
(A
n
)
x
,
oraz
(A
′
)
x
= (A
x
)
′
.
Stąd wynika, że
R jest σ−ciałem zawierającym wszystkie zbiory postaci
A
× B, gdzie A ∈ M
1
, B
∈ M
2
. Stąd dostajemy, że
R ⊂ M.
Niech f : X
× Y → R będzie dowolną funkcją mierzalną. Wówczas dla
dowolnego x
∈ X niech ϕ
x
: Y
→ R będzie taką funkcją, że ϕ
x
(y) = f (x, y)
a dla dowolnego y
∈ Y niech ψ
y
: X
→ R będzie funkcją określoną wzorem
ψ
y
(x) = f (x, y).
Przy powyższych oznaczeniach mamy
Twierdzenie 14.7 (Toneliego) Jeżeli funkcja f : X
× Y → R jest dowol-
ną funkcją mierzalną nieujemną, to dla dowolnego x
∈ X funkcja
Y
∋ y → f(x, y) ∈ R
jest funckją mierzalną i
∫
X
×Y
f dµ =
∫
X
(∫
Y
f (x, y)dµ
2
)
dµ
1
75

15
Miary zespolone
Zakładamy, że M jest σ
−ciałem podzbiorów zbioru X. Mówimy, że ciąg
(A
n
) zbiorów należących do M jest rozbiciem zbioru A
∈ M jeżeli zbiory A
n
są parami rozłączne i A =
∪
∞
n=1
A
n
.
Definicja 15.1 Mówimy, że funkcja µ : M
→ C jest miarą zespoloną, jeżeli
dla dowolnego A
∈ M i dowolnego rozbicia (A
n
) zbioru A zachodzi równość
µ(
∞
∪
n=1
A
n
) =
∞
∑
n=1
µ(A
n
).
Jeżeli natomiast wartości µ(A) są liczbami rzeczywistymi, to mówimy, że µ
jest miarą rzeczywistą
Definicja 15.2 Dla dowolnej miary zespolonej µ na M określamy wariację
|µ| tej miary przyjmując
|µ|(A) = sup{
∞
∪
n=1
|µ(A
n
)
| : (A
n
) rozbice A
}
(48)
Oczywiście zachodzi nierówność µ(A)
¬ |µ|(A) dla dowolnego zbioru A ∈ M,
na ogół równość nie musi zachodzić.
Twierdzenie 15.1 Wariacja
|µ| dowolnej miary zespolonej jest miarą do-
datnią skończoną.
Dowód. Weźmy dowolny zbiór A
∈ M i jego rozbicie (A
n
). Niech (C
m
)
będzie dowolnym rozbiciem zbioru A. Wówczas dla dowolnego n
∈ N ciąg
(C
m
∩ A
n
) jest rozbiciem A
n
więc
|µ|(A
n
)
>
∞
∑
m=1
|µ(A
n
∩ C
m
)
|,
zatem
∞
∑
n=1
|µ|(A
n
)
>
∞
∑
n=1
∞
∑
m=1
|µ(A
n
∩ C
m
)
| =
∞
∑
m=1
∞
∑
n=1
|µ(A
n
∩ C
m
)
|
∞
∑
m=1
|
∞
∑
n=1
µ(A
n
∩ C
m
)
| =
∞
∑
n=1
|µ(A ∩ C
m
)
| =
∞
∑
n=1
|µ(C
m
)
|.
Stąd dostajemy nierówność
∞
∑
n=1
|µ|(A
n
)
|µ|(A).
76

Aby udowodnić odwrotną nierówność weźmy dowolne ε > 0. Istnieją takie
rozbicia (C
n,m
) zbiorów A
n
, że
∞
∑
m=1
|µ(C
n,m
)
| > |µ|(A
n
)
−
ε
2
n
.
Wówczas (C
n,m
) jest rozbiciem A więc
|µ|(A)
∞
∑
n=1
∞
∑
m=1
|µ(C
n,m
)
|
∞
∑
n=1
|µ|(A
n
)
− ε.
Twierdzenie 15.2 Jeżeli µ jest dowolną miarą zespoloną na M, to
|µ|(X) <
∞ więc |µ| jest miarą skończoną.
Lemat 15.1 Dla dowolnych liczb zespolonych z
1
, . . . , z
n
istnieje zbiór skoń-
czony S
⊂ 1, . . . n taki, że
∑
j
∈S
z
n
1
6
n
∑
j=1
|z
n
|.
Dowód twierdzenia. Udowodnimy najpierw, że jeżeli E
∈ M jest takim
zbiorem, że
|µ|(E) = ∞, to istnieją dwa zbiory A, B ∈ M, że E = A ∪ B
oraz
µ(A) > 1,
|µ|(B) = ∞.
Rzeczywiście ponieważ
|µ|(E) = ∞ więc istnieje pokrycie (E
n
) zbioru E
takie, że
∞
∑
n=1
|µ(E
n
)
| > 6(1 + |µ(E)|).
Istnieje takie m
∈ N, że
m
∑
n=1
|µ(E
n
)
| > 6(1 + |µ(E)|).
Ale na podstawie lematu znajdziemy taki zbiór S
⊂ {1, . . . , m}, że
|
∑
n
∈S
µ(E
n
)
| > 1 + |µ(E)|.
Weźmy A =
∑
n
∈S
E
n
. Wówczas
|µ(A)| > 1 + |µ(E)| 1. Jeżeli B = E \ A,
to
|µ(B)| = |µ(E) − µ(A)| |µ(A)| − |µ(E)| 1.
Tak więc
|µ(A)| 1 oraz |µ(B)| > 1 i E = A ∪ B tak więc ponieważ |µ jest
miarą więc albo
|µ|(A) = ∞ lub |µ(B) = ∞. Bez straty ogólności możemy
zakładać, że zachodzi drugi przypadek.
77

Przejdźmy teraz do dowodu twierdzenia. Załóżmy nie wprost, że
|µ|(X) =
∞. Wówczas istnieją dwa zbiory rozłączne A
1
, B
1
∈ M takie, że A
1
∪B
1
= X
oraz
|µ(A
1
)
| 1 i |µ|(B
1
) =
∞. Dalej biorąc zamiast zbioru E zbiór
B
1
stwierdzamy, że istnieją dwa zbiory rozłączne A
2
, B
2
∈ M takie, że
A
2
∪ B
2
= B
1
oraz
|µ(A
2
)
| > 1 i |µ|(B
2
) =
∞. Kontynuując tą konstrukcję
dostajemy ciąg zbiorów A
n
∈ M które są parami rozłączne i |µ(A
n
)
| 1.
78
Wyszukiwarka
Podobne podstrony:
wyk.1 teoria miary
5 Teoria miary 1 sigma algebry id 40532 (2)
zagadnienia, punkt 17, XVII Twierdzenia o przechodzeniu do granicy pod znakiem całki Lebesgue'a
CALKI teoria
calki teoria zadania
Stat FiR TEORIA II (miary cd, sggw - finanse i rachunkowość, studia, II semestr, Statystyka ĆW
Teoria, całki wielokrotne
SO i SM FiR TEORIA II (miary?, rozklady ZL) cz1(2)
1 calki oznaczone, teoria
całki i miary
5 - Konstrukcja całki względem miary, Analiza matematyczna
Analiza matematyczna egzamin I (lato) calki teoria, Wykłady - Studia matematyczno-informatyczne
3 calki podwojne, teoria id 33 Nieznany (2)
CALKI teoria
calki teoria zadania
więcej podobnych podstron