TERMODYNAMIKA

Zajęcia wyrównawcze, Częstochowa, 2009/2010

Ewa Mandowska

1. Bilans cieplny
2. Przejścia fazowe
3. Równanie stanu gazu doskonałego
4. I zasada termodynamiki
5. Przemiany gazu doskonałego
6. Silnik cieplny
7. II zasada termodynamiki

ZADANIA

Zad. 1

Mieszanie wody o różnych temperaturach

W jakim stosunku należy zmieszać wodę o temperaturze 100

°C z woda o temperaturze 20°C,

aby temperatura końcowa wody wynosiła 40

°C, jeżeli możemy zaniedbać wymianę ciepła z

otoczeniem.

Odp. 1/3

Zad. 2

Topniejący lód w wodzie

Do wody o masie 560 g i temperaturze 16

°C wrzucono kawałek lodu o masie 80 g i

temperaturze 0

°C. Temperatura wody po stopieniu się lodu zmniejszyła się do 4°C. Oblicz

ciepło topnienia lodu, jeżeli możemy zaniedbać wymianę ciepła z otoczeniem. Ciepło
właściwe wody wynosi

(

)

3

4.19 10 J kgK

⋅

Odp.

5

3.35 10 J kg

⋅

Zad. 3

Topnienie srebra

Oblicz minimalną energię potrzebną do całkowitego stopienia 130 g srebra o temperaturze
początkowej 15

°C. Ciepło właściwe srebra wynosi 236 J/(kg K)a ciepło topnienia 105kJ/kg,

temperatura topnienia srebra 958

°C

Odp. 42.7 kJ

Zad. 4

Zbiornik z wodą w garażu

Jednym ze sposobów zapobieżenia zbyt silnemu wychłodzeniu garażu w czasie silnego mrozu
jest umieszczenie w nim zbiornika wypełnionego wodą. Przyjmij, że zbiornik zawiera 125 kg
wody o temperaturze początkowej 20

°C. Ile energii musi oddać do otoczenia ta ilość wody,

aby w całości zamarznąć? Ciepło właściwe wody wynosi

(

)

4.19

a ciepło topnienia

lodu

k J kgK

⋅

3

33 kJ kg

Odp. 52 kJ

Zad. 5

Lód w termosie

Dwie kostki lodu o masie 50 g każda wrzucono do termosu zawierającego 200g niesłodzonej
herbaty. Jaka będzie temperatura końcowa po osiągnięciu przez układ równowagi
termodynamicznej jeżeli herbata początkowo miała temperaturę 25

°C a lód wyjęto z

zamrażarki w której panowała temperatura -15

°C. Jaka byłaby temperatura końcowa gdyby

wzięto tylko jedna kostkę lodu? Załóż, że herbata jest czystą wodą. Ciepło właściwe wody i
lodu wynosi odpowiednio

(

)

4.19

k J kgK

⋅

(

)

2.22 k J kgK

⋅

a ciepło topnienia lodu

333 kJ kg

Odp. 273 K, 275.5 K

Zad. 6

Para wodna i lód w izolowanym zbiorniku

Ile pary wodnej o temperaturze 100

°C trzeba wpuścić do izolowanego cieplnie zbiornika

zawierającego 150 g lodu o temperaturze topnienia, aby w stanie końcowym otrzymać wodę o
temperaturze 50

°C. Ciepło skraplania pary wodnej wynosi 2256 kJ/kg.

Odp. 33 g

Zad. 7

Hel i argon w zamkniętych naczyniach

W naczyniach o jednakowej objętości znajdują się równe masy helu i argonu. Ile razy
cieśninie helu jest większe od ciśnienia argonu, jeżeli temperatury obu gazów są identyczne?
Masa molowa helu wynosi 4 g/mol, masa molowa argonu 40 g/mol

Odp. 10

Zad. 8

Rozprężanie gazu podczas ogrzewania pod stałym ciśnieniem

O ile procent wzrośnie objętość gazu, który ogrzano pod stałym ciśnieniem od temperatury
80

°C do temperatury 120°C

Odp. 11.3%

Zad. 9

Rozprężanie gazowego tlenu

Gazowy tlen, który w temperaturze 40

°C pod ciśnieniem 101 kPa zajmuje objętość 1000cm

3

rozpręża się do 1500cm

3

. Jednocześnie jego ciśnienie osiąga wartość 106 kPa. Oblicz

temperaturę końcową i liczbę moli tlenu.

Odp. 220

°C, 0.0388 mol

Zad 10

Zmiana objętości wypływającego pęcherzyka powietrza z dna jeziora

Pęcherzyk powietrza o objętości 20cm

3

znajduje się na dnie jeziora na głębokości 40 m w

wodzie o temperaturze 4

°C. Pęcherzyk wznosi się w kierunku powierzchni jeziora, gdzie

panuje temperatura 20

°C. Przyjmijmy, że temperatura powietrza w pęcherzyku jest taka sama

jak temperatura wody. Jaka będzie objętość pęcherzyka w chwili, gdy osiągnie on
powierzchnię? Gęstość wody wynosi 1000kg/m

3

a ciśnienie atmosferyczne 1000 hPa.

Odp. 100 cm

3

Zad. 11

Przemiana izobaryczna i izotermiczna gazu wieloatomowego

Gaz wieloatomowy rozszerzając się wykonuje pracę 245 J. Jaką ilość ciepła otrzymał gaz jeśli
była to przemiana izobaryczna a jaką gdy izotermiczna

Odp. 980 J, 245 J

Zad. 12

Zmiana energii wewnętrznej gazu

Podczas zmniejszania się objętości tlenu od 20dm

3

do 10dm

3

jego ciśnienie wzrosło od

100 kPa do 250 kPa. Jaka była zmiana energii wewnętrznej gazu?

Odp. 1.25 kJ

Zad. 13

Sprawność silnika Carnota

Oblicz wydajność silnika Carnota, pracującego pomiędzy źródłem ciepła o temperaturze
127

°C a chłodnicą o temperaturze 27°C

Odp. 25%

Zad. 14

Sprawność silnika Carnota

Gaz pracujący w cyklu Carnota oddaje do chłodnicy 3/5 ciepła pobranego ze źródła. Jaka jest
wydajność tego cyklu?

Odp. 40%

Zad. 15

Cykl Carnota

Gaz wykonuje cykl Carnota. Temperatura bezwzględna źródła ciepła jest trzy razy większa od
temperatury bezwzględnej chłodnicy. Jaką część pobranego ciepła oddaje gaz chłodnicy?

Odp. 1/3

Literatura:

D. Halliday, R. Resnick, J. Walker, Podstawy fizyki , tom 2, PWN, Warszawa 2003
J. Kalisz, M. Massalska, J.M. Massalski, Zbiór Zadań z Fizyki z Rozwiązaniami, PWN, Warszawa 1971
M. S. Cedrik, Zbiór zadań z fizyki, PWN, Warszawa 1972
K. Chyla, Zbiór prostych zadań z fizyki, ZAMKOR, Kraków 2000

TEORIA

Bilans cieplny

Jeżeli ogrzewamy ciało to ciepło mu dostarczone (Q) możemy wyznaczyć:

(

)

=

−

w

k

p

Q c m T

T

(1)

m - masa ogrzewanego ciała
T

k

, T

p

- temperatury odpowiednio końcowa i początkowa ciała

c

w

- ciepło właściwe substancji z jakiej jest wykonane ogrzewane ciało

(

)

=

⋅

2

wH O

c

4180 J kg K

W układzie izolowanym termicznie suma ilości ciepła przekazanego przez ciała danego
układu jest równa zero

+

+ +

=

…

1

2

n

Q

Q

Q

0 (2)

Q

1

, Q

2

, ...Q

n

- ciepła przekazywane przez poszczególne ciała układu,

n – liczba ciał.
Uwaga: Podstawiając dane do wzoru (2) zawsze trzeba odejmować od temperatury końcowej
temperaturę początkową.

Przejścia fazowe

Ciepło przemiany c

przem

– ilość energii, która w postaci ciepła trzeba przekazać jednostkowej

masie substancji, aby uległa ona przemianie fazowej

przem

Q

c

m

= ±

(3)

Ciepło pobierane przez ciało podlegające przemianie jest dodatnie (znak +) a ciepło
oddawane jest ujemne (znak -)

Topnienie

Parowanie

Substancja

( )

t

T K

(

)

t

c kJ kg

( )

p

T K

(

)

p

c kJ kg

Woda

273 333 373 2256

Tlen

54.8 13.9 90.2 213

Srebro

1235 105 2323 4730

Gaz doskonały

(gaz idealny) - model gazu, spełniający następujące warunki:

1. składa się on z identycznych cząsteczek
2. cząsteczki znajdują się w ciągłym chaotycznym ruchu, który podlega zasadom

dynamiki Newtona

3. liczba cząsteczek gazu jest nieskończenie duża
4. cząsteczki traktujemy jak punkty materialne czyli objętość cząsteczek jest znikoma w

stosunku do objętości gazu

5. odległość miedzy cząsteczkami jest bardzo duża w porównaniu z ich rozmiarami
6. cząsteczki oddziałują ze sobą tylko w momencie zderzenia
7. zderzenia cząsteczek są doskonale sprężyste (spełniona jest zasada zachowania energii

i zasada zachowania pędu)

8. tor ruchu cząsteczek miedzy zderzeniami jest linią prostą

Równanie stanu gazu doskonałego (równanie Clapeyrona)

=

pV

nRT (4)

p – bezwzględna wartość ciśnienia,
n – liczba moli gazu w próbce,

=

n m

µ

)

(m – masa gazu,

µ

- masa 1 mola)

T – temperatura bezwzgledna gazu,

(

=

R 8.31 J mol / K

- stała gazowa (ma taką samą wartość dla wszystkich gazów)

W przypadku mieszaniny różnych gazów spełniających równanie gazu doskonałego jej
parametry opisuje równanie:

(

)

=

+

+ +

…

1

2

i

pV

n

n

n RT

(5)

n

1

, n

2

, ...n

i

– liczby moli poszczególnych składników mieszaniny

=

A

R

k

N

(6)

−

=

⋅

23

k 1.38 10

J / K

- stała Boltzmana

−

=

⋅

23

1

A

N

6.02 10 mol

- liczba Avogadra (liczba atomów lub cząsteczek w jednym molu)

=

A

N

n

N

(7)

N – liczba cząsteczek lub atomów w próbce
Z (4) i (6) i (7) wynika:

=

pV

NkT (8)

Równanie stanu gazu doskonałego obowiązuje też dla gazów rzeczywistych o bardzo małych
gęstościach.

I Zasada termodynamiki

Energia wewnętrzna układu

E

w

wzrasta, jeśli układ pobiera energie w postaci ciepła Q i

maleje, kiedy wykonuje on pracę W.

w

E

Q

W

∆

= ∆ − ∆ (9)

E

w

jest funkcja stanu układu a nie zależy od sposobu przejścia od stanu 1 do 2. Dla gazu

doskonałego

E

w

jest funkcja tylko temperatury.

Przemiany gazu doskonałego

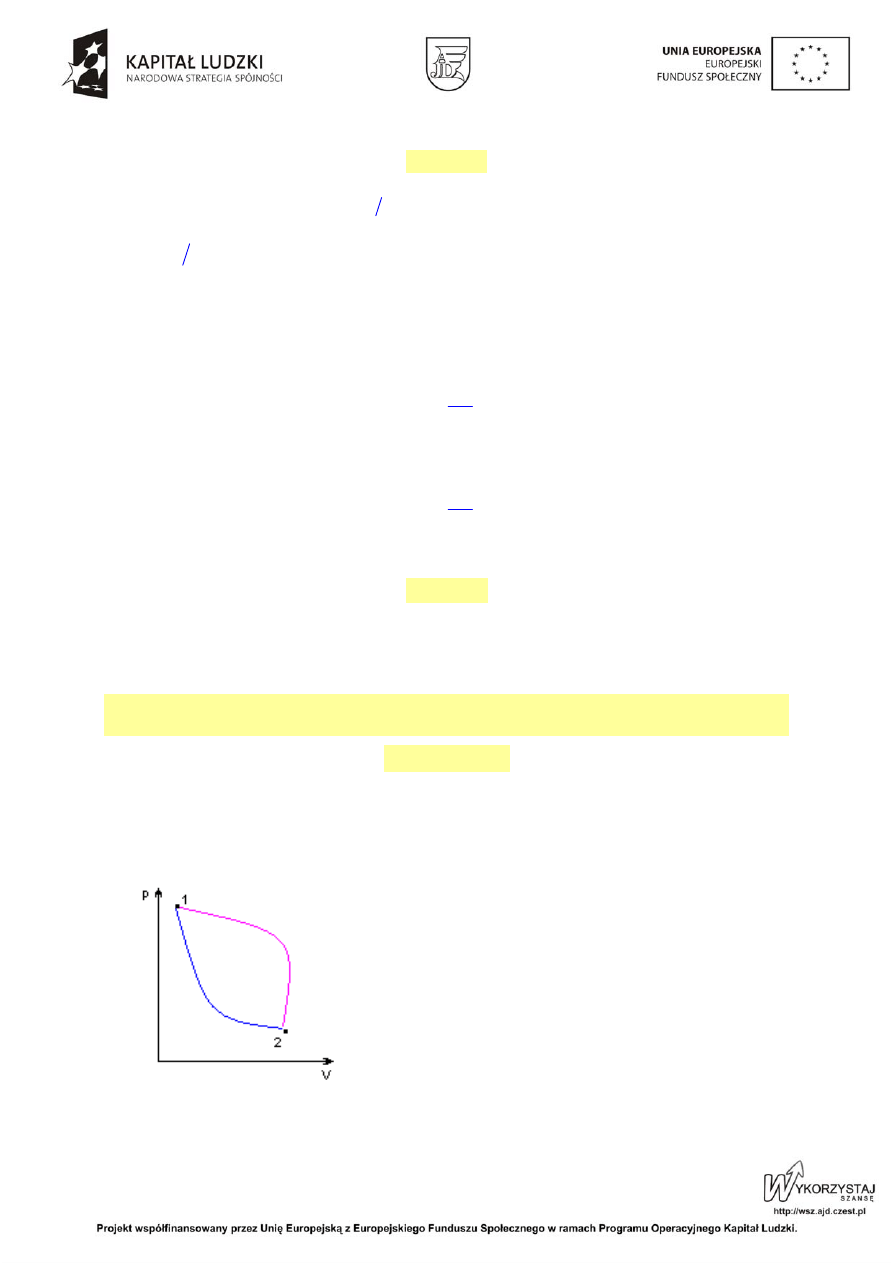
Przejście gazu ze stanu

1 określonego parametrami p

1

,

V

1

, T

1

do stanu

2 określonego parametrami p

2

, V

2

, T

2

może odbywać się po różnych drogach. Parametry
p, V, T wszystkich stanów pośrednich spełniają
równanie stanu.
Równanie przemiany podaje się najczęściej w postaci
związku funkcyjnego miedzy dwoma parametrami
stanu.

Przejście gazu ze stanu 1 do 2

C

p

– ciepło molowe przy stałym ciśnieniu

C

V

– ciepło molowe przy stałej objętości



 =





⋅

p

V

J

C ,C

mol K

Ciepło molowe to ilość ciepła, jaką należy dostarczyć

1 molowi gazu, aby ogrzać go o 1K

p

p

V

C

c

C

V

c

= µ

= µ (10)

gdzie

µ

- masa 1 mola gazu,

c

p

, c

v

– ciepło właściwe gazu odpowiednio pod stałym

ciśnieniem i stałą objętością

p

V

C

C

R

−

=

(11)

V

i

C

2

= R (12)

i - liczba stopni swobody cząsteczki gazu (liczba niezależnych rodzajów ruchu)
i=3 dla gazu jednoatomowego (3 stopnie swobody w ruchu postępowym)
i=5 dla gazu dwuatomowego (3 stopnie swobody w ruchu postępowym i dwa dla ruchu

obrotowego)

i=6 dla gazu wieloatomowego

=

T

const

1 1

2 2

=

→

=

pV

const

p V

p V

Przemiana izotermiczna

Z pierwszej zasady termodynamiki wynika, że całe ciepło doprowadzone do gazu
doskonałego w procesie izotermicznym jest zużywane na wykonanie pracy przeciwko siłom
zewnętrznym.

Q

W

∆ = ∆

=

p const

1

2

1

2

=

→

=

const

T

T

V

V

Przemiana izobaryczna

V

T

)

1

(

)

(

2

1

2

1

2

w

w

p

E

E

c m T

T

p V

V

−

=

−

−

−

(

)

(

2

1

2

1

2

w

w

p

)

1

E

E

C n T

T

p V

V

−

=

−

−

−

=

V

const

1

2

1

2

=

→

=

p

p

p

const

T

T

T

Przemiana izochoryczna

(

)

2

1

2

w

w

V

1

E

E

c m T

T

−

=

−

(

)

2

1

2

w

w

V

1

E

E

C n T

T

−

=

−

Q 0

∆ =

1 1

2 2

1

χ

χ

χ

=

→

=

χ =

p

V

pV

const

p V

p V

gdzie

C C

>

Przemiana adiabatyczna

w

E

W

∆

= −∆

Silnik cieplny

Silnik cieplny

Cykl Carnota

Sprawność silnika

η

to stosunek uzyskanej pracy

W w całym cyklu do pobranego ciepła Q

1

1

W
Q

=

∆

η

∆

(12)

W procesie cyklicznym parametry stanu początkowego i końcowego są takie same, więc

i (9)

→ W Q

1

w

E

E

=

2

w

2

1

Q

=

−

→ (12)

1

1

Q

Q

Q

2

−

=

η

(13)

Najbardziej sprawna maszyna cieplna to

maszyna Carnota, która pracuje w cyklu zwanym

cyklem Carnota (dwie przemiany izotermiczne i dwie adiabatyczne). Jeżeli T

1

to temperatura

źródła a

T

2

to temperatura chłodnicy to sprawność takiego silnika wynosi:

1

2

1

c

T

T

i

T

c

−

=

>

η

η η

(14)

II Zasada termodynamiki

Ciepło może zostać w silniku cieplnym zamienione częściowo na pracę tylko wtedy, gdy
przepływa od ciała o wyższej temperaturze

T

1

do ciała o niższej temperaturze

T

2

(

T

1

>T

2

)

Niemożliwe jest zbudowanie perpetum mobile drugiego rodzaju tzn. silnika pracującego
cyklicznie i czerpiącego ciepło z jednego źródła ciepła tzn. takiego silnika, który nie
oddawałby ciepła do chłodnicy (nie miałby chłodnicy).

Nie można przeprowadzić ciągu procesów, których jedynym rezultatem jest oddanie energii
w postaci ciepła przez ciało chłodniejsze ciału cieplejszemu