WM

Z5/25. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH -

ZADANIE 25

1

Z5/25. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH –

ZADANIE 25

Z5/25.1. Zadanie 25

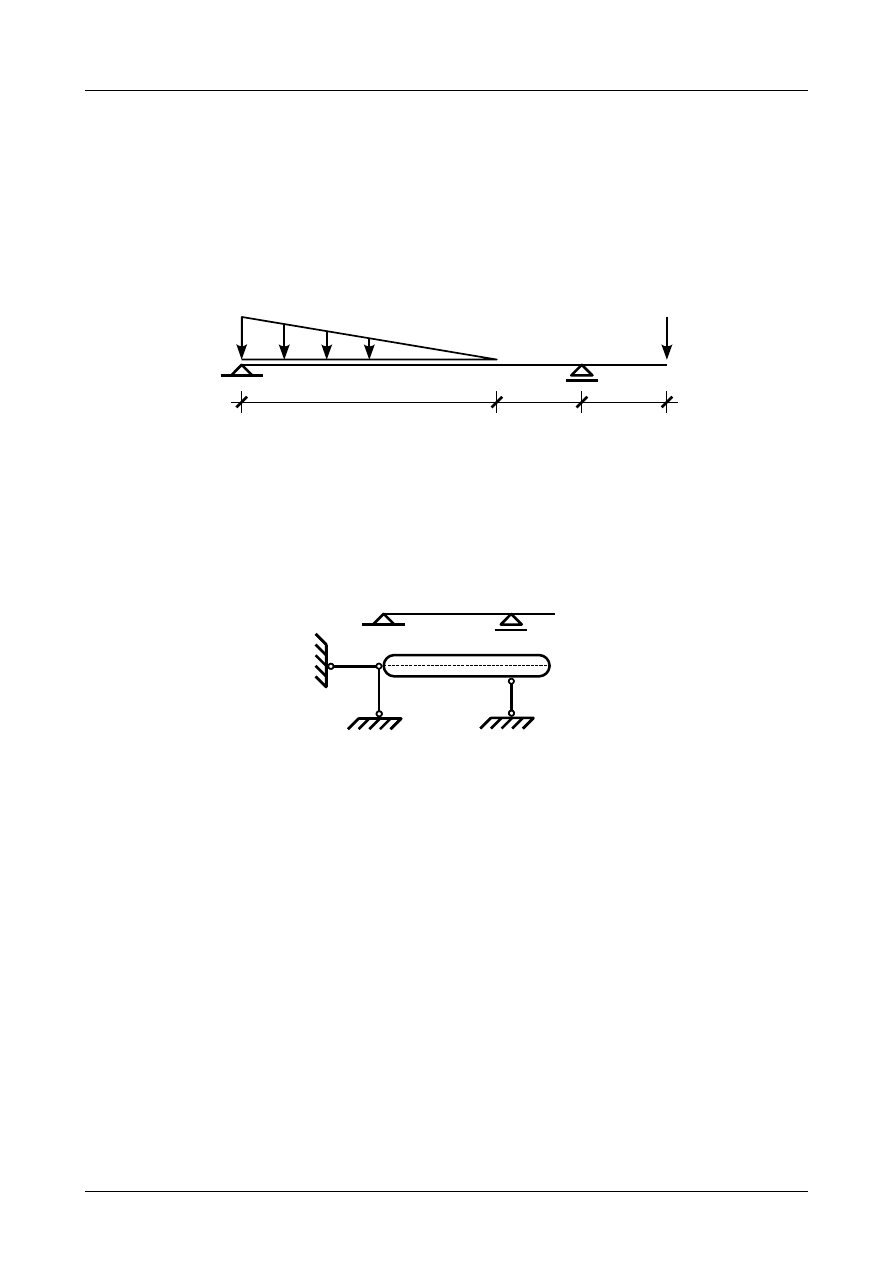
Narysować metodą ogólną wykresy sił przekrojowych dla belki prostej przedstawionej na rysunku

Z5/25.1. Wymiary belki podane są w metrach.

A

B

C

D

12,0 kN

24,0 kN/m

6,0

2,0

2,0

[m]

Rys. Z5/25.1. Belka prosta

Z5/25.2. Analiza kinematyczna belki

Rysunek Z5/25.2 przedstawia belkę prostą traktowaną w analizie kinematycznej jako płaską tarczę

sztywną.

1

2

3

I

A

C

D

Rys. Z5/25.2. Belka prosta jako płaska tarcza sztywna

Jak widać na rysunku Z5/25.2 tarcza sztywna posiada trzy stopnie swobody. Tarcza ta jest podparta

trzema prętami podporowymi 1, 2 i 3. Wszystkie te więzy odbierają razem trzy stopnie swobody. Został
więc spełniony warunek konieczny geometrycznej niezmienności (2.4). Belka może więc być układem
geometrycznie niezmiennym i statycznie wyznaczalnym.

Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie

przecinają się w jednym punkcie. Został więc spełniony także i warunek dostateczny geometrycznej nie-
zmienności dla tej tarczy sztywnej. Jest więc ona geometrycznie niezmienna i statycznie wyznaczalana.

Z5/25.3. Wyznaczenie reakcji podporowych

Aby wyznaczyć wartości i zwroty reakcji podporowych musimy najpierw przyjąć ich dodatnie zwroty.

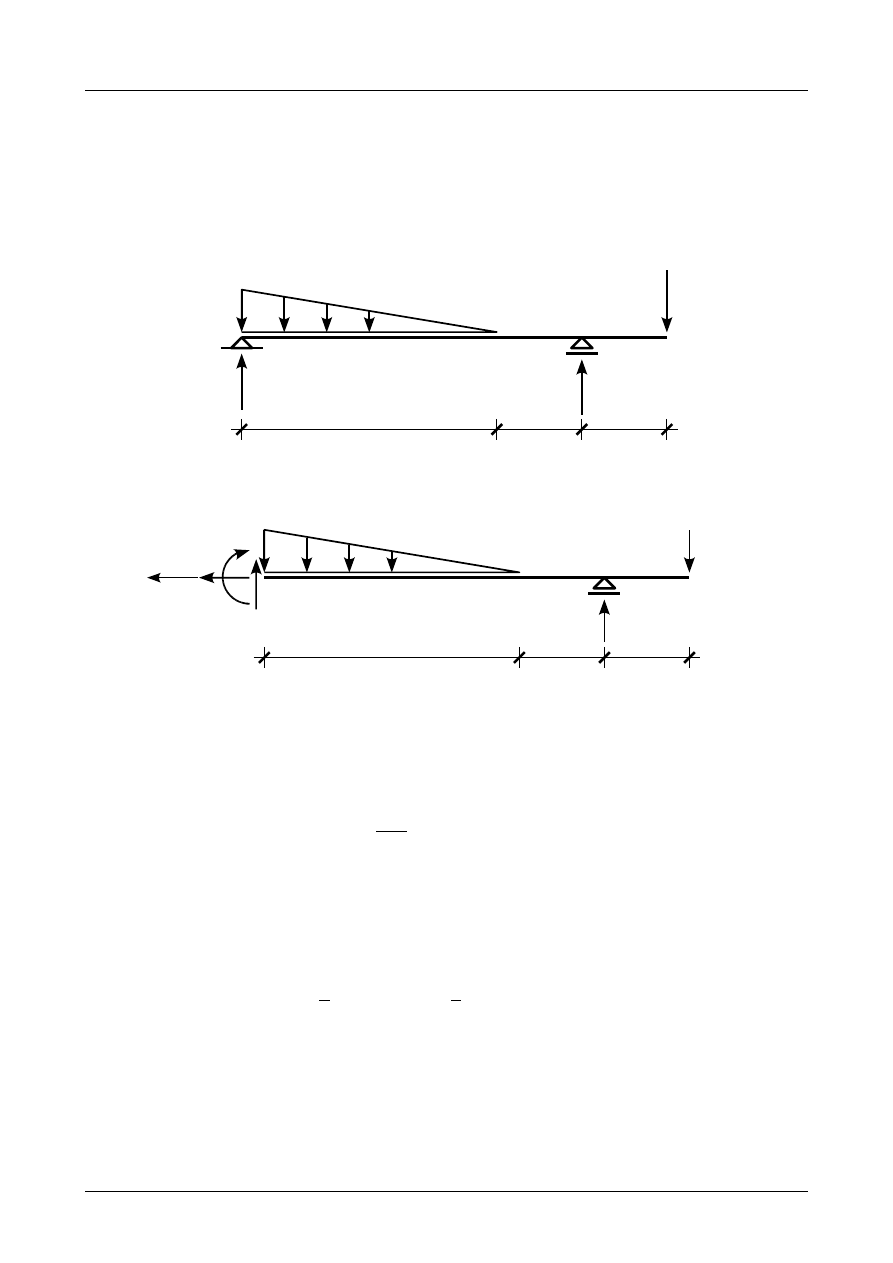
Rysunek Z5/25.3 przedstawia założone zwroty reakcji we wszystkich podporach belki.

Poziomą reakcję na podporze A wyznaczymy z równania sumy rzutów wszystkich sił działających na

belkę na oś poziomą X.



X =H

A

=

0

H

A

=

0,0 kN

.

(Z5/25.1)

Dr inż. Janusz Dębiński

WM

Z5/25. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH -

ZADANIE 25

2

A

B

C

D

12,0 kN

24,0 kN/m

6,0

2,0

2,0

[m]

X

Y

V

A

H

A

V

C

Rys. Z5/25.3. Założone zwroty reakcji podporowych

Pionową reakcję na podporze A otrzymamy z równania sumy momentów wszystkich sił działających

na belkę względem punktu C.



M

C

=

V

A

⋅

8,0−

1
2

⋅

24,0⋅6,0⋅



2,0

2
3

⋅

6,0





12,0⋅2,0=0

V

A

=

51,0 kN

.

(Z5/25.2)

Reakcja ma więc zwrot zgodny z założonym.

Pionową reakcję na podporze C otrzymamy z równania sumy momentów wszystkich sił działających

na belkę względem punktu A.



M

A

=−

V

C

⋅

8,0

1
2

⋅

24,0⋅6,0⋅

1
3

⋅

6,012,0⋅10,0=0

V

C

=

33,0 kN

.

(Z5/25.3)

Reakcja ma więc zwrot zgodny z założonym.

W celu sprawdzenia obliczeń reakcji pionowych zastosujemy równanie sumy rzutów wszystkich sił

działających na belkę na oś pionową Y.



Y =V

A



V

C

−

1

2

⋅

24,0⋅6,0−12,0=51,033,0−72,0−12,0=0

.

(Z5/25.4)

Możemy więc stwierdzić, że pionowe reakcje działające na belkę zostały obliczone poprawnie i znajdują się
w równowadze.

Rysunek Z5/25.4 przedstawia prawidłowe wartości i zwroty reakcji we wszystkich podporach danej

belki.

Z5/25.4. Funkcje sił przekrojowych w przedziale AB

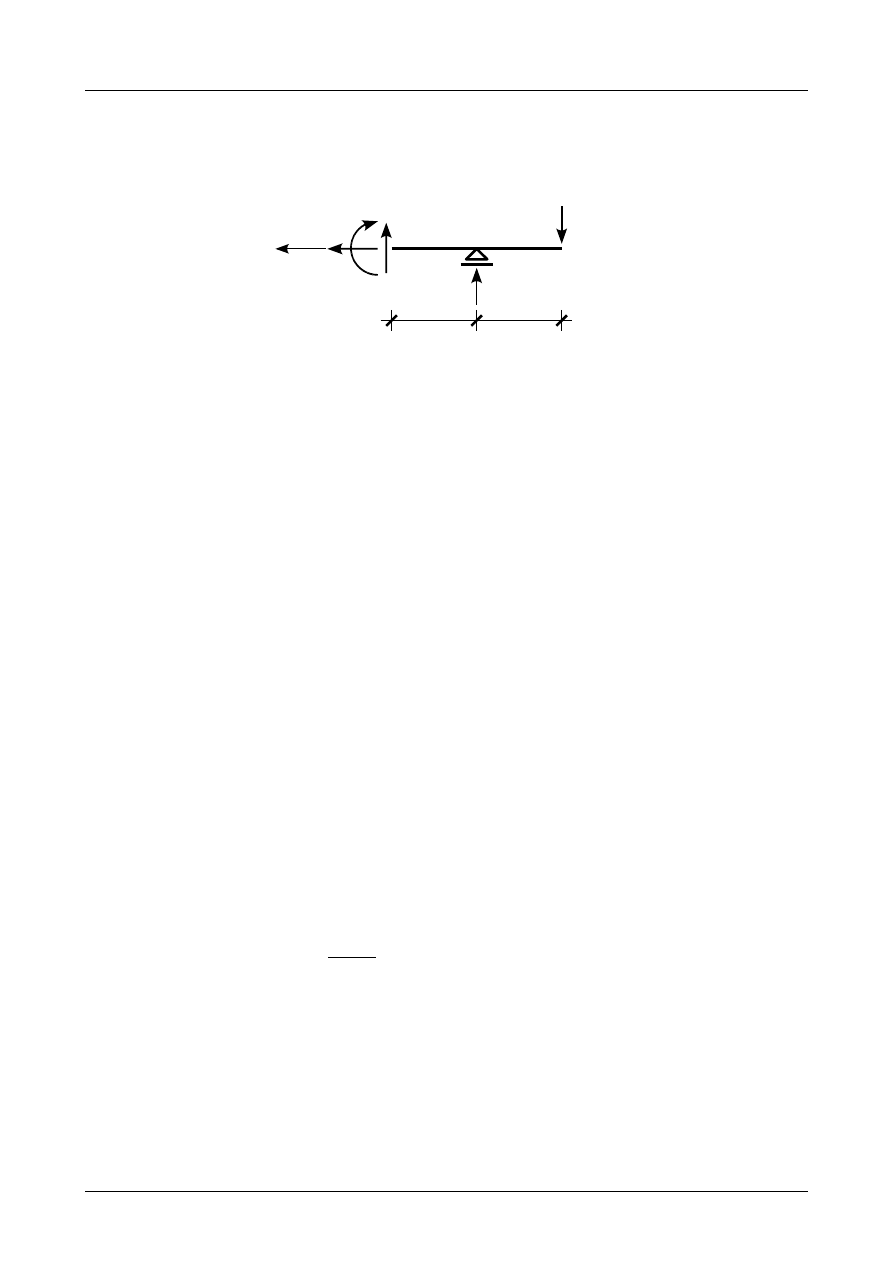
Rysunek Z5/25.5 przedstawia siły działające na odciętą część belki w przedziale AB. Na rysunku tym

są zaznaczone dodatnie siły przekrojowe.

W dalszej części przy wyznaczaniu postaci funkcji siły normalnej lub poprzecznej oraz momentu

zginającego będziemy korzystali z następujących zasad:

•

siły, które działają zgodnie z dodatnim zwrotem siły normalnej lub poprzecznej będziemy zapisywać
z minusem

Dr inż. Janusz Dębiński

WM

Z5/25. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH -

ZADANIE 25

3

•

siły, które działają przeciwnie do dodatniego zwrotu siły normalnej lub poprzecznej będziemy
zapisywać z plusem

•

siły i momenty skupione, które kręcą zgodnie z dodatnim zwrotem momentu zginającego będziemy
zapisywać z minusem

•

siły i momenty skupione, które kręcą przeciwnie do dodatniego zwrotu momentu zginającego
będziemy zapisywać z plusem.

A

B

C

D

12,0 kN

24,0 kN/m

6,0

2,0

2,0

[m]

51,0 kN

33,0 kN

Rys. Z5/25.4. Prawidłowe wartości i zwroty reakcji we wszystkich podporach belki prostej

B

C

D

12,0 kN

x

2,0

2,0

[m]

33,0 kN

q(x)

N(x)

T(x)

M(x)

X

Rys. Z5/25.5. Siły działające w przedziale AB

Funkcja obciążenia ciągłego trójkątnego prostopadłego do osi belki będzie miała, zgodnie ze wzorem

(5.3), postać

q



x



=

24,0

6,0

⋅

x=4,0⋅x

.

(Z5/25.5)

Jak widać na rysunku Z5/25.5 funkcja siły normalnej jest równa zero. Siłę poprzeczną wyznaczymy

z równania sumy rzutów wszystkich sił działających na odciętą część belki na kierunek tej siły. Funkcja ta
ma postać

T



x



=−

33,012,0

1

2

⋅

q



x



⋅

x =−21,0

1
2

⋅

4,0⋅x⋅x=−21,02,0⋅x

2

.

(Z5/25.6)

Funkcja siły poprzecznej jest funkcją kwadratową i aby ją jednoznacznie narysować musimy wyznaczyć jej
wartości w trzech punktach. Wartości tej funkcji na końcach przedziału wynoszą

T



0,0



=−

21,0 kN

T



6,0



=−

21,02,0⋅6,0

2

=

51,0 kN

.

(Z5/25.7)

Dr inż. Janusz Dębiński

WM

Z5/25. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH -

ZADANIE 25

4

Siła poprzeczna ma na obu końcach przedziału wartości różnych znaków. Będzie ona miała więc w prze-
dziale AB miejsce zerowe, które znajduje się w odległości

−

21,02,0⋅x

0

2

=

0

x

0

=

3,240 m

(Z5/25.8)

od początku przedziału czyli od punktu B. Współczynnik przy x

2

jest dodatni więc parabola siły poprzecznej

będzie miała „brzuszek” w dół. Ekstremum tego wykresu znajduje się w punkcie B, w którym obciążenie
trójkątne ma wartość zero.

Moment zginający wyznaczymy z równania sumy momentów wszystkich sił działających na odciętą

część belki względem punktu, w którym wyznaczamy moment zginający.

M



x



=

33,0⋅



x2,0



−

12,0⋅



x4,0



−

1
2

⋅

q



x



⋅

x⋅

1
3

⋅

x=21,0⋅x18,0−

1
2

⋅

4,0⋅x⋅x⋅

1
3

⋅

x

M



x



=−

2

3

⋅

x

3



21,0⋅x18,0

.

(Z5/25.9)

Funkcja momentu zginającego jest wielomianem trzeciego stopnia i aby ją jednoznacznie narysować
potrzebujemy jej wartości w czterech punktach. Wartości tej funkcji na końcach przedziału oraz w miejscu
ekstremum wynoszą

M



0,0



=

18,0 kNm

M



3,240



=−

2

3

⋅

3,240

3



21,0⋅3,24018,0=63,37 kNm

M



6,0



=−

2
3

⋅

6,0

3



21,0⋅6,018,0=0,0 kNm

.

(Z5/25.10)

Jak wiadomo dodatni momenty zginające rozciągają dolną część przekroju pręta i będziemy je odkładać na
dole. Czwartym punktem funkcji będzie fakt, że „brzuszek” jej musi być skierowany w stronę obciążenia
trójkątnego czyli w dół.

Oś X układu współrzędnych jest skierowana w lewo, zastosujemy więc różniczkowe równania rów-

nowagi (5.31) i (5.32). Pierwsze z nich ma postać

dT



x



dx

=

4,0⋅x=q



x



.

(Z5/25.11)

Drugie ma postać

dM



x



dx

=

21,0−2,0⋅x

2

=−

T



x



.

(Z5/25.12)

Jak więc widać oba różniczkowe równania równowagi zostały spełnione.

Wykresy funkcji siły poprzecznej i momentu zginającego w przedziale AB przedstawia rysunek

Z5/25.8. Są to także i ostateczne wykresy tych sił przekrojowych.

Dr inż. Janusz Dębiński

WM

Z5/25. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH -

ZADANIE 25

5

Z5/25.5. Funkcje sił przekrojowych w przedziale BC

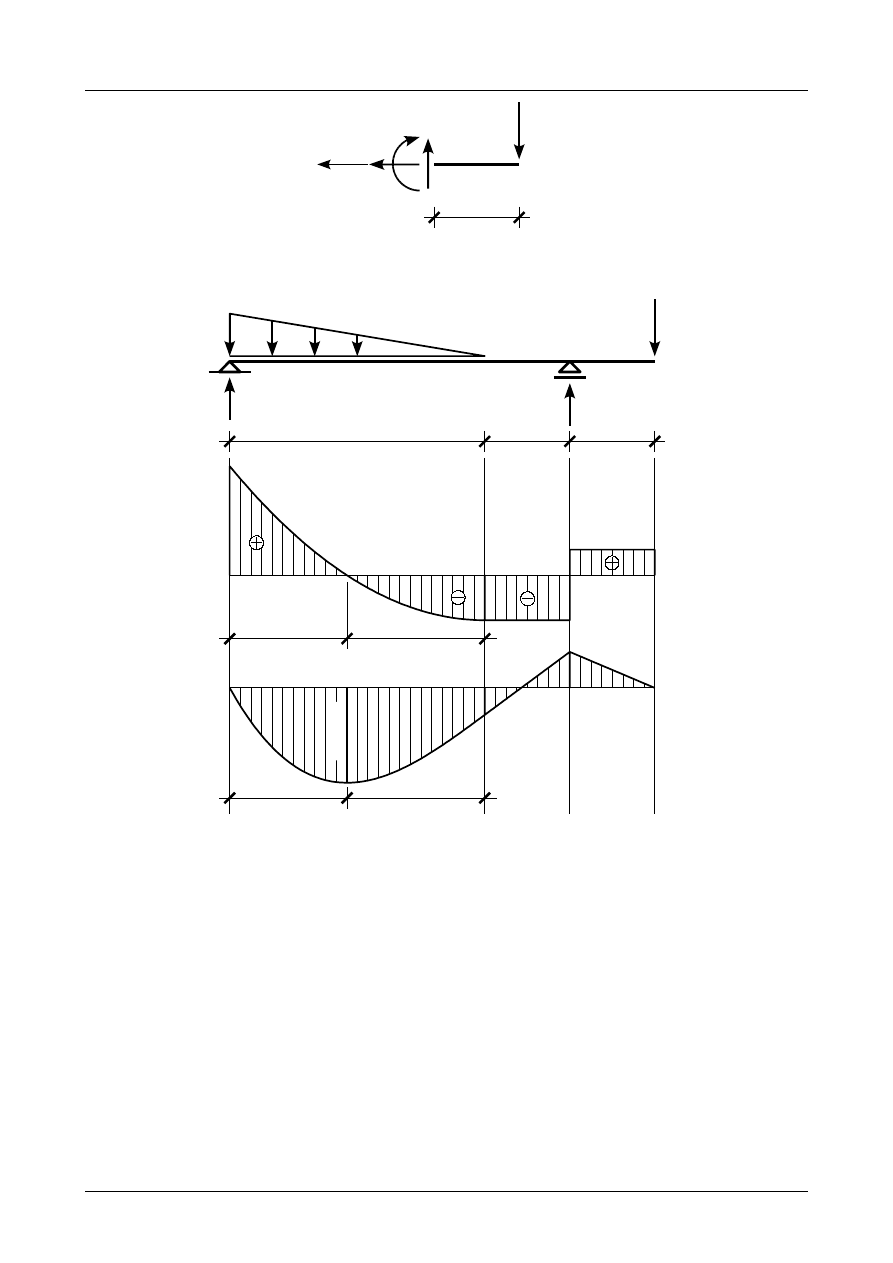
Rysunek Z5/25.6 przedstawia siły działające na odciętą część belki w przedziale BC. Na rysunku tym

są zaznaczone dodatnie siły przekrojowe.

C

D

12,0 kN

x

2,0

[m]

33,0 kN

N(x)

T(x)

M(x)

X

Rys. Z5/25.6. Siły działające w przedziale BC

Funkcja obciążenia ciągłego równomiernie rozłożonego prostopadłego do osi belki będzie zerowa.

Jak widać na rysunku Z5/25.6 funkcja siły normalnej w tym przedziale jest równa także zero. Siła
poprzeczna ma postać

T



x



=−

33,012,0=−21,0 kN

.

(Z5/25.13)

Moment zginający w przedziale BC będzie miał postać

M



x



=

33,0⋅x−12,0⋅



x2,0



=

21,0⋅x−24,0

.

(Z5/25.14)

Funkcja momentu zginającego jest funkcją liniową i aby ją jednoznacznie narysować musimy wyznaczyć jej
wartości w dwóch punktach. Wynoszą one

M



0,0



=−

24,0 kNm

M



2,0



=

21,0⋅2,0−24,0=18,0 kNm

.

(Z5/25.15)

Jak wiadomo ujemne momenty zginające rozciągają górną część przekroju pręta i będziemy je odkładać na
górze, dodatnie zaś na dole.

Oś X układu współrzędnych jest skierowana w lewo, zastosujemy więc różniczkowe równania

równowagi (5.31) i (5.32). Zastosujemy tylko równanie drugie. Ma ono postać

dM



x



dx

=

21,0=−T



x



.

(Z5/25.16)

Jak więc widać różniczkowe równanie równowagi zostało spełnione.

Wykresy funkcji siły poprzecznej i momentu zginającego w przedziale BC przedstawia rysunek

Z5/25.8. Są to także i ostateczne wykresy tych sił przekrojowych.

Z5/25.6. Funkcje sił przekrojowych w przedziale CD

Rysunek Z5/25.7 przedstawia siły działające na odciętą część belki w przedziale CD. Na rysunku tym

są zaznaczone dodatnie siły przekrojowe.

Dr inż. Janusz Dębiński

WM

Z5/25. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH -

ZADANIE 25

6

D

12,0 kN

x

N(x)

T(x)

M(x)

X

Rys. Z5/25.7. Siły działające w przedziale CD

A

B

C

D

12,0 kN

24,0 kN/m

6,0

2,0

2,0

[m]

51,0 kN

33,0 kN

T(x) [kN]

M(x) [kNm]

2,760

3,240

2,760

3,240

51

,0

21,0

12,0

0,

0

18

,0

24

,0

0,

0

63

,3

7

Rys. Z5/25.8. Wykresy funkcji siły poprzecznej i momentu zginającego w belce prostej

Funkcja obciążenia ciągłego równomiernie rozłożonego prostopadłego do osi belki będzie zerowa.

Jak widać na rysunku Z5/25.7 funkcja siły normalnej w tym przedziale jest równa także zero. Siła
poprzeczna ma postać

T



x



=

12,0 kN

.

(Z5/25.17)

Moment zginający w przedziale CD będzie miał postać

M



x



=−

12,0⋅x

.

(Z5/25.18)

Funkcja momentu zginającego jest funkcją liniową i aby ją jednoznacznie narysować musimy wyznaczyć jej
wartości w dwóch punktach. Wynoszą one

Dr inż. Janusz Dębiński

WM

Z5/25. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH -

ZADANIE 25

7

M



0,0



=

0,0 kNm

M



2,0



=−

12,0⋅2,0=−24,0 kNm

.

(Z5/25.19)

Jak wiadomo ujemne momenty zginające rozciągają górną część przekroju pręta i będziemy je odkładać na
górze.

Oś X układu współrzędnych jest skierowana w lewo, zastosujemy więc różniczkowe równania rów-

nowagi (5.31) i (5.32). Zastosujemy tylko równanie drugie. Ma ono postać

dM



x



dx

=−

12,0=−T



x



.

(Z5/25.20)

Jak więc widać różniczkowe równanie równowagi zostało spełnione.

Wykresy funkcji siły poprzecznej i momentu zginającego w przedziale CD przedstawia rysunek

Z5/25.8. Są to także i ostateczne wykresy tych sił przekrojowych.

Dr inż. Janusz Dębiński