1

00518 Termodynamika D

TEORIA

00518

Termodynamika D

Część 3

Kinetyczna teoria gazów

Cykl Carnota.

II i III zasada termodynamiki.

Entropia

Instrukcja dla zdającego
1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 12
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

9.

Znak * dotyczy wiadomości wykraczających poza
ramy programu „maturalnego”.

ś

yczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Październik

ROK 2008

Dane osobowe właściciela arkusza

2

00518 Termodynamika D

TEORIA

Temat: 86

Kinetyczna teoria gazów.

1.

Gaz składa się z olbrzymiej liczby cząsteczek znajdujących się w stanie bezładnego ruchu
cieplnego. Cząsteczki te zderzają się ze sobą, wskutek czego ich prędkości ulegają nie-
ustannym zmianom zarówno co do kierunku, zwrotu, jak i wartości. Jednakże wszystkie
kierunki ruchu są jednakowo prawdopodobne, a większość cząsteczek porusza się z pręd-
kościami niewiele różniącymi się od prędkości średniej

r

v

, która jest tym większa, im

wyższa jest temperatura bezwzględna T gazu. Zderzenia cząsteczek gazu są doskonale
sprężyste, przy czym ze względu na duże odległości między nimi i krótki zasięg działania
sił międzycząsteczkowych nie działają na nie, poza chwilą zderzenia, żadne siły.

2.

Jeżeli gaz znajduje się w zbiorniku, to efektem olbrzymiej liczby zderzeń cząsteczek z jego
ś

ciankami jest wywierane przez gaz ciśnienie. Wskutek dużej częstotliwości i powtarzal-

ności tych zderzeń oraz zupełnie jednakowego prawdopodobieństwa ruchu cząsteczek w
każdym kierunku - ciśnienie gazu jest jednakowe we wszystkich punktach zbiornika (pra-
wo Pascala). Wielkość tego ciśnienia można z pewnym uproszczeniem obliczyć zakłada-
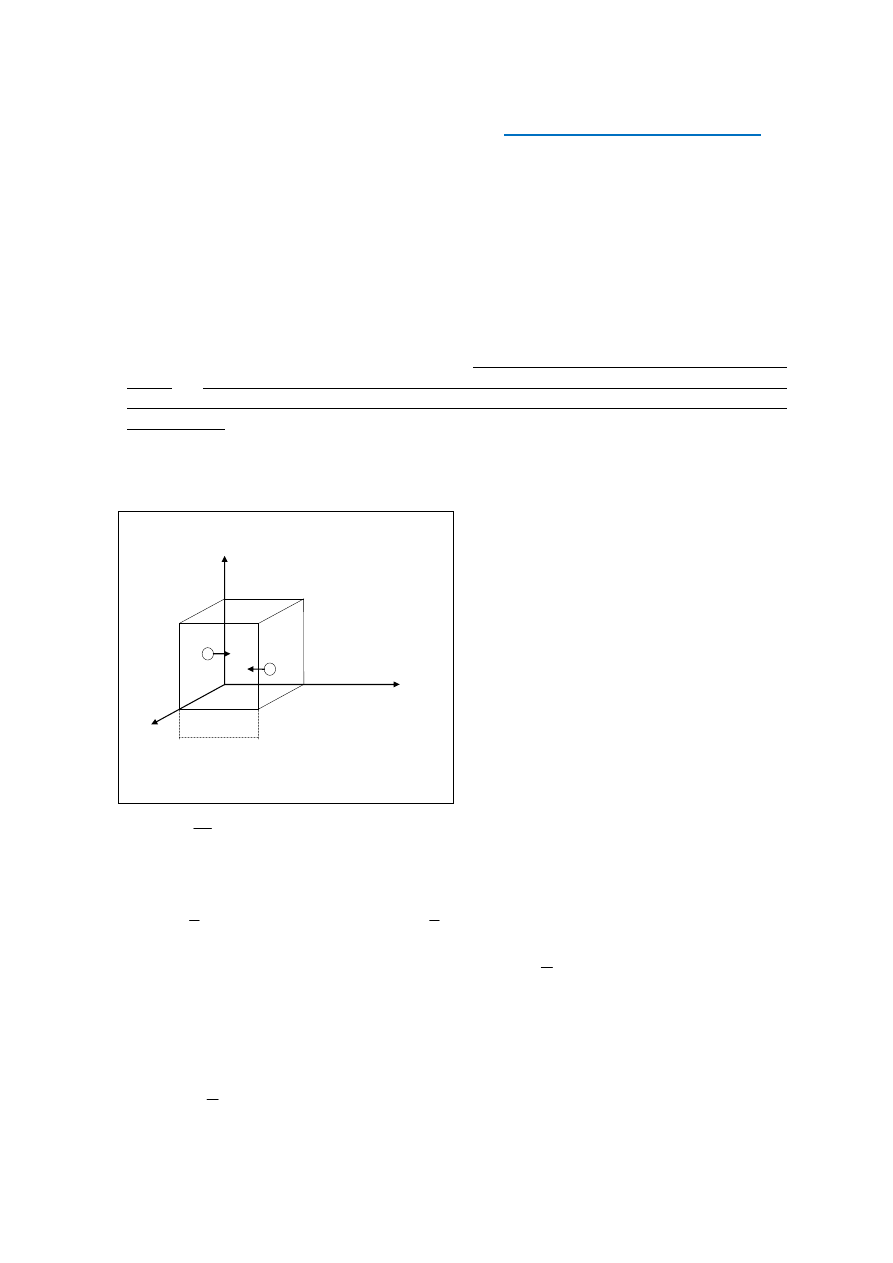
jąc, że zbiornik w kształcie sześcianu (rys. 1) o długości krawędzi l wypełnia gaz chemicz-
nie jednorodny, przy czym w zbiorniku znajduje się N cząsteczek gazu, z których każda
ma masę m’.

y

r

v

r

v

x

z l


Rys. 1

( )

1

2

t

l

v

=

.

W wyniku uderzenia o ścianę zbiornika cząsteczka gazu zmieni swój pęd o wartość

2m v

'

⋅

(zmiana pę

du:

∆

p

m v

v

m v bo v

v

= ⋅ −

=

⋅

= −

' (

)

' ,

0

0

2

), ponieważ zaś w rozpatrywaną ścianę

uderza

1

3

N cząsteczek o łącznej masie

1

3

N m

⋅

' , to zgodnie z ogólną postacią II zasady

dynamiki, całkowita zmiana pędu w czasie t wynosząca

2

3

N m v

⋅ ⋅

' jest równa udzielonemu

ś

cianie zbiornika popędowi siły parcia F, wywieranego przez cząsteczki. Matematycznie

rozumowanie to można przedstawić następująco:

(2)

F t

p

⋅ = ∆

ogólna postać II zasady dynamiki

(3) F t

N m v

⋅ =

⋅ ⋅

2

3

' II zasada dynamiki w naszym przypadku

Ponieważ ruch cząsteczek jest całkowicie
chaotyczny, czyli każdy z kierunków tego
ruchu jest jednakowo prawdopodobny,
można przyjąć, że w każdym z trzech kie-
runków [x; y; z] przestrzeni porusza się
jedna trzecia całkowitej liczby cząsteczek.
Między dwoma kolejnymi uderzeniami o tę
samą ściankę sześcianu cząsteczka gazu
przebywa drogę 2l. Zakładając, że na swej
drodze cząsteczka nie zderza się z żadnymi
innymi cząsteczkami, a prędkość jej jest
równa prędkości średniej v - czas między
dwoma kolejnymi uderzeniami o ścianę
wyniesie:

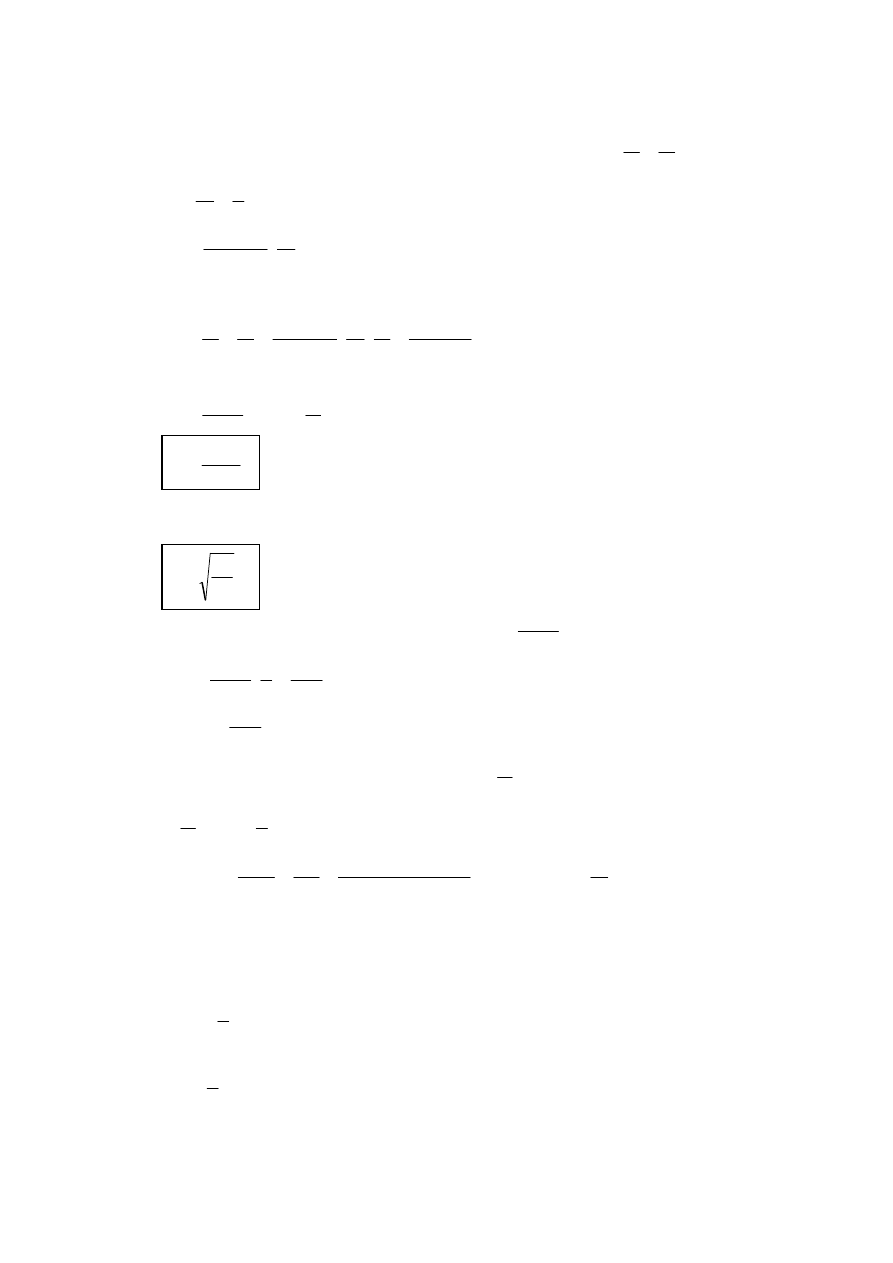
3

00518 Termodynamika D

TEORIA

Pamiętając, że czas określiliśmy wzorem (1) oraz, że ciśnienie wywierane przez gaz rów-

na się stosunkowi siły parcia do powierzchni ściany zbiornika p

F

S

F

l

=

=











2

, otrzymamy:

( )

'

(5)

'

4

2

2

3

2

3

2

F

l

v

N m v

F

N m v v

l

⋅

=

⋅ ⋅

=

⋅ ⋅ ⋅

Mając siłę parcia określoną wzorem (5) wyznaczamy za pomocą wzoru definicyjnego ci-
ś

nienie gazu:

( )

'

'

6

2

3

2

1

3

2

2

2

3

p

F

S

F

l

N m v v

l l

N m v

l

=

=

=

⋅ ⋅ ⋅ ⋅ = ⋅ ⋅

Teraz uwzględniamy zależności: V

l

N m

m

=

⋅ =

3

,

'

i ostatecznie:

( )

,

,

ą

:

(8)

7

3

3

2

2

p

m v

V

ale

m

V

st d

p

v

= ⋅

=

= ⋅

ρ

ρ

Natomiast korzystając ze wzoru (8) możemy wyznaczyć średnią prędkość cząsteczki gazu:

( )

9

3

v

p

=

ρ

Wracamy teraz do równania (7), pamiętając, że

E

m v

k

= ⋅

2

2

:

(

)

,

lub

( )

10

3

2

2

2

3

11

2

3

2

p

m v

V

E

V

p V

E

k

k

= ⋅ ⋅ =

⋅ =

Korzystamy teraz z równania Clapeyrona

p V

m

R T

⋅ = ⋅ ⋅











µ

:

(

)

12

2

3

m

R T

E

k

µ

⋅ ⋅ =

.

Wielkość k

m R

R

N

J mol

mol K

J

K

A

= ⋅ =

=

⋅

⋅

⋅

=

⋅

−

µ

8 314

6 023 10

1 38054 10

23

23

,

,

,

(rachunek dla 1 mola)

nosi nazwę stałej Boltzmanna, a występująca tu wielkość

N

A

, to stała Avogadra wynoszą-

ca

6 023 10

23

,

⋅

cząsteczek w jednym molu gazu.

Uwzględniając powyższe dane i wyznaczając ze wzoru (12) energię kinetyczną cząsteczek
gazu, dostajemy:

(

)

13

3

2

E

k T

k

=

⋅

.

Dla dowolnej liczby moli n, równanie to przyjmie postać:

(14) E

n k T

k

=

⋅ ⋅

3

2

Ponieważ k jest wielkością stałą - z ostatniego równania wynika ważny wniosek stwier-
dzający cieplny charakter ruchu cząsteczek:

4

00518 Termodynamika D

TEORIA

Energia kinetyczna ruchu postępowego cząsteczek gazu jest wprost proporcjonalna
do jego temperatury bezwzględnej.

Łącząc równania (11) i (14) otrzymujemy równanie stanu gazu:

(

)

,

(

)

lub

(

)

15

3

2

3

2

16

17

p V

n k T

czyli

p V

n k T

p V

m

R T

⋅ =

⋅ ⋅

⋅ = ⋅ ⋅

⋅ = ⋅ ⋅

µ

I otrzymaliśmy w ten sposób równanie stanu gazu.

Zależności (9) i (14) stanowiące powiązanie teorii kinetycznej z prawami gazowymi
umożliwiają wyrażenie trudnych do bezpośredniego zmierzenia wielkości mikroskopo-
wych (średnia prędkość lub średnia energia kinetyczna cząsteczek gazu) przez wielkości
makroskopowe (ciśnienie, temperatura bezwzględna), które łatwo można zmierzyć.

Temat: 87

Zjawiska odwracalne i nieodwracalne.

1.

W dotychczasowym opisie zjawisk energetycznych nie uwzględnialiśmy kierunku, w któ-
rym one zachodzą. Rozpatrzmy np. ciało opadające z pewnej wysokości, które następnie
upada na niesprężyste podłoże. W chwili uderzenia jego energia kinetyczna zamieni się na
ciepło, które natychmiast rozproszy się w otoczeniu. Zjawiska tego nie można jednak od-
wrócić, tzn. nie można nieruchomego ciała wprawić w ruch przez ogrzewanie go. Nieod-
wracalne są również wszystkie zjawiska związane z występowaniem sił tarcia, praca bo-
wiem zużywana na przesunięcie ciała i pokonanie siły tarcia zamienia się na ciepło i nie
może być zwrócona przy powrocie ciała do położenia pierwotnego. Także ruch ciepła od
ciała gorętszego do ciała chłodniejszego nigdy nie wystąpi w odwrotnym kierunku i dlate-
go jest procesem nieodwracalnym.

2.

W termodynamice zakłada się istnienie również zjawisk (przemian) odwracalnych. Prze-
mianami takimi są np. izotermiczna oraz adiabatyczne rozprężanie i sprężanie gazu; jed-
nak warunkiem ich odwracalności jest, aby odbywały się nieskończenie wolno, tzn. skła-
dały się z nieskończonej liczby bardzo małych zmian objętości, przy czym po każdej z
nich gaz musi uzyskać stan równowagi wewnętrznej.
Szereg procesów, w wyniku których gaz zostanie z powrotem doprowadzony do stanu po-
czątkowego, nosi nazwę cyklu lub obiegu termodynamicznego. Jeżeli wszystkie przemia-
ny, z których składa się cykl są odwracalne - cykl nazywamy odwracalnym.

5

00518 Termodynamika D

TEORIA

3.

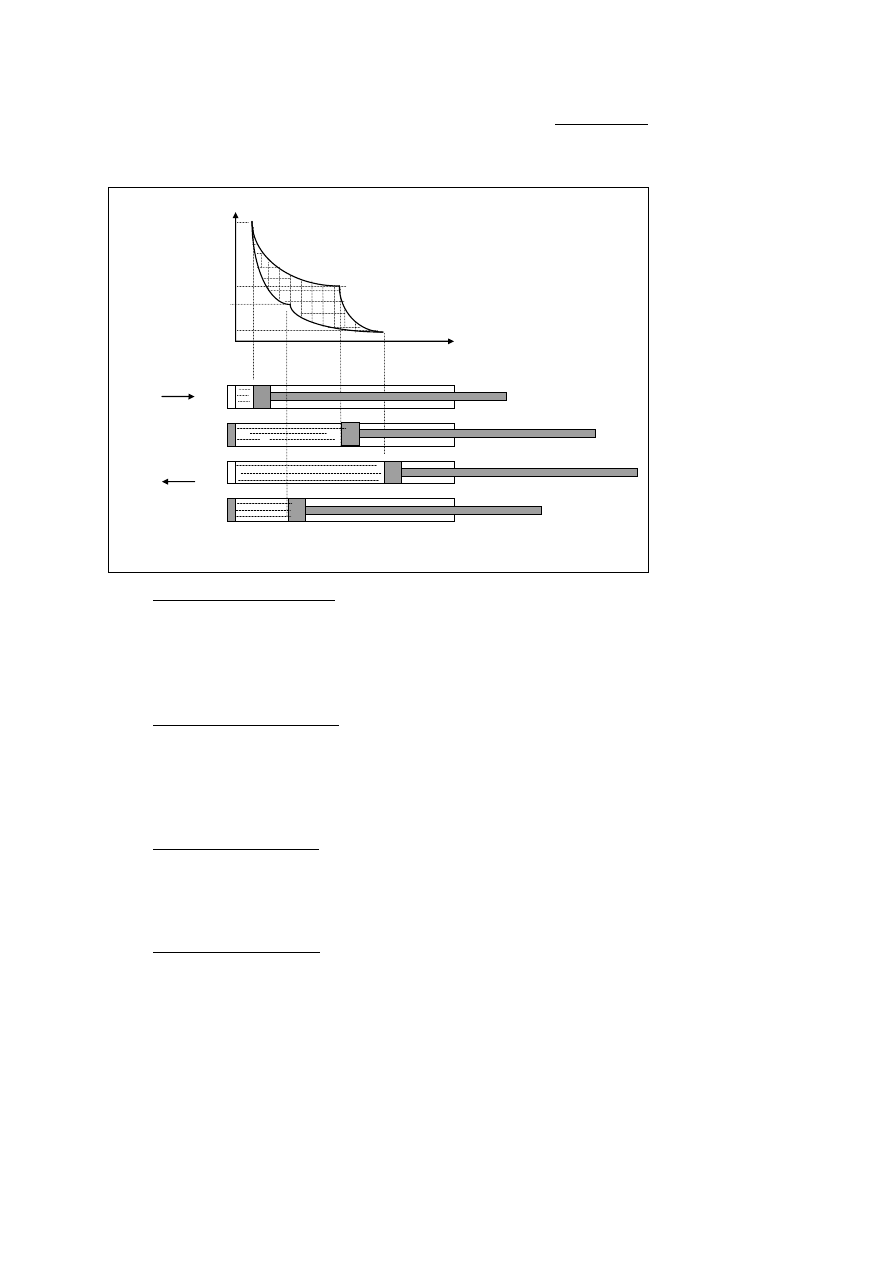
Z punktu widzenia termodynamiki szczególnie ważny jest cykl Carnota, który określa gra-
niczne możliwości zmiany energii cieplnej na mechaniczną. Cykl składa się z czterech
przemian:

p
p

1

1

I
p

2

IV 2

p

3

4

II

p

4

III 3

V
V

1

V

4

V

2

V

3

a) T

1

b) dQ = 0

c) T

2

d) dQ = 0

Rys. 1

a)

rozprężanie izotermiczne - krzywa I. W cylindrze, którego ścianki są izolowane od oto-
czenia, znajduje się gaz doskonały w stanie początkowym p

1

, V

1

, T

1

. Gaz stykając się

ze źródłem ciepła o temperaturze T

1

pochłania energię cieplną Q

1

i ulega izotermicz-

nemu rozprężaniu uzyskując parametry p

2

, V

2

, T

1

. Wykonuje on pracę wyrażoną przez

pole figury V

1

- 1 - 2 - V

2

;

b)

rozprężanie adiabatyczne - krzywa II. Po przerwaniu dopływu ciepła i zamknięciu
ś

cianki czołowej przez izolacyjną pokrywę, gaz bardzo powoli rozpręża się adiabatycz-

nie (brak wymiany ciepła z otoczeniem) do stanu p

3

, V

3

, T

2

, wykonując równocześnie

pracę kosztem swojej energii wewnętrznej pracę wyrażoną przez pole figury V

2

- 2 - 3 -

V

3

;

c)

sprężanie izotermiczne - krzywa III. Po zdjęciu pokrywy izolacyjnej i zetknięciu cylin-
dra z chłodnicą o temperaturze T

2

, gaz zostaje bardzo wolno izotermicznie sprężony do

stanu p

4

, V

4

, T

2

, przy czym praca sprężania wyrażona jest polem figury 3 - V

3

- V

4

- 4 i

zamienia się na ciepło Q

2

- doprowadzone do chłodnicy;

d)

sprężanie adiabatyczne - krzywa IV. Po ponownym przykryciu ścianki czołowej cylin-
dra pokrywą izolacyjną i przesunięciu tłoka w położenie wyjściowe, gaz zostaje bardzo
wolno adiabatycznie sprężony do stanu początkowego p

1

, V

1

, T

1

, przy czym praca ze-

wnętrzna tłoka (jego przesunięcia) wyrażona przez pole figury 4 - V

4

- V

1

- 1 zostaje

przekształcona w równoważny jej przyrost energii wewnętrznej gazu.

Wypadkowa praca W wykonana w czasie cyklu Carnota przedstawiona jest przez zakre-
skowane pole, zamknięte krzywymi I, II, III i IV, ciepło zaś zużyte na jej wykonanie wy-
nosi Q

1

- Q

2

, przy czym zgodnie z I zasadą termodynamiki:

(1) W = Q

1

- Q

2

6

00518 Termodynamika D

TEORIA

Opisany układ złożony ze źródła ciepła, chłodnicy i cylindra z gazem doskonałym działa
jak silnik - wykonując pracę kosztem doprowadzonego ciepła.
Jeżeli cykl Carnota odbywałby się w odwrotnej kolejności (a więc zachodziłyby przemia-
ny IV, III, II, I), to praca sprężania byłaby większa od ciepła doprowadzonego i urządze-
nie realizujące ten cykl pracowałoby jak lodówka.

4.

W analogii do znanego już określenia sprawności maszyn w mechanice

η

=











W

W

użyteczna

ca kowita

ł

-

sprawność maszyny cieplnej

η

c

określa się jako stosunek wykonanej pracy W do energii

cieplnej pobranej ze źródła ciepła Q

1

w czasie jednego cyklu, czyli

(2)

η

c

W

Q

Q

Q

Q

=

=

−

1

1

2

1

Można przy tym wykazać, że w warunkach całkowitego wykorzystania ciepła przy zamia-
nie go na pracę mechaniczną - sprawność teoretyczna silnika zasilanego przez źródło cie-
pła o temperaturze T

1

i oddającego do chłodnicy o temperaturze T

1

ciepło, wynosi

(3)

η

t

T

T

T

= −

1

2

1

Jest to największa sprawność teoretyczna, jaką może osiągnąć silnik cieplny pracujący
między tymi temperaturami. Rzeczywista sprawność silników jest mniejsza od tej warto-
ś

ci, ponieważ występują w nich zarówno straty ciepła, jak i straty energii mechanicznej

związane z tarciem.
O nich warto wiedzieć...

Carnot, Nicolas Leonard Sadi (1796 - 1832) - fizyk francuski. Do 1828 roku był oficerem
wojsk inżynieryjnych. W 1824 podał teorię termodynamicznego procesu kołowego (tzw. cykl
Carnota), obliczył sprawność idealnej maszyny cieplnej. Kilkanaście lat przed R. Mayerem i
J. Joule’em odkrył równoważność ciepła i pracy, wyników tych jednak nie opublikował.
Dzięki swym pracom stał się jednym z twórców podstaw termodynamiki.

Temat: 88

II zasada termodynamiki.

1.

Jak już wiemy, można skonstruować silniki cieplne, które zmieniają pewną ilość ciepła w
energię mechaniczną. Powstaje pytanie: dlaczego nie można zamieniać na energię mecha-
niczną ciepła zmagazynowanego w oceanach? Gdyby nawet wydajność takiego procesu
wynosiła zaledwie 1 %, to uzyskalibyśmy około 10

24

J, podczas gdy, całoroczna produkcja

energii elektrycznej w USA wynosi około 10

18

J. Promieniowanie słoneczne dostarczyłoby

ponownie tej niewielkiej ilości ciepła, która byłaby pobierana z oceanów. Okazuje się, że
istnieje zasadniczy powód, dla którego nie można wykorzystać ogromnej ilości ciepła za-
wartej w oceanach. Jak zobaczymy dalej, druga zasada termodynamiki nie pozwala na
bezpośrednią zamianę ciepła na energię mechaniczną

7

00518 Termodynamika D

TEORIA

2.

Zaczniemy od wymienienia czterech matematycznie równoważnych sformułowań drugiej
zasady termodynamiki:

Nie można zbudować perpetuum mobile drugiego rodzaju.

Gdy dwa ciała o różnych temperaturach znajdą się w kontakcie termicznym,
wówczas ciepło będzie przepływało z bardziej nagrzanego ciała do chłodniej-
szego.

ś

adna cykliczna maszyna cieplna pracująca między temperaturami górną T

1

i

T

2

nie może mieć większej sprawności niż:

η

=

−

T

T

T

1

2

1

D.

W układzie zamkniętym entropia nie może maleć.

3.

Urządzenie zwane perpetuum mobile pierwszego i drugiego rodzaju są przedstawione
schematycznie na rys.1 i 2.

Układ

∆

W

zamknięty ciągły wypływ
energii z naczynia

Rys.1 Perpetuum mobile I rodzaju.

T

2

T

2

T

1

∆

W

obniżanie ciągły wypływ
energii mechanicznej

Rys.2 Perpetuum mobile II rodzaju.

4.

Perpetuum mobile II rodzaju nie narusza wszakże zasady zachowania energii i wskutek
tego bardziej frapuje umysły ludzkie. Taka maszyna miałaby zamieniać ciepło w energię
mechaniczną. Źródło ciepła ustawicznie oziębiałoby się w miarę dostarczania otoczeniu
energii mechanicznej. Gdyby można było skonstruować takie urządzenie, należałoby je
umieścić w oceanach, w których jest zmagazynowane ciepło rzędu 10

26

J, i przekształcić je

w energię mechaniczną. Ta ilość energii znacznie przewyższa ilość dotychczas zużytej
przez ludzkość energii. Niestety, z II zasady termodynamiki wynika, że przekształcenie
chaotycznego ruchu cząsteczek w uporządkowany ruch maszyny czy generatora elektrycz-
nego jest niemożliwe.
W rzeczywistości można pobrać pewną ilość energii z oceanów wykorzystując fakt, że
temperatura powierzchni wody jest wyższa niż temperatura głębszych warstw. Zostały za-
projektowane maszyny cieplne, w których źródło ciepła i chłodnicę stanowią wierzchnia
warstwa wody i dolne warstwy. Wówczas mamy silnik cieplny pracujący między tempera-
turami T

1

i T

2

z maksymalną sprawnością:

η

=

−

T

T

T

1

2

1

Górna granica sprawności takiego silnika wynosi około

1

30

, ponieważ T

1

- T

2

10 K lub

mniej. Omówiliśmy zatem pierwsze sformułowanie II zasady termodynamiki.

Perpetuum mobile pierwszego rodzaju stano-
wiłaby maszyna, która pracowałaby sama
przez się (całkowicie niezależnie od otocze-
nia) i ustawicznie dostarczałaby ciepło oto-
czeniu. Zgodnie z zasadą zachowania energii
oznaczałoby to, że w pudle o skończonej obję-
tości jest zawarte źródło nieskończonej ener-
gii. Jest przeto oczywiste, że perpetuum mobi-
le pierwszego rodzaju po prostu narusza zasa-
dę zachowania energii.

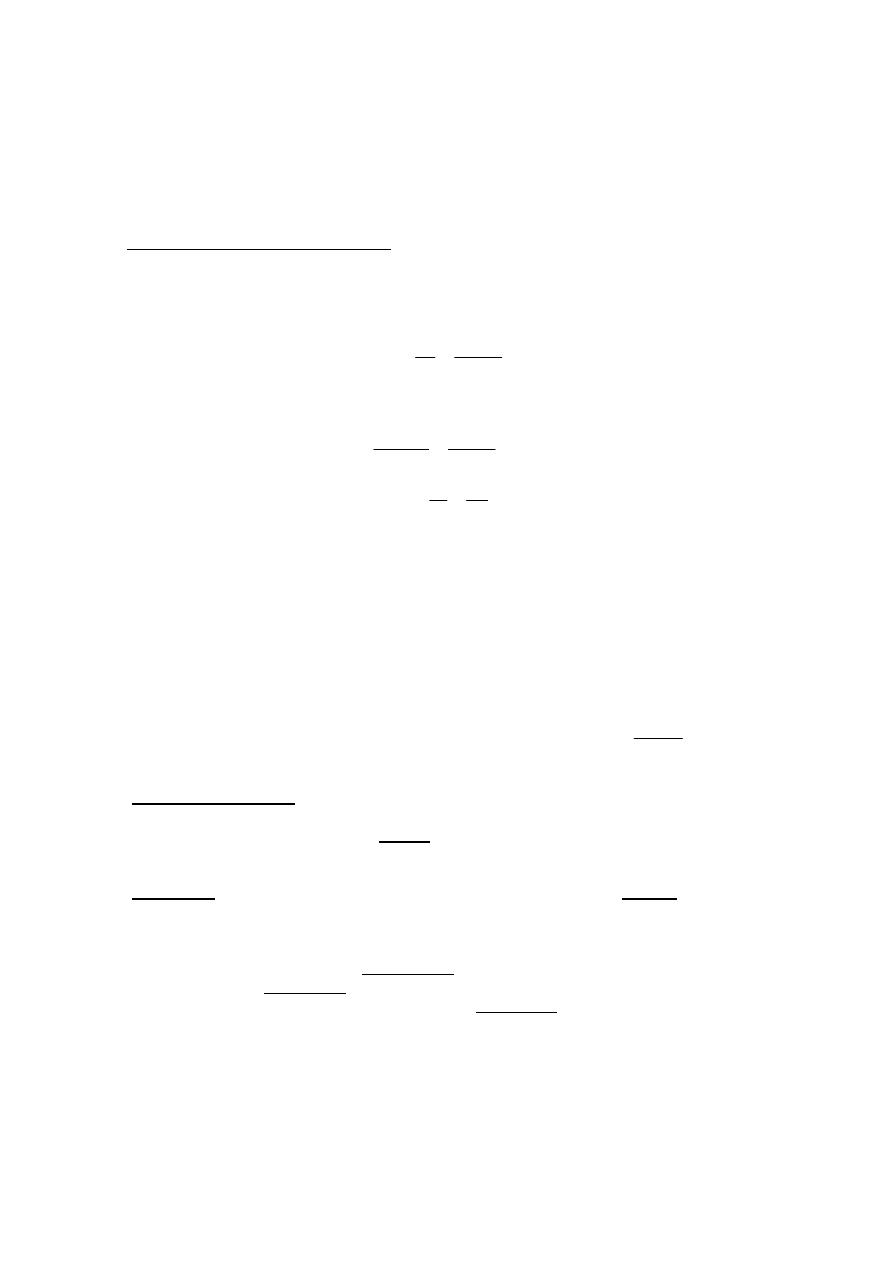
8

00518 Termodynamika D

TEORIA

5.

Gdyby II zasada termodynamiki w drugim sformułowaniu została naruszona, oznaczałoby
to, że ciepło przepływa z chłodniejszego zbiornika do cieplejszego. Gdyby to ciepło zosta-
ło zużyte do uruchomienia maszyny cieplnej, to mielibyśmy perpetum mobile II rodzaju,
co w myśl pierwszego sformułowania jest niemożliwe.

Sformułowanie trzecie pozostawimy do własnej analizy, natomiast czwarte omówimy
przy temacie „Entropia”.

6.

Termodynamiczna skala temperatur.

Nasza pierwotna definicja temperatury jest związana ze średnią energią kinetyczną czą-
steczki (temat 112, wzór 13). Istnieje wszakże równoważna definicja makroskopowa.
Udowodniliśmy właśnie, że niezależnie od ciała roboczego, sprawność silnika Carnota jest
równa:

W

Q

T

T

T

1

1

2

1

=

−

Korzystając z I zasady termodynamiki podstawiamy W = Q

1

- Q

2

i mamy:

Q

Q

Q

T

T

T

1

2

1

1

2

1

−

=

−

, czyli:

T

T

Q

Q

1

2

1

2

=

Zatem stosunek temperatur dwóch dowolnych zbiorników ciepła można zmierzyć mierząc
przenoszenie ciepła podczas jednego cyklu Carnota. W rzeczywistości wzór powyższy
stanowi definicję tak zwanej termodynamicznej skali temperatur. Ponieważ wzór ten wy-
prowadziliśmy posługując się naszą pierwotną makroskopową definicją temperatury,
udowodniliśmy zarazem równoważność tych dwóch definicji temperatury.
Warto zwrócić uwagę, że tak przyjęta skala temperatur nie zależy od żadnych cech wy-
branego ciała termometrycznego, a do jej określenia wystarczy jeden punkt stały (np.
punkt potrójny wody) i dlatego często nazywa się ją bezwzględną skalą temperatur oraz
przyjęto ją za wielkość podstawową układu SI.

Jednostką temperatury termodynamicznej jest kelwin (1 K), to jest

1

273 16

,

część tempe-

ratury termodynamicznej punktu potrójnego wody.
O tym warto wiedzieć:

Proces, który doprowadził do ostatecznego sformułowania II zasady termodynamiki trwał ponad
40 lat. W 1824 roku francuski fizyk Carnot na podstawie rozważań odnośnie cyklu Carnota, do-
chodzi do jakościowego wniosku: ciepło można zamienić na pracę tylko w takim procesie, w któ-
rym następuje przepływ ciepła, matematyczną postać temu wnioskowi Carnota nadał w 1834 roku
Clapeyron. Sam termin: II.z.t. wprowadził w 1851 roku fizyk niemiecki Clasius, który sformuło-
wał ją w ujęciu: niemożliwy jest przepływ ciepła od ciała o niższej do ciała o wyższej temperatu-
rze. W tym samym roku II.z.t. sformułował w wersji: niemożliwy jest proces, w którym ciepło po-
brane od ciała ulegałoby całkowitej zamianie na pracę (a więc niemożliwa jest budowa perpetum
mobile II rodzaju) angielski fizyk W. Thomson (późniejszy lord Kelvin). Ostateczną postać II.z.t
podał w 1865 roku R.E.Clasius wprowadzając i analizując pojęcie entropii. Mikroskopową inter-
pretację II.z.t podał w 1877 roku austriacki fizyk Boltzmann. Wszystkie prawa termodynamiki
mają postać statystycznej tendencji, a nie bezwzględnego prawa. Z mikroskopowego punktu wi-
dzenia są możliwe procesy nie spełniające II.z.t, są one jednak tak mało prawdopodobne, że wy-
stąpienia jakiegokolwiek takiego procesu w skali nawet miliardów lat jest prak

tycznie nierealne.

I zasada termodynamiki doprowadziła do odkrycia zasady zachowania energii, a
więc była od niej pierwsza.

9

00518 Termodynamika D

TEORIA

Temat: 89*

Entropia.

1.

Zasada degradacji energii:

Wszystkie zjawiska zachodzące samorzutnie w przyrodzie są zjawiskami nieodwracalny-
mi. Mają one określony kierunek przebiegu, a mianowicie zawsze taki, że w czasie trwa-
nia takich zjawisk energia określonego rodzaju, np. energia mechaniczna, chemiczna,
elektryczna, magnetyczna przetwarza się na ciepło. Tym zmianom może towarzyszyć po-
wstanie pewnych różnic temperatur. Wiemy jednak, że jeśli obok siebie istnieją dwa ciała
o różnych temperaturach, to samorzutny przepływ ciepła od ciała o temperaturze wyższej
do ciała o temperaturze niższej powoduje wyrównanie się temperatur. Po wyrównaniu się
temperatur ciał niemożliwa jest już przemiana ciepła na pracę. Nawet w idealnym procesie
odwracalnym silnika termodynamicznego z ogólnej ilości ciepła Q

1

, dostarczonej przez

kocioł, na prace przekształca się tylko część ciepła, reszta zostaje oddana do chłodnicy. Ta
reszta stanowi zasób energii trudniejszy już do przetworzenia na pracę lub inny rodzaj
energii. W czasie przemiany np. na pracę ta ilość ciepła wymagałaby użycia nowej chłod-
nicy o jeszcze niższej temperaturze.
Ta kierunkowość przemian w przyrodzie, objawiająca się przetwarzaniu się pracy lub ja-
kiejkolwiek energii na ciepło, odpowiada zasadzie degradacji albo rozpraszania się ener-
gii.
Nawiązując do I zasady termodynamiki powiemy:

W układzie odosobnionym ogólna ilość zasobów energii jest stała, lecz zjawiska
zachodzące samorzutnie w takim układzie prowadzą do zmniejszenia się jej war-
tości użytkowej.

3.

Nierówność Clausiusa.

Omówioną wyżej kierunkowość zjawisk w przyrodzie można ująć ilościowo za pomocą
nowej funkcji stanu układu, zwanej entropią. Zanim przejdziemy do określenia entropii
musimy zająć się tzw. nierównością Clausiusa. Wiemy, że sprawność silnika termodyna-
micznego wynosi:

1

2

1

Q

Q

Q

)

1

(

−

=

η

Dla silnika odwracalnego, pracującego w obiegu Carnota między stałymi temperaturami
kotła i chłodnicy:

1

2

1

t

T

T

T

)

2

(

−

=

η

Sprawność silnika pracującego między temperaturami T

1

i T

2

może być co najwyżej rów-

na

t

η

, czyli:

1

2

1

1

2

1

T

T

T

Q

Q

Q

)

3

(

−

≤

−

czyli:

1

2

1

2

T

T

Q

Q

)

4

(

≥

Mnożąc przez wyrażenie

2

1

T

Q

otrzymujemy:

2

2

1

1

T

Q

T

Q

0

)

5

(

−

≥

10

00518 Termodynamika D

TEORIA

Pamiętając, że Q

2

jest ujemne można nierówność (5) napisać w postaci:

2

2

1

1

T

Q

T

Q

0

)

6

(

+

≥

Znak równości obowiązuje dla odwracalnego obiegu Carnota.
Można udowodnić, że analogiczna zależność może być rozszerzona na większą liczbę
przemian tworzących cykl zamknięty. Niech ilość ciepła odpowiadająca poszczególnym
częścią cyklu wynoszą

n

2

1

Q

,

,

Q

,

Q

∆

⋅⋅

⋅

∆

∆

i będą pobierane lub oddawane (a więc dodatnie

lub ujemne) odpowiednio w temperaturach.

n

2

1

T

,

,

T

,

T

∆

⋅⋅

⋅

∆

∆

. Wtedy:

0

T

Q

T

Q

T

Q

)

7

(

n

n

2

2

1

1

≤

∆

+

⋅⋅

⋅

+

∆

+

∆

Jest to tzw. nierówność Clausiusa. Znak równości obowiązuje przy przemianach odwra-

calnych, znak nierówności - przy przemianach nieodwracalnych. Stosunek

T

Q

∆

- ciepła

pobranego do temperatury, w jakiej jest ono pobierane (lub oddawane) - nazywamy cie-
płem zredukowanym. Przez temperaturę, w której ciepło jest pobierane rozumiemy tempe-
raturę źródła dostarczającego ciepło. Z nierówności Clausiusa wynika, że:

Suma wartości ciepła zredukowanego w przemianie odwracalnej kołowej równa się
zeru, a w przemianie nieodwracalnej jest mniejsza od zera.

3.

Entropia:

p odwracalna
1

2
V
odwracalna
Rys. 1

(8) S = S

2

- S

1

, a równocześnie

∑

∆

=

−

2

1

1

2

T

Q

S

S

)

9

(

Dla elementarnej przemiany odwracalnej możemy zapisać:

dS

T

Q

)

10

(

=

∆

, czyli dQ = TdS, co oznacza

Ciepło dostarczone czynnikowi w elementarnej przemianie odwracalnej wyraża iloczynem
temperatury bezwzględnej i elementarnego przyrostu entropii charakteryzującego tę ele-
mentarną przemianę.

Ciepło zredukowane łączne odpowiadające
przejściu odwracalnemu od stanu 1 do stanu 2
(rys.1), nie zależy od rodzaju przemiany, a
zależy od stanu początkowego i końcowego
(bo zgodnie ze wzorem (7) musi być równa
zeru dla przemian kołowych i odwracalnych).
Wprowadźmy zatem nową funkcję stanu,
zwaną entropią, której zmiana S, odpowiada-
jąca przejściu odwracalnemu od stanu 1 do
stanu 2, wyraża się wzorem:

11

00518 Termodynamika D

TEORIA

p nieodwracalna
1

2
V
odwracalna

Rys. 2

0

T

Q

T

Q

)

11

(

1

a

ln

odwraca

2

2

a

ln

nieodwraca

1

〈

∆

+

∆

∑

∑

Dla przemiany odwracalnej wykorzystamy równość (9):

∑

∆

〉

−

2

a

ln

nieodwraca

1

1

2

T

Q

S

S

)

12

(

Ponieważ układ jest izolowany cieplnie (odosobniony), więc prawa strona równania (12)
jest równa zeru, gdyż układ jako całość nie pobiera i nie oddaje ciepła, czyli:

1

2

1

2

S

S

lub

0

S

S

)

13

(

〉

〉

−

, a zatem:

W układzie odosobnionym zachodzą samorzutnie takie procesy nieodwracalne, podczas
których entropia rośnie. W tej zasadzie wzrostu entropii jest właśnie zawarte kryterium
kierunkowości przemian w przyrodzie.

Temat: 90*

III zasada termodynamiki.

I.

Badanie właściwości ciał stałych i cieczy w temperaturach bliskich zera bezwzględnego
doprowadziły Nernsta (1906 rok) do sformułowania tzw. III zasady termodynamiki. Obec-
nie zwykle jest ona podawana w ujęciu Plancka:

W temperaturze zera bezwzględnego entropia ciał stałych i ciekłych

staje się równa zeru, czyli

0

S

lim

0

T

=

∆

→

W oparciu o III zasadę termodynamiki można teoretycznie wykazać, że w miarę zbli-
ż

ania się do temperatury zera bezwzględnego, ciepła właściwe ciał stałych i współ-

czynniki rozszerzalności dążą do zera. Innymi słowy, w tych warunkach maleją różni-
ce termiczne we właściwościach ciał stałych

Można również wykazać (tego robić nie bę-
dziemy), że w przemianie odwracalnej entro-
pia całkowita układu odosobnionego nie ulega
zmianie.

Aby określić za pomocą entropii kierunkowość
przebiegu zjawisk zachodzących samorzutnie
w przyrodzie, rozważymy w układzie odosob-
nionym taką przemianę jak na rys.2. Całość
przebiegu jest zatem zjawiskiem nieodwracal-
nym, czyli z nierówności Clausiusa mamy:

12

00518 Termodynamika D

TEORIA