2

4

6

6

I

1

I

1

I

1

I

1

I

2

I

2

+25°C

+25°C

-20°C

-20°C

-20°C

t

m

=+20°C

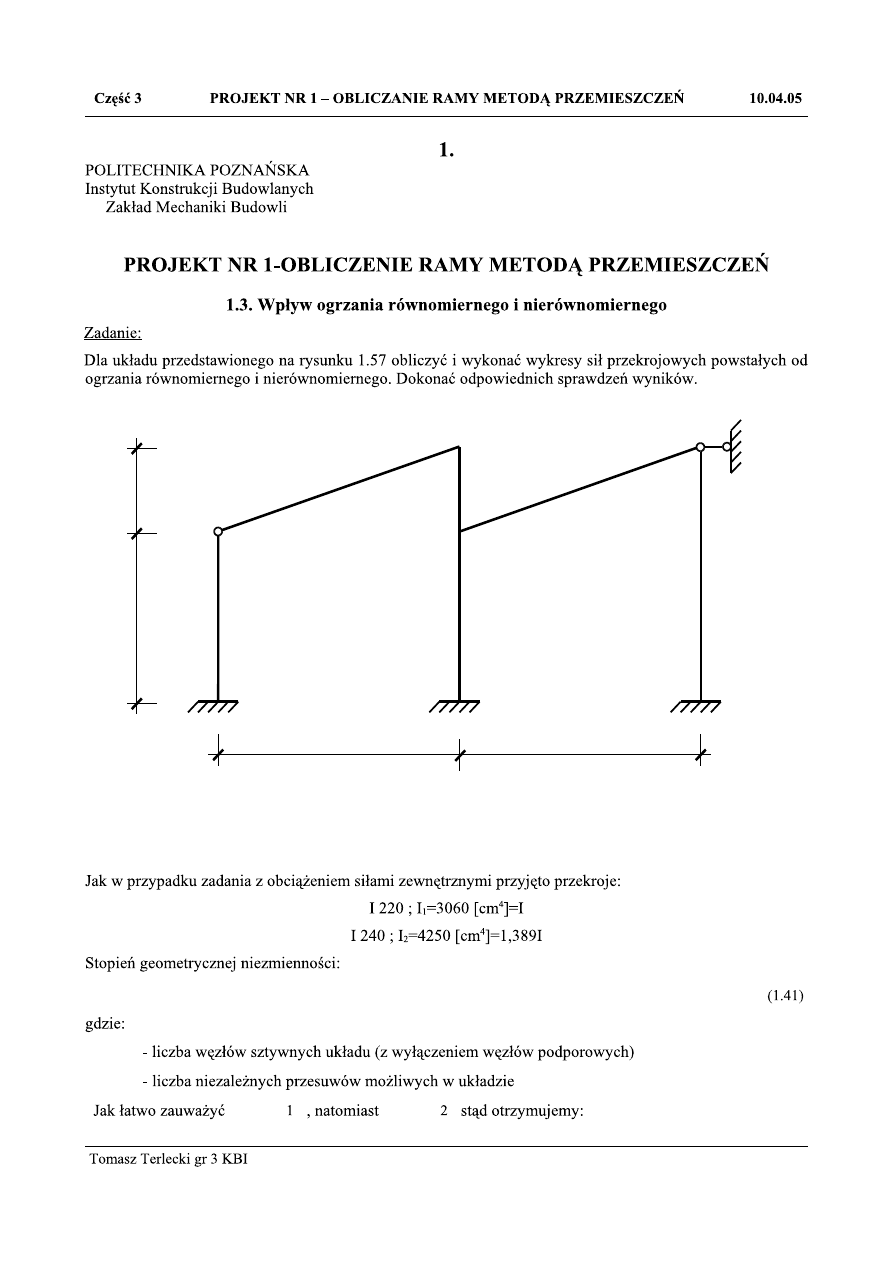
Rys.1.57. Układ statycznie niewyznaczalny poddany działaniu temperatury

SGN =

∑



∑



∑



∑



∑

=

∑

=

1/13

SGN

=3

(1.42)

Układ podstawowy przyjmuję jak w poprzedniej części zadania

2

4

6

6

I

1

I

1

I

1

I

1

I

2

I

2

+25°C

+25°C

-20°C

-20°C

-20°C

t

m

=+20°C

I

1

2

3

R

1

R

3

φ

3

=z

3

u

2

=z

1

φ

2

=z

2

0

1

4

5

6

R

2

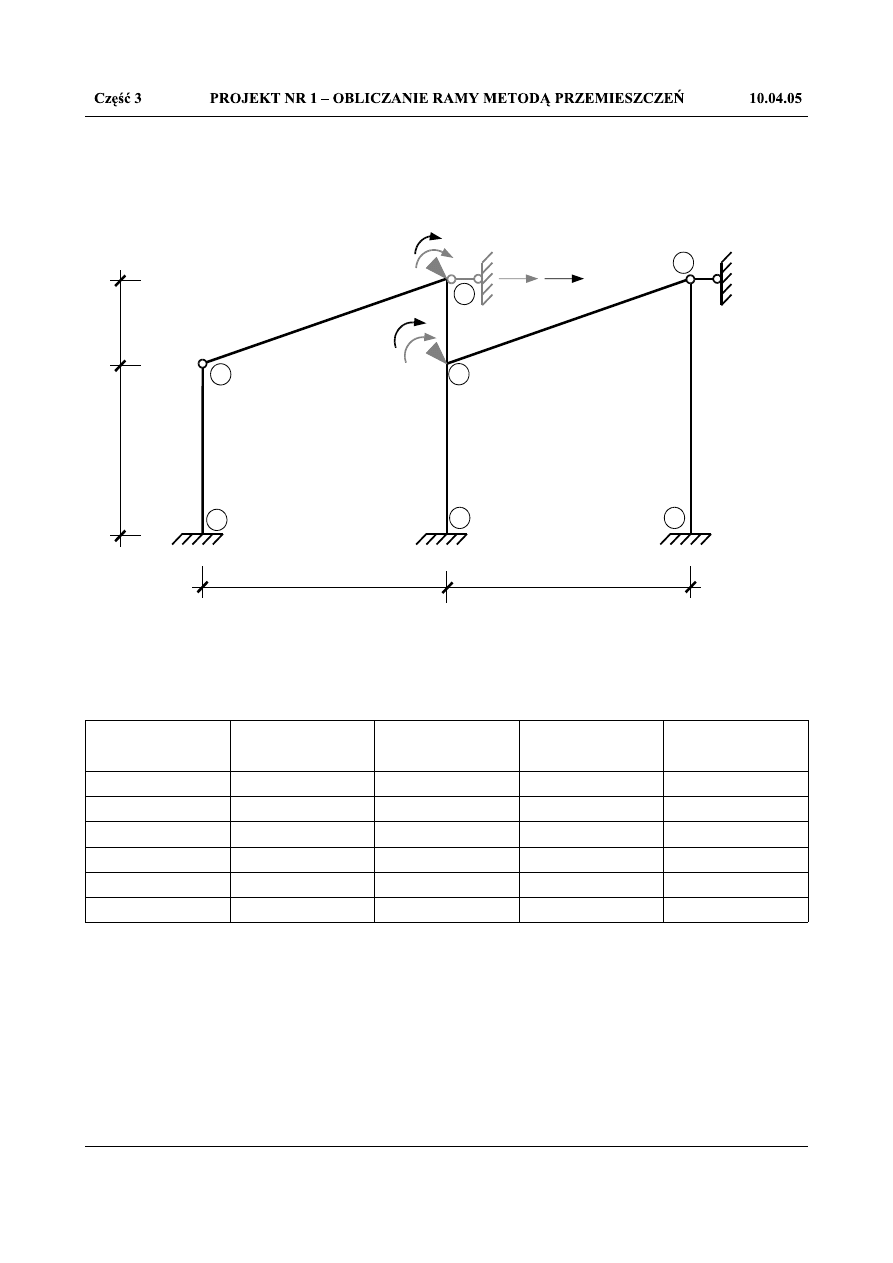
Rys.1.58.Układ podstawowy poddany osiadaniu podpór

Zestawienie parametrów charakterystycznych dla poszczególnych prętów:

numer pręta

moment bezwładności

I[cm

4

]

wysokość przekroju

h [m]

|∆t|

[˚C]

t

0

[˚C]

01

I

0,22

45

-17,5

12

1,389I

0,24

45

-17,5

23

I

0,22

45

-17,5

34

I

0,22

0

+5

35

1,389I

0,24

45

-17,5

56

I

0,22

45

-17,5

Tab.1 Zestawienie charakterystyk prętów

Identyczność statyczną układu podstawowego z wyjściowym zapewnia układ równań kanonicznych:

Tomasz Terlecki gr 3 KBI

2/13

{

R

1

=0

R

2

=0

R

3

=0

}

{

r

11

z

1

r

12

z

2

r

13

z

3

R

1 t

=0

r

21

z

1

r

22

z

2

r

23

z

3

R

2 t

=0

r

31

z

1

r

32

z

2

r

33

z

3

R

3 t

=0

}

(1.43)

Wartości współczynników r

ik

nie zależą od rodzaju obciążenia stąd, jeżeli przyjęto taki sam układ

podstawowy to pozostaną one takie jak w poprzedniej części zadania (rama obciążona siłami zewnętrznymi).
Aby określić wartości współczynników

R

it

wyznaczam w pierwszej kolejności

wartości momentów

zginających wywołanych działającą temperaturą, przy czym korzystając z zasady superpozycji:

M

ik

=M

ik

 t

M

ik

t

0

(1.44)

Wartości momentów zginających powstałych w wyniku ogrzania nierównomiernego wyznaczam
wg odpowiednich wzorów transformacyjnych metody przemieszczeń. Otrzymuję:

M

01

 t

=−

3
2

⋅EI

01

⋅

t

⋅

 t

h

=−1,5 ⋅6273 ⋅1,2 ⋅10

−5

⋅

45

0,22

=−23,09605

M

10

 t

=0

M

12

 t

=0

M

21

 t

=

3
2

⋅EI

21

⋅

t

⋅

 t

h

=1,5 ⋅1,389⋅6273 ⋅1,2 ⋅10

−5

⋅

45

0,24

=29,40704

M

23

 t

=−EI

23

⋅

t

⋅

 t

h

=−6273 ⋅1,2 ⋅10

−5

⋅

45

0,22

=−15,39736

M

32

 t

=EI

23

⋅

t

⋅

 t

h

=6273 ⋅1,2 ⋅10

−5

⋅

45

0,22

=15,397360

M

34

 t

=0

M

43

 t

=0

M

35

 t

=−

3
2

⋅EI

35

⋅

t

⋅

 t

h

=−1,5 ⋅1,389⋅6273 ⋅1,2 ⋅10

−5

⋅

45

0,24

=−29,40704

M

53

 t

=0

M

56

 t

=0

M

65

 t

=

3
2

⋅EI

56

⋅

t

⋅

 t

h

=1,5 ⋅6273⋅1,2 ⋅10

−5

⋅

45

0,22

=23,09605

[kNm]

(1.45)

Wartości momentów zginających powstałych w wyniku ogrzania równomiernego wyznaczam wg wzorów
transformacyjnych metody przemieszczeń pamiętając, że φ

i

to

=0. Otrzymuję:

Tomasz Terlecki gr 3 KBI

3/13

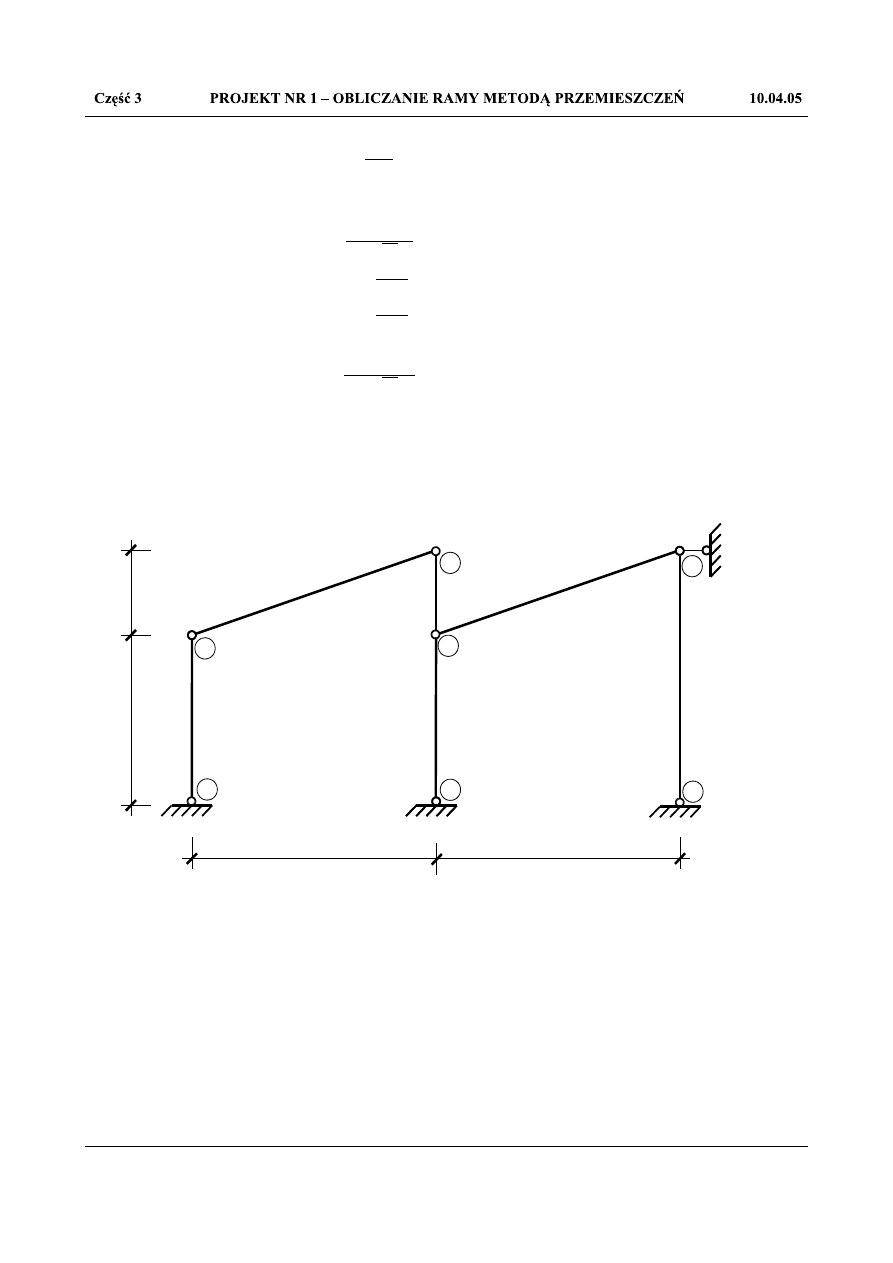
M

01

t

0

=

3 EI

4

⋅−

01

t

0



M

10

t

0

=0

M

12

t

0

=0

M

21

t

0

=

3⋅1,389 EI

2



10

⋅−

12

t

0



M

23

t

0

=M

32

t

0

=

2 EI

2

⋅−3 

23

t

0



M

34

t

0

=M

43

t

0

=

2 EI

4

⋅−3 

34

t

0



M

53

t

0

=0

M

35

t

0

=

3⋅1,389 EI

2



10

⋅−

35

t

0



M

56

 t

=M

65

 t

=0

[kNm]

(1.46)

Na skutek ogrzania równomiernego długości prętów ulegają zmianie, co powoduje obrót prętów. Wartości
kątów



ik

t

0

określam z równań łańcucha kinematycznego w układzie podstawowym:

2

4

6

6

t

m

=+20°C

t

0

= -17,5°C

t

0

= -17,5°C

t

0

=+5°C

0

1

2

3

4

5

6

t

0

= -17,5°C

t

0

= -17,5°C

t

0

= -17,5°C

Rys.1.59. Łańcuch kinematyczny dla ramy poddanej ogrzaniu równomiernemu

Rozpisuję równanie łańcucha kinematycznego dla podanych niżej dróg:

Tomasz Terlecki gr 3 KBI

4/13

65

6

56

t

0

0

56

t

0

0

4356

6

35

t

0

4 1,2 10

−

5

5 2 1,2 10

−

5

17,5 6 1,2 10

−

5

17,5 0

35

t

0

1,8 10

−

4

435

4

34

t

0

2

35

t

0

6 1,2 10

−

5

17,5 0

34

t

0

2,25 10

−

4

432

2

23

t

0

4

34

t

0

0

23

t

0

4,5 10

−

4

01234

6

12

t

0

4 1,2 10

−

5

17,5 2 1,2 10

−

5

17,5 2 1,2 10

−

5

17,5 4 1,2 10

−

5

5 0

12

t

0

1,8 10

−

4

012

4

01

t

0

2

12

t

0

6 1,2 10

−

5

17,5 0

01

t

0

4,05 10

−

4

[rad]

(1.47)

Stąd wartości przęsłowych momentów przywęzłowych powstałych w wyniku ogrzania równomiernego
wynoszą:

M

01

t

0

1,90542

M

10

t

0

0

M

12

t

0

0

M

21

t

0

0,74395

M

23

t

0

M

32

t

0

8,46855

M

34

t

0

M

43

t

0

2,11714

M

53

t

0

0

M

35

t

0

0,74395

M

56

t

0

M

65

t

0

0

[kNm]

(1.48)

Wartości momentów od ogrzania równomiernego i nierównomiernego zgodnie z zasadą superpozycji (patrz
wzór 1.44.):

M

01

t

25,00147

M

10

t

0

M

12

t

0

M

21

t

30,15099

M

23

t

6,92881

M

32

t

23,86591

M

34

t

M

43

t

2,11714

M

53

t

0

M

35

t

30,15099

M

56

t

M

65

t

0

[kNm]

(1.49)

Wykres momentów przyjmie więc postać:

Tomasz Terlecki gr 3 KBI

5/13

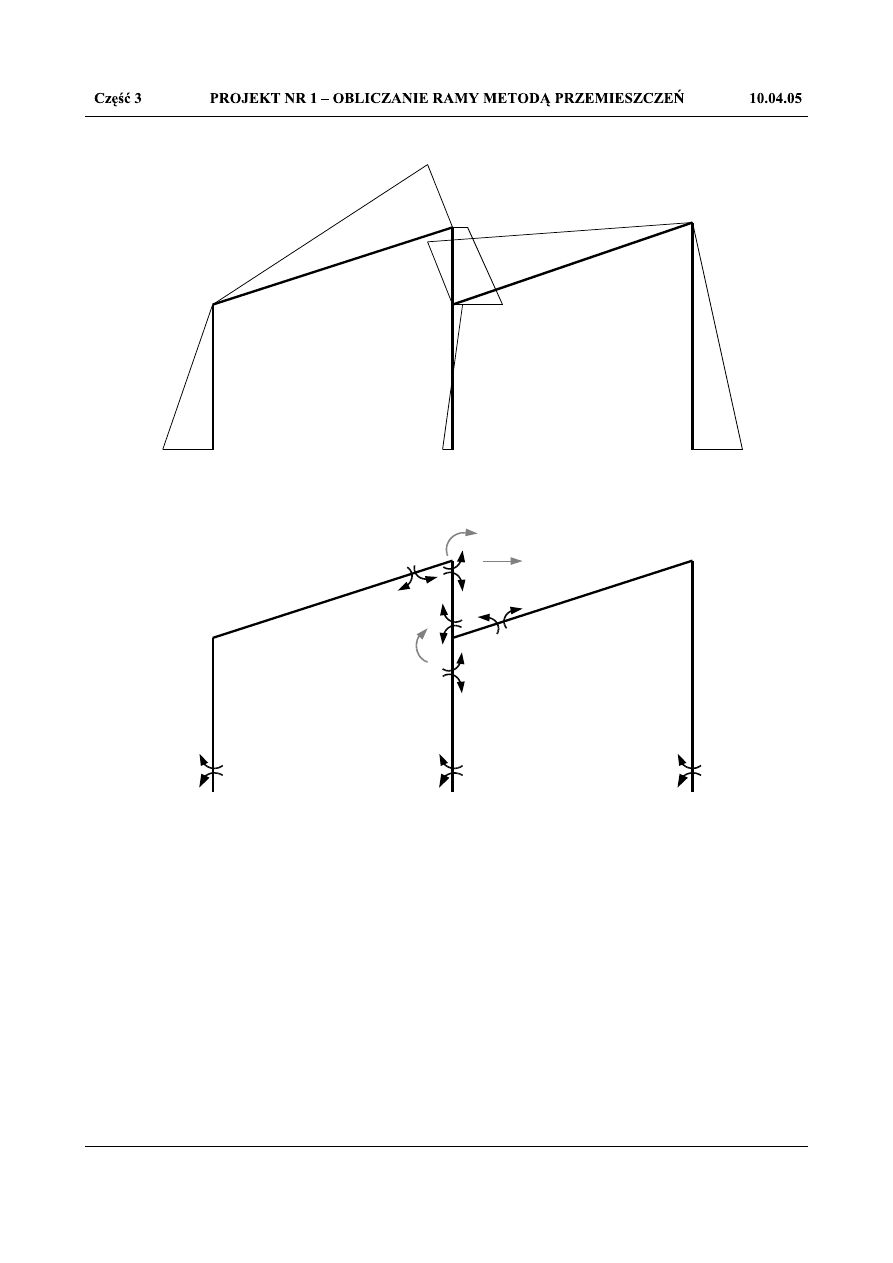
Rys.1.60. Stan t - wpływ ogrzania równomiernego i nierównomiernego M

t

[kNm]

Określenie współczynnika

R

2 t

, R

3 t

z wykorzystaniem równowagi węzła 2 i 3:

R

2 t

=23,22218

R

3 t

=−8,40222

[kNm]

(1.50)

Wartości współczynnika

R

1 t

określam korzystając jak w poprzedniej części zadania z zasady pracy

wirtualnej przy wirtualnym stanie przemieszczeń (patrz rysunek 1.18).

Dla wirtualnego stanu

z

1

=1

obliczając pracę sił w stanie t na przemieszczeniach wirtualnych jak na

rysunku 1.18 otrzymujemy:

Tomasz Terlecki gr 3 KBI

6/13

30,15099

25,00147

30,15099

6,92881

23,86591

2,11714

2,11714

23,09605

R

1t

R

2t

R

3t

30,15099

-25,00147

-6,92881

-30,15099

-23,09605

-2,11714

-2,11714

23,86591

R

1 t

⋅1−25,00147 t

1
4

−6,9288123,86591⋅

1
2

=0 ⇒ R

1 t

=−2,21818 [kN]

(1.51)

Uwzględniając powyższe wartości współczynników r

ik

układ równań kanonicznych 1.43. przyjmie postać:

{

1,547 EI z

1

−1,5 EI z

2

−1,5 EI z

3

−2,21818=0

−1,5 EI z

1

2,659 EI z

2

EI z

3

23,22218=0

−1,5 EI z

1

EI z

2

3,659 EI z

3

−8,40222=0

}

(1.52)

Rozwiązanie powyższego układu jest następujące:

EI z

1

=−13,81731

EI z

2

=−17,00971

EI z

3

=1,28067

(1.53)

Ostateczne wartości momentów zginających w ramie statycznie niewyznaczalnej poddanej działaniu
temperatury jest superpozycją stanów z

1

, z

2

, z

3

, t:

M

ik

n

=M

1

0

⋅z

1

M

2

0

⋅z

2

M

3

0

⋅z

3

M

ik

t

(1.54)

M

01

=

−3 EI

4

⋅

z

1

4

−25,00147=−22,411

M

10

=0

M

12

=0

M

21

=

3

⋅1,389 EI

2



10

z

2

30,15099=18,943

M

23

=EI 2 z

2

z

3

−1,5 z

1

−6,92881=−18,942

M

32

=EI  z

2

2 z

3

−1,5 z

1

23,86591=30,144

M

34

=EI z

3

−2,11714=−0,836

M

43

=0,5 EI z

3

−2,11714=−1,477

M

35

=

3

⋅1,389 EI

2



10

⋅z

3

−30,15099=−29,307

M

53

=0

M

56

=0

M

65

=23,096

[kNm]

(1.55)

Tomasz Terlecki gr 3 KBI

7/13

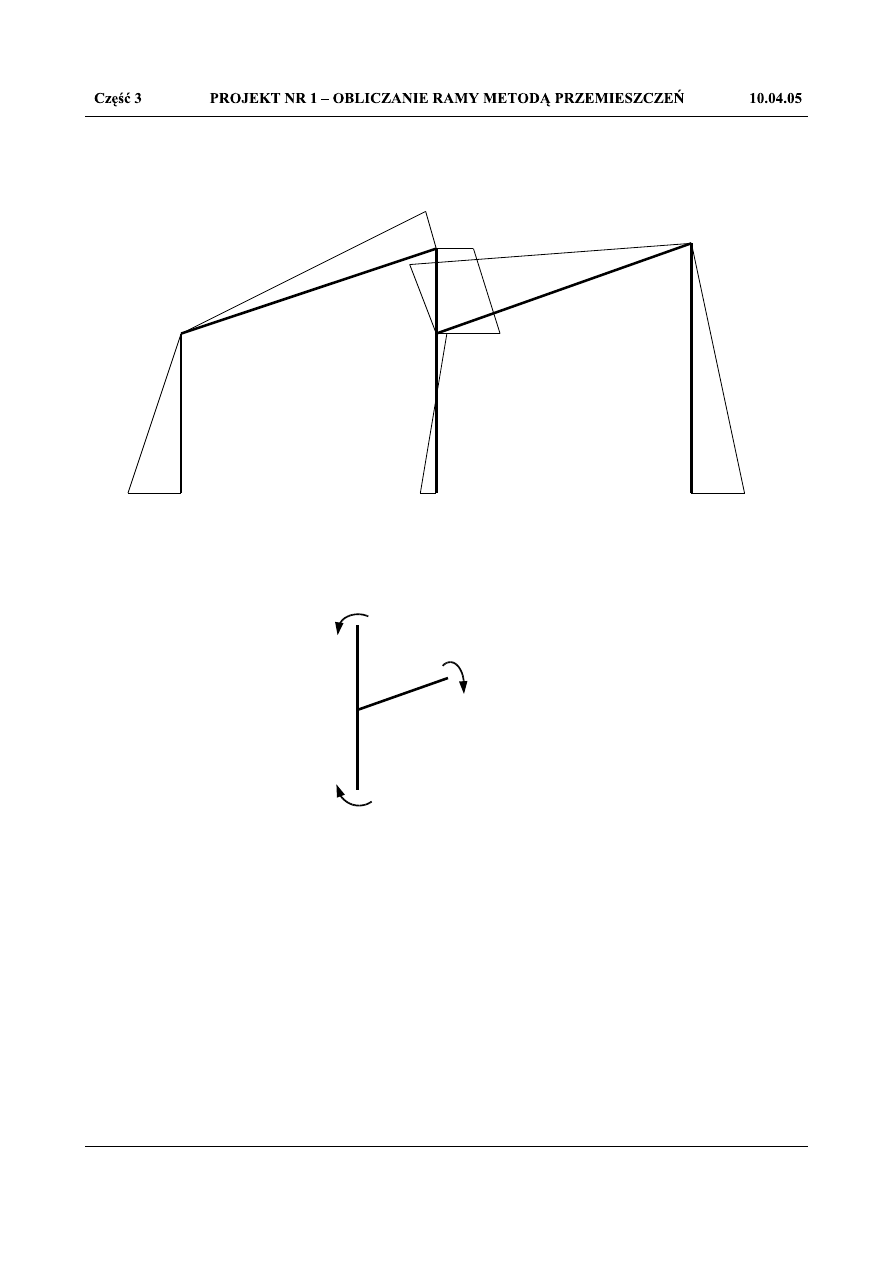
18,943

22,411

29,307

18,942

30,144

0,836

1,477

23,096

Rys.1.61. Momenty zginające w układzie statycznie niewyznaczalnym poddanym działaniu temperatury M

(n)

[kNm]

Wstępną poprawność wyników wykazuję poprzez sprawdzenie równowagi węzła 3:

30,144

29,307

0,836

Rys.1.62. Równowaga węzła 3

∑

M =−30,14429,3070,836=−0,001 ≈0 [ kNm]

(1.56)

Łatwo zauważyć, że również w węźle 2 równowaga jest spełniona bowiem:

∑

M =18,943−18,942=0,001 ≈0 [ kNm]

(1.56)

Tomasz Terlecki gr 3 KBI

8/13

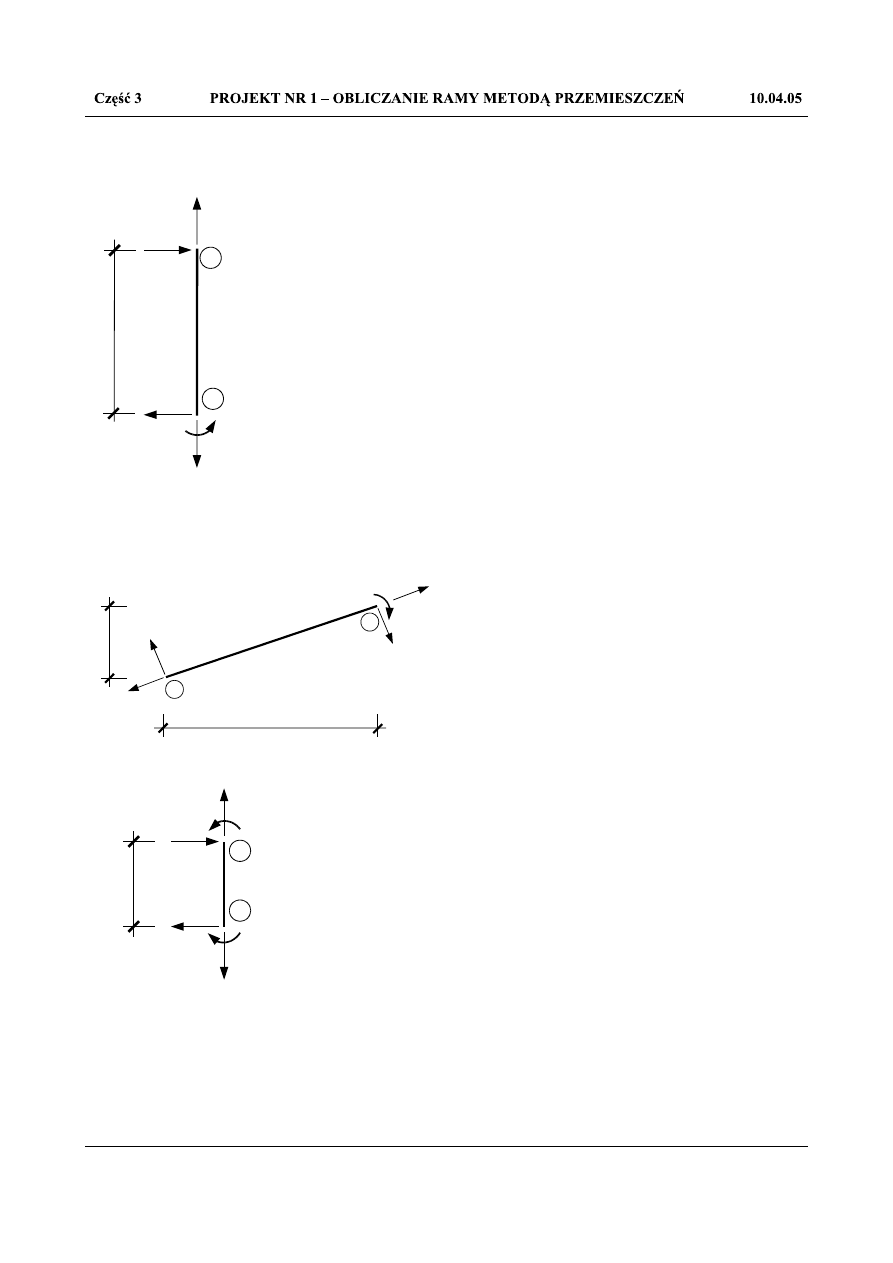
Mając określone wartości momentów zginających na każdym pręcie układu mogę obliczyć wartości sił
tnących w tych prętach :

T

01

=T

10

=5,603 [kN ]

Rys.1.63. Pręt 01

T

12

=T

21

=−2,995 [kN ]

Rys.1.64. Pręt 12

T

32

=T

23

=−5,601 [kN ]

Rys.1.65. Pręt 23

Tomasz Terlecki gr 3 KBI

9/13

I

1

0

1

N

10

N

01

T

01

T

10

22,411

4

2

6

I

2

1

2

N

21

N

12

T

12

T

21

18,943

N

23

N

32

T

32

T

23

30,144

2

I

1

2

3

18,942

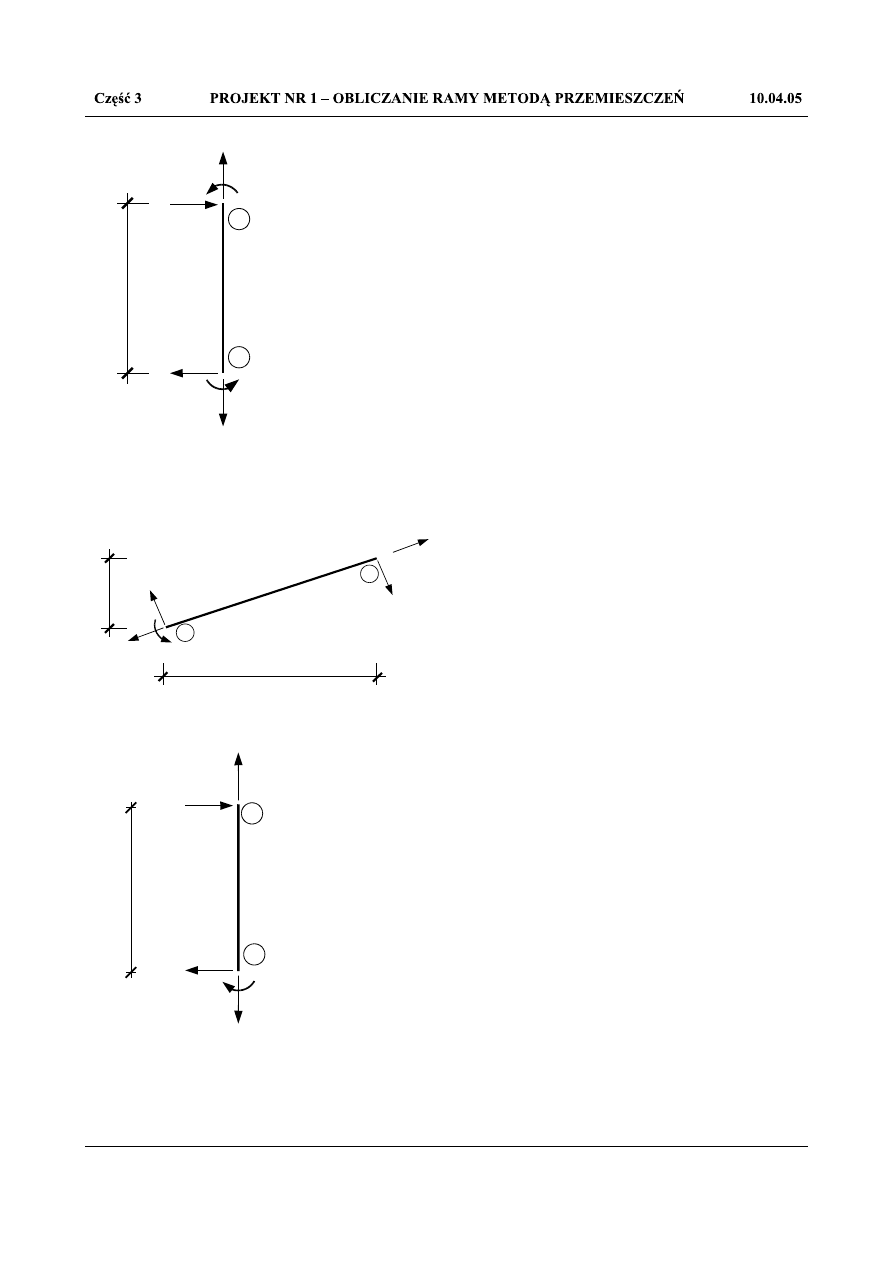
T

34

=T

43

=0,578 [kN ]

Rys.1.66. Pręt 34

T

35

=T

53

=4,634 [kN ]

Rys.1.67. Pręt 35

T

56

=T

65

=−3,849 [kN ]

Rys.1.68. Pręt 56

Tomasz Terlecki gr 3 KBI

10/13

4

I

1

3

4

N

34

N

43

T

43

T

34

1,477

0,836

2

6

I

2

3

5

N

53

N

35

T

35

T

53

29,307

I

1

6

5

N

56

N

65

T

65

T

56

23,096

6

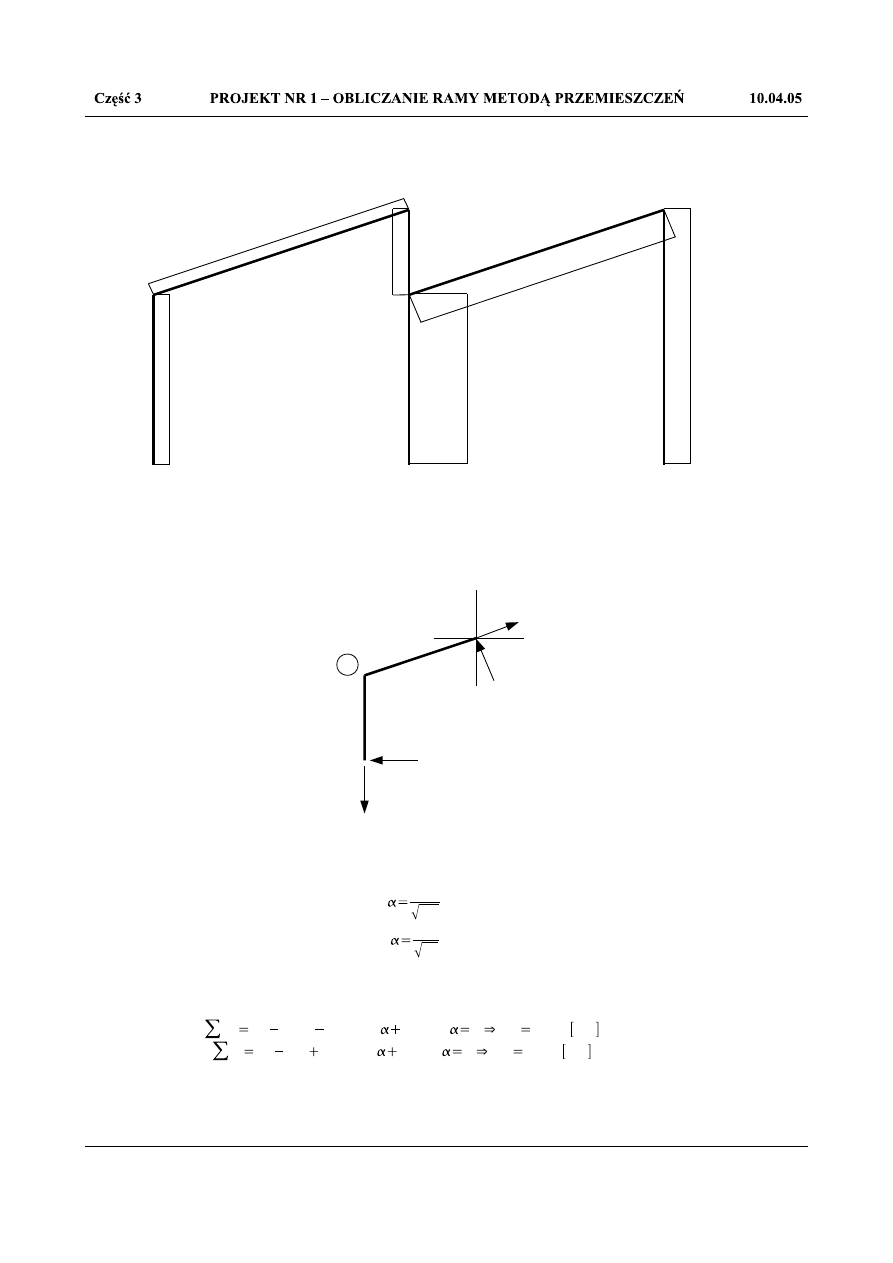
Zestawiając otrzymane wyniki otrzymuję:

2,995

5,603

5,601

0,578

3,849

-

-

+

-

4,634

+

+

Rys.1.69. Siły tnące w układzie statycznie niewyznaczalnym poddanym działaniu temperatury T

(n)

[kN]

Wyznaczając wartości sił normalnych występujących w zadanej ramie korzystam z równowagi węzłów.

2,995

1

α

5,603

N

10

=N

01

α

N

12

=N

21

Rys.1.70. Równowaga węzła 1

Mając dane:

sin

1

10

cos

3

10

(1.57)

Z równowagi węzła 1:

X

0 : 5,603 2,995 sin

N

12

cos

0

N

12

6,904 kN

Y

0 : N

01

2,995 cos

N

12

sin

0

N

01

5,025 kN

(1.58)

Tomasz Terlecki gr 3 KBI

11/13

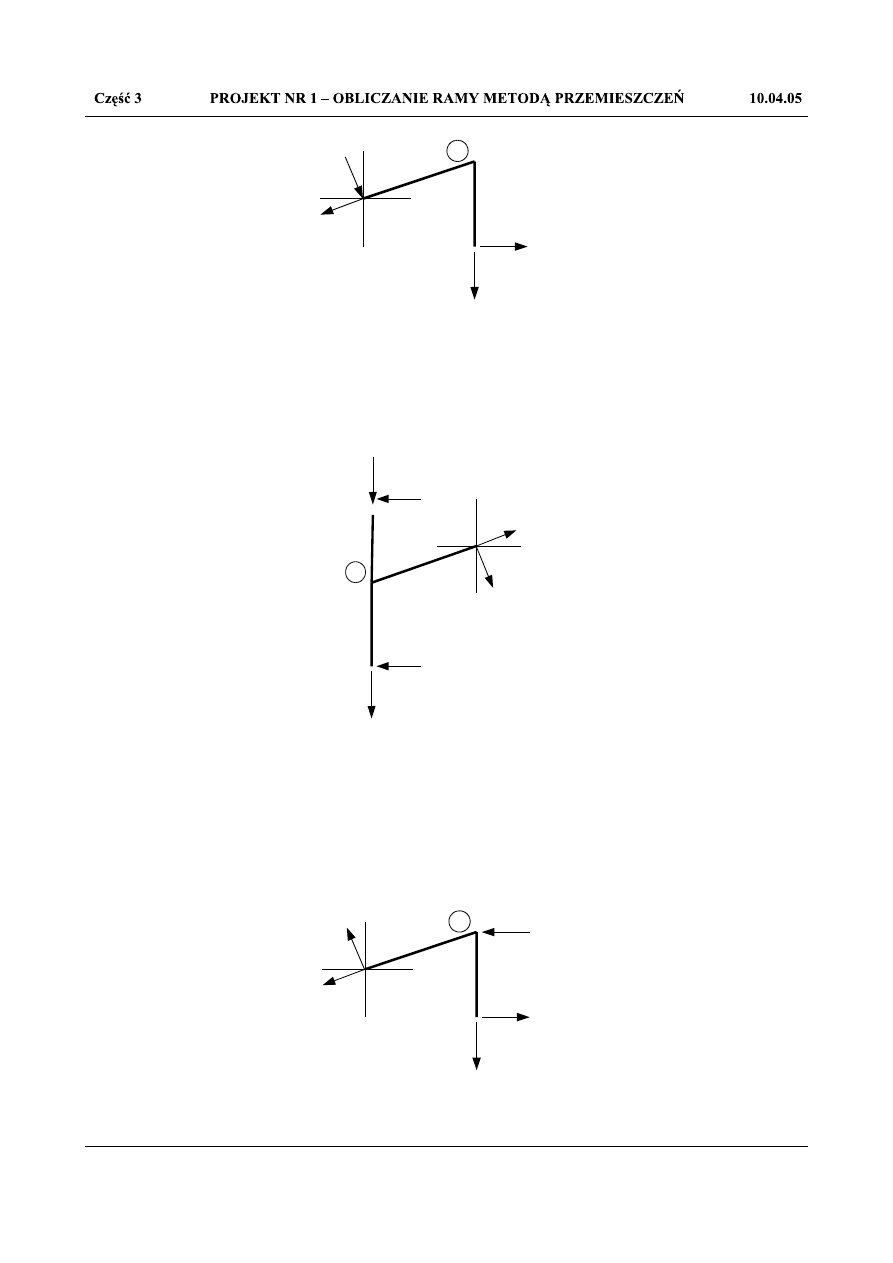
6,904

2,995

2

α

5,601

N

23

α

Rys.1.71.Równowaga węzła 2

Z równowagi węzła 2:

∑

Y =0 :−N

23

−6,904 sin −2,995 cos =0 ⇒ N

23

=−5,025 [kN ]

(1.59)

N

35

4,634

3

α

0,578

N

34

α

5,601

5,025

Rys.1.72.Równowaga węzła 3

Z równowagi węzła 3:

∑

X =0 :−5,601−0,578N

35

cos 4,634 sin =0 ⇒ N

35

=4,969 [kN ]

∑

Y =0 :−5,025− N

34

N

35

sin −4,634 cos =0 ⇒ N

34

=−7,850 [kN ]

(1.60)

Z równowagi węzła 5 określam wartość poziomej reakcji H

5

w podporze występującej w tym węźle.

4,969

4,634

5

α

3,849

N

56

α

H

5

Rys.1.73.Równowaga węzła 5

Tomasz Terlecki gr 3 KBI

12/13

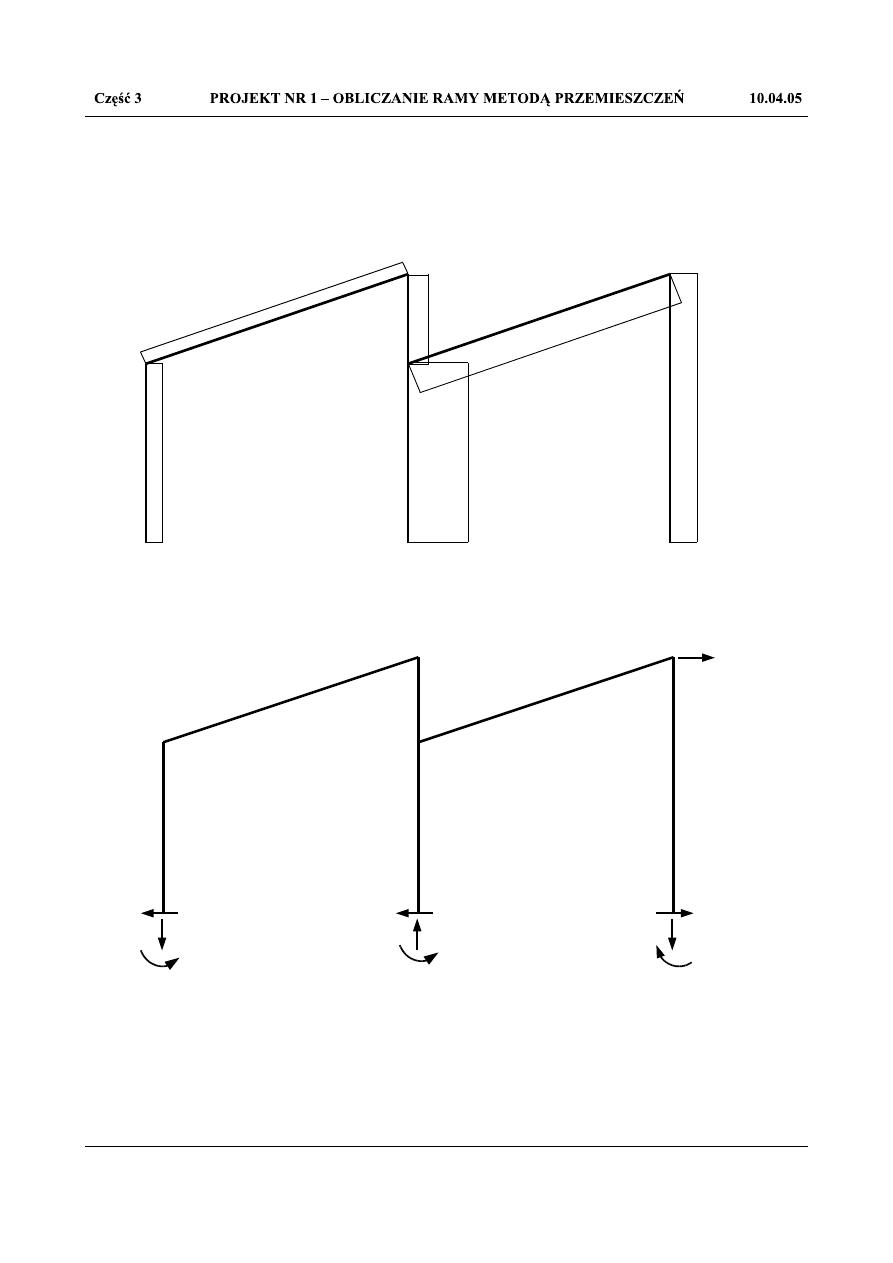
Z równowagi węzła 5:

∑

X =0 : H

5

=−2,330 [kN ]

∑

Y =0 : 4,634 cos −4,969 sin −N

56

=0 ⇒ N

56

=2,825 [kN ]

(1.61)

Zestawiając otrzymane wyniki otrzymuję:

6,904

5,025

5,025

7,850

2,825

+

-

-

+

4,969

+

+

Rys.1.74. Siły normalne w układzie statycznie niewyznaczalnym poddanym działaniu temperatury N

(n)

[kN]

Aby sprawdzić poprawność uzyskanych wyników dokonuję kontroli statycznej:

5,603

0,578

3,849

5,025

7,850

2,825

2,330

22,411

1,477

23,096

Rys.1.75. Kontrola statyczna-siły działające na zadany układ

∑

X =0 :−5,603−0,5783,8492,330=−0,002 ≈0 [ kN ]

∑

Y =0 :−5,0257,850−2,825=0 [ kN ]

∑

M

o

=0 :−22,411−1,47723,096−7,85⋅62,825 ⋅122,330 ⋅6=−0,012 ≈0 [kNm]

(1.62)

Tomasz Terlecki gr 3 KBI

13/13