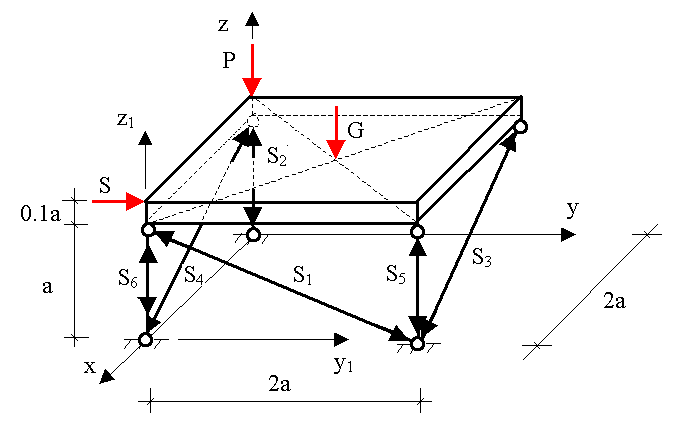
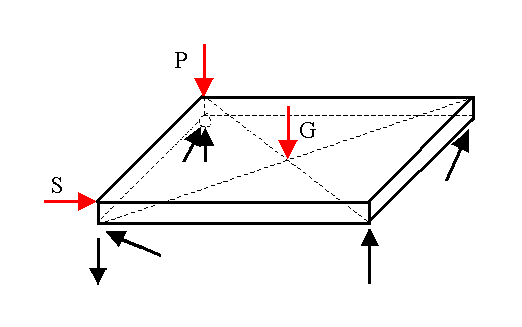
Przykład 5.6. Układ tarczowo-prętowy

Jednorodna płyta prostopadłościenna o ciężarze G spoczywa na układzie 6 prętów połączonych przegubowo. Obliczyć siły w prętach.

Przyjęto: S = G = P

Zakładamy, że w prętach występują siły ściskające, tzn. pręty oddziaływują na płytę siłami

"do płyty". Równowaga pręta jest spełniona tożsamościowo. Rozkładamy siły S1, S3 i S4 na składowe odpowiadające osiom x, y i z.

2 a

2

a

1

S = ,

0

S = − S

= − S

,

S = S

= S

1 x

1 y

1

5

1

a

5

1 z

1

5

1

a

5

2 a

2

a

1

S = − S

= − S

,

S = ,

0

S = S

= S

3 x

3

5

3

a

5

3 y

3 z

3

5

3

a

5

2 a

2

a

1

S = − S

= − S

,

S

= ,

0

S = S

= S

4 x

4

5

4

a

5

4 y

4 z

4

5

4

a

5

Badamy równowagę płyty. Nie znamy sześciu sił w prętach podpierających. Dla przedstawionej na schemacie płyty można zapisać sześć warunków równowagi. Zatem układ jest statycznie wyznaczalny. Równania równowagi są postaci

∑ P = ,0

P

P

ix

∑ = ,0

iy

∑ = 0

iz

∑ M = ,0

M

M

ix

∑

= ,

0

iy

∑

= 0

iz

Kolejność równań jest dowolna. Zatem zapiszemy je tak, aby były one z jedną niewiadomą (jeśli jest to możliwe). Pamiętamy przy tym, że moment siły względem osi jest równy zeru, jeśli wektor siły jest równoległy do osi, linia działania siły przecina się z osią.

∑

2

5

P = 0 S − S

= 0 → S = S

iy

1

5

1

2

∑

3

M

= 0 S ⋅ 2 a − P ⋅ 2 a − Ga = 0 → S = S

iy 1

2

2

2

∑

2

M

= 0 S

⋅ 2 a = 0 → S = 0

iz 1

3

5

3

∑

2

2

P = 0 − S

− S

= 0 → S = 0

ix

4

5

3

5

4

∑

2

2

M = 0 − S ⋅ 1

.

1 ⋅ a − Ga + S

a + S ⋅ 2 a + S

a = 0 → S = 55

.

0

S

ix

1

5

5

3

5

5

∑

1

1

1

P = 0 S + S + S + S

+ S

+ S

− S − G = 0 → S = − 55

.

0

S

iz

2

5

6

1

5

3

5

4

5

6

Znak minus oznacza, że zwrot wektora siły S jest przeciwny do założonego.

6

W celu sprawdzenia poprawności obliczeń korzystamy z warunku równowagi, z którego nie korzystaliśmy poprzednio

∑

2

2

M = 0 − S ⋅ 2 a + S

⋅ 2 a − S ⋅ 2 a + S

⋅ 2 a = 0 → 2 Pa + 0 − 2 Pa = 0

iz

3

5

1

3

5

2

Odp.

3

S = S

2

2

S = 0

4

S = 0

3

5

S = S

S = 55

.

0

S

5

S = 55

.

0

S

1

6

2

3