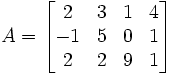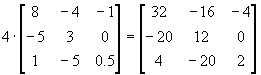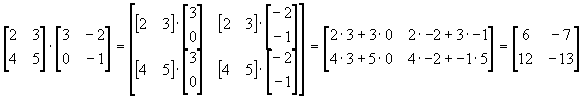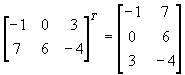Macierze ćw.1
Macierz to uporządkowana prostokątna dwuwymiarowa tablica wielkości z pewnego zbioru wartości (najczęściej utworzona z liczb rzeczywistych lub zespolonych).
Przykładowa macierz
ma trzy wiersze i cztery kolumny.
Wybrane elementy: a = − 1, a = 1 oraz a = 9.
21
13
33
Łatwo zauważyć, że położenie każdego elementu określa się poprzez podanie numeru wiersza i kolumny, na przecięciu których się znajduje (zawsze w tej kolejności: najpierw wiersz, a potem kolumna). Zatem element stojący w pierwszym wierszu i drugiej kolumnie oznaczamy a (w powyższej macierzy jest on równy 3).
12
a – oznacza element leżący w i-tym wierszu i j-tej kolumnie i,j
Macierze zapisujemy na ogół tłustym drukiem - A, B – opisujemy A=[a ]
– oznacza macierz o liczbie wierszy n i liczbie kolumn m, ij nxm
tworzą ją elementy aij
Macierz, której wszystkie elementy są równe zero, nazywamy macierzą zerową lub po prostu zerem, zapisujemy A=0
Dla macierzy kwadratowej możemy wyróżnić przekątną główną, tworzą ją elementy na przekątnej od lewego górnego rogu, do prawego dolnego. Matematycznie jest to ciąg elementów (a , a , ..., a ).
11
22
nn
Macierz kwadratową, której wszystkie elementy oprócz przekątnej głównej są równe zero, nazywamy macierzą diagonalną i zapisujemy diag(a ,a ,...,a ).
11
22
nn
Macierze ćw.1
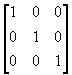
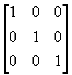
Macierz diagonalną, której wszystkie elementy na przekątnej równe są 1
nazywamy macierzą jednostkową lub po prostu jedynką i oznaczamy I.
np. I=
dla stopnia trzeciego
Macierze ćw.1
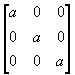
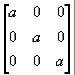
Macierz, która oprócz przekątnej ma same 0, a na przekątnej te same wartości nazywamy macierzą skalarną.
np. A=diag(a,a,a) =
1. Porównywanie macierzy
Dla macierzy A=[a ]
oraz B=[b ]
możemy stwierdzić równość jeżeli
ij nxm
ij nxm
odpowiadające sobie elementy są równe.
Matematycznie zapisujemy:
A=B a =b dla (i=1,2,...,n;j=1,2,...,m)
ij
ij
2. Dodawanie macierzy
Dodawanie (i analogicznie odejmowanie) macierzy jest możliwe tylko dla dwóch macierzy o takich samych wymiarach. Wynikiem dodawania macierzy jest macierz o takich samych wymiarach jak składniki. Elementy macierzy wynikowej są sumą odpowiednich elementów składników.
Matematycznie zapisujemy:
A=[a ]
, B=[b ]
ij nxm
ij nxm
Sumą macierzy A+B nazywamy taką macierz C = [c ]
, że:
ij nxm
c =a +b dla (i=1,2,...,n;j=1,2,...,m)
ij
ij
ij
czyli po prostu:
C=A+B= [a +b ]
ij
ij nxm
analogicznie definiujemy odejmowanie:
D=A-B= [a -b ]
ij
ij nxm
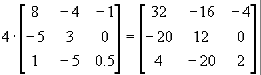
Macierze ćw.1
3. Mnożenie przez skalar
Każdą macierz możemy pomnożyć przez dowolną liczbę rzeczywistą.
Mnożenie przez liczbę rzeczywistą polega na pomnożeniu każdego elementu przez tą liczbę. Mnożenie przez skalar jest przemienne.
Matematycznie:
A=[a ]
– iloczynem axA nazywamy taką macierz C=[c ]
, że:
ij nxm
ij nxm
c =axa
ij
ij
np.
4. Mnożenie macierzy
Mnożenie macierzy jest możliwe dla macierzy o odpowiednich wymiarach.
Jeżeli chcemy przeprowadzić mnożenie AxB to liczba kolumn macierzy A musi być równa liczbie wierszy macierzy B.
Mnożenie macierzy nie jest przemienne tzn. chcąc wykonać mnożenie BxA liczba kolumn macierzy B musi być równa liczbie wierszy macierzy A.
Wynikiem mnożenia macierzy A
xB
jest macierz C o wymiarze nxk
nxm
mxk
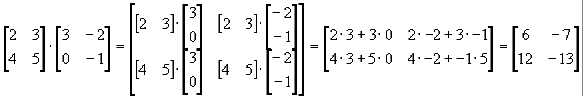
Macierze ćw.1
Jaką postać będzie miała macierz C?
Otóż każdy element macierzy C – c jest równy iloczynowi skalarnemu i-ij
tego wiersza macierzy stojącej po lewej stronie znaku mnożnie, przez j-tą kolumnę macierzy stojącej po prawej stronie znaku mnożenia.
np.
Kilka przydatnych właściwości:
Jeżeli A,B oraz C są macierzami o odpowiednich wymiarach to: 1.
A(BC)=(AB)C
2.
a(AB)=(aA)B
3.
(A+B)C=AC+BC
4.
C(A+B)=CA+CB
5.
IA=A, gdy A
i I
nxn
nxn
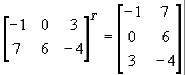
Macierze ćw.1
5. Transpozycja macierzy
Operacja transpozycji to zamiana macierzy tak, aby jej wiersze stały się kolumnami. Transpozycję oznaczamy indeksem górne T.
AT – transpozycja macierzy A
np.
Dla macierzy A=[a ]
macierz B=[b ]
taką, że:
ij nxm
ij mxn
b =a dla i=1,2,...,m; j=1,2,...,n nazywamy transpozycją macierzy A.
ij
ji
Z definicji transpozycji wynika kilka ciekawych właściwości: Jeżeli A=[a ]
oraz B=[b ]
i a jest liczbą, to:
ij nxp
ij pxm
1.
(AT)T=(A)
2.
(AB)T=BTAT
3.
(aA)T=a(A)T
4.
(A+B)T=AT+BT, jeżeli wymiary macierzy A i B są takie same.
Wyszukiwarka
Podobne podstrony:
Ustawa z dnia 25 06 1999 r o świadcz pien z ubezp społ w razie choroby i macierz
macierz BCG
macierze 2
04 Analiza kinematyczna manipulatorów robotów metodą macierz
macierze i wyznaczniki lista nr Nieznany
macierze 1
Macierz przykrycia testów akceptacyjnych Jasiek
MACIERZE
macierze moje i rzad id 275988 Nieznany
ćw 15 Rachunek macierzowy
Lab Wypełnianie macierzy dendro meteo
Potencjał węglowodorowy skał macierzystych i geneza gazu zie, geologia, AGH, SzM, GEOLOGIA
Macierze i wyznaczniki, Politechnika Poznańska, Elektrotechnika, Matematyka, semestr 2
Laboratorium 2 Macierze
Opis macierzy
Zadania macierze
Gotowe Uporzadkowane Macierze
Komórka macierzysta, głodzenie i cukrzyca
więcej podobnych podstron