Rozwiązania zadań B.1 - Funkcje produkcji 1 Małgorzata Nowak Zadanie 1

Krańcowa produktywność sklepu wzrośnie gdy zwiększy się ilość pracowników, ponieważ:

- lepszy podział pracy;

- łatwiej obsłużyć klientów;

- podział na działy – specjalizacje; ale gdy będzie za dużo pracowników produktywność może spaść, ponieważ zaczną sobie przeszkadzać

Zadanie 2

L

całkowity produkt średnia produktywność krańcowy produkt q

il. pracowników il. krzeseł

AP=q/L

MP=dq/dL

1

10

10

10

2

18

9

8

3

24

8

6

4

28

7

4

5

30

6

2

6

28

4 2/3

-2

7

25

3 4/7

-3

MP- w jaki sposób zmieni się całkowity krańcowy produkt jeśli zwiększymy dany czynnik produkcji o najmniejszą jednostkę

b) TAK- MP maleje

c) za dużo pracowników – będą sobie przeszkadzać Zadanie 3

il. zmiennego

produkcja krańcowa

średnia produktywność

czynnika produkcji całkowita produktywność czynnika L

q

MP

AP

0

0

-

-

1

225

225

225

2

600

375

300

3

900

300

300

4

1140

240

285

5

1365

225

273

6

1350

-15

225

Zadanie 1

Funkcja produkcji: F(K,L) = 2KL0,5

I(6)=?

preferencje Cobba-Douglasa

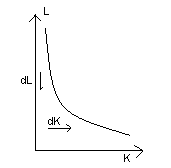
izokwanta (~krzywa obojętności)-> ta sama ilość produkcji Izokwanta jest to zbiór możliwych kombinacji nakładów czynników produkcji pozwalających efektywnie wyprodukować daną ilość dobra.

2KL0,5 =6

K= 3/L0,5

1

Rozwiązania zadań B.1 - Funkcje produkcji 1 Małgorzata Nowak Zadanie 2:

F(K,L) = 2KL0,5 jak zmienia się techniczna stopa substytucji TRS jeżeli zwiększamy pracę L?

MRTS= - MP1/MP2 -> nachylenie izokwanty

-> stopa wymiany wielkość produkcji = const

∆TP=MP1*∆x1 + MP2*∆x2 = 0 (bo izokwanta – krzywa jednakowego produktu) MP1*∆x1=-MP2*∆x2

MRTS= ∆x1/∆x2= -MP1/MP2

Gdy zwiększamy L, to TRS maleje

MP1=MPK=2L0,5

MP2=MPL=K*L-0,5

TRS= -2L0,5/KL-0,5 = -2L/K

Zadanie 4

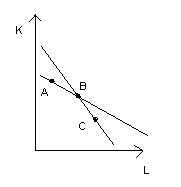
a) z definicji izokwanty nie mogą się przecinać -> ten sam poziom produkcji A->q1

B->q2 q=/= q2

C-> q1 sprzeczność B->q2

b) TAK – np. całkowita liczba pracowników (patrz zadanie 2, 3); c) TAK - izokwanty mogą być rosnące, np. gdy państwo płaci nam za zatrudnianie niepełnosprawnych, to nawet, gdy ich produktywność jest < 0, zo ich zatrudniamy; lub po prostu od pewnego momentu produktywność pracowników < 0 (patrz zad. 2), czyli w krótkim okresie (nie można zwiększyć nakładu kapitału w krótkim okresie) izokwanta jest rosnąca; d) TAK, czynniki produkcji, których nie używa się razem.

Zadanie 5

a)

MRTS zmienia się , malejąca (izokwanty ściśle wypukłe, np. funkcja produkcji Cobb-Douglasa);

2

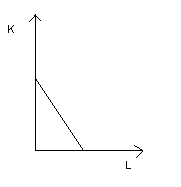
Rozwiązania zadań B.1 - Funkcje produkcji 1 Małgorzata Nowak b)

MRTS=const (czynniki produkcji substytucyjne).

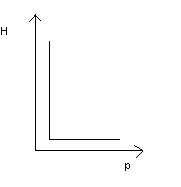
c)

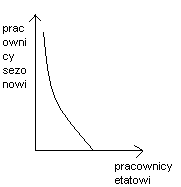
H-ilość maszyn, p- ilość pracowników pełnoetatowych y=min {2H,p} - czynniki produkcji komplementarne; funkcja produkcji Leontiefa.

Zadanie 6

W przypadku doskonałej substytucji MRTS jest stała, by określić jej wysokość musimy znać stosunek zamiany czynników produkcji.

Zadanie 7

MPL=50 czip/h

MRTSLK = ¼ = MPL/MPK

MPK=?

MPK= 4*50= 200 czip/h

Zadanie 8

f(x

0,2

0,3

0,4

0,7

1,x2,x3,x4) = x1

x2

x3

x4

tf(x1,x2,x3,x4) < (tx1)0,2 (tx2)0,3 (tx3)0,4(tx4)0,7

tf(x

0,2

0,3

0,4

0,7

1,x2,x3,x4) < t1,6x1

x2

x3

x4

Rosnące korzyści skali

MRTS

-0,8

0,3

0,4

0,7

0,2

-0,7

0,4

0,7

x1x2 = - (0,2 x1

x2 x3 x4 ) / (0,3 x1

x2

x3 x4 )

3