Testowanie hipotez – algorytm post powania:
1. zało enia
próba losowa, elementy próby niezale ne
2. hipotezy
• hipoteza zerowa – zakłada brak ró nic, np.
H0: p = p0
H0: = 0
H0: 1 = 2
• hipoteza alternatywna np.
HA: p p0
HA: 0
HA: 1 2
lub
HA1: p < p0
HA1: > 0
HA1: 1 > 2
HA2: p > p0
HA2: < 0
HA2: 1 < 2
3. statystyka testu – funkcja elementów próby pozwalaj ca ustali czy hipotez zerow
mo emy odrzuci czy nie.
4. reguła decyzyjna – przy jakich warto ciach statystyki testu odrzucimy H0, a przy
jakich nie.
•
p-warto – prawdopodobie stwo popełnienia bł du I rodzaju przy odrzuceniu H0.
• poziom istotno ci – ( ) na jaki bł d I rodzaju mo emy si zgodzi przy
podejmowaniu naszej decyzji.
• obszar krytyczny (obszar odrzucenia)– zakres wyników do wiadczenia dla
których odrzucimy H0.
5. badania i wyliczenie statystyki testu.
6. decyzja zgodnie z reguł decyzyjn .
Mo liwe bł dy przy podejmowaniu decyzji
Je li: H0: p = p0
HA1: p < p0
HA2: p > p0
Stan faktyczny
HA1
H0
HA2
HA1 decyzja słuszna
Bł d I rodzaju
Bł d III rodzaju
Podj ta
H0
Bł d II rodzaju
decyzja słuszna
Bł d II rodzaju
decyzja HA2 Bł d III rodzaju Bł d I rodzaju decyzja słuszna
Przykład
Chcemy sprawdzi stosunek płci w populacji pewnego gatunku. Czy wi cej jest samców czy
samic?
1. Pobieramy prób losow n=10 osobników. Rozkład liczby osobników jednej z płci
w ród 10 elementowej próby b dzie rozkładem Bernoulliego.
2. Zakładamy, e proporcja płci w populacji jest 1:1, wi c prawdopodobie stwo
wylosowania osobnika jednej z płci jest 0,5 – stan opisywany przez H0. Pozostałe stany s opisane przez hipotezy alternatywne.
H0: p=0,5
HA1: p>0,5
HA2: p<0,5
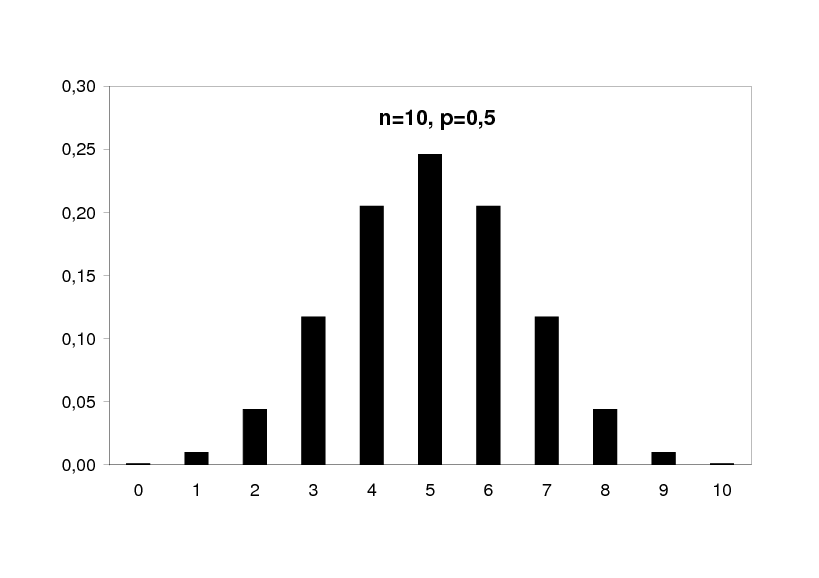
Jaki byłby rozkład prawdopodobie stwa przy zało eniu słuszno ci H0? Mo emy go
wyliczy ze wzoru na prawdopodobie stwo w rozkładzie Bernoulliego dla n = 10,
p = 0,5 i k = 0 do 10.
Liczba prawdopodobie stwo
sukcesów
0
0.001
1
0.010
2
0.044
3
0.117
4
0.205
5
0.246
6
0.205
7
0.117
8
0.044
9
0.010
10
0.001
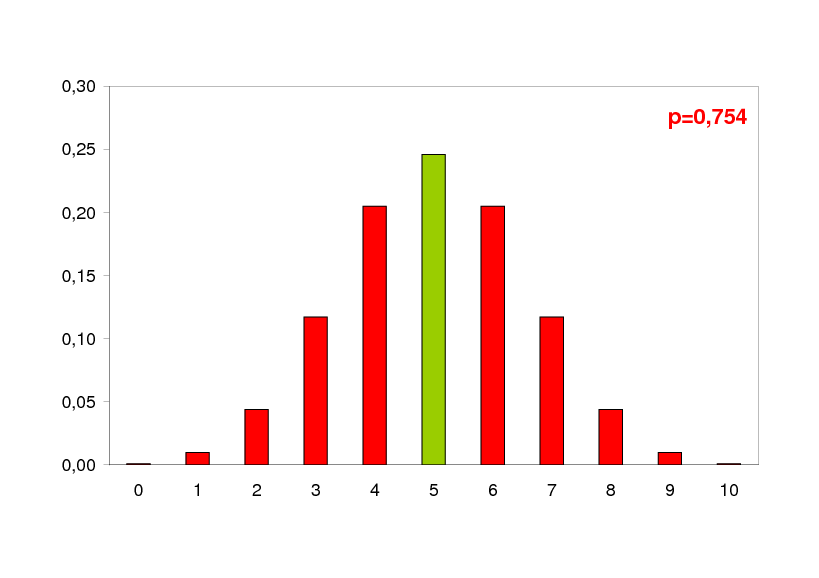
Czy odrzucimy H0 je li w naszej próbie znajd si 4 osobniki jednej płci i 6 drugiej?
Nie, bo prawdopodobie stwo uzyskania wyniku takiego lub bardziej skrajnego wynosi: p = 0,754, wi cej od = 0,05 czyli du o.
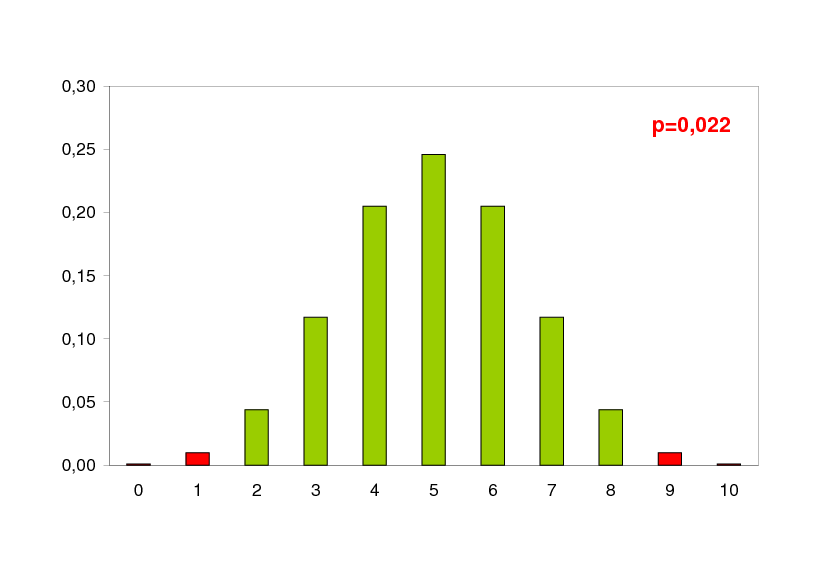
Czy odrzucimy H0 jak w naszej próbie znajdzie si 1 osobnik jednej płci i 9 drugiej?
Tak, bo prawdopodobie stwo uzyskania wyniku takiego lub bardziej skrajnego wynosi: p = 0,022 mniej ni = 0,05 czyli mało.
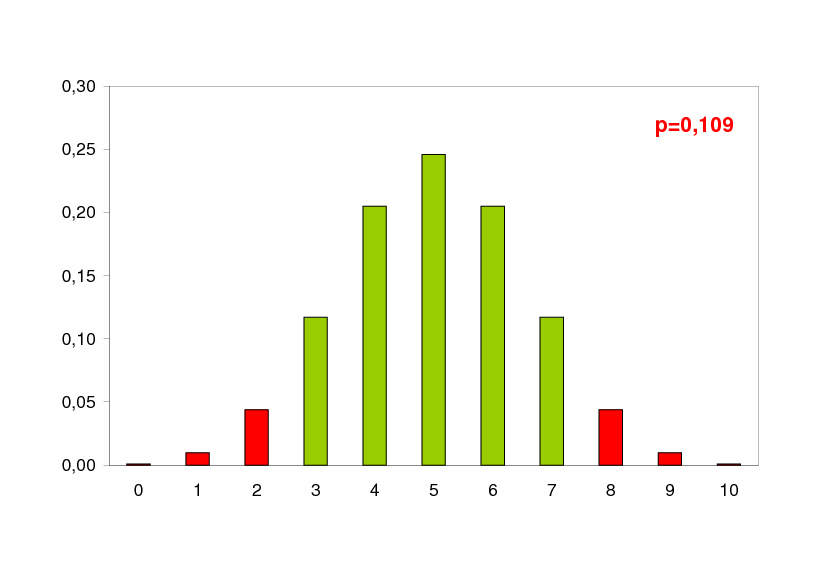
Czy odrzucimy H0 jak w naszej próbie znajdzie si 2 osobniki jednej płci i 8 drugiej?
Nie, bo prawdopodobie stwo uzyskania wyniku takiego lub bardziej skrajnego wynosi: p = 0,109 wi cej ni = 0,05 czyli za du o.
Reguła decyzyjna:
Odrzucimy H0 dla 0, 1, 9 i 10 sukcesów
Nie odrzucimy H0 dla 2, 3, 4, 5, 6, 7 i 8 sukcesów
Hipotezy:
H 0: p= p 0
H A1: p> p 0
H A2: p< p 0
Oszacowanie frakcji na podstawie próby: ˆ p = k / n .
ˆ p − p
Statystyka testu:
0
u =
0
p q
0
0
n
Warto krytyczna: u : P{ U ≥ u =α .
α
α }
Je li
≥ , to na poziomie istotno ci przyjmujemy hipotez H A1: p> p 0;
u
u
0
α
Je li u ≤ u
− , to na poziomie istotno ci przyjmujemy hipotez H A2: p< p 0;
0
α
Je li u ∈( u
− , u ) , to na poziomie istotno ci nie mo emy rozstrzygn mi dzy H A1 a H A2.
0
α
α
Test równo ci dwu frakcji
Hipotezy:
H 0 : p 1 = p 2
H A1 : p 1 > p 2
H A2 : p 1 < p 2
ˆ p − ˆ p
Statystyka testu:
1
2
u =
0
1
1
pq
+
n
n
1
2
ˆ p n + ˆ p n
gdzie p jest redni wa on frakcji sukcesów w obu próbach: 1 1
2
2
p =
n +
n
1
2
Warto krytyczna: u : P{ U ≥ u =α .
α
α }
Je li u ≥ u , to na poziomie istotno ci przyjmujemy hipotez H A1: p 1> p 2.
0
α
Je li u ≤ u
− , to na poziomie istotno ci przyjmujemy hipotez H A2: p 1< p 2.
0
α
Je li u ∈( u
− , u ) , to na poziomie istotno ci nie mo emy rozstrzygn mi dzy H A1 a H A2.
0
α
α