Majczak J Logika Skrypt [2012]

Logika dr Joanna Majczak

Literatura:

Nieznański E., Chodkowski T., Elementy logiki prawniczej. Definicje, podziały i typy argumentacji, Polskie
Wydawnictwo Prawnicze Iuris 2000

Zienkiewicz D., Widła T., Logika, Wydawnictwo C. H. Beck 2006
Lewandowski S., Logika dla prawników, Wydawnictwo prawnicze LexisNexis 2008

Stanosz B., Ćwiczenia z logiki, PWN 2007
Słowo logika pochodzi od gr. słowa logos , które oznacza myślenie, rozumowanie, język. Wg Heraklita to
powszechna prawidłowość świata. Logika jako teoria naukowa rozwinęła się dopiero na początku XX wieku. Duży
wkład w rozwój współczesnej logiki miał Polak Alfred Tarski (1901-1983).
A. Tarski mówił, że współczesna logika dokonała na równi ze współczesną fizyką przewrotu w myśleniu ludzi o
własnym umyśle.

Logika (gr. λόγος, logos - rozum) nauka normatywna, analizująca źródła poznania pod względem prawomocności
czynności poznawczych z nimi związanych. Zajmuje się badaniem ogólnych praw, według których przebiegają
wszelkie poprawne rozumowania, w szczególności wnioskowania. Logika, jako dyscyplina normatywna, nie tylko
opisuje jak faktycznie przebiegają rozumowania, ale także formułuje twierdzenia normatywne, mówiące o tym, jak
rozumowania powinny przebiegać.

Zenon z Elei (490-430 p.n.e.)- Zajmował się poszukiwaniem prawdy, wykorzystując do tego argumenty
słowne. Jego polem zainteresowania były spekulacje językowe. Uważany był za twórcę dialektyki, rozumianej
wówczas jako zdolność do posługiwania się słowem.

Sokrates (469-399 p.n.e.) Sokrates zajmował się problemem definiowania, stając się prekursorem tego nurtu w
rozwoju logiki. Tworzenie definicji odbywało się w drodze kolejnych przybliżeń. Sokrates stał się prekursorem
zasad wnioskowania eliminacyjnego. Tworzył pojęcia przez definicje. Uważany jest również za prekursora
indukcji, choć nie odróżniał twierdzeń indukcyjnych od definicji.

Platon (427-347 p.n.e.)Platona uważa się za twórcę pojęcia rozumowania dedukcyjnego jako podstawy
rozumowania w matematyce. Zajmował się również problemami stosunków nadrzędności i przeciwieństwa oraz
stworzył podstawy podziału logicznego.

Arystoteles z Stagiry(384-322 p.n.e.) Twórca teorii indukcji i pojęcia sylogizmu. Jego teorie powstały w wyniku
zainteresowania rozumowaniem indukcyjnym, a zwłaszcza tworzenia pewnych form indukcji eliminacyjnej.
Stworzył podstawy teorii definicji (wcześniej definiowaniem zajmowali się Sokrates i Platon). Wkład Arystotelesa
w rozwój logiki to również sformułowanie podstawowych zasad myślenia, m.in. zasady sprzeczności oraz zasady
wyłączonego środka.

Boecjusz (480-524) rzymski filozof, tłumacz Arystotelesa, teolog chrześcijański i polityk

Piotr Hiszpan (1226-1277) papież Jan XXI, upowszechniał dorobek Arystotelesa

Duns Szkot (ok. 1266-1308), filozof i teolog szkocki. Sformułował prawo zwane „prawem Dunsa Szkota”,
przedstawiające własności implikacji.

Kartezjusz (1596-1650) francuski filozof, matematyk i fizyk, jeden z najwybitniejszych uczonych
XVII wieku, uważany za prekursora nowożytnej kultury umysłowej.

Gottfried Wilhelm Leibniz, znany także pod nazwiskiem Leibnitz (1646-1716) niemiecki polihistor:
filozof, matematyk, prawnik, inżynier–mechanik, fizyk, historyk i dyplomata. Zwany ostatnim z tych,
którzy wiedzieli wszystko.

Leonhard Euler (1707 -1783) szwajcarski matematyk i fizyk, stworzył wykresy obrazujące stosunki
zakresowe podmiotu i orzecznika w zdaniach kategorycznych, tzw. koła Eulera

Twórcy algebry logiki

1 August de Morgan (1806-1871) angielski matematyk i logik. Nazwisko utożsamiane jest z prawami
logicznymi: negacji koniunkcji i negacji alternatywy. Olbrzymi wkład wniósł w rozwój teorii relacji.

2 George Boole (1815-1864) angielski matematyk, filozof i logik. Zajmowął się logiką nazw. W algebrze
Boole’a trzy działania logiczne: generalizacja, specjalizacja i negacja nazywane są dodawaniem,
mnożeniem i odejmowaniem logicznym.

3 William Stanley Jevons (1835-1882) – angielski logik i ekonomista. Według niego logika to nauka o
myśleniu, a jej podstawowymi działami są: dział o terminach, dział o zdaniach, dział o sylogizmach i dział
o metodzie

4 Bertrand Arthur William Russell, (1872-1970) brytyjski filozof, logik, matematyk, działacz społeczny
i eseista. Laureat Nagrody Nobla w dziedzinie literatury za rok 1950. Zainicjował w 1954 roku kampanię
pokojową Pugwash. Zajmował się teorią zdań i relacji oraz logiką orzeczników.

5 Gottlob Frege (1848-1925) niemiecki matematyk, logik i filozof, profesor matematyki w Jenie.
Definiował logikę jako teorię zbiorów i relacji. Proponował „wyprowadzenie matematyki z logiki”.
Uważany jest za twórcę teorii kwantyfikatorów.

polscy logicy
1) prof. Jan Łukasiewicz (1878-1956) polski logik, matematyk, filozof. Minister wyznań religijnych i
oświecenia publicznego w rządzie Ignacego Paderewskiego (1919

2) Alfred Tarski (1901-1983) polski logik pracujący od 1939 r. w Stanach Zjednoczonych. Twórca m.in.
teorii modeli i semantycznej definicji prawdy, uważany jest współcześnie za jednego z najwybitniejszych
logików wszech czasów

3) Stanisław Leśniewski (1886-1939) polski filozof i logik, był profesorem Uniwersytetu Warszawskiego.

4) Kazimierz Ajdukiewicz (1890-1963) polski filozof i logik, reprezentant szkoły lwowsko-warszawskiej,
profesor Uniwersytetu Stefana Batorego, Uniwersytetu im. Adama Mickiewicza i Uniwersytetu
Warszawskiego, członek Polskiej Akademii Nauk i Polskiej Akademii Umiejętności.

5)Tadeusz Marian Kotarbiński (1886-1981) – polski filozof, logik i etyk, twórca etyki niezależnej,
przedstawiciel szkoły lwowsko-warszawskiej, nauczyciel i pedagog

Logika prawnicza (gr. λόγος, logos - rozum) - przedmiot wykładany na wyższych uczelniach. Stosunkowo młoda
nauka zajmująca się stosowaniem logik formalnych i nieformalnych (teorii argumentacji). Wprowadzona w celu
usprawnienia formułowania swoich myśli w słowa, jak i interpretacji zawiłych przepisów prawnych.

Logika formalna - są to rachunki zdań z wykorzystaniem kwantyfikatorów nazw i zdań. Łudząco przypominająca
logikę matematyczną. W jej skład wchodzi logika deontyczna zajmująca się zdaniami, w których występują
wyrażenia normatywne (zakaz, nakaz, dozwolenie, fakultatywność i indyferentność).

Logika nieformalna - zajmuje się procesem przytaczania argumentacji (głównie pro i contra ). Występuje w
procesach sądowych w postaci przytaczania dowodów i ich odpierania. Zainteresowanie prawników przyciąga
również związana z nią retoryka. Bardzo mocno związana z sylogizmem prawniczym (subsumcja, czyli
"podciągnięcie" stanu faktycznego do określonej normy prawnej).

LOGIKA
Formalna
- charakter sformalizowany
- postać rachunków
- operacje na symbolach
- czy jest działem matematyki, czy może matematyka jest jej działem?
- ograniczone działanie, jeśli chodzi
o nauki społeczne
-służy do uzasadniania czegoś

Teoria argumentacji (logika materialna)
- spełnia potrzeby humanistyki
- zasadniczo zajmuje się tymi samymi problemami, co logika formalna
- używa normalnych reguł i zdań
- ma przekonać kogoś do czegoś
- retoryka - jak argumentować i uzasadniać twierdzenia, aby przekonać osobę do naszych twierdzeń

Teoria negocjacji – jak negocjować, aby skłonić drugą stronę do akceptacji naszego stanowiska.

Działy logiki
Logika formalna
Semiotyka (Syntaktyka Semantyka Pragmatyka)
Ogólna metodologia nauk

Logika formalna zajmuje się teorią wynikania.

Semiotyka jest definiowana jako nauka o znakach. Semantyka koncentruje się na znaczeniu znaków języka,
syntaktyka dotyczy zasad ich łączenia po to, by utworzyć wyrażenia złożone. Pragmatyka zaś analizuje związki
między wyrażeniami języka a podmiotem, który się nim posługuje.

Ogólna metodologia nauk obejmuje m.in. uzasadnianie twierdzeń

Działy logiki formalnej nazywane są rachunkami , np.:
a) rachunek zdań,
b) rachunek nazw,
c) rachunek predykatów,
d) rachunek relacji.

Rachunki:
a) klasyczne:
· oparte na zasadzie dwuwartościowości - prawda lub fałsz,
b) nieklasyczne:
· oparte na zasadzie wielowartościowości - więcej niż tylko prawda i fałsz.

Jan Łukasiewicz (1878-1956) stworzył logikę trójwartościową. Uważał bowiem, że ograniczanie się do
logiki dwuwartościowej, opartej na prawdzie i fałszu, nie jest właściwe w sytuacji, gdy posługujemy się
wyrażeniem zawierającym zwrot „jest możliwe”.
Tak więc w zdaniu: „Od dziś za rok będę w Warszawie” nie możemy określić jego fałszu albo prawdy.
Łukasiewicz proponuje nieograniczanie się do dwóch podstawowych wartości, określanych symbolem „0”
w przypadku fałszu i „1” w przypadku prawdy, wprowadzając „1/2” jako trzecią wartość logiczną.
W wyniku rozważań nad koncepcją Łukasiewicza powstała logika wielowartościowa
Logika deontyczna (lata 50. XX wieku); twórcy: von Wright, J. Kalinowski;
szczególny typ logiki zajmujący się wypowiedziami normo-podobnymi (zdaniami deontycznymi) - mają
one tzw. operator deontyczny:

· jest nakazane, · jest zakazane, · jest dozwolone.

Logika modalna - teoria logiczna, która bada pojęcia możliwości, konieczności i ich wariantów.
Występują wyrażenia: musi, może.
Logiki niemonotoniczna (lata 70. XX wieku)
np. X wyrządził szkodę → X jest zobowiązany do jej naprawienia
Nie zawsze, gdyż mogą zajść pewne okoliczności, w których nie trzeba będzie naprawić szkody.

Logiki monotoniczne
p→q
Zawsze, jeżeli zachodzi p, musi zajść q.

Teorie argumentacji nie mają charakteru symbolicznego, sformalizowanego, przyjmują postać pewnych
wskazówek, poleceń, zaleceń.
a) Retoryka - pierwszy historycznie przykład teorii argumentacji. Zajmują się skutecznym
przekonywaniem - perswazją.
b) Teoria negocjacji - jak wynegocjować korzystne warunki.
c) Teoria dyskursu - sposoby dochodzenia do konsensusu.
d) Metodologia - nauka o metodach stosowanych w różnych dziedzinach nauki, zawiera elementy logiki
formalnej i teorii argumentacji:

· Metodologia opisowa (deskryptywna) - opisuje metody, które stosuje się

w różnych dziedzinach,

· Metodologia normatywna – ustala standardy, jakie powinno się stosować.

Logika zdań (rachunek zdań)

Wyrażenia składają się z:
a) zmienne zdaniowe - małe litery p,q,r,s… lub …
b) stałe logiczne - funktory zdaniotwórcze o argumentach zdaniowych (funktory prawdziwościowe).
Wartość zdania zbudowanego przy pomocy funktora prawdziwościowego zależy wyłącznie od wartości
logicznej zdań, które ten funktor łączy, a nie od ich treści.

Zdania:
· w gramatyce - każda wyrażenie od kropki do kropki.
· zdania w sensie logicznym - wypowiedzi naszego języka, którym można przypisać wartość logiczną
(prawdy - 1 lub fałszu - 0). O każdym zdaniu w sensie logicznym można powiedzieć, że jest
prawdziwe lub fałszywe. Są to tylko zdania oznajmujące.
„Padało”, „Wyszedł” - wypowiedzi niezupełne (eliptyczne), aby stały się prawdziwe lub fałszywe muszą
zostać uzupełnione:
„Padało dziś w Toruniu o godzinie 16.”

Zdania w sensie logicznym:
a) analityczne - zdanie, którego prawdziwość lub fałsz wynika z sensu użytych w tym zdaniu pojęć (czyli z
przyjętej konwencji terminologicznej):
„Godzina ma 60 minut.” (zdanie prawdziwe)
„Kwadrans jest figurą trójboczną.” (zdanie fałszywe)
b) syntetyczne - prawdziwość tego zdania zależy od jego zgodności lub niezgodności z faktami, należy ustalić
zgodność z rzeczywistością:
„Bitwa pod Grunwaldem miała miejsce w 1410 roku.” (zdanie prawdziwe)
„W Puszczy Białowieskiej żyją lamparty.” (zdanie fałszywe)
Do skonstruowania sensownego zdania, poza użyciem nazw niezbędne jest użycie dodatkowych innych wyrażeń,
które nie są ani nazwami, ani zdaniami, lecz służą do wiązania nazw czy zdań w wyrażenia złożone i mogą
występować jako części zdań lub jako części nazw. Takie wyrażenia nazywamy funktorami .
Funktory występują jako cześć zdania lub cześć nazwy złożonej z kilku wyrazów.

Funktor - wyrażenia, przy pomocy których tworzymy zdania, oceny, normy, performatywy; np. „jest”, „nad”.

Przyjmując za kryterium rodzaj wyrażenia otrzymanego w wyniku zastosowania (czyli dodania funktora do jego
argumentu lub argumentów) funktory dzielimy na:
- nazwotwórcze (w wyniku użycia powstaje nazwa złożona),
- zdaniotwórcze (w wyniku użycia powstaje zdanie),
- funktorotwórcze (w wyniku użycia powstaje funktor o zmodyfikowanej treści).

Wyraz czy wyrażenie wiązane w złożoną całość przez funktor nazywamy argumentem funktora.
z – zdanie; n – nazwa; (kreska ułamkowa) – funktor
oznaczenie tego, co tworzy funktor
argument funktora

a) Funktory nazwotwórcze służą do budowy nazw złożonych z dwu lub więcej wyrazów.

· mądry student n / n (funktor nazwotwórczy o jednym argumencie nazwotwórczym)

· Nakło nad Notecią; dziura w jezdni n / n n (funktor nazwotwórczy o dwóch argumentach
nazwotwórczych)

· dom między lasem a rzeką n / n n n (funktor nazwotwórczy o trzech argumentach nazwotwórczych)

b) Funktor zdaniotwórczy łącznie ze swoimi argumentami tworzy zdanie.
· Piotr idzie. z / n (funktor zdaniotwórczy od jednego argumentu nazwowego)

· Koń jest ssakiem. z / n n (funktor zdaniotwórczy od dwóch argumentów nazwowych)

· Jan wymienił dolary na złotówki. z / n n n (funktor zdaniotwórczy od trzech argumentów nazwowych)

· Warszawa jest stolicą Polski i Warszawa leży nad Wisłą. z / z z (funktor zdaniotwórczy od dwóch
argumentów zdaniowych)

c) Funktory funktorotwórcze wraz ze swoimi argumentami tworzą inne funktory. Funktorami funktorotwórczymi
są najczęściej przysłówki, które są nazwami sposobu, czasu, miejsca, stopnia, np. głośno, gdzieniegdzie, dziko,
dobrze. Argumentem funktora funktorotwórczego jest zawsze funktor.

· Jan jest uczciwym człowiekiem.n z/nn n/n n
· Nieprawda, że Jan jest dobrym studentem. z/z n z/nn n/n n

Rachunek zdań - zmienne zdaniowe p, q i funktory prawdziwościowe: ~

⋀ Ѵ ⇒ ⇔

Osobliwości funktorów: są to tzw. funktory prawdziwościowe (wartość logiczna funktora zależy od
wartości logicznej argumentu)

Zmienne zdaniowe - w każdym miejscu za daną zmienną trzeba podstawić to samo zdanie.

Koniunkcja - w języku potocznym odpowiada mu spójnik zdaniowy „i”.

W języku potocznym słowo i może być używane w wielu znaczeniach.
Nie lubię tego i koniec. – W tym zdaniu i nie pełni roli spójnika (rozpoczyna tylko wtrącenie).
Nie zjadłem obiadu i byłem głodny. – Druga część tego zdania wynika z pierwszej (zamiast i
moglibyśmy użyć więc).
Pada i pada od samego rana. – Tu i wyraża nasilenie pewnych czynności, (pełni rolę partykuły, a nie
spójnika).
Włożyłem sweter i włożyłem kurtkę. – W tym zdaniu i jest spójnikiem łączącym dwa zdania, z których jedno
jest uzupełnieniem drugiego.

W logice, budując zdania złożone, używamy słowa „i” wyłącznie jako spójnika, który łączy zdania. Zdanie
otrzymane z dwóch prostszych zdań przez połączenie ich spójnikiem i nazywamy koniunkcją.
„Warszawa jest stolicą Polski i Warszawa leży nad Wisłą”.
Koniunkcja jest prawdziwa wtedy i tylko wtedy, gdy wszystkie jej argumenty są prawdziwe

„2*2 = 5 i Warszawa jest stolicą Polski” - koniunkcja fałszywa

p ʌ q

1
1
0
0

1
0
1
0

1
0
0
0

Prawo przemienności argumentów koniunkcji, czyli Jeżeli zdanie „Warszawa jest stolicą Polski i
leży nad Wisłą” jest prawdziwe, to prawdziwe jest także zdanie „Warszawa leży nad Wisłą i jest stolicą
Polski”.

Alternatywa w języku potocznym odpowiada mu spójnik zdaniowy „lub”.
W języku polskim słowo lub oznacza często to samo co albo.
Paweł jest teraz w kinie lub u kolegi. – W tym zdaniu spójnik lub łączy dwie części zdania, nawzajem się
wykluczające (zamiast lub możemy użyć albo).
Zjem ciastko lub zjem lody. – To zdanie zbudowane jest ze zdań, które się nie wykluczają (zamiast lub nie
możemy użyć albo, można przecież zjeść oba te smakołyki).

W logice przyjmujemy, że zdania połączone spójnikiem lub nie muszą się wykluczać wzajemnie.
Zdanie otrzymane z dwóch prostszych zdań przez połączenie ich spójnikiem lub nazywamy alternatywą
tych zdań.
Alternatywa jest prawdziwa wtedy i tylko wtedy, gdy przynajmniej jeden argument jest prawdziwy.

„Delfin jest rybą lub delfin jest ssakiem” (alternatywa prawdziwa)
„Nowy Jork jest stolicą Polski lub Bonn jest stolicą Polski” (alternatywa fałszywa)

p v q

1
1
0
0

1
0
1
0

1
1
1
0

Wyróżniamy trzy rodzaje alternatywy:
a) nierozłączna p v q „lub”
Alternatywa nierozłączna jest prawdziwa, kiedy przynajmniej jeden z argumentów jest prawdziwy,
np. Toruń leży nad Wisłą lub Toruń leży nad Wartą.

b) rozłączna p ┴ q „albo”
Alternatywa rozłączna jest prawdziwa, gdy jeden człon jest prawdziwy, a drugi fałszywy,
np.: Albo Toruń jest stolicą województwa kujawsko-pomorskiego, abo Bydgoszcz jest stolicą województwa
kujawsko-pomorskiego.

c) dysjunkcja p / q „bądź”
Dysjunkcja jest prawdziwa, kiedy przynajmniej jeden z argumentów jest fałszywy.
Dysjunkcja jest fałszywa, kiedy oba człony są prawdziwe.
Negacja (nie; nieprawda, że…)

Negacja

W języku polskim zaprzeczenia zdań można tworzyć na różne sposoby.
Na przykład zaprzeczeniem zdania Nie lubię poniedziałku jest zdanie Lubię poniedziałek.
Zaprzeczeniem zdania Jest gorąco jest zdanie Nieprawda, że jest gorąco.|
A zaprzeczeniem zdania Istnieją ostre przyprawy jest Każda przyprawa jest łagodna.
Zdanie otrzymane przez zaprzeczenie danego zdania nazywamy negacją tego zdania.
Negacja zdania prawdziwego jest zdaniem fałszywym, a negacja zdania fałszywego jest zdaniem prawdziwym.
Negacja to funktor zdaniowy o jednym argumencie „nieprawda, że p”.

2 typy negacji:
· zewnętrzna , np. „Nieprawda , że Jan jest sędzią.”
· negacja wewnętrzna , np. „Jan nie jest sędzią.”
Oba zdania są równoznaczne.

Z negacją wiążą się dwa podstawowe prawa logiczne:
a) zasada sprzeczności :
Nieprawdą jest, że za razem p i nie p.
~ (p ʌ ~ p)
Jedno zdanie jest prawdziwe, drugie fałszywe. Zdanie sprzeczne to zdanie i jego negacja.
np.: Bonn jest stolicą Polski i Bonn nie jest stolicą Polski.

Zdania sprzeczne nie mogą być oba fałszywe.

Kwestię sprzeczności odróżnić należy od zdań przeciwnych.
Zdania te to takie, w których pierwsze nie jest negacją drugiego. Poza tym nie mogą być oba prawdziwe, ale mogą
być oba fałszywe.
np. Jan jest teraz w Toruniu, Jan jest teraz w Nowym Jorku.
b) zasada wyłączonego środka : p v ~ p

Prawo podwójnej negacji. Negacja negacji danego zdania równa jest temu zdaniu. ~ (~ p) p
np. Jan jest prawnikiem = Nieprawda, że Jan nie jest prawnikiem
Negacja zdania zanegowanego jest równoważna temu zdaniu (2 razy nie).

.
.

Implikacja „Jeżeli..., to...”
W języku potocznym zdania, w których występują wyrażenia jeżeli…, to …, odbieramy jako wynikanie – z
pierwszej części zdania ma wynikać druga część. Za absurdalne uważamy połączenie dwóch zdań, których
treść nie ma ze sobą związku
np. Jeśli zdrowo się odżywiasz, to liczba 4 jest parzysta.

W logice nie rozstrzygamy, czy treść budowanych zdań jest absurdalna czy nie. W logice tego typu
zdania uważamy za poprawnie zbudowane i powinniśmy umieć określić ich wartość logiczną.
Funktor implikacji kłóci się ze znaczeniem potocznym.
p q - „p implikuje q” lub „jeżeli p, to q”
(p to poprzednik, q to następnik)

p => q

Jeżeli Polska leży nad Bałtykiem, to Polska ma granicę morską”.
poprzednik implikacji następnik implikacji
(implikacja prawdziwa)

„Jeżeli 2*2 = 5, to Polska jest najbogatszym państwem świata.” (implikacja prawdziwa)
„Jeżeli cukier jest słodki, to sól jest słodka.” (implikacja fałszywa).
Implikacja jest fałszywa wtedy i tylko wtedy, gdy poprzednik jest prawdziwy, a następnik fałszywy.
(Jeżeli p implikuje q, to q nie może być fałszywe).

Jeżeli zamienimy poprzednik z następnikiem danej implikacji, to otrzymamy implikację, którą nazywamy
odwrotną do danej.
IMPLIKACJA zdanie 1 => zdanie 2
IMPLIKACJA ODWROTNA zdanie 2 => zdanie 1

np. Jeśli woda jest metalem, to istnieje metal, który jest cieczą. (implikacja prawdziwa)
Jeśli istnieje metal, który jest cieczą, to woda jest metalem. (implikacja odwrotna jest fałszywa)

Implikacja odwrotna do prawdziwej nie zawsze jest implikacją prawdziwą.

Twierdzenia matematyczne często są formułowane w postaci implikacji. Poprzednik takiej implikacji
nazywamy założeniem, a następnik – tezą.
Prawa zastępowania implikacji: (p=>q) <=> ~(pʌ~q)
Jeżeli p implikuje q, to nie może być prawdziwe zarazem p i nie q.

Dla danego twierdzenia p => q , które możemy nazwać prostym, twierdzenia: , q=>p, (~q)=>(~p),
(~p)=>(~q)

nazywać będziemy odpowiednio odwrotnym, przeciwstawnym i przeciwnym.

Twierdzenia proste i przeciwstawne oraz, odpowiednio, odwrotne i przeciwne są jednocześnie prawdziwe
albo jednocześnie fałszywe.

Równoważność (ekwiwalencja) - „…wtedy i tylko wtedy, gdy…”
Gdy połączymy spójnikiem implikację oraz implikację do niej odwrotną, to otrzymane zdanie możemy zapisać
krócej za pomocą symbolu .

Dwa zdanie połączone wyrażeniem wtedy i tylko wtedy, gdy nazywamy równoważnością.
Równoważność jest prawdziwa wtedy i tylko wtedy, gdy oba argumenty mają taką samą wartość logiczną.
p q - „p wtedy i tylko wtedy, gdy q”

p <=> q

„Delfin jest zwierzęciem lądowym wtedy i tylko wtedy, gdy delfin jest ssakiem.”
(równoważność fałszywa)

„Warszawa jest stolicą Polski wtedy i tylko wtedy, gdy Warszawa leży w Europie.”
(równoważność prawdziwa)
(p<=>q)<=>(p=>q)

⋀(p=>q)

Dwa zdania są równoważne wtedy i tylko wtedy, gdy pierwsze z nich implikuje drugie, a drugie implikuje
pierwsze.
Zdania równoważne:

Woda jest cieczą, która wrze wtedy i tylko wtedy, gdy ma temperaturę 100 ° C.
Jeśli woda jest cieczą, która wrze, to ma temperaturę 100 ° C.
i Jeżeli dana ciecz wrze w temperaturze 100 ° C, to jest to woda.

PRAWA RACHUNKU ZDAŃ – TAUTOLOGIE

Prawo logiczne (tautologia)
Prawem logicznym (tautologią) nazywamy każde wyrażenie zbudowane ze stałych logicznych i zmiennych, które
to wyrażenie przyjmuje wartość prawdy dla wszystkich podstawień za zmienne.

Prawa logiczne (tautologie) to takie wyrażenia, które we wnioskowaniu nigdy nie doprowadzą nas od prawdziwych
przesłanek do fałszywych wniosków.

Zdanie logiczne nazywamy tautologią, jeśli jest zawsze prawdziwe, niezależnie od wartości logicznych zmiennych
zdaniowych w nim występujących.

Dowody matematyczne składają się z prostych kroków polegających na uznaniu za prawdziwe pewnych
zdań (wniosków), w logicznej konsekwencji prawdziwości innych zdań (przesłanek). Te
elementarne ogniwa dowodów opierają się na regułach wnioskowania (dowodzenia). Każda z nich jest
implikacją związaną z pewną tautologią.

Prawu przechodniości implikacji [(p=>q)ᴧ(q=>r)]=>(p=>r)

odpowiada reguła wnioskowania, którą zapisujemy:
p=>q, q=>r
p=>r

PRÓBNY TEST !!!!!!!!!!!!!

Wybierz jedną (prawdziwą) spośród czterech zaproponowanych odpowiedzi:

1. Spójniki logiczne dwuargumentowe to
a) koniunkcja, implikacja, negacja,
b) równoważność, negacja, alternatywa,
c) alternatywa, koniunkcja, równoważność,
d) negacja, implikacja, równoważność.

2. Dane jest wyrażenie [(pvq)=>r]<=>[(rᴧp)<=>q]
a) Jeśli p-prawdziwe, q-prawdziwe, r-fałszywe, to zdanie jest prawdziwe.
b) Jeśli p-prawdziwe, q-fałszywe, r-fałszywe, to zdanie jest prawdziwe.
c) Jeśli p-fałszywe, q-prawdziwe, r-fałszywe, to zdanie jest fałszywe.
d) Jeśli p-fałszywe, q-prawdziwe, r-prawdziwe, to zdanie jest prawdziwe.

3. Implikacja jest fałszywa, gdy:
a) poprzednik i następnik jest prawdziwy,
b) poprzednik jest fałszywy, a następnik fałszywy,
c) poprzednik i następnik jest fałszywy,
d) poprzednik jest prawdziwy, a następnik fałszywy.

4. Wskaż równoważność prawdziwą:
a) Delfin jest zwierzęciem lądowym wtedy i tylko wtedy, gdy delfin jest ssakiem.
b) Warszawa jest stolicą Polski wtedy i tylko wtedy, gdy Warszawa leży w Europie.
c) Delfin jest zwierzęciem morskim wtedy i tylko wtedy, gdy delfin jest rybą.
d) Warszawa jest stolicą Polski wtedy i tylko wtedy, gdy Warszawa leży nad Odrą

Lista zadań:
1. Sprawdzić, czy następujące wyrażenie jest tautologią
a) p=>(pvq)
b) -(p v q)<=>(-p ᴧ -q)
c) -(p ᴧ q) <=> (-p v -q)
d) (p=>q) <=> (-q => -p)
e) (p => q) => [p => (q v r)]
f) [(p v q) v r] => {-p => [(q v r) ᴧ -]}
g) {[(p ᴧ q) => r] ᴧ [(p ᴧ q) => -r]} <=> [(r ᴧ p) <=> q]

2. Dane jest wyrażenie [(p v q) => r] <=> [(r ᴧ p) <=> q]
Odpowiedz TAK lub NIE
a) jeśli p prawdziwe, q prawdziwe, r fałszywe to zdanie jest prawdziwe
b) jeśli p prawdziwe, q fałszywe, r fałszywe to zdanie jest prawdziwe
c) jeśli p fałszywe, q prawdziwe, r fałszywe to zdanie jest prawdziwe
d) jeśli p fałszywe, q prawdziwe, r prawdziweto zdanie jest fałszywe

3. Dane jest wyrażenie [(p ᴧ q) <=> r] => [p => (q ᴧ r)]
Odpowiedz TAK lub NIE
a) jeśli p prawdziwe, q fałszywe, r fałszywe to zdanie jest prawdziwe
b) jeśli p prawdziwe, q fałszywe, r prawdziwe to zdanie jest fałszywe
c) jeśli p fałszywe, q fałszywe, r fałszywe to zdanie jest prawdziwe
d) jeśli p fałszywe, q prawdziwe, r fałszywe to zdanie jest prawdziwe

Utworzyć twierdzenie odwrotne, przeciwstawne i przeciwne przyjmując jako twierdzenie
proste twierdzenie: jeżeli dwa boki przeciwległe czworokąta są równe i równoległe, to
czworokąt jest równoległobokiem.

Zad.Wykazać, że wyrażenie [(-q)=>(-p)]=>(p=>q) jest tautologią. Rozwiązanie:
I sposób

-p

-q

(-p)=>(-q)

p=>q

L=P

0
1
0
1

0
0
1

1
0
1
0

1
1
0
0

1
0
1
1

1
1
1
1

Wyrażenie jest tautologią.

II sposób (Nie wprost)
Załóżmy, że implikacja jest fałszywa.
[(-q)=>(-p)]=>(p=>q)
1 1/0 0 0 1 0 0

Sprzeczność, zatem implikacja jest prawdziwa.

Jest to prawo transpozycji.

Prawu przechodniości implikacji [(p->q)˄(q=>r)]=>(p=>r)

odpowiada reguła wnioskowania, którą zapisujemy:

p=>q
q=>r
p=>r

Zad.Wykazać, że schemat p, p=>q / q jest regułą wnioskowania (tzw. regułą odrywania).

Rozwiązanie:
Wykażemy, ze wyrażenie [p˄(p=>q)]=>q jest tautologią

p=>q

p˄(p=>q)

[p˄(p=>q)]=>q

1
1
0
0

1
0
1
0

1
0
1
1

1
0
0
0

1
1
1
1

Wyrażenie jest tautologią, zatem schemat jest regułą wnioskowania.

PRÓBNY TEST !!!!!!!!!!!!!!!!!!!

Wybierz jedną (prawdziwą) spośród czterech zaproponowanych odpowiedzi:

2. Dane jest wyrażenie [(pvq)=>r] <=> [(r˄p)<=>q]

a) Jeśli p-prawdziwe, q-prawdziwe, r-fałszywe, to zdanie jest prawdziwe.
b) Jeśli p-prawdziwe, q-fałszywe, r-fałszywe, to zdanie jest prawdziwe.
c) Jeśli p-fałszywe, q-prawdziwe, r-fałszywe, to zdanie jest fałszywe.
d) Jeśli p-fałszywe, q-prawdziwe, r-prawdziwe, to zdanie jest prawdziwe.

Warszawa jest stolicą Polski wtedy i tylko wtedy, gdy Warszawa leży nad Odrą.

Predykaty
Rachunek predykatów:
- jednoargumentowy (rachunek predykatów)
- wieloargumentowy (rachunek relacji)
P(x) → „x ma własność P”
P(a) → „a ma własność P”

Rachunek predykatów pozwala wyrazić pewne zależności ilościowe.

„dla każdego x ” → kwantyfikator ogólny (duży)

„istnieje x takie, że” → kwantyfikator szczegółowy (mały)

→ „każdy x ma własność P”,
np. Każdy człowiek jest śmiertelny.

→ „istnieje x mające własność P”,
np. Niektórzy ludzie są inteligentni.

Relacje

Zdania stwierdzające relację
Pewne wyrazy i wyrażenia wskazują na stosunki, czyli relacje, jakie zachodzą między różnymi
przedmiotami. Do takich wyrazów należą m. in. wyrazy:
nad, pod, za, przy, braterstwo, mniejszość, itp…
Stosunki między przedmiotami opisujemy w takich zdaniach, jak:
„Jan jest bratem Piotra”, „Paweł jest starszy od Piotra”, itp…

Ograniczymy nasze rozważania do relacji dwuczłonowych opisywanych w zdaniach, w których
mowa jest o dwóch obiektach powiązanych owym stosunkiem. Jednak w rzeczywistości możemy także
wyróżnić relacje
trój-, czwór- i więcej-członowe.
Relacja „pośredniczenia między podmiotami w sprawie nabycia nieruchomości” jest przykładem relacji
czwórczłonowej, zachodzącej pomiędzy sprzedającym, kupującym, pośrednikiem i nieruchomością.

Rachunek relacji - podzbiór rachunku predykatów. Jest to pewna zależność występująca pomiędzy
przynajmniej dwoma argumentami.

a) xRy → „x pozostaje w relacji R do y,
np. „X lubi Y” (predykat dwuelementowy)

b) xRyz → „x pozostaje w relacji R do y i z”,
np. „Toruń leży między Bydgoszczą i Włocławkiem” (predykat trójelementowy)

Gdy istnieje przedmiot y, do którego przedmiot x pozostaje w określonej relacji R, wtedy x nazywamy
poprzednikiem relacji R. Gdy istnieje x, który pozostaje w relacji R do przedmiotu y, wtedy

y jest następnikiem tej relacji.

Na przykład, jeśli weźmiemy stosunek „jest potomkiem”, to jakieś niemowlę może być poprzednikiem
tego w opisie tego stosunku, gdyż można powiedzieć: „To niemowlę jest potomkiem tego
a tego”.
Nie może być jednak następnikiem tej relacji, bo nie można o nikim powiedzieć, że jest potomkiem
jakiegoś niemowlęcia, które właśnie oglądamy.

nazwa relacji
↑
poprzednik relacji ←xRy→ następnik relacji
zbiór poprzedników zbiór następników
to dziedzina relacji to przeciwdziedzina relacji

Dziedzina i przeciwdziedzina tworzą razem pole relacji .

Rozpatrując określoną relację R, czasami ograniczamy zbiór przedmiotów
mogących być elementami jej dziedziny lub przeciwdziedziny. Mówimy wówczas,
że relacja ta jest ograniczona w dziedzinie lub przeciwdziedzinie.
Na przykład relację „bycia ojcem” możemy ograniczyć w dziedzinie do osób obecnie żyjących.

W przypadku niektórych relacji występuje sytuacja polegająca na tym, że wystąpieniu określonego
stosunku R zachodzącego pomiędzy x a y , towarzyszy zawsze wystąpienie innego stosunku Q
pomiędzy y a x . Chodzi przy tym o sytuację, w której określonej jednej relacji x a y , odpowiada
dokładnie jedna relacja występująca pomiędzy y a x .
Mówimy wówczas, że relacja Q jest konwersem relacji R.

Relacja odwrotna do danej relacji (konwers)

xRy ≡ yQx

np. „Y jest żoną X”; „X jest mężem Y”- relacja odwrotna
„X jest starszy od Y”; „Y jest młodszy od X”- relacja odwrotna
(„bycie wyższym - bycie niższym”, „bycie mądrzejszym – bycie głupszym”)

Typy relacji:

a)Relacja symetryczna - relacja jest relacją symetryczną wtedy i tylko wtedy, gdy jeśli zachodzi
pomiędzy poprzednikiem i następnikiem, to zawsze zachodzi też między następnikiem i poprzednikiem.

R ϵ Sym ≡ V x,y (xRy → yRx)

np. Jeżeli x jest kuzynem y, to y jest kuzynem x.

(bycie małżonkiem, bycie krewnym, bycie równouprawnionym, bycie rówieśnikiem)
b) Relacja asymetryczna (przeciwsymetryczna) - występuje wtedy i tylko wtedy, gdy jeśli relacja
zachodzi między poprzednikiem i następnikiem, to nigdy nie zachodzi między następnikiem i
poprzednikiem. R ϵ Asym ≡ V x,y (xRy → ~yRx)

np. Jeżeli x jest starszy od y, to nieprawda, że y jest starszy od x.
(bycie bezpośrednim zwierzchnikiem, bycie mądrzejszym, bycie wyższym)

c) Relacja nonsymetryczna (symetryczna nieregularnie) - występuje wtedy i tylko wtedy, gdy nie
jest prawdą, że dla każdego x i y jeżeli dana relacja zachodzi w jednym kierunku, to musi zachodzić też

w drugim (nie jest to przesadzone, ani wykluczone).

R ϵ Nonsym ≡ 3 x,y (xRy ˄ yRx) ˄ 3x,y(xRy, ˄ -yRx)

np. „x kocha y”; „x jest bratem y” (y może być siostrą lub bratem x!)
(bycie szanowanym, bycie lubianym, bycie znanym)

d) Relacja tranzytywna (przechodnia) - relacja trójelementowa (!)
Relacja jest przechodnia wtedy i tylko wtedy, gdy jeśli zachodzi między pierwszym i drugim elementem
oraz między drugim i trzecim, to zachodzi także między pierwszym i trzecim.

R ϵ Tranz ≡ V x,y,z (xRy ʌ yRz → xRz)

np. Jeśli Jan jest wyższy od Pawła oraz Paweł jest wyższy od Macieja, to Jan jest
wyższy od Macieja.
(bycie starszym, bycie potomkiem, bycie rodzonym bratem, bycie rówieśnikiem,
posiadanie tych samych praw)

e) Relacja atranzytywna (przeciwprzechodnia; intranzytywna)
Relacja jest atranzytywną wtedy i tylko wtedy, gdy jeśli zachodzi miedzy pierwszym i drugim elementem
oraz miedzy drugim i trzecim elementem, to nigdy nie zachodzi między pierwszym i trzecim elementem.

R ϵ Atranz ≡ V x,y,z (xRy ʌ yRz → ~ xRz)

np. Jeżeli Jan jest ojcem Pawła i Paweł jest ojcem Piotra, to Jan nie może być
ojcem Piotra.
(bycie ojcem, bycie najwierniejszym przyjacielem, bycie wasalem)

f) Relacja nontranzytywna (nieprzechodnia)

Relacja jest nieprzechodnia wtedy i tylko wtedy, gdy nie jest prawdą, że jeżeli zachodzi miedzy
pierwszym i drugim elementem oraz między drugim i trzecim, to zachodzi też miedzy pierwszym i trzecim
(może zachodzić, ale nie musi).

R ϵ Nontranz ≡ 3x,y,z(xRy ˄ yRz ˄ xRz) ˄ 3x,y,z(xRy ˄ yRz ˄ -xRz)

np. Jeżeli Jan jest przyjacielem Piotra i Piotr jest przyjacielem Magdy, to
niekoniecznie Jan jest przyjacielem Magdy (ale może być).
(bycie krewnym, bycie przyjacielem, bycie sąsiadem)

g) Relacja zwrotna (refleksywna)
Relacja jest refleksywną wtedy i tylko wtedy, gdy dla każdego x, x pozostaje w relacji sam ze sobą.

R ϵ Zwr ≡ V x (xRx)

np. Bycie identycznym. Każdy człowiek jest identyczny ze sobą.
(bycie rówieśnikiem – każdy człowiek jest swoim własnym rówieśnikiem,
bycie równym wzrostem, bycie jednakowo mądrym, posiadanie tych samych
poglądów, bycie równouprawnionym)
h) Relacja azwrotna (przeciwzwrotna)
Relacja jest azwrotna wtedy i tylko wtedy, gdy nie ma takiego x, że x pozostaje w relacji sam ze sobą.

R ϵ Azwr ≡ V x (~xRx)

np. nikt nie może być mądrzejszy od siebie samego.
(bycie wspólnikiem, bycie pomocnikiem, bycie małżonkiem, bycie
podżegaczem)
i) Relacja nonzwrotne (niezwrotna)
Relacja jest nonzwrotną wtedy i tylko wtedy, gdy x może pozostawać w relacji sam ze sobą, ale nie

musi. R ϵ Nonzwr ≡ 3x(xRx) ˄ 3x(-xRx)
np. bycie krytycznym, x jest zadowolony z y, x utrzymuje y

Stosunki porządkujące i równoważnościowe (ekwiwaletne) w danej klasie przedmiotów

Relację porządkującą nazywamy relację asymetryczną, przechodnią (tranzytywną) i spójną
(liniowy porządek). Bez spójności mamy do czynienia z relacją słabo porządkującą. Przykładem relacji
mocno porządkującej jest relacja „bycia wyższym”.

Relacje porządkujące - powalają one uporządkować pewien zbiór obiektów tak, „że każdy
element zajmuje określone miejsce”,
np. uporządkowanie ludzi według wzrostu.
(bycie starszym, wyższym, mądrzejszym, bycie osobą, która wcześniej stanęła
w kolejce).

Relacje porządkujące dzielą się na:
a) całkowicie porządkujące (muszą być spójne)
Relacja jest spójna wtedy i tylko wtedy, gdy między dwoma dowolnie wybranymi elementami zachodzi
relacja albo w jedną, albo w drugą stronę.

R ϵ Spój ≡ x,y (xRy v yRx)

np. bycie współoskarżonym, bycie większą liczbą zbiorze liczb naturalnych
b) niecałkowicie (słabo) porządkujące

Relacją równoważności nazywamy relację, która jest zwrotna, symetryczna i
przechodnia.
Przykładami takich relacji są relacje równoliczności zbiorów, równoległości prostych, czy też relacja
„bycia rówieśnikiem”.

Relacja równoważnościowa ma w logice istotne znaczenie, stanowi bowiem podstawę podziału
logicznego.
Pozwala ona bowiem dzielić określony zbiór na tzw. klasy abstrakcji, to znaczy klasy przedmiotów
pozostających w stosunku równoważnościowym do określonego elementu tej klasy.

PRÓBNY TEST !!!!!!!!!!!!!!!!!!!!

1 . Bycie małżonkiem, bycie krewnym, bycie równouprawnionym, bycie rówieśnikiem to przykłady
relacji:
a) azwrotnej,
b) tranzytywnej (przechodniej),
c) symetrycznej,
d) asymetrycznej.

2. Bycie rówieśnikiem, bycie równym wzrostem, bycie jednakowo mądrym, to przykłady relacji:
a) atranzytywnej,
b) nontranzytywnej,
c) tranzytywnej,
d) zwrotnej.

3. Relacja równoważności jest:
a) spójna, antysymetryczna i tranzytywna,
b) zwrotna, symetrycznia i przechodnia,
c) spójna, symetryczna i przechodnia,
d) zwrotna, antysymetryczna i przechodnia.

Znak, język, kategorie syntaktyczne
Znak
Podstawowym pojęciem logiki jest znak, bowiem pojęcie to jest nieodzowne dla
omówienia procesu komunikacji pomiędzy ludźmi. W szczególności zrozumienie, czym jest znak, jest
niezbędne dla określenia pojęcia języka, dzięki któremu komunikacja pomiędzy ludźmi ma miejsce.

Znakiem nazywamy stan rzeczy spowodowany przez kogoś, po to, by według przyjętej konwencji
znaczeniowej wiązać z tym stanem myśli o określonej treści.

Użytkownicy znaków <= ZNAK => znaczenie znaku
tj nadawca i odbiorca znaku ↓
nośnik znaku
(tzw. substrat np. dla liczby „4” będzie to krzywa w tym kształcie 4)

Oto kilka przykładów:
1. Dowódca batalionu wystrzelił rakietę, dając znak do rozpoczęcia natarcia.
2. Ktoś zawiązał supełek na chustce do nosa, by nie zapomnieć o zapłaceniu rachunku za telefon.
3. Kierowca pogotowia włączył syrenę i niebieskie światło.

Charles Peirce dokonał podziału znaków na:
ikoniczne – wszystko co pojawia się w kulturze, to co się w niej pojawia
np. kreska będąca linią geometryczną
wskaźniki np. amperomierz
symbole – one nie są arbitralne, nie można całkowicie rozstrzygnąć, ale nie ma tej zupełnej

dobrowolności

Za Morisem wyróżnia się sygnał , czyli znak, który ma wywołać określoną reakcję.

Funkcje znaku:
- komunikowanie, przekaz informacji i treści.
- przedstawiania (ma coś reprezentować, inną rzeczywistość np. flaga na pół masztu),
- ekspresyjna (np. wyraz twarzy może wyrażać cierpienie),
- zdolność oddziaływania, ostrzegania, apelowania.

W myśl powyższej definicji, nie jest znakiem sam przez siebie układ rzeczy czy zjawisko, takie jak
określony dźwięk, czy układ kresek – które nazywamy materialnym substratem znaku – lecz dopiero taki
układ rzeczy czy zjawisko rozpatrywane w powiązaniu z określonymi regułami znaczeniowymi,
nakazującymi wiązać z tym substratem materialnym myśli o określonej treści.

Należy także umieć odróżniać znak od oznaki (objawu, symptomu) jakiegoś stanu rzeczy.
Oznaką jakiegoś stanu rzeczy czy zdarzenia nazywamy wszystko to, co współwystępując z owym
stanem rzeczy czy zdarzeniem powoduje skierowanie nań czyjejś myśli, choć nie istnieją reguły
znaczeniowe, które by takie skierowanie myśli nakazywały.
Oto kilka przykładów:

1. Dym sam przez się jest oznaką ognia (ale nie znakiem);
2. Przylot jaskółek jest oznaką wiosny;

3. Roztrzaskane szkło na jezdni jest oznaką wypadku, który wydarzył się w tym miejscu.
W ostatnim przykładzie: narysowane przez policjanta białe kreski na jezdni są, według ustalonych w
służbie policyjnej reguł znaczeniowych, znakami informującymi o stwierdzonym położeniu pojazdu i
innych przedmiotów po wypadku.
Najważniejszym rodzajem znaków są znaki słowne – ciągi foniczne (słowa mówione) lub ciągi liter,
które mają znaczenie.
Znak słowny stanowiący całość nazywamy wyrazem (np.: logika, długopis itd.).
Wyrażeniem nazywamy z kolei sensowne zestawienie co najmniej dwóch wyrazów, które są powiązane
ze sobą składniowo.
Na przykład wyrażeniem będzie „Uniwersytet Warszawski”, „najwyższy budynek w Poznaniu”,
jak również zdanie „Piotr pije sok pomidorowy”.

Zarówno wyraz, jak i wypowiedź mogą mieć postać słowną oraz postać pisemną.
Wypowiedź jest to wyraz lub wyrażenie pełniące funkcję komunikacyjną. Wypowiedziami są więc
zdania lub równoważniki zdań.

Wypowiedź w zależności od okoliczności, w których ją formułowano (np. czasu, miejsca, osoby), pełni
różne funkcje znaczeniowe. Są to m.in.: funkcja opisowa, ekspresywna, sugestywna i performatywna.
Język, najogólniej rzecz biorąc, to zasób wyrazów, zwrotów i form używanych do
porozumiewania się przez ludzi: członków społeczeństwa, regionu, środowiska, zawodu itp.

Język, jest to system obejmujący wyznaczony przez pewne reguły zbiór znaków
słownych, z którymi odpowiednie reguły nakazują wiązać myśli określonego
typu, a inne reguły określają dopuszczalny sposób wiązania tych znaków w wyrażenia złożone.

Z semiotycznego punktu widzenia język określony jest przez trzy grupy reguł:
1. Reguły wyznaczające zasób danego języka. 2. Reguły znaczeniowe. 3. Reguły składniowe
(syntaktyczne).

Rozróżniamy języki:
- naturalne – takie, których reguły ukształtowane zostały zwyczajowo, w sposób
spontaniczny, a dopiero ktoś później podjął się ich odtworzenia na podstawie obserwacji posługiwania
się danym językiem przez członków jakiejś grupy;
- sztuczne – skonstruowane dla jakiś celów w ten sposób, że reguły tych języków
zaprojektowano z góry.

Reguły znaczeniowe języka naturalnego są bardzo złożone, ponieważ uwzględniają m. in. takie lub inne
elementy sytuacji, w której dana wypowiedź została sformułowana, kontekst innych wypowiedzi, formy
gramatyczne użytych słów, itd.
Te same zespoły dźwięków mowy czy napisy mogą być różnie rozumiane w różnych językach, a z
drugiej strony odmienne słowa z różnych języków mogą być rozumiane jednakowo.

Z punktu widzenia semiotyki ogólnej języki różnią się słownictwem i składnią.
Słownictwo – zasób słów mających ustalone znaczenia w danym języku. Na słownictwo współczesnych
języków narodów cywilizowanych składają się dziesiątki tysięcy wyrazów i liczba ta stale rośnie. Osoba
posługująca się pewnym ograniczonym zasobem słów z danego języka – używa, jak mówimy –
słownika z zakresu danego języka.

Rozróżniamy dwa rodzaje słownika:
- słownik czynny – zasób słów, którymi dana osoba posługuje się umiejętnie oraz
- słownik bierny – zasób słów, które dana osoba zna, ale ich nie używa.
Mówiąc o słownictwie pewnego języka, trzeba zauważyć, że niektóre ze zwrotów są specyficzne tylko
dla danego języka.
Wyróżniamy tutaj przede wszystkim:
1. Idiomy – wyrażenia złożone, które maja swoiste znaczenie, odmienne od tych, które wyznaczałoby

zwykłe znaczenie wyrazów składniowych.
Na przykład idiomami w języku polskim są: podziękować z góry, zapłacić z dołu, spaść z wokandy, tu
jest pies pogrzebany, spiec raka, pleść trzy po trzy.

2. Homonimy – wyrazy (wyrażenia) mające jedno brzmienie (często jedną pisownię), ale posiadające
dwa lub więcej znaczenia. Dużą grupę homonimów stanowią nazwy,
np. róg (krowy, ulicy), rola (ziemia, w teatrze), róża (kwiat, choroba).
Homonimami są również wyrazy, które mogą być rozumiane nie tylko jako nazwy, lecz także jako
funktory,
np. bez (kwiat, „bez” jako przyimek), piec (z kafli jako rzeczownik, „piec ciasto” jako czasownik), tępy
(„nieostry” jako przymiotnik, „nieinteligentny” – również przymiotnik).

3. Synonimy – różne wyrazy lub wyrażenia mające takie samo znaczenie,
np. samochód – auto, lub – albo, godzić – jednać, skłonność – upodobanie, itd.

Składnia – ustalone reguły jakiegoś języka dotyczące sposobu wiązania wyrazów w wyrażenia złożone.
Językoznawstwo zajmuje się m.in. opisem składni poszczególnych języków, natomiast przedmiotem
syntaktyki logicznej jest wyróżnianie ogólnych kategorii wyrażeń (kategorii syntaktycznych) ze względu
na rolę tych wyrażeń w
strukturze należycie zbudowanych wyrażeń bardziej złożonych.

Kryterium rozróżnienia poziomu języka stanowi odniesienie do przedmiotu, o
którym orzeka wypowiedź w danym języku. Jeżeli wypowiedź odnosi się do
otaczającej rzeczywistości i taką rzeczywistość opisuje, to wypowiedź
taka jest sformułowana w języku I stopnia, czyli w języku przedmiotowym .

Wypowiedzią w języku I stopnia jest ta, która nie odnosi się do innych wypowiedzi.
Przykłady:
1. W Czersku znajdują się ruiny średniowiecznego zamku.
2. Deszcz pada.
3. Z niektórych okien hotelu Marriott w Warszawie widać Dworzec Centralny PKP.
Jeżeli przedmiotem, o którym orzeka dana wypowiedź , nie jest zjawisko empiryczne, lecz inna
wypowiedź sformułowana w języku I stopnia, to mamy do
czynienia z wypowiedzią w języku II stopnia, czyli z wypowiedzią w metajęzyku. Wyrażenia w
metajęzyku opisują własności wyrażeń językowych sformułowanych w języku I stopnia.
Przykłady:
1. Fałszywe jest zdanie, że teraz pada deszcz.
2. W języku polskim słowo „kontroler” ma takie same znaczenie, jak słowa „rewident”, „inspektor”.

Ogólnie rzecz biorąc, z wypowiedzią w języku n–tego stopnia (gdzie n≥2 ) mamy do czynienia wtedy,
gdy przedmiotem, o którym orzeka ta wypowiedź, jest
druga wypowiedź sformułowana o jeden stopień niższym.
Przykład:
To prawda, że Jan powiedział, że Piotr śpi.
W rzeczywistości rzadko spotykamy wypowiedzi w języku III stopnia, natomiast przede wszystkim
posługujemy się językami I stopnia, a także językami
II stopnia.

Nazwy

Nazwa to wyraz (wyrażenie), które może być podmiotem albo orzecznikiem w zdaniu.
Na nazwę składa się cały zespół rzeczowników, czasowników, przymiotników, zaimków, przyimków.

Również nazwa może nie być rzeczownikiem, weźmy
np. nazwy zawarte w zdaniach: „Chory cierpi”, „Ten jest podejrzany”.

Nazwy to znaki, którymi posługujemy się, aby wskazać osobę lub przedmiot.
Nazwy mogą być również przyporządkowane pojęciom jako wytworom procesu myślowego,
nienaocznego przedstawiania sobie czegoś.

Każda NAZWA ma jakieś znaczenie, coś znaczy, czyli ma jakiś sens, którym jest właściwe tej
nazwie pojęcie (w rozumieniu logicznym nie psychologicznym), a więc jakaś treść myślowa, na
którą składa się pewien zespół cech istotnych.

O znaczeniu nazwy decyduje jej treść, czyli pewien zespół cech istotnych.
NAZWA znaczy przez swą treść.

Przez znaczenie nazwy (jej konotację) rozumiemy przyporządkowany jej w danym języku sposób jej
rozumienia.
Nazwy nie tylko znaczą jakąś treść, czyli posiadają znaczenie, ale i oznaczają jakieś przedmioty, czyli
wskazują na jakieś przedmioty przez tę nazwę nazywane.
Przedmiot wskazany przez nazwę stanowi jej desygnat (czyli to, co jest wskazane, oznaczane).

Zakres przedmiotów, które NAZWA oznacza, nazywa się jej denotacją.

Determinowanie treści nazwy
Jeżeli do zespołu cech tworzących treść jakiejś nazwy dołączymy dalsze cechy, to przechodzimy w ten
sposób do innej nazwy, o bogatszej treści, ale na ogół o węższym zakresie.
(np. człowiek, lekarz, internista)

Abstrahowanie
Jeśli pomijamy w myśli niektóre cechy składające się na treść jakiejś nazwy, przechodzimy w ten
sposób do nazwy, uboższej w treść, ale na ogół mającej szerszy zakres.
(np. urzędnik, pracownik, człowiek)
Ze względu na liczbę wyrazów wchodzących w skład nazwy rozróżniamy nazwy:
PROSTE - składające się z jednego tylko wyrazu
(np. książka, prokurator, król),
ZŁOŻONE - składające się z więcej niż jednego wyrazu
(np. książki oddane do biblioteki; ten, który był ostatnim królem Polski, student Wydziału Filologii
Polskiej Uniwersytetu Wrocławskiego, egzamin dojrzałości).

Ze względu na to, ile desygnatów obejmuje zakres danej nazwy, rozróżniamy nazwy:
OGÓLNE - to takie, które mają więcej niż jeden desygnat
(np. książka, szafa, pióro),
JEDNOSTKOWE - to takie, które mają tylko jeden desygnat
(np. Piotr Kowalski; najstarszy człowiek na świecie),
PUSTE (bezprzedmiotowe) - to takie, które wcale nie mają desygnatów
(np. krasnoludek, elf, nimfa, Miś Puchatek, pies o wadze 200 kg, obecny król Francji, przewodniczący
Rady Państwa).

Nazwy puste niczego nie oznaczają, niemniej coś znaczą.
Nazwy INDYWIDUALNE to takie, które służą do oznaczania poszczególnych, tych a nie innych
przedmiotów, nie przypisując przez to samo danemu przedmiotowi takich, czy innych właściwości
wyróżniających go.
Nazwa ta służy danemu przedmiotowi tak długo jak zachowuje on ciągłość istnienia i bez względu na
cechy tego przedmiotu, mogą być nadawane nie tylko przedmiotom rzeczywistym, ale i tym
wyobrażonym, np. postaciom literackim
(np. Tatrzański Park Narodowy, Apollo, Rondo ONZ, Wrocław, Dunajec,

Karol Maj).

Nazwy GENERALNE to takie, które przysługują przedmiotom ze względu

na jakieś cechy,

które tym przedmiotom przypisujemy.
(np. Warszawa jest największym miastem w Polsce;
„Najsłynniejsze z pierników miasto w Polsce” – to nazwa generalna, która oznacza to samo, co nazwa
indywidualna „Toruń”).

Treścią jakiejś nazwy generalnej nazywamy taki zespół cech posiadanych przez
desygnat danej nazwy, np. treścią nazwy „pęczak” w języku polskim jest zespół
cech:
1) coś, co jest kaszą, 2) jęczmienną, 3) bardzo grubą.
Wszystko, co te trzy cechy posiada może być nazwane pęczakiem i tylko to, co te trzy cechy łącznie
posiada.

Zastanówmy się jakie cechy ma każdy „kwadrat”. Jest to:
1. figura płaska;
2. czworoboczna;
3. równoboczna;
4. prostokątna;
5. o bokach parami równoległych;
6. o równych przekątnych;
7. o połowiących się przekątnych;
8. o prostopadłych przekątnych;
9. o obwodzie przy danym polu stosunkowo najmniejszym;
10. wpisywalna w okrąg;
11. opisywalna na okręgu.

• Taki zespół cech, który wystarcza do tego, by odróżnić desygnaty danej nazwy od innych przedmiotów,
nazywamy konstytutywnym zespołem cech , a cechy
takie nazwy tworzące – cechami konstytutywnymi .
• Pozostałe cechy wspólne nazywamy konsekutywnymi względem poprzednio wymienionych.
Najprościej wytłumaczyć, co to jest kwadrat, podając
zespół cech 1, 2, 3, 4; znacznie trudniej byłoby zrozumieć, co to jest kwadrat podając cechy np. 1, 2, 9.

Taki konstytutywny zespół cech, który jak najprościej wyjaśnia treść danej nazwy,
nazywamy treścią leksykalną , czyli słownikową nazwy.
Z tego przykładu widać, że nie można utożsamiać rozróżnienia nazw
indywidualnych i generalnych z rozróżnieniem imion własnych i pospolitych w gramatyce.
Nazwy generalne odnoszą się do wszystkich przedmiotów mających pewien określony zespół cech.

Każda NAZWA generalna może występować w trzech supozycjach:
- prostej (np. pies zjadł całą kurę),
- formalnej (np. pies nie lubi alkoholu),
- materialnej (np. wyraz „pies” składa się z 4 liter).
Szczególnym przypadkiem nazw generalnych są tzw. nazwy prywatywne – wskazujące brak pewnej
cechy u desygnatów nazwy generalnej
(np. niewykonane zobowiązania, niepowetowana szkoda)

• Jeżeli nazwa jest używana w wypowiedzi jako znak dla poszczególnego przedmiotu tego właśnie

rodzaju, jako znak dla określonego desygnatu nazwy, to mówimy, ze występuje w supozycji prostej. np.
„Zając przebiegł mi drogę.”

• Jeżeli wyraz jest nazwą dla całego gatunku przedmiotów, jak np. w wypowiedzi „Zając jest pospolity w
Polsce”, to mówimy, że jest on w supozycji formalnej. Nazwa używana w tej supozycji staje się nazwą
abstrakcyjną.

• Supozycją materialną nazywamy użycie jakiegoś wyrazu jako znaku dla niego samego. „ZAJĄC” w
supozycji materialnej składa się z dwóch sylab, z pięciu liter i wielokrotnie jest powtarzany w tej części
wykładu Nazwy indywidualne mogą występować tylko w supozycji prostej lub materialnej.
Ze względu na to, do czego nazwy się odnoszą, rozróżnić trzeba:
- nazwy KONKRETNE to jest takie, które są znakami rzeczy albo osób, ewentualnie czegoś, co sobie
wyobrażamy jako rzecz lub osobę
(np. prokurator, skrypt, budynek, Harry Potter, stół ekonomista, nimfa, kwiat paproci),
nazwy ABSTRAKCYJNE to jest takie, które nie są znakami rzeczy, czy osób ani czegoś, co sobie jako
rzeczy, czy osobę wyobrażamy.

Nazwy abstrakcyjne są nazwami:
· klas obiektów, np. umowa komisu, sprawiedliwość, cel umowy, błąd, zła wiara,
· zdarzeń, np. bitwa, opieka, postępowanie nieprocesowe
· relacji, np. wyższość, bliskość, powinowactwo, zstępność,
· własności, np. dobroć, purpura,
· liczb.

Wskazują one na pewną cechę wspólną wielu przedmiotów (np. „białość), na pewne zdarzenie czy
stan rzeczy (np. „płacz”, „kradzież”, „cisza”) albo na
pewien stosunek miedzy przedmiotami (np. „braterstwo”, „wyższość”).
(np. bitwa, braterstwo, opieka, dobroć, purpura, wyższość, bliskość).
Nazwy, których desygnatami są nie poszczególne rzeczy, lecz takie przedmioty, które traktujemy jako
agregaty złożone z poszczególnych rzeczy, nazywamy NAZWAMI ZBIOROWYMI (kolektywnymi)
„las” (agregat drzew), „biblioteka” (agregat książek), „stado” (agregat zwierząt), „spółdzielnia” (agregat
osób).
(np. kodeks cywilny, sąd okręgowy, terytorium Wielkiej Brytanii, system komputerowy, sejm, las, Senat
UWr).

Natomiast wszystkie inne nazwy tj. takie, których desygnatami nie są zbiory o określonym wyżej
charakterze, nazywać będziemy NAZWAMI NIEZBIOROWYMI.
Do nazw niezbiorowych należeć będą nie tylko nazwy, których desygnatami są pojedyncze niedające
podzielić się na części przedmioty
(np. Mont Blanc, Bajkał, Wisła, Jan Kowalski),
lecz także nazwy, których desygnaty tworzą zbiory w sensie dystrybutywnym
(np. krzesło, prawnik, student).

Nie jest więc desygnatem nazwy zbiorowej „Sejm Rzeczpospolitej” ktoś, kto jest desygnatem nazwy
„poseł na Sejm Rzeczypospolitej” – i odwrotnie. Co innego poseł, a co innego Sejm, agregat posłów.
Często można spotkać się z tym, że ktoś utożsamia agregat – całość złożona z części – z klasą
wszystkich tych części składowych. Jest to błędem, np. „spółdzielnia” jako całość, a co innego klasa
wszystkich członków tej spółdzielni.
Jeżeli umiemy, znając należycie dany język, bez wątpliwości rozstrzygnąć o każdym napotkanym
przedmiocie, z którym odpowiednio zapoznaliśmy się, czy jest
on, czy też nie jest desygnatem pewnej określonej nazwy, to mówimy, że w danym
języku nazwa ta ma ostry zakres lub w skrócie jest NAZWĄ OSTRĄ.

Jeżeli o pewnych przedmiotach, mimo dobrego zapoznania się z ich cechami, nie umiemy orzec, czy
są, czy nie są desygnatami danej nazwy, to nazwę taką określamy jako NAZWĘ NIEOSTRĄ.

np. kartka papieru. Jeżeli mamy kawałek papieru o rozmiarach 15x20 cm, to wiadomo, że jest to kartka
papieru, jeśli ma 1x1 cm albo 80x120 cm, to nikt tego nie nazwie kartką. Ale od jakich rozmiarów
„zaczyna się” kartka?

(np. dzieło sztuki, młodociany, nietrzeźwy, dobra wiara).
Nieostrość zakresu wiąże się z tym, że niektóre nazwy nie mają wyraźnej treści ,
to znaczy, że nawet ten, kto dobrze zna język nie umiałby podać takiego zespołu
cech, które pozwoliłyby w sposób stanowczy odróżniać desygnaty danej
nazwy od innych przedmiotów, np. słowo „rzeka”.

Nazwy stają się nazwami ostrymi dzięki temu, że są nazwami wyraźnymi – tzn. umiemy podać zespół
cech wystarczających do odróżnienia desygnatów danej nazwy od innych przedmiotów, lub dzięki temu,
że są nazwami dla nas intuicyjnymi – tzn. że na podstawie ogólnego wyglądu danego przedmiotu, bez
zastanawiania się nad treścią danej nazwy, umiemy określić, czy jest on, czy nie jest desygnatem tej
nazwy.

Zapamiętajmy, że nazwy można podzielić na:
• Proste i złożone – wg liczby wyrazów składowych;
• Konkretne i abstrakcyjne – wg charakteru tego, do czego się odnoszą;
• Generalne i indywidualne – wg sposobu identyfikowania desygnatu;
• Ogólne, jednostkowe, puste – wg liczby desygnatów;
• Zbiorowe i niezbiorowe – wg struktury desygnatów.
• Ostre i nieostre – wg desygnatów danej nazwy

Stosunki między zakresami nazw

Zagadnienie dotyczące stosunków zakresowych nazw wymaga przypomnienia, co to jest zakres nazwy.
Jest to zbiór jej desygnatów, czyli przedmiotów oznaczanych przez daną nazwę.
Musimy także wprowadzić pojęcie klasy uniwersalnej (zwanej universum ), a więc zbioru desygnatów
wszystkich istniejących nazw. Jeśli z klasy uniwersalnej wyłączymy przedmioty określone nazwą
„ekonomista”, wówczas pozostała część tworzy klasę negatywną : „nie-ekonomista”.

Nazwa i jej dopełnienie (czyli klasa negatywna) stanowi klasę uniwersalną.
np. klasa negatywna – zbiór desygnatów nazwy „nie-ekonomista” – obejmuje
wszystko to, co nie wchodzi w zakres nazwy „ekonomista” ( a więc obejmuje
wszystkie przedmioty, wyłączając ekonomistów).

Stosunek pomiędzy zakresami nazw (na przykładzie kół Eulera).
Przedstawione stosunki odnoszą się do sytuacji, w której nazwy nie są nazwami pustymi.

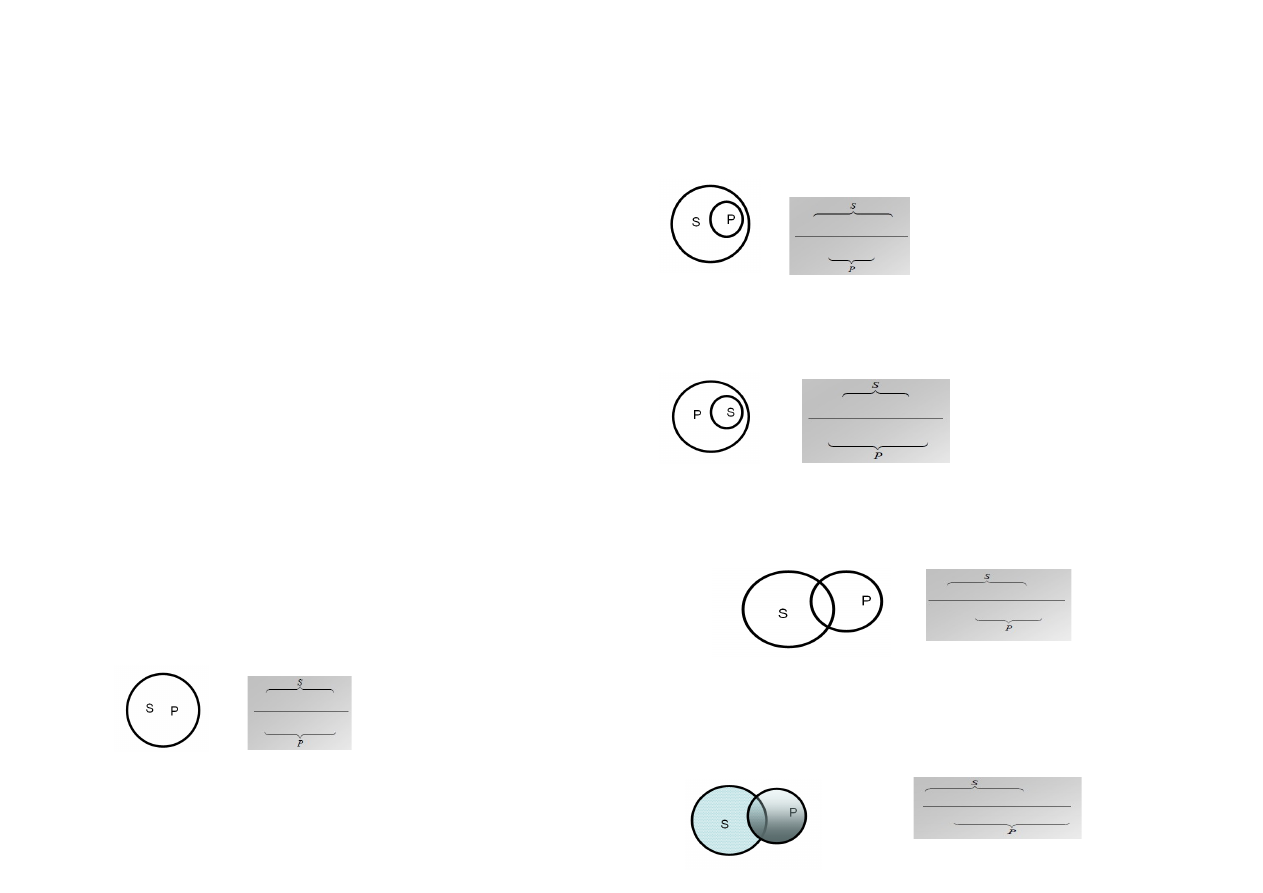
1. STOSUNEK ZAMIENNOŚCI S WZGLĘDEM P

Nazwę „auto” oznaczmy jako „S”
Nazwę „samochód” oznaczmy jako „P”

Desygnaty S są desygnatami nazwy P; każde S jest P, każde P jest S.

(Zakresy nazw S i P pozostają w stosunku zamienności, gdy się ze sobą pokrywają. Nie ma takich P,

które nie byłyby S i nie ma takich S, które nie byłyby P).
Inny przykład: flaga i chorągiew

2. STOSUNEK NADRZĘDNOŚCI S WZGLĘDEM P
Nazwę „prawnik” oznaczmy jako „S”
Nazwę „sędzia okręgowy” oznaczmy jako „P”

Każde P jest S, lecz nie każde S jest P; istnieją bowiem S, które nie są P.

Inny przykład: lekarz i chirurg (S ma szerszy zakres)

3. STOSUNEK PODRZĘDNOŚCI S WZGLĘDEM P
Nazwę „prokurator” oznaczmy jako „S”
Nazwę „prawnik” oznaczmy jako „P”

Każde S jest P, lecz nie każde P jest S; istnieją bowiem P, które nie są S.

Inny przykład: pies i ssak (P ma szerszy zakres)

4. STOSUNEK KRZYŻOWANIA SIĘ – NIEZALEŻNOŚCI S WZGLĘDEM P

Nazwę „prawnik” oznaczmy jako „S”
Nazwę „polityk” oznaczmy jako „P”

Zakresy dwóch nazw krzyżują się wtedy i tylko wtedy, gdy są takie S, które są P i są takie P, które są S,
ale są S, które nie są P i są takie P, które nie są S.
Ponadto oprócz S i P istnieją inne przedmioty (przynajmniej jeden).
4. STOSUNEK KRZYŻOWANIA SIĘ – PODPRZECIWIEŃSTWA
Nazwę „prawnik” oznaczmy jako „S”
Nazwę „nie-adwokat” oznaczmy jako „P”

Niektóre S są P i niektóre P są S; istnieją bowiem S, które nie są P i istnieją P, które nie są S.
Inny przykład: prawnik i nie-notariusz
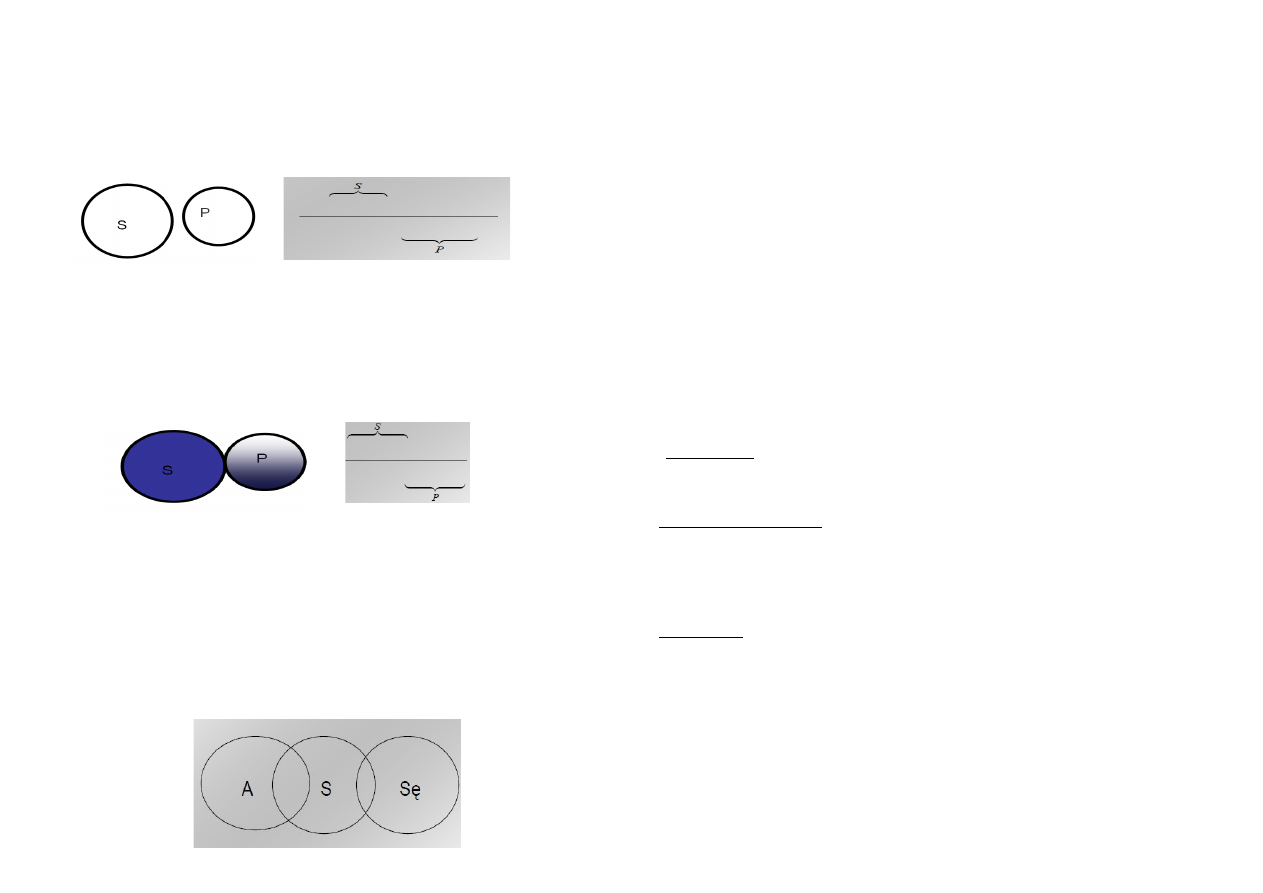
5. STOSUNEK WYKLUCZANIA SIĘ – PRZECIWIEŃSTWA
Nazwę „prokurator” oznaczmy jako „S”
Nazwę „radca prawny” oznaczmy jako „P”

Nie istnieją S, które byłby P i nie istnieją P, które byłby S.

Oprócz S i P istnieją inne przedmioty.

(Nie mamy do czynienia z nazwami sprzecznymi, ale żadne S nie jest P i żadne P nie jest S).

Inny przykład: prokurator i sędzia ciało stałe i ciecz

5. STOSUNEK WYKULCZANIA SIĘ – SPRZECZNOŚCI
Nazwę „prokurator” oznaczmy jako „S”
Nazwę „nie-prokurator” oznaczmy jako „P”

Żadne S nie jest P i żadne P nie jest S.

Poza S i P nie ma żadnych innych przedmiotów.

Inny przykład: sędzia i nie-sędzia

Wykresy wcześniejsze obejmują stosunki zakresów dwóch nazw. Jednakże często musimy sięgać do
prezentacji, które pozwolą nam na określenie stosunków zakresowych trzech, czterech i więcej nazw.
Najczęściej używane do tego są wykresy kołowe. Dla przykładu pokażemy stosunek trzech nazw:
S – sportowiec, A – adwokat, Sę – sędzia.

Opisane wcześniej stosunki pomiędzy zakresami nazw odnoszą się do sytuacji,
w której nazwy nie są nazwami pustymi. Zakresy dowolnych nazw pustych są
zamienne. Ważne jest odróżnianie stosunków zakresowych nazw od relacji części do całości, np.
samochód – silnik.

Jeżeli mamy określić stosunek zakresowy nazw: „rada gminy” i „radny”, wówczas mając na uwadze
fakt, że nie odnosimy się do związków części do całości, stwierdzamy, że „rada gminy” nie jest radnym
i radny nie jest rada gminy, a
zatem zachodzi stosunek wykluczania się (przeciwieństwo). Podobnie stosunek
wykluczania się zachodzi pomiędzy nazwą w liczbie pojedynczej i w liczbie mnogiej, np. drzewo –
drzewa.

PRÓBNY TEST !!!!!!!!!!!

1. Jeśli pomijamy w myśli niektóre cechy składające się na treść jakiejś nazwy, przechodzimy w ten
sposób do nazwy, uboższej w treść, ale na ogół mającej szerszy zakres. (np. urzędnik, pracownik,
człowiek).
Jest to definicja:
a) determinowania,
b) abstrahowania,
c) zastępowania,
d) wnioskowania.

2. Ze względu na to, ile desygnatów obejmuje zakres danej nazwy, rozróżniamy nazwy:
a) ogólne, jednostkowe, puste,
b) proste, złożone,
c) indywidualne, generalne,
d) konkretne, abstrakcyjne.

Teoria definicji

Definiowanie jako metoda precyzowania pojęć oraz określania, czy
charakteryzowania przedmiotów jest niezwykle pożądane. Pozwala
na wyeliminowanie wieloznaczności, nieostrości wyrażeń, wzbogacenie języka
poprzez wprowadzenie nowych wyrażeń o określonej treści i zakresie.
Definiowanie jest metodą porządkowania i kształtowania języka.

Definicja jest wypowiedzią określającą znaczenie danego wyrazu (wyrażenia)
albo podającą jednoznaczną charakterystykę definiowanego przedmiotu.

Wg „Zasady techniki prawodawczej” należy sformułować definicję danego
określenia, jeżeli:

1) dane określenie jest wieloznaczne,
2) dane określone jest nieostre, a pożądane jest ograniczenie jego nieostrości,
3) znaczenie danego określenia nie jest powszechnie zrozumiałe,
4) ze względu na dziedzinę regulowanych spraw istnieje potrzeba ustalenia
nowego znaczenia danego określenia.

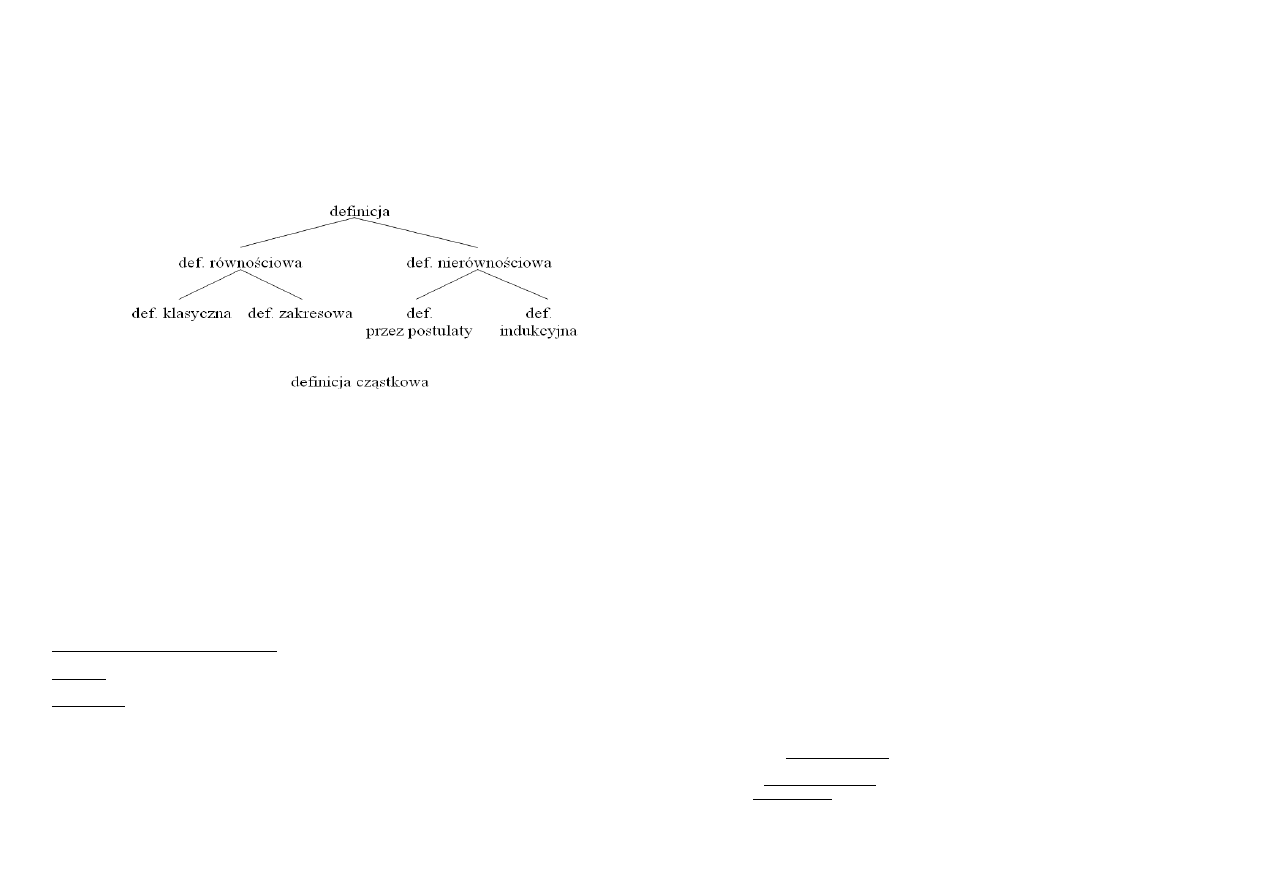
Rodzaje definicji

A. Podział definicji ze względu punkt odniesienia
REALN AI NOMINALNA

Definicja realna odnosi się do przedmiotu. Mówimy „zegar to urządzenie służące do mierzenia czasu”.
W ten sposób charakteryzujemy przedmiot, a nie znaczenie wyrazu. Definicja realna jest sformułowana
w języku I stopnia.

Definicja nominalna polega na zastępowaniu jednych wyrażeń innymi wyrażeniami, przy czym ten
proces zastępowania może zmierzać ku znajdowaniu wyrażeń równoznacznych ze względu na treść lub
równoważnych ze względu na zakres występujących nazw.
Definicja nominalna jest definicją metajęzykową, ponieważ nie odnosi się bezpośrednio do przedmiotów,
lecz dotyczy języka, w którym zostały użyte definiowane nazwy. Definicja nominalna podaje informacje o
znaczeniu definiowanego słowa, jest więc wypowiedzią w języku II stopnia.
np. „herbicyd – substancja chemiczna używana do niszczenia chwastów”
Definicja ta informuje, jak na gruncie określonego języka należy rozumieć pewne wyrażenie.

B. Podział definicji ze względu na zdania szczegółowe
a) sprawozdawcza
b) projektująca
- konstrukcyjna
- regulująca

a) Definicja sprawozdawcza skierowana jest ku przeszłości lub teraźniejszości i stanowi wyraz tego,
jak dane wyrażenie rozumiane jest (lub) było w określonym języku. Jest to swego rodzaju sprawozdanie
oddające znaczenie danej nazwy.

np. Jeśli nauczyciel w szkole przekazuje definicję pojęcia „repatriacja”, stwierdzając, że jest to „powrót

obywateli do kraju, do ojczyzny,

np. jeńców wojennych, uchodźców, przesiedleńców”, wówczas definicja
ta jest sprawozdaniem nauczyciela.
- gdy zmierzamy do odtworzenia zastanego w języku J znaczenia wyrażenia A,
- gdy zachodzi potrzeba wiernego odtworzenia znaczenia pewnego terminu należącego do określonego
języka.
Metody budowania definicji sprawozdawczych:
• etymologiczna:

- zaleca następujące postępowanie:

- wyrażenie definiowane należy rozłożyć na części
składowe,
- należy odnaleźć sens, jaki posiadają poszczególne
cząstki słowotwórcze w języku, z którego pochodzą,
- w oparciu o sens cząstek słowotwórczych utworzyć należy

sens całego wyrażenia definiowanego,

- antropomorfizm - to pogląd, który dopatruje się istnienia własności

i stosunków charakterystycznych dla świata ludzkiego w pewnych

sferach zjawisk nie związanych bezpośrednio z człowiekiem,
• sokratyczna (indukcyjna):

- wersja mocna zaleca następujące postępowanie:

- należy rozważyć

wszystkie

przypadki użycia terminu

definiowanego,

- należy znaleźć cechy wspólne tych przypadków użycia

terminu definiowanego, które odróżniają je od przypadków
użycia innych terminów,
- na podstawie wyróżnionych cech wspólnych należy zbudować
znaczenie terminu definiowanego.

- wersja słaba zaleca następujące postępowanie:

- należy rozważyć

wybraną próbę

przypadków użycia terminu

definiowanego,

- należy znaleźć cechy wspólne tych przypadków użycia

terminu definiowanego, które odróżniają je od przypadków
użycia innych terminów,
- na podstawie wyróżnionych cech wspólnych należy zbudować
znaczenie terminu definiowanego
2. Definicja projektująca mówi o znaczeniu wyrażania na przyszłość.

np. „Bank genów jest to ośrodek, gdzie genotypy są przechowywane poza ich normalnym
środowiskiem, wyposażony w niezbędne budowle i urządzenia”.
Prawodawca projektuje znaczenie tego wyrażenia i oczekuje, że wyrażenie to będzie
występowało powszechnie w zaprezentowanym znaczeniu.

- gdy chcemy wyrażeniu A nadać znaczenie nowe, całkowicie odbiegające od wyrażenia
zastanego w języku J,
- gdy zachodzi potrzeba wzbogacenia języka o nowe pojęcie,

np. disco polo, oszołom, recykling
Przez „recykling rozumie się taki odzysk, który polega na powtórnym przetwarzaniu substancji lub
materiałów zawartych w odpadach w procesie produkcyjnym w celu uzyskania substancji lub materiału
o przeznaczeniu pierwotnym lub o innym przeznaczeniu”.
Inne przykłady:
- kierownika suwnicy elektrycznej nazywać się będzie w niniejszej ustawie ‘suwnicowym’ ;
- słowem ‘płaszczynka’ oznaczać będziemy płaskie butelki do atramentu
do wiecznych piór, służące zarazem jako kałamarz.
2a) Definicja konstrukcyjna dotyczy nowych słów lub nowego znaczenia słów,
nie nawiązuje ona do dotychczasowego ich znaczenia.

np. „maluch” jako „uczeń pierwszej klasy gimnazjum”

2b) Definicja regulująca ustala znaczenie danego wyrazu.

np. „hałas” to dźwięk o częstotliwości od 16 Hz do 16 000 Hz,
„młodociany” to sprawca, który w chwili popełnienia czynu zabronionego
nie ukończył 21 lat i w czasie orzekania wyroku 24 lat.

gdy chcemy wyrażeniu A nadać znaczenie, w którym częściowo dostosowujemy
się do znaczenia zastanego, zarazem częściowo je zmieniając,
gdy zachodzi potrzeba modyfikacji znaczenia pewnego terminu dokonanej w taki
sposób, aby zmiana znaczenia nie była zbyt radykalna i uwzględniamy elementy
dotychczasowego znaczenia wyrażenia.

odział definicji ze względu na budowę

1. Definicja równościowa (definicja pełna, normalna) składa się z 3 elementów:
- definiendum, czyli części definicji zawierającej nazwę definiowaną,
- łącznik definicyjny,
definiens, czyli zwrotu definiującego.

np.

Pełnoletni

jest to

osoba, która ukończyła lat 18

definiendum

łącznik definicyjny

definiens

Prawodawcy powinni używać w nazwie łączników zwrotów „jest to”,
„jest równoznaczne”, „znaczy”, „A znaczy B”, nie powinni natomiast używać „jest”.

Spójnik definicyjny (spójka definicyjna) - to, co łączy definiendum z definiendem.

Definiens - wyrażenie, przy pomocy którego definicja informuje o znaczeniu wyrazu definiowanego.

Definiendum - jeden z trzech składników każdej definicji. Może mieć budowę jednowyrazową lub
wielowyrazową.
Przykład definicji:

Treść charakterystyczna nazwy N

jest to

zespół cech taki, że przysługuje wszystkim desygnatom nazwy

N i tylko im

definiendum:

Treść charakterystyczna nazwy N

spójnik definicyjny:

jest to

definiens:

zespół cech taki, że przysługuje wszystkim desygnatom nazwy N i tylko im

Wyrażenie definiowane połączone jest z wyrażeniem definiującym za pomocą spójki definicyjnej o
charakterze równości, ustalającej równoznaczność
lub równozakresowość wyrażenia definiowanego i wyrażenia definiującego.

np. „Przepisem prawa nazywamy najmniejszą jednostkę systematyzacyjną aktu prawnego”.
„Żołnierz jest osobą pełniącą czynną służbę wojskową”.
„Standard emisji to dopuszczalna wielkość emisji”.

Desygnat - przedmiot, dla którego dana nazwa jest znakiem; desygnatem danej nazwy jest wtedy
każdy przedmiot, o którym trafnie orzec można daną nazwę,
np. to, co masz pod nogami, jest jedynym desygnatem nazwy „glob ziemski”.
„Ziemia to kula u nogi” Hugo Steinhaus
Definicje równościowe mogą być tworzone na dwa sposoby: jako definicje klasyczne albo
zakresowe .

Definicje o budowie klasycznej składają się z określonego rodzaju i różnicy gatunkowej.
np. „Pełnoletnim jest ten, kto ukończył lat osiemnaście”.
Ten rodzaj definiowania polega na podaniu nazwy o zakresie szerszym, a następnie
zawężeniu zakresu.
Pełnoletnim jest więc człowiek, lecz nie każdy, a tylko ten, kto ukończył lat osiemnaście.
Tak więc np. „dom jest to budynek mieszkalny”. Dom to budynek, lecz nie jakikolwiek budynek, ale tym
różniący się od innych, że mieszkalny.
To jest właśnie różnica gatunkowa wyróżniająca „gatunek” dom od innych przedmiotów z „rodzaju”
budynek.
W definicji zakresowej (nieklasyczne) określanej jako definicja przez wyliczanie wskazujemy
zakresy poszczególnych nazw, łącznie dające zakres nazwy definiowanej.
np. „PCB – rozumie się przez to polichlorowane difenyle, polichlorowane trifenyle,
monometylotetrachlorodifenylometan, (…)
„Zbożem w rozumieniu niniejszego rozporządzenia jest pszenica, żyto, jęczmień, owies, kukurydza,
gryka i proso”.

Ten sposób konstruowania definicji wskazuje na zamienność nazwy definiowanej „zboże” z sumą
zakresów wszystkich nazw wymienionych w definiensie.

Ogólnym schematem definicji klasycznych jest formuła „A jest to B mającą cechę C”, zaś definicji
nieklasycznych określenie „A jest B lub C lub D lub…”.
Nominalna definicja równościowa może być skonstruowana w trzech wysłowieniach – w zależności od
tego, czy nazwy stanowiące definiendum i definiens są użyte jako cudzysłowowe, czy też są
traktowane jak nazwy przedmiotowe. Owe wysłowienia nazywane są stylizacjami.
Definicja może przyjąć formę stylizacji:
- słownikowej,
- semantycznej,
przedmiotowej.

Stylizacja słownikowa (metajęzykowa) - jest to wyrażenie podające informację o znaczeniu
jakiegoś słowa (słów), dostarcza informacje o tym, jakie inne wyrażenie jest wyrażeniem
równoznacznym z wyrażeniem definiowanym.

np. słowo „materialista” znaczy to samo, co wyrażenie: „człowiek, który uznaje istnienie jedynie
materii”,
słowo ,,adekwatny” znaczy tyle samo, co „odpowiedni”,
słowo „borsalino” znaczy tyle, co „kapelusz filcowy z szerokim, miękkim rondem”.

Jeśli definicja jest dobra, to sens nie ulegnie zmianie.
Stylizacja semantyczna zdanie, które głosi, że pewien wyraz czy wyrażenie oznacza pewien
przedmiot lub odnosi się do przedmiotu określonego rodzaju, do rzeczy, wyrażeń.
np. słowo „słód” oznacza wszelkie zboże sztucznie kiełkowane,
(słód – skiełkowane i wysuszone ziarna zbóż służące jako jeden z surowców do produkcji
piwa lub whisky)

słowo „buchmacher” denotuje osobę pośredniczącą przy zawieraniu zakładów na wyścigach
konnych albo imprezach sportu zawodowego.
Stylizacja przedmiotowa odnosi się do definicji realnej.
Zdanie, które zawiera jednoznaczną charakterystykę jakiegoś przedmiotu, czy przedmiotów
pewnego rodzaju, wskazując cechy im i tylko im wspólne.
Charakterystyka ma być tak dobrana, aby można było na jej podstawie wnioskować o możliwie
wszystkich ważnych cechach tych przedmiotów.
Ma ona być najzwięźlejszym ujęciem wiedzy o przedmiotach danego rodzaju. Jest to wypowiedź, która
formułuje twierdzenia o cechach wspólnych dla jakichś uprzednio wydzielonych przedmiotów. Opiera się
na założeniu, że uprzednio widzieliśmy przedmioty, które zaliczymy do przedmiotów danego rodzaju.

np. Bursztyn jest naturalną żywicą skamieniałą.
Księgarnia to sklep, w którym sprzedaje się książki.
Zegar to urządzenie służące do mierzenia czasu.
2. Definicje nierównościowe (definicje cząstkowe) charakteryzowane są jako te, które nie
mają budowy właściwej dla definicji równościowej. W definicjach nierównościowych nie
występuje spójnik definicyjny (znaczy, oznacza, jest to).
Ten rodzaj definicji jest mniej popularnym sposobem ich konstruowania.
Jednym z rodzajów definicji nierównościowych jest definicja przez postulaty (aksjomatyczna).
Jej istotą jest umieszczenie definiowanego wyrazu w kilku wzorcowych zdaniach w sensie
gramatycznym, na podstawie których możemy zrozumieć, jakie znaczenie mu się przypisuje.

np. „Przez umowę przechowania przechowawca zobowiązuje się zachować w stanie nie
pogorszonym rzecz ruchomą oddana mu na przechowanie”.

W budowie definicji indukcyjnej (rekurencyjnej) wyróżnia się wyraźnie dwie części: warunek
wyjściowy i warunek indukcyjny.

np. „Nie może być świadkiem przy sporządzaniu testamentu osoba, dla której w testamencie została
przewidziana jakakolwiek korzyść. Nie mogą być również świadkami: małżonek tej osoby, jej krewni i
powinowaci pierwszego i drugiego stopnia oraz osoby pozostające z nią w stosunku
przysposobienia”.
Przy omawianiu budowy definicji należy zwrócić uwagę na definicje cząstkowe. Są to definicje niepełne,
na co wskazuje ich nazwa. Nie podają one całkowitej charakterystyki definiowanego wyrazu
(wyrażenia), czyli wyjaśniają tylko częściowo jego znaczenie.

Rodzaje definicji cząstkowych ze względu na warunek:
- warunek wystarczający
np. Jeśli ktoś kształci się na UJ, to jest studentem.

- warunek konieczności
np. czynnik A jest warunkiem koniecznym czynnika B i jest tak, że jeśli czynnik B występuje, to
występuje również czynnik A, jeśli zaś czynnik A nie występuje, nie występuje też czynnik B.
Błędy w definiowaniu
Problematyka poprawnego budowania definicji była przedmiotem dociekań w starożytności. Definicje
służyły bowiem budowaniu argumentacji w sporach słownych. Problemy związane z występowaniem
błędów w definicjach mają jednak charakter ponadczasowy.

A. Błędne koło w definiowaniu (circulum in definiendo) – błąd polega na określaniu definiowanego
wyrazu poprzez odwołanie się do niego samego.

- błędne koło bezpośrednie (idem per idem) - to samo przez to samo –

polega na zdefiniowaniu jakiegoś wyrażenia przy pomocy tego samego
wyrażenia
(np. masło maślane;
Logika jest nauką o myśleniu zgodnym z prawidłami logiki.)

- błędne koło pośrednie powstaje wówczas, gdy jedno wyrażenie
definiujemy za pomocą innego wyrażenia
(np. Logika to nauka o poprawnym myśleniu, które jest logiką.
Gatunek jest to wszelkie zbiorowisko form, które nie obejmuje
form należących do innego gatunku.)
B. Nieznane przez nieznane (ignotum per signatum)
Błąd polega na tym, że wyrażenie nieznane zostało zdefiniowane za pomocą wyrażenia nieznanego.
np. Fakt prawny to tyle, co okoliczność opisana w hipotezie normy prawnej.

C. Nieadekwatność definicji - może występować jedynie w definicji sprawozdawczej.
Polega na tym, że zakres definiensa nie jest równy zakresowi definiendum:
- definicja za wąska
np. Oficerowie to kapitanowie i porucznicy.
(definicja za wąska, bo nie obejmuje wszystkich przedmiotów)
„Trójkąt to figura geometryczna o trzech

równych

bokach”.

- definicja za szeroka
np. prokurator to pracownik prokuratury
(definicja za szeroka; w prokuraturze pracuje wiele osób, np. sprzątaczki)
„Zabytek to rzecz zasługująca na trwałe zachowanie ze względu na posiadaną wartość artystyczną”.

- krzyżowanie się zakresów
np. Prawnik to pracownik Ministerstwa Sprawiedliwości.

- wykluczanie się zakresów
np. Nietoperz jest to prowadzący nocny tryb życia ptak o bardzo dobrze rozwiniętym
zmyśle słuchu.
Szczególnym przypadkiem wykluczania się zakresów jest błąd przesunięcia
kategorialnego . Ma on miejsce, gdy w definiendum i definiensie występują wyrażenia z różnych
kategorii ontologicznych (kategorii bytów), czyli rzeczy, cechy, stany i stosunki, np.: „czerń to tyle, co
rzecz czarna”.

Należy podkreślić, że błędy nieadekwatności odnoszą się jedynie do definicji sprawozdawczych, które
mogą być prawdziwe albo fałszywe. Definicje projektujące, o których była mowa wcześniej, nie są ani
prawdziwe ani fałszywe. Są to bowiem arbitralne stwierdzenia, że pewnym wyrazom lub wyrażeniom
zostaje nadane określone znaczenie.

Próbny test !!!!!!!!!!!!!!!!!!!
1. Z definiendum, łącznika definicyjnego i definiens zbudowana jest definicja:
a) indukcyjna,
b) cząstkowa,
c) równościowa,
d) sprawozdawcza.

2. Podział definicji ze względu na punkt odniesienia wyróżnia definicje:
a) realne i nominalne,

b) sprawozdawcze i projektujące,
c) równościowe i nierównościowe,
d) klasyczne i zakresowe.

Podział logiczny
Na przykład tort funktor możemy podzielić na trzy części:
• nazwotwórczy,
• zdaniotwórczy,
• funktorotwórczy.

Podział logiczny zakresu nazwy A to zbiór zakresów nazw B

, B

, …, B

podrzędnych względem

zakresu nazwy A, parami rozłącznych i takich, że ich suma równa się zakresowi nazwy A.
Definicja ta zawiera w sobie dwa warunki:
• warunek rozłączności (…parami rozłącznych…);
• warunek adekwatności, inaczej zupełności (… ich suma równa się zakresowi nazwy A).
Zakres nazwy A to całość dzielona (totum divisionis).
Zakresy nazw B

, B

, …, B

to człony podziału (membra divisionis).

Wśród

funktorów

wyróżniamy:

całość dzielona

• funktory

nazwotwórcze

• funktory

zdaniotwórcze

człony podziału

• funktory

funktorotwórcze

Zasada podziału to cecha, z uwagi której wyróżniane są człony podziału.
Wedle jakiej innej cechy możemy dokonać podziału nazwy funktor?
np. Zasadą podziału ludzi na kobiety i mężczyzn jest płeć.

Zauważmy także, że wyróżnienie członów podziału ze względu na jednolitą zasadę podziału jest bardzo
istotne z punktu widzenia poprawności podziału.
np. Podział Polaków na blondynów i rolników – jest całkowicie wadliwy (nierozłączny i niezupełny!)
Podział logiczny może być sztuczny lub naturalny. Niełatwo ustalić, co się przez te dwa określenia
rozumie, rozróżnienie nie jest tu ostre, niemniej rozróżnienie to jest potrzebne.
Typowym podziałem naturalnym nazywamy taki podział, przy którym w każdym członie podziału grupują
się przedmioty pod wieloma ważnymi dla nas względami podobne, a niepodobne na ogół do
przedmiotów z innych członów podziału.

Natomiast typowym podziałem sztucznym jest taki, przy którym do jednego członu podziału trafiają
przedmioty podobne pod jakimś jednym tylko względem, a pod wieloma innymi niepodobne do siebie.
np. Podział ludzi według pierwszej litery ich nazwiska jest podziałem sztucznym, natomiast ich podział ze
względu na wiek, płeć czy wykonywany zawód jest podziałem naturalnym.

Podział dychotomiczny według cech sprzecznych: to taki podział logiczny, w którym wyróżnia się dwa
człony tego podziału według następującej zasady: do jednego zalicza się wszystkie elementy całości
dzielonej, które posiadają wskazaną cechę w zasadzie podziału, do drugiego zaś te – które owej cechy
nie posiadają.

Przykłady:
1. podział liczb całkowitych na parzyste i nieparzyste;
2. podział kręgowców na ssaki i nie-ssaki;
3. podział ludzi na kobiety i na nie-kobiety.

Często jednak podział dychotomiczny według cech sprzecznych jest niewystarczający. Rozróżniamy
więc inny rodzaj podziału tzw. podział według zasady specyfikacyjnej , czyli podział według różnych
odmian określonej cechy. Cecha, według której dokonujemy podziału nazywamy determinandą , jej
odmiany –
determinatami .
Przykład:
Buty możemy podzielić według determinandy rozmiar, a determinatami będą numery …,10, 11, 12, 13,
…, 45, 46,…

Klasyfikacja jest to wielostopniowy podział logiczny.

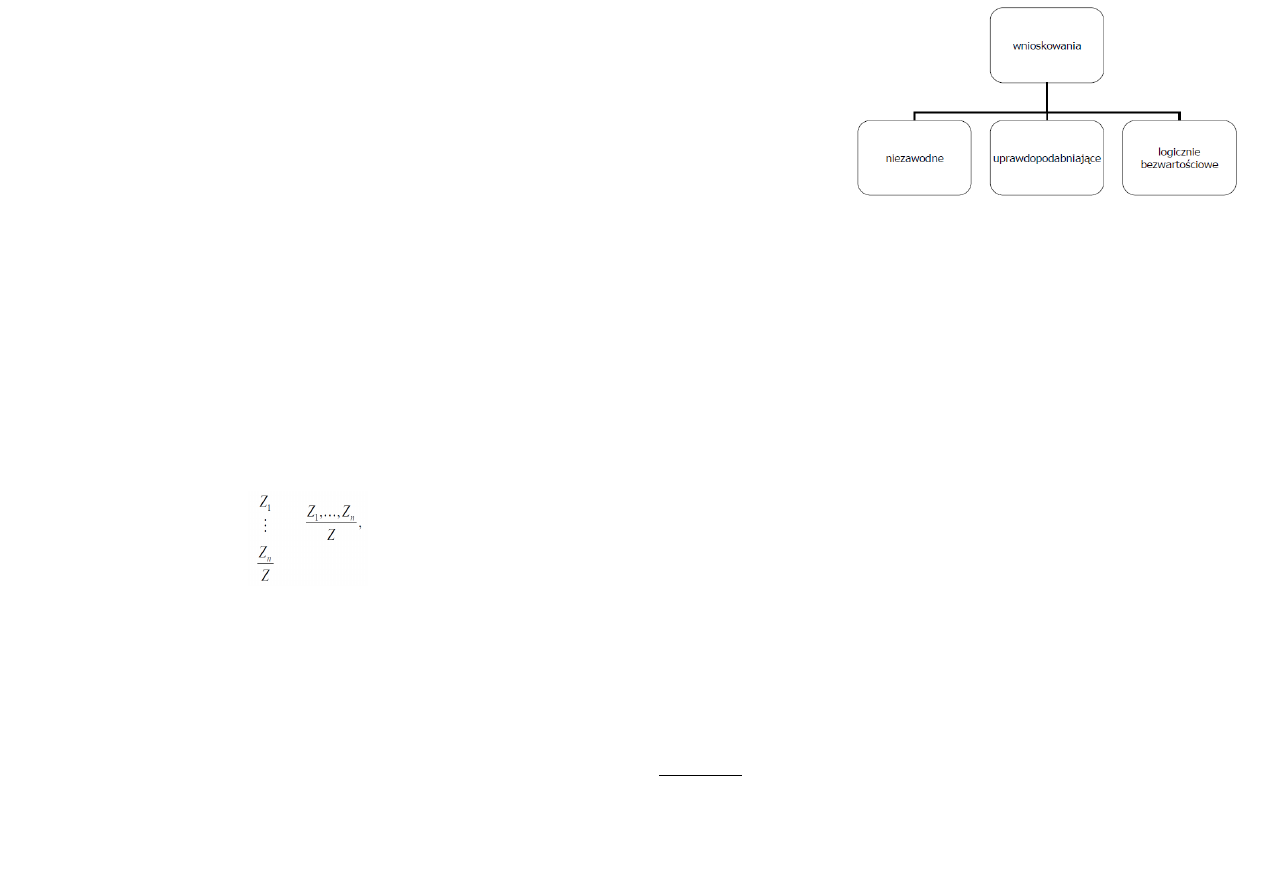
Od podziału logicznego należy odróżniać wyróżnianie typów przedmiotów.
W tym drugim przypadku rozważamy, w jakim stopniu przedmioty z pewnego zbioru mają cechy zbliżone
do przedmiotu o interesujących nas cechach. Przedmioty, które stosunkowo mało różnią się od
przedmiotu wzorcowego, z którym je porównujemy, nazywamy przedmiotami typowymi.

Pewne przedmioty mogą znajdować się na pograniczu dwóch zbliżonych typów i można by je zaliczać do
obu tych typów.
Dlatego przy wyróżnianiu typów nie ma warunku rozłączności i adekwatności.
Partycja jest to wyróżnienie części składowych pewnego przedmiotu.
Wnioskowanie
Wnioskowanie jest to proces myślowy, w którym na podstawie mniej lub bardziej
stanowczego uznania pewnych zdań – zwanych przesłankami – dochodzimy do uznania
innego zdania – wniosku, którego bądź dotychczas nie uznawaliśmy wcale, bądź uznawaliśmy mniej
stanowczo; przy czym stopień stanowczości uznania wniosku nie przewyższa stopnia uznania
przesłanek.

Wnioskowania wypowiadamy za pomocą wypowiedzi inferencyjnych:
ponieważ Z

,…,Z

, zatem Z;

,…,Z

, zatem Z;

skoro Z

,…,Z

, to Z;

,…,Z

, więc Z;

Z, ponieważ Z

,…,Z

, itd.

Reprezentujemy w takich oto obrazkach:

Gdzie Z

,…,Z

symbolizują przesłanki, zaś Z – wniosek.

Często jednak wnioskowania ubieramy w formę wypowiedzi argumentacyjnych – wypowiedzi, za pomocą
których chcemy nakłonić kogoś do przyjęcia, bądź odrzucenia pewnych poglądów.
Wypowiedzi argumentacyjne oprócz wnioskowań (składników logicznych)
zawierają również składniki retoryczne – nieistotne z punktu widzenia logiki, ale istotne jako środki
perswazji.
Rozważmy taką oto wypowiedź argumentacyjną:
Tylko ślepy nie widzi, że X to faszysta. Czy nie faszyści właśnie, jak jeden mąż, jak stado baranów,
opowiadają się zawsze za dyktaturą? I otóż nasz X zaleca dyktaturę właśnie jako panaceum na wszelkie
trudności, przed którymi stajemy po latach niewoli. Cóż, widocznie ten człowiek nie czuje się dobrze w
demokracji. I we własnym kraju. Chce, żebyśmy się znowu zgodzili na łańcuchy.
Jeśli to nie faszyzm, to jak to nazwać?

W gruncie rzeczy można ją sprowadzić do wnioskowania następującego:

Wszyscy faszyści opowiadają się za dyktaturą.

X opowiada się za dyktaturą.

______________________________

X jest faszystą.

Niezawodne – wnioskowania, w których mamy prawo uznać wniosek z takim samym stopniem
pewności, z jakim uznajemy przesłanki.

Wnioskowania uprawdopodabniające – w których mamy prawo uznać wniosek, jednak z mniejszym
stopniem pewności, niż przesłanki.

Przykładem wnioskowania niezawodnego jest wnioskowanie dedukcyjne – takie wnioskowanie, w
którym wniosek wynika logicznie z koniunkcji przesłanek.

Jeżeli Jaś kocha Małgosię, to przynosi jej dużo kwiatów. Jaś kocha Małgosię.

Jaś nosi Małgosi dużo kwiatów.

Wnioskowanie postaci: Z1,....,Zn
Z
jest dedukcyjne wtedy i tylko wtedy, gdy formuła ( A1 ʌ … ʌ An) => B
jest tautologią.

Schemat wnioskowania dedukcyjnego nazywamy niezawodnym schematem
wnioskowania.

Błędy we wnioskowaniu dedukcyjnym

Błąd materialny popełniamy wtedy, jeżeli bierzemy we wnioskowaniu przesłanki fałszywe, mylnie
uważając je za prawdziwe.

Przykład:

Każde zwierzę żyjące w głębinach morza jest rybą.

Każdy wieloryb jest zwierzęciem żyjącym w głębinach morza.

Każdy wieloryb jest rybą.

Błąd formalny polega na tym, że ktoś uważa swoje wnioskowanie za dedukcyjne, a w rzeczywistości
dany wniosek nie wynika logicznie z przesłanek, to znaczy, że wzór wedle którego przebiega
wnioskowanie nie jest w rzeczywistości prawem logicznym, a więc to wnioskowanie w rzeczywistości nie
jest wnioskowaniem dedukcyjnym.
Przykład:Każdy prokurator jest urzędnikiem. Każdy urzędnik jest prokuratorem.

Z prawdziwej przesłanki otrzymujemy fałszywy wniosek, a powyższe wnioskowanie nie jest dedukcyjne.

Wnioskowania uprawdopodabniające są to wnioskowania, w których mamy prawo uznać wniosek,
jednak z mniejszym stopniem pewności niż przesłanki.

Zajmiemy się trzema rodzajami wnioskowań uprawdopodabniających:
- wnioskowaniami redukcyjnymi,
- wnioskowaniami przez analogię,
- wnioskowaniami statystycznymi.

We wnioskowaniu redukcyjnym wniosek nie wynika logicznie z przesłanek, natomiast:
albo: (I) przesłanki wynikają logicznie z samego tylko wniosku,
albo (II) z wniosku i niektórych przesłanek wynikają logicznie przesłanki pozostałe.

Przykładem przypadku (I) jest tzw. wnioskowanie przez indukcję enumeracyjną
niezupełną:

Mój kot miauczy żałośnie, gdy jest głodny.

Kot sąsiada miauczy żałośnie, gdy jest głodny.

Kot Justyny też miauczy żałośnie, gdy jest głodny.

Wszystkie głodne koty miauczą żałośnie.

W tym wnioskowaniu z przesłanek jednostkowych stwierdzających, że pewne konkretne przedmioty
określonego rodzaju (np. koty – mój, sąsiada, Justyny) mają pewną cechę (miauczą żałośnie, gdy są
głodne), wyprowadza się wniosek ogólny, że wszystkie przedmioty owego rodzaju mają ową cechę.

Schemat wnioskowania przez indukcję enumeracyjną niezupełną wygląda
następująco:

Łatwo zauważyć, że ze zdania ogólnego Wszystkie S mają P przesłanki szczegółowe wynikają logicznie
(czyli, że w takim wnioskowaniu wniosek jest racją, a przesłanki następstwem).
Jednakże, nawet jeśli wszystkie przesłanki takiego wnioskowania są prawdziwe, to nie mamy gwarancji,
że wniosek również jest prawdziwy.
Przesłanki uprawdopodabniają wniosek, ale nic poza tym.

Im więcej przebadamy przedmiotów rodzaju, o którym chcemy wnioskować – czyli im większą liczbą
przesłanek będziemy dysponować – tym wniosek będzie lepiej uprawdopodobniony.

Im bardziej różnorodne będą nasze jednostkowe przesłanki (np. zróżnicowane pod względem
pochodzenia lub rasy kotów) – tym wniosek będzie bardziej uprawdopodobniony.

Zawsze może się jednak zdarzyć, że trafimy na kota upośledzonego albo na
twardego kota ekstremistę, albo na łagodnego kota – taoistę – takiego,
który nie będzie miauczał.
(II) z wniosku i niektórych przesłanek wynikają logicznie przesłanki pozostałe.
Przykładem takiego rozumowania jest tzw. wnioskowanie z uznanego następnika:
p=> q q/p

Wniosek nie wynika tu logicznie z przesłanek, ale z wniosku postaci p i
przesłanki postaci p q wynika logicznie przesłanka q.

We wnioskowaniu przez analogię z faktu, że jakieś przedmioty są do siebie podobne pod pewnym
względem wnioskujemy, że są do siebie podobne również pod innym:

Mój kot miauczy żałośnie, gdy jest głodny.

Kot sąsiada miauczy żałośnie, gdy jest głodny.

Kot Justyny też miauczy żałośnie, gdy jest głodny.

Kot Beaty zapewne również miauczy, gdy jest głodny.

Schemat wnioskowania przez analogię wygląda następująco:
S1 jest P
S2 jest P
S3 jest P
…..
Sn jest P
S(n-1) jest P

Od schematu indukcji enumeracyjnej niezupełnej różni się więc tym, że wniosek nie jest tu zdaniem
ogólnym, mówiącym o wszystkich przedmiotach badanego rodzaju, ale zdaniem szczegółowym,
mówiącym o następnym przedmiocie badanego rodzaju.

Wnioskowanie przez analogię może mieć nieco inną strukturę:

Przedmiot X ma własności A, B, C i D.

Przedmiot Y ma własności A, B, C.

Przedmiot Y ma własność D.

Przykład:

Zenkowi, Jurkowi i Włodkowi nie udało się naprawić tej pralki.

Zdzisiowi też się to nie uda.

Zauważmy, że własności z uwagi, na które stwierdza się podobieństwo rozważanych obiektów, nie
zawsze są określone wyraźnie, jak choćby w tym przykładzie:
Co takiego może łączyć czterech panów, że z faktu, że trzech z nich nie dało rady pralce,
uprawdopodabniałby wniosek, że czwartemu również się nie uda?

Wiarygodność wnioskowania przez analogię zależy od tego, czy podobieństwo między rozpatrywanymi
przedmiotami jest konsekwencją związku wewnętrznego między ich cechami, czy też jest czysto
przypadkowe, jedynie zewnętrzne.
[K. Szymanek, Sztuka argumentacji. Słownik terminologiczny]
Stąd też następujące wnioskowanie specjalnie wiarygodne nie jest:
Pierwszy świadek ma na imię Jan, jest łysy, garbaty i kłamie, a drugi – również
Jan – też jest łysy i garbaty, więc pewnie ten drugi również kłamie.

We wnioskowaniu statystycznym na podstawie stwierdzonych cech niektórych elementów pewnego
zbioru Z wnioskuje się o statystycznych własnościach całego zbioru Z.
Zbiór Z nazywany jest populacją (wzgl. zbiorowością ogólną), natomiast zespół elementów o
własnościach znanych nazywa się próbą (próbą losową).

Wnioskowania statystycznie nie są wnioskowaniami niezawodnymi. Z reguły wynikiem takiego
wnioskowania jest stwierdzenie, że populacja ma z określonym prawdopodobieństwem własność,
będącą przedmiotem wnioskowania.
[K. Szymanek, Sztuka argumentacji. Słownik terminologiczny]

Wróćmy do wnioskowania o kotach:

Mój kot miauczy żałośnie, gdy jest głodny.

Kot sąsiada miauczy żałośnie, gdy jest głodny.

Kot Justyny też miauczy żałośnie, gdy jest głodny.

Wszystkie głodne koty miauczą żałośnie.

Nawet jeśli przesłanki owego wnioskowania są prawdziwe, to nie mamy gwarancji, że wśród
nieuwzględnionych przez nas przypadków – kotów, których nie znamy – nie ma takiego przypadku, który
wnioskowi ogólnemu by przeczył; wniosek nie wynika tu więc logicznie z przesłanek.

Zauważmy, że jeśli w indukcji enumeracyjnej niezupełnej dołożymy jeszcze jedną przesłankę
stwierdzającą, że w przesłankach jednostkowych wymienione są wszystkie przedmioty badanego
rodzaju, to mamy wtedy do czynienia z indukcją enumeracyjną zupełną.

Schemat indukcji enumeracyjnej zupełnej wygląda następująco:

Takie rozumowanie jest wnioskowaniem dedukcyjnym: z przesłanek jednostkowych i przesłanki
gwarantującej kompletność listy badanych przedmiotów wniosek ogólny wynika logicznie.

Test próbny !!!!!!!!!!!!!
1. Wyróżniamy wnioskowania
a) niezawodne, dedukcyjne, logicznie bezwartościowe,
b) niezawodne, enumeracyjne, dedukcyjne,
c) niezawodne, uprawdopodabniające, logicznie bezwartościowe,
d) dedukcyjne, enumeracyjne, logicznie bezwartościowe.

2. Rodzaje wnioskowań uprawdopodabniających to wnioskowania:
a) redukcyjne, przez analogię, statystyczne,
b) niezawodne, enumeracyjne, dedukcyjne,
c) dedukcyjne, enumeracyjne, logicznie bezwartościowe,
d) niezawodne, dedukcyjne, logicznie bezwartościowe.

3. Każdy prokurator jest urzędnikiem/każdy urzędnik jest prawnikiem to

a) błąd materialny,
b) wnioskowanie niezawodne,
c) wnioskowanie uprawdopodabniające,
d) błąd formalny.

Przekazywanie myśli

Pytania i odpowiedzi
Pytania są zdaniami w sensie gramatycznym, ale nie w sensie logicznym. Pytania nic bowiem nie
stwierdzają, niczego nie opisują i w związku z tym nie można im przypisać żadnej wartości logicznej.
Np. „Czy byłeś wczoraj w kinie?”
„Kto jest najlepszym skoczkiem narciarskim świata?”
„Jak doszło do upadku Cesarstwa Rzymskiego?”
Nie sposób orzec czy są to wypowiedzi prawdziwe, czy fałszywe. Wartość logiczną mogą mieć dopiero
odpowiedzi na te pytania.
Pytania można dzielić na zamknięte i otwarte.

Zadając pytanie zamknięte, wyznaczamy równocześnie schemat odpowiedzi. Pytając „Ilu posłów
wchodzi w skład Sejmu?” oczekujemy odpowiedzi „W skład sejmu wchodzi n posłów”, gdzie n jest
odpowiednią liczbą naturalną.

Z kolei pytanie „Czy Prezydentowi przysługuje inicjatywa ustawodawcza?” przesądza, że odpowiedzią,
jakiej się spodziewamy, jest zdanie
„Tak, Prezydentowi przysługuje inicjatywa prawodawcza” albo „Nie, Prezydentowi nie przysługuje
inicjatywa prawodawcza”.

Pytaniami zamkniętymi są też pytania ankietowe z zamkniętą listą odpowiedzi.
Odmiennie przedstawia się sytuacja w przypadku pytań otwartych.
Odpowiedzi na pytania otwarte np. „Jak doszło do tego wypadku samochodowego?” lub „Dlaczego
wielu absolwentów szkół średnich chce studiować prawo?” wymagają dłuższego wywodu.

Nie sposób przewidzieć, z ilu zdań i jak zbudowanych, będzie składać się wypowiedź.
Inny podział pytań wyróżnia: pytania rozstrzygnięcia i pytania dopełnienia.

Pytania rozstrzygnięcia zaczynają się od partykuły „czy”.
np. „Czy umiesz grać w brydża?” i pytania, które można sprowadzić do takiej struktury np. „Pożyczysz mi
100 zł?”.
Pozostałe pytania nazywamy pytaniami dopełnienia.
Budowę pytań i odpowiedzi prześledzimy na przykładzie pytania
„Który z kontynentów jest największy?”.

Wyznacza ono schemat odpowiedzi „x jest największym kontynentem”, gdzie x należy do zbioru
kontynentów.

Ten będący funkcją zdaniową schemat odpowiedzi zwany jest osnową pytania. Zbiór wszystkich x, który
określimy jako zbiór Z (zbiór wszystkich kontynentów), to tzw. zakres niewiadomej

pytania.

Jeżeli w odpowiedzi na dane pytanie wystąpi element z zakresu niewiadomej pytania, to odpowiedź
będzie odpowiedzią właściwą.

Natomiast, gdy partykułę zastąpimy elementem nienależącym do tego zakresu, otrzymamy odpowiedź
niewłaściwą.

Odpowiedzią właściwą może być zarówno zdanie prawdziwe, jak i fałszywe.
Odpowiedź właściwa i niewłaściwa.

Odpowiedzią właściwą na postawione pytanie będą m.in. zdania „Azja jest największym kontynentem”,
„Europa jest największym kontynentem”, ale odpowiedź „Polska jest największym kontynentem” będzie
uznana za niewłaściwą.

Pozytywne założenie pytania jest stwierdzeniem, że wśród odpowiedzi właściwych na dane pytanie
istnieje przynajmniej jedno zdanie prawdziwe.

Poprzez negatywne założenie pytania stwierdzimy zaś, że w zbiorze takich odpowiedzi jest co najmniej
jedno zdanie fałszywe.
Jeżeli w przypadku jakiegoś pytania jego pozytywne lub negatywne założenie jest zdaniem fałszywym, to
wówczas mamy do czynienia z pytaniem niewłaściwie postawionym.
Np. „Kto z Polaków otrzymał Nagrodę Nobla w dziedzinie ekonomii?” ma fałszywe pozytywne założenie
pytania, a pytanie „Które z państw nadbałtyckich leży w Europie?” – fałszywe negatywne
założenie pytania.
Do grupy pytań niewłaściwie postawionych zaliczymy także skierowanie
do uczciwego człowieka pytanie „Czy przestałeś się już zajmować paserstwem?”.

Właściwie postawione pytania rozstrzygnięcia mogą być pytaniami dwu- albo wieloczłonowymi.

Pytanie „Czy wczoraj padał deszcz?” jest dwuczłonowe, gdyż posiada ono tylko dwie odpowiedzi
właściwe: „Wczoraj padał deszcz” oraz „Wczoraj nie padał deszcz”, będące względem siebie
odpowiedziami sprzecznymi.

Natomiast pytanie „Czy najtrudniejszym przedmiotem na pierwszym roku studiów prawniczych jest
logika, wstęp do prawodawstwa czy prawo rzymskie?” jest już wieloczłonowym pytaniem
rozstrzygnięcia.
Występują tu więcej niż dwie odpowiedzi właściwe.

Oprócz podziału odpowiedzi na odpowiedzi prawdziwe i fałszywe
oraz na właściwe i niewłaściwe możemy wyróżnić odpowiedzi całkowite wprost, całkowite niewprost i
częściowe.
Odpowiedź:całkowita wprost, całkowita niewprost, częściowa.

Jeżeli na pytanie „Które miasto jest stolicą Polski?” padnie odpowiedź „Warszawa jest stolicą Polski”, to
będziemy mieć do czynienia
z odpowiedzią całkowitą wprost .
Odpowiedzią całkowitą niewprost byłaby odpowiedź „Warszawa jest głównym miastem Polski i
siedzibą wszystkich najważniejszych organów władzy państwowej”.
Odpowiedź ta przekazuje informacje, z których jednoznacznie wynika odpowiedź właściwa.

Odpowiedź częściowa natomiast, nie mając cech odpowiedzi całkowitej, eliminuje jednak część
spośród wszystkich wchodzących w rachubę odpowiedzi właściwych.
Na powyższe pytanie odpowiedzią częściową jest np. zdanie „Stolicą Polski jest miasto leżące na
Mazowszu”.

Perswazja i dyskusja

Przekazywanie myśli może następować nie tylko w drodze udzielania odpowiedzi na postawione
pytania, lecz również poprzez wypowiedź w pewnej mierze spontaniczną, niesprowokowaną żadnymi
pytaniami.

Już w starożytności doceniono umiejętność poprawnego, pięknego i skutecznego
wysławiania się. Z tych czasów pochodzi określenie retoryka – sztuka wymowy. Wtedy też
ukształtowały się dwa zasadnicze style retoryczne: azjanizm i attycyzm.

Azjanizm charakteryzował się ozdobnością i kwiecistością wypowiedzi, attycyzm – prostotą i jasnością
myśli.

W okresie średniowiecza retoryka zaliczana była do sztuk wyzwolonych.
Za podstawowy cel retoryki uznawano i uznaje się w dalszym ciągu perswazję. Środkiem
umożliwiającym realizację tego celu ma być przestrzeganie trzech zasad retoryki: organiczności,
stosowności i funkcjonalności.

Zasada organiczności nakazuje traktować wypowiedź jako organiczną całość i wymaga
zachowania wewnętrznego porządku całości.

Zasada stosowności wskazuje, że w każdym przypadku niezbędne jest odpowiednie dobranie środków
retorycznych.

Zasada funkcjonalności przypomina, że funkcją wypowiedzi jest przekonanie słuchacza i realizacji tego
właśnie zadania należy podporządkować całą wypowiedź.

Jeżeli proces przekonywania odbywa się w formie wymiany zdań między pewną liczbą osób, to wtedy
mamy do czynienia z dyskusją .
Poprawna logicznie dyskusja powinna być klarowna, merytoryczna i konkluzywna.

Klarowność polega na konieczności określenia języka dyskusji tak, aby był w pełni zrozumiały dla
wszystkich dyskutantów, merytoryczność wymaga określenia przedmiotu dyskusji, a konkluzywność – jej
założeń.
Umiejętność dyskutowania rozumiana jako sztuka prowadzenia sporów określana jest mianem erystyki .

Do najbardziej znanych chwytów erystycznych zaliczamy:
- argumentum ex contesso , który odznacza się dostosowywaniem prezentowanej argumentacji do
człowieka, z którym toczy się spór; stosując tę metodę, na potwierdzenie swojego stanowiska używa się
racji przeciwnika, czyli próbuje się wyprowadzić wnioski z przyjętych przez przeciwnika przesłanek,

- argumentum ad personam jest skierowany do osoby, a właściwie przeciwko osobie, z którą prowadzi
się spór; zamiast dyskutować o przedmiocie sporu, atakuje się personalnie przeciwnika,

- argumentum ad baculum to inaczej groźba użycia przemocy; obowiązujące regulacje prawne
najczęściej wprost zakazują korzystania z tego siłowego argumentu,

- argumentum ad crumenam - punktem odniesienia są tu interesy materialne osób uczestniczących w
dyskusji lub przysłuchujących się jej, tego rodzaju argumentem jest obietnica łapówki, a w
łagodniejszej formie – wskazywanie, że przyjęcie danego rozwiązania zwiększy dochody
zainteresowanych osób,
-argumentum ad misericordiam – zamiast do racji merytorycznych następuje odwołanie się do
czynników mających wzbudzić litość; przykładem może być powoływanie się na trudną sytuację
życiową, rodzinną, zdrowotną i finansową
(np. oskarżonego, obwinionego), na fakt, że nikt nigdy go nie lubił i nie rozumiał,

- argumentum ad verecundiam – polegający na szukaniu poparcia swoich też w wypowiedziach
autorytetów, którym oponent lub decydent raczej się przeciwstawi,

- argumentum ad invidiam – sposób argumentacji zmierzający do wywoływania zawiści słuchaczy,

- argumentum ad vanitatem – odwołuje się do próżności słuchaczy; mówiący poprzez prawienie
słuchaczom pochlebstw liczy na to, że zyska ich przychylność, niezależnie od wartości merytorycznej
prezentowanej argumentacji,

- argumentum ad populum – słuchaczom mówi się nie to, co odpowiada rzeczywistości, lecz to, co
chcieliby oni usłyszeć.
Sofizmat – rozumowanie niepoprawne, które jest prowadzone tak, by stwarzać pozory poprawności.
Osoba w ten sposób przeprowadzająca rozumowanie stara się świadomie ukryć występujący w nim błąd
logiczny.

np. Sofizmat o Elektrze, który przedstawia się następująco:
Elektra wie, że Orestes jest jej bratem, lecz gdy staje on przed nią zasłonięty, Elektra nie wie tego, co
wie.
Innym przykładem starożytnego problemu erystycznego jest paradoks nauczyciela i ucznia. Otóż grecki
sofista Protagoras z Abdery, udzielając jednemu ze swoich uczniów lekcji wymowy sądowej, umówił się
z nim, że zapłatę za naukę otrzyma, o ile ten wygra swój pierwszy proces. Uczeń jednak po skończonej
nauce w ogóle nie podejmował żadnej sprawy sądowej. Zniecierpliwiony Protagoras sam wytoczył mu
proces o zapłatę. W sądzie uczeń ten przyjął następującą obronę: „Jeżeli przegram ten proces, to

stosownie do umowy z moim nauczycielem nie będę musiał mu płacić, natomiast gdy wygram proces,
to brak obowiązku zapłaty będzie wynikać wprost z rozstrzygnięcia sądowego”. Z kolei
Protagoras replikował: „Jeżeli uczeń przegra proces, to w myśl orzeczenia sądu będzie musiał mi
zapłacić, jeżeli zaś wygra proces, a przecież będzie to jego pierwszy i w dodatku wygrany
proces, to też będzie musiał zapłacić, bo tak się umówiliśmy”.

Niestety, nie jest wiadome ani, jaką decyzję w tej sprawie podjął sąd, ani nawet to, czy historia ta
rzeczywiście miała miejsce, czy też jest tylko kolejnym paradoksem wymyślonym przez starożytnych
filozofów.
Szkoła mówców z Megary wsławiła się analizowaniem słynnych paradoksów.

Do historii przeszedł już paradoks „kłamcy” Eubulidesa, ucznia Euklidesa, którego treść jest
następująca: „Czy prawdę mówi, kto mówi, że to, co mówi, jest „fałszem?”.

Inny przykład paradoksu to paradoks „łysego”, a więc: „Ile włosów
trzeba mieć, aby nie być łysym?”, czy też paradoks „rogacza”:
„Rogów nie zgubiłeś, a czegoś nie zgubił, to posiadasz, więc masz rogi”.
Błędy w przekazywaniu myśli

Celem przekazywania myśli, przekształconych do postaci odpowiedniego komunikatu słownego, jest
uzyskanie porozumienia między nadawcą tego komunikatu a jego odbiorcą.
Przekazana informacja ma wywołać u odbiorcy myśli zgodne z intencją nadawcy.
W przypadku, gdy informacja nie wywoła u odbiorcy żadnych myśli, będziemy mieć do czynienia z
sytuacją niezrozumienia, gdyż odbiorca nie zrozumie przekazanego komunikatu.

Jeżeli komunikat spowoduje powstanie u odbiorcy określonych myśli, które jednak będą odbiegały od
intencji nadawcy, to powiemy, że doszło do nieporozumienia.
Błędy mogące wystąpić przy przekazywaniu myśli mogą być związane z wieloznacznością
poszczególnych wyrazów tworzących dane wyrażenie.

Są to błędy ekwiwokacji.

Takim błędem obarczona jest wypowiedź „Jan interesuje się zamkami” bez wyjaśnienia, o które ze
znaczeń wieloznacznego wyrazu „zamek” chodzi.

Szczególnym przypadkiem błędu ekwiwokacji jest błąd czterech terminów.

Polega na użyciu jako terminu nazwy wieloznacznej w różnych znaczeniach
lub różnych supozycjach.
Np. Każdy zamek jest budowlą.
Niektóre zamki są urządzeniami blokującymi drzwi.
Niektóre urządzenia blokujące drzwi są budowlami.

Błędem ekwiwokacji jest też błąd figuralnego myślenia polegający na dosłownym rozumieniu wyrazów
czy wyrażeń użytych przenośnie.
np. rozumowanie dosłowne „robienie z igły widły” wskazywałoby na działanie niemożliwe do
zrealizowania.
Popełnienie błędu ekwiwokacji może także wystąpić wskutek użycia wyrażenia okazjonalnego, czyli
wyrażenia, które nie ma trwale określonego zbioru desygnatów.

Denotacja wyrażeń takich jak: „ja”, „twoja żona”, „dwa lata temu”, „jutro”, „stolica tego państwa”, „tutaj”
rozumiana jako ich zakres, zależna jest od okoliczności (okazji), w jakich użyto tych wyrażeń.

Wypowiedzi „Ci ludzie spóźnili się na nasze zebranie”, „Było tam bardzo ciekawie” czy „On uważa, że nie
powinien wtedy podpisywać umowy” stwarzają pole do różnych interpretacji dopóty, dopóki nie ustali się,
do kogo albo czego odnoszą się wyrażenia okazjonalne z tych wypowiedzi.
Druga grupa błędów związanych z wieloznacznością wyrażeń dotyczy wieloznaczności składniowej.
Mówimy wówczas o błędzie amfibologii.

Polega on na tym, że źródło wieloznaczności danego wyrażenia tkwi w jego strukturze, a nie w
pojedynczych wyrazach.
np. napis w sklepie „guma do żucia dla dzieci bez cukru” prowadzi do wątpliwości, czy chodzi o gumę
bez cukru, czy o dzieci bez cukru.

Nieporozumienie albo nawet niezrozumienie może być również skutkiem posługiwania się wyrażeniami
nieostrymi.

Nazwa „wysoki człowiek” wywoła inne skojarzenia u przedszkolaka, a inne u dorosłego człowieka
mierzącego 198 cm wzrostu.

Także inne wyrażenia wchodzące w skład zdania mogą charakteryzować się pewną chwiejnością
znaczeniową, co może spowodować różne zrozumienie danego komunikatu słownego przez jego
nadawcę i odbiorcę.

Zdania „Jaś lubi Małgosię” czy też „Jacek umie wysoko skakać” nie przez każdego będą rozumiane w
ten sam sposób.
Innym jeszcze błędem przy przekazywaniu informacji może być niedopowiedzenie występujące w dwóch
postaciach: niedopowiedzenie kwantyfikacji albo jako niedopowiedzenie relatywizacji.

Niedopowiedzenie kwantyfikacji wystąpi wówczas, gdy w naszej wypowiedzi
nie zostanie określone, czy dotyczy ona niektórych, czy wszystkich elementów danej klasy.
Wypowiedź „Niemcy dbają o porządek” inaczej będzie rozumiana po objęciu kwantyfikatorem ogólnym
(„Każdy Niemiec dba o porządek”), a inaczej - kwantyfikatorem szczegółowym („Niektórzy Niemcy dbają
o porządek”).

Niedopowiedzenie relatywizacji wiąże się z brakiem wskazania punktu odniesienia. Błąd taki popełni
dyskutant na międzynarodowym sympozjum prawa karnego, mówiąc, że za kradzież z włamaniem grozi
kara pozbawienia wolności od roku do lat 10 i nie dodając, którego państwa system karny ma na myśli.

Podobnie jest ze stwierdzeniem, że relacja „bycia wyższym” jest spójna, bez określenia, w jakiej klasie.

Próbny test !!!!!!!!!!!!!!!!!!!!!

1. Poprawna logicznie dyskusja powinna być;
a) klarowna, merytoryczna, konkluzywna,
b) merytoryczna, zrozumiała, konkluzywna,
c) prosta, zrozumiała, konkluzywna,
d) klarowna, stosowna, celowa.

2. Pytanie „Która rzeka jest najdłuższa w Polsce?”
a) jest pytaniem otwartym,
b) skłania do udzielenia odpowiedzi częściowej niewprost „Wisła jest rzeką, która ma 1047 km długości,
jej źródła znajdują się w południowej Polsce,
na wysokości 1106 m n.p.m., na zachodnim stoku Baraniej Góry w Beskidzie Śląskim, deltowatym
ujściem wpływa do Zatoki Gdańskiej”,
c) jest pytaniem rozstrzygnięcia,
d) skłania do udzielenia odpowiedzi całkowitej wprost „Wisła jest najdłuższą rzeką Polski”.

Wypowiedzi oceniające

W praktyce obok zdań opisujących rzeczywistość (analitycznych i syntetycznych), którym możemy
przypisać wartość prawdy lub fałszu, formułujemy często wypowiedzi, które zawierają naszą ocenę
rzeczywistości.
W takich wypowiedziach wyrażamy naszą aprobatę lub dezaprobatę jakiegoś stanu faktycznego.
Mówimy: „dobrze, że student Jan jest zdolny”, „źle, że sesja zimowa na Wydziale Chemii trwa tylko dwa
tygodnie”.

Takie wypowiedzi nazywamy wypowiedziami oceniającymi. Nie są one zdaniami w sensie
logicznym, gdyż nie można przypisać im wartości logicznej.
Mówiąc inaczej, wypowiedź oceniająca zawiera nasz sąd o stanie rzeczy S
ze względu na wartość C, której wystąpienie w stanie S uważamy za cenne (ewentualnie za niedobre).
Przedmiotem aprobaty lub dezaprobaty może być wszystko – stany rzeczy teraźniejsze, przyszłe lub
przeszłe, nawet stany rzeczy pomyślane tylko przez oceniającego, stan wiedzy, fakty przeżywania ocen
i inne.

Sformułowanie wypowiedzi oceniającej wymaga przyjęcia kryterium
i przeprowadzenia oceny.

Kryterium oceny jest to ogólny sąd o wartości wyrażony w zdaniu ogólno-twierdzącym lub ogólno-
przeczącym, na podstawie którego jest dokonywana ocena.
Kryterium to może przyjąć jedną z dwóch postaci:
- „wszystkie obiekty rodzaju R są cenne w sposób C” (przy aprobacie),
- „wszystkie obiekty rodzaju R są niedobre w sposób C” (przy dezaprobacie).

Biorąc pod uwagę stopień ogólności kryterium, rozróżniamy takie, które wyrażają ogólne oceny o
wartości (kryteria niepodporządkowanie) i są podstawą
do formułowania konkretnych sądów o wartości, jak też same konkretne sądy o wartości
sformułowane w oparciu o kryteria ogólne (konkretne sądy).
Kryteria stosowane przy formułowaniu wypowiedzi oceniających są często obarczone nieostrością, w
zależności od sposobu określenia wartości, którą uważamy za cenną.

Nieostre jest odwołanie do kryteriów estetycznych (co jest piękne, zależy od subiektywnego odczucia,
nie ma obiektywnego wzorca piękna), do kryteriów moralnych, bardziej precyzyjne są zaś kryteria
odwołujące się do wartości ekonomicznych (np. cena), czy do wartości użytkowych (np. trwałość).

Oceną nazywamy sąd dotyczący jednostkowego, konkretnego stanu rzeczy, kiedy to, posługując się
przyjętym kryterium oceny, pozytywnie lub negatywnie przeżywamy przypisane temu stanowi rzeczy
określonej wartości W.
np. wartości piękna, sprawiedliwości, oszczędności, dobra.

Odniesienie do jednostkowego, konkretnego stanu rzeczy odróżnia ocenę od kryterium
(które jest zawsze sądem ogólnym). Dokonanie oceny wymaga uprzedniego przyjęcia kryterium oceny
oraz uznanie tego kryterium za słuszne i przydatne do zastosowania w danej sytuacji.
Szczególnego rodzaju ocenami są oceny instrumentalne i oceny preferencyjne.

Przez ocenę instrumentalną rozumiemy sąd o przydatności czegoś jako środka
do osiągnięcia zamierzonego celu, np. pozytywnie oceniamy fakt wyposażenia samochodu w ABS,
mając na uwadze nasze bezpieczeństwo w czasie używania tego samochodu.

Z kolei ocena preferencyjna sprowadza się do porównania dwu lub więcej stanów rzeczy i wskazania
tego z nich, który w zestawieniu z pozostałymi, podlegającymi porównaniu stanami rzeczy, jest naszym
zdaniem lepszy albo gorszy ze względu na przypisane tym stanom określone wartości W.

np. grypę uznamy za lepszą (łagodniejszą) chorobę od gruźlicy, mimo że obie oceniamy negatywnie,
gdyż stanowi ona mniejsze zło dla osoby chorej;
natomiast akwarelę X uważamy za bardziej wartościową od samochodu Y, biorąc za kryterium ich ceny.

W rezultacie takiej oceny dwa przedmioty lub więcej przedmiotów podlega uszeregowaniu jako w
większym lub mniejszym stopniu spełniające kryterium.
Przez wypowiedź oceniającą rozumiemy taką wypowiedź, która zawiera ocenę jednostkowego,
konkretnego stanu rzeczy.
Wypowiedzi oceniające formułowane są na podstawie kryteriów uznanych przez formułującego
wypowiedź za słuszne.
Ma to miejsce, gdy formułujący wypowiedź poddaje określony stan rzeczy ocenie z punktu widzenia
wartości uznanych za cenne w przyjętym kryterium.

Wypowiedź ta zawiera sąd o wartości W i w wypowiedzi tej pozytywnie lub negatywnie przeżywamy
przypisane jakiemuś jednostkowemu, konkretnemu stanowi rzeczy określonej wartości W.

Wypowiedź oceniająca orzeka o relacji pomiędzy ocenianym jednostkowym stanem rzeczy, a kryterium.

Do wypowiedzi oceniających zaliczamy też wypowiedzi optatywne zawierające ocenę stanu rzeczy
przyszłego.
np. dobrze byłoby ze względu na stan psychiczny rodziców Jana (kryterium), gdyby Jan zaliczył w
pierwszym terminie egzamin ze statystyki (przyszły stan rzeczy).
Normy postępowania

Przez normę będziemy rozumieli wypowiedź zawierającą wzór postępowania, którego twórca normy
żąda w przyszłości od określonej osoby lub osób wtedy, gdy ta osoba lub osoby znajdą się w określonej
sytuacji.
Norma jest dyrektywą postępowania zmierzającą do wywołania w przyszłości określonego zachowania
się osób, do których jest skierowana.
Norma żąda wskazanego prostego zachowania lub zespołu zachowań (działań lub zaniechań), które
łącznie służą do spowodowania określonego stanu rzeczy.

Twórcą normy jest normodawca , przez którego rozumiemy osobę lub osoby ustanawiające normy.
Osobę (lub osoby), do których kierowana jest norma, nazywamy adresatem normy.

Normodawca za pomocą norm oddziałuje na postępowanie adresatów norm, wtedy gdy adresaci norm z
jakiegoś względu podlegają władzy normodawcy.
Odrębnym problemem jest budowa normy.
Niektórzy teoretycy przyjmują koncepcję trójelementową struktury normy prawnej: hipoteza – dyspozycja
- sankcja.

Koncepcja norm sprzężonych J. Landego zakłada dwuelementową budowę: hipotezę i dyspozycję.

Hipoteza normy to część normy zawierająca określenie adresata normy oraz określenie sytuacji, w
której adresat normy winien zastosować się do dyspozycji normy. Wskazuje skończoną liczbę
przedmiotów indywidualnych oraz określoną liczbę zachowań tych przedmiotów, od których wystąpienia
w danym stanie faktycznym zależy zaktualizowanie się obowiązku adresata postępowania zgodnego z
nakazem zawartym w dyspozycji normy.
Zakresem normowania normy nazywamy zbiór zachowań adresatów normy, które ta norma reguluje.
Zbiór ten może obejmować zarazem działania, od których adresat winien się powstrzymać,
jak i działania, które adresat powinien wykonać.
Wyróżniamy normy tetyczne i prawne.
Przepis normatywny (prawny) to jednostka systematyki tekstu prawnego, oznaczona jako artykuł,

paragraf, punkt, litera itp. Jest wypowiedzią, poprzez którą przekazywana jest informacja o
ustanowionej przez prawodawcę normie prawnej.
Norma prawna może być ujęta w jednym lub kilku przepisach prawnych.

Akt normatywny jest to opatrzony tytułem, usystematyzowany zbiór przepisów prawnych regulujących
daną dziedzinę spraw, ustanowiony przez organ władzy publicznej i wydany na podstawie posiadanej
przez ten organ kompetencji prawodawczej.
Aktami normatywnymi w polskim porządku prawnym są akty prawa powszechnie obowiązującego
(Konstytucja, ustawy, ratyfikowane umowy międzynarodowe i rozporządzenia), akty prawa
wewnętrznego (zarządzenie i uchwały) oraz akty prawa miejscowego.

Akt normatywny jest obiektem empirycznym, jest tekstem obejmującym określony zbiór przepisów
prawnych, które są elementami konstrukcyjnymi tego tekstu.

Zakresem zastosowania normy nazywamy zbiór wszystkich stanów faktycznych, w których norma
znajduje zastosowanie. Zakres ten ustalany jest na podstawie hipotezy normy.

Dyspozycja normy to część normy, w której następuje określenie zachowania będącego powinnością
(nakazanego, zakazanego, dozwolonego). Dyspozycja wskazuje te działania lub zaniechania adresata
normy, które są pożądane przez normodawcę.

Wyszukiwarka

Podobne podstrony:
Logika skrypt
NoPiP skrypt 2012, Bezpieczeństwo Wewnętrzne, Nauka o Państwie i Polityce
Brożek A, Logika. Skrypt Logika-Skrypt-2
Logika, skrypty
logika - skrypt, Edukacyjnie, M, Materiały WSPOL, Logika
Prawo prywatne międzynarodowe - skrypt 2012, Prawo, Prawo Prywatne Międzynarodowe
Brozek A Logika Skrypt Logika Skrypt I (2)
LOGIKA SKRYPT(1)
logika skrypt, Prawo, Prawo KUL I rok
Logika Psychologia N 2012 2013 Nieznany
LOGIKA skrypt z logiki

więcej podobnych podstron