Przygoda z uśmiechem zabawy matematyczne

Dodatkowe zabawy matematyczne, przewodnik cz. 1

Tydzień1.
Zajęcia: Znaczki

Grupowanie / klasyfikowanie różnorodnych obiektów według wybranych cech
Dzieci powinny mieć codziennie okazję do grupowania / klasyfikowania przedmiotów znajdujących
się w przedszkolu (także w domu) według różnych kryteriów np.:

- porządkując zabawki po zabawie - odkładają lalki do lalek, misie do misiów itd., przy
okazji mogą przeliczać ile czego jest na wskazanej półce, w rzędzie, w pudełku …,
- mogą grupować zabawki ze względu na wielkość kolor, materiał itp.,
- mogą grupować obrazki ze względu na to co na nich jest,
-zbierając rekwizyty (pomoce) po zabawach ruchowych także je grupują np. szarfy według
kolorów,
- sprzątając po posiłku wkładają do pojemników (ustawiają na tacach) osobno talerze,
osobno kubki, osobno sztućce itd.

Tydzień 2.
Zajęcia: Znamy magiczne słowa

Wykorzystujemy różnorodne sytuacje, w których mogą występować różnorodne regularności.
1) Podczas ćwiczeń gimnastycznych można tworzyć regularności, w których powtarzają się
sekwencje ruchów.
Np. zabawa ruchowa – dzieci stoją w kole. Prowadząca pokazuje dzieciom ciąg 2 lub 3 ruchów
(ewentualnie liczeniem nadając rytm), które dzieci rytmicznie wykonują (rytm ruchowy).
Następnie dzieci mogą samodzielnie wymyślać sekwencje ćwiczeń do wykonania. Np. każde
pokazuje układ, a pozostałe powtarzają zawsze po 3 razy.

2) Podczas zajęć muzycznych tworzymy sekwencje dźwiękowe (słowami, sylabami albo za
pomocą instrumentów muzycznych) i rytmicznie je powtarzać – powstaje regularność dźwiękowa.
Dzieci mogą same tworzyć takie układy, może je również podawać nauczyciel nakłaniając dzieci do
powtarzania i kontynuacji.
3) Podczas zajęć muzyczno-ruchowych.
4) Podczas zajęć plastycznych tworzymy regularności z kształtów, z plam. Mogą to być
regularności liniowe (np. szlaczki) albo płaszczyznowe (posadzki, parkietarze, mozaiki, ornamenty,
mandale).
5) Podczas rozwijania sprawności manualnej i wielokrotnego powtarzania tego samego wzoru
(rysowanie wzorów literopodobnych), nawlekanie na sznurek koralików według regularnego
wzoru.

Tydzień 4.
Zajęcia: Bezpieczne przejście przez jezdnię

Omawiamy pracę sygnalizatora dla pieszych uwzględniając kolor świateł – ich naprzemienność.
Najpierw werbalnie: czerwone, zielone, czerwone, zielone itd. Można to zakodować za pomocą
okrągłych kartoników w kolorze czerwonym i zielonym tworząc szlaczek zmieniających się świateł
(zob. szlaczki dla magicznych słów). Powstanie regularność wzrokowa, w której powtarza się
sekwencja 2-wyrazowa.

Analogicznie można omówić i opisać działanie sygnalizatora dla kierujących pojazdami: czerwone
(c), pomarańczowe (p), zielone (z), pomarańczowe (p), czerwone (c), pomarańczowe (p), zielone
(z), pomarańczowe (p), itd. Tu pojawia się regularność, w której powtarza się sekwencja 4-
wyrazowa. By to wyraźnie zobaczyć (nie tylko usłyszeć) warto zakodować ten rytm okrągłymi
kartonikami w trzech kolorach. Oznaczając kartoniki pierwszymi literami nazw kolorów powstaje
szlaczek: c, p, z, p, c, p, z, p, c, p, z, p, itd.

Tydzień 5.
Zajęcia: Jabłka, gruszki, śliwki...

Liczenie i porównywanie liczebności różnych zbiorów
Ważne by dzieci mogły codziennie coś policzyć i by mogły porównywać liczebności zbiorów
używając określeń: tyle samo, więcej, mniej i ustalając o ile mniej/więcej.
Sytuacje, w których łatwo to zrobić:
- Codziennie rano, sprawdzamy czy wszystkie dzieci są obecne. Pytamy: Czy wszyscy są? Kogo nie
ma? Ilu osób brakuje? Ile dzieci jest? Gdy dzieci wymieniają imiona nieobecnych, N. jednocześnie
prostuje palce – po jednym dla każdego nieobecnego, zachęca dzieci, by robiły to samo – w ten
sposób uczą się jak liczyć obiekty, których nie mogą zobaczyć ani dotknąć, N. pokazuje swoje
wyprostowane palce tak, by wszyscy je widzieli.
- Podczas zabaw ruchowych z szarfami, woreczkami, skakankami pytamy czy
szarf/woreczków/skakanek jest tyle samo co dzieci? Ile ich jest? Podczas zabaw w grupach, pytamy
ile dzieci jest w każdej grupie. Czy w każdej jest tyle samo?
- Podczas posiłków i nakrywania do stołu pytamy czy talerzy/kubków/łyżek/widelców jest tyle
samo co dzieci? Ile ich jest?
- Przeliczamy zabawki i ustalamy czy wystarczy dla każdego dziecka samochodów/lalek/misiów
itp. Czego jest mniej: dzieci czy autek i o ile? Porównujemy liczby zabawek np. autek ciężarowych
i autek osobowych itp.

Tydzień 6.
Zajęcia: Warzywa

Zajęcia z wykorzystaniem cebuliPrzypominamy sobie wiersz o cebuli. Możemy przynieść koszyk
cebul oraz talerzyki (albo inne pojemniki na cebulę np. 6 sztuk). Polecenie: Ustawcie talerzyki w
rzędzie. Ile jest talerzyków? Na pierwszym połóżcie jedną cebulę. Na każdym następnym połóżcie
o 1 cebulę więcej niż na poprzednim. Ile cebul jest na drugim/ trzecim/ … / ostatnim talerzyku?

Na którym talerzu są 3 cebule? Pokażcie tyle palców ile jest cebul na trzecim talerzu. Teraz
wszystkie cebule pogrupujcie po 3 (w każdej grupie mają być 3 cebule). Jak można rozdzielić 3
cebule, by ułożyć je na dwóch talerzykach? Ile będzie na pierwszym, a ile na drugim? Wniosek:
Trzy cebule to dwie i jedna albo jedna i dwie. Można też rozłożyć po jednej, ale na trzech
talerzykach.]

Tydzień 7.
Zajęcia: Zabawy kasztanami i żołędziami.

Warto wykonać również i to ćwiczenie z kasztanami

Na którym miejscu jest kasztan z jasnymi plamkami? Na którym miejscu jest kasztan cały brązowy
(bez łupinki)? Na którym miejscu jest zielony kolczasty kasztan? Na którym miejscu jest kasztan z
połową łupinki?

Ile jest wszystkich kasztanów? (To ważne powtórzenie pytania, które już padło na początku.

Ważne by dzieci miały pewność ile jest kasztanów i odpowiadały potem ile jest kasztanów po
zmianie ich ułożenia.)
N. na oczach dzieci zamienia miejscami kasztany np. zamienia pierwszego z trzecim i pyta: A ile
jest teraz kasztanów? Czynność zamiany kasztanów miejscami powtarza jeszcze ze 2 razy
zamieniając np. drugi z czwartym lub pierwszy z drugim bądź jeszcze inaczej, i po każdej takiej
zamianie pyta: A ile jest teraz kasztanów?
Warto też rozsunąć kasztany tak, aby szereg przez nie tworzony był dłuższy niż na początku i
zapytać: A ile jest teraz kasztanów? Potem ścieśnić kasztany by szereg był krótszy niż na początku
i znowu zapytać: A ile jest teraz kasztanów? [Zapewne niektórym dzieciom będzie się wydawać,
że zmiana ułożenia powoduje zmianę liczby kasztanów. To sygnał, że należy zadbać, by dzieci
gromadziły doświadczenia będące podstawą uświadomienia sobie, że zmiana ułożenia lub zmiana
kierunku liczenia nie zmienia liczby przedmiotów (uznawanie stałości ilości nieciągłych).]
Można postawić kosz z kasztanami, z którego każde dziecko powinno wziąć tyle kasztanów ile
jest na obrazkach (ile było w wierszu). Każde ma ustawić swoje kasztany w szereg i je policzyć.
Następnie pierwszy w szeregu przenieść na koniec szeregu i sprawdzić ile jest ich teraz. Znów
zamienić miejscami drugi z trzecim i sprawdzić ile jest teraz itp. Mogą też przeliczyć kasztany
ustawiając je „parami”. Ważne by dzieci same doświadczały stałości liczby kasztanów przy
zmianie ich ułożenia.

Tydzień 8.
Zajęcia: Grzybobranie

Warto wykonać jeszcze ćwiczenie odwrotne do zawartego w przewodniku:
Na którym miejscu jest borowik / muchomor / kurka/ kozak/ maślak?
Czy możemy policzyć te grzyby od drugiej strony? Policzmy. Który grzyb jest TERAZ pierwszy/
drugi/ trzeci/ czwarty/ piąty?
Na którym miejscu jest TERAZ borowik / muchomor / kurka/ kozak/ maślak?
Dajemy w ten sposób okazję do doświadczania (w przyszłości zrozumienia), że przy zmianie
porządku zmieniają się liczby porządkowe, w przeciwieństwie do niezmienności liczby
kardynalnej (liczebności zbioru).

Ile jest wszystkich grzybów? A ile będzie gdy zamienimy miejscami borowika z muchomorem?

Zamieniamy i sprawdzamy. A ile będzie gdy zamienimy miejscami kurkę z koźlakiem? itp. A ile
będzie gdy włożymy grzyby do koszyka?

Jedno z dzieci wkłada grzyby (obrazki) do koszyka. Dzieci sprawdzają ile grzybów

(obrazków) jest w koszyku (to doświadczanie na stałość liczebności zbioru).

N.: Nie mamy prawdziwych grzybów, więc weźcie tyle patyczków ile jest grzybów. Ile

patyczków masz? [Pyta kolejno kilkoro dzieci.] Wyobraźcie sobie, że te patyczki to grzyby
i wkładacie je do dwóch koszyków. Rozdzielcie grzyby na dwie części (do dwóch koszyków). Jak ty
rozdzieliłaś/łeś? [Pyta kolejno kilkoro dzieci.]. Dzieci pokazują i omawiają swój sposób
rozdzielenia patyczków – grzybów. Jest to przygotowanie do rozkładu liczby 5 na dwa składniki.
Wykorzystanie patyczków jest ważnym doświadczeniem. Chodzi o to, by dzieci dostrzegły, że
gdy nie mają możliwości manipulować rzeczywistymi obiektami (tu grzybami), mogą posłużyć
się przedmiotami zastępczymi (tu patyczkami).

Scenariusze dodatkowe:

Lista materiałów potrzebnych do realizacji zajęć: zabawki znajdujące się w przedszkolu, karty

logiczne „misie” (z wyprawki), jedna karta inna (z wyprawki), karta pracy 1.

Scenariusz pracy

1. Klasyfikacja zabawek.

Zapoznanie dzieci z zabawkami w przedszkolu. Dzieci gromadzą się w kąciku z
zabawkami, w którym zabawki nie są pogrupowane rodzajami (zaplanowany
nieporządek). Pytamy jakie zabawki są w kąciku. Dzieci wymieniają nazwy zabawek np.
lalki, misie, pluszami, pojazdy, klocki, i inne. Polecamy dzieciom porządkowanie
zabawek np. poprzez układanie ich na półkach, albo na podłodze w rzędzie, tak aby
zabawki tego samego rodzaju były razem (wyodrębnianie podzbiorów). Wyodrębnione
podzbiory możemy dalej dzielić według różnych kryteriów np. pojazdy na samochody,
samoloty, pociągi, statki. Samochody możemy z kolei dzielić na ciężarowe i osobowe.
Wszystkie zabawki możemy dzielić na plastikowe, drewniane, metalowe, gumowe i
ewentualnie inne. Podobnie można postępować z klockami dzieląc je według różnych
kryteriów np. materiału (plastikowe, drewniane), koloru, wielkości, kształtu. Wszystko
zależy od pomysłowości dzieci. By wzbogacić pomysły dzieci, zwracamy im uwagę na
różne cechy. Pytamy o te cechy np. Jakiego jest koloru? Jaką ma wielkość? Jakie
przeznaczenie? Z czego jest zrobione?. Prosimy o przeliczenie zabawek określonego
rodzaju. Pytamy np. Ile jest autek osobowych? Ile jest lalek dużych. Ile jest pluszowych
misiów? Itp.

2. Klasyfikacja z użyciem kart logicznych. Każde dziecko ma swój zestaw kart.

Zaprezentowanie kart logicznych osiem misiów tj. ośmiu kart wielkości tych do gry w
brydża. Znajdują się na nich rysunki misiów: brązowych albo białych (2 kolory), małych
albo dużych (2 wielkości), z krawatem albo z muchą (2 rekwizyty). Każdy miś jest inny,
narysowany według schematu, jak w tabeli (tyle misiów ile zacieniowanych okienek,
nauczyciel wykonuje rysunki misiów zgodnie z kryteriami podanymi w tabelce).

białe

brązowe

małe
duże

krawat

mucha krawat

mucha

Zadania dla dzieci.

Czy te misie są jednakowe?
Jakie są te misie? Dzieci opisują je. Ważne by wyodrębniły 2 kolory, 2 wielkości i 2
rekwizyty.
Pogrupujcie te misie tak, aby razem były misie podobne.
Obserwujemy co robią dzieci. Prosimy o wyjaśnienie dlaczego tak pogrupowały. Każde
dziecko wyjaśnia swój sposób (co mają podobnego, a czym się różnią), a pozostałe dzieci
przyglądają się i oceniają czy tak można.
Mogą się pojawić różne podziały na dwa podzbiory:
- podział ze względu na kolor,
- podział ze względu na wielkość,
- podział ze względu na rekwizyt.
Podziały na 4 podzbiory:
- ze względu na kolor i wielkość,
- ze względu na kolor i rekwizyt,
- ze względu na wielkość i rekwizyt.
Gdyby nie pojawiły się te kombinacje pytamy: Jak jeszcze można podzielić misie?
Albo wydajemy jedno z poleceń:
Pogrupujmy misie tak, by razem były misie tego samego koloru. Ile ich jest?
Pogrupujmy misie tak, by razem były misie takiej samej wielkości. Ile ich jest?
Pogrupujmy misie tak, by razem były misie z krawatami i razem misie z muchami. Ile ich
jest?

Pytania o liczbę misiów.
Ile jest misiów białych?
Ile jest małych?
Ile jest z krawatem? Ile z muchą?
Ile jest białych z krawatem?
Ile jest dużych z muchą?
Ile jest małych brązowych?
Ile jest małych, białych z krawatem?
Ile jest dużych, brązowych z muchą?
Nie oczekujemy natychmiastowej odpowiedzi, czekamy aż dzieci poukładają i policzą
wskazane misie.
Dla ułatwienia powtarzamy pytania, by dzieciom było łatwiej zapamiętać o jakie misie
chodzi.

Dobierz misie w pary tak, aby różniły się tylko jedną cechą.
Prosimy dzieci, aby poukładały (połączyły) wszystkie misie w pary.
Np. mały, biały z krawatem do niego pasuje albo mały, biały z muchą albo mały brązowy
z krawatem albo duży biały z krawatem.

Tworzenie łańcucha z jedną różnicą.
Podnieście do góry kartę z małym brązowym misiem w krawacie. Połóżcie kartę przed
sobą. To pierwsza karta.
Podnieście do góry kartę z dużym brązowym misiem w krawacie. Połóżcie kartę przed
sobą obok poprzedniej. To druga karta.
Czym różnią się misie na tych kartach? [wielkością].
Podnieście do góry kartę z dużym białym misiem w krawacie. Połóżcie kartę obok
tamtych. To trzecia karta.
Czym różnią się miś na drugiej i trzeciej karcie? [kolorem].

Jako czwartą połóżcie kartę z misiem, który różni się od ostatniego (trzeciego) jedną
cechą.
Jaki to może być miś? Jakiego misia położyłeś? [Odp. to może być miś duży, biały z
muchą albo mały, biały z krawatem. Jest jeszcze jeden miś różniący się od ostatniego
jedną cechą: duży, brązowy z krawatem, ale ten już został ustawiony na drugiej pozycji w
tworzonym łańcuchu.]
Układaj misie dalej tak, aby następny różnił się jedną cechą od poprzedniego.

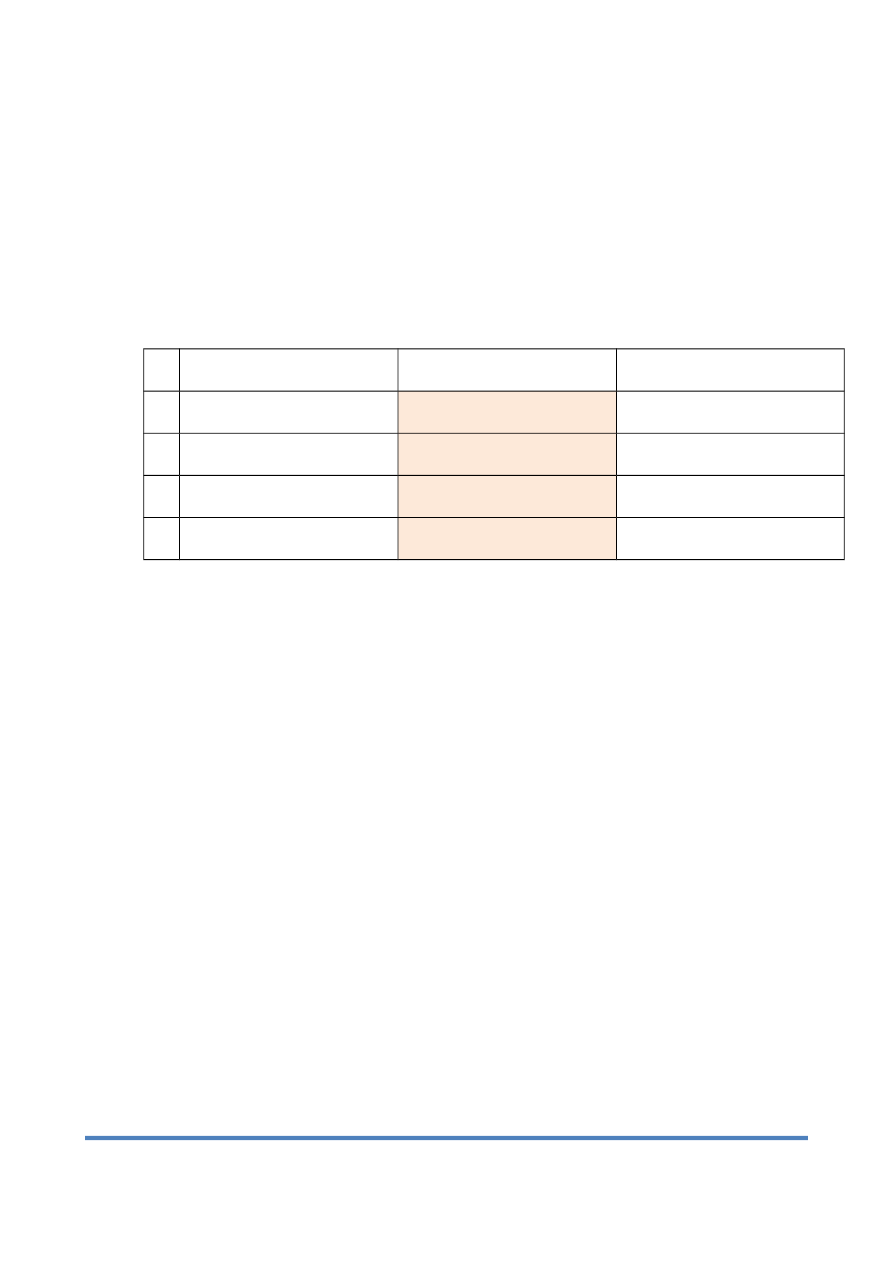
Szukamy trzeciego misia. N. poleca dzieciom ułożyć przed sobą dwie kary takie jak
karty dane w kolejnych przykładach w tabeli. Należy znaleźć i położyć między nimi kartę
z takim misiem, który różni się od każdego ze swoich sąsiadów tylko jedną cechą.
Kolejno podajemy przykład 1., potem 2. aż do 4.

Dana karta

Rozwiązanie (szukana
karta)

Dana karta

P1
.

mały, biały z krawatem

mały, biały z muchą

duży, biały, z muchą

P2
.

duży, brązowy z krawatem

mały, brązowy z krawatem

mały, biały z krawatem

P3
.

duży, biały z muchą

duży, brązowy z muchą

duży, brązowy z krawatem

P4
.

mały, brązowy z muchą

duży, brązowy z muchą

duży, biały z muchą

3. Gry z kartami logicznymi (ćwiczenie w respektowaniu umów, hartowanie odporności

emocjonalnej, ćwiczenie pamięci, porównywanie obiektów – szukanie cech wspólnych i
różnic, a więc ćwiczenie analizy i syntezy wzrokowej).

Gra MEMORY, z udziałem dwu graczy (dzieci grają w parach). Zwycięża ten gracz,
który uzbiera więcej par. Rekwizyty np. dwa komplety kart z obrazkami misiów czyli 16
kart ułożonych na stoliku obrazkami do dołu w układzie 4 rzędy po 4 karty. Gracze na
przemian odwracają po dwie karty. Jeżeli stanowią one parę – są identyczne (w wersji
trudniejszej można dobrać inne kryteria tworzenia par) gracz je zabiera. Jeżeli nie są
identyczne, wracają na swoje miejsce nadal odwrócone obrazkiem do dołu, a karty
odwraca drugi gracz i tak na zmianę.
Gdy wszystkie karty zostaną zebrane, gracze wyłaniają zwycięzcę poprzez porównanie
liczb zebranych par (albo liczb zebranych kart). Zwycięża ten gracz, który uzbiera więcej
par (albo więcej kart).

Gra typu CZARNY PIOTRUŚ, z udziałem dwu graczy (dzieci grają w parach).
Zwycięża ten gracz, który pozbędzie się wszystkich kart, przegrywa ten, któremu w ręce
zostaje „Czarny Piotruś”. Rekwizyty: dwa komplety kart z obrazkami misiów czyli 16
kart i dodatkowa karta (siedemnasta) np. z rysunkiem klauna, która na odwrocie ma
identyczny wzór jak karty z misiami. Gracze tasują kary i rozdają wszystkie, sobie po
równo. Każdy gracz układa swoje karty w wachlarz, tak by przeciwnik nie widział
obrazków. Gracze sprawdzają, czy wśród swoich kart mają pary (identyczne karty). Jeżeli
tak odkładają wszystkie na bok. Z pozostałych w ręce kart przeciwnika losują na przemian
po jednej karcie i sprawdzają, czy nie tworzy ona pary, z którąś z wcześniej posiadanych.
Jeśli tak, to gracz odkłada nową parę na bok, a kartę losuje przeciwnik.
Gra toczy się do momentu, gdy któremuś graczowi zostanie jedna karta bez pary (klaun).
Ten gracz przegrywa – zostaje klaunem.

Klasyfikacja z uwzględnieniem dwóch cech.
Dzieci siedzą w kole i układają przed sobą karty według polecenia.
Np. Podziel misie na białe i te z krawatem.
Na środku koła leżą dwie szarfy. N. poleca, aby jedno z dzieci ułożyło w jednej szarfie
misie białe, a w drugiej misie z krawatem.
Tu pojawia się sytuacja konfliktowa ponieważ dwa białe misie z krawatem (jeden duży, a
drugi mały) powinny być zarówno w jednej jak i w drugiej części. Co zrobić? Może jakieś
dziecko będzie miało pomysł jak z tego wybrnąć. Jeśli nie, to sugerujemy by przesunąć
jedną z szarf tak, by częściowo zachodziła na drugą. Wówczas powstaje część wspólna
obu szarf – jest to miejsce dla misiów pasujących do obydwu zbiorów.
Kolejne przykłady:
Podziel misie na małe i misie brązowe.
Podziel misie na duże i misie brązowe.
Podziel misie na duże i misie z muszką. Itp.

Lista materiałów potrzebnych do realizacji zajęć: klocki - najlepiej sześcienne po jednym dla
każdego dziecka, kwadratowe kartoniki w czterech kolorach po jednym dla każdego dziecka.
Scenariusz pracy

4. Diagnoza wiedzy dzieci na temat procedur i zakresu umiejętności liczenia. Równocześnie

kształtowanie znajomości liczebników, procedury liczenia

porównywania liczebności

zbiorów (porównywania: o ile więcej, o ile mniej

Wykorzystywanie zbiorów zastępczych

(klocki zamiast dzieci).
Przeliczanie dzieci (realizujemy niezależnie od liczebności grupy).

a) Ustalanie liczby dzieci w grupie. Dzieci stoją w kole. Czy wiecie ile dzieci jest w grupie? Kto

potrafi policzyć? Chętne dziecko wchodzi do koła i wskazując kolejne dzieci przelicza je. W
razie potrzeby nauczyciel podpowiada kolejne liczebniki (nie krytykuje) ewentualnie pomaga
dziecku wskazywać (pokazuje jak to robić) i jednocześnie wypowiadać kolejne liczebniki
główne. Po przeliczeniu przez dziecko pytamy: Ile jest dzieci? Chodzi o sprawdzenie czy
dzieci wiedzą, że ostatni liczebnik oznacza liczbę policzonych obiektów. Przeliczanie
powtarzamy jeszcze jeden lub dwa razy. Za każdym razem robi to inne dziecko zaczynając
liczenie od innego miejsca (innego dziecka) i za każdym razem pytamy ile jest dzieci.
Następnie liczymy wspólnie: jedno dziecko wskazuje, a wszystkie dzieci głośno wymawiają
kolejne liczebniki [chodzi o to, by dzieci zapoznały się z ciągiem liczebników i dostrzegły
rytm liczenia i by ustaliły jak liczna jest ich grupa].

b) Porównywanie liczby chłopców i liczby dziewczynek. Pytamy: Ile jest dziewczynek a ile jest

chłopców? Dzieci ustawiają się w dwóch równoległych szeregach w jednym dziewczynki, a
w drugim chłopcy. Szeregi w odległości około 2 metrów tak, aby dzieci z jednego szeregu
mogły obserwować te z drugiego. Jeden z chłopców przelicza ile jest dziewczynek. Dzieci
odpowiadają ile jest dziewczynek. Inny chłopiec, na polecenie Policz dziewczynki zaczynając
liczyć z drugiej strony, powtarza czynność przeliczania zaczynając „od końca" (zmieniając
zwrot liczenia). Odpowiada ile jest dziewczynek. W analogiczny sposób dziewczynki
ustalają ilu jest chłopców. Czy chłopców i dziewczynek jest tyle samo? Jak to sprawdzić?
Wysłuchujemy pomysłów dzieci. Dobrze byłoby, aby dzieci stanęły parami: chłopiec z
dziewczynką. Tych dzieci jest więcej, które zostały bez pary. Jeżeli liczby dzieci się różnią,
pytamy: Kogo jest więcej? Dziewczynek czy chłopców? O ile więcej jest np. dziewczynek niż

chłopców? O ile mniej jest np. chłopców niż dziewczynek?

c) Porównywanie liczb klocków. Przygotowujemy pudło z klockami jednakowego kształtu i

rozmiaru, najlepiej klocki sześcienne. Mogą różnić się kolorem. Każde dziecko bierze do
ręki jeden klocek. Resztę klocków chowamy. Możemy też przydzielić dziewczynkom klocki
np. żółte, a chłopcom np. czerwone, wtedy będziemy mogli zamiennie określać klocki raz
mówiąc „klocki dziewczynek”, a raz „klocki żółte”. Pytamy: Czy każde dziecko ma klocek?
Czy klocków jest tyle samo co dzieci? Skąd to wiadomo? [Bo każde dziecko ma jeden
klocek.] Następnie prosimy, by dziewczynki zbudowały na podłodze ze swoich klocków
„pociąg” [kolejno układają swoje klocki jeden za drugim, bez odstępów między klockami –
klocki mają przylegać ściankami]. Pytamy: Z ilu klocków jest zbudowany pociąg
dziewczynek?/pociąg żółty? Dzieci głośno przeliczają klocki w pociągu. To samo robią
chłopcy – budują pociąg ze swoich klocków. Pytamy: Z ilu klocków jest zbudowany pociąg
chłopców?/pociąg czerwony?, Dzieci głośno przeliczają klocki w pociągu. Czy pociągi
dziewczynek i chłopców są tak samo długie?, Który jest krótszy?, O ile klocków krótszy?,
Który jest dłuższy?, O ile klocków dłuższy? By sprawdzić oceny dzieci należy oba pociągi
przysunąć (ustawić obok siebie) tak, by zaczynały się „równo” i by łatwe było porównanie
ich długości: np.

■■■■■■■
□□□□ tu widać, że dłuższy jest pociąg z ciemnych klocków i widać, że dłuży jest
o tyle kloców, ile ciemnych „wystaje” czyli o 3.

5. Liczenie i porównywanie liczebności zbiorów, podział ze względu na kolor. W pudełku

umieszczamy kwadratowe kartoniki w czterech kolorach np. żółte, czerwone, niebieskie i
zielone. Każde dziecko podchodzi i losuje/wybiera jeden kartonik. Polecenie: Dzielimy się
na grupy. W jednej grupie mają być dzieci z kartonikami w tym samym kolorze. Dzieci
dobierają się w grupy i gromadzą się obok siebie. Grupa zielonych podnosi kartoniki w
górę. Następuje sprawdzenie, czy wszystkie „zielne” dzieci trafiły do grupy i czy nie ma
tam innych kolorów. Prosimy o ocenę pozostałe dzieci. Pytamy np.: Czy wszyscy „zieloni”
są w swojej grupie? Tak samo sprawdzamy pozostałe grupy. Pytamy: Ile jest dzieci w grupie
zielonych? A ile w grupie czerwonych? Czy w grupie zielonych jest tyle samo dzieci co w
grupie czerwonych? Jeżeli nie, pytamy. W której grupie jest mniej/więcej?, O ile
mniej/więcej? Sprawdzamy odpowiedzi poprzez ustawienie równoległych szeregów dzieci z
obu grup tak, by dziecko z jednego szeregu tworzyło parę z dzieckiem z drugiego szeregu.
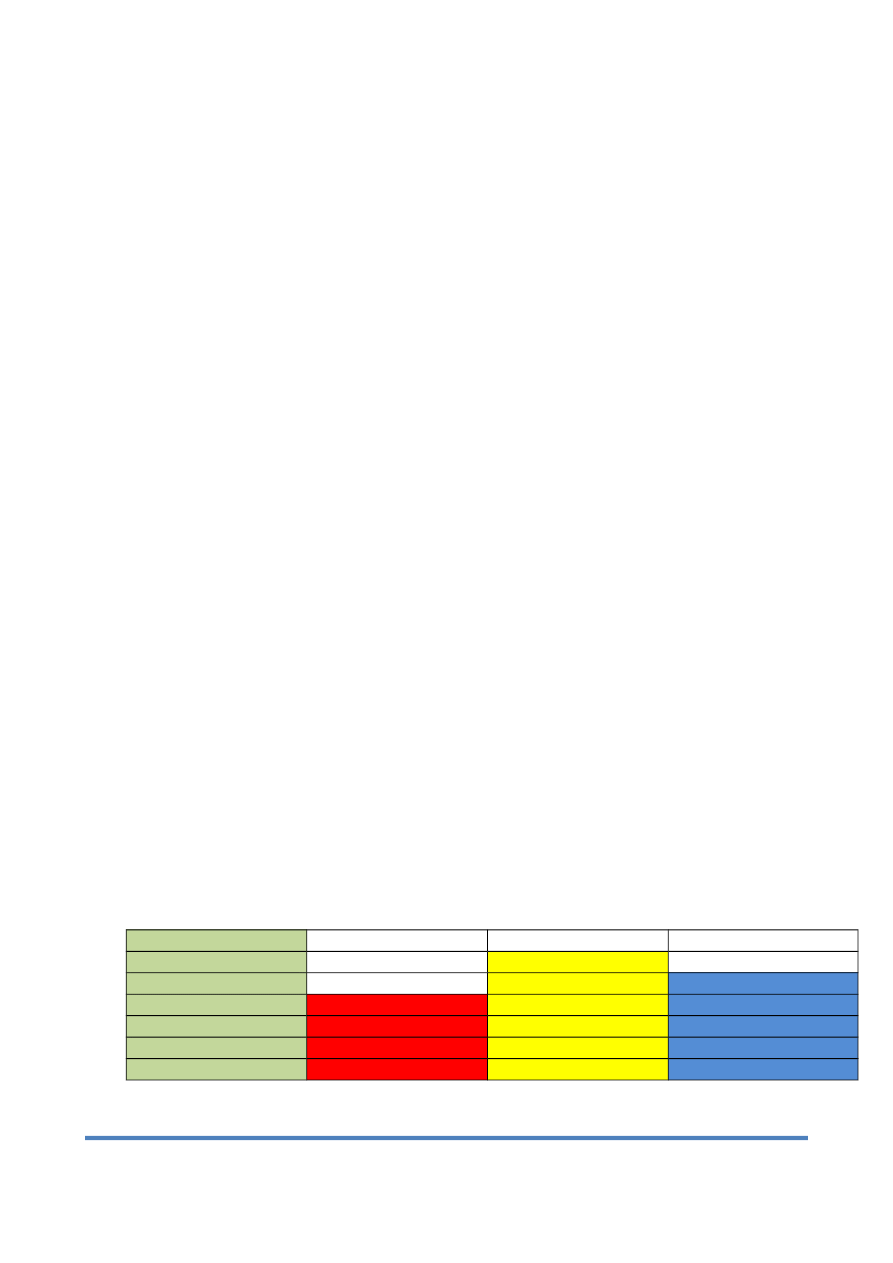
Analogicznie porównujemy liczebności pozostałych grup. Następnie porównujemy ilości
kartoników w różnych kolorach. Grupa zielonych układa na podłodze swoje kartoniki
(buduje pociąg) jeden kartonik za drugim (tak jak słupek na wykresie), obok drugi pociąg
(słupek) układają „czerwoni” itd.
Tworzy się „wykres”, zatem łatwo porównać których kartoników jest najwięcej, a których
najmniej. O ile więcej jest kartoników jednego koloru niż kartoników drugiego koloru np.:

Można uporządkować słupki kartoników od najniższego do najwyższego (rosnąco albo
malejąco).

Podsumowujemy: najmniej jest czerwonych kartoników, więc są na początku na pierwszym
miejscu. Niebieskich więcej niż czerwonych i są na drugim miejscu, żółtych więcej niż
niebieskich i są na trzecim miejscu, a na czwartym miejscu są kartoniki zielone - jest ich
najwięcej.

6. Przeliczanie palców u rąk. Dzieci siedzą w kole.

a) Ile jest palców w jednej ręce? (możemy jednocześnie ustalić, że w lewej ucząc rozróżniać
rękę lewą i prawą). Niezależnie od tego czy dzieci znają odpowiedź, zachęcamy do
przeliczenia. Wyprostowujemy kolejne palce (demonstrujemy jak to robić np. kolejno:
kciuk, wskazujący, środkowy, serdeczny i mały – można przy okazji podać nazwy palców) i
prosimy, by dzieci zrobiły tak samo. Wszyscy głośno wymawiają kolejny liczebnik przy
każdym kolejnym wyprostowanym palcu. Stwierdzamy jest ich pięć. Analogicznie
przeliczamy palce drugiej ręki – teraz prawej (kciuk, wskazujący, środkowy, serdeczny i
mały).
b) Czy palców w jednej ręce jest tyle samo co w drugiej? Jak to sprawdzić?
Sprawdzenie równoliczności palców obu dłoni poprzez np. równoczesne wyprostowywanie:
obu kciuków, obu palców wskazujących, obu środkowych, serdecznych i małych, albo
poprzez dotykanie – łączenie w pary palca małego lewej dłoni i palca małego prawej dłoni,
następnie palców serdecznych, środkowych itd.
c) Ile jest palców w obu dłoniach?
Głośne przeliczenie palców obu rąk z jednoczesnym ich wyprostowywaniem. Stwierdzenie,
że jest ich dziesięć.
d) Ile palców ma kolega?
Dzieci łączą się w pary i przeliczają wzajemnie palce kolegi. Następnie sprawdzają czy
mają po tyle samo palców [przez odwzorowanie – dotykanie tak, jak z dwiema własnymi
dłońmi].
e) Ile palców pokazuję?
N. pokazuje np. trzy wyprostowane palce prawej dłoni i pyta ile palców pokazał. Powtarza
to dla różnych układów palców (liczb). Dzieci odpowiadają ile palców pokazano.
Następnie dzieci bawią się w parach: jedno dziecko pokazuje pewną liczbę swoich palców, a
drugie ustala ile ich jest i tak na zmianę.
W dalszej kolejności to ćwiczenie będzie wykorzystywane do wyznaczania sumy liczb: N.
pokaże np. dwa palce lewej ręki i zapyta ile ich jest i, nie chowając tych palców, na drugiej
ręce pokaże np. cztery palce i zapyta ile ich jest. Następnie cały czas pokazując te palce
pyta: Dwa palce i cztery palce to ile jest razem?
f) Liczenie palców z użyciem liczebników porządkowych: pierwszy palec, drugi palec …

7. Karta pracy z dwoma ćwiczeniami.

a) Prostokątna ramka w niej rysunek siedmiorga dzieci i ośmiu piłek ułożonych w

rozsypce. Pytanie w ramce Czy piłek jest tyle samo co dzieci? odczytuje N. A dzieci (po
ćwiczeniach praktycznych) powinny wymyśleć sposób porównania liczebności zbiorów.
Najlepiej, aby tworzyły pary: dziecko – piłka poprzez łączenie ich kreskami albo
otaczanie pętlą. Pytania dodatkowe nauczyciela: Czego jest więcej?, O ile więcej?,
Czego jest mniej?, O ile mniej?, Ile jest dzieci?, Ile jest piłek?

Czy piłek jest tyle samo co dzieci?

d p d p

d d
p d p

b) Prostokątna ramka w niej rysunek kilku wież z klocków, każda z innej liczby klocków:

1, 2, 3, 4, 5, 6, 7. Wieże nie są uporządkowane ani od najniższej do najwyższej ani
odwrotnie. To ma zrobić dziecko. Na rys. strzałka od wieży o wysokości jednego klocka
do wieży o wysokości dwóch klocków. I polecenie: Strzałka pokazuje wieżę o jeden
klocek wyższą. Dorysuj pozostałe strzałki.

Strzałka pokazuje wieżę o jeden klocek wyższą. Dorysuj pozostałe strzałki.

Dodatkowe zabawy matematyczne, przewodnik cz. 2

Tydzień 9
Zajęcia: Parasole

Dodatkowe zadania z wykorzystaniem parasoli.

Czy możemy policzyć te parasole od drugiej strony? Policzmy. Który parasol jest TERAZ
pierwszy/ drugi/ trzeci/ czwarty/ piąty/ szósty?
Na którym miejscu jest TERAZ parasol w esy-floresy/ kratkę/ kółka/ kwiatki/ kropki/ ciapki?
Ile jest TERAZ wszystkich parasoli?

Jedno dziecko zasłania opaską oczy (lub odwraca się), a w tym czasie drugie (przy ewentualnej
pomocy N.) zamienia miejscami dwa parasole np. pierwszy z drugim. Po zdjęciu opaski pierwsze
dziecko mówi, które parasole zostały zamienione miejscami i ile jest parasoli po tej zmianie oraz
układa je w pierwotnym układzie. Ćwiczenie warto powtórzyć 2 – 3 razy, za każdym razem inne
dziecko dokonuje zamiany i inne dziecko odgaduje co się zmieniło oraz ustala ile jest parasoli po
zmianie.

Już wiecie jakie parasole mają dzieci z wiersza, a teraz pokażcie swoje parasole (N.

poprzedniego dnia polecił dzieciom przynieść swoje (albo rodzica) prawdziwe parasole, każde
dziecko bierze swój parasol). Obejrzyjmy swoje parasole. Każdy powie jaki jest jego parasol.
Dzieci kolejno prezentują parasole (otwierają je – na chwilę, by widać było jakie one są) podają
kolor swojego parasola i nazywają wzór, o ile taki występuje oraz ewentualnie opisują
dodatkowe elementy takie jak napisy, falbanki lub dodatki specyficzne dla dziecięcych parasoli
np. „uszy myszki”, „oczy kota” itp. Mogą też określać wymiary parasoli: mały, malutki, duży,
wielki.

N. poleca dzieciom połączyć się w pary (lub większe grupy) na zasadzie podobieństwa parasoli
np. ze względu na kolor, wielkość, wzór albo na dodatkowy element.
Dzieci w parach (lub w grupach) omawiają co łączy ich parasole. W ten sposób podają kryteria
tworzenia podzbiorów. Pozostałe dzieci oceniają trafność połączenia.
Po prezentacji wszystkich par (grup), N proponuje zabawę ruchową „Sześć parasoli”. Dzieci
ze złożonymi parasolami swobodnie przemieszczają się po sali, a na sygnał N. łączą się w grupy
tak, aby w każdej było sześć parasoli. Nie jest ważne jakie cechy mają parasole tylko to, by było
ich sześć. Jeśli liczba parasoli/dzieci nie jest wielokrotnością liczby sześć, to dzieci, którym nie
udało się utworzyć „szóstki” mówią ile mają parasoli i ile brakuje im do sześciu, a reszta dzieci
to ocenia. Ćwiczenie powtarzamy 2 – 3 razy z obowiązkiem zmiany partnerów.
Przy ostatnim układzie (na koniec zabawy ruchowej) każda „szóstka” dzieci prezentuje swoje
parasole w taki sposób, że część z nich jest złożona, a część rozłożona. Dzieci mówią jaki układ
prezentują. Np. Mamy sześć parasoli. Dwa są rozłożone i cztery złożone [jest to rozkład liczby 6
na dwa składniki]. Kolejna „szóstka” ma to zrobić inaczej. Dzieci starają się, by żaden układ się
nie powtórzył i wymyślają różne możliwości: 1 i 5, 2 i 4, 3 i 3, 4 i 2, 5 i 1. Jeśli jest grupa
dzieci, mniejsza niż 6-osobowa, to jej członkowie powinni zaprosić do siebie tyle innych dzieci
(z „szóstki” już zaprezentowanej), by również mogli przedstawić swój pomysł.

Podsumowując zabawę można poprosić jedną grupę dzieci, by stanęły w rzędzie ze złożonymi
parasolami. Ile jest parasoli złożonych? Następnie pierwsze dziecko w rzędzie rozkłada parasol i
dzieci (ewentualnie przy pomocy N.) komentują: Sześć parasoli; jeden rozłożony i pięć złożonych.
Drugie dziecko rozkłada parasol i komentarz: Sześć parasoli; dwa rozłożone i cztery złożone. itd.
kolejne dziecko w rzędzie rozkłada parasol, aż wszystkie parasole będą rozłożone. Każdą sytuację
należy omówić/skomentować.

Tydzień 11
Zajęcia: Domy i domki

„Budujemy domy” – zabawa matematyczna polegająca na konstruowaniu domów w kształcie różnych

figur geometrycznych oraz z klocków. Ćwiczenie poprawności odtwarzania układów płaskich,

przestrzennych; rozpoznawanie kształtów.

„Dwa domy” – słuchanie wiersza Anny Łady-Grodzickiej.

Kolorowe figury – te duże i małe,
są do układania mozaiki doskonałe.
Wezmę dwa prostokąty, ułożę dwa domy.
Jeden będzie złocisty, a drugi zielony.
Pierwszy będzie wysoki, a drugi niziutki.
W dużym zamieszkają ludzie, w małym krasnoludki.
Dopasuję do każdego trójkątny daszek,
może zechce usiąść na nim jakiś ptaszek?
Z małych prostokątów w obu domach drzwi zrobię,
ludzie i krasnoludki będą chodzić sobie.
Małe, niebieskie kwadraty będą oknami,
a żółte koło będzie słońcem nad dachami.
Jeszcze przy dachach domów kominów brakuje,
zaraz je z małych prostokątów dobuduję.

Po pierwszym czytaniu wiersza, czytamy go ponownie bardzo wolno równocześnie wykonując
opisane czynności związane z układaniem domów z wyciętych kartoników takich, jak opisane w
wierszu. N. tworzy konstrukcje na tablicy, a dzieci - na kartkach. Kolejny fragment wiersza
odczytujemy po wykonaniu czynności opisanej w poprzednim fragmencie. N. może przypinać
kartoniki magnesami, zaś dzieci mogą je naklejać.
Rozmowa na temat „zbudowanych” domków:
Jaki kształt mają ściany tych domów?
Jaki kształt mają dachy? Jaki kształt mają drzwi, a jaki mają okna. Jaki kształt mają kominy.
Jakiego kształtu jest słońce.
Ile jest na tym obrazku prostokątów [6]/ trójkątów [2]/ kwadratów [zależy ile okien się zmieści, np.
w tym dużym domu – 3-kondygnacyjnym może być osiem okien, a w małym – parterowym dwa,
czyli razem dziesięć]/ kół [1]? [formalnie każdy kwadrat jest prostokątem, ale dla małych dzieci
kwadrat to inny kształt niż prostokąt, więc mówiąc „prostokąt” – myślimy o takim, który nie jest
kwadratem].
Czy można nasze kompozycje wzbogacić / upiększyć? Czego tu brakuje? [np. drzew, kwiatów,
zwierząt, ludzi, krasnali, pojazdów itp.]
Każde dziecko ma zaprojektować i wykonać kolejne elementy (choć jeden dodatkowy element)

kompozycji – ważne, by były one, tak jak domki, kompozycjami geometrycznymi, czyli z pudełek
w kształcie figur geometrycznych.
Prezentowanie i omawianie wytworów dzieci. Zwracamy szczególną uwagę na używanie nazw
kształtów, różnicowanie wielkości (większy – mniejszy, niższy – wyższy, węższy – szerszy, dłuższy
– krótszy itp.).
N. z kwadratowego, trójkątnego i okrągłego pudełka konstruuje na tablicy budę dla psa.
Pyta: Jaki kształt mają kartoniki, z których zrobiłem tę kompozycję? Jak myślicie, co to jest? Czyim
domem jest buda? Jakie inne domy – dla ludzi i nie dla ludzi – znacie? [jurta mongolska, tipi lub
wigwam indiański, namiot, szałas, igloo, przyczepa campingowa, ule dla pszczół, budki dla szpaków,
gniazda dla ptaków, muszle dla ślimaków, nory dla lisów, dziuple dla wiewiórek, mrowiska dla
mrówek… ]
Środki dydaktyczne: pudełka w kształtach i kolorach zgodnych z tekstem wiersza oraz dodatkowo
inne pudełka w różnych kształtach i kolorach, nożyczki (by można było przyciąć niektóre z nich),
klej.

Kto szybciej i lepiej zbuduje dom – zabawa matematyczna polegająca na tworzeniu budowli z
klocków według wzoru. Poprawne odtwarzanie układów przestrzennych, rozpoznawanie kształtów,
kolorów i liczby klocków oraz ich wzajemnego położenia.
Środki dydaktyczne: 3 identyczne komplety klocków. W każdym komplecie (zestawie) ma być
tyle samo jednakowych klocków ( nie mniej niż dziesięć i nie więcej niż piętnaście).
Dzielimy dzieci na dwie drużyny. Każda drużyna dostaje po jednym zestawie (komplecie) klocków,
a trzecim dysponuje nauczyciel. N. ze swoich klocków buduje prostą budowlę (wieżę, domek itp.).
Za pierwszym razem nie musi wykorzystać całego zapasu klocków. Przy kolejnych powtórzeniach
zabawy może zwiększać liczbę użytych elementów i stopień skomplikowania budowli.
Każda z drużyn wybiera swojego przedstawiciela (inżyniera), który zbuduje z klocków (jakimi
dysponuje jego drużyna) identyczną budowlę jak budowla nauczyciela: używając tyle samo i takich
samych klocków jak we wzorze. Liczy się czas i dokładność. Pozostali zawodnicy kibicują
inżynierom i kontrolują poprawność. Inżynier, który skończy budowanie mówi „stop”. Wówczas
drugi musi przerwać układanie klocków. Następuje ocena poprawności wykonania zadania. Punkt
zdobywa ta drużyna, której przedstawiciel dokładniej odwzorował budowlę

Zabawę powtarzamy kilka razy wskazując w drużynach innych inżynierów (można budować
parami) i ewentualnie zastępując N. jakimś dzieckiem.

Tydzień 14
Zajęcia: Kolorowe sukienki

Krawcowa przyszywa guziki
Krawcowa przygotowała trzy guziki do przyszycia.
Najpierw przyszyła pierwszy guzik i zostały jej jeszcze do przyszycia dwa.
Potem przyszyła drugi guzik i został jej jeszcze jeden do przyszycia.
Gdy przyszyła trzeci guzik, to do przyszycia zostało jej ZERO guzików.
Opowiadamy historyjkę i jednocześnie demonstrujemy to na guzikach (odsuwając kolejne
przyszywane guziki. Można też na tablicy do rysunku bluzki dopinać magnesami kartonowe
rysunki guzików albo magnesy traktować jak guziki).

Zatem co oznacza ZERO? [oznacza, że nie ma żadnego guzika do przyszycia]

Seria zadań - liczymy dzieci ubrane w …
Ile w grupie jest dzieci, które ubrane są dzisiaj w spodnie? [np. 17]
Ile w grupie jest dzieci, które ubrane są dzisiaj w spódniczki? [np. 7]
Ile w grupie jest dzieci, które ubrane są dzisiaj w sukienki? [odpowiedź np. 0, bo nikt nie włożył
dzisiaj sukienki – chociaż mogłaby być dziewczynka w sukience] itp. Ilu chłopców jest w naszej
grupie? [np. 13]
Ilu chłopców ma na imię Adam? [np. 2]
Ilu chłopców ma na imię np. Filip? [podajemy imię, które w grupie nie występuje – wtedy
odpowiedź 0]
Ile dziewczynek jest w naszej grupie? [np. 11]
Ile dziewczynek ma na imię np. Julia? [np. 3]
Ile dziewczynek ma na imię np. Stefania? [podajemy imię, które w grupie nie występuje – wtedy
odpowiedź 0]

Wycieczka do pracowni krawieckiej
Warto wybrać się z dziećmi do pracowni krawieckiej – zobaczyć na czym polega praca
krawcowej/krawca i przynieść ścinki tkanin.

Projektowanie ubrań
Ze ścinków tkanin, poprzez przycinanie i naklejanie na kartkę, można projektować ubrania.

Zgadnij ile mam guzików w zamkniętej dłoni
Każde dziecko ma np. po pięć guzików. Dzieci dobierają się parami.
Najpierw jedno dziecko z pary bierze wszystkie swoje guziki w obie dłonie np. do jednej 2, a do
drugiej 3. Pokazuje partnerowi obie zamknięte dłonie z guzikami. On wskazuje jedną dłoń, która
zostaje otwarta i widzi ile jest w niej guzików. Zadanie polega na podaniu liczby guzików w drugiej
– nadal zamkniętej dłoni. Może to ustalić poprzez liczenie w pamięci albo poprzez liczenie
przedmiotów zstępczych (swoich palców albo swoich guzików, których ma tyle samo co partner).
Podana odpowiedź sprawdzana jest poprzez otwarcie tej drugiej dłoni i przeliczenie guzików.
Potem zamieniamy role.
Zabawę powtarzamy kilka razy.

Tydzień 15
Zajęcia: Ubieramy choinkę

Można zaproponować kolorowankę:
prostokątne pole (obrazek) podzielone jest dość gęstymi liniami na małe obszary.
W tych obszarach zapisane są różne cyfry od zera do siedem. Pola z tymi cyframi należy
pokolorować według kodu [tu chodzi o rozpoznawanie cyfr] tak, że dzięki kolorowaniu wyłoni się
z tego ilustracja np. choinki albo prezentu pod choinką ….
Przykład kodu:
0 – plamka niebieska,
1 – plamka żółta,
2 – plamka czerwona …
7 – plamka zielona.

Plątaninka
Rysunek dzieci (np. trzy postacie) i rysunki trzech prezentów. Między dziećmi a prezentami
plątanina delikatnych szarych linii. By rozszyfrować, który prezent dostanie dane dziecko, należy
pokonać drogę od dziecka do prezentu wzdłuż poplątanych linii. Przebywając tę trasę warto ją
pokolorować / zaznaczyć kredką.

Konstruowanie bombek choinkowych
Narysuj/wklej w tabeli (pudełku) odpowiednie (pasujące) bombki choinkowe.

Rys./szkic
okrągłej
bombki

Rys./szkic
bombki
szyszki

Rys./szkic
bombki
grzybka

Rys./szkic
bombki
dzwonka

Rys./szkic
bombki sopel
lodu

Plamka
czerwona
Plamka żółta
Plamka
niebieska
Plamka
różowa

Wykonywanie choinki z kółek:

Choinkę można wykonać z większej liczby kółek (będzie wyższa).
Można na zielone kółka nałożyć białe kółka i uzyskać efekt pokrycia drzewka śniegiem.
Zadania matematyczne: klasyfikacja kółek ze względu na wielkość i kolor, przeliczanie elementów.

Naklejanie np. pięciu bombek (kółek) czerwonych, trzech niebieskich, sześciu różowych itp.

Tydzień 16
Zajęcia: Śniegowe gwiazdki

„Śniegowe gwiazdki” – zabawy matematyczne związane z poszukiwaniem osi symetrii figur,
wycinaniem figur osiowo symetrycznych, obserwowaniem odbić w lusterku.
By scenariusz tworzył spójną całość, proponuję szukać w gwiazdkach osi symetrii (linii
podziału na dwie równe – identyczne części). W tym celu należy składać gwiazdki na dwie
części (połowy) tak, by wzór się pokrył. Dla każdej gwiazdki można wskazać w istocie sześć
osi symetrii: trzy przechodzące przez wierzchołki przeciwległych ramion i trzy przechodzące
między ramionami. W celu ułatwienia dzieciom zadania – by mogły sprawdzać swoje działania

– należy każdemu dziecku dać wydrukowany na kalce technicznej (lub półprzeźroczystym
papierze) w kształcie kwadratu wzór płatka śniegu tak ułożonego, żeby złożenie kartki wzdłuż
przekątnych kwadratu wystarczyło, by znaleźć dwie różne osie symetrii płatka albo tak
ułożonego, by składając kartkę wzdłuż symetralnych boków kwadratu móc również znaleźć
dwie różne osie symetrii płatka.
Dzieci składają płatek na dwie równe części tak, aby wzór się „pokrył/nałożył” [mogą to
kontrolować dzięki przeźroczystości kalki/papieru]. Pokazują kolegom jaką linię podziału
znalazły. Kolorują tę linię na czerwono i szukają innej, a po jej znalezieniu kolorują tę inną np.
na niebiesko. Chętne dzieci mogą znaleźć wszystkie sześć osi i każdą oznaczyć innym kolorem.
Poprzez zginanie kartek i nakładanie wzorów odkrywają własności figur osiowo
symetrycznych.
By wzbogacić doświadczenia dzieci (co służy pogłębieniu rozumienia pojęć) można
zaproponować zadania z wycinaniem wzorów z kartek złożonych na pół (ewentualnie dla
chętnych - na dwa zgięcia).

Zad. 1.
N. rozdaje dzieciom zgięte kartki z rysunkiem połowy choinki (albo: motyla, gwiazdki,
pajacyka, koszyczka, itp. albo różne dzieci – różne wzory). Pyta co powstanie, jeżeli dokonają
cięcia wzdłuż narysowanej linii [sprawdzamy czy dzieci potrafią przewidzieć co powstanie].
Jeżeli nie są w stanie wyobrazić sobie co zostanie wycięte, to polecamy wyjęcie lusterek
(wyprawka) i przyłożenie ich równo wzdłuż zgięcia kartki. Lusterko przykładają wszystkie
dzieci – nawet te, które przewidziały efekt cięcia. One kontrolują swoje wyobrażenia. Wszystkie
powinny zobaczyć w odbiciu brakującą (drugą) część choinki – zobaczą to co powstanie po
wycięciu. Następnie dzieci tną wzdłuż linii. Kartka rozpada się na dwie części. Dzieci
rozkładają obie części i oglądają je. Jedna część to kartka z otworem w kształcie choinki, a
druga część, to wycięta choinka, którą można włożyć do otworu. Zarówno otwór jak i choinka,
to figury symetryczne [zbudowane z dwóch identycznych części – połówek]. Można czerwoną
kredką narysować w choince linię podziału na równe części.

Zad. 2.
Na zgiętej kartce N. rysuje każdemu dziecku (na jego oczach), odpowiednio – przy zgięciu,
połowę serca.
Dzieci przewidują co powstanie po wycięciu. Kontrolują swoje pomysły za pomocą odbicia
lustrzanego, tną kartkę wzdłuż linii i obserwują efekt pracy. Omawiają co im powstało.

Zad. 3.
Dzieci same zginają kartki, kreślą samodzielnie dowolną linię zaczynającą się na zgięciu i
kończącą się na zgięciu. Przewidują co wyjdzie [albo planują coś i tak rysują, by właśnie
otrzymać to co chcą], tną kartkę wzdłuż linii i obserwują co powstało. Nazywają swoje wzory.
Omawiają jaką własność posiadają wycięte elementy [wszystkie mają 2 równe części, można
złożyć na części, które idealnie się pokrywają].

Tydzień. 18
Zajęcia: Ptasia stołówka

Zadania z danymi liczbowymi
Zad. 3.

Do ptasiej stołówki, aby się pożywić, przyleciały też sikorki. Najpierw 4 sikorki. Ułóżcie tyle
sikorek ile przyleciało. [dzieci układają liczmany]. Potem przyleciały jeszcze 2. [dzieci dokładają
2 ptaki] Ile razem sikorek przyleciało do karmnika?
Każde dziecko samodzielnie układa obrazki sikorek zgodnie z treścią zadania (zgodnie z
danymi) i przelicza ile jest razem. Każde ma też mieć szansę na podanie odpowiedzi.
Analogicznie rozwiązujemy kolejne zadanie:
Zad. 4.
W karmniku było 6 sikorek (to wynik poprzedniego zadania), a na gałęzi obok siedziały jeszcze
2 sikorki. Ile było wszystkich sikorek?

Zadania o tym ile ziarenek/pestek zjadły ptaki
Zad. 5
Wróbelek zjadł najpierw 4 ziarenka zboża, a potem jeszcze 3 ziarenka. Ile wszystkich ziarenek
zjadł wróbelek?

W tym przypadku dzieci mogą układać prawdziwe ziarenka i zliczać je (zwłaszcza, że powinien
być ich zapas do karmnika).
Jednak, ponieważ ziarenka są małe i trudno jest je układać, można zaproponować dzieciom, by
zamiast ziarenek układały i liczyły kasztany lub patyczki. Wtedy jednak może się zdarzyć, że
niektóre dzieci nie będą potrafiły rozwiązać zadania, bo trudno im będzie zrozumieć, że wynik
liczenia dużych kasztanów, ma być odpowiedzią na pytanie ile małych ziarenek zjadł wróbelek.
Takie dzieci nie potrafią w rozwiązywaniu zadań

Tydzień 19
Zajęcia: Kwiaty dla Babci i Dziadka

Modyfikacja zabawy drugiej: Można ustalić, że razem ma być zawsze 6 (albo 7), ale wówczas
nie dla każdego wyniku w rzucie pierwszą kostką da się dobrać tyle oczek na drugiej, aby
zostały spełnione warunki zabawy. Gdy na pierwszej wypadnie 0, to na drugiej nie ma tylu
oczek, by razem było 6! A w przypadku sumy 7, brak jest rozwiązania zarówno dla 0, jak i dla 1.
W takiej wersji gry dziecko rzucające drugą kostką zdobywa punkt także wtedy, gdy wyjaśni (na
miarę swoich umiejętności) brak możliwości wyrzucenia tylu oczek, by razem było 6 (albo 7).

Środki dydaktyczne: kostki sześcienne z wyprawki (ścianki z kropkami od 0 do 5) dla dzieci,
dwie duże kostki do pokazowe dla nauczyciela, kasztany lub inne drobne przedmioty – jako
punkty w zabawie, klej do sklejenia kostek.

Dodatkowe zabawy matematyczne, przewodnik cz. 3

Tydzień 21
Zajęcia: Przygotowania do balu

„Pary na balu” – zabawa matematyczna: porównywanie liczebności zbiorów przez wzajemnie
jednoznaczne odwzorowanie, pojęcia: para, tyle samo, więcej, mniej, doświadczanie
przechodniości równoliczności zbiorów, których elementy różnią się wielkością, przeliczanie w
zakresie większym niż 10.

Zad. pary: strój karnawałowy – rekwizyt
Wcześniej była rozmowa na temat: „Kim będę na balu”, czyli za kogo można się przebrać.
Nawiązując do tej rozmowy pokazujemy dzieciom obrazki, na których są elementy strojów
karnawałowych oraz rekwizyty do nich pasujące (lecz nie do każdego stroju) np.:

Turban i spodnie Aladyna

Lampa Aladyna

Pół czarna, pół biała peruka Cruelli de Mon

Szczeniak dalmatyńczyk

Korona i strój królewny Śnieżki

Nadgryzione jabłko

Czerwona peleryna z kapturkiem

Koszyczek z jedzeniem

Kapelusz i maska Zorro

Szpada Zorro

Kapelusz i buty Kota w butach

-----

Maska i peleryna Batmana

-----

Czarny szpiczasty kapelusz czarownicy

Miotła

Stożkowate nakrycie głowy wróżki

Różdżka

Strój Spider-mana

Pajęczyna

Polecamy dzieciom, by połączyły w pary strój i pasujący do niego rekwizyt (o ile taki jest) oraz
wyjaśniły, dlaczego one pasują do siebie i o jaką postać bajkową chodzi. Wyjaśniamy także
znaczenie określenia PARA (jako dwie rzeczy w pewien sposób powiązane np. para butów, para
rękawiczek, para dzieci, ale też dwa różne elementy). Pytamy: Czy wszystkie stroje na obrazkach
mają dodatkowe rekwizyty? Czy strojów jest tyle samo, co rekwizytów? Czego jest więcej i o ile?
Czego jest mniej i o ile?

Zad. Pary: dziewczynka - chłopiec
Dzieci na balu będą tańczyć. Możemy zapytać: Czy każda dziewczynka będzie miała do pary
chłopca? Czy chłopców jest tyle samo, co dziewczynek? Jeśli nie, to pytamy O ile więcej/mniej
jest chłopców niż dziewczynek? Jak to sprawdzić? Tworzymy pary: chłopiec- dziewczynka.

Zad. Pary: dziecko – butelka, butelka – zakrętka

Dzieci stoją w kole, na środku pudło (kosz) z butelkami [Rekwizyty: czyste i puste, butelki np.
po wodzie mineralnej, albo po soczku marchwiowym. Każda butelka z zakrętką. Butelek co
najmniej tyle ile dzieci (może być o kilka butelek więcej niż dzieci)].

Nauczyciel mówi np.: Na bal karnawałowy potrzebne są nie tylko stroje, ale także coś do picia.
Wyobraźcie sobie, że w tych butelkach w koszu mamy sok na bal.

N. pyta: Jak myślicie czy tych butelek jest tyle samo, co dzieci? A może więcej, albo mniej?
Słucha odpowiedzi dzieci, nie ocenia ich. Pyta: Dlaczego tak sądzisz? Jak możemy to
sprawdzić?

Dobrym pomysłem jest ten, by każde dziecko podeszło, wzięło jedną butelkę i wróciło na
miejsce. Tworzone są pary: dziecko i butelka. Jeżeli nie zostanie żadna butelka, to znaczy, że
jest ich tyle samo, co dzieci. Jeśli zostaną butelki, to znaczy, że jest ich więcej niż dzieci. W
tym drugim przypadku liczymy ile butelek zostało. Ustalamy, o ile więcej było butelek niż
dzieci oraz o ile mniej było dzieci niż butelek. Następnie chowamy nadmiar butelek i pytamy:
A teraz jak jest? Czy butelek i dzieci jest tyle samo? Ile jest butelek?
Niezależnie od tego, czy dzieci potrafią podać liczbę butelek, czy też nie, proponujemy
przeliczyć butelki: Wskazane dziecko podnosi do góry swoją butelkę i mówi jeden, następne w
kole, podnosi swoją butelkę i mówi dwa, kolejne mówi trzy itd. aż przeliczą wszystkie. N. w
razie potrzeby może podpowiadać dzieciom kolejne liczebniki, nawet w zakresie ponad
dwadzieścia. Dzieci mają okazję poznać liczebniki w większym zakresie i przyswoić sobie
rytm liczenia rytm liczenia.
Ponownie pytamy: Czy butelek i dzieci jest tyle samo?
Po uzyskaniu pozytywnej odpowiedzi, prosimy, aby dzieci ustawiły butelki w jednym rzędzie
wewnątrz koła i wróciły na swoje miejsce w kole. Pytamy: A teraz jak jest? Czy butelek i dzieci
jest tyle samo?
Ponownie prosimy by dzieci zabrały swoje butelki i ponawiamy pytanie: A teraz jak jest? Czy
butelek i dzieci jest tyle samo?
Po uzyskaniu pozytywnej odpowiedzi, pytamy o zakrętki. Czy każda butelka ma zakrętkę? [tu
są pary: butelka i zakrętka] Czy zakrętek jest tyle samo co butelek? Czy zakrętek jest tyle
samo co dzieci? Dlaczego? [sprawdzamy, czy dzieci są świadome przechodniości równości].
Ile jest zakrętek?
Polecamy odkręcić zakrętki z butelek i każde dziecko układa swoją zakrętkę wewnątrz koła,
tak, by zakrętki były w jednym rzędzie. Warto liczyć kolejno układane zakrętki: dziecko
kładzie pierwszą zakrętkę i mówi jeden, następne dziecko kładzie swoją zakrętkę i mówi dwa,
kolejne mówi trzy itd. aż położą i przeliczą wszystkie. Pytamy: A teraz jak jest? Czy zakrętek
jest tyle samo, co butelek? Niektóre dzieci mogą sądzić, że zakrętek jest mniej niż
butelek/dzieci, bo zakrętki są małe i zajmują mniej miejsca niż butelki/dzieci. Dlatego ważnym
dla nich doświadczeniem jest późniejsze ponowne łączenie zakrętek z butelkami tak, by
widziały, że każda butelka/każde dziecko ma zakrętkę, więc jest ich tyle samo. Nie oceniamy i
nie komentujemy wypowiedzi dzieci. Troszczymy się tylko o to, by dzieci zdobywały
doświadczenia. Dlaczego? Czy zakrętek jest tyle samo co dzieci? Dlaczego?
Dzieci zabierają kolejno swoje zakrętki i nakładają na butelki. Pytamy: A teraz jak jest? Czy
zakrętek jest tyle samo co butelek?
W zależności od potrzeby dzieci (gdy nie wszystkie są przekonane, że zawsze jest tyle samo)
prosimy, by ułożyły zakrętki w kole tak, aby ich układ tworzył okrąg. Następnie zadajemy
pytania jak wcześniej.
Można też wrzucić zakrętki po pudełka i znowu zadawać te same co wcześniej pytania.

Zad. Pary: dziecko – balonik
Można wykonać też ćwiczenia z innymi rekwizytami. Można przygotować dla dzieci i ułożyć
w pudełku np. balony do nadmuchiwania. Pytamy: Czy wystarczy balonów dla dzieci, tak aby
każdy miał jeden balon? Co trzeba zrobić by to sprawdzić? Każde dziecko podchodzi i bierze
jeden balonik. Tworzą się pary: dziecko i balonik. Jeżeli każde dziecko będzie miało w ręku
balon i nie będzie już w pudle balonów, to jest ich tyle samo co dzieci. W przeciwnym razie
przeliczamy: o ile więcej było balonów niż dzieci. Chowamy nadmiar balonów tak, by zostało
ich tyle samo, co dzieci. Pytamy: Czy balonów i dzieci jest tyle samo? Czy baloników i butelek
jest tyle samo? [chodzi o butelki z poprzedniego zadania]. Czy baloników i zakrętek do butelek
jest tyle samo?
Dzieci nadmuchują swoje balony. Pytamy: A teraz jak jest? Czy balonów i dzieci jest tyle
samo? Nadmuchane balony układamy w rzędzie pod ścianą, potem w kole na środku sali i za

każdym razem pytamy: A teraz jak jest? Czy balonów i dzieci jest tyle samo?

Środki dydaktyczne: obrazki, na których są elementy strojów karnawałowych oraz rekwizyty do
nich pasujące (lecz nie do każdego stroju) np.:

Turban i spodnie Aladyna

Lampa Aladyna

Pół czarna, pół biała peruka Cruelli de Mon

Szczeniak dalmatyńczyk

Korona i strój królewny Śnieżki

Nadgryzione jabłko

Czerwona peleryna z kapturkiem

Koszyczek z jedzeniem

Kapelusz i maska Zorro

Szpada Zorro

Kapelusz i buty Kota w butach

-----

Maska i peleryna Batmana

-----

Czarny szpiczasty kapelusz czarownicy

Miotła

Stożkowate nakrycie głowy wróżki

Różdżka

czyste i puste, butelki z zakrętkami po wodzie mineralnej, albo po soczku marchwiowym, co
najmniej tyle ile dzieci (może być o kilka butelek więcej niż dzieci), baloniki do
nadmuchiwania (co najmniej tyle ile jest dzieci).

Tydzień 24
Zajęcia: Ogień

„Ogniowe przygody” – zabawy matematyczne połączone z grą planszową.

Rozmowa z dziećmi
Z czym wam się kojarzy ogień?

Co dobrego daje/dawał nam ogień?
- ogrzewanie (ciepło): ognisko, kominek, piec, centralne ogrzewanie;
- możliwość przygotowania posiłku: na ognisku, na kuchni węglowej, na kuchni gazowej, na grillu;
- oświetlenie: światło z ogniska, pochodnia, świeca (różne świece), lampa naftowa, lampa gazowa.
Co oznacza określenie: „Ogień to niebezpieczny żywioł”?
Jakie szkody wyrządza ogień?
- pożar lasu, łąki, budynków (straty w ludziach, zwierzętach, straty materialne, zniszczenia w
przyrodzie);
- wybuch wulkanu – ognista (gorąca) lawa.

Klasyfikacja obrazków
Po rozmowie z dziećmi N. prezentuje obrazki, na których przedstawiony jest ogień w sytuacjach, gdy
jest przydatny i niebezpiecznych (jak omówione wyżej). Dzieci omawiają obrazki, dokonują ich
podziału (np. tak jak w tabeli poniżej) na sytuacje dobre i niebezpieczne.

ogień
sytuacje korzystne/dobre

sytuacje niebezpieczne

ogrzewanie (ciepło)

gotowanie:

oświetlenie

ognisko, kominek,
piec, centralne
ogrzewanie

na ognisku, na kuchni
węglowej, na kuchni
gazowej, na grillu

światło z ogniska,
pochodnia, świeca,
lampa naftowa,
lampa gazowa

pożar lasu, łąki,
budynków,
wybuch wulkanu

Gra planszowa
N. proponuje dzieciom skonstruowanie i rozegranie gry planszowej, w której bohaterem będzie ogień.

W fabule gry można uwzględnić pomysły N. i dzieci.

Rekwizyty: Duży arkusz szarego papieru na narysowanie trasy (chodniczka do gry – około 60 lub
mniej pól/płytek), kolorowe pisaki, kostka sześcienna do gry, różnobarwne pionki – po jednym dla
każdej drużyny, naklejki lub obrazki z ogniem w sytuacjach korzystnych albo niebezpiecznych
(można wykorzystać obrazki z zadania poprzedniego).

Przykładowa plansza: kręty chodniczek liczbowy na którym jest około 60 pól (płytek), zaznaczony
start i meta, i strzałka - kierunek poruszania się.

Wybrane płytki na trasie (około 10 płytek) pomalowane są na zielono, na nich zapisane liczby

(np. liczby od 2 do 6) – premie, a przy nich „dobre” symbole ognia. Gdy gracz zatrzyma się na takiej
zielonej płytce z dobrym symbolem ognia (ma albo oświetloną trasę, albo okazję do zagrzania się,
albo możliwość zjedzenia czegoś gotowanego i nabrania sił), dostaje premię i przesuwa się do przodu
o tyle kroków/pól, jaka jest liczba na zielonej płytce.

Na trasie są także wyróżnione płytki czerwone (około 10 takich płytek) oznaczające

niebezpieczeństwo, także z zapisanymi na nich liczbami (np. liczby od 0 do 5) – karami, a przy nich
symbole z ogniem, który zagraża. Gdy gracz zatrzyma się na takiej czerwonej płytce z symbolem
niebezpieczeństwa, musi wycofać się z niebezpiecznej strefy (cofnięcie o tyle kroków/pól, jaka jest
liczba na czerwonej płytce), albo musi przeczekać niebezpieczeństwo (traci kolejkę, gdy na płytce
czerwonej zapisana jest liczba zero).

W zależności od możliwości dzieci, można jeszcze wprowadzić pola pomarańczowe (kilka np.

8 pól) . Gdy gracz się zatrzyma na takim polu ma wykonać zadanie dodatkowe np. rzucić dwiema
kostkami z wyprawki, ze ściankami, na których jest od 0 do 5 oczek, oraz podać sumę oczek na obu
kostkach. Jeśli gracz wykona zadanie poprawnie, przesuwa się o jeden krok do przodu, jeśli
niepoprawnie, cofa o jeden krok. Tak może być na każdym polu pomarańczowym, albo na każdym
polu pomarańczowym można wykonywać inne zadanie (zadania można zmieniać). Np. można liczyć
na planszy wszystkie pola zielone/ czerwone/ pomarańczowe albo liczyć klaśnięcia nauczyciela. N.
może podać dziecku garść kasztanów i polecić by je przeliczyło itp.

Można grać w dwóch zespołach. Zespoły na przemian rzucają kostką i wykonują swoim pionkiem
tyle kroków do przodu, ile oczek wypadło na kostce. Jeżeli zatrzymają się na wyróżnionym polu –
wykonują kolejne ruchy (do przodu lub do tyłu zgodnie z regułami gry).
Zwycięża ten zespół, który pierwszy dotrze do mety.
Po rozegraniu jednej partii i wyłonieniu zwycięzcy należy powtórnie rozegrać grę, by dać szansę
przegranym na rewanż.
W trakcie gry uczymy respektowania umów, właściwego zachowania, panowania nad emocjami.
Uwaga! Ważne jest zwracanie uwagi na sposób przemieszczania pionków w grze – chodzi o to by
dzieci liczyły wykonane ruchy pionkiem/kroki, a nie pola, bo licząc pola często zaczynają liczenie od
pola, na którym stoi pionek, a nie (jak powinno być) od pola następnego.

Środki dydaktyczne: obrazki: ognisko, kominek, piec kaflowy, centralne ogrzewanie,

kociołek nad ogniskiem, garnek na kuchni węglowej, patelnia na kuchni gazowej,
mięso/kiełbasa na grillu, światło z ogniska, pochodnia, świeca (różne świece), lampa naftowa
(różne lampy), lampa gazowa, pożar lasu, łąki, budynków, wybuch wulkanu (ognista lawa);
rekwizyty do gry planszowej: duży arkusz szarego papieru na narysowanie trasy, kolorowe
pisaki, kostka sześcienna do gry, różnobarwne pionki – po jednym dla każdej drużyny, naklejki
lub obrazki z ogniem w sytuacjach korzystnych albo niebezpiecznych do przyklejenia na planszy,
sześcienne kostki z wyprawki ze ściankami, na których jest od 0 do 5 oczek.

Dodatkowe zabawy matematyczne, przewodnik cz. 4

Tydzień 33
Zajęcia: Kolorowe ule

Ćwiczenie rozwijające kreatywność i twórcze myślenie
I wersja

Zabawa polegająca na tym, że dzieci kolejno podają nazwy par przedmiotów o
przeciwstawnych cechach, a grupa ma podać te przeciwstawne cechy. Np.:
człowiek i samolot [tu jest wiele możliwości podania cech przeciwstawnych: wolny (wolno
poruszający się) i szybki (szybko poruszający się), mały i duży, obiekt żyjący i nieożywiony,
ciepły i zimny, miękki i twardy itp.],
herbata i lody [ciepłe i zimne, płynne i stałe],
piłka i cegła [okrągłe i nieokrągłe, lekkie i ciężkie, miękkie i twarde, gładkie
i szorstkie/kanciaste]
arbuz i cytryna [duże i małe, ciężkie i lekkie, zielone i niezielone, słodkie i kwaśne],
ocet i miód [kwaśny i słodki, rzadki i gęsty, bezbarwny i posiadający kolor miodowy].

II wersja (łatwiejsza)

Zabawa polega na tym, że dzieci kolejno podają, jedno dziecko – nazwę cechy, a drugie
dziecko - nazwę cechy przeciwnej, itd..
Np. jedno dziecko mówi ciepło, następne zimno, kolejne mówi jasny, a następne ciemny itd.
Środki dydaktyczne: obrazki uli takie, by były wśród nich pary uli: wysoki i niski, wąski i
szeroki, jednobarwny i wielobarwny, stary i nowy, mały i duży, w jasnym kolorze i w
ciemnym kolorze, okrągły (np. wydrążony z pnia drewna) i nieokrągły, obrazki
„Przeciwieństwa” z wyprawki.

Tydzień 35
Zajęcia: Wśród owadów

Bingo „owadowe”
Dzieci mają rozmieścić na planszy o wymiarach 3 na 3 (9 okienek) obrazki 9 owadów (3 biedronki,
3 motyle i 3 pasikoniki) – można wykorzystać liczmany z wyprawki, w ten sposób, by w każdym
rzędzie poziomym i w każdej kolumnie były 3 różne owady (w żadnym rzędzie i w żadnej
kolumnie nie może się pojawić 2 razy ten sam owad. Przykładowe rozwiązanie (b – biedronka, m –
motyl, p – pasikonik):

Można zadanie utrudnić, rozmieszczając w tabeli 4 na 4 (16 pól) 16 owadów (4 biedronki, 4
motyle, 4 pasikoniki i 4 osy; kod – osy to litera „o”).

Zabawa „Inna matematyczna gąsienica” (Ćwiczenia przygotowujące do posługiwania się osią
liczbową i grafami strzałkowymi.)
Każde dziecko wycina z papieru kółko, na którym nakleja/zapisuje swoją ulubioną liczbę.
Następnie dzieci siadają w kręgu. Wewnątrz kręgu dzieci i nauczyciel układają gąsienicę (węża) ze
swoich kółek, w ten sposób, że pierwsze kółko z liczbą kładzie N. Kolejno dzieci dokładają swoje
kółka, tworząc gąsienicę. Dziecko kładąc swoje kółko ma podać działanie umożliwiające przejście
od ostatniej liczby do tej jaka jest na jego kółku np. leży kółko z liczbą 5, dziecko dokłada kółko z
liczbą 3. By przejść od 5 do 3 należy odjąć 2 bo 5 – 2 = 3 [można mówić o cofnięciu o 2 kroki z
pola 5 na pole 3 na chodniczku liczbowym zilustrowanym poniżej

]. Gdy następne dziecko kładzie

kółko z liczbą np. 7, to by przejść od liczby 3 do liczby 7 należy dodać 4, bo 3 + 4 = 7 itd.

By ułatwić dzieciom zadanie, można na długim pasku szarego papieru, podzielonym na segmenty,

zapisać liczby od 0 do 10 (por. rys. poniżej) i korzystać z takiego chodniczka liczbowego przy
ustalaniu co zrobić, by „przejść z jednej liczby do następnej”.

Środki dydaktyczne: długi sznurek, papierowe koła (segmenty gąsienicy) co najmniej 10, na
których zapisane są liczby od 0 do 10 – niektóre liczby mogą się powtarzać, tabliczki/kartoniki
z napisem „start”, „meta”, pudełko na koła z liczbami, tabela 3 na 3 (albo 4 na 4) oraz rysunki
owadów (3 – 4 biedronki, 3 – 4 motyle i 3 – 4 pasikoniki, 4 osy) do „owadowego” bingo,
papierowe koła, po jednym dla każdego dziecka do naklejeni/zapisania ulubionej liczby nie
większej niż 10.

Tydzień 36
Zajęcia: Święto Mamy i Taty

Zabawa – ilustrowanie gestami wiersza „Tydzień” Ewy Stadtmüller:
Można zapoznać dzieci

z wierszem Ewy Stadtmüller "Tydzień" oraz wspólne ilustrować z nimi treść wiersza
ruchem i gestami podczas głośnego czytania tekstu przez nauczyciela.
Poniedziałek wstał zaspany,
Ziewnął smacznie i powiada:
- Nie lubię być po niedzieli,
lecz ktoś musi, trudna rada.
Wtorek zabrał się do pracy,
nie ma czasu, by narzekać.

- Jestem drugim dniem tygodnia,
huk roboty na mnie czeka.
Środa ślicznie się uśmiecha,
siedzi braćmi otoczona.
Z tego miejsca, w samym środku,
chyba jest zadowolona.
Czwartek – czwarty w kolejności
ciągle ma kłopoty z czasem.
Tyle jeszcze do zrobienia,
a tu piątek już za pasem.
Piątek – piąty też się spieszy,
aż nań biją siódme poty.
Czas pokończyć, co zaczęte,
chciałby zdążyć do soboty.
A sobota jak sobota,
okna myje, łóżka ścieli.
Już nie może się doczekać
siostry swej – niedzieli.
Ufff – nareszcie jest niedziela.
- Chodźcie – mówi – moi mili.
Czas odsapnąć sobie trochę,
boście bardzo się zmęczyli.

Tydzień 37
Zajęcia: Bawimy się razem

Wersja II zabawy matematycznej: Początek jak w wersji I (tzn. dzielimy dzieci na zespoły 3 –
4 osobowe. Każdy zespół rysuje kredą/patykiem (na boisku, podwórku) planszę jak na rys.
poniżej (plansza „chłopek”). Potrzebne dwie kostki do gry.

Pierwsza osoba staje na polu START i wykonuje rzut dwiema kostkami. Ustala, ile e

wypadło oczek łącznie na obu kostkach (albo dodaje liczby oczek, albo dolicza do oczek jednej
kostki, oczka drugiej, albo przelicza wszystkie razem). Stojąc na STARCIE podaje łączną
liczbę oczek na obu kostkach. Przeskakuje na kolejne pole i podaje liczbę o 1 większą od
uzyskanej na poprzednim polu. Na każdym kolejnym polu wypowiada kolejny liczebnik, aż
dotrze do okrągłego pola. Tam podskokiem odwraca się i od tego miejsca, skacząc nadal,
wymienia liczby w kolejności malejącej (na kolejnych polach wymienia liczbę o 1 mniejszą od
poprzedniej).
Np. Zawodnik staje na polu START i rzuca kostkami. Na jednej wypadło 5 oczek, na drugiej 3
oczka. To razem 8. Stojąc na starcie mówi osiem. Przeskakuje na kolejne pole i wypowiada
kolejny liczebnik, czyli 9. Skacze dalej, wymieniając kolejne liczby: 10, 11, 12, 13 (skacze
obunóż na polach niebieskich), 14 na „szyi”, 15 (jednocześnie wykonując skok obunóż na obu
półkolach). Następnie podskokiem odwraca się na okrągłym polu i nadal, skacząc,(teraz w
przeciwną stronę) wymienia liczby malejąco, powtarza 15 na „głowie” i dalej liczy wstecz: 14,
13 itd. aż dotrze do pola META.

Po poprawnym wykonaniu zadania zdobywa punkt (np. kamyk/ kasztan lub fasolkę, albo
narysowaną kredą kreskę). Następne w kolejce dziecko postępuje analogicznie. Zabawa trwa
określoną liczbę kolejek np. po 5 dla każdego uczestnika. Na koniec wyłaniamy zwycięzcę –
tego kto zdobył najwięcej punktów.

Środki dydaktyczne: kreda do rysowania planszy na betonie lub patyk do rysowania na ziemi,
oraz kostki do gry np. kostki sześcienne z wyprawki ze ściankami na których jest od 0 do 5
oczek, drobne przedmioty (kasztany, kamyki lub fasolki) do zliczania punktów.

Tydzień 38
Zajęcia: Porządki w kąciku książki

Zadania z rozmieszczaniem książek na półkach

Ze stosu książek na biurku weź tyle książek, ile masz palców u rąk.
Ile wzięłaś książek? [10]
Ułóż te książki na regale na dwóch jego półkach (dolnej i górnej).
Ile książek jest na górnej półce?
Ile książek jest na dolnej półce?
Czy na dolnej i górnej jest tyle samo książek?
Jeżeli książki nie zostały rozłożone po równo, to pytamy:
Na której półce jest więcej książek? O ile jest więcej książek na górnej/ dolnej półce niż na
dolnej/górnej?
Zapiszmy matematycznie to rozłożenie książek.
układamy z kartoników działanie: 10 to 6 i 4. 10 = 6 + 4.
Jak jeszcze inaczej można ułożyć te książki na tych dwóch półkach?
Dzieci pokazują różne sposoby rozkładu liczby 10 na 2 składniki, „zapisując” swoje pomysły za
pomocą kartoników z liczbami.

Kolejne zadania z książkami
1. Przypomnijcie ile książek ułożono na tych dwóch półkach. (10)

Zabierzmy z jednej półki 2 książki. Ile książek zostanie? (było 10, zabrano 2, zostało 8, bo 10
odjąć 2 to jest 8).

2. Jeśli od tych 8 książek zabierzemy jeszcze 3, to ile książek zostanie (było 8, zabrano 3, zostało

5, bo 8 odjąć 3 to jest 5).

3. Na półkach jest 5 książek. Dołóżmy do nich 2 książki. Ile teraz będzie książek? (było 5,

dołożono 2, jest teraz 7, bo 5 dodać 2 to jest 7)itp.

Te zadania dzieci powinny rozwiązywać przez układanie książek na półkach. Niektóre z nich

zapewne potrafią wykonać obliczenia na palcach lub w pamięci Z uwagi na to, że nie
wszystkie dzieci posiadają takie umiejętności należy dosłownie realizować sytuację opisaną w
zadaniu.

Środki dydaktyczne: materiały do demonstracji: książki albo rysunki okładek książek, np.

1. tytuł w górnej części książki, a ilustracja w dolnej części,
2. tytuł w dolnej części książki, a ilustracja w górnej części,
3. tytuł w środkowej części książki, a ilustracje wokół: i nad tytułem, i pod tytułem;

prawdziwe książki (co najmniej 10 do zadań z rozkładaniem na półkach).

Tydzień 39
Zajęcia: Tęczowe kolory

Rozwiązywanie zagadek celem utrwalenia znajomości nazw miesięcy

N. rozwiązuje wspólnie z dziećmi zagadki, utrwalając w ten sposób nazwy miesięcy (M. Przybysz-
Piwko Zbiór przysłów i zagadek dla dzieci, Warszawa 1995).
N. omawia z dziećmi niezrozumiałe zwroty, następnie czyta dzieciom zagadkę dzieci odgadują
nazwę miesiąca i wskazują ją na tarczy z dwunastoma miesiącami.

Jaki to miesiąc zamyka szkoły i daje dzieciom urlop wesoły?

Choinkę przynoszę, więc lubią mnie ludzie. Na wigilię proszę, nazywam się ...

Imię swoje zdobi kwiatem. Zawsze zimę z wiosną splata. A w ogóle – chytra sztuka – bacz, by
ciebie nie oszukał!

Słońce mocno przygrzewa, zboże szybko dojrzewa. W lipach brzęk pszczół rozbrzmiewa. W jakim
miesiącu tak bywa?

Przynoszę deszcze, szarugi, dzień krótki, a wieczór długi. Perkoza wysyłam za morza i jeża
usypiam w borze. Z drzew liście ostanie spadły. Świat już utracił jesienne barwy.

Na ślizgawkę, narty, sanki, ciepłą kurtkę włóż i buty. Już niedługo przyjdzie wiosna, choć panuje
jeszcze ...

Mówią, że w nim jak w garncu, nieustanna zmiana. Słońce grzeje w południe, mrozek szczypie z
rana, a do tego jeszcze przelatują deszcze!

On dziesiąty jest w kolejce, gdzie stoi dwanaście miesięcy.

W jakim miesiącu pod cięciem kosy oraz żniwiarek padają kłosy?

Noworocznych wiele życzeń niesie dzieciom mroźny ...

Ten miesiąc we wrzosie, szuka rydzów po lesie. A kiedy rosa zginie, szuka orzechów w leszczynie.

Chociaż to miesiąc długi, to najkrócej się nazywa. I co roku tym się chlubi, że zielenią świat
okrywa.

Na koniec dzieci głośno wymieniają nazwy kolejnych miesięcy i jednocześnie palcem wskazują ich
położenie na tarczy 12 miesięcy. Trwa to tak długo, aż dzieci dwukrotnie okrążą tarczę. Ważne
jest, by dzieci zauważyły stałe następstwo miesięcy.

Środki dydaktyczne: ilustracje miesięcy z ich nazwami, kartoniki z numerami miesięcy od 1. do 12,
można wykorzystać 12-kartkowy kalendarz (jedna kartka na jeden miesiąc) ze zdjęciami
krajobrazów charakterystycznych dla danego miesiąca, z wyprawki tarcza do 12 miesięcy.