Celem analiz ró¿nych materia³ów

jest uzyskanie wiarygodnego wyniku.
Aby to osi¹gn¹æ, metoda analizy mu-
si byæ dobrze opracowana i spraw-
dzona. Do niedawna, a w niektórych
laboratoriach w dalszym ci¹gu poda-
je siê wynik analizy jako wartoœæ X
bez okreœlenia odchylenia standardo-
wego b¹dŸ przedzia³u ufnoœci, czyli
zakresu wartoœci, w jakim mo¿e znaj-
dowaæ siê X z okreœlonym prawdopo-
dobieñstwem. Wprawdzie bardzo
czêsto wraz z wynikiem podaje siê
odchylenie standardowe, lecz naj-
czêœciej jest to precyzja aparatu, czy-
li zgodnoœæ wyników otrzymanych
w tych samych warunkach. Nale¿y
zaznaczyæ, ¿e nowoczesne urz¹dze-
nia analityczne umo¿liwiaj¹ otrzyma-
nie wyniku z precyzj¹ nawet <1%.
Czy to oznacza, ¿e wartoœæ stê¿enia
sk³adnika w próbce oznaczana jest
z precyzj¹ 1%? Nie. Na precyzjê
oznaczenia wp³ywa nie tylko precyzja
aparatu, ale precyzja ca³ego toku
przygotowania próbki i uzyskania wy-
niku analitycznego.

Wynik i precyzja oznaczenia obej-

muje ca³oœæ procesu analitycznego,
poczynaj¹c od etapu pobrania próbki,
rozdrobnienia, ujednorodnienia (ho-
mogenizacji) i przeprowadzenia jej
do roztworu, oddzielenia lub masko-
wania interferentów, oddzielenia ana-
litów i ostateczny pomiar stê¿enia
analitu [1]. Nale¿y wiêc zastanowiæ
siê, co tak naprawdê wp³ywa na pre-
cyzjê i dok³adnoœæ (czyli zgodnoœæ
wyniku otrzymanego z wartoœci¹
prawdziw¹, wyra¿ana jako odzysk
procentowy) uzyskanego wyniku
oraz jak oszacowaæ jego niepew-
noœæ. Jest to problem niezwykle wa¿-

ny w iloœciowej analizie kryminali-
stycznej, gdzie jakoœæ wyników anali-
tycznych ma bardzo du¿e konse-
kwencje. Na przyk³ad, przy oznacza-
niu THC w próbkach konopi bardzo
wa¿na jest okreœlona granica jego
zawartoœci równa 0,20% w suchej
masie. Gdy w próbce oznaczono
THC i uzyskano wartoϾ 0,21%, to
by³oby to du¿¹ nieœcis³oœci¹ podawa-
nie wyniku analizy jako 0,21%. Nie
jest mo¿liwe oznaczenie sk³adnika ze
stuprocentow¹ precyzj¹. Nale¿y
wzi¹æ pod uwagê precyzjê przygoto-
wania próbki (niepewnoœæ kolb, pipet
itp.), roztworów kalibracyjnych (nie-
pewnoœæ kolb, pipet, wzorca wyjœcio-
wego) oraz precyzjê aparatu. Te
wszystkie sk³adniki powoduj¹, ¿e nie-
pewnoϾ wyniku na pewno jest istot-
na. Oczywiœcie komplikuje to inter-
pretacjê wyniku. Podanie 0,21% za-
wartoœci THC u³atwia interpretacjê
prawa w s¹dzie (zawartoœæ THC po-
wy¿ej 0,20%) ni¿ podanie wyniku ja-
ko 0,21 ± 0,02%. Taki wynik obejmu-
je wartoœæ graniczn¹ 0,20% i trudno
jest okreœliæ, czy w próbce jest 0,19%
czy 0,23%. Mimo tych trudnoœci nale-
¿y wzi¹æ pod uwagê, ¿e nawet nowo-
czesne metody analityczne maj¹
swoje ograniczenia. Nale¿y d¹¿yæ do
zmniejszenia wartoœci niepewnoœci
wyniku, maj¹c na uwadze, ¿e nigdy
nie uda siê jej zmniejszyæ do zera.
Celem prowadzonych badañ opisa-
nych w artykule jest podanie metody
szacowania niepewnoœci wyniku na
przyk³adzie oznaczania pierwiastków
technik¹ ICP-OES. Nale¿y zazna-
czyæ, ¿e szacowanie wyniku jest ana-
logiczne we wszystkich technikach
analitycznych. Artyku³ mo¿e byæ wiêc

pomocny szerokiej grupie analityków,
nie tylko zwi¹zanych z wyznacza-
niem sk³adu pierwiastkowego.

Podstawy teoretyczne szacowania
niepewnoœci wyniku

Szacowanie niepewnoœci typu A i B

Wynik pomiaru jest tylko przybli¿e-

niem wartoœci prawdziwej, dlatego
bêdzie on dopiero wtedy kompletny,
gdy podamy go wraz z wartoœci¹ jego
niepewnoœci (parametr zwi¹zany
z wynikiem pomiaru, który charakte-
ryzuje rozrzut wartoœci przypisanych
analitowi) [2]. Na niepewnoϾ wyniku
sk³adaj¹ siê ró¿norodne sk³adniki,
które mo¿na podzieliæ na dwie grupy
w zale¿noœci od metody ich wyzna-
czania:

TYP A – uzyskane metodami sta-

tystycznymi;

TYP B – uzyskane innymi meto-

dami.

Szacowanie niepewnoœci standar-

dowej na podstawie analizy staty-
stycznej wielu wyników nazywane
jest szacowaniem niepewnoœci typu
A. Sk³adnik niepewnoœci w kategorii
A jest reprezentowany przez staty-
stycznie wyznaczone odchylenie
standardowe Sd, obliczone z tych
wyników.

Dla takiego sk³adnika standardo-

wa niepewnoœæ ui, równa jest odchy-

leniu standardowemu (ui = Sd).

Przyk³adem mo¿e byæ oszacowa-

nie niepewnoœci spektrometru ICP-
-OES. W tym celu wykonano 10-kro-
tny pomiar stê¿enia analitu (wykona-
no oznaczanie cynku w próbce kono-

31

PROBLEMY KRYMINALISTYKI 248/05

Marzena Kuras
Marek Jan Wachowicz

Szacowanie niepewnoœci
metody analitycznej
w praktyce
eksperta kryminalistyki

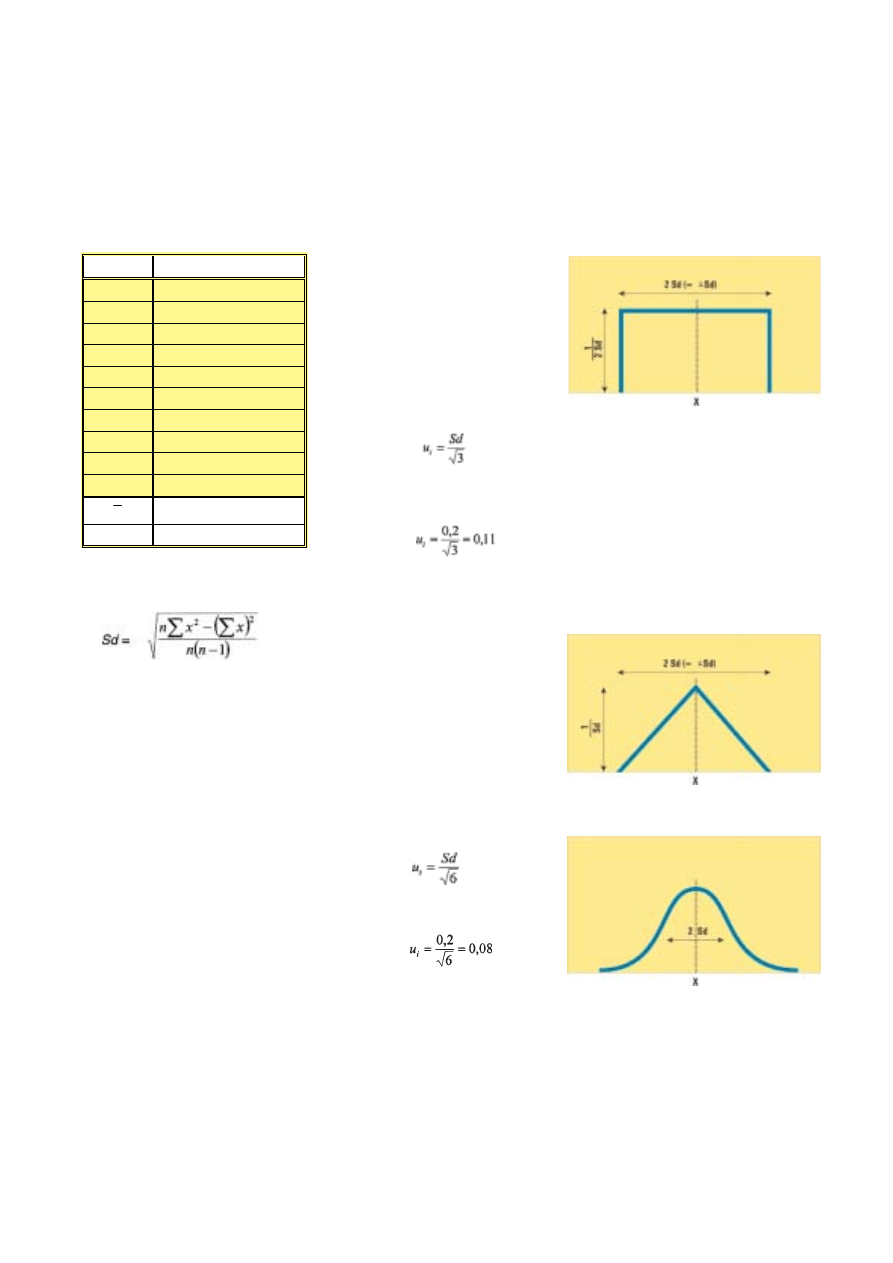
pi). Uzyskane wyniki przedstawiono
w tabeli 1.

gdzie:
n – liczba pomiarów,
x

РwartoϾ wyniku.

Wynik podany jest jako:

x

± Sd

(wartoœæ œrednia ± niepewnoœæ stan-
dardowa). Zatem wynik oznaczania
cynku uwzglêdniaj¹c tylko precyzjê
aparatu wynosi 1,85 ± 0,01 mg/l.

Szacowanie niepewnoœci typu B

zazwyczaj jest oparte na wiedzy na-
ukowej, dostêpnych informacjach,
które mog¹ obejmowaæ:

– wczeœniejsze wyniki pomiarów,
– doœwiadczenie lub ogóln¹ wie-

dzê na temat zachowania i w³a-
œciwoœci próbek oraz aparatu,

– specyfikacje producenta,
– dane dostarczone w dokumen-

tach kalibracji,

– niepewnoœci dostarczone przez

producenta wraz z wartoœciami
certyfikowanymi zawartoœci ana-
litu w próbce.

Do szacowania niepewnoœci typu

B niezbêdna jest wiedza na temat
podstawowych rozk³adów prawdopo-
dobieñstwa i sposobów ich stosowa-
nia w analizie danych. Na przyk³ad,
kolba miarowa w swoim certyfikacie
ma podan¹ objêtoœæ 25 ± 0,2 ml. Nie
jest jednak podany poziom ufnoœci
(czyli prawdopodobieñstwo, z jakim
ta wartoœæ zosta³a wyznaczona).
Nale¿y wiêc za³o¿yæ, ¿e prawdopo-
dobieñstwo wyst¹pienia objêtoœci
w zakresie 24,8

÷25,2 ml jest rów-

ne, czyli w tym przypadku przyjmu-
je siê prostok¹tny rozk³ad prawdo-
podobieñstwa (ryc. 1). Dla tego ty-
pu rozk³adu niepewnoœæ standar-
dow¹ (ui) podaje siê, jako:

W omawianym przyk³adzie

czyli objêtoœæ kolby wraz z nie-

pewnoœci¹ wyniesie 25 ± 0,11 ml.

Je¿eli natomiast z pomiarów

grawimetrycznych objêtoœci kolby
wynika, ¿e wiêkszoœæ wyznaczo-
nych wartoœci jest prawie równa
wartoœci 25,0 ml, to nale¿y przyj¹æ
trójk¹tny rozk³ad prawdopodobieñ-
stwa (ryc. 2). Oznacza to, ¿e war-
toœci te s¹ bardziej prawdopodob-
ne ni¿ wartoœci skrajne, tj. 24,8
i 25,2 ml. Przy zastosowaniu tego
rozk³adu prawdopodobieñstwa
wartoœæ niepewnoœci wyniesie:

W omawianym przyk³adzie

czyli objêtoœæ kolby wraz z nie-

pewnoœci¹ wyniesie 25 ± 0,08 ml.

Porównuj¹c te dwa przyk³ady wi-

daæ wyraŸnie, ¿e uzyskanie dodatko-
wych informacji na temat uk³adu
umo¿liwi³o zmniejszenie wartoœci
niepewnoœci uzyskanego wyniku

(wartoœæ niepewnoœci 0,11 w pierw-
szym i 0,08 w drugim przyk³adzie).

W przypadku gdy podanemu prze-

dzia³owi ufnoœci towarzyszy dodatko-
wo poziom ufnoœci (p%), czyli wynik
± Sd przy p%, nale¿y spodziewaæ
siê, ¿e wyniki podlegaj¹ normalnemu
rozk³adowi prawdopodobieñstwa

(ryc. 3). Wtedy, aby uzyskaæ wartoœæ
niepewnoœci standardowej, nale¿y
odchylenie standardowe podzieliæ
przez odpowiedni¹ wartoœæ procento-
wego wskaŸnika rozk³adu normalne-
go dla danego poziomu ufnoœci. Na
przyk³ad, specyfikacja wagi podaje
jej precyzjê jako ± 0,2 mg, przy pozio-

mie ufnoœci 95%. Z tabel statystycz-
nych rozk³adu normalnego dla pozio-
mu ufnoœci 95% wartoœæ wskaŸnika
wynosi 1,96. Nale¿y wiêc wartoœæ od-

PROBLEMY KRYMINALISTYKI 248/05

32

Tabela 1

Wyniki oznaczenia cynku

w próbce konopi

Results of zinc determination

in cannabis sample

Ryc. 1. Prostok¹tny rozk³ad prawdopodobieñstwa
Fig. 1. Rectangular distribution of probability

Ryc. 2. Trójk¹tny rozk³ad prawdopodobieñstwa
Fig. 2. Triangular distribution of probability

Ryc. 3. Normalny rozk³ad prawdopodobieñstwa
Fig. 3. Regular distribution of probability

P

Po

om

miiaarr

W

Wy

yn

niik

k [[m

mg

g//ll]]

1

1

1,85

2

2

1,86

3

3

1,84

4

4

1,85

5

5

1,85

6

6

1,87

7

7

1,84

8

8

1,86

9

9

1,85

1

10

0

1,87

x

1

1,,8

85

5

SSd

d

0

0,,0

01

1

Odchylenie standardowe Sd obli-

czono wed³ug wzoru:

chylenia standardowego wagi po-
dzieliæ przez odczytan¹ wartoœæ.
W ten sposób uzyskuje siê wynik nie-
pewnoœci:

Etapy procesu szacowania

niepewnoœci pomiaru

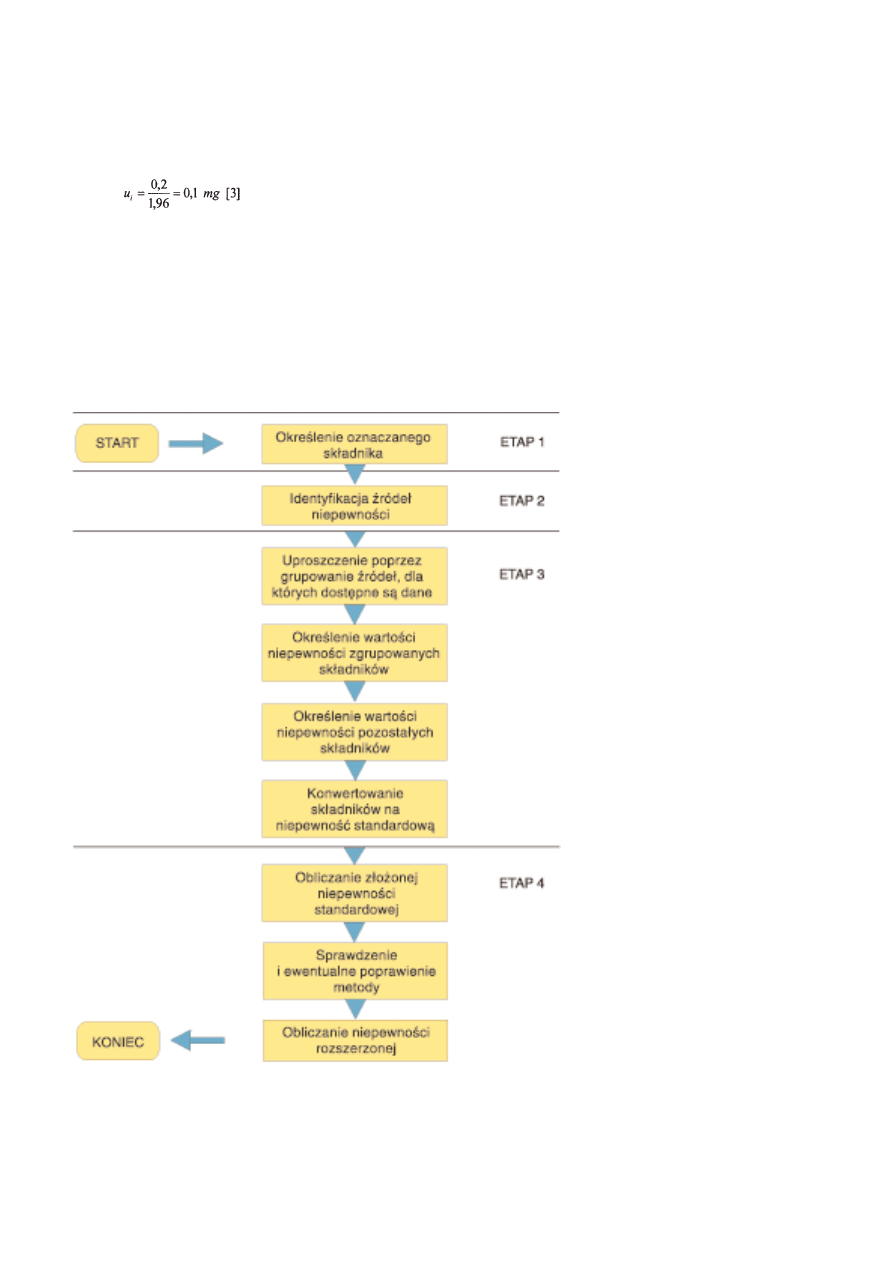
Szacowanie niepewnoœci [3] jest

proste, gdy analityk dobrze zna swój
aparat i potrafi zidentyfikowaæ para-
metry, które wp³ywaj¹ na niepewnoœæ
pomiaru. Proces szacowania niepew-

noœci mo¿na podzieliæ na kilka eta-
pów (ryc. 4).

ETAP 1

Okreœlenie oznaczanego sk³adnika

W pierwszym etapie nale¿y okre-

œliæ, jaki analit bêdzie oznaczany i ja-
kie wystêpuj¹ zale¿noœci miêdzy
analitem i parametrami wejœciowymi
(np. intensywnoœæ sygna³u, stê¿enie
wzorca kalibracyjnego itp.). Nale¿y
wiêc opracowaæ model matematycz-
ny otrzymywania koñcowego wyniku
oznaczenia. Je¿eli np. wynik iloœcio-
wy uzyskuje siê metod¹ krzywej kali-

bracyjnej (regresji liniowej), to model
matematyczny bêdzie równaniem re-
gresji, do którego bêd¹ podstawione
wartoœci intensywnoœci sygna³u dla
odpowiednich stê¿eñ oznaczanych
sk³adników. Nastêpnie na podstawie
równania krzywej kalibracyjnej, zna-
j¹c intensywnoœæ oznaczanego
sk³adnika w nieznanej próbce, wyli-
cza siê jego stê¿enie. Reasumuj¹c,
nale¿y zrobiæ to co zwykle robi apa-
rat, czyli na podstawie intensywnoœci
uzyskanego sygna³u na kartce papie-
ru wyliczyæ stê¿enie sk³adnika. Z do-
œwiadczenia wiadomo, ¿e jest to je-
den z trudniejszych etapów szacowa-
nia niepewnoœci, lecz dla analityka
znaj¹cego metodê analizy nie powin-
no stanowiæ to wiêkszego problemu.

ETAP 2

Identyfikacja Ÿróde³ niepewnoœci

W drugim etapie nale¿y okreœliæ

mo¿liwe Ÿród³a niepewnoœci. Obej-
muje to Ÿród³a, które bêd¹ mia³y
wp³yw na wielkoœci okreœlone w mo-
delu matematycznym wyznaczonym
w etapie 1. Na przyk³ad gdy wynik
uzyskuje siê metod¹ krzywej kalibra-
cyjnej, to Ÿród³a niepewnoœci obej-
muj¹ miêdzy innymi:

– niepewnoœæ kolby, w której przy-

gotowywane s¹ wzorce,

– niepewnoœæ wzorca wyjœciowe-

go, z którego przygotowywane
s¹ wzorce robocze,

РniepewnoϾ pipetowania.

ETAP 3

Szacowanie sk³adników niepewnoœci

W trzecim etapie nale¿y zmierzyæ

lub oszacowaæ wartoœci niepewnoœci
standardowej ka¿dego ze sk³adników
zidentyfikowanych w etapie 2.

ETAP 4

Obliczanie niepewnoœci z³o¿onej

W czwartym etapie informacje

uzyskane w etapie trzecim nale¿y
„po³¹czyæ” i obliczyæ niepewnoœæ z³o-
¿on¹.

Ogóln¹ zale¿noœæ miêdzy niepew-

noœci¹ standardow¹ wartoœci mierzo-
nej x i niepewnoœci¹ standardow¹

PROBLEMY KRYMINALISTYKI 248/05

33

Ryc. 4. Etapy procesu szacowania niepewnoœci pomiaru
Fig. 4. Stages of determination of uncertainty

niezale¿nych parametrów, od których
ona zale¿y, y

1

, y

2

,...y

n

mo¿na wyra-

ziæ, jako:

u(x (y

1

, y

2

,... y

n

)) =

gdzie:
x

(y1, y2,...yn) – funkcja ró¿nych para-

metrów y1, y2,...yn,

ci – wspó³czynnik czu³oœci wyliczony

z zale¿noœci

Do obliczania niepewnoœci z³o¿o-

nej bardzo pomocne s¹ programy
komputerowe. Istnieje wiele opraco-
wanych programów, w których nale¿y
tylko wpisaæ wartoœci i odchylenia
standardowe okreœlone w poprzed-
nich etapach i automatycznie wyli-
czona zostanie niepewnoœæ z³o¿ona
otrzymanego wyniku. Nale¿y do nich
miêdzy innymi program GUM Work-
bench. Warto zaznaczyæ, ¿e nawet
takie programy wymagaj¹ opracowa-
nia dok³adnego modelu matematycz-
nego w celu uzyskania prawid³owego
wyniku. Natomiast istnieje bardzo
prosty schemat szacowania niepew-
noœci wyniku, który mo¿na stworzyæ
samemu w

programie Microsoft

Excel pakietu Microsoft Office.

Aby przybli¿yæ metodykê tworze-

nia takiego arkusza, zostanie przed-
stawiony prosty przyk³ad obliczania
niepewnoœci wyniku uzyskanego po
odjêciu intensywnoœci sygna³u dla
œlepej próbki od sygna³u dla próbki.
Jak wiadomo wszelkie oznaczenia
analitów musz¹ byæ skorygowane
o wartoœæ dla œlepej próbki.

Analizie metod¹ ICP-OES podda-

no próbkê oraz œlep¹ próbkê. Ka¿dy
pomiar wykonano 3 razy. Uzyskano
wiêc œredni¹ intensywnoœæ emisji
pierwiastka w próbce wraz z odchyle-
niem standardowym. Analogiczne
wyniki uzyskano dla œlepej próbki. Na
niepewnoœæ koñcowego wyniku
wp³ywaj¹ wiêc dwa parametry: nie-
pewnoœæ uzyskania sygna³u dla
próbki oraz niepewnoœæ uzyskania

sygna³u dla œlepej próbki. Poniewa¿
odchylenie standardowe mierzonych
wartoœci wyznaczono na podstawie
trzech obserwacji, mo¿na wiêc je
przekszta³ciæ na niepewnoœæ stan-
dardow¹ wed³ug typu A szacowania
niepewnoœci, czyli u

c

= Sd. Model

matematyczny uzyskanego wyniku
to: X = I

p

– I

sp

.

Dla podanego przyk³adu zosta³

utworzony arkusz kalkulacyjny w pro-
gramie Microsoft Excel, który przed-
stawiono na rycinie 5.

Objaœnienia:

a) w kolumnie wartoœæ x nale¿y

wpisaæ wartoœci œrednie inten-
sywnoœci dla próbki i œlepej
próbki,

b) w kolumnie Sd (x) nale¿y wpi-

saæ wartoœci odchyleñ standar-
dowych dla próbki i œlepej prób-
ki,

c) w kolumnie Ux nale¿y wpisaæ,

obliczone wed³ug zasad zawar-
tych w szacowaniu niepewnoœci
typu A i B, wartoœci niepewnoœci
standardowych dla próbki i œle-
pej próbki. W omawianym przy-
k³adzie w komórkach E3 i E4
wpisane s¹ formu³y przenosz¹-
ce wartoœci z komórek kolumny
D ((E3) = D3, (F4) = D4),

d) kolumna RUx

% zawiera

wzglêdne procentowe niepew-
noœci standardowe dla próbki
i œlepej próbki oraz wartoœæ x,
obliczone wed³ug wzoru:

(przek³adaj¹c na formu³y:
(F3) = (E3/C3) *100)
i (F4) = (E4/C4) *100),

e) nastêpnie tworzy siê tabelê

sk³adaj¹c¹ siê z tylu wierszy
i kolumn, ile zdefiniowano para-
metrów wejœciowych. Poniewa¿
w omawianym przyk³adzie ma-
my dwa parametry wejœciowe
(intensywnoœci próbek i œlepej
próbki), powstanie wiêc tabela
o wymiarach 2x2 pola (obszar
H3:I4 z opisanymi wierszami
i kolumnami zgodnie z ryc. 5),

f) po przek¹tnej tej tabeli, w ko-

mórkach oznaczonych H3 i I4

sumowane s¹: wartoœæ x+Ux,
co po prze³o¿eniu na formu³ê
wygl¹da nastêpuj¹co:

(H3) = C3+E3 i (I4) = C4+E4,

g) w pozosta³ych komórkach tabe-

li z pkt f (H4 i I3) wpisuje siê
wartoϾ x dla danego parame-
tru ((H4) = C4 i (I3) = C3),

h) w komórkach oznaczonych C5,

H5 i I5 wpisuje siê formu³ê ilu-
struj¹c¹ opracowany model
matematyczny. W analizowa-
nym przyk³adzie jest to Ip – Isp
((C5) = C3 – C4

(H5) = H3 – H4, (I5) = I3 – I4,

i) w wierszu ró¿nica oblicza siê

w komórkach oznaczonych H6
i I6 ró¿nice miêdzy wartoœciami
obliczonymi x

1

i x

2

a wartoœci¹

obliczon¹ z parametrów wejœcio-
wych wartoœæ x (przek³adaj¹c
na formu³y: (H6) = C5 – H5, (I6)
= C5 – I5),

j) w wierszu ró¿nica

^2

liczony jest

kwadrat wartoœci z wiersza ró¿-
nica dla poszczególnych komó-
rek ((H7) = H6^2, (I7) = I6^2),

k) w wierszu suma ró¿nica

^2

su-

muje siê wartoœci ró¿nica

^2

z obu komórek ( (I8) = H7 + I7),

PROBLEMY KRYMINALISTYKI 248/05

34

( )

( )

∑

∑

=

=

=

n

i

i

n

i

i

i

y

x

u

y

u

c

,

1

2

,

1

2

2

,

i

i

y

x

c

∂

∂

=

%

100

%

∗

=

x

wartosc

Ux

RUx

Ryc. 5. Arkusz kalkulacyjny stworzony dla obliczenia niepewnoœci
Fig. 5. Spreadsheet designed for calculating uncertainty

l) wartoœæ niepewnoœci z³o¿onej:

Ux (komórka = E5), to pierwia-
stek kwadratowy z wartoœci
w wierszu suma ró¿nica

^2

(E5

= pierwiastek I8).

W utworzonym arkuszu jest wiersz

o nazwie INDEX %. Obliczenie war-
toœci tego wskaŸnika pozwala na
identyfikacjê parametru, który ma
najwiêkszy wk³ad w obliczon¹ nie-
pewnoœæ wyniku. Oblicza siê go dzie-
l¹c ka¿d¹ z wartoœci ró¿nica

^2

przez

wartoœæ suma ró¿nica

^2

i otrzymany

wynik mno¿¹c przez 100 (w postaci
formu³ wygl¹da to nastêpuj¹co: ((H9)
= (H7/I8) *100, (I9) = (I7/I8) *100).
W omawianym przyk³adzie okazuje
siê, ¿e precyzja uzyskania intensyw-
noœci œlepej próbki nie ma ¿adnego
wp³ywu na niepewnoœæ standardow¹
otrzymanego wyniku. Natomiast aby
zmniejszyæ niepewnoœæ standardow¹
wyniku, nale¿a³oby poprawiæ precy-
zjê sygna³u uzyskanego dla próbki.
Metoda ta wiêc nie tylko pozwala na
szacowanie niepewnoœci standardo-
wej w sposób prosty i szybki, lecz
równie¿ jest dobrym narzêdziem do
identyfikacji g³ównych Ÿróde³ niepew-
noœci standardowej uzyskanego
wyniku. Pozwala to na skuteczn¹
poprawê metody, prowadz¹c do
zmniejszenia niepewnoœci wyniku.

Szacowanie niepewnoœci
oznaczania cynku
w próbce konopi
metod¹ ICP-OES

Przyk³ad sposobu szacowania

niepewnoœci standardowej opisany
wczeœniej zosta³ wybrany tak, aby ja-
sno okreœliæ zasady wyliczania nie-
pewnoœci z³o¿onej. Jednak w co-
dziennej pracy laboratoryjnej oblicza-
nie wyniku analizy jest du¿o bardziej
skomplikowane. W pracowni emisyj-
nej spektrometrii atomowej CLK KGP
opracowano metodê niepewnoœci
otrzymywanych wyników analitycz-
nych. Aby zrozumieæ ca³y model ma-
tematyczny otrzymywania wyniku,
nale¿y dok³adnie omówiæ poszcze-
gólne etapy procedury analitycznej.

Metoda ICP-OES to metoda roz-

tworowa. Oznacza to, ¿e próbki
poddawane analizie musz¹ byæ

w postaci roztworu. Bardzo czêsto
niezbêdna jest analiza sk³adu pier-
wiastkowego próbek sta³ych. Zatem
takie próbki nale¿y rozpuœciæ w od-
powiednich odczynnikach. Nie jest
problemem na przyk³ad roz-
puszczanie metali. Wystarczy do-
braæ odpowiedni kwas lub mieszani-
nê kwasów. Jednak w przypadku
próbek o bardziej skomplikowanej
matrycy np. próbek roœlinnych u¿y-
cie kwasów do rozpuszczania nie
jest skuteczne. Niezbêdne jest za-
stosowanie techniki mineralizacji
mikrofalowej [4]. W rutynowych ana-
lizach odwa¿a siê oko³o 250 mg
próbki, dodaje 3 ml 65% kwasu azo-
towego (V) oraz 1 ml 30% nadtlenku
wodoru. Tak przygotowan¹ próbkê
poddaje siê mineralizacji mikrofalo-
wej. Po mineralizacji otrzymuje siê
bezbarwny roztwór, który przeno-
szony jest iloœciowo do kolby o po-
jemnoœci 10 ml.
Nastêpnie kolbê
dope³nia siê wo-
d¹ dejonizowan¹
do kreski i pod-
daje siê analizie. Aby uzyskaæ wyni-

ki iloœciowe nale¿y wykonaæ krzyw¹
kalibracyjn¹. W tym celu analizie
poddawane s¹ trzy wzorce o wzra-
staj¹cym znanym stê¿eniu oznacza-
nego pierwiastka. Wzorce do kali-
bracji przygotowywane s¹ w kol-
bach miarowych przez odpowiednie
rozcieñczanie wzorca wyjœciowego
o certyfikowanym stê¿eniu. Wynik
oznaczania pierwiastka w próbce
podawany jest w mg/kg.

Omawiany schemat szacowania

niepewnoœci wyniku najlepiej prze-
œledziæ na konkretnym przyk³adzie
stosowanym w rutynowych pracach
Wydzia³u Chemii CLK KGP. W tym
celu autorzy wybrali proces oznacza-
nia cynku w próbkach ziela konopi.
Aby oszacowaæ niepewnoœæ wyniku
oznaczania cynku w próbce konopi,
nale¿y uwzglêdniæ czynniki, które
maj¹ na ni¹ wp³yw zgodnie z przed-
stawionym wczeœniej schematem.

Etap pierwszy

szacowania niepewnoœci wyniku

oznaczania cynku w próbce

ziela konopi

Polega on na identyfikacji ozna-

czanego sk³adnika i tworzeniu mode-
lu matematycznego otrzymywania
wyniku. W próbce konopi oznacza siê
cynk, a wynik uzyskuje metod¹ krzy-
wej wzorcowej. Równanie krzywej
wzorcowej mo¿na przedstawiæ nastê-
puj¹co:

y = ax + b

gdzie:

y – intensywnoœæ sygna³u analityczne-

go,

a – nachylenie krzywej,
b – punkt przeciêcia krzywej z osi¹ x.

Wartoœæ a oblicza siê ze wzoru:

Wartoœæ b oblicza siê ze wzoru:

gdzie:
x

i – wartoœæ stê¿enia wzorca,

yi – wartoœæ sygna³u analitycznego.

Stê¿enie nieznanej próbki w mg/l

oblicza siê z nastêpuj¹cej zale¿noœci:

gdzie:
x

o – wartoœæ stê¿enia [mg/l],

yo

x

– wartoœæ œrednia sygna³u anali-

tycznego dla nieznanej próbki
[mg/l],

yosp – wartoœæ œrednia sygna³u anali-

tycznego dla œlepej próbki
[mg/l].

Aby przekszta³ciæ stê¿enie wyra-

¿one w mg/l na mg/kg nale¿y
uwzglêdniæ masê próbki oraz objê-
toœæ kolby, w której j¹ przygotowano:

PROBLEMY KRYMINALISTYKI 248/05

35

(

)(

) (

)(

) (

)(

) (

)(

)

(

) (

) (

) (

)

2

4

2

3

2

2

2

1

4

4

3

3

2

2

1

1

x

x

x

x

x

x

x

x

y

y

x

x

y

y

x

x

y

y

x

x

y

y

x

x

a

−

+

−

+

−

+

−

−

−

+

−

−

+

−

−

+

−

−

=

(

)(

) (

)(

) (

)(

) (

)(

)

(

) (

) (

) (

)

4

4

4

3

2

1

2

4

2

3

2

2

2

1

4

4

3

3

2

2

1

1

4

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x

y

y

x

x

y

y

x

x

y

y

x

x

y

y

x

x

y

y

y

y

b

+

+

+

∗

−

+

−

+

−

+

−

−

−

+

−

−

+

−

−

+

−

−

−

+

+

+

=

(

)

a

b

y

y

x

osp

ox

o

−

−

=

gdzie:

C – wartoœæ stê¿enia [mg/kg],

x

0 – wartoœæ stê¿enia [mg/l],

Vp – objêtoœæ kolby, w której przygoto-

wano próbkê [ml],

m – masa próbki [g].

Po po³¹czeniu tych wszystkich

wzorów otrzymuje siê nastêpuj¹cy
model matematyczny:

Nale¿y dodatkowo uwzglêdniæ

fakt, ¿e wzorce kalibracyjne zosta³y
przygotowane przez rozcieñczanie
odpowiedniego wzorca wyjœciowego.
Zatem stê¿enie wzorca do kalibracji
wyra¿one bêdzie jako:

gdzie:

Cwz – stê¿enie wzorca wyjœciowego

[mg/l],

Vi – objêtoœæ odpipetowanego wzorca

[ml],

Vk – objêtoœæ kolby, w którym przygo-

towywano wzorzec [ml].

Tê zale¿noœæ nale¿y wstawiæ

w miejsce x1, x2, x3 do modelu ma-
tematycznego. Poniewa¿ to jeszcze
bardzie komplikuje model matema-
tyczny zrezygnowano ze wstawiania
tego wzoru w tym miejscu. Natomiast
ca³y model matematyczny jest
uwzglêdniony w skoroszycie Micro-
soft Excel.

Etap drugi szacowania niepewnoœci

wyniku oznaczania cynku w próbce

ziela konopi

Polega on na identyfikacji sk³adni-

ków niepewnoœci metody. Na nie-
pewnoϾ metody oznaczania cynku
w próbce konopi technik¹ ICP-OES
wp³ywa wiele czynników. Mo¿na je
pogrupowaæ na wiele sposobów, przy

czym najlepszym kryterium jest po
prostu przeœledzenie ca³ego procesu
otrzymywania wyniku.

Niepewnoœæ wynikaj¹ca z procesu

przygotowania próbki obejmuje na-
stêpuj¹ce sk³adniki:

РniepewnoϾ wyznaczania masy

próbki (niepewnoœæ wagi anali-
tycznej),

– niepewnoœæ kolby, w której przy-

gotowywana jest próbka.

NiepewnoϾ wyznaczania kalibra-

cji i oznaczania cynku w próbce ko-
nopi obejmuje trzy rodzaje sk³adni-
ków:

a) sk³adniki niepewnoœci zwi¹zane

z

przygotowywaniem roztworów

wzorcowych:

– niepewnoœæ wzorca wyjœciowe-

go, z którego w wyniku rozcieñ-
czenia przygotowywane s¹
wzorce robocze,

– niepewnoœæ objêtoœci pipetowa-

nego wzorca (niepewnoϾ pipe-
ty),

–

niepewnoœæ kolb, w których
przygotowywane s¹ wzorce ro-
bocze;

b) sk³adniki niepewnoœci zwi¹zane

z analiz¹ wzorców roboczych metod¹
ICP-OES:

РniepewnoϾ wyznaczenia inten-

sywnoœci sygna³u dla cynku we
wzorcach roboczych;

c) sk³adniki niepewnoœci zwi¹zane

z analiz¹ próbki konopi:

РniepewnoϾ wyznaczenia inten-

sywnoœci sygna³u dla cynku
w próbce konopi,

РniepewnoϾ wyznaczenia inten-

sywnoœci sygna³u dla cynku
w œlepej próbie.

Etap trzeci szacowania niepewnoœci

wyniku oznaczania cynku w próbce

ziela konopi

Jest to grupowanie sk³adników

niepewnoœci metody i szacowanie ich

wartoœci. Sk³adniki niepewnoœci zi-
dentyfikowane w poprzednim punk-
cie nale¿y pogrupowaæ w zale¿noœci
od tego, jakim typom szacowania nie-
pewnoœci podlegaj¹ (A czy B).
W omawianym przyk³adzie typ A sza-
cowania niepewnoœci bêdzie obejmo-
wa³ sk³adniki, które zosta³y wyzna-
czone doœwiadczalnie, tj. intensyw-
noœæ próbki, intensywnoœæ œlepej
próbki i intensywnoœci wzorców. Dla

tych sk³adników jak wspomniano
wczeœniej jest to ui = Sd.

Sk³adniki podlegaj¹ce typowi B

szacowania niepewnoœci to: objêtoœæ
kolb, w których przygotowywano prób-
kê i wzorce robocze, objêtoœæ pipeto-
wanego wzorca oraz masa próbki.

Prostok¹tnemu rozk³adowi praw-

dopodobieñstwa, dla którego

podlegaj¹ objêtoœci kolb, w któ-

rych przygotowywano próbkê i wzor-
ce robocze oraz objêtoœæ pipetowa-
nego wzorca. Natomiast masa prób-
ki, czyli niepewnoœæ wagi bêdzie pod-
legaæ trójk¹tnemu rozk³adowi praw-
dopodobieñstwa, dla którego

Etap czwarty szacowania niepewnoœci

wyniku oznaczania cynku w próbce

ziela konopi

Jest to obliczanie niepewnoœci

z³o¿onej i rozszerzonej. Aby obliczyæ
niepewnoœæ z³o¿on¹, stworzono od-
powiedni arkusz kalkulacyjny w pro-
gramie Microsoft Excel, który przed-
stawiono na ryc. 6a i 6b.

Formu³y z wierszy i kolumn w po-

szczególnych komórkach tabel
z ryc. 6a i 6b opisanych tak samo,

PROBLEMY KRYMINALISTYKI 248/05

36

(

)

(

)(

) (

)(

) (

)(

) (

)(

)

(

) (

) (

) (

)

(

)(

) (

)(

) (

)(

) (

)(

)

(

) (

) (

) (

)

2

4

2

3

2

2

2

1

4

4

3

3

2

2

1

1

4

3

2

1

2

4

2

3

2

2

2

1

4

4

3

3

2

2

1

1

4

3

2

1

0

4

4

x

x

x

x

x

x

x

x

y

y

x

x

y

y

x

x

y

y

x

x

y

y

x

x

m

x

x

x

x

x

x

x

x

x

x

x

x

y

y

x

x

y

y

x

x

y

y

x

x

y

y

x

x

y

y

y

y

y

y

V

kg

mg

C

sp

ox

p

−

+

−

+

−

+

−

−

−

+

−

−

+

−

−

+

−

−

∗









+

+

+

∗

−

+

−

+

−

+

−

−

−

+

−

−

+

−

−

+

−

−

−

+

+

+

−

−

∗

=













Vk

V

Cwz

x

i

i

∗

=

3

Sd

=

i

u

6

Sd

=

i

u

m

V

x

C

p

∗

=

0

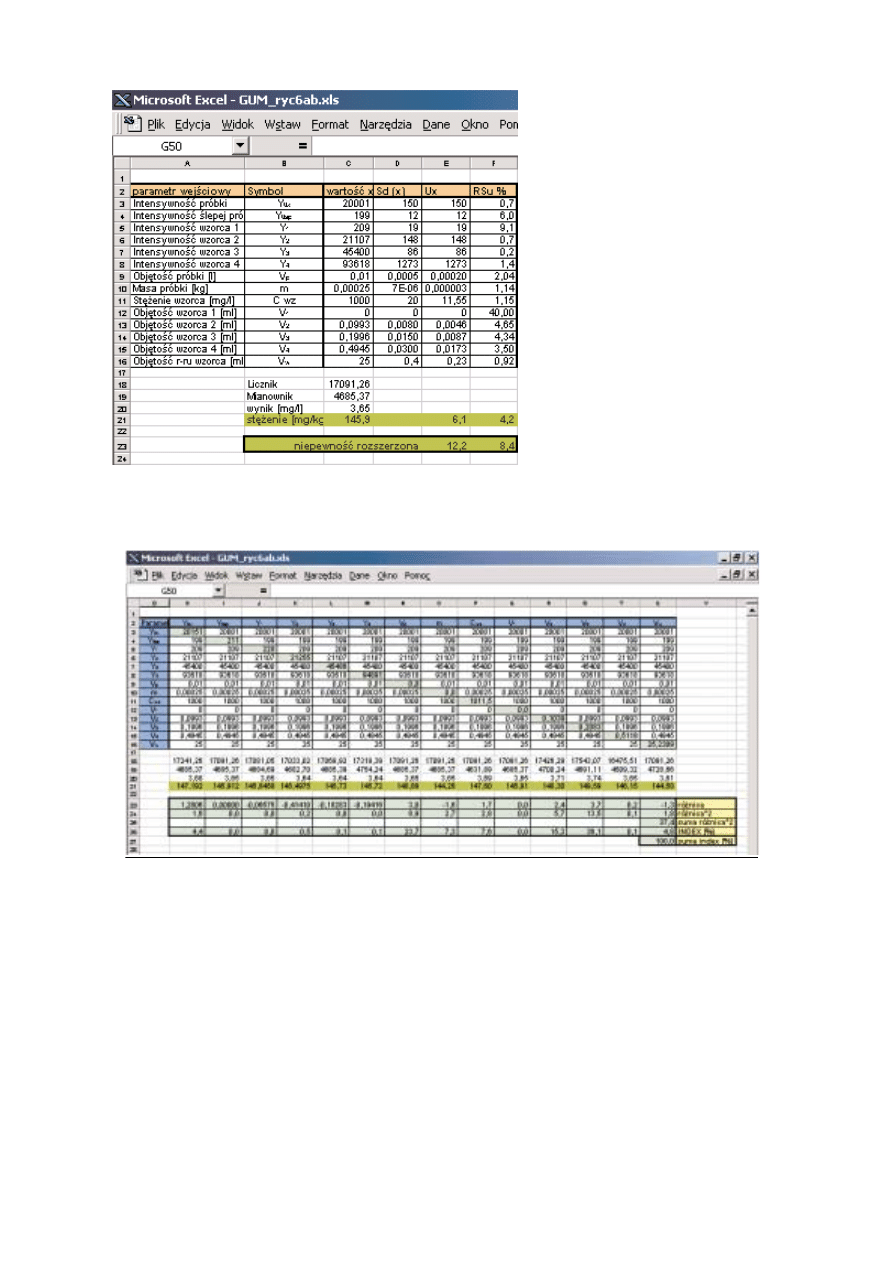
jak w tabeli z ryc. 5 odpowiadaj¹ so-
bie. Natomiast ostateczny wynik li-
czony jest etapami (wiersze licznik
i mianownik) i zawarty jest w wier-
szu wynik ((C20) = C18/C19).

Zatem wynik oznaczania cynku

w próbce konopi metod¹ ICP-OES
wynosi 145,9 ± 6,1 mg/kg.

Nale¿y jednak zaznaczyæ, ¿e ana-

lityk nigdy nie jest w stanie zidentyfi-
kowaæ i oszacowaæ wszystkich sk³ad-
ników niepewnoœci metody, dlatego
te¿ przyjêto podawaæ wartoœæ nie-
pewnoœci rozszerzonej. Uzyskuje siê
j¹ mno¿¹c wartoœæ niepewnoœci z³o-
¿onej przez 2 lub 3. Najczêœciej sto-
suje siê 2Ux. Uwzglêdniaj¹c wiêc nie-
pewnoœæ rozszerzon¹ otrzymujemy
nastêpuj¹c¹ postaæ wyniku analitycz-
nego: 145,9 ± 12,2 mg/kg. Niepew-
noœæ rozszerzona metody wyra¿ona
w % wynosi 8,4%.

Co nale¿y zrobiæ, aby poprawiæ

i zmniejszyæ wartoœæ niepewnoœci
metody?

PROBLEMY KRYMINALISTYKI 248/05

37

Formu³a licznik wygl¹da nastêpuj¹co: = (C3 – (((ŒREDNIA (C5:C8)) – (((((C11*C12)/C16) – ((((C11*C12)/C16) +
+ ((C11*C13)/C16) + ((C11*C14)/C16) + ((C11*C15)/C16))/4)) * (C5 – (ŒREDNIA (C5: C8))) + (((C11*C13)/C16) –
– ((((C11*C12)/C16) + ((C11*C13)/C16) + ((C11*C14)/C16) + ((C11*C15)/C16))/4)) * (C6 – (ŒREDNIA (C5: C8))) +
+ (((C11*C14)/C16) – (((C11*C12)/C16) + ((C11*C13)/C16) + ((C11*C14)/C16) + ((C11*C15) /C16))/4)) * (C7 –
– (ŒREDNIA (C5:C8))) + (((C11*C15)/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16) + ((C11*C14)/C16) +
+ ((C11*C15)/C16))/4)) * (C8 – (ŒREDNIA (C5:C8))))/(((((C11*C12/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16)
+ ((C11*C14)/C16) + ((C11*C15)/C16))/4))^2) + ((((C11*C13)/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16) +
+ ((C11*C14)/C16) + ((C11*C15)/C16))/4))^2) + ((((C11*C14)/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16) +
+ ((C11*C14)/C16) + ((C11*C15) C16))/4))^2) + ((((C11*C15)/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16) +
+ ((C11*C14)/C16) + ((C11*C15)/C16))/4))^2)) * (((((C11*C12)/C16) + ((C11*C13)/C16) + ((C11*C14)/C16) +
+ ((C11*C15)/C16))/4))))))

Ryc. 6a. Arkusz kalkulacyjny stworzony do obliczania niepewnoœci z³o¿onej oznaczania cynku w
próbce konopi metod¹ ICP-OES
Fig. 6a. Calculation spreadsheet for complex uncertainty of determining zinc in cannabis sample by
ICP-OES method

Ryc. 6b. Arkusz kalkulacyjny stworzony do obliczania niepewnoœci z³o¿onej oznaczania cynku w próbce konopi metod¹ ICP-OES (cd.)
Fig. 6b. Calculation spreadsheet for complex uncertainty of determining zinc in cannabis sample by ICP-OES method (continued)

Stworzony arkusz kalkulacyjny to

dobre narzêdzie do oszacowania,
które czynniki najbardziej wp³ywaj¹
na niepewnoϾ otrzymywanego wy-
niku. Jak wspomniano wczeœniej in-
formacje takie zawiera wartoϾ IN-
DEX [%]. W omawianym przyk³adzie
czynniki limituj¹ce niepewnoœæ
w najwiêkszym stopniu to niepew-
noϾ pipetowania wzorca 2 i 3 (nie-
pewnoœæ pipety, u¿ywanej do odmie-
rzenia wzorca wyjœciowego w proce-
sie przygotowywania wzorca 2 i 3)
oraz niepewnoœæ kolby, w której
przygotowano próbkê. Zatem aby
poprawiæ niepewnoœæ metody nale-
¿a³oby zakupiæ pipety i kolby o mniej-
szej wartoœci niepewnoœci.

Informacje takie s¹ niezwykle u¿y-

teczne szczególnie w sytuacji, gdy la-
boratoria poddawane s¹ procesowi
akredytacji.

Podsumowanie

Szacowanie niepewnoœci wyniku

jest zagadnieniem niezwykle istot-
nym we wspó³czesnej analizie che-
micznej. Wynik uzyskany nawet naj-
bardziej rzeteln¹ i sprawdzon¹ meto-
d¹, bez podania jego niepewnoœci,
jest bezwartoœciowy. Niejeden do-
œwiadczony analityk mo¿e stwierdziæ,
¿e jego wyniki s¹ rzetelne, poniewa¿
metoda jest dobrze opracowana i na
bie¿¹co sprawdzana. Nale¿y przy-
znaæ mu racjê, ale nie zwalnia go to
z obowi¹zku udokumentowania pro-
cedury badawczej. A najlepsz¹ doku-
mentacj¹ metody jest podanie nie-
pewnoœci wyniku. Zatem podejmuj¹c
siê tworzenia modelu szacowania
niepewnoœci dokumentuje siê meto-
dê, co jest pierwszym etapem do jej
akredytacji.

BIBLIOGRAFIA

1. Rubel S.: Metody sprawdzania wia-

rygodnoœci wyników analizy w: Kabata-
-Pendias A., Szteke B.: Problemy jakoœci
analizy œladowej w badaniach œrodowiska
przyrodniczego, Wydawnictwo Edukacyj-
ne Zofii Dobkowskiej, Warszawa 1998.

2. Taylor B N., Kuyatt C.E.: Guideli-

nes for evaluating and expressing the un-
certainty of NIST measurement results,
NIST „Technical Note”, 1994, nr 1297.

3. EURACHEM/CITAC Guide: Quanti-

fying Uncertainty in Analytical Measure-
ment, Second edition, final draft: April
2000.

4. Wachowicz M., Kuras M.: Minerali-

zacja mikrofalowa jako technika przygoto-
wania próbek w analizie kryminalistycz-
nej, „Problemy Kryminalistyki” 2002, nr
238, s. 8–23.

PROBLEMY KRYMINALISTYKI 248/05

38

Formu³a mianownik wygl¹da nastêpuj¹co: = (((((C11*C12)/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16) +
+ ((C11*C14)/C16) + ((C11*C15)/C16))/4)) * (C5 – (ŒREDNIA (C5:C8))) + (((C11*C13)/C16) – ((((C11*C12)/C16) +
+ ((C11*C13)/C16) + ((C11*C14)/C16) + ((C11*C15)/C16))/4)) * (C6 – (ŒREDNIA (C5:C8))) + (((C11*C14)/C16) –
– ((((C11*C12)/C16) + ((C11*C13)/C16) + ((C11*C14)/C16) + ((C11*C15)/C16))/4)) * (C7 – (ŒREDNIA (C5:C8))) +
+ (((C11*C15)/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16) + ((C11*C14)/C16) + ((C11*C15)/C16))/4)) * (C8 –
– (ŒREDNIA (C5:C8))))/(((((C11*C12)/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16) + ((C11*C14)/C16) +
+((C11*C15)/C16))/4))^2) + ((((C11*C13)/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16) + ((C11*C14)/C16) +
+ ((C11*C15)/C16))/4))^2) + ((((C11*C14)/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16) + ((C11*C14)/C16) +
+ ((C11*C15)/C16))/4))^2) + ((((C11*C15)/C16) – ((((C11*C12)/C16) + ((C11*C13)/C16) + ((C11*C14)/C16) +
+ ((C11*C15)/C16)) /4))^2)))

Wybuch i jego skutki...

Tadeusz Baran, Aldona Policha,

Informujemy, i¿ ukaza³ siê „Zeszyt Metodyczny” nr 21

pt. „Wybuch i jego skutki – kryminalistyczne badania
materia³ów i urz¹dzeñ wybuchowych”.

Zamówienia prosimy kierowaæ na adres:

Centralne Laboratorium Kryminalistyczne KGP
Biblioteka
Al. Ujazdowskie 7,
00-583 Warszawa
tel. [phone]
faks ([phone]

format B5

oprawa kartonowa

160 stronic

cena 1 egz. 37 z³

JUŻ DO NABYCIA