ĆWICZENIE NR 57 C

BADANIE EFEKTU HALLA

I.

Zestaw przyrządów:

1.

Hallotron umieszczony w polu magnetycznym wytworzonym przez magnesy
trwałe. Magnesy zamocowane są tak by możliwy był pomiar zmian orientacji
pola magnetycznego względem płaszczyzny hallotronu.

2.

Zasilacz hallotronu.

3.

Miliamperomierz do pomiaru natężenia prądu sterującego.

4.

Woltomierz do pomiaru napięcia Halla.

II.

Cel ćwiczenia:

1.

Wyznaczenie charakterystyk hallotronu.

2.

Wyznaczenie czułości hallotronu.

3.

Wyznaczenie koncentracji elektronów swobodnych.

4.

Wyznaczenie czułości kątowej układu.

III.

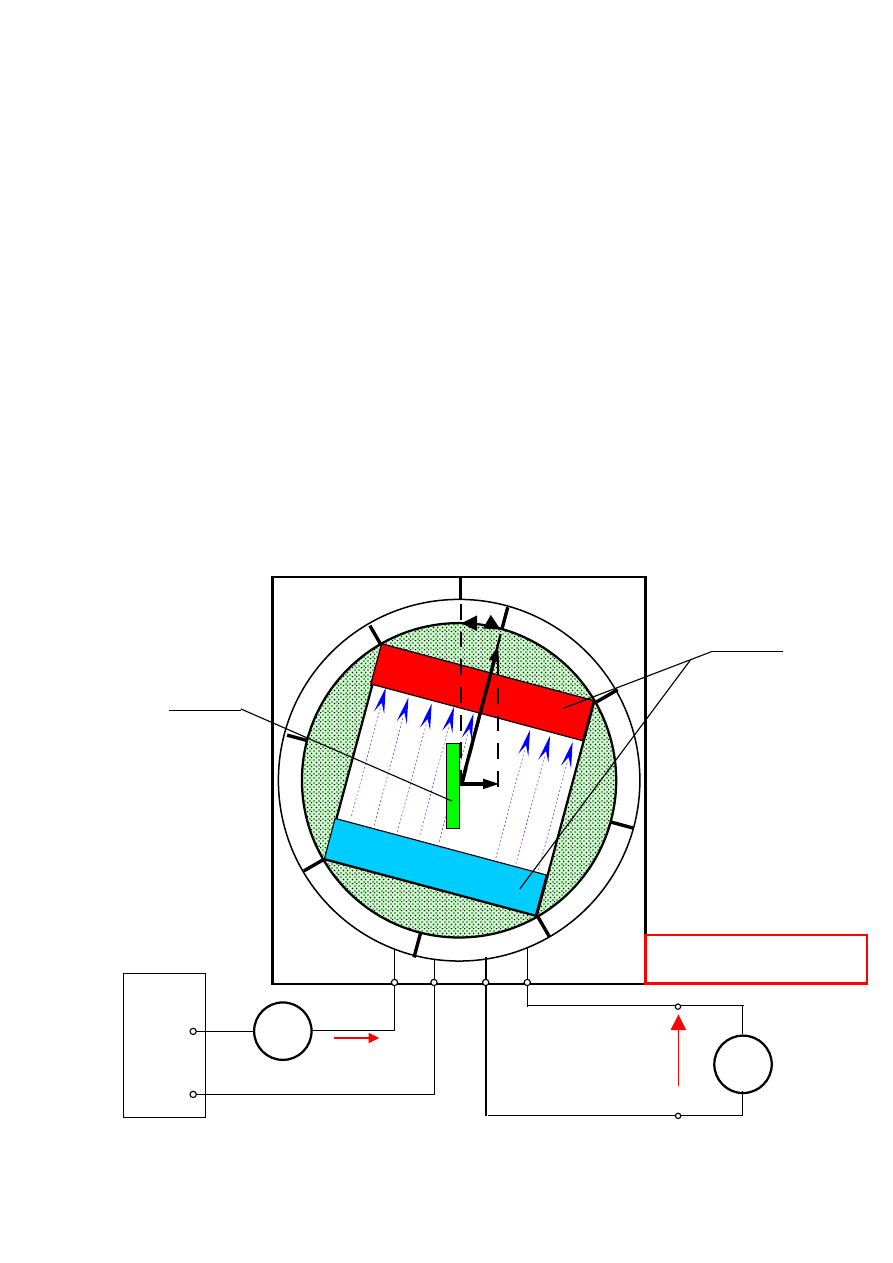
Schemat układu pomiarowego :

1

B

n

B

o

0

°

„0”

180

°

270

°

215

°

135

°

S

N

155

°

mA

V

Zasilacz
hallotronu

I

s

U

H

hallotron

magnesy

B

n

= B

o

⋅

sin(

α

-

α

o

)

α

I

s

U

H

α

o

Wersja podstawowa

IV.

Przebieg pomiarów:

1.

Połączyć układ zasilający hallotron.

2.

Wyznaczyć zależność napięcia Halla U

H

od indukcji magnetycznej U

H

(B) przy

ustalonym natężeniu prądu płynącego przez hallotron I

S

= const. Włączyć woltomierz

oraz zasilacz hallotronu. Ustalić wartość prądu zasilania hallotronu I

S

wskazaną przez

prowadzącego (z przedziału

5 – 15 mA ). Obrócić magnesy

w położenie przy którym napięcie Halla U

H

= 0 - kierunek pola magnetycznego jest

wtedy równoległy do powierzchni hallotronu – zanotować to położenie jako

α

0

.

Wykonać pomiary zależności napięcia Halla od kąta pomiędzy kierunkiem indukcji
magnetycznej B i powierzchnią hallotronu. Pomiary wykonać w przedziale od zera do
360

0

co 10

0

.

V.

Opracowanie wyników pomiarów :

1.

Narysować wykres zależności napięcia Halla od kąta odczytanego z podziałki
hallotronu.

2.

Korzystając z tego wykresu odczytać wartość α

0

przy której U

H

= 0 .

3.

Wyznaczyć maksymalną wartość czułości kątowej hallotronu ΔU

H

/Δα obliczając

nachylenie wykresu U

H

(α) dla wartości U

H

z przedziału od -0,5U

Hmax

do +0,5 U

Hmax

Można skorzystać z metody regresji liniowej.

4.

Narysować wykres zależności napięcia Halla od wartości składowej normalnej
indukcji B

n

= B

0

sin (α – α

0

) .

5.

Korzystając z regresji liniowej obliczyć współczynniki kierunkowe prostych
opisujących zależności U

H

(B) przy I

s

= const..

7.

Korzystając z wartości współczynników kierunkowych obliczyć czułość hallotronu γ.

8.

Oszacować niepewność wyznaczenia czułości hallotronu.

9.

Obliczyć koncentrację elektronów swobodnych oraz wyznaczyć jej niepewność
bezwzględną (metodą różniczki zupełnej lub pochodnej logarytmicznej) i względną
korzystając z wyrażenia:

n

e d

= ⋅ ⋅

1

γ

gdzie:

d - grubość płytki hallotronu ( d = 2 μm )
e - ładunek elementarny (e = 1,6 x 10

–19

C )

przyjąć : B

0

= ( 0,500

±

0,05 ) T

∆

d

d

=

5%

VI.

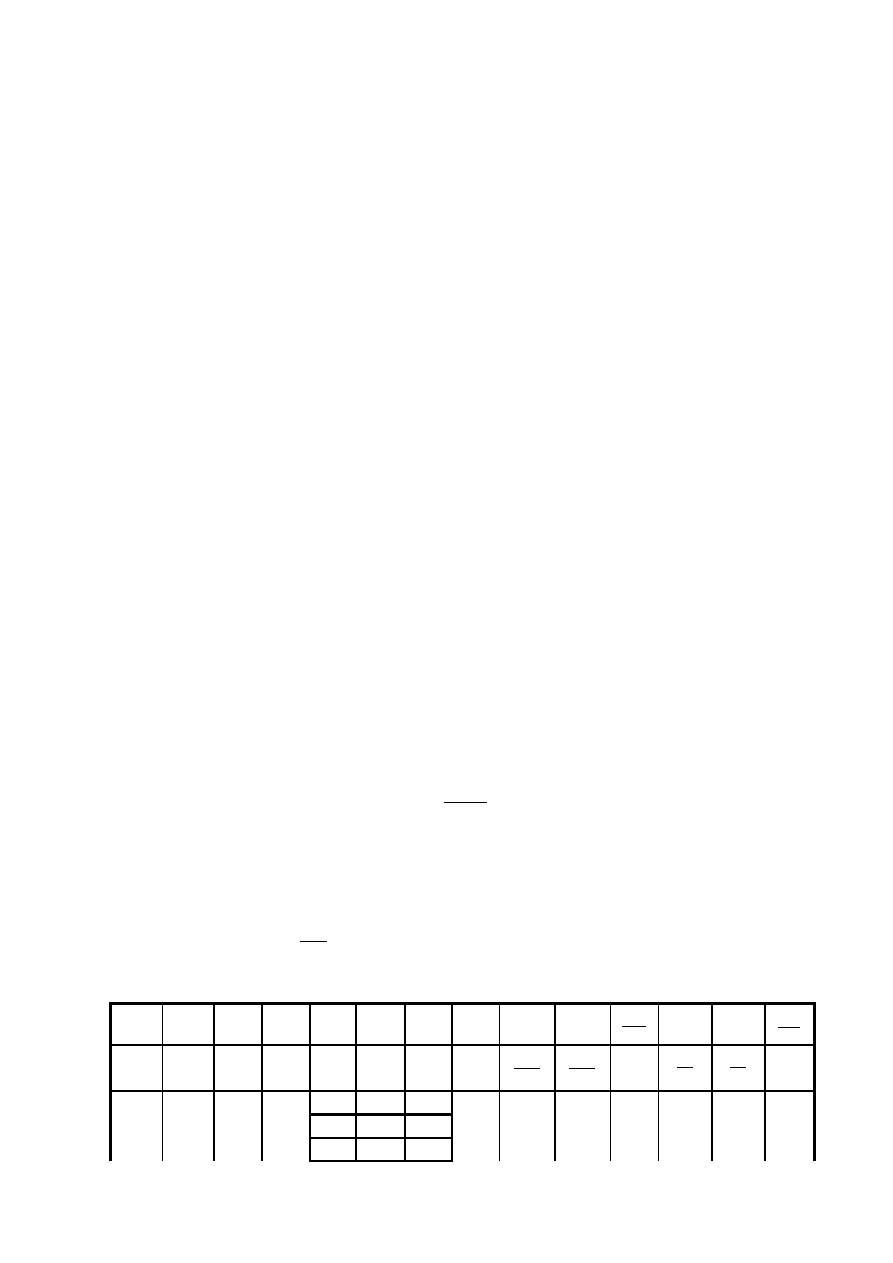
Proponowana tabela pomiarowa

I

s

∆

I

s

B

∆

B

U

H

∆

U

H

α

∆α

γ

∆γ

∆

γ

γ

n

∆

n

∆

n

n

[mA

]

[mA

]

[T]

[T] [V] [V]

[

°

]

[

°

]

[ ]

V

A T

⋅

[ ]

V

A T

⋅

%

[ ]

3

1

m

[ ]

3

1

m

%

2

...

...

...

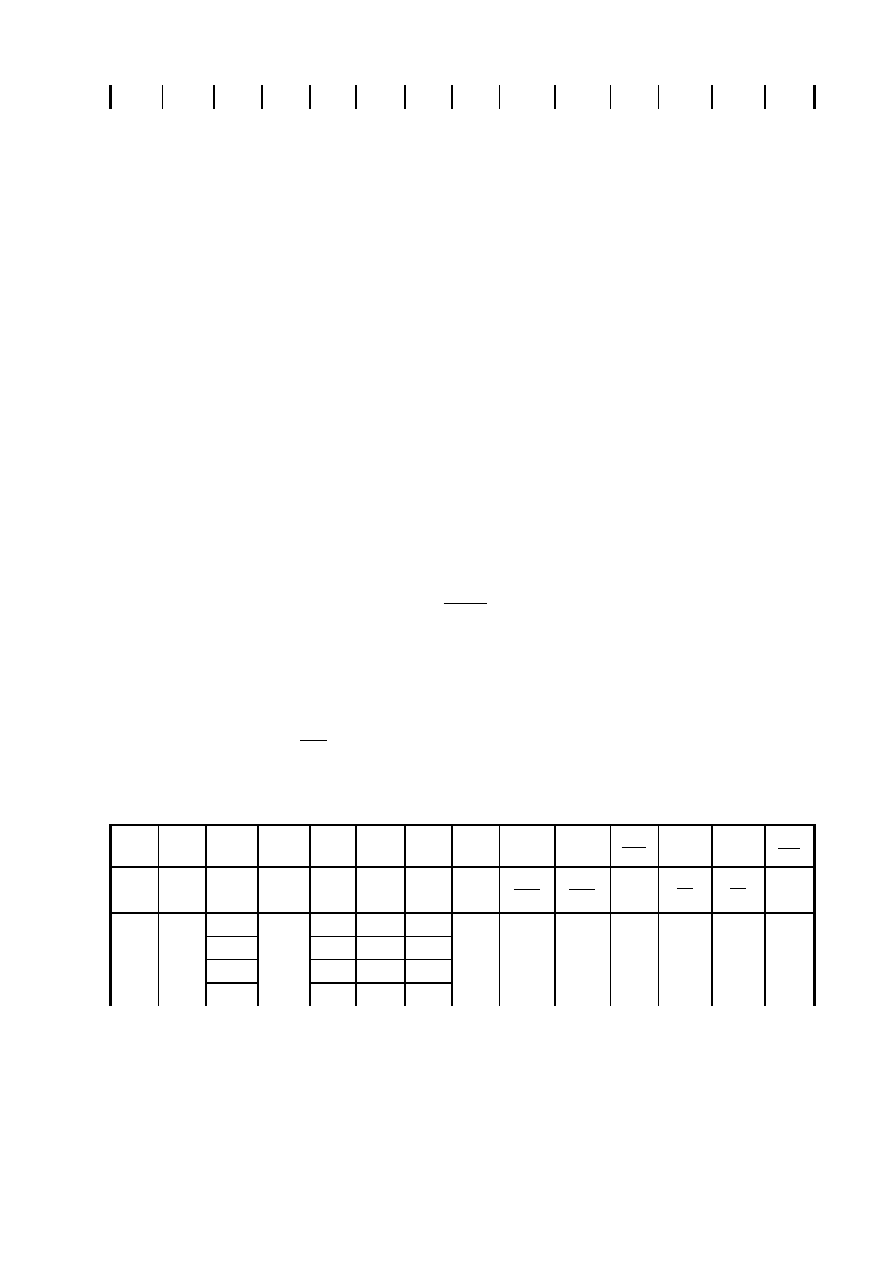
Wersja dodatkowa

IV.

Przebieg pomiarów:

1.

Połączyć układ zasilający hallotron.

2.

Wyznaczyć zależność napięcia Halla U

H

od natężenia prądu I

S

płynącego przez

hallotron U

H

(I

s

), przy ustalonej wartości indukcji magnetycznej B. Ustawić

magnesy pod kątem wskazanym przez prowadzącego. Przeprowadzić pomiary
zależności napięcia Halla U

H

od natężenia prądu sterującego I

S

w zakresie od 1

mA do 15 mA co 1 mA;

V.

Opracowanie wyników pomiarów :

1.

Narysować wykres zależności napięcia Halla U

H

od natężenia prądu I

s

płynącego

przez hallotron.

2.

Korzystając z regresji liniowej obliczyć współczynniki kierunkowe prostych
opisujących zależności U

H

(I

s

) przy B

n

= const.

3.

Korzystając z wartości współczynników kierunkowych obliczyć czułość hallotronu γ.

4.

Oszacować niepewność wyznaczenia czułości hallotronu.

5.

Obliczyć koncentrację elektronów swobodnych oraz wyznaczyć jej niepewność
bezwzględną (np. metodą pochodnej logarytmicznej) i względną korzystając z
wyrażenia:

n

e d

= ⋅ ⋅

1

γ

gdzie:

d - grubość płytki hallotronu ( d = 2 μm )
e - ładunek elementarny (e = 1,6 x 10

–19

C )

przyjąć : B

0

= ( 0,500

±

0,05 ) T

∆

d

d

=

5%

VI.

Proponowana tabela pomiarowa

B

∆

B

I

s

∆

I

s

U

H

∆

U

H

α

∆α

γ

∆γ

∆

γ

γ

n

∆

n

∆

n

n

[T]

[T]

[mA

]

[mA

]

[V] [V]

[

°

]

[

°

]

[ ]

V

A T

⋅

[ ]

V

A T

⋅

%

[ ]

3

1

m

[ ]

3

1

m

%

...

...

...

...

3