> restart:
> with(plots):
> with(CurveFitting);
[ ArrayInterpolation, BSpline, BSplineCurve, Interactive, LeastSquares, PolynomialInterpolation, RationalInterpolation, Spline, ThieleInterpolation ]
Aproksymacja
Aproksymacja funkcji dyskretnej wielomianami
> n:=10;
:=
n
10
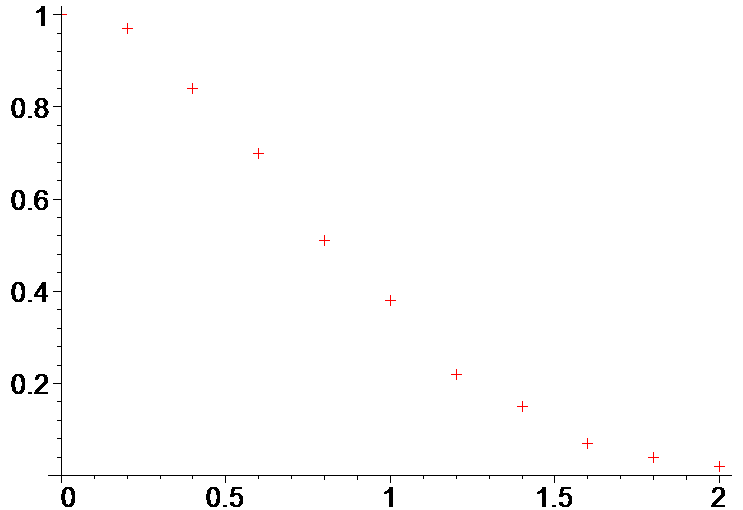
> lx:=array(0..n,[0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0]):
> ly:=array(0..n,[1.,0.97,0.84,0.7,0.51,0.38,0.22,0.15,0.07,0.04,0.02]):
> plot(zip((x,y)->[x,y],lx,ly),style=point,symbol=cross,symbolsize=20);
> pkt:=%:
> m:=4; Digits:=20; # dla m=10
m := 4
:=
Digits
20
Generowanie i rozwiązywanie układu równań na współczynniki wielomianu aproksymującego a[ j]
n
m
j 2
S [ y a x ]
k
j
k
k 0
j 0
> S:=add((ly[k]-add(a[j]*lx[k]^j,j=0..m))^2,k=0..n); 2
2
S := ( 1. a ) ( 0.971.0 a 0.2 a 0.04 a 0.008 a 0.0016 a ) 0
0
1
2
3
4
2
2
( 0.841.0 a 0.4 a 0.16 a 0.064 a 0.0256 a ) ( 0.71.0 a 0.6 a 0.36 a 0.216 a 0.1296 a ) 0
1
2
3
4
0
1
2
3
4
2
2
( 0.511.0 a 0.8 a 0.64 a 0.512 a 0.4096 a ) ( 0.381.0 a 1.0 a 1.00 a 1.000 a 1.0000 a ) 0
1
2
3
4
0
1
2
3
4
2
2
( 0.221.0 a 1.2 a 1.44 a 1.728 a 2.0736 a ) ( 0.151.0 a 1.4 a 1.96 a 2.744 a 3.8416 a ) 0
1
2
3
4
0
1
2
3
4
2
2
( 0.071.0 a 1.6 a 2.56 a 4.096 a 6.5536 a ) ( 0.041.0 a 1.8 a 3.24 a 5.832 a 10.4976 a ) 0
1
2
3
4
0
1
2
3
4
2
( 0.021.0 a 2.0 a 4.00 a 8.000 a 16.0000 a ) 0
1
2
3
4
> for i from 0 to m do
r||i:=diff(S,a[i])=0;
end do;
:=
r0
22.00 a 22.00 a 30.800 a 48.4000 a 81.06560 a 9.8000
0
1
2
3
4
:=
r1
22.00 a 30.80 a 48.400 a 81.0656 a 141.32800 a 4.8720
0
1
2
3
4
:=
r2
30.800 a 48.400 a 81.0656 a 141.32800 a 253.235840 a 4.26240
0
1
2
3
4
:=
r3
48.4000 a 81.0656 a 141.32800 a 253.235840 a 462.8588800 a 4.651200
0
1
2
3
4
:=
r4
81.06560 a 141.32800 a 253.235840 a 462.8588800 a 858.78442496 a 5.8675200
0
1
2
3
4
> roz:=solve({r||(0..m)},{seq(a[i],i=0..m)}); roz := { a 1.0017482517482517483, a 0.078331390831390831391, a -1.5270250582750582751, 0
1
2
a 1.0035450660450660451, a -0.19121503496503496503 }
3
4
> assign(roz):
> g:=add(a[j]*x^j,j=0..m); # wielomian aproksymujący 2
3
g := 1.00174825174825174830.078331390831390831391 x1.5270250582750582751 x 1.0035450660450660451 x 0.19121503496503496503 4
x
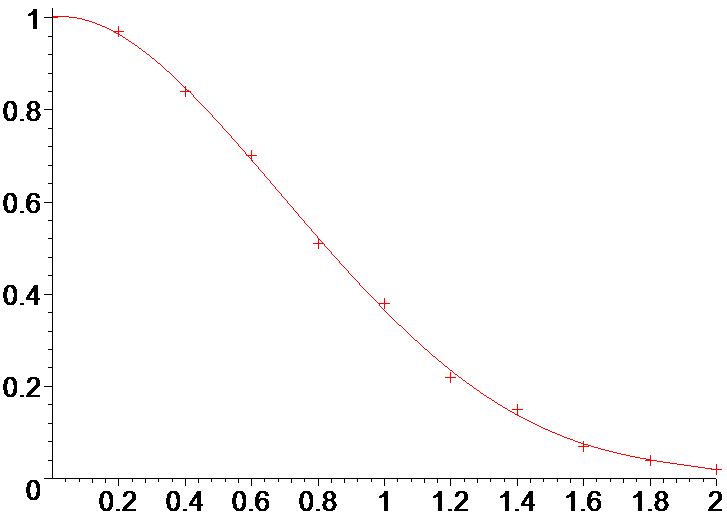
> p:=plot(g,x=0..2):
> display([pkt,p]);
> S;
0.00094871794871794871841
> delta:=sqrt(S);
:=
0.030801265375272307446
> a:='a':
Komenda w Maple'u
Wrócić do m=4
> X:=convert(lx,list): Y:=convert(ly,list):
> w:=add(a[i]*x^i,i=0..m);
:=
2
3
4
w
a
a
0
a 1 x a 2 x 3 x
a 4 x
> gM:=LeastSquares(X,Y,x,curve=w); 2
3
gM := 1.00174825174825174830.078331390831390832734 x1.5270250582750582784 x 1.0035450660450660475 x 0.19121503496503496561 4
x
> g;gM;
1.0017482517482517483 0.078331390831390831391
2
3
x1.5270250582750582751 x 1.0035450660450660451 x 0.19121503496503496503 4
x
1.0017482517482517483 0.078331390831390832734
2
3
x1.5270250582750582784 x 1.0035450660450660475 x 0.19121503496503496561 4
x
> a:='a': # zmienić wartość stopnia wielomianu "m"
>
> restart:
Aproksymacja funkcji okresowej wielomianami trygonometrycznymi
> f:=piecewise(x<-3,x+4,x<-1,-2-x,x<1,x,x<3,2-x,-4+x); # kilka okresow na wykresie
x
4
x-3
2 x
x-1
:=
f
x
x1
2
3
x
x
4 x
otherwise
> plot(f,x=-5..5,scaling=constrained);
>
T 2
2
2
( )cos
i
a
f x
x dx , i 0,1,...
i
T
T
T
2
T 2
2
2
( )sin
i
b
f x
x dx , i 1, 2,...
i
T
T
T
2
> T:=4;
:=
T
4
> m:=5; # 5, 10, 15, 25, 50
m := 5
> for i from 0 to m do
a[i]:=2/T*evalf(Int(f*cos(2*Pi/T*i*x),x=-T/2..T/2)): b[i]:=2/T*evalf(Int(f*sin(2*Pi/T*i*x),x=-T/2..T/2)): end do:
m
1
2 i
2
g( x) a ( a cos x b sin i
x)
2
0
i
T
i
T
i 1
> g:=1/2*a[0]+add(a[i]*cos(2*Pi/T*i*x)+b[i]*sin(2*Pi/T*i*x),i=1..m);
x
3 x
5 x
:=
g
0.8105694690
sin
0.09006327436
sin
0.03242277876
sin
2
2
2
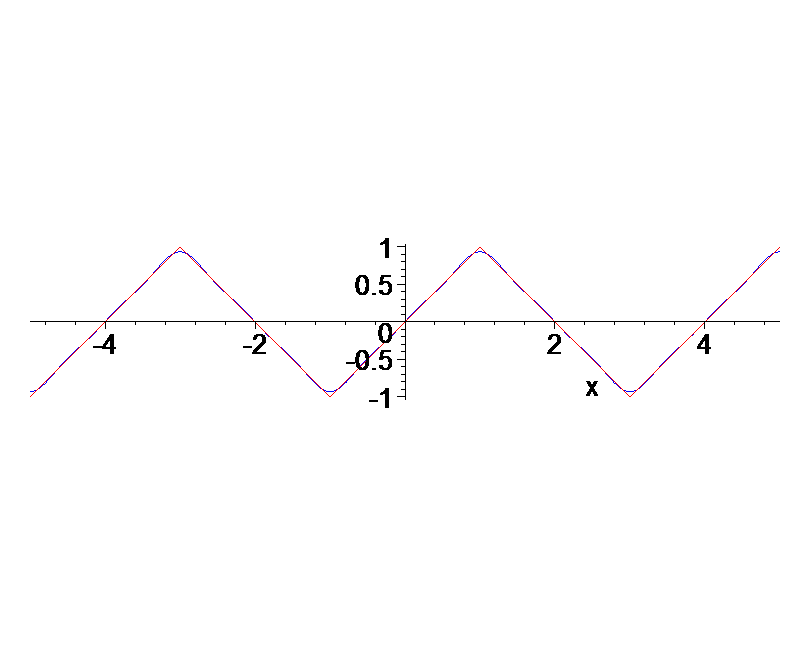
> plot([f,g],x=-5..5,color=[red,blue],scaling=constrained,numpoints=200); # porównanie
>