Warunek przewrócenia klocka sześciennego przez pocisk

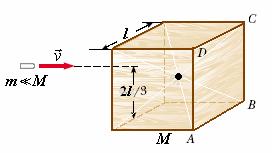
W spoczywający na podłożu poziomym klocek sześcienny o boku l i masie M uderza na wysokości υ

2 l /3 lecący poziomo z prędkością υ pocisk o masie m  M. Obliczyć minimalną wartość prędkości pocisku υmin , przy której możliwe jest przewrócenie klocka. Moment bezwładności sześcianu względem

jego krawędzi wynosi

2

I = (2/3) M l

warunek przewrócenia klocka:

klocek bezpośrednio po uderzeniu pocisku zostaje wprawiony w ruch obrotowy względem osi pokrywającej się z krawędzią AB

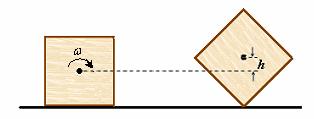
energia kinetyczna ruchu obrotowego zamienia się na energię potencjalną związaną z podniesieniem środka masy klocka w stosunku do położenia pierwotnego podniesienie środka masy klocka na wysokość h (jak na rysunku) jest możliwe, jeżeli wartość prędkości kątowej jest co najmniej równa wartości ωmin z zasady zachowania energii:

1 I

2

ω

= M gh

min

(1)

2

(nie uwzględniamy masy pocisku, który utkwił w klocku, ponieważ m  M) wysokość h wynosi

= l

h

( 2 − )

1

(2)

2

podstawiamy (2) do (1):

1

2

I ωmin =

l

M g ( 2 − )

1 / ⋅2

2

2

M gl

2

ωmin =

( 2 − )

1

(3)

I

prędkość kątowa bezpośrednio po uderzeniu pocisku jest związana z prędkością liniową pocisku – w zderzeniu obowiązuje zasada zachowania momentu pędu L = L’

(4)

L – moment pędu pocisku względem krawędzi AB klocka 2 l

L = mυ ⋅

(5)

3

L’ – moment pędu obracającego się klocka względem krawędzi AB

'

L = I ω

(6)

podstawiamy (5) i (6) do (4): l

2

l

2 mυ

mυ ⋅

= I ω → ω =

3

3 I

zależność obowiązuje dla dowolnych wartości υ i ω, w tym dla minimalnych wartości potrzebnych do przewrócenia klocka υmin i ωmin l

2 mυmin

ω

=

min

(7)

3 I

podstawiamy (7) do (3):

2

 2 l mυmin 

M gl



 =

( 2 − )

1



3 I



I

4 2

2

2

l m υ

M gl

min

=

( 2 − )

1 / : l, ⋅ I

9 2

I

I

4

2

2

l m υmin

= M g ( 2 − )

1

9 I

2

9

υmin =

I

M g

−

( 2

)

1

4

2

l m

(8)

moment bezwładności sześcianu względem jego krawędzi wynosi 2

2

I = M l

(9)

3

podstawiamy (8) do (9):

3 9 2

2

⋅ M l

2

3

υmin =

M g ( 2 − )

1

4

2

2 l m

2

2

M

3

υmin =

⋅ l g ( 2 − )

1

2

m

2

M

3

υmin =

l g ( 2 − )

1

m

2