Politechnika Śląska

ĆWICZENIE PROJEKTOWE Z KONSTRUKCJI METALOWYCH

1

w Gliwicach

KONSTRUKCJA STALOWEJ HALI PRZEMYSŁOWEJ

4.8. Podstawa słupa

a) Założenia

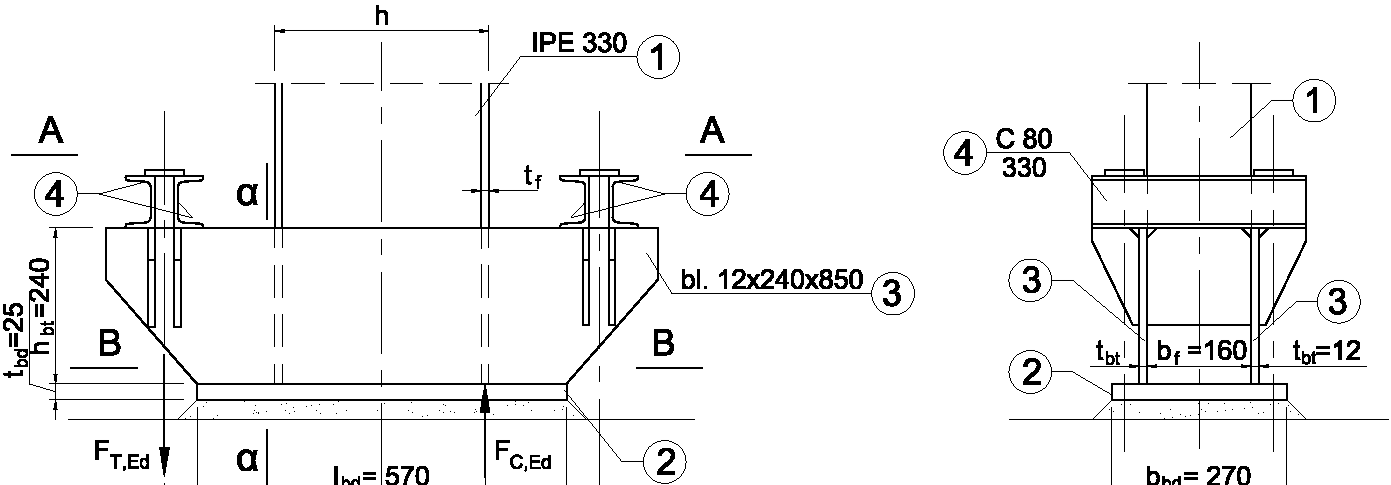
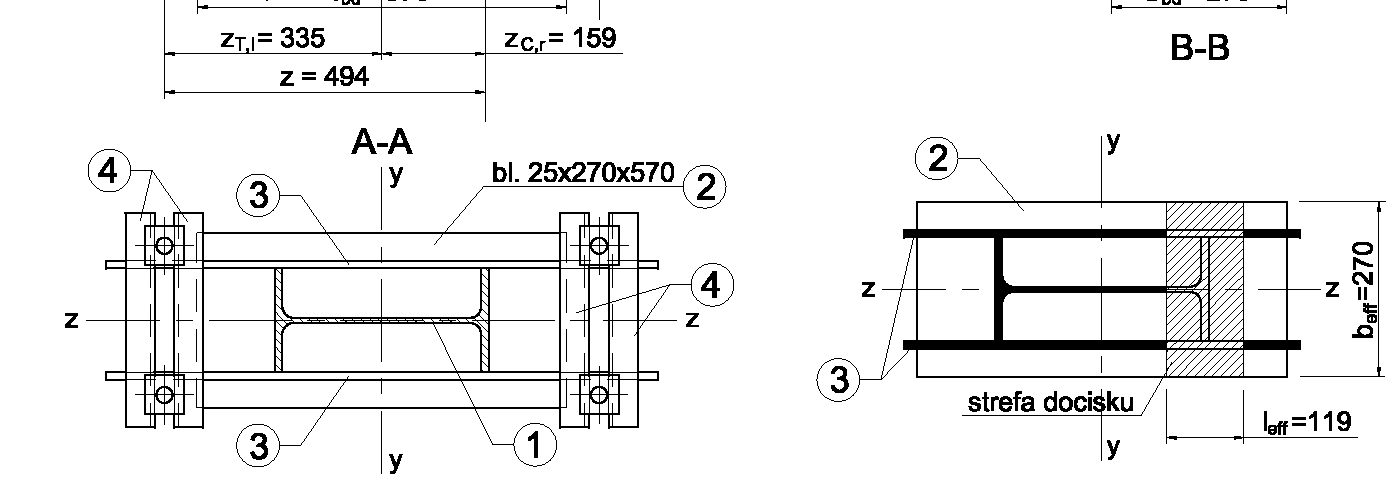
Przyjęto geometrię podstawy jak na rysunku

b) Wytrzymałość betonu

Założenia:

- klasa betonu stopy fundamentowej C25/30,

- wytrzymałość charakterystyczna betonu na ściskanie fck = 25 N/mm2,

- wytrzymałość obliczeniowa betonu na ściskanie fcd = 16,7 N/mm2, Wytrzymałość obliczeniowa połączenia na docisk, wg PN-EN 1993-1-8 [9], p. 6.2.5 oraz PN-EN

1992-1-1:

β ⋅ F

j

R, du

f

=

jd

b ⋅

l

eff

eff

gdzie:

βj – współczynnik materiałowy odniesiony do fundamentu, jego wartość może być przyjmowana jako βj = 2/3,

FR,du – obliczeniowa nośność przy sile skupionej działającej na powierzchnię betonową:

Politechnika Śląska

ĆWICZENIE PROJEKTOWE Z KONSTRUKCJI METALOWYCH

2

w Gliwicach

KONSTRUKCJA STALOWEJ HALI PRZEMYSŁOWEJ

A 1 c

F

= A ⋅ f

≤ 3 f A

Rdu

c 0

cd

cd

c 0

Ac 0

Ac0 – pole powierzchni docisku:

A = b ⋅ l

c 0

eff

eff

beff, leff – szerokość i długość efektywna półki króćca teowego blachy podstawy A

A

c

=

c1 – pole powierzchni rozdziału; dla celów praktycznych można przyjąć 1

1,5

Ac 0

Po przekształceniach otrzymano:

A 1

c

β ⋅ A ⋅ f

j

c 0

cd

β ⋅ F

A

j

R, du

c

2

0

2

f

=

=

= ⋅16,7⋅1,5 =16,7 N/mm

jd

b ⋅

l

A

3

eff

eff

c 0

c) Nośność strefy ściskanej

Maksymalny wysięg strefy docisku

f y

235

c = t

= 25

= 54 mm

p

3 f ⋅γ

3⋅16, 7 ⋅1, 0

jd

M 0

Efektywne: szerokość beff i długość leff półki króćca teowego blachy podstawy, wg [9], p. 6.2.5

 bdb = 270 m

m



b

eff = min

 b

c t

f +

(

 =

2

+ bt ) =160 + (

2 54 +12)

270 m

m

= 292 m

m

0

 ,5( l − h + t + c =

−

+

+ =







bd

)

0,5

f

(570 330) 11,5 54 185 mm

l

= min

 =119 mm

eff

t

 + 2 c =11,5+ 2⋅54 =119 mm



f



Obliczeniowa nośność strefy ściskanej

F

f

l

b

C Rd =

jd ⋅ eff ⋅

eff = 1 ,

6 7 ⋅ 270 ⋅119 = 536 5

7

1 N

,

Obciążenie strefy ściskanej

- ramię dźwigni z przy dominującym momencie zginającym, wg [9], p. 6.2.8: zT,I = 335 mm, zC,r = 0,5( h - tf ) = 0,5(330 – 11,5) = 159,25 mm, z = zT,I + zC,r = 335 + 159 = 494

mm.

Politechnika Śląska

ĆWICZENIE PROJEKTOWE Z KONSTRUKCJI METALOWYCH

3

w Gliwicach

KONSTRUKCJA STALOWEJ HALI PRZEMYSŁOWEJ

- siła ściskająca

Miarodajna kombinacja obciążeń KOMB1→ NEd = 128,65 kN, MEd = 111,81 kN

− NEd ⋅ zT I M Ed −

⋅

,

12 ,

8 65

3

,

0 35

111 8

, 1

F

C Ed =

−

=

−

= 3

− 13 5

, 6 k

N

,

z

z

,

0 494

,

0 494

Warunek nośności strefy ściskanej

F

F

C Ed

= 313 5

, 6 k

N < C Rd = 53 ,

6

k

6 N

,

,

Warunek nośności jest spełniony.

d) Nośność strefy rozciąganej

Przyjęto kotwy fundamentowe P24 ze stali S355: As = 353 mm2, fub = 470 N/mm2

Nośność jednej kotwy fundamentowej, wg [9], tabl. 3.4: k ⋅ f ⋅ A

0, 9 ⋅ 470 ⋅353

2

ub

s

F

=

=

= 119 455 N = 119,45 kN

t , Rd

γ

1, 25

M 2

Przyjęto, że kotew jest odpowiednio zamocowana w betonie i o jej nośności nie decyduje wyrywanie z betonu.

Obciążenie strefy rozciąganej

Miarodajna kombinacja obciążeń KOMB2 → Mmax = 113,54 kN, NEd = 101,55 kN

− NEd ⋅ zC r M Ed −

⋅

,

101 5

, 5

1

,

0 59

113 5

, 4

F

T Ed =

+

=

+

=197 1

, 5 k

N

,

z

z

,

0 494

,

0 494

Warunek nośności strefy rozciąganej

F

F

F

T Ed = 197 1

, 5 k

N < T Rd = 2 ⋅ t Rd = 2 ⋅11 , 9 45 = 238 k

9

,

N

,

,

,

Warunek jest spełniony.

e) Obciążenie siłą poprzeczną

Politechnika Śląska

ĆWICZENIE PROJEKTOWE Z KONSTRUKCJI METALOWYCH

4

w Gliwicach

KONSTRUKCJA STALOWEJ HALI PRZEMYSŁOWEJ

Miarodajna kombinacja obciążeń KOMB4: γ

G

Q

G

WC

Gj

⋅ kj +γ Q ⋅ k =1,0⋅ +1,5⋅

,inf

,inf

,1

,1

→ Vmax =

VEd = 36,96 kN

W celu przejęcia siły poprzecznej, pod blachą podstawy zaprojektowano ostrogę z kształtownika IPE 100, ze stali S235.

Nośność przekroju na ścinanie, wg [2], p. 6.2.6

- powierzchnia pasa:

2

A = b ⋅ t = 64 ⋅ 6, 3 = 403, 2 mm , f

f

f

- powierzchnia środnika:

2

A = d ⋅ t = (120 − 2 ⋅ 7 − 2 ⋅ 6, 3)4, 4 = 411 mm w

w

- ponieważ warunek, wg [2], p. 6.2.6(5): Af

403, 2

=

= 0,98 > 0.6

A

411

w

nośność przekroju należy określić ze wzoru: f y

235

V

A

c Rd =

w

= 411

= 55 7

63 k

N = 55,8 k

N

,

3γ

3

M

⋅ ,10

0

Warunek nośności

V

36, 96

Ed

=

= 0,66 <1

V

55,8

c, Rd

Warunek jest spełniony.

f) Nośność spoin pachwinowych łączących trzon słupa z blachami trapezowymi Grubość spoin anom przyjęto z warunku konstrukcyjnego wg PN-90-03200:

,

0 2 t

t

bt =

,

0 2 ⋅12 = ,

2

m

4

m

 7

,

0

f =

7

,

0 ⋅11 m

5

,

m = m

8

m

 ≤ a

nom =

m

5

m ≤ 

2,5 m

m



16 m

m

Obliczeniowa wytrzymałość spoiny, wg [9], p. 4.5.3.3(3): f / 3

360 / 3

u

2

f

=

=

= 207,85 N/mm

vw, Rd

β ⋅γ

0,8 ⋅

1, 25

w

M 2

gdzie:

βw – współczynnik korelacji dla spoin pachwinowych równy 0,8, wg [9], tabl. 4.1.

Nośność obliczeniowa spoiny na jednostkę długości spoiny:

Politechnika Śląska

ĆWICZENIE PROJEKTOWE Z KONSTRUKCJI METALOWYCH

5

w Gliwicach

KONSTRUKCJA STALOWEJ HALI PRZEMYSŁOWEJ

F

= f

⋅ a = 207,85⋅5 =1039 N/mm

w, Rd

vw, d

nom

Potrzebna obliczeniowa długość spoin:

FC Ed

⋅

,

313 5

, 6 103

l

w potrz =

=

= 75 m

m

,

4 ⋅ F

4

w Rd

⋅1039

,

- przyjęto długość spoin:

 lw potrz = 75 m

m

,

l

w = max

 = 240 m

m

 hbt = 240 m

m 

Uwaga: Jeżeli lw > hbt wówczas należy zwiększyć wysokość blach trapezowych do wymaganej obliczeniowej długości spoin pachwinowych.

g) Nośność układu złożonego z blachy poziomej i blach trapezowych Moment zginający belkę w przekroju α-α



h 





3

330

M

Ed = M T Ed = F

 z

T Ed

T I −

 = 197 1

, 5 ⋅10 335 −

 = 33515⋅103 N ⋅ mm = 3 5

,

3 2 k

N ⋅ m

,

,

,



2 



2 

Klasa przekroju

- środnik zginany

c

h

240

bt

=

=

= 20 < 72ε = 72⋅1 = 72 → klasa1

t

t

12

bt

- ściskana część wspornikowa półki

0,5( b − b − t

c

−

−

bd

f )

bt

0,5(270 160) 12

=

=

=1,72 < 9ε = 9⋅1 = 9 → klasa1

t

t

25

bd

- ściskana część przęsłowa półki

c

bf

160

=

=

= 6,4 < 33ε = 33⋅1 = 33 → klasa1

t

t

25

bd

Przekrój spełnia wymagania klasy 1.

Obliczeniowa nośność plastyczna dwóch blach trapezowych przy ścinaniu, wg [2], p. 6.2.6

Politechnika Śląska

ĆWICZENIE PROJEKTOWE Z KONSTRUKCJI METALOWYCH

6

w Gliwicach

KONSTRUKCJA STALOWEJ HALI PRZEMYSŁOWEJ

- powierzchnia czynna przy ścinaniu:

2

A

= 2 h ⋅ t = 2 ⋅ 240 ⋅12 = 5760 mm v, bt

bt

bt

A

f /

3

5 760 235 /

3

v, bt ( y

)

(

)

3

V

=

=

= 781,5⋅10 N

pl , Rd

γ

1, 0

M 0

- warunek nośności

FC Ed

⋅

,

313 5

, 6 103

=

= ,

0 40 < 1

V

781 5

,

pl Rd

⋅103

,

Warunek nośności jest spełniony.

Obliczeniowa nośność plastyczna układu złożonego przy zginaniu

- ponieważ spełniony jest warunek:

FC, Ed = ,040 < 5,

0

Vpl, Rd

nie zachodzi konieczność uwzględniania ścinania na nośność przy zginaniu, wg [2], p. 6.2.8.

- parametry geometryczne i wytrzymałościowe przekroju, wg rysunku: b ⋅ t ⋅ 0, 5 t

+ 2 h ⋅ t ⋅ (0,5 h + t ) 270 ⋅ 25⋅ 0,5⋅ 25 + 2 ⋅ 240 ⋅12 ⋅ (0,5⋅ 240 + 25) bd

bd

bd

bt

bt

bt

bd

y =

=

=

c

b ⋅ t

+ 2 h ⋅ t

270 ⋅ 25 + 2 ⋅ 240 ⋅12

bd

bd

bt

bt

= 73,5 mm

3

b ⋅ t

 t ⋅ h



⋅

bd

bd

I =

+ b ⋅ t ( y −

t )

3

2

bt

bt

+ 

+ t ⋅ h y − t +

h

 =

+

y

bd

bd

c

bd

bt

bt ( c

( bd

bt ))

3

2

270 25

0, 5

2

0, 5

12

 12



12

+

⋅ (

−

⋅ )

3



⋅



2

12 240

270 25 73, 5

0, 5 25

+ 2 

+12 ⋅ 240(73,5 − (25 + 0,5⋅240))2

4

 = 82 562 872 mm



12





I y

872

562

82



3



=

=

m

431138

m 

 t

h

y

bd +

bt −

25

c

+ 240 −

5

,

73



3

Wy = min

 =

m

431138

m

 I

y

872

562

82

3



=

=

m

304

123

1

m

 y

5

,

73



c



- obliczeniowa nośność przy jednokierunkowym zginaniu, wg [2], p. 6.2.5

W

f

y ⋅

y

431138 ⋅ 235

M c Rd =

=

=1013

17 4

3

0 N ⋅ mm = 101,3 k

N ⋅ m

,

γ

,

1 0

M 0

Politechnika Śląska

ĆWICZENIE PROJEKTOWE Z KONSTRUKCJI METALOWYCH

7

w Gliwicach

KONSTRUKCJA STALOWEJ HALI PRZEMYSŁOWEJ

- warunek nośności

M

33 5

, 2

Ed

=

= 3

,

0 3 < 1

M

101 3

,

c, Rd

Warunek nośności jest spełniony.

h) Nośność spoin pachwinowych łączących blachę poziomą z blachami trapezowymi Grubość spoin anom przyjęto z warunku konstrukcyjnego wg PN-90-03200: 0, 2 t

= 0,2⋅25mm = 5 mm

0,7 t = 0,7 ⋅12 mm = 8, 4 mm

bd

 ≤ a

= 6 mm

bt

≤ 

2,5 mm

nom



1

 6 mm

Sumaryczna długość spoin

∑ l

sp =

(22 lbd − h)= (22⋅570−330)=1620 m m

Naprężenia w spoinach

- od siły pionowej:





3

F



C Ed

⋅



σ

a

l

t

nom ⋅ 2( ,

2 eff − f )

313 5

, 6 10

6 ⋅ (

2 2 ⋅119 −11 )

5

,

2

τ ⊥ =

=

=

= 81 5

,

7 N/mm 



2

σ

τ

⊥ = ⊥ = min

 = 81 5

,

7 N/mm

2

2

2





9

,

0

f

9

,

0

u

⋅360



2

=

= 25 ,

9

2 N/mm



 γ

,

1 25



M



2

- od siły poprzecznej:

Miarodajna kombinacja obciążeń KOMB1→ VEd = 23,89 kN

(2 l h

bd −

)

−

3

(2570 330)

V

V

sp =

Ed

= 23 8

, 9 ⋅10

= 0

7 7

9 N = 7,08 k

N

∑ l

1620

sp

Vsp

7079

2

τ

II =

=

= 491,

6 N/mm

2

2

4 a

4 ⋅ 6

Politechnika Śląska

ĆWICZENIE PROJEKTOWE Z KONSTRUKCJI METALOWYCH

8

w Gliwicach

KONSTRUKCJA STALOWEJ HALI PRZEMYSŁOWEJ

Warunek nośności spoin

[

f

2

u

σ

τ

τ

⊥ + ( 2

2

3 ⊥ + II )]0,5 = [

2

108 1

,

+ (

2

3 108 1

,

+ 49 1

, 6)]0,5

2

= 23 ,

2

4 N/mm ≤

=

β γ

w ⋅

M 2

360

2

=

= 36

0 N/mm

8

,

0 ⋅ ,

1 25

KONIEC OBLICZEŃ