Automatyka i Robotyka –Analiza – Wykład 6 – dr Adam Ćmiel – cmiel@agh.edu.pl RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ
Niech f: R⊃ D→ R , x ∈
0
D.
Oznaczenia: Ot( x 0,δ)= K( x 0,δ)= ( x 0-δ, x 0+δ)∩ D ; S( x 0,δ)= Ot( x 0,δ)-{ x 0}
f ( x 0 + x
∆ ) − f ( x )
Def. Ilorazem różnicowym funkcji f w punkcie x ∈ D nazywamy wyrażenie 0
,
0
x
∆
∆ x≠0, x 0+∆ x ∈ Ot( x 0,δ) Def. Pochodną funkcji f w punkcie x nazywamy właściwą granicę ilorazu różnicowego 0
f ( x + x
∆ ) − f ( x ) df
lim
0
0
'
= f ( x )
( x
0
0 – punkt skupienia zboru D)
x
∆ →0
x
∆
W podobny sposób definiujemy pochodne jednostronne:
'
'
−
f ( x 0 + x
∆ ) − f ( x )
f ( x
0
−
)
0
= f ( x )
0
= lim−
x
∆ →0
x
∆
'
'
+
f ( x 0 + x
∆ ) − f ( x )
f ( x
0
+
)
0
= f ( x )
0
= lim+
x
∆ →0
x
∆
Tw. f '( x ) - istnieje ⇔ istnieją
'
f ( x )
'
f ( x
0
−
i
)
0
+
oraz są sobie równe.
0
Tw. (o przedstawieniu przyrostu funkcji)
Jeżeli funkcja f : R ⊃ Ot( x ,δ ) ma pochodną w punkcie x
0
→ R
0 , to dla każdego ∆ x≠0, takiego,
że x 0+∆ x ∈ Ot( x 0,δ) przyrost wartości funkcji można przedstawić w postaci f ( x + ∆ x) − f ( x )
'
= f ( x ) ⋅ x
∆ + r( x , ∆ x) , przy czym r( x , x o (∆ x) , gdy ∆ x → 0 .
0 ∆ ) =
0
0
0
0
Dow: Niech: r( x , x
. Stąd natychmiast mamy
0 ∆ ) = f ( x 0 +
x
∆ ) − f ( x )
0
− f ' ( x )
0
⋅ x
∆
f ( x + ∆ x) − f ( x )
'
= f ( x ) ⋅ x
∆ + r( x , ∆ x) .Pozostaje jedynie pokazać, że 0
0
0
0
r( x , x
o (∆ x) gdy ∆ x → 0 .
0 ∆ ) =
r( x , x
: x
∆
0 ∆ ) = f ( x 0 +
x
∆ ) − f ( x )
0
− f '( x )
0
⋅ x
∆
r( x , ∆ x)
f ( x + ∆ x) − f ( x) lim
0
= lim
0
'
− f ( x ) = 0 ⇒ r( x , x o (∆ x)
0 ∆ ) =
0
∆ x→0
x
∆ x→0
∆
∆ x
Wniosek. Jeżeli funkcja f ma pochodną w punkcie x 0 to funkcja ta jest ciągła w x 0 , bo f ( x + x
∆ ) − f ( x ) = f '( x ) ⋅ x
∆ + r( x , x
∆ ) .
0
0
0
0
Więc lim ( f ( x + ∆ x) − f ( x ) = , co oznacza ciągłość f w punkcie x 0
0 )
0
∆
0.
x→0
Def. Funkcję f : R ⊃ Ot( x ,δ ) nazywamy różniczkowalną w punkcie x
0
→ R
0 , gdy istnieje stała A∈ R
taka, że dla każdego ∆ x≠0, takiego, że x 0+∆ x ∈ Ot( x 0,δ), f ( x + x
∆ ) − f ( x ) = A ⋅ x
∆ + r( x , x
∆ ) , przy czym r( x , x
o (∆ x) , gdy ∆ x → 0 .
0 ∆ ) =
0
0
0
Def. Różniczka funkcji f w punkcie x
'(
)
, który
0 ∆
0 dla przyrostu ∆ x nazywamy iloczyn f
x
x
df
oznaczamy df ( x , x
0 ∆ ) = f ' ( x )
x
0 ∆
Uwaga. df ( x ,
jest liniową funkcją przyrostu.
0 ⋅ ) :
x
∆ → df ( x , x
0 ∆ ) = f ' ( x )
x
0 ∆
1
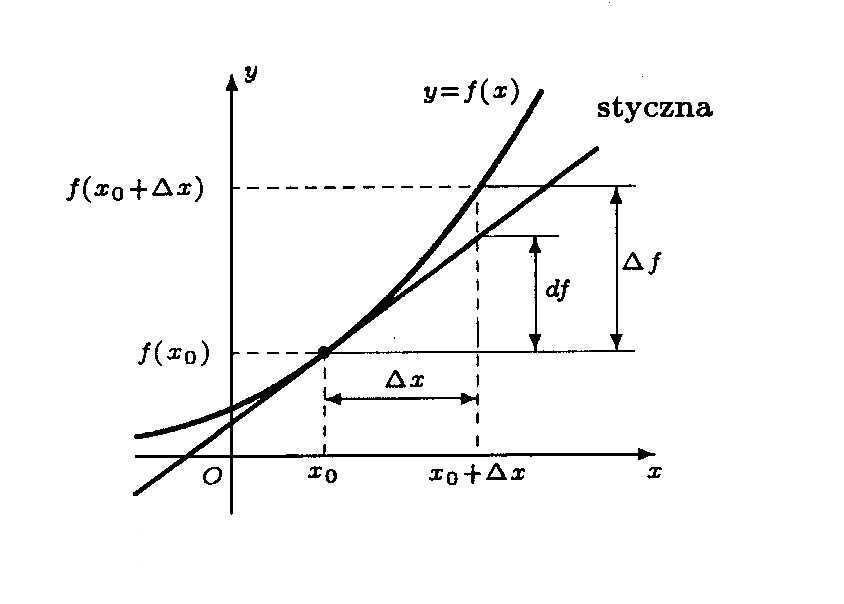
Automatyka i Robotyka –Analiza – Wykład 6 – dr Adam Ćmiel – cmiel@agh.edu.pl nachylenie siecznej
f ( x + ∆ x) − f ( x ) 0
0
= tg β
∆
x
nachylenie stycznej
f ( x + x
∆ ) − f ( x )
lim
0
0
= tg
'
α = f ( x )
0
x
∆ →0
x
∆
f '( x ) określa szybkość zmiany funkcji f w punkcie x 0
0.
Z twierdzenia o przedstawieniu przyrostu funkcji i z przyjętych definicji otrzymujemy
Tw. Funkcja jest różniczkowalna w punkcie x 0 ⇔ funkcja ta ma pochodną w x 0.
Inne oznaczenie dla pochodnej
df ( x , x
dla f ( x) = x dx( x , x
. Stąd
0 ∆ ) = 1⋅
x
∆
0 ∆ ) = f ' ( x )
x
0 ∆
df ( x , x
0 ∆ )
df
f '( x )
0
=
=
dx( x , x
0 ∆ )
dx
Funkcja pochodna i operator różniczkowania
Niech f : R ⊃ I → R ( I – dowolny przedział) będzie różniczkowalna na I.
Def.
Funkcję f ': I ∋ x → f '( x) nazywamy funkcja pochodną.
d
df
Operator (funkcja, odwzorowanie) D =
, który funkcji f przypisuje
= f '( x) nazywamy
dx
dx
operatorem różniczkowania.
Bezpośrednio z definicji wyprowadza się wzory
f ( x)
f ' ( x)
C=const
0
α
α
x
1
−
α x
x
e
x
e
x
a
a x ln a
sin x
cos x
cos x
− sin x
Tw. (o działaniach arytmetycznych). Jeżeli f i g są różniczkowalne w punkcie x (w I), to
f
( f + g) , ( f − g) , ( f ⋅ g) , są różniczkowalne w punkcie x (w I) oraz:
g
1º ( f + g)'( x) = f ' ( x) + g'( x) 2º ( f − g)'( x) = f ' ( x) − g' ( x) 3º ( f ⋅ g)'( x) = f ' ( x) g( x) + f ( x) g' ( x)
'
f
f ' ( x) g( x) − f ( x) g' ( x) 4º =
g( x) ≠ 0 (∀
g( )
∈
x
x I
≠ 0)
2
g
g ( x)
2
Automatyka i Robotyka –Analiza – Wykład 6 – dr Adam Ćmiel – cmiel@agh.edu.pl Tw.
(o pochodnej funkcji złożonej) Jeżeli:
1º h jest różniczkowalna w x (w I) 2º g jest różniczkowalna w h( x) (w h( I)) to funkcja złożona f = g o h jest różniczkowalna w x (w I) i ( g o h)'( x) = g'( h( x)) h'( x) tw. p
o
rzyrosta h
c
Dow. f ( x + ∆ x) − f ( x) = g( h( x + ∆ x)) − g( h( x))
=
= g'( h( x))( h'( x)∆ x + r ( x, x r h x h x
x
h x
2
∆ )) + ( ( ), (
1
+ ∆ ) − ( )) =
= g'( h( x)) h'( x) x
∆ + g'( h( x)) r ( x, x
∆ ) + r ( h( x), h( x + x
∆ ) − h( x))
2
1
Trzeba pokazać, że g' ( h( x)) r ( x, x
∆ )) + r ( h( x), h( x + x
∆ ) − h( x)) = o (∆ x)
2
1
Jeżeli ∆ x → 0 to r = o (∆ x) stąd g' ( h( x)) r ( x, ∆ x)) = o (∆ x) . Ponadto 2
2
0 , h( x + ∆ x) − h( x) = 0
r ( h( x), h( x
x
h x
1
+ ∆ ) − ( )) = r ( h( x), h( x x
h x
1
+ ∆ ) − ( ))
⇒
( h( x + ∆ x) − h( x))
h( x + ∆ x) − h( x)
r ( h( x), h( x + ∆ x) − h( x)) r ( h( x), h( x + ∆ x) − h( x)) h( x + ∆ x) − h( x) Stąd lim 1
= lim 1
= 0 .
∆ x→0
∆ x
∆ x→0
h( x + ∆ x) − h( x)
∆ x
Tw. (o pochodnej funkcji odwrotnej). Niech f : R⊃ I→ R będzie funkcją
• ściśle monotoniczną,
• różniczkowalną w I
• f '( x) ≠ 0 ( w I )
1
− '
1
Wówczas
−1
g = f
jest różniczkowalna na f [ I ] i ( f
) ( f ( x)) = g'( f ( x)) =
f ' ( x)
Dow. Przy przyjętych oznaczeniach mamy : f ( x) = y , f ( x + x
∆ ) = y + y
∆ . Z uwagi na ciągłość i
ścisłą monotoniczność funkcji f funkcja odwrotna
−1
g = f
jest również ciągła i ściśle
monotoniczna. Stąd ∆ y ≠ 0 gdy ∆ x ≠ 0 , ∆ y → 0 ⇔ ∆ x → 0 i g( y + y
∆ ) = x + x
∆ .
g( y + y
∆ ) − g( y)
x + x
∆ ) − x
1
Wobec tego
=
=
.
y
∆
f ( x + x
∆ ) − f ( x)
f ( x + x
∆ ) − f ( x)
x
∆
Przechodząc do granic otrzymujemy tezę .
Uzupełnienie wzorów różniczkowania
f ( x)
f ' ( x)
1
tg x
2
cos x
1
ctg x
−
2
sin x
1
ln x
x
1
log x
a
x ln a
1
arcsin x
x < 1
2
1 − x
3
Automatyka i Robotyka –Analiza – Wykład 6 – dr Adam Ćmiel – cmiel@agh.edu.pl 1
arccos x
−
x < 1
2
1 − x
1
arctg x
2
1 + x
1
arcctg x
−
2
1 + x
Twierdzenia o wartości średniej
Tw. Rolle’a:
f jest ciągła w [ a, b]
f jest różniczkowalna w ( a, b)
⇒ ∃
: f ' ( )
∈
c
c
a b
= 0
( , )
f ( a) = f ( b)
Dowód. Jeżeli f jest stała to twierdzenie jest spełnione w sposób trywialny. Jeżeli f nie jest stała to prawdziwa jest przynajmniej jedna z nierówności inf f ( x) < f ( a) , sup f ( x) > f ( a) .
x [
∈ a, b]
x [
∈ a, b]
Przypuśćmy, że prawdziwa jest inf f ( x) < f ( a) (dla sup f ( x) > f ( a) - analogicznie).
x [
∈ a, b]
x [
∈ a, b]
Z tw. Wierstrassa ∃
: f ( c)
inf f ( x) ale z warunku inf f ( x) < f ( a) wynika, że c∈( a, b).
c [
∈
=
a, b]
x [
∈ a, b]
x [
∈ a, b]
f ( c + ∆ x) − f ( c) ≥
0 g
dy ∆
x > 0
Ale
i istnieje f '( c) bo c jest punktem wewnętrznym.
∆ x
≤
0 g
dy ∆
x < 0
Granice jednostronne ilorazu różnicowego muszą być równe sobie, czyli równe zero.
f ( c + ∆ x) − f ( c) A więc ostatecznie: lim
= 0 ⇔ f '( c) = 0 .
∆ x→0
∆ x
Twierdzenie Cauchy’ego .Jeeżli
1. f i g są ciągłe w [ a, b], 2. f i g są różniczkowalne w ( a, b), to ∃ c∈( a,b) : ( f ( b) – f( a)) g’( c) -( g ( b) – g( a)) f ’( c) =0.
Dowód ϕ( x)=( f ( b) – f( a)) g( x) -( g ( b) – g( a)) f ( x) spełnia zał. tw. Rolle’a , więc istnieje c∈( a, b) takie, że ϕ ’( c)=( f ( b) – f( a)) g’( c) -( g ( b) – g( a)) f ‘( c) - stąd teza.
Interpretacja tw. Cauchy’ego. Wektorowa funkcja ( f( t), g( t)), t∈[ a, b]) jest parametryzacją krzywej płaskiej. Istnieje punkt na krzywej w którym styczna do krzywej jest równoległa do siecznej przechodzącej przez końce krzywej
Z twierdzenia Cauchy’ego można wywnioskować
4
Automatyka i Robotyka –Analiza – Wykład 6 – dr Adam Ćmiel – cmiel@agh.edu.pl Twierdzenie de L’Hospitala . (stosuje również się do granic jednostronnych i niewłaściwych) . Jeżeli f ( x)
f (
′ x)
1º
i
są określone w S ( x ,δ )
g( x)
g (
′ x)
0
2º lim f ( x) = 0 ∧ lim g( x) = 0 [0 albo lim f ( x) = ±∞ ∧ lim g( x) = ±∞ [∞∞ ]
0 ]
x→ x
x
x
x→ x
x
x
0
→ 0
0
→ 0
f (
′ x)
3º Istnieje lim
(właściwa lub niewłaściwa)
x→ x
′
0
g ( x)
f ( x)
f ( x)
f (
′ x)
to istnieje lim
i lim
= lim
x→ x
→
→
′
0 g ( x)
x
x 0 g( x)
x
x 0 g ( x)
f ( x)
f ( x) − f ( x )
f (
′ c)
Szkic dowodu: dla [0 . Przyjmując f( x
0
=
=
(z tw.
0 ]
0)= g( x 0)=0 mamy g( x)
g( x) − g( x )
g (
′ c)
0
f (
′ x)
Cauchy’ego). Ale x
x ⇒
→
c → x . Z istnienia granicy lim
wynika istnienie
0
0
x→ x
′
0
g ( x)
f ( x)
granicy lim
i równość tych granic.
x→ x 0 g( x)
Dla pozostałych przypadków wystarczy sprowadzić do formy [0 .
0 ]
Symbole nieoznaczone
∞
: 0 , ∞ , ∞ − ∞ , 0 ∞, 00, ∞0, 1
0
∞
Przykłady
lim ln x = 1 ,
lim ln x = 0 ,
1
1
1
li (
m
−
) = ,
lim x ctg x = 1,
1
−
ln x
1
−
2
x
1
→ x
x→∞
x
x
1
→
x
x→0
1
−
−
lim x
x = 1 ,
1
tgx
1
lim x x = e ,
lim( 1
= .
2 )
1
+
x→0
x
1
→
→0 x
x
Przykład niewłaściwego użycia tw. de L’Hospitala H
Wiadomo, że lim x+sin x = 1 ale
x+sin x
1+cos x
lim
= lim
nie istnieje (wyjaśnić sprzeczność!)
x+cos
x+cos x
1−cos x
x→∞
x
x→∞
x→∞
5
Wyszukiwarka
Podobne podstrony:
5 Rachunek różniczkowy funkcji jednej zmiennej
C 04,5 Rachunek różniczkowy funkcji wielu zmiennych
11 RACHUNEK RÓŻNICZKOWY FUNKCJI WIELU ZMIENNYCH
wykład, RACHUNEK ROZNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ 63, 1)
,analiza matematyczna 1, rachunek różniczkowy funkcji jednej zmiennej
Matematyka III (Ćw) - Lista 05 - Rachunek rózniczkowy funkcji wielu zmiennych, Odpowiedzi
5 RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ
zadania rachunek różniczkowy jedenej zmiennej, AGH Imir materiały mix, Studia
Rachunek różniczkowy funkcji jednej zmiennej, SZKOŁA, Matematyka, Matematyka
Wykłady z Matematyki, Wykłady - Rachunek Różniczkowy Funkcji Wielu Zmiennych, Dr Adam Ćmiel
RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ 62, Geodezja i Kartografia, I rok, Matematyka
Rachunek rozniczkowy funkcji jednej zmiennej
Matematyka III (Ćw) - Lista 05 - Rachunek rózniczkowy funkcji wielu zmiennych, Zadania
Matematyka III (Ćw) Lista 05 Rachunek rózniczkowy funkcji wielu zmiennych Odpowiedzi
1-RACHUNEK RÓŻNICZKOWY FUNKCJI WIELU ZMIENNYCH, RACHUNEK RÓŻNICZKOWY FUNKCJI WIELU ZMIENNYCH
5 Rachunek różniczkowy funkcji jednej zmiennej
C 04,5 Rachunek różniczkowy funkcji wielu zmiennych
więcej podobnych podstron