Próbne podstawowe równania Maxwella
Prawo Gaussa dla elektryczności
ε 0 ∫ d
E S = q
Istnieją izolowane centra ładunku.
Linie pola elektrycznego pochodzące od ładunków mają swój początek lub koniec.
Prawo Gaussa dla magnetyzmu
∫ BdS = 0
Nie ma izolowanych centrów magnetyzmu.
Linie pola magnetycznego są zamknięte.
d
Prawo indukcji Faradaya
∫
Φ
d
E l = −
B
dt
Zmienne pole magnetyczne wytwarza pole elektryczne.
Prawo Ampere'a
dq
d
B l = µ i = µ
0
0
∫
dt
Przepływający prąd powoduje wytworzenie pola magnetycznego.
Korzystają z zasady symetrii można przypuszczać, że zmieniając pole elektryczne ( dΦ /dt) wytwarzamy pole magnetyczne ( ∫ B dl ).
W analogii do prawa indukcji Faraday’a
∫
dΦ
d
E l = −
B
dt
∫
dΦ
d
B l =
E
µ ε0 0 dt
Maxwell uogólnił prawo Amper’a do postaci
dΦ
d
B l
E
= µ ε
+ µ i
0 0
∫
dt
0
dΦ E
ε 0
ma wymiar prądu i nazywamy go prądem przesunięcia.
dt
∫ d
B l = µ 0( ip + i) Pole magnetyczne może być wytworzone przez prąd przewodzenia lub prąd przesunięcia.
E = ε A
0
dE
1 dq
=
= 1 i
dt
ε A dt ε A
0
0
prąr
przesunięria
dΦ
d
E
( EA)
dE
i = ε
ε
ε
0
= 0
=
A
p
dt
dt
0
dt
czyli
1
i = ε A
i
0
= i
p
ε A
0
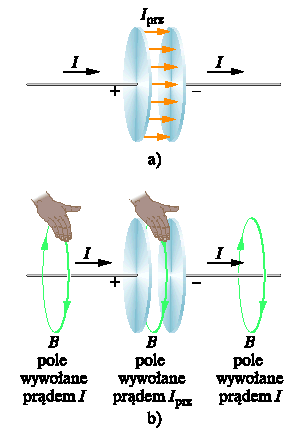
Rys. a) Prąd przesunięcia o natężeniu Iprz między okładkami kondensatora, który jest ładowany prądem o natężeniu I .
Rys b) Reguła prawej dłoni, służąca do wyznaczania kierunku indukcji magnetycznej pola wokół przewodu, w którym płynie rzeczywisty prąd (jak po lewej stronie rysunku), wskazuje również kierunek indukcji magnetycznej pola wokół prądu przesunięcia (jak
w środku rysunku)
Prawo Gaussa dla pola elektrycznego Ładunek wytwarza pole elektryczne o indukcji odwrotnie proporcjonalnej do kwadratu odległości ε ∫ EdS
0
= q
Prawo Gaussa dla pola magnetycznego Nie istnieje w przyrodzie ładunek magnetyczny, linie indukcji są krzywymi zamkniętymi
∫ BdS = 0
Uogólnione prawo indukcji Faradaya
Zmienne pole magnetyczne wytwarza wirowe pole elektryczne, które może wywoływać prąd
= d
Edl
B
elektryczny
∫
Φ
− dt
Uogólnione prawo Ampere'a
Prąd elektryczny lub zmienne pole elektryczne wytwarza wirowe pole magnetyczne
∫
Φ
=
d
Bdl
E
µ ε
0
0
+ i
dt