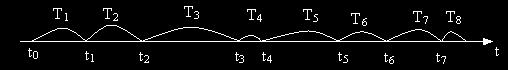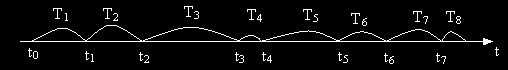1. PRZEDSTAW POJĘCIE NIEZAWODNOŚCI OBIEKTU
Obecnie niezawodność rozumiana jest jako niezawodność techniczna.
Niezawodność obiektu - to jego właściwość określona przez wartości istotnych w określonych przypadkach wielkości charakteryzujących zdolność obiektu do spełnienia wymagań.
Obiekt – wyrób, samochód, proces produkcji.
Spełnienie wymagań – przeżycie określonego okresu czasu, wykonanie określonej pracy, wykonanie określonej liczby czynności, zachowanie zdolności do pełnienia określonych funkcji.
Niezawodność jest jedną z nieodłącznych cech stanowiących o jakości obiektu
Niezawodność jako:
- prawdopodobieństwo spełnienia wymagań:
• Prawdopodobieństwo, że obiekt będzie sprawny w przedziale czasu (t1, t2) bądź (0, t).
• Prawdopodobieństwo, że wartości parametrów określających istotne własności obiektu nie przekroczą w ciągu okresu (t1, t2) dopuszczalnych granic w określonych warunkach życia obiektu
• Prawdopodobieństwo poprawnego wykonywania przez obiekt ustalonych zadań, które mają być realizowane w określonych warunkach i w określonym czasie
Chwile powstawania uszkodzeń, czasy napraw i okresy użytkowania mają charakter przypadkowy mogą być rozpatrywane jako zmienne losowe
- średnia długość okresów sprawności:
Obiekt może poddawać się naprawie po utracie sprawności stąd można mówić o okresach sprawności obiektu. Średnia długość okresów sprawności, poprawnego funkcjonowania, wartości wykonanej pracy, liczby wykonanych czynności, długości przebytej drogi ... może być miarą niezawodności obiektu. Średni czas do utraty sprawności.
2. WSKAZAĆ RÓŻNICE MIĘDZY DYSTRYBUANTĄ ZMIENNEJ LOSOWEJ
NIEZAWODNOŚCI A FUNKCJĄ ZAWODNOŚCI
Różnica między dystrybuantą zmiennej losowej niezawodności a funkcją zawodności .
Funkcja zawodności:
F ( t) = P( T < t) = 1 − R( t) t ≥ 0
T – zmienna losowa oznaczająca czas zdatności obiektów z pewnej populacji
Jeżeli dodatkowo F(t) spełnia warunek F(t)=0 dla t ≤ 0 to F(t) jest dystrybuantą zmiennej losowej T opisującej niezawodność obiektu.
Zakłada się, że funkcja F(t) jest ciągła dla t >0.
4. NA CZYM POLEGA REZERWOWANIE
Rezerwowanie polega na wprowadzeniu dodatkowych elementów do struktury pełniącej rolę elementu rezerwowego dla zwiększenia niezawodności działania systemu.
Rezerwa obciążona – gorąca
Odpowiada włączeniu do systemu równoległych elementów. Elementy te obciążone są od początku pracy systemu.
Dla 2-elementowego systemu czas zdatności:
T=max(T1,T2)
Niezawodność systemu z elementami rezerwowymi Ri
n
R t
( ) 1
1
[
R t
( )],
t
0
r
= −∏ − i
≥
i =1
Dla rozkładu wykładniczego
1
1
ET = 1
( +
+...+ ) ET
r
2
n
Rezerwa nieobciążona - zimna
Elementy rezerwowe nie pracują włączane są w momentach uszkodzeń. Zakłada się że własności niezawodnościowe rezerwy nie zmieniają się podczas eksploatacji.
Dla 2-elementowego systemu czas zdatności
T = T1 + T2
Dla rozkładu wykładniczego intensywność uszkodzeń maleje n-krotnie
λ
λ =
r
n
Rezerwa częściowo obciążona – ciepła
Własności niezawodnościowe elementu rezerwowego ulegają zmianie w okresie eksploatacji.
Czas zdatności zależy od stopnia zmniejszenia zdatności w chwili podmiany
T
T = T + 2
1
T 1
5. NA CZYM POLEGA FMECA
FMECA (Failure Mode Effects and Criticality Analysis) polega na oszacowaniu ryzyka i pojawienia się wad i błędów, ocenie ich znaczenia (konsekwencji) i możliwości wczesnego wykrywania i proponowaniu na tej podstawie rozwiązań preferencyjnych lub korygujących z uwzględnieniem krytyczności wad/błędów.
Metod polega na analitycznym ustaleniu związków przyczynowo – skutkowych powstania potencjalnych wad oraz uwzględnieniu w analizie czynnika krytyczności (ryzyka).
Identyfikacja potencjalnych uszkodzeń w systemie i klasyfikacja stopnia wpływu na funkcjonowanie.
I – określenie potencjalnych miejsc i rodzajów uszkodzeń i ich znaczenia dla działania systemu FMEA (Failure Mode Effects Analysis).
II – klasyfikacja i ocena zagrożeń powodowanych przez określone w I uszkodzenia.
Algorytm postępowania
- zdefiniowanie systemu będącego przedmiotem analizy,
- konstrukcja schematu zależności (blokowego),
- wskazanie miejsc i rodzajów możliwych uszkodzeń,
- przypisanie zagrożeń uszkodzeniom,
- ocena i klasyfikacja zagrożeń,
- raportowanie,
- formułowanie wniosków odnośnie zmiany projektu systemu i sposobów utrzymania w ruchu.
ZESTAW 2
1. PORÓWNAĆ WŁASNOŚCI STRUKTUR OBIEKTU
Struktura obiektu
Dla złożonych obiektów łatwiej jest analizować zagadnienia niezawodności gdy zostaną rozpatrzone jako obiekty składające się z elementów stanowiących strukturę
Struktura „k z n” (k/n) k/n
Dla obiektu składającego się z n elementów jest sprawny gdy co najmniej k jego elementów jest sprawne.
Struktura z redundancją k <n
Z nadmiarem można wyróżnić elementy, które przejmują zadania uszkodzonych.
Struktura szeregowa k=n (n/n) n/n
Najczęściej spotykana wypadkowa niezawodność Rn/n
Rn/n =Π Ri
Struktura równoległa k=1 (1/n) 1/n
R1/n =1- Π(1- Ri)
rezerwowanie
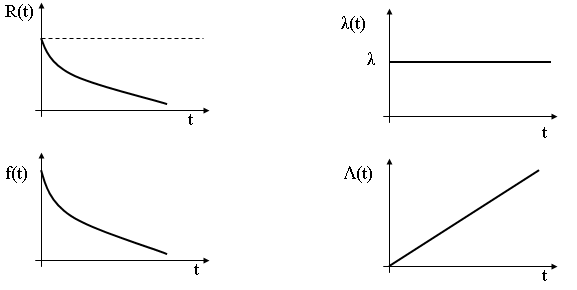
2. PRZEDSTAWIĆ WŁASNOŚCI ROZKŁADU WYKŁADNICZEGO
Opisuje czas zdatności obiektu, którego intensywność uszkodzeń jest stała niezależna od czasu
λ(t) = λ const
Są to obiekty, których własności nie zmieniają się podczas używania, nie starzeją się, nie ulegają zmęczeniu, nie korodują. Podlegają tylko przypadkowym uszkodzeniom, które uniemożliwiają dalsze działanie lub zmieniają ich własności, cechy.
Brak pamięci – nie uszkodzony obiekt jest tak samo zawodny jak obiekt nowy.
Własności rozkładu wykładniczego:
• Zmienna losowa jest zmienną ciągłą jednowymiarową,
• Niezawodność R(t) = exp(- λt),
• Zawodność F(t) = 1- exp(- λt),
• Gęstość
f(t) = λ exp(- λt),
• Skumulowana intensywność Λ(t) = λt,
• Oczekiwany czas zdatności ET = 1/ λ,
• Wariancja Var T = 1/ λ2,
• Entropia
H(T) = log2(e/ λ),
• Prawdopodobieństwo pozostawania w stanie zdatrności przez czas t po upływie czasu s poprawnej pracy jest iloczynem zdatności R(s) i R(t): R(s+t) = R(s) * R(t).
ROZKŁAD WYKŁADNICZY
3. NA CZYM POLEGA REZERWOWANIE
Rezerwowanie polega na wprowadzeniu dodatkowych elementów do struktury pełniącej rolę elementu rezerwowego dla zwiększenia niezawodności działania systemu.
Rezerwa obciążona – gorąca
Odpowiada włączeniu do systemu równoległych elementów. Elementy te obciążone są od początku pracy systemu.
Dla 2-elementowego systemu czas zdatności:
T=max(T1,T2)
Niezawodność systemu z elementami rezerwowymi Ri
n
R t
( ) 1
1
[
R t
( )],
t
0
r
= −∏ − i
≥
i =1
Dla rozkładu wykładniczego
1
1
ET = 1
( +
+...+ ) ET
r
2
n
Rezerwa nieobciążona - zimna
Elementy rezerwowe nie pracują włączane są w momentach uszkodzeń. Zakłada się że własności niezawodnościowe rezerwy nie zmieniają się podczas eksploatacji.
Dla 2-elementowego systemu czas zdatności
T = T1 + T2
Dla rozkładu wykładniczego intensywność uszkodzeń maleje n-krotnie
λ
λ =
r
n
Rezerwa częściowo obciążona – ciepła
Własności niezawodnościowe elementu rezerwowego ulegają zmianie w okresie eksploatacji.
Czas zdatności zależy od stopnia zmniejszenia zdatności w chwili podmiany
T
T = T + 2
1
T 1
4. CO TO JEST HIPOTEZA ZEROWA
Hipoteza zerowa (H0) – (Jest to hipoteza poddana procedurze weryfikacyjnej, w której zakładamy, że różnica między analizowanymi parametrami lub rozkładami wynosi zero.) Hipoteza formułowana na początku, a następnie sprawdzana testem zgodności np. że dana populacja ma rozkład wykładniczy.
Jest ona określana wraz z hipotezą alternatywną w pierwszym punkcie budowy testu istotności.
H0 odrzuca się dla liczonego poziomu istotności α (alfa), jeśli zn - obliczona wartość próby należy do obszary krytycznego, natomiast nie ma podstaw do odrzucenia H0 dla liczonego poziomu istotności α (alfa), jeśli zn leży poza obszarem krytycznym.
5. NA CZYM POLEGA FMECA
FMECA (Failure Mode Effects and Criticality Analysis) polega na oszacowaniu ryzyka i pojawienia się wad i błędów, ocenie ich znaczenia (konsekwencji) i możliwości wczesnego wykrywania i proponowaniu na tej podstawie rozwiązań preferencyjnych lub korygujących z uwzględnieniem krytyczności wad/błędów.
Metod polega na analitycznym ustaleniu związków przyczynowo – skutkowych powstania potencjalnych wad oraz uwzględnieniu w analizie czynnika krytyczności (ryzyka).
Identyfikacja potencjalnych uszkodzeń w systemie i klasyfikacja stopnia wpływu na funkcjonowanie.
I – określenie potencjalnych miejsc i rodzajów uszkodzeń i ich znaczenia dla działania systemu FMEA (Failure Mode Effects Analysis).
II – klasyfikacja i ocena zagrożeń powodowanych przez określone w I uszkodzenia.
Algorytm postępowania
- zdefiniowanie systemu będącego przedmiotem analizy,
- konstrukcja schematu zależności (blokowego),
- wskazanie miejsc i rodzajów możliwych uszkodzeń,
- przypisanie zagrożeń uszkodzeniom,
- ocena i klasyfikacja zagrożeń,
- raportowanie,
- formułowanie wniosków odnośnie zmiany projektu systemu i sposobów utrzymania w ruchu.
ZESTAW 3
1. OPISZ TEST ZGODNOŚCI χ2
Jeden z najstarszych testów zaproponowany przez K.Pearsona na początku XX wieku.
Statystyka służąca do budowy obszaru krytycznego ma graniczny rozkładu χ2.
Z populacji o dystrybuancie F(t) wybrano n-elementową próbę prostą n-kilkadziesiąt.
Wyniki grupowane po ni w r klasach. Otrzymano szereg wyników próby tzw. rozkład empiryczny.
„Sprawdzić zgodność rozkładu empirycznego z określonej postaci rozkładem teoretycznym.”
Inaczej zweryfikować hipotezę H0:F(t)=F0(t) wobec hipotezy H1:F(t)≠F0(t) gdzie F0(t) jest zadaną
hipotetyczną dystrybuantą
Tok postępowania:
1.Z rozkładu hipotetycznego wyznacza się dla każdej klasy prawdopodobieństwa p = P{ x ≤ X ≤ x } = F ( x ) − F( x ) i
0 i
i
1
0
i
1
0 i
dla
i = ,
1 ,
2 .. r
.
2.Dla każdej klasy wyznacza się liczebności teoretyczne npi , które powinny wystąpić w n-elementowej próbie, gdyby rozkład był zgodny z hipotezą H0
r
r
∑ np = n∑ p = n
i
i
i=1
i=1
3. Oblicza się wartość statystyki
2
(
)
2
χ
∑ r n np
i −
=
i
1
np
i=
i
Duże wartości statystyki świadczą przeciwko hipotezie zerowej
4. Buduje się obszar krytyczny oparty na rozkładzie granicznym χ2
2
2
2
Q = {χ : χ ≥ χ }
α
Gdz
χ i2αe jest odczytaną z tablicy rozkładu χ2 o r-1 stopniach swobody wartością krytyczną dla przyjętego poziomu istotności α tj
{χ 2
P
≥ χ 2
α } = α
5. Sprawdza się czy wartość statystyki leży w obszarze Q jeżeli tak hipotezę odrzuca się przeciwnie nie ma podstaw do odrzucenia hipotezy
2. WŁASNOŚCI ROZKŁADU NORMALNEGO (LAPLACE’A, GAUSSA)
Modeluje zjawiska eksploatacji zależne od wielu czynników jednocześnie, uszkodzenia powodowane są stopniowo zachodzącymi nieodwracalnymi zmianami np.. starzenie Własności rozkładu normalnego:
• Zmienna losowa jest zmienną ciągłą jednowymiarową przyjmującą dowolne wartości rzeczywiste z przedziału (-∞,+∞),
• Postać funkcji gęstości:
( t
2
−µ )
−
σ
( ) =
1
2
2
∈
f t
e
t
R
σ 2π
Rozkład normalny, co wynika z powyższego wzoru, jest określony przez 2 parametry : µ oraz σ, gdzie: µ=ET – wartość oczekiwana czasu zdatności, σ2=var
T – wariancja czasu zdatności,
• Zwykle korzysta się z tablic standaryzowanego rozkładu normalnego f0(t) (µ=0,σ =1).
Standa f ry
(−z
t)o
=w
f a
( t n
) y rozkład jest symetryczny:
0
0
1
t − µ
f t
( ) =
f
σ 0 σ
I f(t) można wyrazić:
• Funk1cj∞a nie( x z−aµw2
) odn
1 oś
c
t i
− :µ
R t
( ) =
∫
exp−
2
dx =
R
σ π
2
σ
2
σ 0 σ
t
Gdzie:
∞
1
x 2
R t()
0
=
∫exp− dx
2π
2
t
• Intensywność t −uµszkodzeń:
f
0
σ
λ( t) =
t − µ
σ R
0 σ
3. OPISZ DRZEWO USZKODZEŃ
Drzewo uszkodzeń
Drzewo uszkodzeń
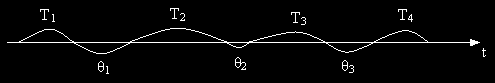
Działania:
1) Określenie granicznych warunków działania systemu.
2) Analiza stanów pracy, które mogą doprowadzić do niebezpiecznego działania systemu.
3) Określenie zdarzeń do określenia relacji.
4) Rysowanie drzewa – budowane jest od góry.
Drzewo
-porażenie pierwotne,
-porażenie wtórne,
-porażenie inicjowane.
Analiza za pomocą drzewa uszkodzeń jest techniką analizy niezawodności. Drzewa awarii mogą być pomocne w szczegółowym określeniu
ciągu zdarzeń, normalnych i dotyczących awarii, które prowadzą do analizowanej awarii lub niepożądanego
zdarzenia na poziomie elementu (analiza „od góry do dołu”). Niezawodność jest obliczana przez konwersję
pełnego drzewa uszkodzeń na odpowiedni układ równań. Można to zrobić, wykorzystując algebrę zdarzeń nazywaną również algebrą Boolowską. Podobnie jak w przypadku analizy FMEA, dane dotyczące prawdopodobieństwa potrzebne do obliczeń mogą być trudne do uzyskania.
4. CO TO JEST STRUMIEŃ ODNOWY.
Strumień odnowy
Odnowa polega na naprawie, przywróceniu własności, wymianie na nowy obiekt, regulacji i kalibracji.
Przedziały czasowe zdatności Ti i niezdatności θi – odnowy (naprawy) są realizacjami zmiennych losowych: T1, θ1 ,T2, θ2 ,T3, θ3 ,T4, ... Ti ....
Proces odnowy natychmiastowy z zerowym czasem odnowy:
Proces odnowy rzeczywisty alternatywny:
Można również określić strumień odnowy natychmiastowy przez ciąg sum zmiennych losowych
Sn = T1 + T2 + T3 + T4 +...+ Tn dla n=1,2,3...
Analogicznie dla rzeczywistego alternatywnego strumienia odnowy
θ(n)=(T1+θ1)+(T2+θ2)+...+(Tn+θn)
Alternatywny strumień odnowy – czasy między odnowami
Alternatywny strumień uszkodzeń – czasy między uszkodzeniami (strumień złożony)
5. FUNKCJA ZAWODNOŚCI
Zawodność obiektu nieodnawialnego jest prawdopodobieństwem zdarzenia przeciwnego określana jest przez funkcję F( T ) = P( T < t) = 1− R( t) , gdzie t ≥ 0
T – zmienna losowa oznaczająca czas zdatności obiektów z pewnej populacji charakteryzuje dwustanowy proces stochastyczny – model niezawodności obiektu.
Prawdopodobieństwo uszkodzenia się obiektu do chwili t
Przedział czasu (0 – t) czas zdatności, lub trwałość obiektu.
Jeżeli dodatkowo F(t) spełnia warunek F(t)=0 dla t <= 0 to
F(t) jest dystrybuantą zmiennej losowej T opisującej niezawodność obiektu.
Zakłada się że funkcja F(t) jest ciągła dla t >0.
Dopuszcza się nieciągłość w t=0 wtedy R0 =1 określaną jako wadliwość początkową dla obiektów które rozpoczynając pracę ulegają awarii.
Niezawodność początkowa R(0) = P(T=0) prawdopodobieństwo przejścia w stan niezdatności w chwili t=0
Zawodność początkowa.
ZESTAW 4
1. WYMIENIĆ LICZBOWE WSKAŹNIKI NIEZAWODNOŚCI.
Liczbowe wskaźniki niezawodności:
Pierwszy moment - wartość oczekiwana:
∞
ET = ∫ R( t) dt
0
oczekiwany czas do uszkodzenia.
Warian2cja: 2 ∞
∞
Var T = ET − ( ET ) = 2∫ t ⋅ R( t) dt − (∫
2
R( t) dt)
0
0
Entropia:
H ( t) = [
E log f ( T )]
2
Mediana: jest to wartość (zmiennej losowej T) czasu zdatności, dla której R(t)=1/2.
Moda: wartość zmiennej losowej, dla której funkcja gęstości osiąga największą wartość.
Kwanty: rzędu p zmiennej losowej T jest to wartość spełniająca równanie: R(t)=p (forma tego równania – nie wiem, czy jest poprawna).
2. SCHARAKTERYZOWAĆ SPOSOBY ZWIĘKSZENIA NIEZAWODNOŚCI.
Rezerwowanie dla zwiększenia niezawodności działania systemu wprowadza się dodatkowy element do struktury pełniącej rolę elementu rezerwowego. (WIĘCEJ W PUNKCIE 1.4) 3. CZYM RÓŻNIĄ SIĘ METODY WNIOSKOWANIA PARAMETRYCZNEGO I
NIEPARAMETRYCZNEGO
Wnioskowanie parametryczne:
Warunkiem stosowania jest znajomość rozkładu prawdopodobieństwa badanej cechy populacji (dystrybuanty F(t)).
Weryfikacja hipotez statystycznych co do wartości parametrów rozkładu cechy T
Estymacja nieznanych parametrów cechy T badanej populacji (statystyk populacji) Rozróżnić można metody
- graficzne - siatki funkcyjne,
- analityczne
Metody nieparametryczne
Testy nieparametryczne stosowane:
– Rozmiar próby duży,
– Próba prosta (losowanie niezależne),
– Poziom ufności nie mniejszy od 0,01
Polega na badaniu zgodności uzyskanego w próbie rozkładu z rozkładem hipotetycznym określonym w weryfikowanej hipotezie H0.
Ważne jest sprawdzenie czy próba jest losowa. Przeprowadza się testy losowości.
4. PODAĆ PRZYKŁAD GENERATORA LOSOWEGO.
Generatorami losowymi nazywamy urządzenia lub programy, które podają na swoje wyjście ciąg liczb losowych, np. czarna skrzynka generująca liczby losowe.
Przykłady:
• Π (3,1415926535), e – ciągi liczb mają bardzo dobre właściwości,
• LCG – liniowy generator losowy: np. mieszanyx+1=(axn+b)modM-(231-1,16807,0,x0),
• Generatory oparte na rejestrach przesuwanych:
• bi=(ai bi-1+…+ ak bi-1)mod2,
• Fibonacciego: xn =(xn-r + xn-s)modM,
• Generatory nieliniowe:
ICG: xn+1=(ax-1+bx)modM.
Zastosowanie generatorów losowych:
1. przygotowanie reprezentatywnej próbki populacji
2. zadania numeryczne (np. rozwiązywanie równań różniczkowych) 3. symulacja i modelowanie zjawisk
4. kryptografia
5. telekomunikacja.
ZESTAW 5
1. PRZYKŁADY ROZKŁADÓW SŁUŻĄCYCH DO MODELOWANIA WŁASNOŚCI
OBIEKTÓW
ROZKŁADY
Najczęściej stosowane rozkłady do modelowania niezawodności obiektów
• WYKŁADNICZY – modelowanie uszkodzeń nagłych, modelowanie obciążenia i
wytrzymałości, modelowanie struktur niezawodnościowych progowych,
• WEIBULLA – modelowanie uszkodzeń stopniowych, modelowanie problemów
wytrzymałości, zwłaszcza wytrzymałości zmęczeniowej, modelowanie struktur
niezawodnościowych szeregowych i szeregowo-równoległych,
• NORMALNY – modelowanie obciążeń statycznych i problemów wytrzymałości
modelowanie struktur niezawodnościowych szeregowych,
• LOGNORMALNY – modelowanie zużycia tribologicznego, modelowanie problemów
wytrzymałości i obciążenia,
• GUMBELA – modelowanie uszkodzeń katastroficznych, zużycia zmęczeniowego,
modelowanie struktur niezawodnościowych szeregowych i szeregowo-równoległych,
• FRECHETA – modelowanie zużycia korozyjnego, uszkodzeń katastroficznych, obciążenia, modelowanie struktur niezawodnościowych równoległych,
• RAYLEIGHA – modelowanie problemów obciążeń,
• GAMMA – modelowanie problemów wytrzymałości,
• RÓWNOMIERNY – problemów eksploatacji,
• PODWÓJNIE WYKŁADNICZY – modelowanie uszkodzeń wywoływanych przez pitting i skojarzone procesy erozyjno-korozyjne
2. HIPOTEZA ZEROWA
Hipoteza zerowa (H0) – (Jest to hipoteza poddana procedurze weryfikacyjnej, w której zakładamy, że różnica między analizowanymi parametrami lub rozkładami wynosi zero.) Hipoteza formułowana na początku, a następnie sprawdzana testem zgodności np. że dana populacja ma rozkład wykładniczy.
Jest ona określana wraz z hipotezą alternatywną w pierwszym punkcie budowy testu istotności.
H0 odrzuca się dla liczonego poziomu istotności α (alfa), jeśli zn - obliczona wartość próby należy do obszary krytycznego, natomiast nie ma podstaw do odrzucenia H0 dla liczonego poziomu istotności α (alfa), jeśli zn leży poza obszarem krytycznym.
3. W JAKI SPOSÓB GENERUJE SIĘ ZMIENNE LOSOWE O ROZKŁADZIE
LOSOWYM Z UŻYCIEM GENERATORA O ROZKŁADZIE RÓWNOMIERNYM.
Odwracanie dystrybuanty. (Jeżeli funkcja posiada taką odwrotną funkcję, zaproponować nową zmienna losową, która zostanie potraktowana tą odwrotną)
Rozkład równomierny
X=F-1(R) F(R)- dystrybuanta
Wystarczy znaleźć funkcje odwrotną i według niej zrobić zmienne, które będą miały zadany rozkład.
Rozkład wykładniczy: F(x)=1-e-x
F-1(n)=-ln(1-r) (obliczając tę funkcję dostajemy dane o rozkładzie)
4. W JAKI SPOSÓB GENERUJE SIĘ ZMIENNE LOSOWE O ROZKŁADZIE
LOSOWYM Z UŻYCIEM GENERATORA O ROZKŁADZIE NIERÓWNOMIERNYM
W jaki sposób generuje się zmienne losowe o rozkładzie nierównomiernym:
R – zmienna losowa o rozkładzie nierównomiernym (0,1)
F – dystrybuanta
Definiuje się: x=F-1(R)
P[x ≤ X]=P{ F-1(R) ≤ x}=P{R ≤ F(x)}
F(x)=1-e-x
F-1(x)=-ln(1-n)=x
5. NA CZYM POLEGA REZERWOWANIE
Rezerwowanie polega na wprowadzeniu dodatkowych elementów do struktury pełniącej rolę elementu rezerwowego dla zwiększenia niezawodności działania systemu.
Rezerwa obciążona – gorąca
Odpowiada włączeniu do systemu równoległych elementów. Elementy te obciążone są od początku pracy systemu.
Dla 2-elementowego systemu czas zdatności:
T=max(T1,T2)
Niezawodność systemu z elementami rezerwowymi Ri
n
R t
( ) 1
1
[
R t
( )],
t
0
r
= −∏ − i
≥
i =1
Dla rozkładu wykładniczego
1
1
ET = 1
( +
+...+ ) ET
r
2
n
Rezerwa nieobciążona - zimna
Elementy rezerwowe nie pracują włączane są w momentach uszkodzeń. Zakłada się że własności niezawodnościowe rezerwy nie zmieniają się podczas eksploatacji.
Dla 2-elementowego systemu czas zdatności
T = T1 + T2
Dla rozkładu wykładniczego intensywność uszkodzeń maleje n-krotnie
λ
λ =
r
n
Rezerwa częściowo obciążona – ciepła
Własności niezawodnościowe elementu rezerwowego ulegają zmianie w okresie eksploatacji.
Czas zdatności zależy od stopnia zmniejszenia zdatności w chwili podmiany
T
T = T + 2
1
T 1
ZESTAW 6
1. OKREŚLIĆ FUNKCJĘ RYZYKA
Funkcja ryzyka - Zależność określająca zdolność do spełniania wymagań
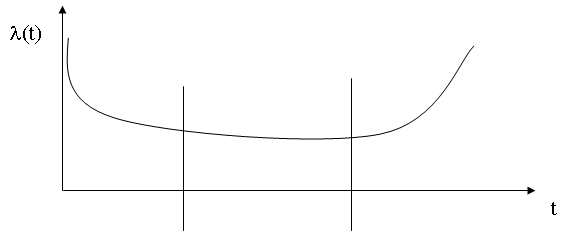
λ(t) – prawdopodobieństwo niespełnienia wymagań w chwili (t+dt), ryzyko, intensywność ubywania lub intensywność uszkodzeń
Funkcja λ - funkcja intensywności, wartość λ(t) – intensywność
Gdy wartość λ(t) maleje własności niezawodnościowe polepszają się
Najczęściej spotykany przebieg λ(t) to przebieg typu U (wannowy)
2. OKREŚL STRUMIEŃ ODNOWY
Strumień odnowy
Odnowa polega na naprawie, przywróceniu własności, wymianie na nowy obiekt, regulacji i kalibracji.
Przedziały czasowe zdatności Ti i niezdatności θi – odnowy (naprawy) są realizacjami zmiennych losowych: T1, θ1 ,T2, θ2 ,T3, θ3 ,T4, ... Ti ....
Proces odnowy natychmiastowy z zerowym czasem odnowy:
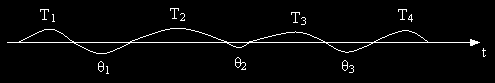
Proces odnowy rzeczywisty alternatywny:
Można również określić strumień odnowy natychmiastowy przez ciąg sum zmiennych losowych
Sn = T1 + T2 + T3 + T4 +...+ Tn dla n=1,2,3...
Analogicznie dla rzeczywistego alternatywnego strumienia odnowy
θ(n)=(T1+θ1)+(T2+θ2)+...+(Tn+θn)
Alternatywny strumień odnowy – czasy między odnowami
Alternatywny strumień uszkodzeń – czasy między uszkodzeniami (strumień złożony)
3. SPOSÓB PRZEPROWADZANIA TESTÓW ZGODNOŚCI
Polega na badaniu zgodności uzyskanego w próbie rozkładu z rozkładem hipotetycznym określonym w weryfikowanej hipotezie H0 Ważne jest sprawdzenie czy próba jest losowa.
Przeprowadza się testy losowości.
Dla przeprowadzenia weryfikacji próbę dzieli się na 2 części
1-sza do obliczenia statystyki
2-ga do sprawdzenia hipotezy
Przebieg:
1. Określenie hipotezy zerowej H0 i hipotezy alternatywnej H1,
2. Przyjęcie poziomu istotności (alfa) im wyższy poziom istotności tym większa szansa odrzucenia hipotezy (alfa=0,1; 0,05; 0,001)
3. Wylosowanie n-elementowej próby i wyznaczenie statystyki Zn, której rozkład jest znany przy założeniu prawdziwości hipotezy zerowej.
4. Wybór obszaru krytycznego w zależności od hipotezy alternatywnej.
5. Obliczenie z próby wartości zn statystyki Zn i sprawdzenie czy należy do obszaru krytycznego.
4.
5. CECHY KOMPUTEROWEGO OPROGRAMOWANIA W WSPOMAGANIU
CECHY FMECA (Failure Mode Effects and Criticality Analysis):
• Ciągłe rozwijanie od lat 60. i zastosowanie w coraz to nowszych dziedzinach;
• Możliwe wykorzystanie do procesów bardzo złożonych zarówno w produkcji masowej jak i jednostkowej;
• Posiada miary oceny, które między innymi biorą pod uwagą znaczenie wady dla klienta;
• Można stosować w różnych fazach powstania:
o -Koncepcji produktu,
o -Przed wdrożeniem do produkcji,
o -W czasie wdrażania produktu na skalę masową,
o -Produkcji,
o -Eksploatacji;
• Możliwe zastosowanie dla:
o -Całego wyrobu,
o -Pojedynczego podzespołu lub elementu
o konstrukcyjnego,
o -Całego procesu technologicznego,
o -Jego dowolnej operacji.
FUNKCJA NIEZAWODNOŚCI
Niezawodność obiektu nieodnawialnego określana jest przez funkcję
R( t) = P( T ≥ t)
t ≥ 0
T – zmienna losowa oznaczająca czas zdatności obiektów z pewnej populacji charakteryzuje dwustanowy proces stochastyczny – model niezawodności obiektu
Prawdopodobieństwo nie uszkodzenia się obiektu co najmniej do chwili t
Przedział czasu (0 – t) czas zdatności, lub trwałość obiektu.
Jeżeli funkcja niezawodności jest ciągła to można przedstawić ją w postaci:
F( t) = P( T < t) =1− R( t) t ≥ 0
∞
R t
( ) = ∫ f ( x) dx
t ≥ 0
t
EMPIRYCZNA FUNKCJA NIEZAWODNOŚCI
n( t)
n − m t
( )
m( t)
R t
( ) =
=
= 1−
n
n
n
Funkcja niezawodności w rozkładzie Weibulla
−
α
λ( t− t )
0
R( t) = e
t ≥ t
0