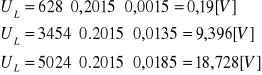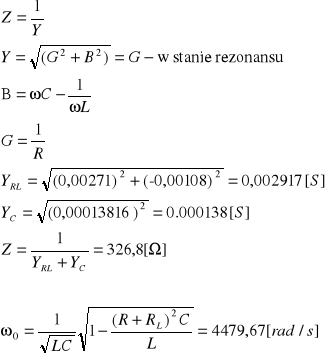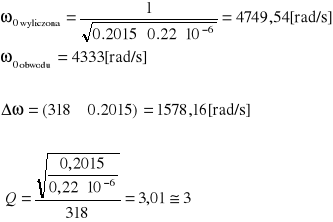Wiadomości ogólne.

Celem ćwiczenia jest zbadanie własności szeregowego i równoległego obwodu rezonansowego złożonego z elementów rzeczywistych R,L,C i wyznaczenie charakterystyk częstotliwościowych napięć i prądów.

Stan obwodu R,L,C zasilanego przebiegiem sinusoidalnym , przy którym pulsacja zasilania jest równa pulsacji drgań swobodnych obwodu nosi nazwę rezonansu, a pulsacja ω pulsacji rezonansowej.

W obwodzie R,L,C zjawisko rezonansu może być wywołane przy stałych parametrach R,L,C poprzez zmianę częstotliwości zasilania lub poprzez zmianę wartości elementów R,L,C.

W zależności od sposobu połączenia elementów R,L,C w obwodzie może wystąpić zjawisko rezonansu napięć (rezonans szeregowy ) lub zjawisko rezonansu prądów (rezonans równoległy).

POMIARY

A. Wyznaczanie charakterystyk częstotliwościowych w układzie zeregowym RLC

Schemat pomiarowy:

Oznaczenia :

G - generator napięcia zmiennego o regulowanej częstotliwości

R1 - opornik dekadowy

L,R - cewka powietrzna o indukcyjności L i rezystancji R

3. kondensator o pojemności C

V- woltomierze cyfrowe

1. amperomierz magnetoelektryczny

U=	8	R1=	200	L=	0,2015	R=	118	C=	2,2E-07
	z pomiaru					z obliczeń
Lp.	f	omega	I	Url	Uc	Ul	Ur	Z	fi
	Hz	rad/s	mA	V	V	V	V	Om	deg
1	100	628	1,5	0,25	8	0,190	0,177	7118,55	-87,44
2	200	1256	2,75	0,75	8,5	0,696	0,325	3380,90	-84,60
3	300	1884	4,5	1,75	9,5	1,708	0,531	2057,76	-81,11
4	400	2512	7	7	11	3,543	0,826	1341,56	-76,29
5	550	3454	13,5	9,5	16,75	9,396	1,593	696,81	-62,85
6	600	3768	16,5	13	18	12,528	1,947	548,64	-54,58
7	650	4082	20	18	20	16,450	2,360	431,06	-42,46
8	690	4333	24,5	19,5	21,5	21,392	2,891	363,38	-28,94
9	750	4710	21	20,5	18,2	19,930	2,478	318,40	-2,88
10	800	5024	18,5	19,4	15	18,728	2,183	335,71	18,69
11	900	5652	14	15,5	10	15,944	1,652	461,65	46,46
12	1000	6280	10,5	13,5	6,8	13,287	1,239	628,07	59,58
13	1200	7536	7	9,2	2,95	10,630	0,826	969,00	70,84
14	1500	9420	5	9	1,9	9,491	0,590	1450,88	77,34
15	1600	10048	4,7	8,9	1,75	9,516	0,555	1604,13	78,57
pulsacja rez.[rad/s]			4749,54
szer. pasma przep.			1578,16
Q			3,01

W obliczeniach skorzystałem z następujących wzorów.

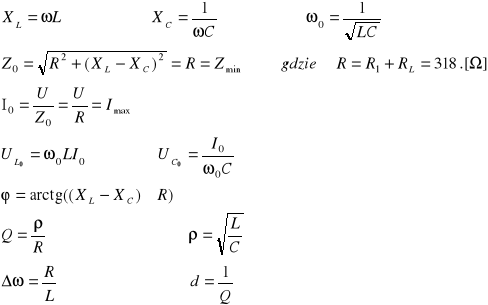
Obliczenia na wartościach:

Wszystkie obliczenia przeprowadziłem dla pulsacji z punktów 1, 5, 10 w tabeli A.

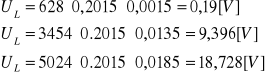
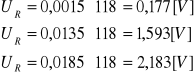
Porównuję wartości pulsacji i szerokość pasma przepustowego wyznaczoną na podstawie pomiarów i wartości elementów obwodu.

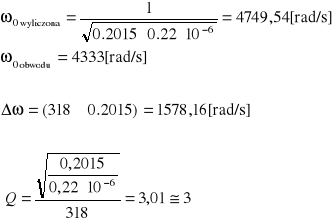
W momencie rezonansu wartość prądu jest maksymalna impedancja osiąga wartość minimalną a kąt fazowy φ osiąga wartość zero. Na podstawie tych wykresów można z dużym przybliżeniem określić wartość pulsacji rezonansowej. Wartość ta dla danych odczytanych z wykresów wynosi 4772 [rad/s], wartość pulsacji wyznaczona na podstawie pomiarów wynosi 4333 [rad/s] a na podstawie wartości elementów wynosi 4749 [rad/s].
Ewentualne rozbieżności wynikają stąd iż wzory te są prawdziwe jedynie dla idealnych elementów R,L,C.

Trudno jest także na podstawie takich pomiarów jakich dokonaliśmy na pracowni określić te wartości z dużą dokładnością, a ponadto podczas przeprowadzania pomiarów wyraźnie był widoczny wpływ przyrządów pomiarowych na badany układ (szczególnie dobrze jest ot widoczne na wykresach przedstawiających charakterystyki częstotliwościowe w funkcji prądu). Dlatego mogliśmy jedynie określić wartości przybliżone. Pomimo tego różnice pomiędzy wartościami obliczonymi a zmierzonymi są niewielkie.

B. Wyznaczanie charakterystyk częstotliwościowych w układzie równoległym RLC

Schemat pomiarowy:

Oznaczenia :

G - generator napięcia zmiennego o regulowanej częstotliwości

R1 - opornik dekadowy

L,R - cewka powietrzna o indukcyjności L i rezystancji R

4. kondensator o pojemności C

V- woltomierze cyfrowe

2. amperomierz magnetoelektryczny

	U=8	R1=200	L=0,2015	R=118	C=2,2E-7
Lp.	f	omega	I	I1	I2	Z
		Hz	rad/s	mA	mA	mA	om
1	100	628	22	22,5	1,25	326,80
2	200	1256	17	18,25	2,5	365,38
3	300	1884	12,5	15	3,5	410,88
4	400	2512	8,6	12	4,5	449,33
5	550	3454	4,6	9,5	6,5	483,85
6	600	3768	3,7	8,75	7	489,29
7	650	4082	3	8	7,5	492,12
8	700	4396	2,7	8	8,25	492,69
9	750	4710	2,8	7,25	8,75	491,33
10	800	5024	3,4	5,7	9,5	488,35
11	900	5652	4,9	6	10,5	478,66
12	1000	6280	6,4	5,5	11,75	465,54
13	1200	7536	9,5	4,5	14	434,31
14	1500	9420	13,5	3,75	17,75	385,80
15	1600	10048	15	3,5	19	370,58
pulsacja rez.[rad/s]			4479,67

Przykładowe obliczenia :

W stanie rezonansu wartość impedancji jest największa co można zauważyć na załączonym wykresie.

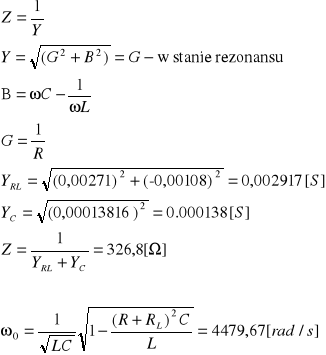
Pulsacja otrzymana na drodze pomiarowej (minimalna wartość prądu I i minimalna wartość admitancji (maksymalna impedancji) ) wynosi 4396 [rad/s], wartość pulsacji wyznaczona na podstawie wartości elementów wynosi 4479,6 [rad/s].

Jak widać istnieje pewna rozbieżność wyników. Pulsacja rezonansowa obliczona na podstawie podanego wyżej wzoru jest większa niż pulsacja wyznaczona przez nas na podstawie pomiarów. Rozbieżności te spowodowane są tym, że podane wyżej wzory są prawdziwe dla idealnych elementów RLC, ponadto różnice powiększać może niedokładność pomiarów, oraz niezbyt dobrą precyzją urządzeń pomiarowych. Podobnie tak jak w poprzednim układzie wyraźnie jest widoczny wpływ mierników na rozpływ prądów w obwodzie. Szczególnie dobrze jest to widoczne na wykresie przedstawiającym charakterystyki prądowe. Dla prądu I1 w gałęzi zawierającej amperomierz A1 przy prądzie około 8 mA musieliśmy zmienić zakres aby móc prowadzić pomiary. W wyniku tego zmalała impedancja obwodu co na wykresie obserwujemy jako skok prądu w okolicy częstotliwości 650 Hz.

Wnioski

Ponieważ różna jest inpedancja wewnętrzna mierników na poszczególnych zakresach pomiarowych. Chcąc uniknąć przynajmniej częściowo rozbieżności pomiędzy wynikami pomiaru a wartościami obliczonymi, w rozważaniach teoretycznych należałoby uwzględnić impedancję dołączonych mierników, lub użyć woltomierzy o odpowiednio dużej rezystancji wewnętrznej (10-20 M i amperomierzy o odpowiednio małej rezystancji aby zminimalizować ich wpływ na badany obwód.

---
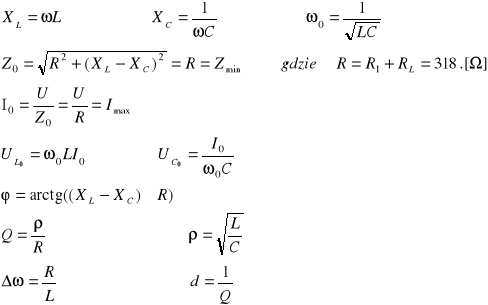
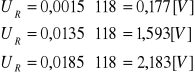