Sprawozdanie z ćwiczenia B-12.

Kołodziejski Zbigniew	Zespół 7
Wydział Elektryczny A i R	Ocena z przygotowania:
4 .01.1996	Ocena za sprawozdanie:
Czwartek 11.15-14.00	Zaliczenie:
Prowadzący :Dr Jaworski	Podpis:

Badanie właściwości statystycznych elektronów

emitowanych z katody lampy próżniowej.

Podstawy fizyczne:

Dla gazu doskonałego ( gdzie można zaniedbać rozmiary cząsteczek oraz ich wzajemne oddziaływanie) można stosować zasady statystycznego rozkładu Maxwella. W myśl tych zasad możemy napisać dwie funkcje rozkładu względnej liczby cząsteczek według posiadanej przez nie energii:

prędkości:

gdzie:

N - liczba wszystkich cząsteczek

n- liczba cząsteczek posiadających daną energię lub prędkość

k - stała Boltzmana

m - masa cząsteczki

Jako przykład gazu doskonałego możemy traktować elektrony emitowane z katody lampy próżniowej. Przesłanką upoważniającą do takiego podejścia jest między innymi fakt, że koncentracja elektronów, które opuściły metal jest o 10 - 15 rzędów niniejsza niż elektronów w metalu, co pozwala na zaniedbanie oddziaływań między nimi.

W lampie próżniowej zachodzi zjawisko termoemisji czyli wysyłania elektronów pod wpływem nagrzania metalu. W wysokich temperaturach elektrony znajdujące się na wyższych poziomach energetycznych mogą pokonać siły wiążące je z metalem i wydostać się poza barierę potencjału na zewnątrz. Temperaturę katody można regulować poprzez zmianę natężenia prądu żarzenia.

Wykonanie ćwiczenia:

W celu zbadania zależności ilości elektronów docierających do anody lampy próżniowej od temperatury zbudowaliśmy następujący układ:

Badania przeprowadziliśmy dla 3 prądów żarzenia, czyli dla 3 temperatur katody. Sprawdzaliśmy zależność natężenia prądu anodowego od przyłożonego napięcia hamowania. Na prąd anodowy składa się ilość elektronów jaka dociera do anody. Jeśli przyjmiemy, że elektrony termiczne spełniają rozkład Maxwella, to zależność między prądem anodowym a napięciem anodowym można zapisać:

Logarytmując stronami otrzymamy:

gdzie:

e - ładunek elektronu =

k - stała Boltzmanna =

Iao - prąd bez napięcia hamowania.

Zauważamy, że wykres zależności ln(Ia/Iao) od Ua, jest linią prostą, której współczynnik kierunkowy wynosi:

a =

Przekształcając otrzymujemy temperaturę żarzenia katody:

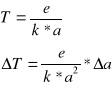
Uak [V]	n	I a[mA] Iż=0,6[A]	ln(Ia/Iao) Iż=0,6[A]
0	0	59	0
-0,02	10	55,1	-0,16
-0,04	20	47	-0,32
-0,056	30	40,2	-0,48
-0,073	40	34,5	-0,63
-0,09	50	29,5	-0,79
-0,1	60	25,5	-0,94
-0,12	70	22	-1,08
-0,14	80	18,5	-1,26
-0,15	90	16	-1,40
-0,168	100	14	-1,54
-0,18	110	12	-1.69
-0,2	120	10	-1.87
-0,21	130	8,5	-2.03
-0,23	140	7,3	-2.18
-0,25	150	6,1	-2.37
-0,26	160	5,4	-2.49
-0,28	170	4,8	-2.61
-0,29	180	4	-2.79
-0,3	190	3,1	-3.04
-0,32	200	2,4	-3.30
-0,34	210	1,9	-3.53
-0,35	220	1,4	-3,84
-0,37	230	1,1	-4,02
-0,39	240	0,9	- 4,14
-0,42	250	0,7	- 4,28
-0,43	260	0,5	- 4,37
-0,46	270	0,4	- 4,48
-0,48	280	0,2	- 4,59
-0,49	290	0,1	- 4,64
-0,51	300	0,08	- 4,78

Pomiary umieszczone w tabeli są częścia pomiarów.

Współczynnik a	Temperatura	I żarzenia
10,04 0,29	(1146 09)K	0,6A

Opracowanie błędów:

Dokonane przez nas obliczenia temperatury żarzenia katody są obarczone błędem, który wynika z:

- niedokładności przyrządów pomiarowych;

- z założenia, że emitowane elektrony zachowują się jak gaz doskonały.

Współczynnik kierunkowy a oraz ich błędy zostały wyznaczone metodą najmniejszych kwadratów. Obliczyliśmy go stosując wzory:

średnie odchylenia standardowe obliczyliśmy :

gdzie:

Mając a i średnie odchylenie standardowe obliczyliśmy metodą różniczki zupełnej błąd z jakim została wyznaczona temperatura:

Wnioski:

Zbadaliśmy zależność prądu anodowego od napięcia hamującego,. Stwierdziliśmy, że wartość prądu anodowego (Ia) maleje wraz ze wzrostem napięcia hamującego (Ua). Ponieważ wartość Ia zależy od ilości elektronów docierających do anody wnioskujemy, że elektrony emitowane z katody mają różne energie ,także prędkości. Rozkład ich energii (prędkości jest zgodny z teoretycznym rozkładem Maxwella. Pozwala to na obliczenie temperatury żarzenia katody, co przedstawia tabela.

Uzyskane przez nas wyniki są obarczone stosunkowo dużym błędem ,ponieważ używane przyrządy nie odpowiadały wymogom co do dokładności. Przy pomiarach wielkości rzędu mikrojednostek przewody pomiarowe powinny być ekranowane równierz mikroamperomierz musi być osłonięty aluminiowym ekranem.

---