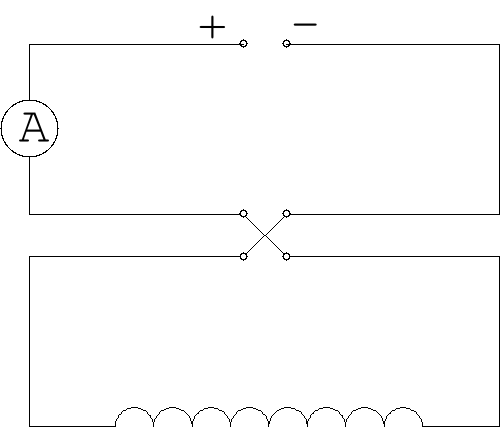
rys1. Schemat układu pomiarowego:
a - obwód pomiaru napięcia Halla,
b - obwód zasilania halotronu,
k1,k2 - styczniki,
B - bateria,
P - potencjometr,
Sprawozdanie z ćwiczenia B-11
Wydział |
Czwartek 1115-1400 |
Nr zespołu |
|||
Elektryczny |
1996.11.21 |
20 |
|||
1.Marcin Domański |
Ocena z |
Ocena z |
Ocena |
||
|
przygot. |
sprawozd. |
|
||
2.Marcin Szulc |
|
|
|
||
|
|
|
|
||
Prowadzący: |
Podpis |
||||
E. Szerewicz |
prowadzącego |
||||
Temat: Badanie efektu Halla.
Cel ćwiczenia:
Celem ćwiczenia jest zapoznanie się z efektem Halla, poznanie budowy i zasady działania halotronu oraz pomiar zależności napięcia Halla UH od natężenia prądu sterującego IS i od indukcji B pola magnetycznego, w którym znajduje się badana próbka.
1. Podstawy fizyczne
Ładunek elektryczny poruszający się w polu magnetycznym o indukcji z prędkością jest pod działaniem siły Lorentza
Halotron jest to cienka (grubość d * 0,1 mm) warstwa półprzewodnika na nieprzewodzącym podłożu i posiadająca cztery elektrody. Prąd sterujący halotronu przepływa wzdłuż warstwy półprzewodnika o długości l, a tym samym przez przekrój db, gdzie b jest szerokością naparowanej warstwy.
Nośnikami prądu w halotronie mogą być dziury lub elektrony, działa na nie siła Lorentza skierowana prostopadle do kierunku przepływu prądu sterującego i do indukcji magnetycznej. Siła ta powoduje zakłócenie ruchu nośników wzdłuż linii sił pola elektrycznego przyłożonego do halotronu, wynikiem tego jest gromadzenie się ładunków na powierzchni bocznego przekroju warstwy w kierunku działającej siły. Dzieje się tak, aż do momentu, gdy pole elektryczne nie skompensuje siły Lorentza. Obecność zgromadzonych nośników można wykryć mierząc różnicę potencjałów UH, między bocznymi powierzchniami półprzewodnika
gdzie:
b - szerokość warstwy półprzewodnika,
B - indukcja pola magnetycznego, w którym znajduje się badana próbka v - prędkość nośników prądu w kierunku wytworzonego w próbce pola elektrycznego,
tzw. prędkość dryftowa, która jest równa połowie przyrostu prędkości uzyskanej między
zderzeniami nośników, prędkość ta jest wprost proporcjonalna do natężenia pola
elektrycznego w próbce:
gdzie:
- prędkość dryftowa [m/s],
- natężenie pola [V/m],
μ - ruchliwość [m2/Vs],
Prędkość nośników jest tym większa im większe jest natężenie prądu sterującego płynącego przez halotron i im mniejsza jest koncentracja nośników prądu w półprzewodniku:
gdzie:
Is - natężenie prądu sterującego,
n - koncentracja nośników,
e - ładunek nośnika prądu,
d - grubość warstwy półprzewodnika,
Wykorzystując prędkość w podanym wzorze i podstawiając ją do wzoru na napięcie Halla, otrzymujemy:
Natomiast wykorzystując prawo Ohma i definicję natężenia prądu otrzymamy:
gdzie:
U - spadek napięcia wzdłuż halotronu,
U/l - natężenie pola elektrycznego,
Z podanych wyżej wzorów możemy wyznaczyć koncentrację nośników i ruchliwość:
Iloczyn koncentracji i ruchliwości jest odwrotnie proporcjonalny do rezystancji warstwy półprzewodnika:
Wykonanie ćwiczenia
Dane do ćwiczenia:
grubość halotronu d=(100±1)μm
szerokość b=(2,5±0,1)mm
długość l=(10,0±0,1)mm
maksymalna wartość prądu sterowania próbki 15mA
maksymalna wartość prądu elektromagnesu 3A
wyznaczenie napięcia Halla przy stałym polu magnetycznym
Pomiarów dokonano przy polu magnetycznym o indukcji B=1,44*10-1T
Is[mA] |
UH[V] |
Is[mA] |
UH[V] |
Is[mA] |
UH[V] |
Is[mA] |
UH[V] |
Is[mA] |
UH[V] |
|
-0,31 |
|
+0,27 |
|
-0,17 |
|
+0,11 |
|
-0,02 |
12,5 |
+0,31 |
10,5 |
-0,26 |
7,5 |
+0,18 |
5 |
-0,12 |
2 |
+0,02 |
|
-0,30 |
|
+0,26 |
|
-0,17 |
|
+0,12 |
|
-0,02 |
|
+0,31 |
|
-0,26 |
|
+0,18 |
|
-0,13 |
|
+0,02 |
Montujemy układ pomiarowy jak na rysunku 1.
rys1. Schemat układu pomiarowego:
a - obwód pomiaru napięcia Halla,
b - obwód zasilania halotronu,
k1,k2 - styczniki,
B - bateria,
P - potencjometr,

rys2. Obwód zasilania elektromagnesu
Do uzyskania wyników końcowych z przeprowadzonych prób i otrzymanych wyników zastosowaliśmy metodę najmniejszych kwadratów.
Do obliczenia wartości koncentracji nośników zastosowaliśmy wzór:
-wyprowadzenie jednostki:
e = 1,6*10-19 [C]
[IS] = A
[B] = T
[UH] = V
[d] = m.
gdzie:
Korzystając z metody najmniejszych kwadratów sprowadzamy liczoną wartość do zależności liniowej:
y = (a+Δa)*x+(b+Δb)
gdzie:
Wykres zależności napięcia Halla UH od natężenia prądu sterującego I
Przy wykorzystaniu metod komputerowych otrzymaliśmy podany wyżej wykres i wartości współczynników kierunkowych a i b:
a = (27,2±0,9)
b = (-26,1±7,7)*10-3
Wykorzystując otrzymane wartości możemy obliczyć koncentrację nośników:
Podstawiając wzory do powyższego wzoru otrzymaliśmy:
n = 33,1*1019
Błąd koncentracji policzyliśmy z różniczki logarytmicznej:
ΔB = 0,01*10-1[T]
Δn = 1,7*1019
wobec powyższego błąd względny obliczony ze wzoru:
wyniósł:
Δnwzg = 5,1%
Otrzymaliśmy wynik końcowy:
n=(33,1±1,7)*1019
wyznaczenie napięcia Halla przy stałym natężeniu prądu sterującego
Pomiary zostały wykonane przy prądzie sterującym o natężeniu Is=11mA
B[T]*10-1 |
UH[V] |
B[T]*10-1 |
UH[V] |
B[T]*10-1 |
UH[V] |
B[T]*10-1 |
UH[V] |
|
+0,09 |
|
-0,1 |
|
+0,14 |
|
-0,17 |
0,43 |
-0,1 |
0,54 |
+0,13 |
0,73 |
-0,16 |
0,82 |
+0,18 |
|
+0,08 |
|
-0,12 |
|
+0,16 |
|
-0,18 |
|
-0,08 |
|
+0,11 |
|
-0,15 |
|
+0,17 |
|
|
|
|
|
|
|
|
|
+0,2 |
|
-0,24 |
|
+0,27 |
|
-0,31 |
0,98 |
-0,21 |
1,14 |
+0,25 |
1,27 |
-0,26 |
1,41 |
+0,31 |
|
+0,21 |
|
-0,25 |
|
+0,28 |
|
-0,3 |
|
-0,2 |
|
+0,24 |
|
-0,28 |
|
+0,3 |
|
|
|
|
|
|
|
|
|
+0,34 |
|
-0,35 |
|
+0,41 |
|
-0,49 |
1,54 |
-0,34 |
1,65 |
+0,35 |
1,76 |
-0,41 |
1,91 |
+0,48 |
|
+0,35 |
|
-0,37 |
|
+0,42 |
|
-0,47 |
|
-0,35 |
|
+0,37 |
|
-0,42 |
|
+0,47 |
Wykorzystaliśmy układ pomiarowy z ćwiczenia poprzedniego (rys1. i rys2.).
Do uzyskania wyników końcowych z przeprowadzonych prób i otrzymanych wyników zastosowaliśmy metodę najmniejszych kwadratów.
Do obliczenia wartości koncentracji nośników zastosowaliśmy wzór:
gdzie:
Korzystając z metody najmniejszych kwadratów sprowadzamy liczoną wartość do zależności liniowej:
y = (a+Δa)*x+(b+Δb)
gdzie:
Przy wykorzystaniu metod komputerowych otrzymaliśmy podany niżej wykres i wartości współczynników kierunkowych a i b:
Wykres zależności napięcia Halla UH od indukcji pola magnetycznego B
a = (24,8±1,0 )*10-1
b = (-3,0±1,2 )*10-2
Wykorzystując otrzymane wartości możemy obliczyć koncentrację nośników:
Podstawiając wzory do powyższego wzoru otrzymaliśmy:
n = 27,7*1019
Błąd koncentracji policzyliśmy z różniczki logarytmicznej:
ΔIS = 5,0*10-4[A]
Δn = 2,7*1019
Z powyższego wynika , że błąd względny wynosi:
Δnwzg = 1,0%
Otrzymaliśmy wynik końcowy:
n = (27,7±2,7)*1019
Wnioski
Porównując obie metody doszliśmy do wniosku, iż metoda druga (pomiary przy stałym prądzie sterującym) jest dokładniejsza ze względu na mniejszą niepewność względną. Brak możliwości skonfrontowania otrzymanych wyników z wynikami rzeczywistymi uniemożliwia potwierdzenie tej tezy. Na otrzymane niepewności pomiarowe z pewnością mogło mieć wpływ to, iż brak było stabilnego połączenia z bateryjką co było wynikiem niemożności używania nowego, dobrego sprzętu.