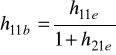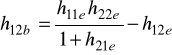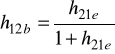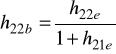Modele liniowe tranzystora dzielimy na dwie grupy :
modele końcówkowe ( modele czwórnikowe)
modele fizyczne (schematy zastępcze zbudowane z elementów odpowiadających określonym procesom fizycznym w tranzystorze).
Czwórnik liniowy
u1 = z11 i1 + z12 i2
równania impedancyjne
u2 = z21 i1 + z22 i2
i1 = y11 u1 + y12 u2
równania admitancyjne
i2 = y21 u1 + y22 u2
u1 = h11 i1 + h12 u2
równania mieszane (hybrydowe)
i2 = h21 i1 + h22 u2
przy czym i1, i2 u1, u2 - wartości chwilowe prądów i napięć małych sygnałów zmiennych na wejściu i wyjściu czwórnika.
Równania te można zapisać w postaci macierzowej:
![]()
= z ![]()
przy czym macierze z, y, h mają postać:
![]()
= y ![]()
z = 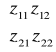
; y = 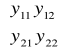
; h = 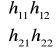
![]()
= h ![]()
Parametry impedancyjne są mierzone w warunkach rozwarcia wejścia lub wyjścia czwórnika.
Np. ![]()
przy i2 = 0 czyli przy rozwarciu wyjścia, a ![]()
przy i1 = 0, czyli przy rozwarciu wejścia itd.
Parametry admitancyjne są mierzone przy zwarciu wejścia lub wyjścia a parametry hybrydowe przy rozwarciu wejścia lub zwarciu wyjścia czwórnika. Należy podkreślić, że nie chodzi tu o zwarcie i rozwarcie w sensie galwanicznym gdyż uniemożliwiłoby to spolaryzowanie tranzystora w określonym punkcie pracy. Chodzi tu wyłącznie o zapewnienie specyficznych warunków sterowania i obciążenia tranzystora dla sygnału zmiennego.
Przykładowo rozwarcie wejścia oznacza, że z zacisków wejściowych czwórnik „widzi” impedancję znacznie większą niż jego impedancja wejściowa. Zwarcie wyjścia oznacza, że z zacisków wyjściowych czwórnik „widzi” impedancję znacznie mniejszą niż jego impedancja wyjściowa.
Układ włączania tranzystora przy pomiarze parametrów typu h.
Parametry macierzy h i y są najczęściej stosowane w praktyce, przedstawimy je zatem bardziej szczegółowo:
![]()
- impedancja wejściowa
![]()
- współczynnik oddziaływania zwrotnego
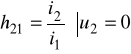
- współczynnik wzmocnienia prądowego
![]()
- admitancja wyjściowa
![]()
- admitancja wejściowa
![]()
- admitancja zwrotna
![]()
- admitancja przejściowa (transadmitancja)
![]()
- admitancja wyjściowa
Należy przy tym zauważyć, że: ![]()
lecz h22 ≠ y22
gdyż h22 jest admitancją wyjściową mierzoną przy i1 = 0 (tzw. rozwarciowa admitancja wyjściowa), a y22 jest admitancją wyjściową, mierzoną , przy u1 = 0
(tzw. zwarciowa admitancja wyjściowa).
Trzy sieci równoważne równaniom: impedancyjnym(a), hybrydowym (b),
admitancyjnym (c).
Równoważność poszczególnych sieci wynika z równoważności poszczególnych par równań czwórnika, a więc istnieją również związki tożsamościowe między parametrami macierzy różnych typów:
Związki tożsamościowe miedzy parametrami macierzy z, h, y.
Macierz |
z |
h |
y |
z |
z11 z12 z21 z22 |
|
|
h |
|
h11 h12
h21 h22 |
|
y |
|
|
y11 y12
y21 y22 |
∆z = z11 z22 - z12 z21 ,, ∆h = h11 h22 - h12 h21 , ∆y = y11 y22 - y12 y21
z
u1 = z11 I1 + z12 I2 1/
u2 = z21 I1 + z22 I2 2/
h
u1 = h11 I1 + h12 U1 3/
I2 = h21 I1 + h22 U2 4/
Przykład 1. Wyrazić parametry macierzy [z] za pomocą [h].
Równanie 3/ ma postać
u1 = h11 I1 + h12 U2 5/
Porównujemy z równaniem 1/
z 4/ wyznaczamy U2 → 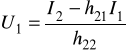
i podstawiamy do 5:
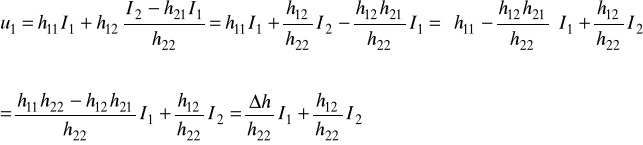
ostatnie równanie porównujemy z 1/ i widzimy, że:
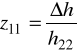
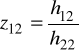
Równanie 2/ ma postać:
u2 = z21I1 + z22I2 6/
porównujemy z 4/
Wniosek - porównać trudno, więc:
z 4/ wyznaczamy u2 →:
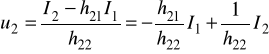
ostatnie równanie porównujemy z 6/ i widzimy, że:
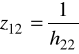
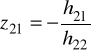
Przykład 2. Wyrazić parametry [z] za pomocą [Y]
u1 = z11I1 + z12I2 1/
u2 = z21I1 + z22I2 2/
I1 = y11u1 + y12u2 3/
I2 = y21u1 + y22u2 4/
Równanie 1/ ma postać
u1 = z11I1 + z12I2
porównujemy go z 3/ i widzimy, że porównać trudno, więc:
z 3/ wyznaczamy u1:
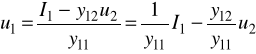
5/
ostatnie równanie porównujemy z 1/ i widzimy, że porównać trudno, więc:
z 4/ wyznaczamy u2 →:
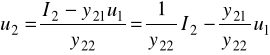
to równanie podstawiamy do 5/
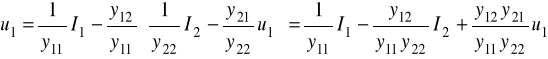
Przekształcamy go ( wyrazy z u1 przenosimy na lewą stronę równania ):
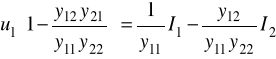
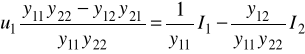
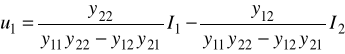
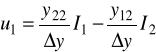
ostatnie równanie porównujemy z 1/ i widzimy, że:
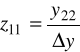
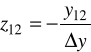
Równanie 2/ ma postać:
u2 = z21I1 + z22I2
porównujemy go z 4/ i widzimy, że porównać trudno, więc:
z 4/ wyznaczamy u2:
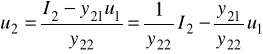
porównujemy go z 2/ i widzimy, że porównać trudno, więc:
z 3/ wyznaczamy u1:
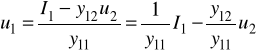
ostatnie równanie podstawiamy do 7/
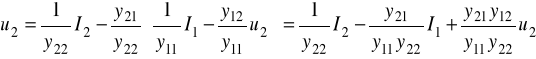
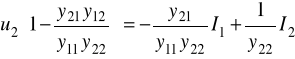
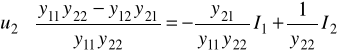
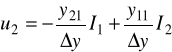
ostatnie równanie porównujemy z 2/ i widzimy, że:
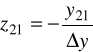
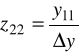
Wartości parametrów czwórnikowych zależą od układu włączenia tranzystora. Przykładowo, parametr h21, wyznaczający wzmocnienie prądowe, przyjmuje następujące wartości:
w układzie WB - α (ok. 0,99)
w układzie WE - β (ok. 100)
w układzie WC - β + 1
Rodzaj układu włączenia jest oznaczony indeksem literowym:
b - dla układu OB (WB)
e - dla układu OE (WE)
c - dla układu OC (WC)
Np. h11b jest impedancją wejściową w układzie OB. (WB) itp.
W literaturze angielskiej i w katalogach często indeks dwucyfrowy zastępuje się jedną literą wg następującego klucza (na przykładzie parametrów h):
h11 = hi (input - wejście)
h12 = hr (reverse - oddziaływanie zwrotne)
h21 = hf (forward - przenoszenie w przód)
h22 = ho (output - wyjście)
Zatem: hib = h11b
hfe = h21e itp.
Zależności między parametrami macierzy [h] w trzech układach włączenia.
Układ włączenia
Parametr |
WE |
WB |
WC |
h11 |
h11e |
|
h11C = h11e |
h12 |
h12e |
|
h12C = 1 - h12e |
h21 |
h21e |
|
h21C = (1 + h21e) |
h22 |
h22e |
|
h22C = h22e |
Np. znając parametry typu h dla układu WE można wyznaczyć parametry tej macierzy dla układu WB i WC, a ponadto korzystając z przedostatniej tabelki można nawet wyznaczyć parametry dowolnej macierzy dla dowolnego układu włączenia tranzystora.
Wyszukiwarka
Podobne podstrony:
Geodezja wykład 5 pomiary liniowe i pomiary kątowe (04 04 2011)
Wykład 6 Stabilność liniowych układów automatyki (2013)
MOO wyklad Progr Liniowe i Alg Sympleks
jkf wyklad ukld liniowych2008 09
wyklad 8 czworniki
wyklad 9 Regresja liniowa wielokrotna
ekonometria wyklad model liniowy WSB 13 14
Geodezja wykład 5 pomiary liniowe i pomiary kątowe (04 04 2011)(1)
Wyklady, Wyklad4, PRZESTRZENIE LINIOWE
3 wyklad algebra liniowa
wyklad 9 czworniki
Ryszard R Andruszkiewicz Wykłady z algebry liniowej
Wykład 6 Stabilność liniowych układów automatyki (2013)
MOO wyklad Progr Liniowe i Alg Sympleks
więcej podobnych podstron