Ćwiczenia Wytrzymałość 5 - 20 -
Zadanie 18
Stalowy pręt o zmiennej skokowo średnicy i wymiarach jak na rysunku 18 umieszczono bez luzu i wcisku pomiędzy dwoma prostopadłymi do osi pręta, nieskończenie sztywnymi podporami. Pręt podgrzano równomiernie na całej długości o Δt = 800C. Obliczyć naprężenia w pręcie, jeżeli średnice pręta są równe: D = 4 cm, d = 3 cm, a współczynnik rozszerzalności
cieplnej liniowej α = 1,39·10-5 C-1, moduł Younga E = 2,1·105 MPa i Rs = ± 350 MPa.
D d l1 = 1,1 m
l2 = 1,5 m
l1 l2 Rys.18
Rozwiązanie
Zadanie to jest jednokrotnie statycznie niewyznaczalne, więcej informacji na ten temat patrz strona 160 w książce Statyka i Wytrzymałość Materiałów autor Jan Misiak.
Pręt po podgrzaniu i uwolnieniu z więzów przedstawiono na rysunku 18a
Rys.18a
Δl1t
l1 l2 Δlt =Δl1t +Δl2t = l1αΔt + l2αΔt
![]()
Pręt pod działaniem sił oddziaływania podpór po usunięciu podpory przedstawia rysunek 18b
R
Δl1R
l1 l2 ΔlR = Δl1R + Δl2R
Rys.18b
![]()
, ![]()
![]()
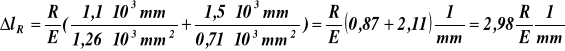
Sumaryczne wydłużenie pręta Δl = Δlt +ΔlR = 0
![]()
,![]()
Wartości naprężeń 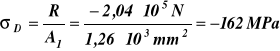
, ![]()
Ponieważ obliczone naprężenia są niższe od granicy proporcjonalności użyte wzory do określenia wartości wydłużenia są zgodne z rzeczywistością.
Zadanie 19 - 21 -
Określić długość zerwania jednorodnego pryzmatycznego pręta, zbudowanego z materiału o ciężarze własnym γ = 78 N/dcm3 i Rm = 450 MPa (rys.19)
Rozwiązanie
x N1 N = N1
l
x1
N l - x
dN dx1
Rys.19
x x x1
A przekrój pręta, dN = Adx1γ, ![]()
![]()
, Nmax=Aγl, *max = lγ![]()
lr wystąpi dla *max = Rm
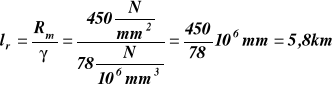
Zadanie 20
Wykonać wykresy sił wewnętrznych i momentu gnącego dla belki wysięgnikowej przedstawionej na rysunku 20. Dane α = 400, q = 1300N/m
z α
q
0 x
l = 2 m Rys.20
Rozwiązanie
Robimy myślowy przekrój w odległości x od brzegu swobodnego i odciętą część belki równoważymy siłami N,T i momentem gnącym Mx (rys.20a)
dQ α
Mx
q dQ = qdx1
01 N
0 x
x1 dx1 T
x Rys.20a
Równowaga odciętej części 001
![]()
, ![]()
, ![]()
![]()
,![]()
![]()
, ![]()
![]()
, 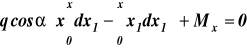
- 22 -
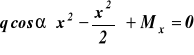
, ![]()
Wykresy sił normalnej N i tnącej T oraz momentu gnącego Mg = Mx (rys.20b)
N
Nx=l = -qlsinα = -1300(N/m)2(m)sin400
Rx = -1671 N
T Tx=l = -qlcosα = 1300·2·cos400 = -1992N
Rz = -1992N
Mg Mx=l = -0.5ql2 cosα=
= -0.5·1300(N/m)4(m2)cos400
Mx=l = -1992Nm
z
x = l
Rys.20b
Zadanie 21
Dla belki z zadania 20 dobrać przekrój kwadratowy z warunku, że naprężenia od zginania nie mogą przekroczyć *dop = 100 MPa.
Rozwiązanie
Wzór na naprężenia 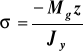
(rys.21) (a)
z
x
dA
g *
z
y
Rys.21
y
gdzie Jy jest momentem bezwładności pola przekroju względem y określonym wzorem (b)
Wzór (a) jest słuszny jeśli moment odśrodkowy względem osi y,z Jyz = 0
Jyz jest określony wzorem (c)
![]()
(b)
![]()
(c)
Wyprowadzenie wzoru na Jyz względem osi symetrii dla prostokąta (rys.21a) - 23 -
z
dz
z
h y dA = dzdy
a
y dy Rys.21a
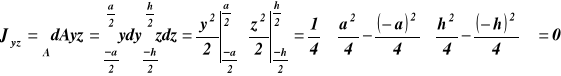
Wyprowadzenie wzoru Jy dla prostokąta względem osi głównych centralnych
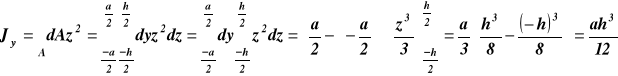
![]()
![]()
Maksymalne naprężenia występują dla Mgmax , zmax i -zmax czyli
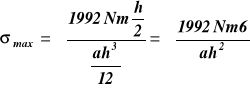
dla przekroju kwadratowego a = h

Wyszukiwarka
Podobne podstrony:
Wytrzymałość materiałów, cwiczeniawytrzymalosc6, Ćwiczenia wytrzymałość 6
Lista 4(1), PWR [w9], W9, 3 semestr, Mechanika i wytrzymałość materiałów, Ćwiczenia
Wytrzymałość materiałów ćwiczenie 9
Lista 5, PWR [w9], W9, 3 semestr, Mechanika i wytrzymałość materiałów, Ćwiczenia
Lista 2, PWR [w9], W9, 3 semestr, Mechanika i wytrzymałość materiałów, Ćwiczenia
Lista 1, PWR [w9], W9, 3 semestr, Mechanika i wytrzymałość materiałów, Ćwiczenia
wierszyki 3, Materiały i cwiczenia z emisji głosu
Badanie gardła, Materiały i cwiczenia z emisji głosu
Statyczna próba zginania materiału Ćwiczenie 5
materiały ćwiczenia
METODY I FORMY KSZTAŁCENIA, Materiały z ćwiczeń
chemia material cwiczeniowy 2013 pr model
Materialy cwiczenia 3
METODY AKTYWNE W NAUCZANIU I WYCHOWANIU, Materiały z ćwiczeń
Materialy cwiczenia 3 nowy
materiały ćwiczeniowe mech obronne całość VI, psychiatria
Ćwiczenia podniebienia miękkiego, Materiały i cwiczenia z emisji głosu
Kształcenie aparatu mowy- oddech i przepona, Materiały i cwiczenia z emisji głosu
więcej podobnych podstron